1 Introduction

The role of low temperature detectors (LTDs) has become critical in many applications of modern particle physics that require an extremely good energy resolution  [1,2,3,4,5]. These high-resolution detectors are based on the detection principle of a complete thermal calorimeter in which the energy input is fully converted to the thermal energy of the detector. By the means of measuring the temperature increase in the detector system with a sensitive temperature sensor, the energy input can be determined at high resolution. LTD sensor technologies such as semiconductor thermistors, transition edge sensors (TESs), and magnetic microcalorimeters (MMCs), make it possible to realize such sensitive thermal calorimetric detection [5,6,7]. Thermistors are heavily doped semiconductors of ion-implemented Si devices or neutron transmuted-doped (NTD) Ge sensors [8]. The resistance values of these materials are a strong function of temperature at tens of mK. TESs utilize an abrupt change in the resistance upon any temperature change at their superconducting transition. The temperature-dependent magnetization of a paramagnetic material is utilized to measure the temperature increase caused by an energy input in a calorimetric detection with an MMC.

In a simplified model of a thermal calorimeter, the detector is composed of an absorber and a temperature sensor with heat capacities of \(C_\text {a}\) and \(C_\text {s}\), respectively. An energy input \(\Delta E\) causes a subtle temperature increase \(\Delta T\) of the absorber and the sensor by an amount of \(\Delta E / (C_\text {a}+ C_\text {s})\) assuming a tight thermal connection between the detector components and a loose thermal contact of the detector system with the thermal bath. Then, the detector measures the resistance change \(\Delta R = (\partial R / \partial T) \cdot \Delta E / (C_\text {a}+ C_\text {s})\) in a detector with a resistive sensor of a semiconductor thermistor or a TES. In the case of a detector with an MMC sensor, it measures the magnetization change \(\Delta M = (\partial M / \partial T) \cdot \Delta E / (C_\text {a}+ C_\text {s})\).

Most LTD experiments in astroparticle physics applications require long-term data collection while maintaining a base temperature as stable as possible at a few tens of mK. Generally, the heat capacities of the detector components are temperature dependent. For instance, it is proportional to \(T^3\) for a dielectric crystal absorber and to T for a metal absorber. Moreover, the sensor responsivities (i.e., the partial derivative terms in the expressions of \(\Delta R\) and \(\Delta M\)) typically vary as the temperature changes for all resistive or magnetic sensors. Thus, any short- or long-term instability of the base temperature may result in a short-term sensitivity fluctuation or a long-term gain drift, respectively. Temperature instability can be one of the major sources that degrade the energy resolution of the detector.

A dilution refrigerator is popularly chosen as the major refrigeration tool of an LTD experiment for a high-resolution detection and long-term data collection. Major cooling to a mK temperature takes place in a unit called a mixing chamber in a dilution refrigerator system. The temperature of a metal plate housing the mixing chamber is regulated with a thermometer and a heater attached to it.

A low-noise AC resistance bridge is commonly used to measure the resistance of a semiconductor thermometer made of carbon, Ge, or RuO2. A temperature controller can be adopted to regulate the current of the heater with a feedback system connected to the resistance bridge. However, there is a limit of the temperature stability maintained at a constant temperature within the range of 10–20 mK. The stability limit of the control system with a resistance bridge originates from the bias current limit to minimize the Joule heating in the thermometer and the frequency-dependent sensitivity limits of the bridge preamp and the AC detection speed.

In this work, we instrumented a second temperature control system in addition to a normal temperature regulation system with a resistance bridge. We employed a dummy MMC channel as the thermometer for the additional control system with another heater. This second system was designed to operate together with the first-stage system.

Fig. 1
figure 1

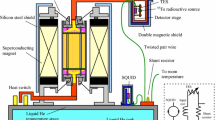
Schematic of the detector setup of AMoRE-I with an additional MMC sensor used for the 2nd-PID system. Top-left is a simplified diagram of the thermal system relevant to the temperature controls. The MCP has a strong thermal connection to the MC. H1, TR1, and TR2 are attached to the MCP. The DP is connected to MCP with a finite thermal conductance \(G_{\mathrm {CR}}\). H2 and TM are attached to the DP. In the TM, the MMC is connected to its copper plate with gold wires of thermal conductance \(G_{\mathrm {GW}}\) (color figure online)

Full size image

2 Experimental Setup

The dilution refrigerator system that hosted the AMoRE-Pilot experiment [9, 10] has currently been used for its successive AMoRE-I phase with 18 crystal modules and 36 MMC detection channels [11]. The lowest temperature reached 9 mK at the mixing chamber plate (MCP) and detector plate (DP) for this phase. The detector modules of AMoRE-I were assembled for simultaneous heat and light detection and stacked in a four-column tower. Because of the size of this AMoRE-I detector tower, we removed the mass spring dampers used for the second-stage vibration mitigation. The spring suspended still with Eddy current dampers remained in the cryostat [12].

Figure 1 illustrates the MCP, the radiation shield, and the detector tower of AMoRE-I, which are mechanically and thermally connected to each other. The radiation shield composed of clean lead and copper remained from the Pilot configuration. At the early installation step of the shield structure, the 5 cm thick lead bricks were sandwiched between copper plates with copper bolts to enhance conduction cooling for the superconducting lead. Then, two radiation shielding layers of the clean Cu–Pb–Cu structure with a total thickness 6.5 cm were bolted to the 3.5 cm thick MCP with six copper bolts with a 1 cm diameter. Copper spacers with clamping features were placed to ensure the thermal connection between the copper plates and the 1 cm copper bolts. During the early test stage for the pilot phase, the 180 kg structure of the radiation shield did not cause a noticeable delay in cooling the system from 4 K to 10 mK with the dilution unit. Moreover, no measurable temperature gradient was found between the MCP and the bottom copper plate labeled the DP, as shown in Fig. 1, when no extra heat input was applied. On the other hand, when external heat is applied to the DP, nonnegligible temperature gradient can be developed between MCP and DP. This result indicates that one can configure a temperature control system for the temperature of DP or the detector tower with better temperature sensitivities [13].

As indicated in Fig. 1, two RuO2 thermometers denoted TR1 and TR2 and the heater H1 were anchored to the MCP as the main temperature control system. Two low-noise AC resistance bridges (AVS-47B by PICOWATT) read the resistance values of the two RuO2 thermometers, independently. One bridge is connected to a temperature controller (TS530 by PICOWATT) with the heater as the main PID system. The other bridge is used as a real-time temperature monitor for MCP with a DAQ.

For the present experiment with the AMoRE-I setup, we installed a 37th MMC channel at the top of the detector tower as indicated in Fig. 1. This MMC sensor, having served as the thermometer of the DP and denoted as TM, was fabricated in a common batch with new MMCs used for additional AMoRE-I detection channels. We investigated the low temperature properties such as the magnetization and the heat capacity of the sensor material as functions of temperature as reported in the previous paper [14].

A strong thermal connection made with ten gold bonding wires was placed between the MMC Ag:Er layer and the copper sample holder as shown in the magnified view of Fig. 1. This gold wire thermal connection determines the response time of the TM with respect to the temperature change in the copper plate as \(C_{\mathrm {MMC}}/G_{\mathrm {GW}} (={0.6}\,\hbox {m}\hbox {s})\) where \(C_{\mathrm {MMC}}={0.3}\,\hbox {nJ}/\hbox {K}\) is the heat capacity of the MMC sensor and \(G_{\mathrm {GW}}={500}\,\hbox {nW}/\hbox {K}\) is the thermal conductance of the gold wires.

Fig. 2
figure 2

The response signal of the TM from a temperature sweep between 9 and 13 mK (color figure online)

Full size image

Figure 2 shows the result of the DC measurement result for both thermometers. This figure also shows the expected values of the SQUID output calculated from the magnetic property of the MMC sensor at the temperatures with 100 mA field current [14]. The TM does not measure the absolute values but instead measures the changes in magnetic flux. Both values of the measured and calculated data were set to zero at 12 mK with no multiplicative scale factors applied. The good agreement between the two curves indicates that the MMC thermometer (TM) works as expected from the MMC properties at mK temperatures. Practically, a small change in \(\delta \varPhi \) can convert to the temperature scale in the unit of K based on this measurement where only 2 percent difference was found between the slopes of measured and calculated curves at 12 mK.

A slow current ramp on H1 results in a temperature sweep of the system including MCP, DP, and the detector tower. During a wide temperature sweep, a long-term DC measurement can be made for the bridge readings of TR1 and the SQUID output of TM.

During the DC measurements of TR1 and TM, the heater H1 attached to the MCP was used. The ramping-up speed of the heater power changed a few times. These sudden changes resulted in the rate of temperature increase in the measurement shown in Fig. 2. The 36 MMC channels were active with all the corresponding SQUIDs operating during the DC measurement. The total heat dissipation of approximately 44 nW from the SQUID operations supplied to the detector tower as a heat load through DP. It was regarded as a background heat input to the system because the long-term data taking should be made with all the channels active.

We implemented the second-stage PID setup with this TM and the heater (H2). The main PID is performed with the thermometer TR1 and the heater H1 because the TM can detect the relative temperature change. The second-stage PID system focuses on even small temperature fluctuations, so we set the power of the H2 to approximately 200 nW, 10% of the H1 power. PID software was configured with a DAQ to read the SQUID output and a power supply to control the current to H2.

3 Results and Discussion

The TM was calibrated against the calibrated RuO2 thermometer TR1 comparing the bridge readings and the SQUID output in the flux lock loop (FLL) mode. In this mode, the SQUID output has a linear behavior with respect to the change of the temperature. The output occasionally jumps in an integer number of the feedback current equivalent to changing one flux quantum in the SQUID loop. A simple logic for jump detection was employed to cancel the sudden change in the SQUID output in the program used for the second-stage PID. We set both the sampling rate of the TM signal and the control rate for the heater current to 10 Hz. This rate was found to be sufficient to take the jump signals into account in the PID feedback for stable continuous operation. Noninteger jumps in the SQUID output have not been found during the past 3 months of continuous operation of the SQUID system.

Fig. 3
figure 3

Noise spectra of RuO2 (TR2) and TM under different PID conditions. The dashed and solid lines indicate a set of noise spectra measured at the same time in each PID condition without and with the second-stage PID, respectively. All the measurements were made with a 10 Hz sampling rate. The second-stage PID results in a temperature gradient between MCP and DP (color figure online)

Full size image

We set the first-stage PID system for MCP temperature regulation in a conventional method with TR1 and H1. No filter or data acquisition system was connected in the analog PID system with an AC bridge and a temperature controller. The MCP temperature was monitored with the additional thermometer TR2 read with its own bridge. The resistance values of TR2 were calibrated with TR1 resulting in similar values and noise.

The two dotted lines in Fig. 3 indicate the noise spectra measured with TR2 and TM when the first-stage PID was applied to maintain MCP at 12 mK with zero heat at the second heater H2 at DP. The temperature readings of the two thermometers TR2 and TM show rms values of 19 μK and 9 μK for 100 min measurements, respectively, when the analog PID system was set at 12 mK. The frequency responses of the two thermometers resulted in quite different levels because the limits of the thermometer noise levels were found to be 4 \(\upmu \hbox {K}/\sqrt{\mathrm {Hz}}\) and 80 \(\hbox {n}\hbox {K}/\sqrt{\mathrm {Hz}}\) for TR2 and TM at 5 Hz measurement frequency, respectively. However, they follow one another at low frequencies below 20 mHz when the low-frequency noise dominates over the noise limit of TR2.

The Two-stage PID system aimed to keep the DP temperature at 12 mK as stable as possible in the present study of AMoRE-I. Because we wanted to apply a sufficient current on H2 and to operate two PID setups independently, the PIDs were set to maintain MCP at 11 mK with approximately 1.3 \(\upmu \hbox {W}\) on H1 and DP at 12 mK with approximately 0.2 \(\upmu \hbox {W}\) on H2. When the second-stage PID was active, the both thermometer readings of TR2 and TM became quieter with the rms values of 11 μK and 0.5 μK for 100 min measurements, respectively.

The noise improvement with the second PID is apparent in the frequency response of TM. As shown in Fig. 3 much less noise is acquired at frequencies below 1 Hz. However, only modest improvement was noticeable in the TR2 signals with the second PID. Different parameter selections for the second PID vary the level of the low-frequency noise in the mHz region and its cutoff frequency appears near 30 mHz. Another cutoff frequency is found near 1 Hz in the TM noise spectra under both PID conditions. The origin of the cutoff at that frequency is not clear. We infer that this result may be attributed to the finite thermal conductance between MCP and the thermometer TM. Because the thermal conductance between MCP and DP can be found from the temperature gradient caused by the H2 heat input, the effective copper mass coupled to the TM thermometer with the 1 Hz cutoff frequency is approximately 0.24 kg. Two other cutoff frequencies of TM noise exist when the measurement is extended for higher frequencies. One frequency is at 300 Hz associated with the gold bonding wires connecting the MMC to the copper plate as \(2\pi f_c = G_{\mathrm {GW}}/C_\mathrm {MMC}\). The other frequency is the SQUID bandwidth that is 100 kHz.

Fig. 4
figure 4

Energy spectra measured in AMoRE-I modules of a CaMoO4 and a Li2MoO4 during the calibration campaigns of 7 and 3 days, before and after implementing the second-stage PID, respectively. The DP temperatures were 12 mK for both measurements with 9 μK and 0.5 μK rms fluctuations for single and Two-stage PID systems, respectively (color figure online)

Full size image

The two-stage PID system improved not only the fluctuations of the DP temperature but also the energy resolutions of the detector modules of AMoRE-I. Figure 4 shows the energy spectra measured with selected modules for both CaMoO4 and Li2MoO4 cases in calibration runs. The Two-stage PID led to improved energy resolutions of the heat channels in a similar ratio for all the modules. Long-term gain drifts of the modules were corrected with stabilization heater pulses embedded for each crystal [15]. However, the major resolution limitation of energy resolutions originates from the vibration of the cryostat from pulse tube operation, which also appears in the TM noise spectra peaks at 1.4 Hz and its multiples.

4 Conclusion

The two-stage PID system has been successfully implemented for long-term data collection in AMoRE-I. It demonstrated a stable temperature control and consequent resolution improvements in the detector channels. This result is mainly because the temperature sensitivity of TM is significantly higher than that of resistance thermometers.

Generally, the PID system with a TM can be applied to any low temperature experiment that requires a stringent temperature stability. To ensure a long-term operation in a certain temperature point, this kind of TM can provide a good complement to the temperature control system with a resistance thermometer.