The Casimir effect is a phenomenon that arises due to fluctuations in the quantum vacuum. In its simplest version, uncharged metal plates that are spaced much closer than a micron freeze out the long wavelength modes of these fluctuations [1,2,3]. The lower density of modes between the plates in comparison with the density of modes outside the plates gives rise to a net attractive force between the plates. One can refer to the space between the plates as a Casimir vacuum, a region where the energy density is less than that found in free space. The Casimir vacuum can be considered a region of negative energy, leading one to ask if such a place can have an influence on the transition temperature a superconductor. Ref. [4] discusses this possibility in detail.

In the simple case, the net attractive force between the plates separated by d is given by:

$${\text{Force/area}} = - {\hbar}c\pi^{2} /240d^{4}$$
(1)

Note the factor of ħ in the numerator. This is purely a quantum mechanical effect. As ħ goes to zero, so does the force. The other thing to note in Eq. (1) is the dependence on the fourth power of the separation, 1/d4. This is in contrast to gravitational or electrostatic forces which scale as 1/d2. The Casimir force has been seen experimentally a number of times [5,6,7,8,9,10,11] and can typically only be detected for plate separations below a few hundred nanometers which requires that the plates be kept strictly parallel. Because of this parallelism requirement, one often uses a sphere-plate geometry, for which the resulting force becomes:

$${\text{Force}} = - {\hbar}Rc\pi^{3} {/}360d^{3}$$
(2)

Note that in Eq. (1) one calculates a force per unit area (of the plates) while in Eq. (2) one calculates a total force. In Eq. (2) R is the radius of the sphere which is assumed to be much larger than the separation, d. Figure 1 shows a typical experimental setup for detecting the force [6].

Fig. 1
figure 1

Shown is a typical experimental setup for detecting the Casimir force. This approach leverages the pN force sensitivity one can obtain with a commercial MEMS accelerometer. Using a micro-gluing technique, a sphere (a), roughly 100 microns in diameter (scale bar is 100 microns), is attached to the accelerometer proof mass (b). The springs holding the proof mass are the four purple serpentine structures (c). A gold-coated plate (d) is moved to within 100 nm of the sphere, creating a force on and a displacement of the proof mass. This displacement is sensed by interdigitated capacitor displacement sensors (e) and the integrated electronics (f) that surrounds the proof mass. This figure is from Ref. [6] (Color figure online)

Full size image

The first unambiguous observation of the effect was made by Lamoreaux in Ref [8]. Ref. [9] discusses repulsive Casimir forces as opposed to the attractive forces one normally sees. Ref. [10] discusses unusual Casimir effects between micropatterned surfaces. In Ref. [5] we discuss nonlinearities induced in the AC response of a MEMS harmonic oscillator using a geometry similar to that being used here. In Ref. [6], we discuss a different MEMS Casimir metrology platform we have developed, leveraging a commercial sensor, that could be the basis for the metrology approach developed in this paper.

In this paper, we show how one can use the extreme sensitivity of the force on the sphere-plate separation to build a quantum displacement amplifier (QDA). This quantum mechanical object amplifies small DC displacements and creates much larger AC oscillation amplitudes and changes in frequency. We do this by using the Casimir force to couple displacements of a sphere to a mechanical parametric amplifier [12]. We use the Casimir interaction between the sphere and plate to pump energy into the parametric amplifier. In Ref. [12] we have linearized the equations and derived the results within that approximation. This linearization approach illuminates some of the essential physics but misses other important parts. The approach discussed here builds upon Ref. [12] and is a full nonlinear simulation of the system that finds a new feature, stable high gain fixed points in the system response. Our approach is one of “experimental mathematics” where one uses simulation tools to calculate the full dynamic response of a fundamentally nonlinear system to observe its behavior. This approach is commonly used in the chaos community to explore the response of nonlinear systems.

The quantum gain of the system can be as large as a million or more. Given that one can routinely detect picometer displacements [5, 6], this combination gives us a system where zeptometer displacements can be measured. The combination of a mechanical parametric amplifier and a Casimir vacuum produces a QDA that lets one amplify small DC displacements of a sphere into large changes in AC amplitude or frequency which can be measured using conventional approaches. In other work [13], we show how one can use this device to detect attoTesla magnetic fields and how one might use this system to detect the magnetic field generated by the heart or brain. In this paper, we discuss measurements of displacement and show how one might get into a regime where this could potentially be of interest in gravitational wave detection [14]. We argue that QDA’s are an important new tool in creating quantum metrology systems with unprecedented sensitivity.

1 Method of Operation

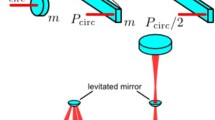
The basic operation of the device is shown in Fig. 2A. The sphere is driven resonantly at \(\omega\). The sensor is driven at 2\(\omega\). The Casimir coupling between the sphere and the sensor is used to pump energy into the resonant mode of the sphere, forming a parametric amplifier. The amplitude of the sphere, oscillating at \(\omega\), can be amplified or de-amplified, depending on the phase of the Casimir 2\(\omega\) driving term.

Fig. 2
figure 2

Shown is the system layout (a) and the potential energy terms (b) for our system. The Casimir coupling between the sphere and the sensor is increased as they move closer to each other. The sphere oscillates at ω and the sensor at 2ω. The amount of parametric pumping from the sensor on the sphere depends sensitively on their relative positions. Small DC displacements of the sensor manifest themselves as large changes in the AC amplitude of the sphere. This is the quantum gain of the system. In (b) one sees the potential energy terms for the system. The dotted line is the SHO term for the sphere, the dashed line is the Casimir term and the solid line the sum of the two. The lower panel is from ref. [5]. The 1/d5 dependence is derived in ref. [12] (Color figure online)

Full size image

The potential energy diagram in 2b is instructive. The dotted line is the potential energy of the sphere with typical behavior of a simple harmonic oscillator. The potential energy scales as X2. The dashed line shows the Casimir term. There is an attractive interaction between the sphere and the sensor. The solid line in 2b is the sum of these two terms. The potential well becomes asymmetric and by tuning the Casimir term, the sphere can be trapped in a shallow minimum. As can be seen by the diagram, as one tunes the system the oscillation amplitude becomes asymmetric and the restoring force of the system is reduced producing a change in resonant frequency of the sphere. As we will discuss later, one can use this change in resonant frequency as a high-resolution way to determine the sensor’s position.

2 Analysis

This system is highly nonlinear and a full, analytical solution is not feasible. In order to study the system in detail, including all the nonlinear effects where much of the interesting physics lies, we have done an extensive modeling using the Simulink simulation platform. This platform allows one to model the full nonlinear system and study, in detail, how it evolves in time as a result of all the system parameters.

Figure 3 shows our simulation platform. In our simulation, block A is our damped linear oscillator, block B is used to kick start it to resonate at its resonant frequency ω, block C is a Simulink subroutine to calculate the Bode plots shown later, block D measures the AC amplitude of oscillation and the DC offset, E shows the amplitude versus time and the phase plot of position versus velocity, F is the Casimir block where the parametric pumping force is calculated, G produces a unity amplitude square wave obtained from the proof mass position, H derives a sine wave at ω/2, I calculates the period of oscillation, J calculates a sine wave at ω and K derives a sine wave at 2ω. The inputs to the simulation that are changed on a regular basis are the 1ω and 2ω phase delays, the 2ω amplitude and the static position of the sensor. The metrology blocks measure the AC amplitude, the DC position and the period of oscillation of the proof mass. The system parameters are tuned so the bare damped linear oscillator (block A) has a resonant frequency of 1.00 kHz and a Q of 1000. The units used in the simulation are MKS with times in seconds and distances in meters. The proof mass is assumed to have a mass of 10–9 kg. The details of this simulation platform are given in Ref. [13]. In our simulation, we calculate the effects of mass 2, the sensor, via the Casimir force, on mass 1, the gold sphere. We assume that the sensor is much heavier than the sphere and don’t calculate the back-action force of the sphere on the sensor.

Fig. 3
figure 3

Shown is our Casimir parametric amplifier simulation tool. Block A is the damped oscillator, B kick starts the system, D, E and F are metrology blocks, C produces Bode plots, F is the Casimir block and H, J and K produce sine waves at ω/2, ω and 2ω (Color figure online)

Full size image

Figure 4 shows Bode plots for the bare system (A) and for the Casimir loaded system (B). The bare system has a resonant frequency of 1 kHz and a Q of 1000 while the loaded system has a resonant frequency of 890.5 Hz and a Q of 1000. As shown in Fig. 2, the Casimir loaded system reduces the effective restoring force of the spring and therefore should reduce the resonant frequency which is what we see in the simulations. In the Casimir loaded system, the sensor is being driven at 2ω.

Fig. 4
figure 4

Shown is the Bode plot for the bare oscillator system (a) and the system with the Casimir term applied (b). The bare system has a resonant frequency of 1 kHz and a Q of 1000. The Casimir couple system has a resonant frequency of 890.5 Hz and a Q of 1000. In the Casimir loaded system, the sensor is being driven at ω (Color figure online)

Full size image

To run a simulation, one first needs to phase lock the system at its resonant frequency, ω. The simulation tool creates a clean sine wave at ω and this signal is phase shifted by the time delay block associated with block J and then fed back into the drive input. With the signal phase locked, one varies the time delay and obtains a maximum in the oscillating amplitude.

With the system optimally phase locked at ω, one can then feed the Casimir signal into the system. The parametric Casimir signal is calculated in the following way. The initial distance between the sphere and the sensor is chosen. This is the position parameter in the simulation. A typical number is ~ 100 nm. The time dependent, parametric Casimir force is calculated by subtracting the amplitude of oscillation and the amplitude of the 2ω drive from the position. This gives an adjusted distance that is used to calculate the Casimir force that is fed back to the system. As shown in Fig. 5, the response of the system depends on the phase of the 2ω signal. In the simulation tool, one specifies the amplitude of the 2ω drive, typically 0.2 nm and its phase. In panel A in Fig. 5 one can see the response of the system for a phase shift of zero. The parametric signal rings up the amplitude over the time scale of the simulation. As expected, one sees both the DC offset (~ 10 nm) and an AC amplitude that starts at about 11 nm and grows to ~ 35 nm because of the parametric pumping. Panel B in Fig. 5 shows a phase plot where velocity is plotted on the X-axis and amplitude on the Y-axis. As expected from the discussion of Fig. 2, as the amplitude rings up, it becomes asymmetric with the positive amplitude being larger than the negative going amplitude. Panel C shows what happens for a different phase of the 2ω signal. In this case the amplitude rings down to a small, symmetric response but still offset from zero. The phase plot shows a response where instead of expanding outward as a function of time, it spirals inward.

Fig. 5
figure 5

Shown are the response of the system for two different phases of the 2ω drive. In the upper row, one has parametric amplification and in the lower row, deamplification. The LH figures show the position of the system as a function of time and the RH figures show the phase plots, position versus velocity with time an implicit, not explicit plot parameter. The 2ω amplitude is 0.2 nm for both sets of plots. The ω amplitudes are given in the figure (Color figure online)

Full size image

Figure 6a, b shows how the period of oscillation evolves over time for the data shown in Fig. 5a, c. As would be expected from examining Fig. 2b, for the data shown in Fig. 5a, as the amplitude rings up the effective restoring force on the system is reduced, increasing the period. For the data shown in Fig. 5c, as can be seen in Fig. 6b, the period slowly decreases during early times and then stays constant as the amplitude rings down.

Fig. 6
figure 6

Upper panel shows how the period evolves for the data shown in Fig. 5a and the lower panel shows how it evolves for the data shown in Fig. 5c (Color figure online)

Full size image

Figure 7 shows the amplitude of oscillation as a function of the 2ω phase. Qualitatively one sees a typical parametric response with both amplification and de-amplification as a function of phase. There are three types of responses in Fig. 7: unstable amplification, de-amplification and a new feature, stable amplification. The stable amplification peaks are the ones of interest here, particularly the larger one at ~ 180°. These stable peaks are an unexpected result for this system and had not been seen in studies done by linearizing the equations of motion [12]. In this system, the nonlinear response is not small in comparison with the linear response and so a full treatment of the nonlinearities is required, as done here. This is contrast to our earlier paper, Ref. [12].

Fig. 7
figure 7

Shown is the AC amplitude of oscillation as a function of the 2ω phase. One sees the typical response for a parametric system with both amplification and deamplification, depending on the phase. The ω amplitude is given in the plot. The 2ω amplitude is 0.2 nm (Color figure online)

Full size image

By sitting at particular places on the phase response curve, one can determine the quantum gain. The quantum gain comes from the response of the system where small changes in DC position due to the static force on the sensor can cause larges changes in the AC amplitude or frequency. Figure 8 shows such a plot. Plotted is the AC amplitude as a function of sensor position. One sees that at approximately 99.7 nm the AC response diverges. This means small changes in DC position get transferred into large AC amplitudes. This is the quantum gain of the system. The data shown in Fig. 8 can be analyzed to directly extract this gain.

Fig. 8
figure 8

(Above) Shown is the AC amplitude of oscillation as a function of DC position of the sensor relative to the sphere. The Casimir force depends strongly on distance and the parametric pumping amplifies the response. This is data from Fig. 7 and uses those values of ω and 2ω amplitudes (Color figure online)

Full size image

Plotted in Fig. 9 is the quantum gain. It is a measure of the local slope of the curve shown in Fig. 8. For the data shown, the maximum gain we see is 80,000. This means the small changes in the sensor position due to an applied force produces large (80,000 times larger) changes in AC amplitude or frequency.

Fig. 9
figure 9

(Below) shown is the quantum gain extracted from Fig. 8 (Color figure online)

Full size image

The analysis of the ultimate positional sensitivity can be obtained from the data shown in Fig. 8. A typical positional resolution of the MEMS proof mass is 1 pm [5, 6]. With a quantum gain of 80 k, this implies that by measuring the proof mass AC amplitude, one can detect changes in the sensor’s position to a resolution of 1 pm/80 k or 1.25 × 10–17 m. Another, more sensitive mode of operation is possible, measuring the frequency. As shown in Fig. 6, there is a frequency shift due to the Casimir induced pumping of the mode. In the analysis above, we assume measurement of the proof mass amplitude, which can typically be done to one part in 104 in a1 s averaging time. However, one can typically measure frequencies much better, at least to a part in 106, perhaps 107–108 with one second averaging so the resolution using frequency detection would be a hundred (or perhaps more) times better. This implies a positional resolution of ~ 100 zeptometers or below. Ref. [13] discusses, in detail, the application of using this approach for magnetometry. In that reference we show how using a magnet as the sensing mass might enable aT/cm sensitivities.

3 Thermal and Quantum Noise

So far, in this analysis, we have ignored the issue of thermal noise and whether one could actually use this much sensitivity to detect zeptometers or attoTelsas. As shown in Ref. [15], for \(\omega < \omega_{{\text{o}}}\), the mechanical thermal noise for a linear, damped harmonic oscillator is:

$$\left| x \right|\sim \left( {4k_{b} T/\omega_{\text{o}}^{3} mQ} \right)^{1/2}$$
(3)

At room temperature with a Q of 1000, a resonant frequency, ωo, of 2π × 103 rad/s and a mass of a microgram, we obtain a thermally driven mechanical noise of ~ 0.3 pm/Hz1/2. In order to actually use the sensitivity calculated here to detect zeptometers, one could work at milli-Kelvin temperatures, with a Q of a million, a mass of 10 µg and with a resonant frequency of 10 kHz. This would provide a thermal noise amplitude of ~ 150 zm/Hz1/2. Each of these conditions has been demonstrated many times on their own, accomplishing all of these in a single experiment would be challenging but is achievable.

It is an open question as to how much one should rely on Eq. (3) to predict the behavior of our system. This result is derived for a linear, damped harmonic oscillator and our system is highly nonlinear. Equation (3) is unlikely to be quantitatively correct but it probably gives the right order of magnitude and the right qualitative dependences on the various system parameters. Understanding the effect of thermal noise on our system, in detail, will require a separate study, using the modeling approaches described here, and is beyond the scope of this paper.

The quantum limit (ħω~kbT) for the 10 kHz resonator would be reached at a temperature of ~ 3 microKelvin. The thermal/quantum noise at this point would be ~ 8 zm/Hz1/2. This would not be possible to reach in any conventional experimental setup. The ultimate performance of the Casimir approach would be limited by thermal, not quantum, noise. It is an open question as to how much of this sensitivity calculated here can actually be realized in practice. The point of this paper is to outline a path to zeptometer positional resolution. The key point is that leveraging the Casimir effect gives one a tool that can resolve these types of displacements. Considerable cryogenic engineering will be required to actually get there.

The quantum noise discussion above demonstrates an important point. Getting a 10 kHz resonator into the quantum regime is not going to be possible for a very long time, perhaps never. However, the Casimir approach discussed here allows one to approach sensitivities of the kind promised by working in the quantum regime but with a much looser set of experimental requirements. Casimir sensing leveraging quantum fluctuations is quantum metrology of a kind that will be much easier to achieve than conventional approaches using effects requiring quantum coherence. The purpose of this paper is to demonstrate this point.

4 Conclusions

In this paper, we have shown how one could use a MEMS parametric amplifier and a Casimir vacuum to achieve zeptometer positional sensing. This system represents an entirely new class of quantum sensors that open the door to unprecedented sensitivity in a wide range of applications. The device converts small changes in DC position to large changes in AC amplitude and AC frequency of a parametrically pumped MEMS device. This approach leverages quantum fluctuations to build a device with performance that can’t be achieved with classical systems. This approach is very different from sensors requiring quantum coherence and may be much easier to implement in practice.