Noise Thermometry for Ultralow Temperatures

Abstract

In recent years, current-sensing dc-SQUIDs have enabled the application of noise thermometry at ultralow temperatures. A major advantage of noise thermometry is the fact that no driving current is needed to operate the device and thus the heat dissipation within the thermometer can be reduced to a minimum. Such devices can be used either in primary or relative primary mode and cover typically several orders of magnitude in temperature extending into the low microkelvin regime. Here we will review recent advances of noise thermometry for ultralow temperatures.

1 Introduction

Measuring the temperature at low temperatures is a particular challenge, as only very small power can be used. While for moderately low temperatures down to about 20 mK many suitable choices for thermometry exist, measuring even lower temperatures still remains a difficult task and the number of applicable methods is rather limited. Overviews on the different methods available for thermometry at low temperatures can be found for example in [1, 2].

In recent years noise thermometry has emerged as a new way of determining low temperatures with the potential to be used over a wide range of cryogenic temperatures and in particular going down to ultralow temperatures. It is based on the Brownian motion of electrons in conductors, a phenomenon that was already considered by Einstein in his second paper on the theory of Brownian motion in 1906 [3]. The existence of this effect was discovered experimentally more than two decades later by Johnson, who showed that any resistor exhibits thermally driven voltage fluctuations that depend only on two parameters, the resistance R itself and the equilibrium temperature T [4, 5]. The theoretical description was worked out by Nyquist, who calculated the resulting power spectral density [6]:

$$\begin{aligned} S_U = {\big \langle U^2\big \rangle \over \varDelta f} = 4 h f R \left[ {1\over 2}+ {1\over e^{hf/k_{\mathrm{B}}T}-1} \right] \, , \end{aligned}$$

(1)

with f denoting the frequency and ${\varDelta f}$ the bandwidth over which the fluctuations are measured. For temperatures and frequencies fulfilling the condition $hf/k_{\mathrm{B}}T \ll 1$ this expression can be expanded, with the two leading terms given by

$$\begin{aligned} S_U = {\big \langle U^2\big \rangle \over \varDelta f} \approx 4 k_{\mathrm{B}} T R \left[ 1+ {1\over 12}{hf\over k_{\mathrm{B}}T} \right] \, . \end{aligned}$$

(2)

The first term $S_U = 4 k_{\mathrm{B}} T R$ is often referred to as classical approximation of the Nyquist noise. For the typical conditions relevant to practical noise thermometers the classical expression is fully sufficient. Even for temperatures as low as $10\,\upmu \hbox {K}$ the corresponding frequency is 200 kHz, and thus exceeding the bandwidth of a typical noise measurement for thermometry purposes. In practice, an important prerequisite for using this relation to determine the temperature is that the sensor resistance does not change in the temperature range for which the thermometer is used. Depending on the temperature range and resistance type, different challenges are encountered to meet this condition. Kondo impurities, for example, are a particular problem for cryogenic applications of noise thermometry and must typically be avoided at a sub-ppm level [7, 8].

The precision measurement of thermal voltage fluctuation across a resistor to determine the thermodynamic temperature is well established and has a rich history (see for example [9,10,11,12,13,14]). Recently this technology helped to determine the Boltzmann constant used in the redefinition of the Kelvin in the new International System of Units (SI) [15,16,17,18].

Utilizing noise thermometry based on voltage fluctuations across a resistor for low temperatures, is much more challenging because the corresponding power spectral densities become rather small and require amplifiers with extremely low noise. Although several different concepts for measuring cryogenic temperatures with noise thermometers were proposed already in the late fourties [19,20,21] it took until 1959 to its first realization [22]. Here the temperature of the lambda point of helium was measured with an estimated uncertainty of 8%.

More than a decade later the development of SQUID amplifiers made the application of noise thermometry at temperatures below 1 K feasible. Early attempts concentrated on the use of resistive point-contact rf-SQUIDs for readout [23]. Here a dc-biased resistor is integrated in the rf-SQUID loop and the voltages across the resistor were converted into frequencies according to the Josephson relation $f_{\mathrm{J}}= (2e/h)V_{\mathrm{J}}$. In this case, the thermal voltage fluctuations—the measure of temperature—are superimposed to the dc voltage and lead to frequency fluctuations. One major disadvantage of this type of thermometer is the long integration times needed to reach an acceptable precision. The relative statistical uncertainty of the temperature is given for all noise thermometers by the relation

$$\begin{aligned} {\varDelta T\over T} = {1\over \sqrt{\varDelta t\,\varDelta f}} \, , \end{aligned}$$

(3)

where $\varDelta t$ denotes the measuring time and $\varDelta f$ the bandwidth of the measurement. To obtain a statistical uncertainty of better the $10^{-3}$ typically integration times of several hours were necessary, which made this kind of noise thermometer unpractical.

Nonetheless, it was used by metrology laboratories to extend the International Temperature Scale ITS-90 [24,25,26,27] to lower temperatures and thus to establish the Provisional Low Temperature Scale 2000 (PLTS-2000) [28]. Despite of improvements made to this technology in terms of device fabrication, experimental setup and readout schemes, the long integration times required remained a major drawback and limited the use of this type of noise thermometer. In addition, problems with hot electron effects and poor thermal coupling prevented the use of such devices at ultralow temperatures (see for example [29]).

An alternative way to determine the temperature using Johnson noise was also already introduced in the seventies [30]. Here, the resistive temperature sensor is shorted by an input coil of a SQUID. The Brownian motion in the resistor causes current fluctuations in the LR circuit, where L is the inductance of the SQUID input coil. In the early days such current-sensing noise thermometers (CNST) used rf-SQUIDs, until reliable thin film dc-SQUIDs [31] became available in the eighties [32,33,34]. The much higher sensitivity of dc-SQUIDs allowed one to open up the bandwidth and thus speed up the measurement process by several orders of magnitude. Following up this work about 15 years later, practical current noise thermometers were developed and characterized over a wide range of temperatures [35,36,37,38,39,40,41].

In 2005 a variant of the current-sensing noise thermometer was introduced, which today is known as the magnetic flux fluctuation thermometer (MFFT) [42]. This thermally very robust version of a noise thermometer is based on the inductive readout of the current fluctuation in a massive resistor using a superconducting flux transformer. In the following years, it was developed further, in terms of practical use [43, 44], expanding the temperature range [45, 46], creating a commercially available version [47,48,49], and developing a device that can be used in primary mode for metrology purposes [50, 51]. Combined with a two-channel SQUID readout and cross-correlating the signals to minimize amplifier noise the measurement of temperatures down to below $50\,{\upmu }K$ was recently demonstrated with an MFFT [45], covering five orders of magnitude in temperature with a precision of better than 0.5% in 400 s.

Here, we will provide an overview on recent developments of both CSNTs and MFFTs for ultralow temperatures.

2 Current-Sensing Noise Thermometers

Fig. 1

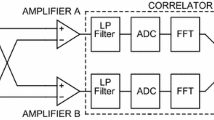
a Principle scheme of a current-sensing noise thermometer. b Power spectral density of current fluctuations for a current-sensing noise thermometer with sensor resistance of $R=5\,{\upmu \Omega }$ and SQUID input inductance of $L=5\,\hbox {nH}$ at a temperature of $T=1.4\,\hbox {K}$ (Color figure online)

The basic scheme for a current-sensing noise thermometer is shown in Fig. 1a. Here the resistor that functions as a temperature sensor is connected to the input coil of a sensitive dc-SQUID. Thus resistor and inductor form a one pole low-pass filter circuit with a cut-off frequency given by $f_0= (1/2\pi ) L/R$. In the classical limit, the spectral power density of the current fluctuations in this circuit can be expressed as

$$\begin{aligned} S_I = {\big \langle I^2\big \rangle \over \varDelta f} = {4 k_{\mathrm{B}} T\over R}{1\over 1 + (f/f_0)^2}. \end{aligned}$$

(4)

From this, it becomes immediately clear that with decreasing sensor resistance, the white-noise plateau increases, while the cut-off frequency decreases. This means that for any of such devices a compromise in terms of speed and sensitivity has to be made. Figure 1b shows the frequency dependence of the power spectral density at $1.4\,\hbox {K}$ calculated for a CSNT with $R = 5\,{\upmu \Omega }$ and $L= 5\,\hbox {nH}$ resulting in a cut-off frequency of $f_0 = 160\,\hbox {Hz}$.

Fig. 2

a Schematic of the sensor unit and b readout scheme of the current-sensing noise thermometer developed by Lusher et al. (after [36]) (Color figure online)

A first realization of a current noise thermometer reaching temperatures below 1 mK was developed by Lusher et al. in 2001. A schematic of the device is shown in Fig. 2a. The noise generating resistive sensor consisted of a thin copper foil that was grounded on one side to a copper post to improve the thermal contact. The resistor glued to a MACOR [52] base plate and connected via a pair of niobium leads to Nb screw terminals also positioned on the MACOR base plate. In one of the leads a small coil was incorporated enclosing an Al ring, whose transition temperature served as an internal reference point. The dc-SQUID was placed at 4 K and connected via twisted pair of superconducting leads with the Nb screw terminals. It was operated in flux lock loop (FLL) mode and readout by a spectrum analyzer.

This thermometer was measured against a $^3$He melting curve thermometer in the mK range and against a platinum NMR thermometer below 1 mK. Figure 3a shows the power spectral density of current noise $S_I$ as a function of frequency for these devices at different temperatures. The shape of these curves resembles the expected characteristic of a low-pass filter and stays the same over a wide range of temperatures, indicating that the resistance of the noise-generating copper foil is temperature independent in this temperature range. At the lowest temperatures, at which the noise power is lowest, there is a small distortion of the spectra at high frequencies, caused by amplifier noise. In Fig. 3a the temperatures calculated from the white-noise plateau of these spectra were plotted against the temperatures of a $^3$He melting curve thermometer and the ones of a platinum NMR thermometer. With a one-point calibration, the noise thermometer showed excellent agreement with the $^3$He melting curve thermometer in relative primary mode in the entire range with a standard deviation of below 2% after integrating for 160 s. However, a small heat leak of a few fW led to a thermal decoupling of the electrons in the noise generating $0.34\,\hbox {m}\Omega$ resistor below 1 mK and prevented the use of this thermometer in relative primary mode in this range [37].

Fig. 3

a Power spectral density of current noise as a function of frequency at different temperatures obtained with a noise-generating copper foil of resistance $R= 0.34\,{\hbox {m}\Omega }$ and b Temperatures resulting from these spectra plotted against the temperatures obtained with a $^3$He melting curve thermometer ($\bullet$) and with a platinum NMR thermometer ($\circ$) (after [36])

An improved version of this type of noise thermometer has been used to demonstrate the applicability in relative primary mode down to about 0.3 mK before similar decoupling effects occur [38]. Figure 4a shows the power spectral density of current noise $\langle I^2_{\mathrm{N}}\rangle$ at 500 mK as a function of frequency for three current-sensing noise thermometers with noise-generating copper foils having different resistances. For all three noise thermometers, the spectral shape can be perfectly described by Eq. (4). For the thermometer with the largest resistance of $R=1.29\,\Omega$ having a total inductance of 1.315 $\upmu$H, the cut-off frequency is 156 kHz, which allows obtaining a temperature reading in 100 ms with a precision of near 1%, demonstrating that noise thermometry can be very fast even at low temperatures. In Fig. 4 the temperatures obtained with these three noise thermometers are plotted against a temperature scale established with a Ge resistor, a $^3$He melting curve thermometer and a platinum NMR thermometer. At high temperatures, all three CSNT thermometers agree well with the reference scale. At low temperatures, thermal decoupling is observed at different temperatures for the different resistors. Modeling the effect assuming a constant heat leak into the resistors and a metallic thermal link to the nuclear stage results in a good qualitative description of the data. Clearly, there is a systematic correlation between the resistance of the copper foil and the temperature where the decoupling occurs. For the noise thermometer with the lowest resistance the decoupling starts at about $300\,\upmu \hbox {K}$, which demonstrates that such a thermometer can be used in relative primary mode down to this temperature.

In 2016 Shibahara et al. [39] investigated the use of CSNT thermometers in terms of metrology applications and studied the influence of systematic errors originating from amplifier noise, from temperatures dependencies of both the resistance and the inductance of the devices and from the removal of identifiable discrete noise peaks originating from electromagnetic interference. They carefully evaluated all uncertainties and demonstrated in a primary mode measurement a relative uncertainty of 1.53% and very good overall agreement with the PLTS-2000.

Fig. 4

a Power spectral density of current noise as a function of frequency obtained with current-sensing noise thermometers with different resistors at $T=500\,\hbox {mK}$. The solid lines represent fits with (4). b Comparison of the temperatures obtained with the three noise thermometers and three reference thermometers. The dotted line represents a modeling of the decoupling of the thermometer assuming a metallic link to the demagnetization stage and constant heat leak to the thermometers (after [38]) (Color figure online)

Very recently an alternative way of defining the noise-generating resistor was introduced by Ständer et al., which allows separating the choice of electrical resistance of the noise-generating resistor and its thermal resistance to the cold-stage of the cryostat [41]. In this case, the noise-generating resistor is a massive piece of high-purity silver which allows for a robust thermal coupling and the electrical resistance is defined by the size of niobium contact pads.

Figure 5 shows an illustration of this kind of current-sensing noise thermometer. For readout, the input coils of two dc-SQUIDs are connected in series and bonded to two niobium pads with radius $R=75\,\upmu \hbox {m}$, which were sputter-deposit approximated on the silver noise resistor. If the spatial separation of the niobium pads is large compared to their size the resistance is given in good approximation by $R= \varrho /(\pi r)$, where $\varrho$ is the specific resistance of the bulk silver and r the radius of the contact pads. For silver, with a RRR of 25, this geometry results in a resistance of $R= 5\,\upmu \Omega$. Combined with a small total inductance of $L=5$ nH the cut-off frequency of such a device is $f_0=160\,\hbox {Hz}$ (see also Fig. 1).

Fig. 5

a Schematic illustration of the sensor element of the C3NT noise thermometer. The first-stage SQUID chip carrying two dc SQUIDs is glued onto a silver half-cylinder which serves as a noise-generating resistive element. b Enlargement of the first-stage SQUID amplifiers showing the superconducting bonds to the Nb contact pads (after [41]) (Color figure online)

The readout scheme for this device consists of two channels with two-stage SQUID amplification each. Since the readout of this current-sensing noise thermometer involves cross-correlation it was termed cross-correlated current noise thermometer C3NT [41]. The circuits for signal amplification and processing of the two channels having a low-temperature and a room-temperature section are illustrated in Fig. 6. The low-temperature section of each channel consists of a first-stage dc-SQUID that is used to read out the current noise of the resistor. The second stage, consisting of a dc-SQUID array, serves as a low-noise low-temperature amplifier to raise the signal to a level that the noise of the room-temperature electronics is negligible.

The first-stage SQUID forms a sub-circuit with a gain resistor $R_{\mathrm{g}}$ and the input coil $L_{\mathrm{i2}}$ of the second-stage SQUID array. The current fluctuations in the noise-generating resistor cause a change of magnetic flux $\Delta \varPhi _{1}$ in the first-stage SQUID, and the resulting voltage drop drives a current $\Delta I_{{\text{S}}}$ through the input coil of the second-stage SQUID array. With the gain resistor appropriately chosen this leads to a moderate flux to flux amplification given by

$$G_{\Phi } = \frac{{\Delta \varPhi _{2} }}{{\Delta \varPhi _{1} }} = M_{{{\text{iS}}2}} \frac{{I_{{\text{S}}} }}{{\Delta \varPhi _{1} }}$$

(5)

where $\varPhi _{\mathrm{2}}$ denotes the flux change at the SQUID array and $M_{\mathrm{iS2}}$ stands for the mutual inductance of the input coil $L_{\mathrm{i2}}$ and the SQUIDs of the second amplifier stage. Since the noise of the second-stage SQUID array scales under ideal circumstances with $\sqrt{N}$ the overall amplifier noise power density of the system is given by

$$\begin{aligned} S_{\varPhi } = S_{\varPhi _1} + {S_{\varPhi _2}\over G_{\varPhi }^{\,2}} + {S_{U}\over V_{\varPhi _{\mathrm{S}}}^2 G_{\varPhi }^2 N^2}. \end{aligned}$$

(6)

Here $S_{U}$ represents the power spectral density of the input voltage noise of the room-temperature FLL electronics and N the number of dc-SQUIDs coupled in series in the second-stage array.

Fig. 6

Double-stage SQUID readout for C3NT noise thermometers (after [41]) (Color figure online)

To further reduce the overall noise cross-correlation of the two channels is used. This technique is commonly used in signal processing and has been employed also for noise thermometry early on [10, 53] and more recently for cryogenic noise thermometers [41, 45, 50]. Reading out the noise signal u(t) of the resistor with two independent channels results in two output signals given by $a_1(t)= u(t) + n_2(t)$ and $a_2(t)= u(t) + n_1(t)$, where $n_1$ and $n_2$ are the amplifier noise contributions of the two channels, respectively. Fourier transformation of these two output signals results in two frequency-dependent complex functions:

$$\begin{aligned} \tilde{a}_1(f) &= \tilde{u}(f) + \tilde{n}_1(f) \end{aligned}$$

(7)

$$\begin{aligned} \tilde{a}_2(f) &= \tilde{u}(f) + \tilde{n}_2(f)\, , \end{aligned}$$

(8)

from which the cross-correlated spectrum

$$\begin{aligned} \tilde{a}_1 (f) {\tilde{a}}^{*}_2(f) = \tilde{u}(f) {\tilde{u}}^{*}(f) + \tilde{u}(f) {\tilde{n}}^{*}_2(f) + \tilde{u}(f) {\tilde{n}}^{*}_1(f) + {\tilde{n}}^{*}_1(f) {\tilde{n}}^{*}_2(f) \, , \end{aligned}$$

(9)

can be calculated. Under the assumption that u(t), $n_1(t)$ and $n_2(t)$ are pairwise uncorrelated, cross-correlation leads to a suppression of amplifier noise and this expression can be reduced to

$$\begin{aligned} {{|\tilde{a}_{\mathrm {i}}|}}^2 = \tilde{a}_1(f) {\tilde{a}}^{*}_2(f) = \tilde{u} \left( f \right) {\tilde{u}}^{*}\left( f \right) , \end{aligned}$$

(10)

where ${{|\tilde{a}_{\mathrm {i}}|}}^2$ represents the power spectral density of the cross-correlated signals. In practice, a typical reduction of amplifier noise by a factor 10 can be achieved by this method.

The room temperature part of the readout chain of the C3NT includes a two-channel XXF-1 flux-lock-loop electronics [54]. After anti-aliasing filtering and analog-to-digital conversion, the signals were processed subsequently using a standard PC.

Fig. 7

Power spectral density measured with a C3NT thermometer with two independent channels at $T=5.2\,\hbox {mK}$ in comparison to the cross-correlated spectrum. (after [41]) (Color figure online)

Figure 7 shows noise spectra taken with two independent channels of the C3NT thermometer at $T=5.2\,\hbox {mK}$ in comparison with the cross-correlated spectrum using these two channels. In the frequency range were the amplifier noise dominates, the cross-correlation technique leads to a clear improvement resulting in an effective noise temperature of the readout of $T_{\mathrm{N}}\approx 0.5\,\upmu \hbox {K}$ for this setup. At lower frequencies the spectra for the two channels agree very well, indicating that amplifier noise is not a significant factor in this range.

To obtain the temperature with this thermometer the following procedure was followed: First power spectral densities with both channels at a reference temperature of $T_{\mathrm{ref}}= 100\,\hbox {mK}$ with an integration time of $\varDelta t= 900$ s were measured and the cross-correlated spectrum was calculated. The relatively long integration time was chosen to reach a sufficiently good statistical uncertainty for determining the shape of the spectrum. This reference spectrum was then approximated by a fit, to obtain a smooth representation of it. Subsequently, cross-correlated power spectral densities obtained with $\varDelta t = 35$ s at different temperatures are divided by this representation of the reference spectrum to ensure that all frequency bins are weighted equally in the analysis. The resulting data are shown in Fig. 8a. For all temperatures, flat spectra over several orders of magnitude are obtained indicating not only that the parameters R and L are constant in this temperature range, but that the usable bandwidth $\varDelta f$ extends far beyond the cut-off frequency $f_{\mathrm{c}}=160\,\hbox {Hz}$.

In Fig. 8b the temperatures measured with the C3NT are plotted against a reference temperature provided by an MFFT thermometer that was previously calibrated with a superconducting fix-point device SRD-1000 [55]. The two thermometers agree to better than 0.3% within 35 s. With a thermal resistance of less than $1.5\,\upmu \Omega$ and a noise temperature of $T_{\mathrm{N}}\approx 0.5\,\upmu \hbox {K}$ the C3NT thermometer is expected to be a practical solution not only for the millikelvin range but down to the lowest cryogenic temperatures produced today.

Fig. 8

a Normalized power spectral densities of flux noise measured with a C3NT thermometer at different temperatures as a function of frequency. b Temperatures obtained with the C3NT noise thermometer plotted against an MFFT reference thermometer. The solid line represents identical temperatures for both thermometers (after [41]) (Color figure online)

3 Magnetic Flux Fluctuation Thermometers

Closely related to the current-sensing noise thermometers are the flux-sensing noise thermometers, for which the name magnetic flux fluctuation thermometers or MFFT has become generally established. This type of noise thermometer was introduced by Netsch et al. [42] in 2005. It differs from the current-sensing noise thermometers discussed in the previous section by the fact that here the noise source is read out inductively. The general scheme is depicted in Fig. 9a. The noise-generating resistor is situated in a superconducting coil, which forms a flux transformer with the input-coil of a dc-SQUID. Alternatively, one can place a dc-SQUID sensor with planar miniature multiloop coils [56] directly onto the noise-generating resistor for a more compact geometry [43].

The power spectral density of thermal flux noise is given by

$$\begin{aligned} S_\varPhi (f,T) = {4 k_{\mathrm{B}} T \mathfrak {R}(Z(f))\over (2\pi f)^2}\, , \end{aligned}$$

(11)

where $\mathfrak {R}(Z(f))$ is the real part of the complex impedance of the detection coil interacting with a metallic noise-generating sensor, which depends on the geometries of both the conductor and the detection coil as well as on the electrical conductivity of the conductor. For the simple geometry of a loop of wire wrapped tightly around a long conducting cylinder with radius r and conductivity $\sigma$ the power spectral density of flux noise inside it has the constant value

$$\begin{aligned} S_\varPhi = 4 k_{\mathrm{B}} T \sigma {G\over 2\pi }\mu _0^2 r^3\, , \end{aligned}$$

(12)

up to the cut-off frequency $f_{\mathrm{c}}\simeq 4.5/(\pi \mu _0\sigma r^2)$, which is determined by self-shielding of magnetic field fluctuations generated by high-frequency currents inside the noise source due to the skin effect. Here G is a dimensionless geometry factor of the order of unity. Figure 9b shows the result of a FEMM simulation [57] for the frequency dependence of the power spectral density of a copper cylinder with $RRR = 28$. As expected $S_\varPhi$ is constant at low frequencies and decreases above the cut-off frequency similar to but weaker than a low-pass filter characteristic.

Fig. 9

a Principle scheme of a magnetic flux fluctuation thermometer. b Power spectral density of flux fluctuations of an MFFT with a cylindrical noise-generating copper sensor and a niobium pickup coil at $T=20\,\hbox {mK}$. The solid line corresponds to a FEM simulation for this geometry (after [58]) (Color figure online)

This concept was first realized by Netsch et al. [42, 59]. A schematic of the sensor setup is shown Fig. 10a. It consists of a metallic cylinder made of high-purity (5N) gold, 2 mm in diameter and 10 mm long, that is in good thermal contact with a copper holder. The cylinder is surrounded by a pickup coil consisting of two times 17 turns of niobium wire that form a first-order coaxial gradiometer. This coil is connected via a twisted pair of superconducting leads to the input coil of a current-sensing SQUID thermally anchored at the 1 K-pot of a dilution refrigerator. The readout scheme of this thermometer is depicted in Fig. 10b.

Fig. 10

a Schematic of the sensor unit and b readout scheme of the MFFT noise thermometer developed by Netsch et al. (after [42]) (Color figure online)

Fig. 11

a Power spectral density of flux noise in the first-stage SQUID measured with an MFFT thermometer at different temperatures as a function of frequency. b Temperatures obtained from the MFFT thermometer in comparison to a temperature scale calibrated with an SRD-1000 superconducting fix-point device. The solid line represents identical temperatures for both thermometers (after [59]) (Color figure online)

The results of the first proof of principle measurement are shown in Fig. 11a. Here the power spectral density is plotted as a function of frequency at seven different temperatures that are determined by a superconducting fix-point thermometer SRD-1000 [55]. The red solid lines represent fits of these spectra with the result of a FEM simulation for this geometry. Obviously, the data are equally well described at all temperatures using Eq. (11) indicating that the resistivity of the noise-generating sensor does not change noticeably in the observed temperature range. This is a necessary condition to operate such a thermometer in relative primary mode. The temperatures deduced from these noise spectra are shown in Fig. 11b plotted against a temperature scale calibrated by an SRD-1000 device. The statistical uncertainty obtained in this measurement was better than 0.4% after 100 s averaging time.

To use this type of thermometer for temperatures in the microkelvin range an advanced double-channel readout scheme utilizing cross-correlation has been developed by Rothfuss et al. [45]. Two dc-SQUIDs [56] serving as the depicted first amplification stage were mounted at the mixing chamber of a dilution refrigerator. The noise source, a high-purity copper cylinder was thermally anchored at the nuclear demagnetization stage of the cryostat. Two superconducting flux transformers were used to couple the flux noise generated by the copper cylinder inside the two pickup coils into the SQUIDs as depicted schematically in Fig. 12.

Fig. 12

a Photo of the copper noise source of an MFFT for ultralow temperatures with the two parts of the gradiometric pickup coils. b Schematic illustration of the setup including the SQUID amplification stage thermally attached to the mixing chamber and the cooper noise source mounted on top of the demagnetization stage. Both are connected via superconducting flux transformers and shielded with niobium tubes (after [60]) (Color figure online)

A schematic of the readout is shown in Fig. 13. Each of the two flux transformers is made of a gradiometric pickup coil of a few turns of 90 $\upmu \hbox {m}$ niobium wire-wound around the noise generating copper cylinder and is run as twisted pair to the SQUID stage where it is hooked up to the input coil of one of the SQUIDs. The room temperature part includes two units of XXF-1 flux-loop electronics [54]. These low-noise and fast SQUID electronics are used to control and read out the SQUIDs, transforming the detected magnetic flux signals into proportional voltage signals.

At room temperature, each signal then passes through a low-pass filter before being amplified by a battery-powered, ac-coupled operational amplifier. The combination of the low-pass filter used and the ac-coupled amplifier corresponds to the function of a bandpass filter as depicted in the equivalent circuit diagram in Fig. 13. This filter has a passband of 0.1 Hz to 145 kHz. Since the operational amplifier used has a gain-bandwidth product of 8 MHz, it also acts as a low-pass filter with a cut-off frequency of about 80 kHz at a gain of $G = 100$.

Fig. 13

MFFT readout scheme for ultralow temperatures (after [60]) (Color figure online)

After passing through this signal chain, the two analog voltage signals of the SQUID electronics are digitized with an A/D converter with a sampling rate of $f_{\mathrm{s}}=150\,\hbox {kHz}$ each, just enough to fulfill the Nyquist-Shannon theorem [61]. Further processing was done by using a standard PC. After FFT of the signal, the cross-correlated spectra were calculated.

The power spectral density of flux noise obtained via cross-correlation of the two signals as a function of frequency at different temperatures between $42\,\upmu \hbox {K}$ and 800 mK is shown in Fig. 14. The lowest temperature was given by the minimum temperature reached in this particular demagnetization cycle starting at 4 T and 12.6 mK and the highest temperature was limited by the use of Al bonding wires within the superconducting flux transformer. The temperatures assigned to these spectra have been obtained by a $\hbox {RuO}_2$ resistance thermometer, that was calibrated in situ by a superconducting fix-point device SRM 768 from NIST (formerly NBS) [62] and by a pulsed platinum NMR thermometer $^{195}\hbox {Pt}$ which was read out by a PLM4 electronics [63].

Clearly, the spectral shape is not changing with temperature indicating that the specific electrical resistance of the copper sensor is sufficiently constant over more than four orders of magnitude in temperature and that the temperature-independent defect scattering dominates in this regime. The recording time for one cross-correlation spectrum was 400 s leading to a statistical precision of better than 0.5% for the given bandwidth of about 100 Hz. The solid lines in Fig. 14 represent an empirical fit using the same parameters for all curves, except the prefactor, which is expected to be proportional to temperature. The temperatures obtained from these cross-correlated spectra are plotted in Fig. 14b against the reference temperatures. The resulting nearly perfect linear dependence over almost five orders of magnitude clearly demonstrates the capability of this type of noise thermometer of being a relative primary thermometer.

Fig. 14

a Power spectral density of flux noise measured with an MFFT thermometer at different temperatures as a function of frequency. The solid lines represent an empirical fit with constant parameters that is scaled to all spectra. b Temperatures obtained with the noise thermometer plotted against reference temperatures provided by a calibrated Ge resistance thermometer and a platinum NMR thermometer. The solid line shows the equality of noise and reference temperature, and the dashed lines are shifted by $\pm 5\,\%$ to give an impression of the overall accuracy of the measurement. (after [45]) (Color figure online)

In this case, the parasitic heating power into the noise thermometer is estimated to be about 1 fW considering the thermal conductance of the niobium wires of the flux transformer and the back-action of the two SQUID amplifiers. This value is six orders of magnitude lower than the total parasitic heating power into the nuclear stage of about 1 nW. Based on the Widemann-Franz law the thermal link between the copper noise source and the nuclear stage has a thermal conductance corresponding to an electrical resistance of about $1\,\upmu \Omega$, which means that even a heating power of 1 pW into the noise-generating copper resistor would not change the temperature of it by more than 1% at the lowest temperature of about $50\,\upmu \hbox {K}$. This clearly demonstrates that MFFTs are thermally very robust and can be cooled to ultra-low temperatures even with a residual heat input up to a few pW.

An alternative geometry for MFFTs has been developed by Beyer et al. [43] shortly after the general concept had been introduced. Here the dc-SQUID is placed directly onto the noise-generating sensor and a micro-fabricated gradiometric flux transformer as an integral part of the SQUID chip is used for enhanced flux coupling. In this configuration, the power spectral density of flux noise at a distance z above the conducting plate of thickness d in the limit $d\ll z$ is given in good approximation by [64]

$$\begin{aligned} S_\varPhi (f,T) = 4 k_{\mathrm{B}} T\sigma d{\mu _0^2\over 32\pi z^2}{1\over 1+(2f/\pi f_{\mathrm{c}})^2}\, , \end{aligned}$$

(13)

where $\mu _0$ is the permeability of free space and $f_{\mathrm{c}}$ the cut-off frequency, which for this geometry is given by $f_{\mathrm{c}}=1/(4\mu _0\sigma zd)$. Again the shape of this spectrum is similar to a low-pass filter characteristic. A more general discussion of the flux coupling including the optimization of SQUID geometries and flux transformers for MFFTs is given in Kirste et al. [65].

Based on this concept a compact and simple to use noise thermometer called MFFT-1 has been developed [43, 48] that is commercially available since 2008 [49]. For this device, a calibration service at the Physikalisch Technische Bundesanstalt is offered [66]. The readout concept is similar to the one depicted in Fig. 10. The set-up of the sensor element is shown in Fig. 15. The fact that the SQUID chip is mounted directly onto the copper noise source results in heat deposition into the copper due to the heat dissipation of the SQUID of about 100 pW. Despite this rather substantial residual heat input, this device shows a linear temperature dependence between 1 mK and 1 K in very good agreement with the PLTS-2000 scale [67] due to the high thermal conductance of the bulk copper and the good thermal coupling to the demagnetization stage of the cryostat.

Fig. 15

Commercial magnetic flux fluctuating thermometer MFFT-1. a Schematic illustration, b photo of the inner part, and c photo of the fully assembled sensor element (after [48]) (Color figure online)

Fig. 16

a Power spectral density of flux noise measured with the MFFT-1 thermometer at different temperatures as a function of frequency. b Temperatures obtained from the MFFT-1 thermometer in relative primary mode in comparison to the temperature scales PLTS-2000 and ITS-90. The solid line represents a linear fit. The green arrow indicates the reference temperature for the MFFT-1 calibration at 15.5 mK (after [67]) (Color figure online)

The power spectral density of flux noise for the MFFT-1 thermometer measured in the temperature range between 1 mK and 1.6 K is shown in Fig. 16a. The general shape of the spectra is basically identical at all temperatures, indicating that the resistivity of the noise-generating resistor is constant. There are deviations at the lowest temperatures at low frequencies and high frequencies due to non-negligible 1/f and white flux noise contributions of the SQUID. The temperatures were obtained by fitting (13) to the power spectral density at the reference temperature of $T_{\mathrm{ref}}=15.5\,\hbox {mK}$ in the frequency range between 50 Hz and 3 kHz after removing obvious noise peaks and subsequently by scaling the fit with fixed parameters to all other spectra treated in the same way.

Using the simple relation $T= T_{\mathrm{ref}} [S(T)/S(T_{\mathrm{ref}})]$ the temperatures can be determined in relative primary mode. The reference temperature was given by the tungsten superconducting transition. The resulting temperatures are plotted in Fig. 16b against a temperature scale obtained for a $^3\hbox {He}$ melting curve thermometer below 1 K (PLTS-2000) and a rhodium-iron thermometer above 1 K (ITS-90). In the whole temperature range, no overheating or thermal decoupling effects have been observed and temperatures down to $T=400\,\upmu \hbox {K}$ were measured with the MFFT-1 thermometer [67].

A special variant of the integrated MFFT was introduced by Kirste et al. in 2014 [50] called p-MFFT. This version of an MFFT has several new additions to the concept specifically for use as a primary thermometer for metrology applications. Both the sensor and the coil geometry were optimized to enable practicable analytical modeling. In addition, it has a separate calibration coil which allows the electrical resistivity of the temperature sensor and the flux-to-voltage calibration coefficients of the two SQUID gradiometer channels to be determined independently of each other.

A photo of this device is shown in Fig. 17. It consists of a massive high-purity copper cylinder, having a residual resistivity ratio RRR of about 100. The cylinder is thinned in the middle section from both sides to form a 2 mm thin plate with lateral dimensions of $13\,\hbox {mm} \times 18\,\hbox {mm}$ that is used as a noise-generating sensor. In the center part, a blue silicon chip is visible that carries two planar gradiometric detection coils for the flux noise and is mounted face down parallel to the copper flat. A similar silicon chip having a planar gradiometric calibration coil is mounted face down on the opposite side of the copper flat. Detection and calibration coils have similar geometries and both chips reside on a small rim that separates them from the copper flat by $100\,\upmu \hbox {m}$ and $50\,\upmu \hbox {m}$, respectively. At both ends of the detection chip, a printed circuit board is located that is equipped with a current-sensing dc-SQUID.

Fig. 17

Photo of the p-MFFT sensor (after [13]) (Color figure online)

A schematic diagram of the readout circuit of the p-MFFT is depicted in Fig. 18. There are two detection coils that are read out individually by two current-sensing SQUIDs. At room temperature, each SQUID sensor is connected to an FLL (flux-locked loop) electronics, and the output voltages of both channels are read out simultaneously by a spectrum analyzer. As mentioned a calibration coil is located on the other side of the temperature sensor. By feeding a known direct or alternating current into the calibration coil, a calculable magnetic flux can be generated in the detection coils. In the case of direct current, this coil is used to determine the ratio between the magnetic flux in the detection coils and the output voltage of the SQUID electronics. In the case of alternating current, this arrangement allows one to determine the electrical conductivity of the temperature sensor.

Fig. 18

Readout scheme of the p-MFFT thermometer (after [50]) (Color figure online)

The cross-correlation of the signals is realized for the p-MFFT in the following way: Together with the superconducting input coils of two almost identical SQUID current sensors, the detection coils form superconducting flux transformers. In this way, the thermal noise signals from which the temperature is determined are fully correlated in the two SQUID sensors. Both channels are read independently, and a two-channel data acquisition system is used to digitize the SQUID output signals. The contributions of amplifier noise should therefore ideally occur completely uncorrelated in the output signals. However, it should be noted that both SQUID sensors are inductively coupled via the flux transformers, which means that any coupling between the input coils of the SQUIDs and their feedback coils leads to a certain correlation of the nominally uncorrelated amplifier noise contributions. With appropriate dimensioning, this coupling can be made very small and the cross-correlation of the SQUID signals to determine the temperature drastically reduces the effect of amplifier noise.

Fig. 19

a Comparison of measured and calculated flux noise as a function of frequency at 4.2 K. b Relative deviations of the temperature measured with the p-MFFT in relative primary mode from a copy of the PLTS-2000. (after [50]) (Color figure online)

In the first series of experiments, the p-MFFT was used and characterized as a relative primary thermometer. Figure 19a shows a high-precision measurement of the magnetic flux noise at a temperature of 4.2 K. It is in very good agreement with an analytical calculation that reflects how well this setup is designed, fabricated, and understood. In the relative primary mode, measurements were performed with the p-MFFT between 9 mK and 4.2 K, with $T_{\mathrm{ref}} = 478\,\hbox {mK}$ selected as the reference temperature. The temperatures obtained were compared to a calibrated thermometer that represented a copy of the PLTS-2000. The relative deviations of the two thermometers for temperatures below $T=1\,\hbox {K}$ are shown in Fig. 19b. With few outliers at temperatures between 18 mK to 35 mK, most data points are well within an interval of $\pm 0.5\,$% with a typical relative uncertainty of 0.25% dominated by the $T_{\mathrm{ref}}$ uncertainty and the statistical uncertainty.

Subsequently, measurements were carried out in primary mode in the temperature range from 15 mK to 700 mK with very good agreement between the measured and calculated spectra [51]. Very long measurement times of 40 min and 700 min were chosen to minimize the influence of the statistical uncertainty. A very careful analysis of the systematic errors led to a relative uncertainty of 0.59% in the absolute temperature. In Fig. 20 the relative deviations to the PLTS-2000 are shown.

Between 16 mK and 672 mK, the p-MFFT is in good agreement with the PLTS-2000. However, there is a slight tendency to negative values at 15 mK. For comparison, Fig. 20 also shows the deviations of the background data on which the PLTS-2000 is based, from the PLTS-2000. Clearly, further measurements at lower temperatures and higher precision are needed to resolve the evident discrepancies between the data sets at very low temperatures. Here noise thermometry can and likely will play an important role in the future.

Fig. 20

Relative deviations of the p-MFFT noise temperatures from the PLTS-2000, obtained with two different measurement times as a function of temperature. The dashed green line indicates the uncertainty of the PLTS-2000 with respect to the absolute temperature. The green open diamonds represent fixed points of the $^3\hbox {He}$ melting curve. The light green area defines a deviation band of $\pm 1\,$% from PLTS-2000. The background data (PTB, NIST, University of Florida) on which the PLTS-2000 is based are shown as solid lines. (after [51]) (Color figure online)

4 Summary

The development of noise thermometry at ultralow temperatures has advanced enormously over the last two decades. This progress was largely only possible due to the availability of modern micro-fabricated current-sensing dc-SQUIDs. Based on this technology, several variants of practical noise thermometers have been realized, so that noise thermometry is not only available today for metrological applications in special laboratories, but is increasingly becoming the standard in all low-temperature laboratories. There are two different versions, the current-sensing noise thermometer CSNT and the magnetic flux fluctuation thermometer MFFT, both of which are suitable for use in a wide temperature range. For over 10 years, commercially available MFFT type noise thermometers have been on the market, covering a temperature range between 1 mK and 4 K. In addition, concepts for the use of such thermometers in the low microkelvin range and also in primary mode for metrological purposes have been developed and demonstrated. Despite all these advances, a major challenge remains, namely the realization of cryogenic noise thermometers that can be used in combination with high magnetic fields. This would certainly be a breakthrough for a number of important applications and still makes noise thermometry for ultra-low temperatures a current topic of research.