1 Introduction

Thermal conductivity of superfluid \(^{3}\)He consists of two components: diffusive conductivity due to the quasiparticle motion and hydrodynamic conductivity caused by the superfluid–normal fluid counterflow effect [1]. The hydrodynamic conductivity is most important just below the superfluid transition temperature \(T_\mathrm{c}\), as it requires the presence of the normal component, whose amount decreases exponentially with temperature. Diffusive conductivity has been discussed in a few theoretical publications [2,3,4,5] and has been measured using a heat-pulse method [6, 7]. Measurements of the total thermal conductivity have been made only on a narrow temperature span near the \(T_\mathrm{c}\) [8, 9] at a selection of pressures, and at a single point at the \(^{3}\)He crystallization pressure in the ballistic quasiparticle regime [10].

Our interest in the matter is related to our adiabatic melting experiment that aims to cool \(^{3}\)He and saturated \(^{3}\)He–\(^{4}\)He mixture to ultra-low temperatures at the \(^{4}\)He crystallization pressure 2.564 MPa [11, 12]. The method is capable of reaching temperatures below 0.1 mK by melting solid \(^{4}\)He and mixing it with liquid \(^{3}\)He. At the lowest achievable temperatures, our quartz tuning fork thermometers become insensitive [13], and a computational modeling of the system is required to evaluate the temperature. To carry out the simulation, we need good understanding of the thermal couplings within the system, of which one of the key components is the thermal conductivity of superfluid \(^{3}\)He. Also, the thermal boundary resistance between liquid helium and the cell wall and between liquid and the sintered heat-exchanger is needed.

Fig. 1
figure 1

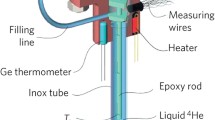
Simplified drawing of the experimental cell, showing phases, heat flows and temperatures in the system during precool. Liquid in the main volume is at \(T_\mathrm{L}\), in the heat-exchanger volume at \(T_\mathrm{V}\), while all container walls are thermalized to the precooler (nuclear stage) at \(T_\mathrm{NS}\). The main thermometer QTF (\(f_{32}\)) is located on the top section of the main volume (Color online)

Full size image

Our experimental setup provides a unique opportunity to map such intricate thermal parameters across a wide temperature range at various thermal loads, as the total heat capacity of the system can be varied by altering the amount of mixture in the system by changing the size of the \(^{4}\)He crystal. Temperatures from 10 mK down to 0.5 mK were reached by cooling the system by a nuclear demagnetization refrigerator, while temperatures below that were accessible by the adiabatic melting method. We were thus able to study the thermal conductivity of \(^{3}\)He down to the low temperature limit of our thermometry.

2 Thermal Model

The experimental cell, shown schematically in Fig. 1, consisted of a main volume (77 cm\(^{3}\)), and a sinter-filled heat-exchanger volume (5 cm\(^{3}\)), connected together by a tubular channel [12]. The main volume was filled with pure solid \(^{4}\)He, saturated liquid \(^{3}\)He–\(^{4}\)He mixture and pure liquid \(^{3}\)He at varying proportions, whereas the heat-exchanger volume and the connecting channel were always filled by pure \(^{3}\)He. There may have also been small amount of mixture trapped in the porous sinter. The main volume was monitored by two-quartz tuning fork oscillators (QTFs): one situated in an extension at the top of the main volume to always keep it in the pure \(^{3}\)He phase, while the other was in the middle of the main volume, and thus in the mixture phase, or frozen in solid \(^{4}\)He, depending on the size of the \(^{4}\)He crystal. Additionally, our setup had a cold valve (not shown in Fig. 1) that could be used to restrict the channel, but it was kept open during the measurements described here. The cell was precooled by copper nuclear adiabatic demagnetization cooler, whose temperature was measured by a pulsed \(^{195}\)Pt NMR thermometer.

There were two filling lines to the cell: a normal capillary attached to the heat-exchanger volume and a superleak line to the main volume. The normal capillary was used to introduce \(^{3}\)He to the system, but after that it was blocked by solid helium, while the superleak line was usually open to a reservoir at about 10 mK temperature, and to Kelvin-range environment from there on. The superleak line was a capillary filled with tightly packed metal-oxide powder, whose large impedance allows only superfluid flow. The crystallization pressure in porous materials is larger than in bulk, which is why the superleak can be used to transfer \(^{4}\)He to (or from) the cell at the bulk crystallization pressure to grow (or melt) the solid phase.

We have a univariant three-phase system, as solid \(^{4}\)He fixes the pressure to its crystallization pressure 2.564 MPa [14], while the presence of the pure \(^{3}\)He phase ensures that the mixture is at its saturation concentration \(8.12\%\) [15], leaving only temperature T as a free variable. When the cell is cooled down, \(^{3}\)He becomes A-phase superfluid at \(T=T_\mathrm{c}=2.6\) mK [14], while the transition to the B-phase occurs at \(T_{AB}=0.917T_\mathrm{c}\) [16] \(\approx \) 2.4 mK.

During external cooling, heat flows from the main volume of the experimental cell (\(T_\mathrm{L}\)) to the precooler (\(T_\mathrm{NS}\)) via two paths: directly through the plain cell wall, which becomes rather unimportant below the \(T_\mathrm{c}\), and through the sinter of the heat-exchanger volume via the connecting channel. Due to better thermal connection to the precooler, the liquid in the heat-exchanger volume (\(T_\mathrm{V}\)) follows temperature changes faster, while the main volume lags behind. This gives us an opportunity to evaluate the thermal conductivity of superfluid \(^{3}\)He in the connecting channel.

The Kapitza resistance \(R_\mathrm{K}\) from liquid helium to the cell wall and to the sinter is assumed to obey a power law

$$\begin{aligned} R_\mathrm{K}=\frac{R_{0}}{AT^{p}}, \end{aligned}$$
(1)

where A is the surface area, while \(R_{0}\) and p are the constants that depend on the temperature range and materials in question, as discussed in Refs. [17,18,19,20,21]. We measured the sinter to have approximately 10 m\(^{2}\) surface area, while the cell wall area was estimated to be 0.12 m\(^{2}\). In the following treatment, we combine \(R_{0}\) and A into one parameter \(r=A{/}R_{0}\). Thus, the heat flow across the Kapitza resistance becomes

$$\begin{aligned} \dot{Q}_{K}\left( p,r,T\right) =\intop _{T}^{T_\mathrm{NS}}\frac{\mathrm {d}T'}{R_{K}}=\frac{r}{p+1}\left( T_\mathrm{NS}^{p+1}-T^{p+1}\right) , \end{aligned}$$
(2)

where r and p have different values for the sinter and the plain cell wall.

Pure \(^{3}\)He phase and the mixture phase in the main volume (L) are assumed to have uniform temperature, and thus, the heat balance there reads

$$\begin{aligned} C_\mathrm{L}\dot{T}_\mathrm{L}\left( t\right) =\dot{Q}_\mathrm{melt}+\dot{Q}_\mathrm{ext}+\dot{Q}_f+\dot{Q}_\mathrm{direct}+\dot{Q}_\mathrm{tube}. \end{aligned}$$
(3)

A dot above a symbol indicates derivative with respect to time t. Here, \(C_\mathrm{L}=n_{3}^\mathrm{L}C_{3}+n_{{m,3}}^\mathrm{L}C_{{m,3}}\) is the heat capacity of the liquid in the main volume, with \(n_{3}^\mathrm{L}\) and \(n_{{m,3}}^\mathrm{L}\) the amounts of \(^{3}\)He in the pure \(^{3}\)He phase and in the saturated \(^{3}\)He–\(^{4}\)He mixture phase, respectively, while \(C_{3}\) and \(C_{{m,3}}\) are their heat capacities per mole of \(^{3}\)He, respectively. The first term on the right side is the heat absorbed (or released) when solid \(^{4}\)He is melted (or grown), \(\dot{Q}_\mathrm{melt}=T_\mathrm{L}\dot{n}_{\mathrm {3}}\left( S_{{m,3}}-S_{3}\right) \) [22], where \(\dot{n}_{\mathrm {3}}\) is the rate at which \(^{3}\)He is transferred between the liquid phases, and \(S_{3}\) and \(S_{{m,3}}\) are the entropies of pure \(^{3}\)He and saturated \(^{3}\)He–\(^{4}\)He mixture per mole of \(^{3}\)He, respectively. Each \(C_{3}\), \(C_{{m,3}}\), \(S_{3}\) and \(S_{{m,3}}\) is a function of temperature, and they are as given by Ref. [22]. (We assume that the heat capacity of pure solid \(^{4}\)He is negligibly small.) Next, \(\dot{Q}_\mathrm{ext}\) is the background heat leak to the main volume, while \(\dot{Q}_f\) represents losses occurring when there is flow through the superleak line. Lastly, \(\dot{Q}_\mathrm{direct}=\dot{Q}_\mathrm{K}\left( p_\mathrm{L},r_\mathrm{L},T_\mathrm{L}\left( t\right) \right) \) is the heat flowing to the precooler through the plain wall Kapitza bottleneck, given by Eq. (2), and \(\dot{Q}_\mathrm{tube}\) is the heat leaving the main volume through the connecting channel for the heat-exchanger volume. During the precooling period, both \(\dot{Q}_\mathrm{melt}\) and \(\dot{Q}_f\) can be omitted, as solid \(^{4}\)He is neither grown nor melted. This applies to all cases considered in this paper.

Next, for the heat balance of the heat-exchanger volume (V), we get

$$\begin{aligned} C_\mathrm{V}\dot{T}_\mathrm{V}\left( t\right) =\dot{Q}_{\mathrm {sinter}}-\dot{Q}_\mathrm{tube}, \end{aligned}$$
(4)

where \(C_{\mathrm{V}}=n_{3}^{\mathrm{V}}C_{3}+n_{{m,3}}^{\mathrm{V}}C_{{m,3}}\), is similar to the first term of Eq. (3), \(\dot{Q}_{\mathrm{sinter}}=\dot{Q}_\mathrm{K}\left( p_{\mathrm{V}},r_{\mathrm{V}},T_{\mathrm{V}}\left( t\right) \right) \) is the heat flowing to the precooler through the sinter Kapitza resistance, again given by Eq. (2), and \(\dot{Q}_{\mathrm{tube}}\) is the heat coming from the main volume through the channel. Here, \(n_{3}^{\mathrm{V}}\) includes liquid \(^{3}\)He in the connecting channel as well, but assumes, for simplicity, that the entire channel is at the same temperature as the heat-exchanger volume. Having the channel to be at \(\left( T_{\mathrm{V}}+T_{\mathrm{L}}\right) /2\) would not modify the simulations notably, since the heat capacity of the small \(^{3}\)He amount in the channel is insignificant next to the heat capacity of the heat-exchanger volume. Note that \(n_{{m,3}}^{\mathrm{V}}\) can be nonzero due to the mixture trapped into the sinter. We estimated that the sinter can hold maximum of 7 mmol of \(^{3}\)He.

All the heat that is not transmitted through the cell wall must flow through the connecting channel to the heat-exchanger volume and then through the sinter to the precooler. The thermal resistance of the cylindrical channel is

$$\begin{aligned} R_\mathrm{T}=\frac{4l}{\kappa \left( T\right) \pi d^{2}}, \end{aligned}$$
(5)

where \(\kappa \left( T\right) \) is the thermal conductivity of pure \(^{3}\)He, and \(l\approx 15\) cm and \(d\approx 2.5\) mm are the length and the effective diameter of the channel. In reality, the channel is not equally wide along its complete length, and thus 5–10% uncertainty in \(D=\frac{\pi d^{2}}{4l}\) results. The heat flow through such channel is given by the integral

$$\begin{aligned} \dot{Q}_{\mathrm{tube}}=\intop _{T_{\mathrm{V}}}^{T_{\mathrm{L}}}\frac{\mathrm{d}T'}{R_\mathrm{T}}=D\intop _{T_{\mathrm{V}}}^{T_{\mathrm{L}}}\kappa \left( T'\right) \hbox {d}T'. \end{aligned}$$
(6)

In the normal state of pure \(^{3}\)He, from \(T=T_\mathrm{c}=2.6\) mK [14], up to our range of interest (\(T \approx 10\) mK), its thermal conductivity follows \(\kappa \left( T\right) =\kappa _{0}/T\) dependence, with the coefficient \(\kappa _{0}=9.69\cdot 10^{-5}\,\mathrm {\frac{W}{m}}\) interpolated from the data of Ref. [23]. But below the \(T_{\mathrm{c}}\), the situation becomes more complicated, as the behavior of \(\kappa \left( T\right) \) is not well established. We can proceed by first dividing the heat flow integral of Eq. (6) into above and below the \(T_{\mathrm{c}}\) parts, and then linearizing it below the \(T_{\mathrm{c}}\). This is a valid course of action as long as the temperature of the heat-exchanger volume \(T_{\mathrm{V}}\) does not drop far below the \(T_{\mathrm{c}}\) until the main volume temperature \(T_{\mathrm{L}}\) is there as well. The integral of Eq. (6) may thus be written as

$$\begin{aligned} \begin{aligned} \dot{Q}_{\mathrm{tube}}&=D\intop _{\max \left( T_{\mathrm{V}}\left( t\right) ,T_\mathrm{c}\right) }^{\max \left( T_{\mathrm{L}}\left( t\right) ,T_\mathrm{c}\right) }\frac{\kappa _{0}}{T'}\hbox {d}T'+D\intop _{\min \left( T_{\mathrm{V}}\left( t\right) ,T_\mathrm{c}\right) }^{\min \left( T_{\mathrm{L}}\left( t\right) ,T_\mathrm{c}\right) }\kappa \left( T'\right) \hbox {d}T'\\&=D\kappa _{0}\ln \left[ \frac{\max \left( T_{\mathrm{L}}\left( t\right) ,T_\mathrm{c}\right) }{\max \left( T_{\mathrm{V}}\left( t\right) ,T_\mathrm{c}\right) }\right] +D\kappa _{1}\left( T_{\mathrm{tube}}\right) \left[ \min \left( T_{\mathrm{L}}\left( t\right) ,T_\mathrm{c}\right) -\min \left( T_{\mathrm{V}}\left( t\right) ,T_\mathrm{c}\right) \right] , \end{aligned} \end{aligned}$$
(7)

where \(\kappa _{1}\left( T_{\mathrm{tube}}\right) \) is the superfluid \(^{3}\)He thermal conductivity at the average channel temperature \(T_{\mathrm{tube}}\).

3 Results

The results presented here were obtained by analyzing 8 precools from about 10 mK (\(\approx 4T_\mathrm{c}\)) to 0.5 mK (\(\approx 0.2T_\mathrm{c}\)), 9 low temperature precools between 1.5 mK (\(\approx 0.6T_\mathrm{c}\)) and 0.5 mK, as well as 5 warm-up periods after melting of solid \(^{4}\)He at temperatures below 0.5 mK. The thermal transport parameters presented here were determined so that all those precools and warm-ups could be computationally reproduced within reasonable accuracy.

The challenge is that the three heat conduction paths: direct conduction through the plain cell wall, conduction through the connecting channel and conduction through the sinter, are intertwined; hence, none of them can be determined truly independently. Fortunately, certain stages of the precool are more sensitive to one than the others. At the beginning of the precool, the temperature is so high that heat conduction through the surface of the main cell volume brings along a significant contribution to the total heat transfer, even if the surface of the cell is hundred times less than the surface area of the sinter. On the other hand, thermal conductivity of \(^{3}\)He in the connecting channel plays important role near the \(T_\mathrm{c}\) of the main cell volume, as its conductivity increases significantly due to the superfluid–normal fluid counterflow effect. The Kapitza resistance of the sinter is somewhat difficult to discern, since it contributes to the heat flow over the entire temperature range. However, it is effectively decoupled from the main volume due to the relatively poor thermal conductivity along the connecting channel at temperatures well above the \(T_\mathrm{c}\). The path through the channel and the sinter is overwhelmingly dominant anywhere below the \(T_\mathrm{c}\), which was obviously intended, as the sole purpose of the sinter was to enable precooling the experimental cell to as far below 1 mK as possible.

Fig. 2
figure 2

Flowchart of the analysis procedure. Measured quantities are indicated by solid outline, computed quantities by dotted lines, and quantities obtained by other means by dashed lines (\(\kappa _{0}\) from Ref. [23], helium quantities from our log, and Kapitza parameters from Ref. [21])

Full size image

Further challenge is provided by the varying background heat leak \(\dot{Q}_{\mathrm{ext}}\) to the main cell volume. This is mostly consequential at temperatures below 1 mK. We observed that it depended on whether the cold valve was filled with liquid helium or not, and if there had been flow through the superleak recently. In our analysis, we have let it vary from 20 to 300 pW to make computations match with the experimental observations. The highest heat leak occurred when the magnetic field of the nuclear demagnetization stage was changing, while the maximum idle state heat leak was about 80 pW. For each precool and post-melting warm-up period, we used a constant heat leak value.

The procedure used to resolve the thermal conductivity of \(^{3}\)He below the \(T_\mathrm{c}\) is illustrated in Fig. 2. First, we solve differential Eqs. (3) and (4) for \(T_\mathrm{V}\left( t\right) \), as the main volume temperature \(T_\mathrm{L}\) is known based on the QTF measurements, and the nuclear stage temperature \(T_\mathrm{NS}\) from the PLM measurement. Throughout the measurement, we kept a log of the amount of helium in the different phases to calculate the heat capacities at each stage. For the plain cell wall Kapitza resistance, we used the values \(r_\mathrm{L}=0.69\) W K\(^{-3.6}\) and \(p_\mathrm{L}=2.6\), determined by analyzing the precooling data near 10 mK. The heat-exchanger volume Kapitza parameters on the other hand were \(r_{\mathrm{V}}=0.18\) W K\(^{-2.7}\) and \(p_{\mathrm{V}}=1.7\), which were determined at temperatures below 2 mK by repeatedly growing or melting small amount of solid \(^{4}\)He to alter the heat capacity of the system, and studying how that changed the relaxation time of the system toward the precooler temperature. The detailed account of that analysis can be found in Ref. [21].

Fig. 3
figure 3

Thermal conductivity of superfluid \(^{3}\)He at 2.564 MPa as a function of temperature relative to the superfluid transition temperature \(T_\mathrm{c}\) is shown in red with the shaded gray area representing the confidence bounds. Thermal conductivity values are scaled by the normal fluid value at the \(T_\mathrm{c}\) (\(0.037\,\mathrm {\tfrac{W}{K\,m}}\) [23]). The solid black line is a multi-Gaussian fit \(G\left( T\right) \) to the data, and the dotted black lines show the extrapolation of the fit at \(T<0.1T_\mathrm{c}\) and at \(T>0.92T_\mathrm{c}\). From \(0.92T_\mathrm{c}\) to the \(T_\mathrm{c}\), three possible options are given: (A) linear increase from 4.3 to \(8.0\,\tfrac{\kappa }{\kappa (T_\mathrm{c})}\), (B) constant \(4.3\,\tfrac{\kappa }{\kappa (T_\mathrm{c})}\) and (C) \(G\left( T\right) \) up to the \(T_\mathrm{c}\). Thermal conductivity data by Johnson et al. [9] at 2.00 MPa (\(\Circle \)) and at 2.96 MPa (\(\square \)), scaled by the normal fluid conductivity at the \(T_\mathrm{c}\) for each pressure, alongside with diffusive thermal conductivity (\(\bigstar \)) by Wellard et al. [6] (further analyzed by Einzel [7]), as well as hydrodynamic conductivity (solid blue line) calculated from Eq. (8) are shown for comparison. The dash-dotted blue line shows the diffusive and hydrodynamic conductivities combined (Color online)

Full size image

Heat transmitted through the channel, as evaluated from Eq. (3), depends on the derivative \(\hbox {d}/\hbox {d}t\) of the liquid helium temperature \(T_{\mathrm{L}}\) in the main volume. To reduce noise in \(\dot{T}_{\mathrm{L}}\left( t\right) \), we averaged the QTF data over 7–20 min intervals, depending on the scatter of the data. Having \(\dot{Q}_{\mathrm{tube}}\), we can then solve \(\kappa _{1}\left( T_{\mathrm{tube}}\right) \) from Eq. (7) as a function of the channel temperature \(T_{\mathrm{tube}}\). We have taken it to be the mean value between \(T_{\mathrm{V}}\left( t\right) \) and \(T_{\mathrm{L}}\left( t\right) \), when both are below the \(T_\mathrm{c}\), and the mean value between \(T_{\mathrm{V}}\left( t\right) \) and \(T_\mathrm{c}\) when only the heat-exchanger volume is below the superfluid transition temperature.

Figure 3 shows the resulting thermal conductivity, averaged across all analyzed precools and warm-ups. The confidence bounds include the measurement spread, as well as 10% uncertainty in the channel dimension parameter D, and in the Kapitza constants \(r_{\mathrm{L}}\) and \(r_{\mathrm{V}}\), and 5% uncertainty in the Kapitza exponents \(p_{\mathrm{L}}\) and \(p_{\mathrm{V}}\). The solid black line indicates a fit to the experimental data of form \(G\left( T\right) =g_{1}\left( T\right) +\left( \mathcal {K}_{2}-g_{2}\left( T\right) \right) +g_{3}\left( T\right) \), where \(g_{i}=\mathcal {K}_{i}\exp \left[ -\left( \left( T-T_{0,i}\right) /\sigma _{i}\right) ^{2}\right] \) is a Gaussian function, with \(\mathcal {K}_{i}\), \(T_{0,i}\) and \(\sigma _{i}\) listed in Table 1. Such an analytic form is handy for the model simulations.

The distinct features of our data are a plateau between \(0.3T_\mathrm{c}\) and \(0.5T_\mathrm{c}\), and a local maximum at \(0.75T_\mathrm{c}\). As we approach the \(T_\mathrm{c}\) from below, the conductivity first decreases from the local maximum value until about \(0.85T_\mathrm{c}\) after which it starts to increase again until about \(0.95T_\mathrm{c}\). Data analysis near the \(T_c\) was challenging due to two things. First, \(^{3}\)He usually undercooled slightly as we crossed the \(T_\mathrm{c}\) from above, i.e., temperature of the liquid was already below the \(T_\mathrm{c}\), but it was not yet in the superfluid state, and second, our QTF calibration formula changed at the \(T_\mathrm{c}\) from normal fluid viscosity-dependent calibration [24] to a phenomenological one. The combined effect of the changing calibration and undercooling of the liquid causes a small artificial jump in the temperature determined from the QTF frequency and width, which results in a large apparent derivative \(\dot{T}_{\mathrm{L}}\left( t\right) \) rendering our analysis inaccurate near the \(T_\mathrm{c}\). As a further complication, at a certain range, we may have a situation, where the main volume is in A-phase of the superfluid, while the heat-exchanger volume is already in the B-phase, and the A–B-phase boundary can be somewhere in the channel causing unpredictable behavior in the determined thermal conductivity. With these issues acknowledged, we conclude that our analysis gives reasonable thermal conductivity data in the B-phase of \(^{3}\)He superfluid (\(T<0.92T_\mathrm{c}\)).

Table 1 List of the parameters used in the multi-Gaussian fit of Fig. 3
Full size table

Johnson et al. [9] reported anomalous thermal resistance behavior in the A-phase near the melting pressure of \(^{3}\)He. Their thermal resistance data converted to thermal conductivity are included in Fig. 3 for comparison, showing roughly the same magnitude with our measurement. Their data are scaled by the normal fluid conductivity at the \(T_\mathrm{c}\) for each pressure (0.047 W/(K m) at 2.00 MPa, 0.032 W/(K m) at 2.96 MPa [23]). Wellard et al. [6] studied the conductivity of superfluid \(^{3}\)He at 2.1 MPa down to \(0.3T_\mathrm{c}\) by observing a time delay of a heat pulse between two vibrating wires that was converted to diffusive conductivity by Einzel [7] as normalized to the normal fluid conductivity. Feng et al. [10] determined area-scaled \(^{3}\)He thermal resistance 6.8 K m\(^2\)/W in 3.6-mm-long channel at 0.4 mK, at the \(^{3}\)He crystallization pressure. That corresponds to thermal conductivity of about \(0.02\kappa /\kappa \left( T_\mathrm{c}\right) \), which is 5–16 times less than the conductivity determined from our measurement. Full correspondence between all the described data sets is not to be expected due to the different conditions in these experiments.

Near the \(T_\mathrm{c}\), we need to take into account the hydrodynamic thermal conductivity, which is given by [1, 9]

$$\begin{aligned} \kappa _{\mathrm {h}}=\frac{d^{2}TS_{3}^{2}}{32\eta V^{2}}, \end{aligned}$$
(8)

where d is the diameter of the liquid column and \(\eta \) its viscosity, while \(V=26.76\) cm\(^3\)/mol [25] is the molar volume of \(^{3}\)He at 2.564 MPa. We used the normalized viscosity data given by Einzel [7] with the normal fluid viscosity given by Ref. [14]. It is evident that such a mechanism is needed to explain the efficient heat transfer close to the \(T_\mathrm{c}\), but the hydrodynamic contribution alone falls off too quickly as the temperature decreases. The sum of diffusive and hydrodynamic conductivities shows fair resemblance to our data, while it still does not reproduce the local maximum at \(0.75T_\mathrm{c}\).

Figure 4 demonstrates how the main volume temperature \(T_{\mathrm{L}}\) is computationally reproduced using various \(^{3}\)He thermal conductivities of Fig. 3. It also shows another crucial element of our analysis, the heat-exchanger volume temperature \(T_{\mathrm{V}}\) calculated from the measured main volume temperature and the precooler temperature \(T_{\mathrm{NS}}\). Scatter in the \(T_{\mathrm{V}}\) data is due to the analysis procedure. We immediately note from the main panel that neither diffusive nor hydrodynamic conductivity alone can reproduce our observed data. The computed \(T_{\mathrm{L}}\), with either, starts to severely lag behind as the heat-exchanger volume goes below the \(T_\mathrm{c}\).

Fig. 4
figure 4

Example of the measured temperature of the main cell volume \(T_{\mathrm{L}}\) (red), the measured precooler temperature \(T_{\mathrm{NS}}\) (blue) and the computed heat-exchanger volume temperature \(T_{\mathrm{V}}\) (magenta) during a cooldown by the nuclear stage. The other curves correspond to calculated main volume and heat-exchanger volume temperatures using various superfluid \(^{3}\)He conductivities. (See Fig. 3.) Main panel (solid black) multi-Gaussian fit \(G\left( T\right) \) using the extrapolation (B), (dashed green) hydrodynamic thermal conductivity and (dash-dotted brown) diffusive thermal conductivity. Inset (solid gray) \(G\left( T\right) \) with extrapolation (A), (solid black) extrapolation (B), (solid green) extrapolation (C) and (dotted black) sum of hydrodynamic and diffusive conductivities. The system had \(570\,\mathrm {mmol}\,\left( \pm \,2\%\right) \) of \(^{3}\)He in total; \(344\,\mathrm {mmol\,\left( \pm \,2\%\right) }\) in the pure \(^{3}\)He phase of the main volume, \(187\,\mathrm {mmol\,\left( \pm \,2\%\right) }\) in the heat-exchanger volume and the connecting channel, \(32\,\mathrm {mmol\,\left( \pm \,5\%\right) }\) in the mixture phase of the main volume and at most 7 mmol stuck as mixture in the sinter. The amount of solid \(^{4}\)He was \(2.98\,\mathrm {mol\,\left( \pm \,0.5\%\right) }\), while the external heat leak was \(40\,\mathrm {pW}\) (Color online)

Full size image

The analysis is problematic in the \(^{3}\)He-A region (from \(0.92T_\mathrm{c}\) to \(T_\mathrm{c}\)), as our treatment is not accurate there. Figure 3 shows three possible extrapolations of the measured data, and the inset of Fig. 4 illustrates the resulting difference. The option (A) with linearly increasing conductivity follows the measured data accurately above the main volume \(T_\mathrm{c}\), but, from there downward, it gives slightly too low temperatures. The opposite is true for the options (B) with constant conductivity, and (C) with the multi-Gaussian fit \(G\left( T\right) \), as both lag slightly behind the measured temperature above the \(T_\mathrm{c}\), but give better correspondence below it. The combined diffusive and hydrodynamic conductivities, based on data from the earlier publications, also reproduce the data with decent accuracy, except at the lowest temperatures. This makes sense as the combined conductivity is within the confidence bounds of our measurements until \(0.6T_\mathrm{c}\), below which it stays too high and thereby the computed main volume temperature would continue to decrease more rapidly than the measured temperature.

4 Conclusions

We have determined the thermal conductivity of superfluid \(^{3}\)He-B at the \(^{4}\)He crystallization pressure \(2.564\,\mathrm {MPa}\) in a tubular channel connecting two volumes, the larger of which contained solid pure \(^{4}\)He, liquid saturated \(^{3}\)He–\(^{4}\)He mixture and liquid pure \(^{3}\)He, while the smaller, sinter-filled heat-exchanger volume, had solely pure \(^{3}\)He (with possible traces of mixture within the sinter). The temperatures down to \(0.25T_\mathrm{c}\) were covered during precooling the experimental cell externally by a copper nuclear demagnetization cooler, while the temperatures down to \(0.1T_\mathrm{c}\) were reached by utilizing the internal adiabatic melting method and then observing the following warm-up. \(0.1T_\mathrm{c}\) was also the low temperature limit of our quartz oscillator thermometry. A handicap in our setup was that we could not directly measure the temperature of the heat-exchanger volume, but instead we had to resolve it from our computational model. To improve the setup, an additional quartz tuning fork should be installed there.

At the onset of the B-phase \(0.92T_\mathrm{c}\), we observed a thermal conductivity 4.3 times larger than that of normal fluid \(^{3}\)He at the \(T_\mathrm{c}\). Then, as the temperature was lowered, the conductivity showed a local minimum at \(0.85T_\mathrm{c}\) (2.5 relative units) followed by a local maximum at \(0.75T_\mathrm{c}\) (3.5). Between \(0.5T_\mathrm{c}\) and \(0.3T_\mathrm{c}\), we observed a plateau at about 1 relative units, below which a monotonically decreasing behavior was observed. At the plateau, our data indicated \(\sim 60\%\) lower overall conductivity than the value obtained from earlier studies [6, 7]. We also showed that our measured temperature data were computationally reproducible using the determined thermal conductivity, meaning that the computational model can be used to estimate the lowest temperatures reached by the adiabatic melting method, when the quartz oscillator thermometer had become insensitive to temperature.