1 Introduction

In the past few decades, great effort has been devoted to the discovery of dark matter [1]. One of the paths which can lead to identify this elusive particle(s) is through direct detection: the goal of this class of experiments is to detect an interaction of a dark matter particle with a nucleus of a target material [2]. In this scenario, cryogenic solid-state detectors are among the leading technologies for the exploration of the low mass dark matter parameter space.

CDMS, CRESST, and EDELWEISS are currently the experiments adopting this technology, and they use different crystals as targets to study dark matter interactions with ordinary matter. EDELWEISS has developed detectors based on germanium single crystals [3], CDMS has used both germanium and silicon [4], while CRESST has focused mostly on \(\hbox {CaWO}_4\) [5, 6]. All these different materials have an important role to probe spin-independent dark matter interactions with nuclei, but they hold a limited probing power for spin-dependent interactions.

The main difference in the cross section for spin-dependent interactions is the lack of the coherence term, \(A^2\); as a result, the presence of a heavy element in the target is not beneficial, while the opposite is true for an experiment focused on spin-independent interactions. However, the kinematic of elastic scattering with nuclei is the same for both type of interactions [7]. Hence, an experiment designed to probe spin-dependent interactions in the sub-GeV dark matter mass region should develop a technology based on a target containing the lightest element possible to maximize the energy transfer. This quite simple picture is complicated by the fact that spin-dependent interactions with ordinary matter can be tested only choosing isotopes with a nuclear ground state angular momentum \(J_\mathrm{N} \ne 0\) [8,9,10], requirement fulfilled by a limited number of isotopes [11]. The lightest element which can be used to probe spin-dependent interactions with a cryogenic solid-state detector is lithium, which is composed of \(^6\hbox {Li}\), with natural abundance of 7.59% and \(J_\mathrm{N}=1\), and \(^7\hbox {Li}\), with natural abundance of 92.41% and \(J_\mathrm{N}=3/2\) [12].

Lithium is also a very attractive element because it could be used to measure the neutron flux in the experimental setup, a significant piece of information for the construction of the background model of a given experiment. For dark matter experiments, this source of background is even more problematic, since neutrons mainly interact through nuclear recoils, the same type of interactions is expected for dark matter particles. If a neutron crosses the volume of a lithium-containing crystal, there is a non-negligible probability that it gets captured by \(^6\hbox {Li}\). If that is the case, the produced \(^7\hbox {Li}\) nucleus promptly breaks up in \(^3\hbox {H}\) and an \(\alpha \) particle with a combined energy of 4.78 MeV. With such a large energy release, the signature of neutron capture is pronounced and very hard to be mistaken. The signature is even more clear if the lithium-containing crystal employed scintillates at 4.78 MeV, since the light yield could be used to discriminate different particles interacting in the crystal. Thus, with the adoption of a light detector it should be possible to measure even a very small neutron flux in an underground laboratory and then possibly reconstruct the energy spectrum of the incoming neutrons with the help of dedicated Monte Carlo simulations.

Some lithium-containing crystals are already known to be good targets for cryogenic experiments, such as \(\hbox {Li}_{{2}}\hbox {MoO}_4\) [13, 14], \(\hbox {Li}_2\hbox {Mg}_2(\hbox {MoO}_4)_3\) [15], and LiF [16, 17], but in this work we will focus on the results obtained using \(\hbox {LiAlO}_2\) [18,19,20], a target never tested before with this technology.

2 Detectors

The first work for the use of lithium-containing crystals to explore the low mass spin-dependent dark matter sector was recently published [21]. In that work, we used a \(\hbox {Li}_{{2}}\hbox {MoO}_4\) crystal, but the large hygroscopicity of such material prevents the full implementation of the CRESST technology. One attractive alternative candidate is \(\hbox {LiAlO}_2\): it is a scintillator at room temperature with a \(340\,\hbox {nm}\) emission peak [22] at which the CRESST-III light detectors have a high absorption rate [23], it contains \(^{27}\hbox {Al}\), another interesting element to study spin-dependent interactions [24], and most importantly the CRESST technology for the direct deposition of a transition-edge sensor (TES) on the crystal surface can be easily applied.

Fig. 1
figure 1

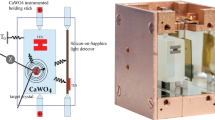
Top left: close-up of module A. It is possible to see the 2.8 g \(\hbox {LiAlO}_2\) crystal instrumented with the NTD sensor looking through the CRESST-III light detector. Bottom Left: module B, constituted by a 2.8 g \(\hbox {LiAlO}_2\) crystal with a TES directly evaporated on the surface. Right: module C, instrumented with two phonon sensors and a light detector (Color figure online)

Full size image

The crystal we use to build the detector modules described in this work was produced at the Leibniz-Institut für Kristallzüchtung (IKZ) in Berlin using the Czochralski technique. The growing procedure of this particular crystal is described in detail in [20]. From the original crystal, we built three different detector modules, labeled as module A, module B, and module C (see Fig. 1). For module A and module B, we use twin (\(2 \times 1\times 0.5)~\hbox {cm}^{3}\) crystals of 2.8 g that were cut from the original crystal; for module C, we use the bulk of \(\hbox {LiAlO}_{{2}}\), which, after a mechanical polishing, amounted to a cylindrical 373 g crystal with a 5 cm diameter and a height of 7 cm. The crystal of module A is instrumented with a Neutron Transmutation Doped (NTD) germanium thermistor [25] glued on one surface, while a CRESST-III light detector [23] is facing the crystal. A \(^{55}\hbox {Fe}\) X-ray source with an activity of \(0.050\,\hbox {Bq}\) is placed at a distance of \(\sim 0.5\,\hbox {cm}\) from the light detector to calibrate its energy response. Module B is instrumented with a TES. This TES has a similar design to the one of the CRESST-III light detectors, and it is the first directly deposited on a \(\hbox {LiAlO}_2\) crystal. Another \(^{55}\hbox {Fe}\) X-ray source is placed in the proximity of the crystal in order to calibrate the energy response of the TES. Module A and module B were simultaneously operated at the Max-Planck-Institut für Physik in Munich, in an above-ground laboratory.

In module C, the 373 g crystal is instrumented with two sensors glued on the top surface: one NTD [25] and a CRESST-II TES evaporated on a \(\hbox {CaWO}_4\) carrier [26]. On the same surface, there is a glued heater to ensure the stability of the detector operation. The crystal is surrounded by reflective foil, and a CRESST-II light detector [27] is facing its top surface. Module C was operated at Laboratori Nazionali del Gran Sasso in an underground test-facility.

Fig. 2
figure 2

Left: energy measured by the CRESST-III light detector versus energy measured by the NTD for each event registered by module A in the presence of an AmBe neutron source during a 9.44 h data collection. Two bands starting from zero energy appear: the one with the higher light emission is constituted by \(\beta /\gamma \) events interacting inside the \(\hbox {LiAlO}_2\) crystal, while the one with lower light emission is caused by the scattering of neutrons within the crystal. At 4780 keV, a different family of events appears, due to the neutron capture of \(^6\hbox {Li}\). In the vicinity of the neutron capture, there is an additional small family of events, at higher energy. This additional family has currently an unknown origin,and the modeling of the anomalously high light yield is particularly challenging. Right: energy spectrum collected during 23 h of measurement with module B. All particle events plus events due to test pulses are given in black, and in light blue, the particle events only. The energy threshold of this detector is equal to \((189.5\pm 11.7)~\hbox {eV}\), the lowest ever achieved with a cryogenic detector employing lithium-containing crystal as a target (Color figure online)

Full size image

3 Cryogenic Characterization of \(\hbox {LiAlO}_2\)

Since \(\hbox {LiAlO}_2\) was never tested as a target for a cryogenic detector, the first step was to gather data about some basic unknown properties. This was done using module A, which allows us to have a first overview on scintillation, light yield, and quenching factors for different particle interactions inside the crystal.

The energy calibration of the light detector was implemented using a combination of injected heater pulses and the 5.893 keV peak from the \(^{55}\hbox {Fe}\) source. After calibration, the baseline resolution of the light detector is \(\sigma _\mathrm{baseline}=(26.6\pm 1.2)~\hbox {eV}\), while the resolution at 5893 eV is \(\sigma _\mathrm{Fe}=(139.1\pm 4.0)~\hbox {eV}\). During the operation of module A, we installed at a distance of \(\sim \,50~\hbox {cm}\) from the center of the dilution refrigerator an AmBe neutron source emitting \(\sim \)80.000 neutrons/s. Thus, for the calibration of the NTD, we used the neutron capture peak appearing at 4780 keV where the energy resolution is \(\sigma _\mathrm{capture}=(8.7\pm 0.8)~\hbox {keV}\). In Fig. 2, we plot the energy measured in the light channel versus the energy measured in the phonon channel for each event registered by our detector during 9.44 h of effective measuring time in the presence of the AmBe neutron source. Three main different families of events can be easily distinguished: \(\gamma \) rays and \(\beta \) particles interacting in the \(\hbox {LiAlO}_2\) form one band starting from zero energy and with a light yield of \(\sim 1.2~\hbox {keV/MeV}\), while neutrons scattering within the crystal exhibit a band starting as well from zero energy but with a much reduced light yield. Finally, at high energies and with a light yield in between the \(\beta /\gamma \) band and the neutron band, the neutron capture by \(^6\hbox {Li}\) appears. The separation between the \(\beta /\gamma \) band and the neutron band starts to become evident at \(\sim 170~\hbox {keV}\); this means that in the energy region of interest for dark matter search (\(\lesssim \) 1–10 \(\hbox {keV}\)) it will be unlikely to achieve an effective particle discrimination based on the light yield even with a substantial improvement of the light collection. The light emission at \(\sim 1~\hbox {MeV}\) is equal to \((1180.5\pm 103.0)~\hbox {eV}\) for \(\beta /\gamma \) events and \((284.3\pm 55.8)~\hbox {eV}\) for neutrons, resulting in a quenching factor for neutrons equal to 0.241. Finally, the light emission is equal to \((3438.2\pm 227.6)~\hbox {eV}\) at 4780 keV; assuming a linear light emission up to this energy in the presence of \(\beta /\gamma \) events, the quenching factor for the \(\alpha \) particles is 0.599.

4 Dark Matter Results

Module B was designed to improve the limits on spin-dependent dark matter interactions obtained with cryogenic experiments [21, 28, 29]. In order to do this, it is essential to reach a low energy threshold \({E}_\mathrm{T}\): in the previous work, we reached \({E}_\mathrm{T}=932~\hbox {eV}\) [21] with one NTD as phonon sensor. In this work, instead, we use a TES directly evaporated on the \(\hbox {LiAlO}_2\) surface, which generally can reach a lower \({E}_\mathrm{T}\) in comparison with a glued NTD.

We collected 23 h of background data with module B. The energy calibration is implemented using a combination of the 5.893 keV peak from the \(^{55}\hbox {Fe}\) source and artificial pulses of discrete energies (called test pulses) periodically injected to continuously monitor the detector response. Using this method, we can obtain an accurate energy calibration taking in account the intrinsic nonlinearity of the TES. The baseline resolution is \(\sigma _\mathrm{baseline}=(39.7\pm 2.5)~\hbox {eV}\). The energy threshold for particle interactions is calculated as \((189.5\pm 11.7)~\hbox {eV}\) using the same method presented in [30]. In this case, however, we set the total rate of counts in the noise above threshold (noise trigger rate) to \(10^5\) counts/(\(\hbox {keV}\,\hbox {kg}\,\hbox {day}\)), the same order than the observed event rate in the 1–5 keV range. In Fig. 2, we show the spectrum of the background measurement: the X-ray peaks from \(^{55}\hbox {Fe}\) decay clearly emerge and a sudden rise of events below 300 eV is also evident, which we mostly attribute to noise triggers. In the flat part of the spectrum, the background rate is in the order of \(2\times 10^5\) counts/(\(\hbox {keV}\,\hbox {kg}\,\hbox {day}\)), similar to the one seen in [5]: this high value is expected, since the detector is operated in an above-ground laboratory without the presence of any kind of shielding or veto system. From this spectrum, we can calculate dark matter exclusion limits for spin-dependent interactions. We choose an energy region of interest ranging from threshold to 4000 eV, and we do not apply any cut to the particle events registered by the detector. The exclusion limit is calculated using Yellin’s optimal interval method [31, 32] in the theoretical framework presented in [21]. For the calculation, we adopt the standard dark matter halo model, which assumes a dark matter halo with a Maxwellian velocity distribution and a local dark matter density of \(\rho _\text {DM} = 0.3\,\hbox {GeV}/(\hbox {c}^{2}\, \hbox {cm}^{3})\) [33]. We also assume \(v_\text {esc} = 544\,\hbox {km/s}\) for the galactic escape velocity [34] and \(v_\odot = 220\,\hbox {km/s}\) for the solar orbit velocity [35]. The limit obtained is shown in Fig. 3.

Fig. 3
figure 3

Exclusion limits set by various direct detection experiments for spin-dependent interactions of dark matter particles with protons. The cross section for this kind of interactions is shown on the y-axis, while the dark matter particle mass is on the x-axis. We plot in red and brown the results obtained from module B and module C data, respectively, with \(^7\hbox {Li}\) and \(^{27}\hbox {Al}\). The first result obtained using \(^7\hbox {Li}\) is plotted in orange. Additionally, we plot limits from other experiments: CDMSlite [28] and EDELWEISS [29] with \(^{73}\hbox {Ge}\); PICO with \(^{19}\hbox {F}\) [37]; Collar [38] with \(^{1}\hbox {H}\). Finally, we plot in dotted black a constraint from Borexino data derived in [39] (Color figure online)

Full size image

5 Underground Measurement at LNGS

The final goal of cryogenic detectors with lithium-containing crystals is to measure simultaneously the neutron flux and eventual interactions of dark matter particles, with a special focus on spin-dependent interactions. In order to do this, it is necessary to achieve a high energy range of operation (up to \(\sim 10~\hbox {MeV}\)) with a good energy resolution while also reaching a low energy threshold (\(\lesssim 1~\hbox {keV}\)). This goal is extremely challenging if using a single phonon sensor technology, but relatively easy to achieve if using simultaneously a TES and a NTD as phonon sensors. Module C follows this concept and proves that this is possible. In fact, the two phonon sensors were simultaneously operated for 9 days inside a dilution refrigerator in an underground test-facility at LNGS: the TES reached an energy threshold of 2.6 keV, while the NTD and the CRESST light detector were used to measure the neutron capture of \(^6\hbox {Li}\) in the presence of a weak neutron source placed in the proximity of the dilution refrigerator. We can see that the energy threshold of module C is sensibly higher than the one achieved by module B: this is mainly due to the large increase in crystal mass, as observed in multiple occasions [36], and the use of a glued phonon sensor. A dark matter limit obtained from 4 h (effective live time) of background data is shown in Fig. 3. The limit was calculated with the same method previously discussed and improves the limit obtained with module B for dark matter particle masses \( > rsim 6~\hbox {GeV}/\hbox {c}^2\). In the next months, we plan to use the data collected in this run to precisely assess the radiopurity of the crystal and to determine the precision of the neutron flux measurement with this detector.

6 Conclusions

Lithium-containing crystals can be used to build cryogenic detectors that can test spin-dependent dark matter interactions while simultaneously measuring the neutron flux in the experimental setup. The first results obtained with \(\hbox {LiAlO}_2\) crystals are extremely promising and support further technological developments headed to explore the dark matter parameter space at low masses.