Excitonic Tunneling in the AB-bilayer Graphene Josephson Junctions

Abstract

We have considered the AB-stacked bilayer graphene tunnel junction construction. The bilayers are supposed to be in the charge equilibrium states and at the half-filling in each of the electronic layers of the construction and at each value of the external gate potential. By considering the interacting bilayers in both sides of the junction and by taking into account both intralayer and interlayer Coulomb interaction effects, we have calculated the normal and excitonic tunnel currents through the junction. The electronic band renormalizations have been taken into account, due to the excitonic pairing effects and condensation in the BLGs. The exact four-band energy dispersions, including the excitonic renormalizations, have been used for the bilayers without any low-energy approximation. The normal and excitonic tunneling currents have been calculated for different values of the gate potential and for different values of the interlayer interaction parameters in both sides of the tunnel junction. We demonstrate the existence of the excitonic Josephson current through the junction which persist even for the non-interacting bilayer graphene junction. For the non-interacting case, the mechanism of the excitonic condensates formation and tunneling between the condensates is attributed to the interlayer hopping between the layers. The role of the charge neutrality point has been discussed in details.

1 Introduction

The existence of the electron-hole bound states for a semimetal with overlapping bands has been postulated long years ago by Keldysh, Kopaev and Kozlov [1,2,3,4,5,6], and a prediction about the superfluidity has been given for a condensed excitonic state. Ulteriorly, it has been the subject of an intense theoretical studies [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Experimentally, the strong evidence of an excitonic insulator (EI) and excitonic Bose–Einstein condensate (BEC) ground states have been determined only in the quantum Hall regime (in a large magnetic field) and under the high pressure, in a series of the experimental works on the rare-earth chalcogenide compounds, transition metal dichalcogenides and tantalum chalcogenides [23, 24]. The exciton condensation was experimentally observed also in quantum Hall bilayers [25,26,27], in the systems of magnons [28] and cavity exciton polaritons [29,30,31]. Recently, other solid-state systems were proposed as possible candidates for the achievement of the BEC of excitons. It concerns the quantum well heterostructures with the excitons trapped in the cavities of the potential wells [32,33,34,35,36,37,38,39,40,41,42,43,44,45] (the structure, utilized in these works, were double-layer GaAs/AlGaAs or InAs/GaSb quantum-wells with the electric field applied perpendicularly to the structure), the double-layer heterostructures and bilayers [46,47,48].

The excitonic gap formation and condensation has been examined also in the bilayer graphene structures [49,50,51,52,53,54,55,56,57]. Namely, the bilayer graphene is very promising for the optoelectronic applications due to its unique gate-controllable band structure properties [58]. The imposition of the external electrical field can tune the bilayer graphene from the semimetal to the semiconducting state. Nevertheless, the excitonic condensation in the bilayer graphene structures remains controversial in the modern solid-state physics because of the complicated nature of the single-particle correlations in these systems [49,50,51,52,53,54,55,56,57]. It has been shown recently [59] that the critical temperature, which describes the transition from the condensate state to the normal state in graphene double-layer structures, can be very high due to the extremely small effective mass of excitons. The coherence in exciton BEC condensates survives at the very high temperatures. An analog conclusion has been drawn in Ref. [56, 57], concerning the bilayer graphene, where the condensate evolution has been analyzed as a function of the interlayer Coulomb interaction parameter in the BLG.

The excitonic condensation has been realized experimentally in the double bilayer graphene heterostructure, in the strong quantum Hall regime, with the help of a combination of the Coulomb drag and current counterflow measurements [60]. They have also found the evidence of strong interlayer coupling between graphene layers, thanks to the observation of quantized Hall “drag plateau”. The zero-valued longitudinal resistance, measured there, confirms the dissipationless (friction-free) nature of the electron-hole condensate state. A quite simple experimental way to observe the excitonic condensate states in the bilayer structures is related to the possibility of engineering of a spatially confined excitonic condensates in the potential traps, and the investigation of the Josephson tunneling effects for excitons [61,62,63,64], related to the tunneling between two trapped Bose condensates [65] that possess the macroscopic phase coherence. The excitonic Josephson tunneling effects and thermal transport properties in the electron-hole type double-layer graphene junctions, separated by a dielectric layer, have been recently considered in Refs. [66, 67].

In the present paper, we study the excitonic tunneling effects in the tunnel junction based on the AB-stacked bilayer graphene structures. We suppose the presence of the macroscopic phase coherent regime with the well-defined condensates phases and amplitudes and we consider only the local, on-site, interlayer excitonic pairing in each side of the junction. We treat the local intralayer and interlayer Coulomb interactions within the bilayer Hubbard model at the half-filling (in each layer of the BLG). Supposing the electronic bilayers, without the initial optical pumping mechanism, we study the normal and excitonic tunneling currents through the BLG/I/BLG junction for different values of the external gate voltage, applied to the heterostructure, including the dc limit (i.e., $V=0$) when a dc excitonic Josephson current passes through the tunnel junction. We will assume the half-filling regime in each layer of the BLG structures, even in the presence of the applied gate potential, thus by supposing that not considerable changes occur in the electron density during the adiabatic switching of the external potential.

Here, by the adiabatic switching, we mean the very slow changes of the external switching potential applied to the junction, which causes the appearance of the ac Josephson current in the junction. The adiabatic changes of the external gate potential are important in many contexts concerning the tunnel junctions. First of all, here the adiabaticity of the external potential is important for the non-perturbative influence of the gate potential on electron densities in the individual bilayer structures, on both sides of the junction. Furthermore, this leads to the possibility of examination of the permitted values of interlayer Coulomb interaction parameters and excitonic gaps for a fixed value of the external gate potential. The half-filling condition in each layer of the BLGs is directly related to the adiabaticity of the external gate potential in the sense that the electronic reconfiguration time $\tau _\mathrm{rec}$ in the BLG system is much faster than the variation time of the external potential $\Delta {\tau }_\mathrm{Field}$: $\tau _\mathrm{rec}<<\Delta {\tau }_\mathrm{Field}$. Such instantaneous changes of the electron densities in the system lead to the well-defined Coulomb potentials, for each value of the external field configuration. On the other hand, we consider the explicit dependence of the condensates phase difference parameter on the external gate potential and we show that the excitonic dc Josephson current appears in the junction array at the zero value of the external gate potential. We show how a finite difference between the static phases of the coherent excitonic condensates in the BLG subsystems leads to the excitonic Josephson dc current through the tunnel junction even in the case of the non-interacting regime in the BLG systems. The adiabatic switching of the external gate potential could be very important in the context of the adiabatic graphene logic constructions similar to the superconductor logic constructions, which are actually under the strong theoretical and experimental investigations [68,69,70]. In such devices, the intrinsic switching speed of the junctions increases rapidly with the increase of the damping resistance, and the phase differences change more adiabatically, which results in a considerable reduction in the energy dissipation of the single logical gates.

Furthermore, we show also that any finite voltage leads to the ac Josephson current irrespective of the phases of coherent condensates in both sides of the junction and we calculate the ac Josephson current as a function of external gate potential, for different values of the interlayer Coulomb interactions in different sides of the junctions. We study the amplitude of the zero voltage Josephson dc current as a function of the interlayer Coulomb interaction parameters in the subsystems. The symmetric and asymmetric interaction cases have been considered straightforwardly. Also, we calculate the normal quasiparticle tunneling current and we show that normal tunneling in the BLG/I/BLG heterostructure is an interaction-protected process and the threshold frequency of the normal tunneling current strongly depends on the values of the Coulomb interaction parameters in the BLGs. We analyze the role of the charge neutrality point (CNP) on the behavior of the normal and excitonic tunneling currents.

2 The Bilayer Graphene Josephson Junction

2.1 Description of the Hubbard Interactions

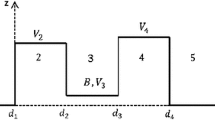
We introduce here our model consisting of two Bernal stacking bilayer graphene (BLG) structures separated by a very thick dielectric layer (We suppose that the thickness of the insulating layer is such that we can neglect the quasiparticle scattering and recombination processes in the layer.) For the convenience, we will denote by a, b and $\tilde{a}, \tilde{b}$ (and their conjugates $a^{\dag }, b^{\dag }$ and $\tilde{a}^{\dag }, \tilde{b}^{\dag }$) the annihilation (creation) fermionic operators corresponding to different sublattice sites A, B in the left bottom, and $\tilde{A}$, $\tilde{B}$ in the left top layer in the left BLG. Similarly, we denote by c, d and $\tilde{c}, \tilde{d}$ (and their conjugates $c^{\dag }, d^{\dag }$ and $\tilde{c}^{\dag }, \tilde{d}^{\dag }$) the annihilation (creation) fermionic operators corresponding to different sublattice sites C, D in the right bottom and $\tilde{C}$, $\tilde{D}$ in the right top layer in the right BLG. In Fig. 1, we have presented the schematic setup of our BLG/I/BLG junction (here I represents the dielectric layer between the BLGs). We assume here that the layers, which have lattice sites A, B and C, D (bottom layer) are biased-$V_{\ell }/2$ (with $\ell =L,R$), and the layers with the lattice sites $\tilde{A}$, $\tilde{B}$ and $\tilde{C}$, $\tilde{D}$ (top layers) $V_{\ell }/2$, so that the potential difference between the two layers is $V_{\ell }$. For the first treatment of such a junction, we suppose the half-filling condition satisfied in both BLG systems, i.e., we suppose that $\langle n^{\ell '}_{\ell } \rangle =1$, where $n^{\ell '}_{\ell }$ is the total particle number operator in each layer with $\ell '=1,2$ of each BLG with $\ell = L,R$. Note, also that we attached the number $\ell '=1$ to the bottom layers and $\ell '=2$ to the top layers, in the heterostructure. The non-interacting tight-binding part of the total tunnel junction Hamiltonian could be written in the usual form

$$\begin{aligned} {H}_{0}=\sum _{\ell =L,R}\hat{H}_{\ell 0} \end{aligned}$$

(1)

with ${H}_{{\ell }0}$, given as

$$\begin{aligned} {H}_{{\ell }0}= & {} -\,\gamma _0\sum _{\left\langle \mathbf{{r}}{} \mathbf{{r}}'\right\rangle }\sum _{X_{\ell },Y_{\ell }}\sum _{\sigma }\left( X^{\dag }_{\ell \sigma }(\mathbf{{r}})Y_{\ell \sigma }(\mathbf{{r}}')+h.c.\right) \nonumber \\&-\,\gamma _1\sum _{\mathbf{{r}},\sigma }\left( P^{\dag }_{\ell \sigma }(\mathbf{{r}})Q_{\ell \sigma }(\mathbf{{r}})+h.c.\right) \nonumber \\&-\,\sum _{\ell '}\sum _{\mathbf{{r}},\sigma }\mu ^{\ell '}_{\ell }n^{\ell '}_{\ell ,\sigma }(\mathbf{{r}}), \end{aligned}$$

(2)

where the fermionic operators $X_{\ell }$ and $Y_{\ell }$ refer to different sublattice fermions, i.e., for $\ell =L$ we have $X_{\ell }=a, \tilde{a}$, and $Y_{\ell }=b,\tilde{b}$, while for $\ell =R$ we have $X_{\ell }=c, \tilde{c}$ and $Y_{\ell }=d,\tilde{d}$. The intralayer hopping parameter $\gamma _0$ is supposed to be the same for both layers and for both BLGs. The fermionic operators $P^{\dag }_{\ell }$ and $Q^{\dag }_{\ell }$ in Eq. (2) are defined such that for $\ell =L$ we have $P_{\ell }=b$ and $Q_{\ell }=\tilde{a}$, whereas for $\ell =R$ we defined $P_{\ell }=d$ and $Q_{\ell }=\tilde{c}$. The parameter $\gamma _1$ denotes the interlayer hopping amplitude between the layers of the BLGs, and it is supposed also the same for both sides of the junction. The variable $\sigma$, in all terms in Eq. (2), describes the fermionic spin variable, which takes two values $\sigma =\uparrow , \downarrow$. The last term in Eq. (2) subjects the chemical potential terms with the chemical potentials coupled to the charge density operators in each layer of separated BLGs. Initially, we suppose that the BLG/I/BLG system is in the Grand canonical equilibrium state with the equal chemical potentials in both layers of each BLG structure. Thus, we have $\mu ^{\ell '=1}_{\ell }=\mu ^{\ell '=2}_{\ell }$ for $\ell =L,R$. The charge density operator $n^{\ell '}_{\ell ,\sigma }(\mathbf{{r}})$, as it was discussed above, describes the total electron density with the spin $\sigma$ in the given layer $\ell '=1,2$ of a given BLG with $\ell =L,R$. For example, for the layer $\ell '=1$ in the BLG with $\ell =L$, we have $n^{(1)}_{L,\sigma }(\mathbf{{r}})=a^{\dag }_{\sigma }(\mathbf{{r}})a_{\sigma }(\mathbf{{r}})+b^{\dag }_{\sigma }(\mathbf{{r}})b_{\sigma }(\mathbf{{r}})$. It is important to notice here that we consider purely electronic graphene layers in both sides of the heterojunction and we do not suppose any initial optical pumping in the BLGs.

Fig. 1

The structure of the BLG/I/BLG tunnel junction. The applied gate potentials and the potential drop (between the layers) are shown in the left ($V_L$) and right ($V_{R}$) sides of the junction (Color figure online)

The fermionic operators, in the individual BLG, systems satisfy the following anticommutation rules

$$\begin{aligned} \left[ X^{l'}_{l}(\mathbf{{r}}),Y^{m'}_{m}(\mathbf{{r}}')\right] _{+}= & {} X^{l'}_{l}(\mathbf{{r}})Y^{m'}_{m}(\mathbf{{r}}')+Y^{m'}_{m}(\mathbf{{r}}')X^{l'}_{l}(\mathbf{{r}}) \nonumber \\= & {} \delta _{ll'}\delta _{mm'}\delta (X-Y)\delta (\mathbf{{r}}-\mathbf{{r}}'). \end{aligned}$$

(3)

The top indices, in Eq. (3), indicates the layers in the BLGs, and the bottom subscripts were introduced for the left- and right BLG, as in Eq. (2). Thus, we suppose the non-vanishing anticommutators only between the fermions on the same type of sublattices in the layers. The sign +, near the parenthesis $[\ldots ]_{+}$, in the left-hand side in Eq. (3), indicates the anticommutation rule. We introduce here also the interaction terms by defining the generalized bilayer Hubbard model, in each side of the junction. Namely, we have for the interaction part

$$\begin{aligned} {H}_\mathrm{int}=\sum _{\ell =L,R} {H}_{i\ell }, \end{aligned}$$

(4)

where ${H}_{i\ell }$ are the interaction Hamiltonians, for both sides of the junction

$$\begin{aligned} {H}_{i\ell }= & {} U_{\ell }\sum _{\ell '}\sum _{\mathbf{{r}},\eta }\left[ \left( n^{\ell '}_{\ell \eta \uparrow }-\frac{1}{2}\right) \left( n^{\ell '}_{\ell \eta \downarrow }-\frac{1}{2}\right) -\frac{1}{4}\right] \nonumber \\&+\,W_{\ell }\sum _{\mathbf{{r}}\sigma \sigma '}\left[ \left( n^{(1)}_{P_{\ell }\sigma }-\frac{1}{2}\right) \left( n^{(2)}_{Q_{\ell }\sigma '}-\frac{1}{2}\right) -\frac{1}{4}\right] , \end{aligned}$$

(5)

where $n^{(1)}_{P_{\ell }\sigma }$ and $n^{(2)}_{Q_{\ell }\sigma }$ are the electron densities in the layers 1 and 2 in the BLGs ($\ell =L,R$) for the $P_{\ell }$ and $Q_{\ell }$-type fermions, introduced above. The parameter $U_{\ell }$ describes the intralayer Coulomb interactions in the layers of the BLG systems. We have attributed only one index notation to $U_{\ell }$ because we suppose in the paper that $U_{\ell }$ is the same for both layers in the individual BLG systems. Moreover, we put $U_{L}=U_{R}=2\gamma _0$ throughout the paper, except the case of the non-interacting BLGs, when $U_{\ell }=W_{\ell }=0$. As we have shown previously [56, 57], this parameter does not play an important role in the formation of the excitonic condensates states in the individual BLG systems, and it leads only to the small modifications of the chemical potential behavior as a function of the interlayer Coulomb interaction parameter $W_{\ell }$. The interlayer Coulomb interaction $W_{\ell }$ in the second term in Eq. (5) is considered as local, i.e., it is defined as the electrostatic Coulomb repulsion between the electrons at the same lattice position in different layers of the BLGs (with $\ell =L, R$). Indeed, this type of local Coulomb interaction is possible to consider in the BLGs due to their stacking order. We have shown also in Ref. [56, 57] that the interaction parameter $W_{\ell }$ is responsible for the excitonic pair formation and excitonic condensates states in the BLG system. It is interesting to emphasize here that at the zero interlayer coupling limit $W_{\ell }=0$ between the layers in the individual BLG system and at the zero value of the on-site intralayer Coulomb interaction $U_{\ell }=0$ the BLG systems are in the condensates states. This becomes clear when calculating (for details see in Ref. [56, 57]) the frequency-summed anomalous excitonic spectral functions $g^{\ell }_{b\tilde{a}}(\mathbf{{k}})$ (in the left BLG with $\ell =L$) and $g^{\ell }_{d\tilde{c}}(\mathbf{{k}})$ (in the right BLG with $\ell =R$) which give the momentum distribution of the spectral functions in the BLG systems. Indeed, the calculations show the existence of a very narrow but finite bandwidth in the momentum space where the excitonic condensate amplitude is not zero. Therefore, the fundamental excitonic state in the BLG system, at the zero interlayer interaction regime, is governed principally by the electron-hole pair condensed phase caused by the interlayer hopping $\gamma _1$, and the individual free excitonic pairs are indeed absent in the BLG structure. This last effect will become clear in the present paper when calculating the excitonic Josephson current for the non-interaction BLGs, i.e., when $U_{\ell }=0$ and $W_{\ell }=0$. We should notice here that the interaction parameter $W_{\ell }$ is not defined for example for the electrons on the lattice sites A (in the bottom layer $\ell =1$, in the left BLG) and $\tilde{B}$ (in the upper layer $\ell =2$, in the right BLG), and, similarly, it is not defined for the electrons on the lattice sites C (in the bottom layer $\ell =1$, in the right BLG) and $\tilde{D}$ (in the upper layer $\ell =2$, in the right BLG). Indeed, these lattice sites have not their local nearest neighbors sites on the opposite layer in the given BLG. Both interaction parameters $U_{\ell }$ and $W_{\ell }$ are positive because we consider, initially, the electronic layers in both BLG systems. Then, we will use the interaction representation for the fermions [71], in which the time dependence of the fermionic operators is given by the unperturbed Hamiltonian ${H}_{L 0}(V)+{H}_{R 0}+H_{iL}+H_{iR}$, where ${H}_{L 0}(V)$ is the tight-binding Hamiltonian of the left side of the junction in the presence of the external gate voltage applied to the BLG/I/BLG (see). We assume that the gate voltage V(t) drops across the barrier and, in general, the Fermi levels in the left- and right-BLG structures will relatively shift by an amount proportional to the potential drop across the junction, i.e., $\bar{\mu }_{L}-\bar{\mu }_{R}=-eV(t)$. We should emphasize here that the Fermi levels $\bar{\mu }_{L}$ and $\bar{\mu }_{R}$ are the functions of the shifted effective chemical potentials in the system which depend on the intralayer and interlayer Coulomb interaction parameters introduced in Eq. (5). For the reasons that will be clear in the following sections, we have denoted by $\bar{\mu }_{l}, l=L, R$ the exact Fermi levels in different sides of the tunnel junction. We suppose here the half-filling conditions for the total electron densities in each layer of the separate BLG structure and we assume that the influence of the external gate voltage on the charge densities in the layers is infinitesimally small, and the excitonic gap parameters $\Delta _{L}=W_{L}\left\langle \tilde{a}^{\dag }_{i}b_{i} \right\rangle$ (in the left bilayer) and $\Delta _{R}=W_{R}\left\langle \tilde{c}^{\dag }_{i}d_{i} \right\rangle$ will not get modified by the external perturbation, i.e., $\delta {V}\nrightarrow \delta {n^{\ell '}_{\ell }}\nrightarrow \delta {\Delta }_{\ell }$, and consequently $\delta {n^{\ell '}_{\ell }}=0$, $\delta {\Delta }_{\ell }=0$. Such a non-perturbative effect on the electron densities and on the excitonic gap parameter permits to include properly the effect of the applied gate voltage on the excitonic properties in the system and do not affect the excitonic condensate state in the system. For a more sophisticated case that evolves the variation of the excitonic condensates states in the junction, one should include the influence of the gate voltage on the excitonic gap parameter and the half-filling assumption will be failed in this case. Such a treatment is out of the scope of the present paper. We will consider the hopping parameter $\gamma _{0}=1$ as the unit of energy measure in the system, and we set $e=1$, $k_{B}=1$, $\hbar =1$ in the paper.

2.2 The Tunneling Hamiltonian

The time evolution of the eigenstates is determined by the perturbation term, given via the quasiparticle tunneling Hamiltonian ${H}_{T}$. In the following, we will transform the total Hamiltonian of the system ${H}={H}_{0}+{H}_\mathrm{int}+H_{T}$ into the Fourier space by introducing the Nambu fermionic spinors $\psi ^{L}_{\mathbf{{k}},\sigma }(t)$ and $\psi ^{R}_{\mathbf{{k}},\sigma }(t)$ in the left and right sides of the junction. We have

$$\begin{aligned} \psi ^{L}_{\mathbf{{k}},\sigma }(t)= & {} \left[ a_{\mathbf{{k}},\sigma }(t),b_{\mathbf{{k}},\sigma }(t),\tilde{a}_{\mathbf{{k}},\sigma }(t),\tilde{b}_{\mathbf{{k}},\sigma }(t)\right] ^{T}, \nonumber \\ \psi ^{R}_{\mathbf{{k}},\sigma }(t)= & {} \left[ c_{\mathbf{{k}},\sigma }(t),d_{\mathbf{{k}},\sigma }(t),\tilde{c}_{\mathbf{{k}},\sigma }(t),\tilde{d}_{\mathbf{{k}},\sigma }(t)\right] ^{T}. \end{aligned}$$

(6)

The tunneling matrix Hamiltonian ${H}_{T}$ will include all possible quasiparticle tunnelings between the BLGs in the junction. Namely, it accounts all sublattice fermions in the hexagonal layers that participate to the tunneling process. Due to the AB stacking order in the BLGs and the form of the interlayer hopping and interlayer interaction terms in Eqs. (2) and (5), some of the sublattice fermions will not participate to the total excitonic tunneling (for example the fermions on the lattice sites $a,\tilde{b}$ and $c, \tilde{d}$), and they will contribute only to the single-particle normal tunneling in the junction. Therefore, the tunneling Hamiltonian ${H}_{T}$, which describe the tunneling of the particles between the similar lattice sites (here the pairs of similar lattice sites in the BLGs are $(\tilde{A},\tilde{C})$, $(\tilde{B},\tilde{D})$, (A, C) and (B, D), where the first letter in the pair (x, y) is the lattice site in the left BLG and the second letter is the lattice site which belongs to the right BLG) will be written in the form

$$\begin{aligned} {H}_{T}= & {} \sum _{\mathbf{{k}},\mathbf{{p}},\sigma }\left[ t_{\mathbf{{k}},\mathbf{{p}}}\left( \tilde{a}^{\dag }_{\mathbf{{k}},\sigma }\tilde{c}_{\mathbf{{p}},\sigma }+{b}^{\dag }_{\mathbf{{k}},\sigma }{d}_{\mathbf{{p}},\sigma }+\right. \right. \nonumber \\&\left. \left. +\,\tilde{b}^{\dag }_{\mathbf{{k}},\sigma }{\tilde{d}}_{\mathbf{{p}},\sigma }+{a}^{\dag }_{\mathbf{{k}},\sigma }{c}_{\mathbf{{p}},\sigma }\right) +h.c\right] . \end{aligned}$$

(7)

where $t_{\mathbf{{k}},\mathbf{{p}}}$ is the tunneling matrix element, which describes the transition probability for the electron from the state $\mathbf{{p}}$ (in the right side of the barrier) to a state $\mathbf{{k}}$ (in the left side of the barrier). We will calculate the total tunneling current through the BLG/I/BLG junction by considering the rate of change of the total electron density in the top layer in the right BLG system.

$$\begin{aligned} I(V,T,t)=-e\langle \dot{N}^{\ell =2}_{R}(t)\rangle , \end{aligned}$$

(8)

where $\langle \dot{N}^{\ell =2}_{R}(t)\rangle$ is the expectation value of the rate of change of the electron number operator ${N}^{\ell =2}_{R}$ in the top right layer of the heterojunction, i.e.,

$$\begin{aligned} {N}^{\ell =2}_{R}(t)=\sum _{\mathbf{{k}},\sigma }\left( \tilde{c}^{\dag }_{\mathbf{{k}},\sigma }(t)\tilde{c}_{\mathbf{{k}},\sigma }(t)+\tilde{d}^{\dag }_{\mathbf{{k}},\sigma }(t)\tilde{d}_{\mathbf{{k}},\sigma }(t)\right) . \end{aligned}$$

(9)

Indeed, we have considered here the change of the electron number operator in the top right layer of the heterojunction, because of the AB stacking order in the right BLG. The local excitons are created between the electrons, at the sites $\tilde{A}$ in the top right layer, and the holes, at the sites B in the bottom layer (or similarly between the sites $\tilde{C}$ and D in the right BLG system). There are no excitons between the electrons at the sites $\tilde{B}$ ($\tilde{D}$) in the top layer and the holes at the sites A (D) in the bottom layer of the left (right) BLG. Thus, considering the zig-zag outermost sites as the sites which are close to the junction contacts with the insulating barrier, the tunneling of the electrons is coming only from the top layer of the right BLG system. Another equivalent geometry for the local excitons in the right BLG is also possible when the electrons at the sites D in the right bottom layer $\ell =1$ are coupled with the holes at the sites $\tilde{C}$ in the top layer $\ell =2$. In this case, we should consider the rate of change of the electron number operator $N^{\ell =1}_{R}(t)$ in the right bottom layer. Those two descriptions are equivalent. We can consider also the tunneling current coming from the rate of change of the hole number operator in the right bottom layer, but, in fact, this contribution is exactly the same as that given by Eq. (8) except the sign in the right-hand side. The sign changing occurs because of the hole type of particles in the right bottom layer. Thus, the rate of total current between the layers will be twice as higher as the tunneling current given in Eq. (8) above. Let us mention also that the consideration of both the electron and hole particle number operator changes in the right BLG has nothing to do with the true excitonic tunneling process, and it defines only the amplitudes of the normal single-particle and excitonic tunneling currents. In reality, the only electron tunneling from the right top layer is sufficient to consider the single-particle and excitonic tunnelings through the junction because the electron-hole recombination times is much large than the single-particle tunneling time $\tau _\mathrm{rec}>>\tau _{T}$ (Here $\tau _{T}$ is the single-particle tunneling time.) The electron tunneling time is of order of $\tau _{T}\sim 10^{-16}$ sec [72], while the time of the electron and hole recombination processes (Auger recombination time for Coulomb scattering) in graphene is of order of $\tau _\mathrm{rec}\sim 1.1 \times 10^{-12}$$\mathrm{sec}$ for electron-hole densities smaller than $10^{12} \mathrm{cm}^{-2}$ [73]. In order to not double counting the single-particle and excitonic tunneling effects, we have not considered the rate of change of the left bottom electron number operator $N^{\ell =1}_{L}(t)=\sum _{\mathbf{{k}},\sigma }(a^{\dag }_{\mathbf{{k}},\sigma }a_{\mathbf{{k}},\sigma }+b^{\dag }_{\mathbf{{k}},\sigma }b_{\mathbf{{k}},\sigma })$. Thus, as a result, we have the single exciton tunneling through the tunnel junction, from left to right. The expectation value $\langle \dot{N}_{R}\rangle$ is given by $\langle \dot{N}_{R}\rangle =Tr(e^{-\beta {H}}\dot{N}_{R})/Tr(e^{-\beta {H}})$, where $\beta =1/k_{B}T$, and H is the total Hamiltonian of the system H. The Heisenberg equation of motion for ${N}^{\ell =2}_{R}$ is

$$\begin{aligned} i\hbar \frac{\mathrm{d}{N}^{\ell =2}_{R}(t)}{\mathrm{d}t}=\left[ {N}^{\ell =2}_{R}(t),H(t)\right] _{-}=\left[ {N}^{\ell =2}_{R}(t),H_{T}(t)\right] _{-}. \end{aligned}$$

(10)

The notation $[\ldots ]_{-}$ refers to the usual Bose-type commutation rule. A very simple calculation shows that

$$\begin{aligned} I(V,T,t)=\frac{2e}{\hbar }\mathfrak {I}\left[ \sum _{\mathbf{{k}},\mathbf{{p}}}\sum _{\sigma }t_{\mathbf{{k}},\mathbf{{p}}}\left\langle \tilde{a}^{\dag }_{\mathbf{{k}},\sigma }(t)\tilde{c}_{\mathbf{{p}},\sigma }(t)+\tilde{b}^{\dag }_{\mathbf{{k}},\sigma }(t)\tilde{d}_{\mathbf{{p}},\sigma }(t)\right\rangle \right] . \end{aligned}$$

(11)

Furthermore, we apply the Rickayzen [74] transformation for the creation and destruction operators in the left-BLG system. Due to the shift of the Fermi levels $\bar{\mu }_{L}-\bar{\mu }_{R}=-eV$ (the similar shit takes the place between the chemical potentials in the usual superconducting Josephson junctions and in the case of the one layer graphene junction arrays, which is not discussed here), the electrons in the left side of the junction gain the additional energy, driven by the external potential and the unperturbed Hamiltonian of the left BLG is given, in this case, as $H_{L}(V)=H_{L}(0)-eVN_{L}$. Here, $N_{L}$ is the total electron density operator in the left BLG: $N_{L}=\sum _{\ell =1,2}N^{\ell }_{L}$. The equations of motion for the electron in the left BLG at $V=0$ will be written as

$$\begin{aligned} i\hbar \frac{d}{\mathrm{d}t}X^{\ell }_{\mathbf{{k}},\sigma }(t)=\left[ X^{\ell }_{\mathbf{{k}},\sigma }(t),H_{L}(0)\right] , \end{aligned}$$

(12)

while, for the case $V\ne 0$, we have

$$\begin{aligned} i\hbar \frac{d}{\mathrm{d}t}\hat{X}^{\ell }_{\mathbf{{k}},\sigma }(t)= & {} \left[ \hat{X}^{\ell }_{\mathbf{{k}},\sigma }(t),H_{L}(V)\right] \nonumber \\= & {} \left[ \hat{X}^{\ell }_{\mathbf{{k}},\sigma }(t),H_{L}(0)\right] +eV\hat{X}^{\ell }_{\mathbf{{k}},\sigma }(t), \end{aligned}$$

(13)

where $\hat{X}^{\ell =2}_{\mathbf{{k}},\sigma }(t)$ and $\hat{X}^{\ell =1}_{\mathbf{{k}},\sigma }(t)$ are the electron destruction operators in the left top and left bottom layers in the left BLG, in the case $V\ne 0$. Here, we have used the anticommutation relation between the fermionic operators given in Eq. (3). Furthermore, we obtain the Rickayzen transformation for the fermionic operators in the left top and left bottom layer of the left BLG

$$\begin{aligned} \hat{X}^{\ell =2}_{\mathbf{{k}},\sigma }(t)= & {} X^{\ell =2}_{\mathbf{{k}},\sigma }(t)e^{i\frac{\Delta {\Phi }_\mathrm{Upper}(t)}{2}}, \nonumber \\ \hat{X}^{\ell =1}_{\mathbf{{k}},\sigma }(t)= & {} X^{\ell =1}_{\mathbf{{k}},\sigma }(t)e^{i\frac{\Delta {\Phi }_\mathrm{Lower}(t)}{2}}. \end{aligned}$$

(14)

We can suppose that the phase differences across the junction, between the upper and lower layers in the BLGs, evolve with voltage according to the relations known in the usual Josephson junctions theory [75], and a good reason for this is related to the fact that the total ground state energy of the separate non-interacting graphene layer equals exactly twice of the chemical potential in the layer $E_{\ell }=2|{\mu }_{\ell }|$ with $\ell =L,R$ [76], which is the case of the usual superconductors according to the Gorkov’s derivations of the energy spectrum of superconductors in the microscopic theory [77]. Therefore, for the phases in Eq. (14) we have the following relations

$$\begin{aligned} \frac{d\Delta {\Phi }_\mathrm{Upper}(t)}{\mathrm{d}t}= & {} \frac{2eV(t)}{\hbar }, \nonumber \\ \frac{d\Delta {\Phi }_\mathrm{Lower}(t)}{\mathrm{d}t}= & {} -\frac{2eV(t)}{\hbar }, \end{aligned}$$

(15)

where $V(t)=(V_{L}(t)-V_{R}(t))/2$. Then after integration in both sides in Eq. (15), from zero to t, we obtain $\Delta {\Phi }_\mathrm{Upper}(t)$ and $\Delta {\Phi }_\mathrm{Lower}(t)$. Furthermore, we will define the time-dependent phase difference parameter ${\Delta \varphi }(t)$ as

$$\begin{aligned} {\Delta \varphi }(t)=\frac{2e}{\hbar }\int ^{t}_{0}\mathrm{d}t'V(t'), \end{aligned}$$

(16)

Next, we will consider the tunneling matrix term $H_{T}$ as the small perturbation turned on adiabatically from $t=-\,\infty$ and which determines the time evolution of the eigenstates in the Heisenberg picture. Therefore, in the first order in $H_{T}$, we have

$$\begin{aligned} I(V,T,t)= & {} \frac{2e}{\hbar }\mathfrak {I}\left[ \left( -\frac{i}{\hbar }\right) \int ^{t}_{-\infty }\mathrm{d}\tau e^{\eta \tau }\right. \nonumber \\&\left. \left\langle \left[ A^{\dag }(t)e^{-i\frac{{\Delta \varphi }(t)}{2}},H_{T}(\tau )\right] _{-}\right\rangle _{H'_{0}}+\left\langle \left[ C^{\dag }(t)e^{-i\frac{{\Delta \varphi }(t)}{2}},H_{T}(\tau )\right] _{-}\right\rangle _{H'_{0}}\right] .\nonumber \\ \end{aligned}$$

(17)

The infinitesimal, positive constant $\eta =0^{+}$ has been introduced in the integral in Eq. (17) in order to assure the convergence of the integral. Here, the averages over the commutators are referred to the unperturbed Hamiltonian $H'_{0}=H_{0}+H_\mathrm{int}$. The time-dependent operators $A^{\dag }(t)$ and $C^{\dag }(t)$ in Eq. (17) have been introduced with respect to the reformulation of the tunneling Hamiltonian in Eq. (7) in terms of the composite tunnel-operators A(t), B(t), C(t) and D(t). Namely, we write

$$\begin{aligned} H_{T}=\left[ A^{\dag }(t)+C^{\dag }(t)+B(t)+D(t)\right] e^{-i\frac{\Delta \varphi (t)}{2}}+h.c., \end{aligned}$$

(18)

where

$$\begin{aligned} A(t)= & {} \sum _{\mathbf{{k}},\mathbf{{p}}}\sum _{\sigma }t^{*}_{\mathbf{{k}},\mathbf{{p}}}\tilde{c}^{\dag }_{\mathbf{{p}},\sigma }(t)\tilde{a}_{\mathbf{{k}},\sigma }(t), \nonumber \\ B(t)= & {} \sum _{\mathbf{{k}},\mathbf{{p}}}\sum _{\sigma }t^{*}_{\mathbf{{k}},\mathbf{{p}}}{d}^{\dag }_{\mathbf{{p}},\sigma }(t){b}_{\mathbf{{k}},\sigma }(t), \nonumber \\ C(t)= & {} \sum _{\mathbf{{k}},\mathbf{{p}}}\sum _{\sigma }t^{*}_{\mathbf{{k}},\mathbf{{p}}}\tilde{d}^{\dag }_{\mathbf{{p}},\sigma }(t)\tilde{b}_{\mathbf{{k}},\sigma }(t), \nonumber \\ D(t)= & {} \sum _{\mathbf{{k}},\mathbf{{p}}}\sum _{\sigma }t^{*}_{\mathbf{{k}},\mathbf{{p}}}{c}^{\dag }_{\mathbf{{p}},\sigma }(t){a}_{\mathbf{{k}},\sigma }(t). \end{aligned}$$

(19)

It is important to note that the phase factor in Eqs. (17) and (18) appears after the Rickayzen transformations, given in Eq. (14), above.

2.3 The Normal Quasiparticle and Excitonic Tunneling

Next, we calculate the commutators in Eq. (17) and we perform the statistical averaging of four-point correlation functions using the Wick’s theorem at the finite temperatures [71]. After the whole averaging procedure, we keep only terms responsible for the normal and excitonic currents in the junction. We obtain for the total tunneling current the following expression

$$\begin{aligned} I(V,T,t)= & {} \frac{2e}{\hbar }\mathfrak {I}\left[ \left( -\frac{i}{\hbar }\right) \int ^{t}_{-\infty }\mathrm{d}\tau e^{\eta \tau }\left( \left\langle \left[ A^{\dag }(t),A(\tau )\right] _{-}\right\rangle _{H'_{0}}+\left\langle \left[ C^{\dag }(t),C(\tau )\right] _{-}\right\rangle _{H'_{0}}\right) e^{i\frac{\Delta {\varphi }(t)-\Delta {\varphi }(\tau )}{2}}\right. \nonumber \\&\left. +\,e^{\eta \tau }\left\langle \left[ B^{\dag }(t),A(\tau )\right] _{-}\right\rangle _{H'_{0}}e^{i\frac{\Delta {\varphi }(t)+\Delta {\varphi }(\tau )}{2}}e^{i\left( \varphi _{L}-\varphi _{R}\right) } \right] , \end{aligned}$$

(20)

where the first term, in the sum in the right-hand side in Eq. (20), gives the normal single-particle tunneling current and the second term in Eq. (20) is responsible for the excitonic tunneling. Concerning the excitonic part, we have neglected the term containing the average of type $\langle \left[ A^{\dag }(t),B(\tau )\right] _{-}\rangle _{H'_{0}}$. This is because the AB-stacked geometry of the BLG structures and the convention that the current (included the excitonic one) is passing from left to right in the junction. We have neglected also all terms in which the following averages appear: $\langle \left[ A^{\dag }(t),B^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$, $\langle \left[ A^{\dag }(t),A^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$, $\langle \left[ B^{\dag }(t),A^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$, $\langle \left[ B^{\dag }(t),B^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$, $\langle \left[ C^{\dag }(t),A^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$, $\langle \big [C^{\dag }(t),B^{\dag }(\tau )\big ]_{-}\rangle _{H'_{0}}$, $\langle \left[ D^{\dag }(t),A^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$ and $\langle \left[ D^{\dag }(t),B^{\dag }(\tau )\right] _{-}\rangle _{H'_{0}}$. Indeed, these mentioned averages are zero because of the symmetry of the Hamiltonian $H'_{0}$ and the structure of the Nambu spinors in Eq. (6). The phase factor $e^{i\left( \varphi _{L}-\varphi _{R}\right) }$, in the last term in Eq. (20), is related to the broken symmetry states in the BLG systems in both sides of the junction and which is the consequence of the excitonic pair formation in the system. We have shown previously [56, 57] that the individual BLG system undergoes the excitonic condensation phase transition when modulating the interlayer interaction parameter $W_{\ell }$. In this case, the macroscopic phase coherent state of the excitonic condensate appears in the BLG. Moreover, we showed that in the weak interaction limit, the pair formation in the BLG is BCS-like and a BCS-BEC crossover occurs when augmenting the interlayer interaction parameter. Therefore, as in the case of the usual superconducting junction array [78, 79], here also we have the symmetry broken state here related to the local gauge invariance of the complex excitonic order parameter $\Delta _{\ell }=|\Delta _{\ell }|e^{i\varphi _{\ell }}$. The phase of the order parameter $\varphi _{\ell }$ cannot be changed arbitrarily because of the presence of the macroscopic excitonic condensate state in each side of the junction. Indeed, the measurable physical quantities in the BLG/I/BLG junction arrays depend only on the difference $\Delta {\varphi }_{0}=\varphi _{L}-\varphi _{R}$ between the phases of the coherent condensate states in different sides of the junction. Furthermore, we can write Eq. (20) in the form

$$\begin{aligned} I(V,T,t)= & {} -\frac{e|t|^{2}}{\pi ^{2}{\hbar ^{2}}}\mathfrak {I}\left[ e^{i\frac{\Delta {\varphi (t)}}{2}} \int ^{\infty }_{-\infty }\mathrm{d}t' e^{\eta (t-t')}\right. \nonumber \\&\times \left( e^{-i\frac{\Delta {\varphi (t-t')}}{2}}N(t') \left. +e^{i\frac{\Delta {\varphi (t-t')}}{2}}F(t')e^{i{\Delta \varphi }_{0}}\right) \right] . \end{aligned}$$

(21)

Here, we have performed a change of variable of integration $t'=t-\tau$ and we have introduced the time-dependent functions N(t) and F(t) for the normal and excitonic counterparts, which are defined with the help of the Kadanoff–Baym Green’s functions [80]. For the normal function N(t), we have

$$\begin{aligned} N(t)= & {} i\Theta (t)\sum _{\mathbf{{k}}}\int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }\mathrm{d}\omega {\mathrm{d}\omega '}e^{i(\omega -\omega ')t'} \nonumber \\&\times \left[ A^{L}_{\tilde{a}}(\mathbf{{k}},\omega )A^{R}_{\tilde{c}}(\mathbf{{k}},\omega ')+A^{L}_{\tilde{b}}(\mathbf{{k}},\omega )A^{R}_{\tilde{d}}(\mathbf{{k}},\omega ')\right] \nonumber \\&\times \left[ n^{L}_{F}(\omega )-n^{R}_{F}(\omega ')\right] \end{aligned}$$

(22)

and for the excitonic function F(t), we get

$$\begin{aligned} F(t)= & {} i\Theta (t)\sum _{\mathbf{{k}}}\int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }\mathrm{d}\omega {\mathrm{d}\omega '}e^{i(\omega -\omega ')t'} \nonumber \\&\times A^{L}_{\tilde{a}b}(\mathbf{{k}},\omega )A^{R}_{\tilde{c}d}(\mathbf{{k}},\omega ')\left[ n^{L}_{F}(\omega )-n^{R}_{F}(\omega ')\right] . \end{aligned}$$

(23)

Th function $n^{\ell }_{F}(\omega )=1/(e^{\beta {\omega }}+1)$ ($\ell =L,R$) in Eqs. (22) and (23) is the Fermi–Dirac distribution function. We have performed the Fourier transformation of the Kadanoff’s Green’s functions [80] in order to obtain the expressions of N(t) and F(t), given in Eqs. (22) and (23), and, also, we have introduced the single-particle spectral functions $A^{\ell }_{X_{\ell }}(\mathbf{{k}},\omega )$ ($X=\tilde{a}, \tilde{b}$ for $\ell =L$ and $X=\tilde{c}, \tilde{d}$ for $\ell =R$) and excitonic spectral functions $A^{L}_{\tilde{a}b}(\mathbf{{k}},\omega )$, $A^{R}_{\tilde{c}d}(\mathbf{{k}},\omega )$. We have supposed in Eqs. (22) and (23) a simple form of the tunneling probability $t_{\mathbf{{k}},\mathbf{{p}}}=\delta _{\mathbf{{k}},\mathbf{{p}}}t$. For a simple treatment, this approximation is sufficient to consider the excitonic effects.

The normal and anomalous (or excitonic) spectral functions in the separate BLGs with the presence of the excitonic pairing interaction have been discussed by us in Ref.[56, 57], where the full four-band theory has been developed without low-energy assumption near the K-point in the Brillouin zone. From the form of the total fermionic action, derived there, it follows that the normal spectral functions in different layers in the left BLG are interconnected:

$$\begin{aligned} A^{L}_{\tilde{a}}(\mathbf{{k}},\omega )= & {} A^{L}_{b}(\mathbf{{k}},\omega ), \nonumber \\ A^{L}_{\tilde{b}}(\mathbf{{k}},\omega )= & {} A^{L}_{a}(\mathbf{{k}},\omega ). \end{aligned}$$

(24)

The same is true also for the right-BLG system. Moreover, the explicit analytical expressions of the normal spectral functions in the bottom layer of the left BLG are [56, 57]

$$\begin{aligned} A^{L}_{a}(\mathbf{{k}},\omega )= & {} \sum _{i=1,\ldots ,4}\alpha ^{L}_{i\mathbf{{k}}}\delta (\omega +\kappa ^{L}_{i\mathbf{{k}}}), \nonumber \\ A^{L}_{b}(\mathbf{{k}},\omega )= & {} \sum _{i=1,\ldots ,4}\beta ^{L}_{i\mathbf{{k}}}\delta (\omega +\kappa ^{L}_{i\mathbf{{k}}}) \end{aligned}$$

(25)

and the similar expressions can be written for the right-BLG structure $\ell =R$. The spectral functions in the upper layers in both BLGs could be obtained after the relations in Eq. (24). The dimensionless coefficients $\alpha ^{\ell }_{i{\mathbf{{k}}}}$, in Eq. (25) with $i=1,\ldots ,4$ and $\ell =L,R$, are given as

$$\begin{aligned} \alpha ^{\ell }_{i{\mathbf{{k}}}} =(-1)^{i+1} \left\{ \begin{array}{ll} \prod ^{}_{j=3,4}\frac{\mathcal{{P}}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})}{\left( \kappa ^{\ell }_{1\mathbf{{k}}}-\kappa ^{\ell }_{2\mathbf{{k}}}\right) }\frac{1}{\left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{j\mathbf{{k}}}\right) },&{} \quad \hbox {if} \quad i=1,2,\\ \prod ^{}_{j=1,2}\frac{\mathcal{{P}}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})}{\left( \kappa ^{\ell }_{3\mathbf{{k}}}-\kappa ^{\ell }_{4\mathbf{{k}}}\right) }\frac{1}{\left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{j\mathbf{{k}}}\right) },&{} \quad \hbox {if} \quad i=3,4, \end{array}\right. \end{aligned}$$

(26)

where $\mathcal{{P}}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})$ is the polynomial of third order in $\kappa ^{\ell }_{i\mathbf{{k}}}$, namely we have

$$\begin{aligned} \mathcal{{P}}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})=(\kappa ^{\ell }_{i\mathbf{{k}}})^{3}+\omega _{1\mathbf{{k}}}(\kappa ^{\ell }_{i\mathbf{{k}}})^{2}+\omega _{2\mathbf{{k}}}\kappa ^{\ell }_{i\mathbf{{k}}}+\omega _{3\mathbf {k}} \end{aligned}$$

(27)

with the coefficients $\omega _{i\mathbf{{k}}}$, $i=1,\ldots ,3$, given as

$$\begin{aligned} \omega ^{\ell }_{1\mathbf{{k}}}= & {} -2\mu ^{\ell }_{2\mathrm eff}-\mu ^{\ell }_{1\mathrm eff}, \nonumber \\ \omega ^{\ell }_{2\mathbf{{k}}}= & {} \mu ^{\ell }_{1\mathrm eff}\left( \mu ^{\ell }_{2\mathrm eff}+2\mu ^{\ell }_{1\mathrm eff}\right) -|\tilde{\gamma }_{\mathbf{{k}}}|^{2}-|\Delta _{\ell }|^{2}, \nonumber \\ \omega ^{\ell }_{3\mathbf{{k}}}= & {} -\mu ^{\ell }_{1\mathrm eff}\left( \mu ^{\ell }_{2\mathrm eff}\right) ^{2}+\mu ^{\ell }_{1\mathrm eff}|\Delta _{\ell }|^{2}+\mu ^{\ell }_{2\mathrm eff}|\tilde{\gamma }_{\mathbf{{k}}}|^{2}. \end{aligned}$$

(28)

The effective chemical potentials $\mu ^{\ell }_{1\mathrm eff}$ and $\mu ^{\ell }_{2\mathrm eff}$ are defined here as a function of the intralayer $U_{\ell }$ and interlayer $W_{\ell }$ (with $\ell =L,R$) Coulomb interaction parameters as

$$\begin{aligned} \mu ^{\ell }_{1\mathrm eff}= & {} \mu _{\ell }+\frac{U_{\ell }}{4}, \nonumber \\ \mu ^{\ell }_{2\mathrm eff}= & {} \mu _{\ell }+\frac{U_{\ell }}{4}+W_{\ell }. \end{aligned}$$

(29)

The energy dispersion parameters $\kappa ^{\ell }_{i\mathbf{{k}}}$ in Eqs. (25) and (26), define the band structures of the interacting BLGs in both sides of the tunnel junction [56, 57]. We have

$$\begin{aligned} \kappa ^{\ell }_{1,2\mathbf{{k}}}= & {} -\frac{1}{2}\left[ \Delta _{\ell }+\gamma _{1}\pm \sqrt{\left( W_{\ell }-\Delta _{\ell }-\gamma _{1}\right) ^{2}+4|\tilde{\gamma }_{\mathbf{{k}}}|^{2}}\right] +\bar{\mu }_{\ell }, \nonumber \\ \kappa ^{\ell }_{3,4\mathbf{{k}}}= & {} -\frac{1}{2}\left[ -\Delta _{\ell }-\gamma _{1}\pm \sqrt{\left( W_{\ell }+\Delta _{\ell }+\gamma _{1}\right) ^{2}+4|\tilde{\gamma }_{\mathbf{{k}}}|^{2}}\right] +\bar{\mu }_{\ell }, \end{aligned}$$

(30)

The parameters $\beta ^{\ell }_{i\mathbf{{k}}}$ are given as

$$\begin{aligned} \beta ^{\ell }_{i\mathbf{{k}}} =(-1)^{i+1} \left\{ \begin{array}{ll} \prod ^{}_{j=3,4}\frac{\mathcal{{P}'}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})}{\left( \kappa ^{\ell }_{1\mathbf{{k}}}-\kappa ^{\ell }_{2\mathbf{{k}}}\right) }\frac{1}{\left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{j\mathbf{{k}}}\right) },&{} \quad \hbox {if} \quad i=1,2,\\ \prod ^{}_{j=1,2}\frac{\mathcal{{P}'}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})}{\left( \kappa ^{\ell }_{3\mathbf{{k}}}-\kappa ^{\ell }_{4\mathbf{{k}}}\right) }\frac{1}{\left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{j\mathbf{{k}}}\right) },&{} \quad \hbox {if} \quad i=3,4, \end{array}\right. \end{aligned}$$

(31)

where $\mathcal{{P}'}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})$ is the polynomial of third order in $\kappa ^{\ell }_{i\mathbf{{k}}}$, namely we have

$$\begin{aligned} {\mathcal {P}'}^{(3)}(\kappa ^{\ell }_{i\mathbf{{k}}})=(\kappa ^{\ell }_{i\mathbf{{k}}})^{3}+\omega '_{1\mathbf{{k}}}(\kappa ^{\ell }_{i\mathbf{{k}}})^{2}+\omega '_{2\mathbf{{k}}}\kappa ^{\ell }_{i\mathbf{{k}}}+\omega '_{3\mathbf {k}} \end{aligned}$$

(32)

with the coefficients $\omega '^{\ell }_{i\mathbf{{k}}}$, $i=1,\ldots ,3$, given as

$$\begin{aligned}&\omega '^{\ell }_{1\mathbf{{k}}} =-2\mu ^{\ell }_{1\mathrm eff}-\mu ^{\ell }_{2\mathrm eff}, \nonumber \\&\omega '^{\ell }_{2\mathbf{{k}}} =\mu ^{\ell }_{1\mathrm eff}\left( \mu ^{\ell }_{1\mathrm eff}+2\mu ^{\ell }_{2\mathrm eff}\right) -|\tilde{\gamma }_{\mathbf{{k}}}|^{2}, \nonumber \\&\omega '^{\ell }_{3\mathbf{{k}}} =-\mu ^{\ell }_{2\mathrm eff}\left( \mu ^{\ell }_{1\mathrm eff}\right) ^{2}+\mu ^{\ell }_{1\mathrm eff}|\tilde{\gamma }_{\mathbf{{k}}}|^{2}. \end{aligned}$$

(33)

As we have mentioned above, the intralayer and interlayer hopping parameters are supposed the same in both sides of the junction. It is particularly important to underline here the role of the bare chemical potentials $\bar{\mu }_{\ell }$ appearing in the expressions of the band structure parameters in Eq. (30). Indeed, they are playing the role of the exact Fermi energies in the BLG structures as it was pointed out in Ref. [56, 57]. For the anomalous (or excitonic) spectral functions in Eq. (23), we have [56, 57]

$$\begin{aligned} A^{L}_{\tilde{a}b}(\mathbf{{k}},\omega )= & {} (\gamma _1+\Delta _{L})\sum _{i=1,\ldots ,4}\gamma ^{L}_{i\mathbf{{k}}}\delta (\omega +\kappa ^{L}_{i\mathbf{{k}}}), \nonumber \\ A^{R}_{\tilde{c}d}(\mathbf{{k}},\omega )= & {} (\gamma _1+\Delta _{R})\sum _{i=1,\ldots ,4}\gamma ^{R}_{i\mathbf{{k}}}\delta (\omega +\kappa ^{R}_{i\mathbf{{k}}}), \end{aligned}$$

(34)

and the parameters $\gamma ^{\ell }_{i\mathbf{{k}}}$ are given as

$$\begin{aligned} \gamma ^{\ell }_{i{\mathbf{{k}}}}= \left\{ \begin{array}{ll} \frac{(-1)^{i}\left( \mu ^{\ell }_\mathrm{eff1} +\kappa ^{\ell }_{i\mathbf{{k}}}\right) ^{2}}{\left( \kappa ^{\ell }_{1\mathbf{{k}}}-\kappa ^{\ell }_{2\mathbf{{k}}}\right) \left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{3\mathbf{{k}}}\right) \left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{4\mathbf{{k}}}\right) },&{} \quad \hbox {if} \quad i=1,2, \\ \frac{(-1)^{i}\left( \mu ^\mathrm{eff}_{1}+\kappa ^{\ell }_{i\mathbf{{k}}}\right) ^{2}}{\left( \kappa ^{\ell }_{3\mathbf{{k}}}-\kappa ^{\ell }_{4\mathbf{{k}}}\right) \left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{1\mathbf{{k}}}\right) \left( \kappa ^{\ell }_{i\mathbf{{k}}}-\kappa ^{\ell }_{2\mathbf{{k}}}\right) },&{} \quad \hbox {if} \quad i=3,4 . \end{array}\right. \end{aligned}$$

(35)

Furthermore, the normal and excitonic tunneling currents can be simply expressed analytically after the Werthamer spectral decomposition [81] and by supposing simultaneously the case of the constant gate voltage, i.e., $V(t)=V=\text {const}$. We have

$$\begin{aligned} e^{i\frac{{\Delta \varphi }(t)}{2}}=\int ^{\infty }_{-\infty }\frac{\mathrm{d}E}{2\pi }W^{*}(E)e^{iEt}, \end{aligned}$$

(36)

and

$$\begin{aligned} W(E)=W^{*}(E)=2\pi \delta \left( E-\frac{e}{\hbar }V\right) . \end{aligned}$$

(37)

Here, we have used the definition of the phase difference function in Eq. (16). The total tunneling current through the tunnel junction will be

$$\begin{aligned} I(V,T,t)= & {} I_{n}(V,T)+I_\mathrm{Exc}(V,T,t) \nonumber \\= & {} \mathfrak {I}\left( N(i\eta +\omega _0)\right) +\mathfrak {I}\left[ e^{i(\Delta \varphi _{0}+2\omega _{0}t)}F(i\eta -\omega _{0})\right] \nonumber \\= & {} I_\mathrm{qp}(V,T)+I_\mathrm{J_{1}}(V,T)\sin (\Delta \varphi _{0}+2\omega _{0}t) \nonumber \\&+\,I_\mathrm{J_{2}}(V,T)\cos (\Delta \varphi _{0}+2\omega _{0}t), \end{aligned}$$

(38)

where $\omega _0$ is the field frequency: $\omega _{0}=\frac{e}{\hbar }V$, and the normal tunneling is equivalent to the single-particle tunneling term $I_{n}(V,T)=\mathfrak {I}(N(i\eta +\omega _0))$, while the coherent Josephson tunneling of excitons is given by the last two terms in Eq. (38). Thus, the total excitonic tunneling current is

$$\begin{aligned} I_\mathrm{Exc}(V,T,t)= & {} I_\mathrm{J_{1}}(V,T)\sin (\Delta \varphi _{0}+2\omega _{0}t) \nonumber \\&+\,I_\mathrm{J_{2}}(V,T)\cos (\Delta \varphi _{0}+2\omega _{0}t), \end{aligned}$$

(39)

and we have $I_\mathrm{J_{1}}(V,T)=\mathfrak {R}(F(i\eta -\omega _{0}))$ and $I_\mathrm{J_{2}}(V,T)=\mathfrak {I}(F(i\eta -\omega _{0}))$.

Finally, after some calculations, we get for the normal tunneling current the following expression

$$\begin{aligned} I_{n}(V,T)= & {} -\frac{e|t|^{2}}{\pi \hbar ^{2}}\left\{ \Theta _\mathrm{T}\left( \Delta _{\omega _{0}},a_{1},b_{1}\right) \sum _{i=1,2}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{1}(x_{i})\alpha ^{R}_{2}(x_{i})+\beta ^{L}_{1}(x_{i})\beta ^{R}_{2}(x_{i})}{|f(x_{i},a_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{1}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{1}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( \Delta '_{\omega _{0}},c_{1},b_{1}\right) \sum _{i=3,4}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{1}(x_{i})\alpha ^{R}_{4}(x_{i})+\beta ^{L}_{1}(x_{i})\beta ^{R}_{4}(x_{i})}{|f(x_{i},c_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{1}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{1}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( -\Delta _{\omega _{0}},a_{1},b_{1}\right) \sum _{i=1,2}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{2}(x_{i})\alpha ^{R}_{1}(x_{i})+\beta ^{L}_{2}(x_{i})\beta ^{R}_{1}(x_{i})}{|f(x_{i},a_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{2}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{2}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( -\Delta '_{\omega _{0}},c_{1},b_{1}\right) \sum _{i=3,4}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{2}(x_{i})\alpha ^{R}_{3}(x_{i})+\beta ^{L}_{2}(x_{i})\beta ^{R}_{3}(x_{i})}{|f(x_{i},c_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{2}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{2}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( \tilde{\Delta }'_{\omega _{0}},a_{1},d_{1}\right) \sum _{i=5,6}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{3}(x_{i})\alpha ^{R}_{2}(x_{i})+\beta ^{L}_{3}(x_{i})\beta ^{R}_{2}(x_{i})}{|f(x_{i},a_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{3}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{3}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( \tilde{\Delta }_{\omega _{0}},c_{1},d_{1}\right) \sum _{i=7,8}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{3}(x_{i})\alpha ^{R}_{4}(x_{i})+\beta ^{L}_{3}(x_{i})\beta ^{R}_{4}(x_{i})}{|f(x_{i},c_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{3}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{3}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( -\tilde{\Delta }'_{\omega _{0}},a_{1},d_{1}\right) \sum _{i=5,6}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{4}(x_{i})\alpha ^{R}_{1}(x_{i})+\beta ^{L}_{4}(x_{i})\beta ^{R}_{1}(x_{i})}{|f(x_{i},a_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{4}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{4}(x_{i})+\omega _{0}\right) \right) \right] \right. \nonumber \\&\quad \left. +\Theta _\mathrm{T}\left( -\tilde{\Delta }_{\omega _{0}},c_{1},d_{1}\right) \sum _{i=7,8}\right. \nonumber \\&\left. \left[ \rho (x_{i})\frac{\alpha ^{L}_{4}(x_{i})\alpha ^{R}_{3}(x_{i})+\beta ^{L}_{4}(x_{i})\beta ^{R}_{3}(x_{i})}{|f(x_{i},c_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{4}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{4}(x_{i})+\omega _{0}\right) \right) \right] \right\} . \nonumber \\ \end{aligned}$$

(40)

Here, we have introduced a product-$\Theta$ function $\Theta _{T}(x,y,z)$, in the following way

$$\begin{aligned}&\Theta _{T}(x,y,z)=\theta (x)\theta (x^{2}-y^{2}-z^{2})\theta \left[ (x^{2}-y^{2}-z^{2})^{2}-4y^{2}z^{2}\right] \\ \nonumber&\theta (\sqrt{x^{4}+4y^{2}z^{2}}-y^{2}-z^{2}), \end{aligned}$$

(41)

where each multiplier, in the total product, is given as a single $\theta$-Heaviside step function. Furthermore, the interaction-dependent parameters $a_{1}, b_{1},c_{1}$ and $d_{1}$, in Eq. (40), are defined as

$$\begin{aligned} a_{1}= & {} W_{R}-\Delta _{R}-\gamma _{1}, \nonumber \\ b_{1}= & {} W_{L}-\Delta _{L}-\gamma _1, \nonumber \\ c_{1}= & {} W_{R}+\Delta _{R}+\gamma _{1}, \nonumber \\ d_{1}= & {} W_{L}+\Delta _{L}+\gamma _1. \end{aligned}$$

(42)

Next, the frequency-dependent parameters ${\Delta }_{\omega _{0}}, {\Delta }'_{\omega _{0}}, \tilde{\Delta }_{\omega _{0}}$ and $\tilde{\Delta }'_{\omega _{0}}$, introduced in Eq. (40), form a detuning matrix

$$\begin{aligned} \hat{\Delta }_{\omega }=\left( \begin{array}{ccrr} {\Delta }_{\omega _{0}} &{}\quad {\Delta }'_{\omega _{0}} \\ \tilde{\Delta }'_{\omega _{0}} &{}\quad \tilde{\Delta }_{\omega _{0}} \end{array} \right) , \end{aligned}$$

(43)

and for each component we have

$$\begin{aligned} {\Delta }_{\omega _{0}}= & {} 2(\omega _{0}-\omega '_0), \nonumber \\ \tilde{{\Delta }}_{\omega _{0}}= & {} 2(\omega _{0}-\tilde{\omega }'_0), \nonumber \\ {\Delta }'_{\omega _{0}}= & {} 2(\omega _{0}-\omega ''_0), \nonumber \\ \tilde{{\Delta }}'_{\omega _{0}}= & {} 2(\omega _{0}-\tilde{\omega }''_0), \end{aligned}$$

(44)

where the detuning frequencies $\omega '_0, \tilde{\omega }'_0, \omega ''_0$ and $\tilde{\omega }''_0$ depend explicitly on the difference between the Fermi energies in different sides of the tunnel junction. Namely, we get

$$\begin{aligned} \omega '_0= & {} \bar{{\mu }}_{R}-\bar{\mu }_{L}-\frac{1}{2}(\Delta _{R}-\Delta _{L}), \nonumber \\ \tilde{\omega }'_0= & {} \bar{{\mu }}_{R}-\bar{\mu }_{L}+\frac{1}{2}(\Delta _{R}-\Delta _{L}), \nonumber \\ \omega ''_0= & {} \bar{{\mu }}_{R}-\bar{\mu }_{L}+\frac{1}{2}(\Delta _{R}+\Delta _{L}+2\gamma _1), \nonumber \\ \tilde{\omega }''_0= & {} \bar{{\mu }}_{R}-\bar{\mu }_{L}-\frac{1}{2}(\Delta _{R}+\Delta _{L}+2\gamma _1). \end{aligned}$$

(45)

Next, eight parameters $x_{i}$ with $i=1,\ldots ,8$, have been introduced in Eq. (40), which are defined as

$$\begin{aligned} x_{1,2}= & {} \pm X({\Delta }_{\omega _{0}},a_{1},b_{1}), \nonumber \\ x_{3,4}= & {} \pm X( {\Delta }'_{\omega _{0}}, b_{1},c_{1}), \nonumber \\ x_{5,6}= & {} \pm X(\tilde{{\Delta }}'_{\omega _{0}}, a_{1},d_{1}), \nonumber \\ x_{7,8}= & {} \pm X(\tilde{{\Delta }}_{\omega _{0}}, c_{1},d_{1}) \end{aligned}$$

(46)

whereas the function X(x, y, z) is defined as $X(x,y,z)=(4\gamma _{0}|x|)^{-1}\sqrt{\left( x^{2}-y^{2}-z^{2}\right) ^{2}-4y^{2}z^{2}}$. The density of states (DOS) function $\rho (x)$ in Eq. (40) appears after transforming the $\mathbf{{k}}$-summation in Eq. (22) into the integration over the continuous variable, i.e., $\sum _{\mathbf {k}}\ldots =\int dx\rho (x)\ldots$. The DOS, in the non-interacting graphene layer, is defined as

$$\begin{aligned} \rho (x)=\sum _{\mathbf{{k}}}\delta (x-\gamma _{\mathbf{{k}}}), \end{aligned}$$

(47)

where $\gamma _{\mathbf{{k}}}$ is the band dispersion in the non-interacting single graphene sheet, i.e.,

$$\begin{aligned} \gamma _\mathbf{{k}}=e^{-ik_{x}d}+2\exp {i\frac{k_{x}d}{2}}\cos {\frac{\sqrt{3}}{2}k_{y}d}. \end{aligned}$$

(48)

The parameter d, in Eq. (48), refers to the carbon–carbon distance in the graphene layers. Beyond the Dirac’s approximation, the DOS can be analytically expressed [58, 82, 83] as

$$\begin{aligned} \rho (x)=\frac{2|x|}{\pi ^{2}|\gamma _{0}|^{2}} \left\{ \begin{array}{ll} \frac{1}{\sqrt{\Lambda \left( |{x}/{\gamma _0}|\right) }}{\mathbf {K}}\left[ \frac{4|x/\gamma _0|}{\Lambda \left( |{x}/{\gamma _0}|\right) }\right] ,&{} \quad 0<|x|<\gamma _0,\\ \frac{1}{\sqrt{4|{{x}/{\gamma _0}}|}}{\mathbf {K}}\left[ \frac{\Lambda \left( |x/\gamma _0|\right) }{4|{x}/{\gamma _0}|}\right] ,&{} \quad \gamma _0<|x|<3\gamma _0, \end{array}\right. \end{aligned}$$

(49)

where ${\mathbf {K}}(x)$ is the Elliptic integral of the first kind [84] ${\mathbf {K}}(x)=\int ^{\pi /2}_{0}dt/\sqrt{1-x^{2}\sin ^{2}t}$ . The function $\Lambda (x)$, in Eq. (49), is given by [82, 83]

$$\begin{aligned} \Lambda (x)=\left( 1+x\right) ^{2}-\frac{\left( x^{2}-1\right) ^{2}}{4}. \end{aligned}$$

(50)

Furthermore, the functions f(x, y, z) in the denominators in Eq. (40) read as:

$$\begin{aligned} f(x,y,z)=\frac{2x\gamma ^{2}_{0}}{\sqrt{y^{2}+4x^{2}\gamma ^{2}_{0}}}+\frac{2x\gamma ^{2}_{0}}{\sqrt{z^{2}+4x^{2}\gamma ^{2}_{0}}}. \end{aligned}$$

(51)

Concerning the excitonic part of the tunneling current, the Josephson current $I_{J_1}(V,T)$, in Eq. (39), is given as:

$$\begin{aligned} I_{J_1}(V,T)= & {} \frac{e}{\pi ^{2}\hbar ^{2}}\mathrm{P.V.}\sum _{\mathbf{{k}}}\int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty }\mathrm{d}\omega \mathrm{d}\omega '\times \nonumber \\&\times \frac{A^{L}_{\tilde{a}b}(\mathbf{{k}},\omega )A^{R}_{\tilde{c}d}(\mathbf{{k}},\omega ')}{\omega -\omega '-\omega _0}\left( n^{L}_{F}(\omega )-n^{R}_{F}(\omega ')\right) . \end{aligned}$$

(52)

Furthermore, we will calculate numerically the principal value $\mathrm{P.V.}$, in Eq. (52), by using the explicit expressions of the excitonic spectral functions, given in Eq. (34), above. For the Josephson current $I_{J_2}(V,T)$, we get

$$\begin{aligned} I_{J_2}(V,T)= & {} -\frac{e|t|^{2}}{\pi \hbar ^{2}}(\Delta _{L}+\gamma _1)(\Delta _{R}+\gamma _1)\sum _{\mathbf{{k}}}\sum _{i,j=1,\ldots ,4}\gamma ^{L}_{i\mathbf{{k}}}\gamma ^{R}_{j\mathbf{{k}}}\delta \nonumber \\&\left( -\kappa ^{L}_{i\mathbf{{k}}}+\kappa ^{R}_{j\mathbf{{k}}}-\omega _{0}\right) \left( n^{L}_{F}(-\kappa ^{L}_{i\mathbf{{k}}})-n^{R}_{F}(-\kappa ^{L}_{i\mathbf{{k}}}-\omega _{0})\right) . \end{aligned}$$

(53)

Again, transforming the summation over the wave vectors into the integration, we obtain for the Josephson current $I_{J_{2}}(V,T)$:

$$\begin{aligned} I_{J_{2}}(V,T)= & {} -\frac{e|t|^{2}}{\pi \hbar ^{2}}(\Delta _{L}+\gamma _1)(\Delta _{R}+\gamma _1)\times \nonumber \\&\times \left\{ \Theta _\mathrm{T}\left( \Delta _{\omega _{0}},a_{1},b_{1}\right) \right. \nonumber \\&\quad \left. \quad \sum _{i=1,2}\left[ \rho (x_{i})\frac{\gamma ^{L}_{1}(x_{i})\gamma ^{R}_{2}(x_{i})}{|f(x_{i},a_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{1}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{1}(x_{i})-\omega _{0}\right) \right) \right] \right. \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( \Delta '_{\omega _{0}},c_{1},b_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=3,4}\left[ \rho (x_{i})\frac{\gamma ^{L}_{1}(x_{i})\gamma ^{R}_{4}(x_{i})}{|f(x_{i},c_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{1}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{1}(x_{i})-\omega _{0}\right) \right) \right] \right. \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( -\Delta _{\omega _{0}},a_{1},b_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=1,2}\right. \left[ \rho (x_{i})\frac{\gamma ^{L}_{2}(x_{i})\gamma ^{R}_{1}(x_{i})}{|f(x_{i},a_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{2}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{2}(x_{i})-\omega _{0}\right) \right) \right] \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( -\Delta '_{\omega _{0}},c_{1},b_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=3,4}\left[ \rho (x_{i})\frac{\gamma ^{L}_{2}(x_{i})\gamma ^{R}_{3}(x_{i})}{|f(x_{i},c_{1},b_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{2}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{2}(x_{i})-\omega _{0}\right) \right) \right] \right. \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( \tilde{\Delta }'_{\omega _{0}},a_{1},d_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=5,6}\left[ \rho (x_{i})\frac{\gamma ^{L}_{3}(x_{i})\gamma ^{R}_{2}(x_{i})}{|f(x_{i},a_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{3}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{3}(x_{i})-\omega _{0}\right) \right) \right] \right. \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( \tilde{\Delta }_{\omega _{0}},c_{1},d_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=7,8}\left[ \rho (x_{i})\frac{\gamma ^{L}_{3}(x_{i})\gamma ^{R}_{4}(x_{i})}{|f(x_{i},c_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{3}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{3}(x_{i})-\omega _{0}\right) \right) \right] \right. \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( -\tilde{\Delta }'_{\omega _{0}},a_{1},d_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=5,6}\left[ \rho (x_{i})\frac{\gamma ^{L}_{4}(x_{i})\gamma ^{R}_{1}(x_{i})}{|f(x_{i},a_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{4}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{4}(x_{i})-\omega _{0}\right) \right) \right] \right. \nonumber \\&\left. +\,\Theta _\mathrm{T}\left( -\tilde{\Delta }_{\omega _{0}},c_{1},d_{1}\right) \right. \nonumber \\&\quad \left. \sum _{i=7,8}\left[ \rho (x_{i})\frac{\gamma ^{L}_{4}(x_{i})\gamma ^{R}_{3}(x_{i})}{|f(x_{i},c_{1},d_{1})|}\left( n^{L}_{F}\left( -\kappa ^{L}_{4}(x_{i})\right) -n^{R}_{F}\left( -\kappa ^{L}_{4}(x_{i})-\omega _{0}\right) \right) \right] \right\} .\nonumber \\ \end{aligned}$$

(54)

In the following section, we will analyze numerically the obtained expressions for the normal and excitonic tunneling currents in the system.

3 The Numerical Results and Discussions

3.1 The Normal Quasiparticle Tunneling

In Fig. 2, we have studied the evolution of the normal quasiparticle tunneling current [given in Eq. (40)] as a function of the applied gate voltage V and for two different limits of the right-BLG interlayer Coulomb interaction parameter $W_R$: the weak and intermediate regime, starting from $W_R=0$ (solid black curve), $W_R=\gamma _0$ (solid blue curve), $W^{*}_R=1.25\gamma _0$ (bold-dashed darker green curve) and $W_R=1.5\gamma _0$ (dashed darker yellow curve) (the value $W_R=1.5\gamma _0$ is chosen very close to the CNP value $W^{C}_{R}=1.48999\gamma _0$) and the high interaction limit, when $W_R=1.8\gamma _0$ (dashed darker blue curve), $W_R=2\gamma _0$ (solid green curve), $W_R=3\gamma _0$ (dot-dashed darker red curve) and $W_R=5\gamma _0$ (solid red curve). In all plots, in Fig. 2, we have set the intralayer Coulomb interaction parameters $U^{\eta }_{\ell }$ equal and $U^{\eta }_{\ell }=2\gamma _0$, for both BLGs $\ell =L,R$ and for all layers in the individual BLGs, i.e., $\eta =1,2$. We denoted by $W^{*}_{R}$ the value of the interlayer Coulomb interaction parameter at which the excitonic gap parameter is maximal: $\Delta _{R}=\Delta ^\mathrm{max}_{R}$. The interlayer interaction parameter in the left BLG is fixed at the value $W_L=0.5\gamma _0$, for all curves in Fig. 2. We see first of all, in Fig. 2, that the normal quasiparticle tunneling through the BLG/I/BLG heterojunction, accompanied with the excitonic pair formations in the system, is a threshold process, and the threshold frequency $\omega _0=(e/\hbar )V$ of the external field depends on the relative values of the Coulomb interaction parameters $W_L$ and $W_R$ at different sides of the construction. We also see that when augmenting the parameter $W_R$ in the interval $W_R\in [0,1.5\gamma _0]$, the curves, corresponding to the positive part of the current function $I_{n}(V,T)$, are shifting into left and the intensity of curves is increased. In turn, the threshold values of the normal tunneling current are also shifting left. Starting from the upper bound (UB) critical CNP value of $W_R$ (i.e., $W_R\ge W^{C}_{R}(UB)$), related to the upper bound solution of the chemical potential in the BLG (see in Ref. [56, 57]), the normal tunneling current is shifting right, on the V-axis. Nevertheless, the same is not true for the negative part of the tunnel current. We see, in Fig. 2, that all curves of the negative part of the quasiparticle tunneling current are displacing to the right when increasing the interlayer Coulomb interaction parameter in the interval $W_R\in [0, 5\gamma _0]$. Only a large jump of the threshold voltages occurs when passing across the lower bound (LB) CNP value $W^{C}_{R}(LB)$, related to the lower bound chemical potential at the CNP. We observe also that for a very large disbalance between the values of the parameters $W_L$ and $W_R$, the additional low-frequency peaks appear in the positive part of the current spectrum, and the threshold frequency values of V are gradually decreasing in these cases. We see also that the amplitudes of the low-frequency peaks are increasing with $W_R$. It is interesting to note that for $W_R=5\gamma _0$ (see the solid red curve in Fig. 2), the threshold frequency $\omega _0$ in the positive part of the normal current is of the order of $\omega _0\sim 2\gamma _1=0.256\gamma _0=0.76$ eV.

Fig. 2

The $I-V$ characteristic of the normal quasiparticle tunneling current, given in Eq. (40), for $W_L=0.5\gamma _0$ and for different values of $W_R$. The low-energy quasiparticle tunneling formation, coming from the condensate states, is shown at the large values of the interaction parameter $W_R$. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Another important observation in Fig. 2 is related to the formation of the four-peak structures in the spectrum of the normal tunneling current (This is due to the strong excitonic excitations in the four-band structure of the BLGs.) Namely, for small values of $W_R$, the spectrum of the normal current is stepwise, which furthermore transforms into the four-peak structure at the intermediate values of $W_R$ ($W_R=1.2\gamma _0$, $W^{*}_R=1.25\gamma _0$, $W_R=1.5\gamma _0$ and $W_R=1.8\gamma _0$). This is more apparent in Fig. 3, where we have chosen very close values of $W_R$, in order to demonstrate the gradual formation of the current four-peak structure.

Fig. 3

The four-bound peaks formations in the normal tunneling current in the BLG/I/BLG system, given in Eq. (40). The interaction parameter in the left BLG is fixed at the value $W_L=0.5\gamma _0$, and different values of $W_R$ are considered. The maximal value of the excitonic gap parameter is shown in the figure, corresponding to the value $W^{*}_R=1.25\gamma _0$. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 4

The $I-V$ characteristic of the normal quasiparticle tunneling current, given in Eq. (40) for equal values of the interlayer Coulomb interaction parameters in both sides of the junction: $W_L=W_{R}$. The values of interaction parameters below the CNP point (upper panel), above the CNP point (middle panel) and in the vicinity of $W^{C}$ are considered in the picture. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

We see in Fig. 3 that for $W_R=\gamma _0$ the structure of the tunneling current is half-stepwise with the well-formed two peaks in the excitation spectrum and at the relatively high values of the gate potential. When slightly augmenting $W_R$ (see the curves at $W_R=1.2\gamma _0$ and $W^{*}_R=1.25\gamma _0$), the current steps become more pronounced and, at the value $W^{*}_{R}=1.25\gamma _0$, the resonant tunneling peaks appear at the place of the current steps. Remember that at $W^{*}_{R}=1.25\gamma _0$ the excitonic gap parameter attains its maximum value (see in Ref.[56, 57]). Moreover, for higher values of $W_R$, the four-peak structure remains present and, additionally, the low-frequency resonant tunneling peaks appear in the electron tunneling spectrum. We relate the four-peak structure to the high energy strong resonant tunneling of single electrons, and the presence of the very large tunneling threshold is a direct consequence of the EI state in the bilayer graphenes. Thus, in order to do the tunneling, the electrons must break their contribution to the excitonic insulator state. Contrary, the additional low-frequency peaks at the large values of the parameter $W_R$, are related to the excitonic condensate states in the BLGs. This is the manifestation of tunneling coming from the coherent excitonic condensates states in the system. Vis-a-vis the high interaction values of $W_R$, accompanying the low-frequency peaks, coming from the excitonic condensates states, we can conclude that the excitonic insulator state and the excitonic condensates states in the system are not identical. These are two different states of matter, and the EI state does not survive at the high values of $W_R$, considered in Fig. 2. This observation is in complete agreement with the ideas retrieved in Ref. [56, 57]. This statement is also in agreement with the recent work in Ref. [66], where it has been shown that the excitonic Josephson current becomes extremely small before the EI state breaks down. A detailed analysis of the role of the CNP point $W^{C}=1.48999\gamma _0$, for the case of interaction balanced BLGs, is given in Fig. 4. Particularly, in the upper panel in Fig. 4, we consider the equal values of $W_L$ and $W_R$, below the upper bound critical value $W^{C}_{L}(UB)=W^{C}_{R}(UB)\equiv W^{C}(UB)$ (The latest was also considered in the figure.) We observe that the tunneling spectrum is perfectly symmetric in this case with respect to the origin. When augmenting the interaction parameter up to the upper bound solution at the CNP point, the positive part of the tunneling spectrum is shifted left (see the upper panel in Fig. 4), while for higher values of $W_R$ ($W_R=W_L \ge W^{C}(UB)$), the spectrum is shifted to right (This behavior is presented in the middle panel, in Fig. 4). In the lower panel, in Fig. 4, we have presented the smooth passage of the tunneling spectrum when crossing the CNP point. Both, lower bound and upper bound curves of the tunneling current have been considered there. It is worth to mention that the electronic band structure of the BLGs is doubly degenerated at $W^{C}$ because of the chemical potential solutions in the system (see in Ref. [56, 57]). We see in the bottom panel in Fig. 4 that the left outermost curve is the UB normal tunneling current in the system. When passing from LB to UB, the tunneling current spectrum still shifted to the left, while for $W>W^{C}(UB)$ the spectrum is transferring to the right. In Fig. 5, we have presented the temperature dependence of the normal tunneling current for a special antisymmetric choice of the Coulomb interaction parameters $W_L$ and $W_R$: $W_L=0.5\gamma _0$ and $W_R=\gamma _0$. As it is clear from the picture, the amplitude of the normal current decreases with increasing the temperature and also leads to the partial suppression of the threshold values of gate voltage, thus promoting a more flexible tunneling of the normal electrons.

Fig. 5

Temperature dependence of the normal quasiparticle tunneling current in the case of the non-equal interlayer Coulomb interactions: $W_L=0.5\gamma _0$ and $W_R=\gamma _0$. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 6

The time dependence of the total excitonic Josephson tunneling current, given in Eq. (39), for different values of the right-BLG interlayer interaction parameter $W_R$ ($W_R=0, 0.5\gamma _0$ and $\gamma _0$, from top to bottom) and for a fixed value of the left-BLG interlayer interaction $W_L=0.5\gamma _0$. Different combinations of the applied gate potential V and the condensate phase difference ${\Delta \varphi }_{0}$ are considered in the panels. The temperature is set to zero, in all panels. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 7

The time dependence of the total excitonic Josephson tunneling current, given in Eq. (39), for $W_R=0$ and for different values of the applied gate potential V. The condensates phase difference is fixed at the value ${\Delta \varphi }_{0}=\pi /2$, and the zero temperature case is considered here. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

3.2 The Excitonic Josephson Tunneling

The time dependence of the total excitonic Josephson current through the BLG/I/BLG heterostructure, given in Eq. (39), above, is evaluated numerically in Fig. 6, for different values of the applied gate potential, interaction parameters and condensates phase difference $\Delta \varphi _{0}=\varphi _{L}-\varphi _{R}$. When calculating numerically the principal value in Eq. (52), three singular points $(-\,1;0;1)$ of the integrand have been straddled properly. For the left BLG, we have $W_L=0.5\gamma _0$ in all panels in Fig. 6, while for the right BLG we have chosen three different values $W_R=0; 0.5\gamma _0$ and $W_R=\gamma _0$, from top to bottom panels in Fig. 6. At $V=0$ and $\Delta {\varphi }_{0}=0$, no tunneling current flows in the system (see the solid black lines on the time axis with the holly triangular plot-markers), while a dc current appears at $V=0$ if the phases of coherent excitonic states, in different sides of the junction, differ by $\Delta \varphi _{0}=\pi /2$ or $\Delta \varphi _{0}=-\pi /2$ (see the solid black lines in Fig. 6). Remarkably, the dc excitonic Josephson current changes the sign when changing the sign of $\Delta \varphi _{0}$, i.e., $\Delta \varphi _{0}\rightarrow -\Delta \varphi _{0} \Rightarrow I_\mathrm{Exc}(t)\rightarrow -I_\mathrm{Exc}(t)$. The change of sign in the total excitonic current is related to the fact that the second part of the total excitonic current is zero, i.e., $I_{J_{2}}(V,T)\cos (\Delta \varphi _{0}+2\omega _{0}t)=0$ because $\omega _{0}=0$ (This is the case $V=0$) and $\Delta \varphi _{0}=\pi /2$ (or $\Delta \varphi _{0}=-\pi /2$ when reversing the sign of the condensates phase difference parameter $\Delta \varphi _{0}$.) The first part in the total excitonic current at $\omega _{0}=0$ is proportional simply to $\sin \Delta \varphi _{0}$ which is odd function of its argument, and the factor $I_{J_1}(V,T)$ is given in Eq. (52), in Sect. 2.3. Such a finite dc current in the system suggests the degeneracy in the ground state of the system, i.e., the U(1) symmetry, and the presence of the excitonic condensates. Moreover, an ac excitonic current appears in the junction for any finite value of V ($V=0.5\gamma _0$ and $V=\gamma _0$, in the picture), even for the case $\Delta \varphi _{0}=0$ (see the blue dotted lines in Fig. 6 with the square plot-markers). The additional phase difference $\Delta {\varphi }_{0}=\pi /2$ only amplifies the excitonic tunneling current amplitude and leads to a phase shift (see the black dashed lines in Fig. 6). We observe also that the amplitude of the tunnel current decreases when increasing the parameter $W_R$ (see the top panel with $W_R=0$ and the middle panel with $W_R=0.5\gamma _0$, in Fig. 6). In the bottom panel in Fig. 6, we have chosen the larger value of the applied gate potential $V=1.5\gamma _0$, and $W_R=\gamma _0$. We see that the oscillations of the tunnel current are multiplied in this case within the same time interval. This effect is clearly seen in Fig. 7, where different values of the applied gate voltage are considered straightforwardly, and the interaction parameter $W_R$ is fixed at the value $W_R=0$, in correspondence with the plots of the excitonic Josephson current in the upper panel in Fig. 6. We see that when multiplying the value of V by an integer number $V'=nV$, where $n=1,2,3,4$, we have for the current wavelength $\lambda '=\lambda /n$, thus a relation of type $\lambda {V}=\text {const}$, between the applied gate potential and the current wavelength, emerges naturally. In Fig. 8, the same function $I_\mathrm{Exc}(t)$ is presented for the case of the fixed applied gate potential $V=0.5\gamma _0$, and for different values of the right-BLG interlayer Coulomb interaction parameter $W_R$, below the critical CNP value $W^{C}_{R}=1.48999\gamma _0$. The condensates phase difference is fixed at the value $\Delta {\varphi }_{0}=\pi /2$. We see, particularly, that when augmenting the interaction parameter $W_R$ (and keeping at the same time $W_L$ fixed at $W_L=0.5\gamma _0$) the amplitude of the excitonic tunneling current is decreasing considerably. The zeros of the current function do not shift in their positions, contrary to the case presented in Fig. 7, where the shift of the zeros is caused by the reduction of the current wavelength in the junction. Thus, we realize that the interlayer Coulomb interaction in the right BLG affects only the current amplitudes, while the changes of the applied gate potential modify principally the frequency of the excitonic current and have not a significant effect on the current amplitudes. Next, in Fig. 9, we have shown the time dependence of the excitonic tunneling current for the values of $W_R$ above the UB charge neutrality point $W^{C}_{R}(UB)$. Contrary to the case, given in Fig. 8, the amplitude of the Josephson tunneling current is increasing with $W_R$. This result is related again to the behavior of the chemical potential and Fermi energies in the BLGs (see in Ref. [56, 57]). In order to compare the results in Figs. 8 and  9, we kept the curve for $W_R=0$, in both cases.

Fig. 8

The time dependence of the total excitonic Josephson tunneling current, given in Eq. (39), for $V=0.5\gamma _0$ and for different values of the right-BLG interlayer Coulomb interaction parameter $W_R<W^{C}$. The parameter $W_L$ is fixed at the value $W_L=0.5\gamma _0$, and the condensates phase difference is fixed at the value ${\Delta \varphi }_{0}=\pi /2$. Zero temperature case is considered here. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 9

The time dependence of the total excitonic Josephson tunneling current, given in Eq. (39), for $V=0.5\gamma _0$ and for different values of the right-BLG interlayer Coulomb interaction parameter $W_R>W^{C}$. The value $W_R=0$ is also considered as a reference. The parameter $W_L$ is fixed at the value $W_L=0.5\gamma _0$, and the condensates phase difference is fixed at ${\Delta \varphi }_{0}=\pi /2$. Zero temperature case is considered here. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

In Fig. 10, we have presented the excitonic Josephson current-voltage dependence on time at $T=0$ and for the balanced values of the interaction parameters $W_L$ and $W_R$. We put $W_L=W_R=0.5\gamma _0$, and we have considered the cases when $\Delta {\varphi }_{0}=0$ or $\Delta {\varphi }_{0}\ne 0$. We observe, in the upper panel in Fig. 10, that for the case $\Delta {\varphi }_{0}=\pi /2$ we have a finite excitonic Josephson tunneling current through the system at $V=0$. At $V\ne 0$, we have principally the same qualitative behavior of the tunneling current for both cases $\Delta {\varphi }_{0}=0$ and $\Delta {\varphi }_{0}=\pi /2$ apart the situation at $t=0$, when there is a large threshold of V at the zero phase difference (see the solid black curve in the lower panel, in Fig. 10). Contrary, for $\Delta {\varphi }_{0}=\pi /2$ and at $t=0$ the excitonic current has been developed in the system (see the solid black curve, in the upper panel, in Fig. 10).

Fig. 10

The time evolution of the total excitonic Josephson tunneling current, given in Eq. (39), for the case of $W_L=W_R=0.5\gamma _0$. The condensates phase difference is fixed at the value $\Delta \varphi _{0}=\pi /2$, in the upper panel, and $\Delta \varphi _{0}=0$, in the lower panel. The temperature is set at zero. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 11

The $I-V$ characteristic of the excitonic Josephson tunneling current, given in Eq. (39), for the equal values of the interlayer Coulomb interaction parameters $W_L=W_R$, below the lower bound critical CNP value $W^{C}_{LB}$. The lower bound critical current is shown in dashed dark yellow curve. The temperature is set at zero. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 12

The $I-V$ characteristic of the excitonic Josephson tunneling current, given in Eq. (39), for the equal values of the interlayer Coulomb interaction parameters $W_L=W_R$, above the critical upper bound CNP value $W^{C}_{UB}$, presented in dashed dark yellow curve. The temperature is set at zero. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 13

The $I-V$ characteristic of the excitonic tunneling current, given in Eq. (39), for $W_L=0.5\gamma _0$ and for different values of $W_R$. The temperature is set at zero. The intralayer Coulomb interaction parameters $U_{L}$ and $U_{R}$ are set equal to $U_{\ell }=2\gamma _0$ ($\ell =L,R$), for all plots in the figure (Color figure online)

Fig. 14

The $I-V$ characteristic of the excitonic tunneling current, given in Eq. (39), for the special case $W_L=W_R=0$ and at $T=0$. The values of numerical solutions of the chemical potentials and the exact Fermi levels in the non-interacting BLGs are shown in the picture. The intralayer Coulomb interaction parameter $U_{\ell }$ (with $\ell =L,R$) is set both to zero (Color figure online)

The I–V characteristics of the excitonic Josephson current, for the case of the equal values of the interlayer interaction parameters, i.e., $W_L=W_R=W$, is shown in Fig. 11. Different values of W are considered in the picture: $W=0.5\gamma _0$ (solid black curve), $W=0.8\gamma _0$ (solid blue curve), $W=\gamma _0$ (solid yellow curve), $W=W^{*}=1.25\gamma _0$ (solid red curve), $W=1.3\gamma _0$ (dot-dashed darker green curve), $W=1.4\gamma _0$ (large-dashed green curve), and $W=W^{C}(LB)=1.48999\gamma _0$ (bold-dashed darker yellow curve). We observe that up to the value $W^{*}=1.25\gamma _0$, which corresponds to the maximum of the excitonic gap parameters in the BLGs, the amplitude of the excitonic Josephson current is increasing (including the dc values at $V=0$). Furthermore, for $W>W^{*}$, the amplitudes are continuously decreasing, for W up to the LB CNP value $W=W^{C}(LB)=1.48999\gamma _0$. The further increase of W, above the LB CNP, leads to a drastic decrease (of about of one order of magnitude) of the excitonic tunnel current amplitude, and this is shown in Fig. 12. It is important to concentrate on another principal difference between the results presented in Figs. 11 and  12. This concerns the first deepest minima of the excitonic Josephson current. In Fig. 11, those minima appear for relatively small voltages, and the positions of the positive (negative) minima are shifting to right (left), for $W\le W^{*}=1.25\gamma _0$. Then, with a further increase of W in the interval $W^{*}<W<W^{C}(LB)=1.48999\gamma _0$, they are slightly shifting to the left (right). On the other hand, the first minima for the curves in Fig. 12, for $W^{C}(UB)\le W\le 3\gamma _0$, appear for very large values of V, and the positions of positive (negative) minima are continuously shifting to right (left) in this case. Therefore, the very large values of V are very promising to observe the ac excitonic Josephson current in the system. Experimentally, this could be achieved with the appropriate choice of the left and right gate voltages, which will change the interlayer Coulomb interactions in the BLGs, until the expected effect takes place. In Fig. 13, we have presented the excitonic tunneling current for the asymmetric values of the interaction parameters $W_L$ and $W_R$ and we see how the increase of $W_R$ in the right BLG, above the symmetric value $W_{R}=0.5\gamma _0$ (the parameter $W_L$ is fixed at the value $W_L=0.5\gamma _0$ for all values of $W_{R}$), leads to the tunneling current transfer into right, on the positive axis of V. It is interesting and straightforward to consider the special case of the non-interacting BLGs and the excitonic Josephson current through the junction in this particular case. This result is shown in Fig. 14. We see that although the zero interaction limit, i.e., when $U_{\ell }=0$ and $W_{\ell }=0$, the excitonic Josephson current still present in the BLG/I/BLG junction, and the values of it are comparable to the case when $W>W^{C}(UB)$, shown in Fig. 12, above. The reason of such excitonic effect is related to the presence of the excitonic condensates states, and the principal mechanism for the formation of the excitonic condensates phase is due to the interlayer hopping between the layer in the individual BLG systems (see in Ref. [56, 57]). In the context of the excitonic Josephson current, discussed here, the finite value of the excitonic current follows from the expressions of the functions $I_{J_1}(V,T)$ and $I_{J_2}(V,T)$, given in Eqs. (50) and (51), in Sect. 2.3. Indeed, the expression of the current amplitude $I_{J_{1}}(V,T)$, in Eq. (52) is proportional to the product of the anomalous spectral functions $A^{L}_{\tilde{a}b}(\mathbf{{k}},\omega )$ and $A^{R}_{\tilde{c}d}$, given in Eq. (34); in Sect. 2.3, thus, the function $I_{J_{1}}(V,T)$ is proportional to the product $(\gamma _{1}+\Delta _{L})(\gamma _{1}+\Delta _{R})$. The same is true for the function $I_{J_{2}}(V,T)$, given in Eq. (53). At the zero interlayer coupling limit $\Delta _{L}=\Delta _{R}=0$ while the functions $I_{J_{1}}(V,T)$ and $I_{J_{2}}(V,T)$ remain finite, due to the finite interlayer hopping amplitude $\gamma _1$. Thus, in the non-interacting regime, the fundamental state of BLG systems in both sides of the junction is represented as the phase coherent macroscopic state of the excitonic condensate and the principal mechanism for such a state is attributed to the finite interlayer hopping between the layers in the BLGs. Another spectacular effect, related to the non-interacting regime in the BLGs, is the presence of a finite solution of the chemical potential and the Fermi energy in the separate BLGs (see in Ref. [56, 57], for more details).

4 Conclusion

We have calculated the normal quasiparticle and excitonic Josephson tunneling currents in the BLG/I/BLG heterostructure with the half-filled, AB-stacked bilayer graphene structures at different sides of the junction. By using the S-matrix approximation, we have derived the analytical expressions of both types of tunneling currents: normal quasiparticle and excitonic. The role of charge neutrality point has been discussed in details. Particularly, we have shown how the current spectrum is changing when passing through the CNP point of the interlayer Coulomb interaction parameters, in different sides of the junction. It has been shown that the normal quasiparticle tunneling, in the junction, is a threshold process, independently of the values of the interlayer Coulomb interactions in the BLGs and the threshold value of field frequency could be modified by changing the interaction parameter in one BLG, while keeping it fixed, at the same time, in another BLG. The formation of the resonant tunneling peaks in the normal tunneling spectrum has been analyzed in details by considering the vicinity of the charge neutrality point in the right BLG. The very large values of the threshold frequency have been obtained for the case of the interaction-symmetric junction $W_L=W_R$, below and above the charge neutrality point. Particularly, from the form of I–V spectrum, in the case of the interaction-asymmetric junction, it is clear that the excitonic insulator state and the excitonic condensate states are two different states of matter in the BLGs. We have shown that the low-frequency peaks appear from the excitonic tunneling in the condensates regime in BLGs, and at the large values of the Coulomb interaction parameter in the right BLG (when the excitonic insulator state breaks down). The temperature dependence of the threshold values of field frequency has been derived for a very large interval of temperature: from zero up to very high temperatures.

Furthermore, the time dependence of the excitonic Josephson tunnel current has been studied in details for different limits of interlayer Coulomb interaction parameter in the right BLG, and the excitonic Josephson dc effect has been found for the case $\Delta {\varphi }_{0}\ne 0$ and $V=0$. Ulteriorly, an ac excitonic Josephson effect has been shown in the junction for nonzero values of the applied gate potential. It has been shown that the phase difference between the excitonic condensates in the BLGs, only amplifies the tunneling current when keeping V constant. It has been shown that a relation of type $\lambda {V}=\text {const}$ is valid in the junction when changing the applied gate potential by the integer values. The time dependence of the excitonic Josephson tunneling current has been analyzed by considering different values of the right-BLG interaction parameter. The $I-V$ characteristics of the excitonic Josephson effect has been found for both interaction-symmetric and interaction-asymmetric cases, and the effects of the charge neutrality point have been discussed in details. It has been shown that the very large values of V are promising to observe the ac excitonic Josephson current in the system. Finally, a particular case of the non-interacting BLGs junction has been considered separately, and the excitonic Josephson tunneling current has been calculated for this case. As a result, we have shown that the nonzero excitonic current is present in this case with the amplitudes comparable to that of the amplitudes of I–V spectrum at the high symmetric values of W . The principal mechanism for the excitonic condensate states and the nonzero excitonic tunneling current, in this case, is attributed to the interlayer hopping between the layers in the individual BLG systems.

We have presented a complete theory of the bilayer graphene-based tunnel junction, and the results, presented here, could represent a veritable framework on which the experimental setup could be made and the results could be compared straightforwardly. The theoretical results in the paper are especially important in the context of the long-standing problem about the excitonic condensation and pair formation in the BLGs and double-layer graphene systems. This is especially important for the theoretical understanding of the nature of the EI state and the coherent excitonic condensate states in such systems: their similarities and differences. The Josephson effect studied in the considered system could be furthermore an important construction in order to build the graphene-based quantum interference devices, which will bring a new idea about the ultra-sensitive magnetometers and voltmeters and will be more sensitive than the usual superconductors-based Quantum Interferometer Devices SQUIDs, due to the exceptional mobility of the electrons in graphene. The excitonic Josephson junctions would be also promising in the context of engineering a new type of ultrafast electronic circuits blocks, which could form a digital logic unit, in the modern ultrafast computers and fast electronics. The results, presented here, could be also important for the building of the new type of adiabatic graphene logic constructions based on the Graphene Quantum Interferometer Devices (Graphene-QUIDs) analog to the Josephson flux transfer logic devices such as the Adiabatic Quantum Flux Parametron (AQFP).