Transport Properties of a Quasi-1D Wigner Solid on Liquid Helium Confined in a Microchannel with Periodic Potential

Abstract

We present transport measurements in a quasi-1D system of surface electrons on liquid helium confined in a 101-$\upmu$m-long and 5-$\upmu$m-wide microchannel where an electrostatic potential with periodicity of 1-$\upmu$m along the channel is introduced. In particular, we investigate the influence of such a potential on the nonlinear transport properties of a quasi-1D Wigner solid (WS) by varying the amplitude of the periodic potential in a wide range. At zero and small values of amplitude, the quasi-1D WS in the microchannel shows expected features such as the Bragg–Cherenkov scattering of ripplons and re-entrant melting. As the amplitude of the potential increases, the above features are strongly suppressed. This behavior suggests the loss of long-range positional order in the electron system, which is reminiscent of re-entrant melting behavior due to lateral confinement of the WS in the channel.

Introduction

A lattice of interacting charged particles driven against an external periodic potential presents an attractive system to model sliding friction, which is relevant to diverse fields of science [1]. The basic model that describes sliding friction between crystalline interfaces, the one-dimensional (1D) Frenkel–Kontorova (FK) model, consists of a chain of particles coupled by a harmonic nearest neighbor interaction and subject to an external spatially periodic potential. The competition between these two interactions determines essential physical features, such as the stick–slip motion when particles are acted upon by an additional adiabatically increasing driving force and the Aubry transition to a superlubricity state. It is understood that these processes are governed by the excitation of topological defects in the system and are strongly influenced by incommensurate periodicities of the lattice and potential [2]. Experimentally, the FK model was studied in diverse physical systems, such as solid interfaces [3, 4], 2D colloidal monolayers [5,6,7] and cold ions in optical lattices [8, 9], and continues to attract a lot of attention.

Electrons on helium present an ultra-clean system of charged particles on a liquid substrate where the FK model can potentially be realized. Owing to the strong Coulomb interaction between electrons, the system crystallizes into a two-dimensional Wigner solid (WS) at densities of order $10^{13}$ m$^{-2}$ and at temperatures around 1 K. Electrostatic pressure exerted by localized electrons in the solid phase causes a commensurate deformation of the liquid surface, the so-called dimple lattice, that couples to the WS and significantly alters its transport along the surface under an external driving electric field. In particular, the coherent Bragg–Cherenkov (BC) emission of surface capillary waves, ripplons, with a wavelength equal to the lattice constant leads to a deepening of the dimples and results in the saturation of the electron current [10, 11]. At high driving fields, electrons decouple from the dimples, and the WS is in a sliding state characterized by much larger values of current [12, 13]. The regime of coherent BC emission of ripplons, where the lattice of electrons couples to the dimples, has a loose analogy to the two-dimensional (2D) case of the FK model particularly for a case in which the mean distance between particles equals the spatial period of the substrate potential. Indeed, it shows some typical features predicted by the FK model, such as a de-pinning transition and hysteresis [14, 15]. However, one main aspect of the FK model, the role of incommensurability between electrons and dimple lattices, is automatically eliminated by the origin of the dimple lattice itself.

Experimental devices for studying transport properties of electrons on helium have generally a structure of the field-effect transistor for a two-dimensional electron gas in semiconductors, for example in a form of thin films [16] or microchannels [17]. It was shown that confining electrons in capillary-condensed microchannel structures facilitates control of the electron system by imposed electrostatic potentials [18,19,20] and allows for observation of new interesting features associated with electron transport and phase transitions in the system, such as clocked electron transport [21], discrete transport through a point-contact constriction [22, 23], suppressed and re-entrant melting of a quasi-1D electron crystal [24,25,26], stick–slip motion of WS [27], inhomogeneous WS [28] and effect of size of a WS on sliding transition [29]. Motivated by these studies and by the possibility of studying the FK model in an electron-on-helium system, we designed and fabricated a microchannel device in which a spatially periodic electrostatic potential of varying amplitude could be imposed on the electrons confined in the channel. Here, we present the results of our preliminary studies of electron transport along the microchannel in the presence of a periodic potential. In particular, we report the strong suppression of typical features associated with the crystalline ordering, such as the re-entrant melting of WS and the nonlinear BC regime of electron transport, by the periodic potential. These results are discussed in terms of the loss of long-range crystalline ordering in the electron system under application of an external potential.

Sample and Methods

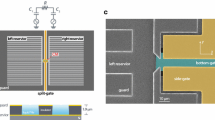
Our microchannel device was fabricated on a silicon oxide substrate using optical and e-beam lithography methods. The device consisted of two large arrays of 5 $\upmu$m microchannels that acted as two electron reservoirs, connected by a central 101 $\upmu$m-long and 5 $\upmu$m-wide microchannel; see Fig. 1a, b. This structure was composed of two patterned gold layers separated by an insulating layer of silicon nitride with a thickness of 550 nm. The bottom gold layer (dark golden color in Fig. 1a) consisted of three electrodes that defined the bottoms of two reservoirs and the central channel. The top gold layer (light gold color in Fig. 1a) consisted of two electrodes, the split-gate and guard electrodes. The insulating layer separating the two gold layers was removed within the microchannels to form rectangular grooves having a height of 550 nm. Microchannels were filled with superfluid $^4$He by capillary action from bulk liquid helium, the level of which was maintained slightly below the device.

Fig. 1

a Microscopic image of the microchannel device used in the experiment. Bottom and top gold layers are indicated by dark and light golden colors, respectively. The central microchannel (CM) connecting the left and right reservoirs, LR and RR, respectively, is shown in detail in the next panel. b False-color scanning electron micrograph of the CM region of the device. The bottom of the channel is formed by two electrically isolated electrodes, Ch1 and Ch2, in the shape of inter-digital capacitor plates. The inset shows a magnified image of these plates. c Variation in the electrostatic potential along the microchannel (x-direction) calculated using FEM at the surface of liquid helium in the middle of CM for $V_\text {sg}=-\,0.8$ V, $V_\text {ch}=1.5$ V and $\varDelta V_\text {ch}=0.5$ V. The inset shows a magnified portion of the potential at the surface at the center of CM (Color figure online)

A special feature of our device is the bottom electrode of the central channel, which consisted of two separate parts, “Ch1” and “Ch2,” in the shape of an inter-digital capacitor with fingers aligned across the channel; see inset of Fig. 1b. Each finger was 250 nm wide, and the adjacent fingers of two electrodes were separated by 250-nm gaps. Thus, by applying a potential difference $\varDelta V_\text {ch}=|V_\text {ch1}-V_\text {ch2}|$ between electrodes Ch1 and Ch2, we could create a spatially periodic electrostatic potential along the channel with a period of 1 $\upmu$m. As an example, Fig. 1c shows the spatial variation in the potential at the center of the channel at a distance of 550 nm above the bottom electrode (that is, approximately at the level of liquid helium filling the channel) calculated using the finite element method (FEM) for $\varDelta V_\text {ch}=0.5$ V. In this case, voltages $V_\text {ch1}=V_\text {ch}+\varDelta V_\text {ch}/2$ and $V_\text {ch2}=V_\text {ch}-\varDelta V_\text {ch}/2$ were assigned to electrodes Ch1 and Ch2, respectively, to have a common bias of 1.5 V at the bottom of the central microchannel.

The surface of the liquid helium filling the microchannels was charged with electrons produced by thermal emission from a tungsten filament placed a few millimeters above the device, while a positive bias was applied to the reservoir’s bottom electrodes and the guard electrode was grounded. Transport of electrons through the central microchannel was measured by the standard capacitive-coupling (Sommer–Tanner) method. An AC voltage $V_\text {ac}$ with frequency $f=99.5$ kHz was applied to one of the reservoir electrodes, while both in-phase and quadrature components of the current I induced by electron motion in the other reservoir electrode were measured with a lock-in amplifier. The response of the device was well described by a lumped RC-circuit [30], in which two capacitances ($\sim 1$ pF) between the left and right reservoir electrodes and the charged surface of the liquid are connected in series with a resistance R of the electrons in the central channel. Due to the large size of the reservoirs, which consisted of a large number of microchannels connected in parallel, the total resistance of the device is dominated by the resistance of electrons in the central microchannel, which justifies the above lumped-RC model. In turn, R depends on the density of electrons in the central microchannel, which is determined by the number of electrons in the reservoirs and the voltages applied to different electrodes of the device.

Experimental Results

Phase Diagram of the Electron System Without Applying a Periodic Potential

First, we checked the performance of the fabricated device by applying the same potential to both electrodes Ch1 and Ch2 of the central microchannel ($V_\text {ch}=V_\text {ch1}=V_\text {ch2}$) and measuring the current in the device I while applying a peak-to-peak AC voltage $V_\text {ac}=5$ mV to the device (Fig. 2) for various values of $V_\text {ch}$ and bias $V_\text {sg}$ applied to the split-gate electrode of the central microchannel. To understand this diagram, it is convenient to use a simplified capacitance model to find the relationship between the density of electrons in the central microchannel and voltages applied to different electrodes of the device [23]. First, we define the total capacitance of the liquid surface in the central microchannel $C_\varSigma =C_\text {ch}+C_\text {sg}$, where $C_\text {ch}$ and $C_\text {sg}$ are capacitances between the liquid surface and the channel’s bottom and split-gate electrodes, respectively. It is also convenient to introduce the dimensionless coupling constants $\alpha =C_\text {ch}/C_\varSigma$ and $\beta =C_\text {sg}/C_\varSigma$, which satisfy the obvious relation $\alpha +\beta =1$. Then, the potential at the uncharged liquid surface can be written as $V_\text {b}=\alpha V_\text {ch}+\beta V_\text {sg}$. When the device is charged with electrons, the potential of the charged liquid surface $V_\text {e}$ must be the same everywhere, owing to high mobility of the surface electrons on liquid helium. The value of $V_\text {e}$ is determined by voltages applied to the reservoir’s bottom and guard electrodes and the number of electrons in the reservoir, and is assumed to be fixed once the device is charged. Note that occasionally, loss of electrons from the device is observed, which is reflected in discontinuous jumps of the measured current I. Such data are not considered here. Then, by the definition of capacitance, we can define the total charge Q of electrons in the channel $Q=C_\varSigma (V_\text {e}-V_\text {b})$. A further simplification can be made by assuming a uniform density distribution of electrons in the channel, that is, $Q=-en_\mathrm{s}S$, where $n_\mathrm{s}$ is the areal density of surface electrons, $e>0$ is the electron charge and S is the channel area. Such a parallel-plate capacitance approximation is partially justified by a large aspect ratio ($\sim 10$) of the wide, shallow microchannel used in our device. Using $C_\text {ch}=\epsilon \epsilon _0 S/d$, where $d=550$ nm is the height of the microchannel in our device, $\epsilon =1.056$ is the dielectric constant of liquid helium and $\epsilon _0=8.85\times 10^{12}$ F/m is the permittivity of free space, we obtain the relation

$$\begin{aligned} n_\mathrm{s}=\frac{\epsilon \epsilon _0}{\alpha e d} \left( \alpha V_\text {ch} + \beta V_\text {sg} - V_\text {e} \right) . \end{aligned}$$

(1)

Fig. 2

Magnitude of electron current I measured as a function of split-gate electrode potential $V_\text {sg}$ and channel potential $V_\text {ch}=V_\text {ch1}=V_\text {ch2}$ at $T=0.86$ K. The dashed (white) line shows potential threshold values for channel opening, as described in the text (Color figure online)

The above equation is useful to characterize the device and to estimate various quantities. For example, the maximum density of electrons corresponds to the condition $V_\text {e}=V_\text {sg}$, in which electrons cease to be confined across the microchannel by the split-gate potential, from which we find $n_s^{(\text {max})}=\epsilon \epsilon _0(V_\text {ch}-V_\text {sg})/(ed)$. In contrast, the zero density of electrons in the central microchannel corresponds to the condition $\alpha V_\text {ch} + \beta V_\text {sg}=V_\text {e}$, which determines the threshold value of the channel voltage for given values of $V_\text {sg}$ and $V_\text {e}$

$$\begin{aligned} V_\text {ch}^{(\text {th})}=\frac{1}{\alpha }V_\text {e}- \frac{1-\alpha }{\alpha } V_\text {sg}. \end{aligned}$$

(2)

Below this threshold value, the potential at the uncharged surface in the central microchannel $V_\text {b}$ is lower than $V_\text {e}$; therefore, the central microchannel is completely depleted of electrons and the current I in the device is zero. The experimental values of $V_\text {ch}^{(\text {th})}$ are plotted in Fig. 2 with a dashed (white) line. By fitting this line using Eq. (2), we obtain $V_\mathbf e =0.92$ V and $\alpha =0.77$ (therefore $\beta =0.23$).

Above the threshold line in the $V_\text {sg}-V_\text {ch}$ plane, see Fig. 2, the current in the device is determined by the resistance R of electrons in the microchannel, which in turn depends on the phase of the electron system. For weak confinement of the electron system, which corresponds to lower values of $V_\text {ch}$ and more positive values of $V_\text {sg}$, the system is in the liquid phase. This corresponds to low resistance R and large current I; see Fig. 2. For stronger confinement of the electron system, which corresponds to larger values of $V_\text {ch}$ and more negative values of $V_\text {sg}$, the system crystallizes into a WS [24, 31]. As a result, the resistance R of electrons in the central microchannel increases due to the formation of the commensurate dimple lattice, and the measured current I drops significantly. A spectacular behavior is observed in the intermediate voltage range, where the current I exhibits a fringed pattern; see Fig. 2. This phenomenon was identified as the re-entrant melting of the WS [25, 26]. As the confining potential, therefore the width of the electron system in the microchannel, is varied by the voltage applied to the electrodes, the WS in the microchannel undergoes intermittent melting as a result of increased fluctuation of electron positions between stable configurations corresponding to different numbers of electron rows across the channel. Therefore, the fringes, which are nearly parallel to the threshold line, see Fig. 2, can be identified by the different number of electron rows in the microchannel. It is worth noting that deep in the WS phase region the threshold line slightly deviates from the fitting line. Apparently, that is because a continuous electron distribution approximation, which is used to derive Eq. (2), may not work so well for the case of a few rows of electrons in the WS state, where the granular nature of electrons has to be taken into account.

Effect of Periodic Potential

Next, we investigate the effect of a spatially periodic potential applied to electrons in the microchannel on the current. To do this, we apply potentials $V_\text {ch1}=V_\text {ch}+\varDelta V_\text {ch}/2$ and $V_\text {ch2}=V_\text {ch}-\varDelta V_\text {ch}/2$ to electrodes Ch1 and Ch2, where $V_\text {ch}=1.5$ V is a fixed common bias applied to two electrodes, and $\varDelta V_\text {ch}$ can be varied from 0 to 2 V. The absolute value of the current I in the device is plotted in Fig. 3 for various values of $\varDelta V_\text {ch}$ and $V_\text {sg}$. For $\varDelta V_\text {ch}\lesssim 0.7$ V, we observe fringes of current due to the re-entrant melting of the WS, as described earlier. For the sake of illustration, the solid (red) line plots the measured current I versus $V_\text {sg}$ for $\varDelta V_\text {ch}=0.25$ V. For $\varDelta V_\text {ch}\gtrsim 0.7$ V, the behavior becomes drastically different; see Fig. 3. The re-entrant melting fringes disappear and the measured current I increases significantly to a value comparable to that for electrons in the liquid phase (c.f. Fig. 2). This behavior might suggest that the application of a sufficiently strong periodic potential suppresses crystallization of the electron system into the WS phase. Under continuous electron distribution approximation, the onset of charging of electrons in the central microchannel $\varDelta V_{\text {ch}}^{(\text {th})}$ can be expressed similarly to Eq. (2). Considering the contribution to $\varDelta V_{\text {ch}}$ by electrodes Ch1 and Ch2, the potential threshold line can be expressed as

$$\begin{aligned} \varDelta V_\text {ch}^{(\text {th})}=\frac{2}{\gamma }\left( -V_{e}+\alpha V_{\text {ch}}+\beta V_{\text {sg}}\right) , \end{aligned}$$

(3)

where $\gamma$ is the coupling constant maximum from the Ch2 electrode. The dashed line plotted in Fig. 3 indicates the potential threshold line determined by the experimental values of $\varDelta V_{\text {ch}}^{(\text {th})}$ in the region of $\varDelta V_{\text {ch}} \ge 0.7$ V. By fitting this line with Eq. (3), we obtain $\gamma =0.02$. For low $\varDelta V_{\text {ch}}$, where signatures of the WS phase are still prominent, again there is a deviation of the threshold line from the fitting line, suggesting that granular nature of electrons cannot be ignored in this regime.

Fig. 3

Magnitude of electron current I measured at $T=0.86$ K for driving AC voltage $V_\text {ac}=0.5$ mV as a function of the split-gate electrode potential $V_\text {sg}$ for different values of potential difference $\varDelta V_\text {ch}=|V_\text {ch1}-V_\text {ch2}|$ between channel electrodes Ch1 and Ch2. The common bias for the two channel electrodes is fixed at $V_\text {ch}=1.5$ V. Solid (red) line shows current I versus $V_\text {sg}$ measured at a fixed value $\varDelta V_\text {ch}=0.25$ V. Dashed (white) line shows potential threshold values for the channel opening, as described in the text (Color figure online)

To understand the effect of the spatially periodic potential on the electron system, it is instructive to estimate the variation in the electron density $n_s$ in the central microchannel using the parallel-plate capacitance approximation. As described earlier, the electron density can be estimated as $n_s=\epsilon _0\epsilon \left( V_\text {b} - V_\text {e} \right) /(\alpha e d)$, where the potential $V_\text {b}$ at the uncharged surface of liquid helium in the central microchannel can be calculated numerically using the FEM; see Fig. 1c. We find that at the middle of the channel the density varies nearly sinusoidally with average value $\bar{n}_s$ and amplitude $\varDelta n_s$. In particular, for $V_\text {e}=0.92$ V, $V_\text {sg}=-\,0.4$ V, $V_\text {ch}=1.5$ V and $\varDelta V_\text {ch}=0.7$ V using the above approximation we estimate $\bar{n}_s=3.9\times 10^{13}$ m$^{-2}$ and $\varDelta n_s=0.4\times 10^{13}$ m$^{-2}$. For an infinite 2D electron system, the melting of the WS is expected to occur when the value of the plasma parameter $\varGamma =e^2\sqrt{\pi n_s}/(4\pi \epsilon _0\epsilon k_\text {B}T)$ exceeds $130 \,\pm \, 10$ [13, 32]. For $T=0.86$ K, the critical density of electrons corresponds to $n_s=1.4\times 10^{13}$ m$^{-2}$. Therefore, a small variation in electron density due to the applied periodic potential estimated above cannot cause melting of WS for an infinite electron system. On the other hand, as was pointed out earlier, the variation in lateral confinement of the electron system in the microchannel can cause a loss of the long-range crystalline order in the quasi-1D WS due to structural transitions between two stable configurations of the electron lattice corresponding to changing the number $N_y$ of electron rows in the channel by one [25, 26]. This is exactly the mechanism that explains the phenomenon of re-entrant melting in this system. Therefore, one can expect that a variation in $N_y$ along the microchannel caused by the applied periodic potential can induce a similar loss of long-range positional order, which in turn strongly changes the transport of the electron system observed in the experiment. For simplicity, we assume that the smallest reciprocal lattice vector of the WS points in the x-direction. The number of electron rows can be estimated as $N_y=\left( 4/3 \right) ^{1/4} w\sqrt{n_s}$, where w is the width of the electron system in the microchannel. For $V_\text {e}=0.92$ V, $V_\text {sg}=-\,0.4$ V, $V_\text {ch}=1.5$ V and $\varDelta V_\text {ch}=0.7$ V, we estimate that w varies from 3.63 to 3.54 $\upmu$m, and $N_y$ changes from 25 to 23. Therefore, $\varDelta N_y\approx 2$. In other words, the variation in the confining potential due to an applied periodic potential with $\varDelta V_\text {ch}=0.7$ V is sufficient to cause a structural transition between $N_y$- and $(N_y+1)$-row configurations, which increases fluctuations in the positions of electrons and suppresses nonlinear transport features usually associated with an electron system in the WS phase.

Fig. 4

Magnitude of electron current I measured at $T=0.86$ K as a function of peak-to-peak driving AC voltage $V_\text {ac}$ at $f=99.5$ kHz for different values of $\varDelta V_\text {ch}$. The common bias for the two channel electrodes was fixed at $V_\text {ch}=1.55$ V, while the split-gate voltage was fixed at $V_\text {sg}=-\,0.25$V (Color figure online)

To confirm suppression of nonlinear transport features associated with the crystalline ordering of the electron system, we measured the current I as a function of the driving amplitude $V_\text {ac}$ in the presence of periodic potential for different values of $\varDelta V_\text {ch}$. A typical set of such IV curves is shown in Fig. 4 for four different values of $\varDelta V_\text {ch}=0$, 0.7, 1.0 and 1.26 V. Without the periodic potential ($\varDelta V_\text {ch}=0$), the IV curve clearly shows two characteristic features of nonlinear transport, namely a BC plateau of current due to coherent emission of ripplons by the driven WS and a sharp rise of current due to sliding of the WS from the commensurate dimple lattice. Application of the periodic potential suppresses both features of nonlinear transport of the WS. In particular, for sufficiently large $\varDelta V_\text {ch}\gtrsim 0.7$ V, both features essentially disappear, and the electron transport approximates that of the electron system in liquid phase. This agrees with the suppression of re-entrant melting described earlier.

Discussion

The re-entrant melting, which results from competition between stable configurations corresponding to different numbers of electron rows, is particularly important in studies of finite-size crystalline systems where the spatial order of particles is strongly affected by their confinement [31]. The interplay between the electron lattice configuration and confining potential is an interesting problem of structural phase transitions [33]. In our experiment, the confinement is spatially modulated by an external periodic potential of varying strength. A characteristic feature of our observation is a threshold value of the amplitude of the periodic potential above which the nonlinear transport of the electron system associated with its crystalline ordering is suppressed. Our estimations presented above show that this corresponds to about 10$\%$ variation in the electron density in the microchannel and variation in the number $N_y$ of electron rows across the channel of the order one. More accurate estimations could be made by calculating the distribution of the electrical potential and electron density across the microchannel (y-direction) using the FEM [26, 30]. However, to properly account for the granular nature of electrons, molecular dynamics (MD) calculation is preferable [31]. Therefore, we did not try to improve the continuous density approximation model used in the previous section. MD calculations for the electron system in our device are currently under development.

As demonstrated in our work, the employed microchannel device can be used to study structural phase transitions in quasi-1D electron systems. Also, we are interested in using similar devices to study the FK model employing a 1D chain of electrons subject to the periodic potential. Of particular interest is the realization of an incommensurate case where the ratio of the mean distance between electrons to the spatial period of potential is equal to the “golden ratio” $(\sqrt{5}+1)/2$. This is the subject of future experimental efforts.

Summary

We have investigated the transport properties of a quasi-1D WS on the surface of liquid helium confined to a 5-$\upmu$m-long microchannel and subjected to an applied electrostatic potential with periodicity of 1 $\upmu$m along the channel. Nonlinear features of WS transport were suppressed by increasing the potential amplitude. We attribute this observation to structural transitions and suppression of the crystalline ordering of the electron system induced by the spatially modulated confinement.