Abstract
Suspended aluminum nanoelectromechanical resonators have been fabricated, and the manufacturing process is described in this work. Device motion is driven and detected with a magnetomotive method. The resonance response has been measured at 4.2 K temperature in vacuum and low-pressure \(^4\hbox {He}\) gas. At low oscillation amplitudes, the resonance response is linear, producing Lorentzian line shapes, and Q values up to 4400 have been achieved. At higher oscillation amplitudes, the devices show nonlinear Duffing-like behavior. The devices are found to be extremely sensitive to pressure in \(^4\hbox {He}\) gas. Such device is a promising tool for studying properties of superfluid helium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In cryogenic fluids like \(^4\hbox {He}\) and \(^3\hbox {He}\), immersed oscillating objects such as tuning forks, wires, grids and spheres have proven to be useful and multifunctional tools acting as thermometers, bolometers, pressure gauges, viscometers, as well as generators and detectors of turbulence, cavitation and sound [1,2,3,4]. Fluid properties are usually determined from measured changes in mechanical resonance response including resonance frequency, line width, amplitude and certain nonlinear effects (for example, nonlinear drag force resulting from turbulence). For high sensitivity, a resonator with a low mass and spring constant together with a high Q value is required. Modern micro- and nanofabrication techniques have enabled creation of ultra-sensitive probes of the quantum fluids [5,6,7]. We are pursuing sensitivity to the force resulting from dynamics of a single quantized vortex attached to a mechanical resonator. This would allow us to study many interesting phenomena, such as Kelvin-wave cascade on a single quantized vortex in \(^3\hbox {He}\) and \(^4\hbox {He}\) [8,9,10]; the role of vortex-core-bound fermions in the vortex dynamics in \(^3\hbox {He}\)-B [11, 12]; vortex friction due to the chiral anomaly, and the synthetic electromagnetic fields created by vortex motion in Weyl superfluid \(^3\hbox {He}\)-A [13]. To reach this goal, we have fabricated suspended aluminum nanoelectromechanical (NEMS) resonators with typical effective mass \(\sim 10\, \hbox {pg}\), dimensions \(\sim 10\,\upmu \hbox {m}\) and rectangular cross section of \({150}\,\hbox {nm} \times {1.1}\,\upmu \hbox {m}\) (see Fig. 1). The goalpost geometry of the devices was inspired by the work of Collin et al. [14]. The geometry allows for relatively low resonance frequency, which is an important factor in keeping damping due to acoustic emission in superfluids small [15].
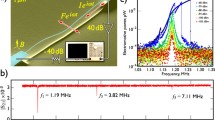
SEM micrographs of one of the samples studied in this work (4NN). a The NEMS resonator comprises of two cantilever feet connected by a paddle. Note the upward curvature of the device away from the Si surface. b Closeup of the device corner, showing typical grain size (\(\sim \,{50}\,\hbox {nm}\)) and the resulting surface roughness (\(\sim \,{10}\,\hbox {nm}\)) of the evaporated Al film
2 Methods
2.1 Fabrication Process
The fabrication process of the NEMS devices is presented schematically in Fig. 2. We start with a \({5}\,\hbox {mm} \times {5}\,\hbox {mm}\) high purity (resistivity \(>{100}\,\Omega \,\hbox {m}\)) silicon chip with 275 nm of \(\hbox {SiO}_2\) on top. First, the chip is cleaned in solvent baths (ethyl pyrrolidinone, acetone and isopropanol) with ultrasound, and a positive tone PMMA (polymethyl methacrylate, 50k/950k) bilayer is spin coated on top of the chip. The device pattern is written by electron beam lithography and developed in MIBK/IPA (1:3) solution. After a brief (15 s) \(\hbox {O}_2\) plasma cleaning, a 150 nm thick aluminum layer is deposited on the surface of the chip with an electron beam evaporator. To release the vibrating structures, the sacrificial \(\hbox {SiO}_2\) layer is etched with isotropic dry HF vapor process. The released structure has typically some upward curvature, as seen in Fig. 1. It originates from internal stress formed in the metal layer due to temperature changes during metal deposition [16].
2.2 Measurement Scheme
Schematic pictures of the chip after each fabrication step (not to scale): a cleaning, b spin coating, c lithography, d metal deposition, e lift-off, and f release etch. The wide structures, such as bonding pads and wires, remain anchored on top of \(\hbox {SiO}_2\), while the nanomechanical resonator is suspended after the isotropic HF vapor release etch (Color figure online)
Magnetomotive Measurement The magnetomotive measurement scheme is depicted in Fig. 3. When a constant magnetic field B is applied in the y-direction, perpendicular to the paddle of length L, and an AC current \(I=I_0 \cos (\omega t)\) is fed through the device, the paddle experiences a Lorentz force \(F = I L B\) in the x-direction. The force drives the resonator into oscillatory motion at the frequency \(\omega \). Numerical finite element method simulations (COMSOL) show that the first eigenmode of the nanomechanical resonator corresponds to out-of-plane and in-phase oscillation of the two cantilever feet connected by a rigid paddle. In this configuration, the motion of the paddle through the magnetic field generates via electromotive force a voltage \(V = \dot{x} L B\) across the paddle, where \(\dot{x}\) is the velocity of the paddle.
Measurement Circuit A schematic of the measurement circuitry is presented in Fig. 4. The excitation current I is generated by an arbitrary waveform generator, followed by a 40 dB attenuator and a \({1.2}\,\hbox {k}\Omega \) resistor connected in series with the resonator. The voltage over the resonator is amplified with a preamplifier (input impedance \(>10\, \hbox {k}\Omega \) at device frequency) and measured with a lock-in amplifier, which is phase-locked with the generator. The high impedance of the excitation and detection lines ensure low magnetomotive losses [17]. Indeed, magnetomotive loading is not observed at the fields \(B< {100}\, \hbox {mT}\) used in this work. The gain of the current and voltage lines has been calibrated to within 5% accuracy at frequencies below 1 MHz. The value of the magnetic field is known within 5%. \(R_w\), \(L_w\) and \(C_s\) present the resistance, inductance and stray capacitance of the device, wires and connected electronics, and they contribute to a background signal, which is a linear function of frequency for narrow sweeps around the mechanical resonance. This background is subtracted from the measured response in further analysis of the results.
The magnetomotive drive and detection scheme (I, B, V) and geometrical parameters (H, L, w, d) of the devices are depicted. The mode shape of the first eigenmode of the sample 4NN obtained from COMSOL simulation is also shown. The model does not incorporate any in-built stress. Values of the geometrical parameters and simulated resonance response for all the three devices studied in this work are listed in Table 1 (Color figure online)
Experimental Setup The NEMS devices are wire-bonded to a printed circuit board (PCB) with aluminum wires. The PCB is attached to a copper plate, which is installed in the vacuum chamber of a dipstick setup. The chamber is immersed in a liquid \(^4\hbox {He}\) bath, which provides a stable 4.2 K temperature enabling the use of a superconducting magnet and ensuring low thermal noise. Twisted pairs of copper wires carry the signals between the PCB at 4.2 K and the room temperature end of the dipstick, and standard coaxial cables are used to connect the dipstick to the measurement electronics at room temperature.
2.3 Theoretical Background
Resonance Response A NEMS device can be treated as a damped oscillator driven by an external force \(F = F_0 \cos ({\omega t})\). At sufficiently small oscillation amplitudes, a harmonic approximation is valid. The equation of motion is
where x, \(\dot{x}\), \(\ddot{x}\) are the displacement, velocity and acceleration of the paddle, \(\gamma \) is the drag coefficient (in units rad/s), and \(\omega _0 = \sqrt{k/m}\) is the natural frequency of the mechanical oscillator where m and k are the effective mass and the spring constant. The solution in the frequency domain is given by the Lorentzian functions for absorption and dispersion
respectively. The maximum amplitude \(\dot{x}_\mathrm {max}\) is obtained at the resonance frequency \(f_0=\omega /2\pi \), and the full width at half height of the absorption curve is \({\Delta }f=\gamma /2\pi \). The Q value is defined as \(Q=f_0/\Delta f\), and it holds for the maximum displacement at resonance that \(x_\mathrm {max} = Q F_0 / k\) [18]. At large oscillation amplitudes, the response becomes Duffing-like nonlinear [19] and shows hysteresis depending on the direction of the frequency sweep. In practice, we measure the voltages \(V_\mathrm {abs}=\dot{x}_\mathrm {abs} B L\) and \(V_\mathrm {disp}=\dot{x}_\mathrm {disp} B L\), which we convert to velocity or displacement of the beam. The oscillation amplitudes of velocity \(\dot{x}_0\) and displacement \(x_0\) are related as \(\dot{x}_0 = 2 \pi f x_0\).
Kinetic Damping The force experienced by an oscillating body moving through low-pressure gas in the ballistic regime is due to momentum transfer in collisions with individual gas molecules. The moving body experiences kinetic damping [20]
where m is the effective mass, \( \langle v \rangle \) is the average velocity of the gas molecules, p is the pressure, and \( A^* \) is the area of the cross section normal to the motion direction \(A=w(2H+L)\) weighted with the velocity profile over the surface. For the NEMS devices considered here, we have \(A^* \approx 0.6 A\).
Squeeze Film Force The vicinity of the Si surface to the oscillating NEMS device results in a squeeze film force, which arises due to compression and decompression of the gas in the narrow gap between the oscillator and the surface. The force has a dissipative and an elastic contribution, and in the ballistic regime the corresponding terms are
where g is the gap between device and Si surface, and
is the diffusion time of \(^4\hbox {He}\) gas out of the narrow gap [20]. The resonance frequency increases from the vacuum value as \( \delta f_\mathrm {sf} \approx f_0 k_\mathrm {sf} / 2k \) due to the small additional spring constant \(k_\mathrm {sf} \ll k\).
Gas Adsorption At low temperatures, \(^4\hbox {He}\) gas adsorbs on all surfaces, including the NEMS device. At low coverages, the Langmuir isotherm
can be used to describe the adsorption process. Here, \(\theta \) is the fraction of occupied adsorption sites, p is the pressure, and K is an empirical constant. We assume that the adsorbed atoms do not induce additional dissipation, but the mass loading results in a decrease of the resonance frequency \(\delta {f} \approx - f_0 \Delta m / 2 m_0 \) where \(m_0\) is the mass of the resonator and \({\Delta }m \ll m_0\) is the mass of the adsorbed gas.
3 Results
Mechanical Properties The geometrical dimensions and measured properties of the NEMS devices are tabulated in Table 1. The resonance frequency \(f_0\), the line width \({\Delta }f\) and the amplitude are obtained from Lorentzian fits (Eq. 2) to linear resonance spectra, such as shown in Fig. 5. The resonance frequencies obtained from the measurements and simulations agree within 4%, justifying the use of bulk values for the elastic modulus and the density of aluminum.
The maximum displacement amplitude as a function of the excitation force for the sample 4UN is shown in Fig. 5. At high oscillation amplitudes, the response is Duffing-like nonlinear. The resonance frequency shifts down quadratically with increasing oscillation amplitude as \(\delta {f} = {-0.010}\, \hbox {Hz}/\hbox {nm}^2 x_{\max }^2\), where \(x_{\max }\) is the oscillation amplitude at resonance when sweeping frequency in decreasing direction. The effective mass m and the spring constant k are extracted from the slope of the displacement-force curve in the linear regime using the relations \(k=\omega _0^2 m=Q x_{\max }/F_0\). For the samples 4NN and 4UN, the simulated values for m and k agree with measurements within 20%. For the sample 4UV, the measured values are a factor of three larger than the simulated ones. Such discrepancy could be explained by an unaccounted contact resistance of \(\sim 2\,\hbox {k}\Omega \) in the excitation line, perhaps due to a defective wire bond to the sample. Simulated values of k and m are used for the sample 4UV in the further analysis.
Pressure Dependence We have measured pressure dependence of the resonance response for the sample 4UV, and the results are presented in Fig. 6. The line width increases linearly, as expected from the theory (Eqs. 3 and 4), and we infer the gap distance \(g\approx {2.3}\,\upmu \hbox {m}\) from the slope of the linear fit. We note that the gap distance approximately doubles from the value inferred from SEM images at room temperature (\(g\approx {1.2}\,\upmu \hbox {m}\)). We expect that the increased deformation results from increased stress due to different thermal expansion coefficients of the aluminum layer and the silicon substrate.
Response of the device 4UN, measured in vacuum at 4.2 K temperature. a Displacement amplitude dependence on the excitation force. The black line is a linear fit to the filled circles (linear response regime). b An example of linear response with Lorentzian line shapes. Such response is observed up to approximately 50 nm deflections. The resonance properties are obtained from fits to Eq. 2 (solid lines). c At higher excitation forces, the response becomes Duffing-like nonlinear with a negative shift in the resonance frequency. The displacement amplitude for panel (a) is taken from the absorption peak height, when sweeping frequency in the decreasing direction. The obtained amplitudes deviate from the linear dependence, indicating nonlinear increase in damping at high oscillation amplitudes (Color figure online)
Interestingly, M. Defoort et al. [21] report on decreased damping and deviation from the linear pressure dependence, as the mean free path of gas \(l_\mathrm {mfp}\) exceeds the gap distance g. In our measurements, the mean free path varies between 5 and 60 gap distances. We plot in Fig. 6 the expected response obtained from the phenomenological model \({\Delta }f \propto p/(1 + b(l_\mathrm {mfp}/g)^a)\) suggested in [21], using the given fit parameters a and b for the gap values \({4}\,\upmu \hbox {m}\) and \({50}\,\upmu \hbox {m}\). We estimate a and b for \(g={2.3}\,\upmu \hbox {m}\) from linear extrapolation of the parameters. In our devices such nonlinearity, originating from the effective limitation of the mean free path by diffusive scattering from the surfaces is not seen. We note that in the work [21] the surfaces were very rough, resulting from the \(\hbox {XeF}_2\) etching step. The HF vapor process used in this work does not attack the underlying Si substrate or the Al device layer and results in surfaces with more specular reflection.
Resonance response of the sample 4UV as a function of pressure, measured in \(^4\hbox {He}\) gas at 4.2 K temperature. The resonance line width \({\Delta }f\) (red circles) increases linearly with pressure as expected from theory (Eqs. 3 and 4). The thick solid line is a linear fit to the data, from which we infer the gap distance \(g\approx {2.3}\,\upmu \hbox {m}\). For comparison, we also plot the response expected from the phenomenological model presented in Ref. [21] using the given fit parameters a and b obtained for gap distances \(g={4}\,\upmu \hbox {m}\) and \(g={50}\,\upmu \hbox {m}\), and extrapolated parameters for gap value \(g={2.3}\,\upmu \hbox {m}\) (thin solid, dashed and dotted lines). The measured frequency shift \(\delta {f}\) (blue filled squares) has contributions from the squeeze film force (Eq. 4) and adsorbed mass. The blue empty squares present the frequency shift with the squeeze film effect subtracted, and it corresponds to the adsorbed mass \({\Delta }m\). The adsorption is well described with a simple Langmuir isotherm (Eq. 5, blue dash-dot line) up to about 0.2 mbar, where the adsorption saturates at coverage \({0.073}{\AA ^{-2}}\), or approximately one monolayer of \(^4\hbox {He}\) (thick dashed line) [22] (Color figure online)
4 Conclusions
Suspended aluminum nanoelectromechanical resonators have been fabricated and operated in vacuum and low-pressure \(^4\hbox {He}\) gas at 4.2 K temperature. Q values up to 4400 have been achieved. The high sensitivity of the devices is demonstrated by large changes in resonance response, as small quantities of \(^4\hbox {He}\) gas are admitted to the vacuum chamber. Such devices show promise as sensitive probes of the quantum fluids.
References
M. Blažková, M. Človečko, V.B. Eltsov, E. Gažo, R. de Graaf, J.J. Hosio, M. Krusius, D. Schmoranzer, W. Schoepe, L. Skrbek, P. Skyba, R.E. Solntsev, W.F. Vinen, Vibrating quartz fork—a tool for cryogenic helium research. J. Low Temp. Phys. 150, 525 (2008)
R. Blaauwgeers, M. Blazkova, M. Človečko, V.B. Eltsov, R. de Graaf, J. Hosio, M. Krusius, D. Schmoranzer, W. Schoepe, L. Skrbek, P. Skyba, R.E. Solntsev, D.E. Zmeev, Quartz tuning fork: thermometer, pressure- and viscometer for helium liquids. J. Low Temp. Phys. 146, 537 (2007)
E. Pentti, J. Rysti, A. Salmela, A. Sebedash, J. Tuoriniemi, Studies on helium liquids by vibrating wires and quartz tuning forks. J. Low Temp. Phys. 165, 132 (2011)
A. Salmela, J. Tuoriniemi, J. Rysti, Acoustic resonances in helium fluids excited by quartz tuning forks. J. Low Temp. Phys. 162, 678 (2011)
D.I. Bradley, R. George, A.M. Gunault, R.P. Haley, S. Kafanov, M.T. Noble, Y.A. Pashkin, G.R. Pickett, M. Poole, J.R. Prance, M. Sarsby, R. Schanen, V. Tsepelin, T. Wilcox, D.E. Zmeev, Operating nanobeams in a quantum fluid. Sci. Rep. 7, 4876 (2017)
P. Zheng, W.G. Jiang, C.S. Barquist, Y. Lee, H.B. Chan, Anomalous damping of a microelectromechanical oscillator in superfluid \(^{3}\)He-B. Phys. Rev. Lett. 117, 195301 (2016)
M. Defoort, S. Dufresnes, S.L. Ahlstrom, D.I. Bradley, R.P. Haley, A.M. Guénault, E.A. Guise, G.R. Pickett, M. Poole, A.J. Woods, V. Tsepelin, S.N. Fisher, H. Godfrin, E. Collin, Probing bogoliubov quasiparticles in superfluid \(^3\)He with a ‘vibrating-wire like’ MEMS device. J. Low Temp. Phys. 183, 284 (2016)
W.F. Vinen, M. Tsubota, A. Mitani, Kelvin-wave cascade on a vortex in superfluid \(^{4}\)He at a very low temperature. Phys. Rev. Lett. 91, 135301 (2003)
A.W. Baggaley, J. Laurie, Kelvin-wave cascade in the vortex filament model. Phys. Rev. B 89, 014504 (2014)
L. Kondaurova, V. L’vov, A. Pomyalov, I. Procaccia, Kelvin waves and the decay of quantum superfluid turbulence. Phys. Rev. B 90, 094501 (2014)
J.T. Mäkinen, V.B. Eltsov, Mutual friction in superfluid \(^{3}\)He-B in the low-temperature regime. Phys. Rev. B 97, 014527 (2018)
N.B. Kopnin, M.M. Salomaa, Mutual friction in superfluid \(^{3}\)He: effects of bound states in the vortex core. Phys. Rev. B 44, 9667 (1991)
T.D.C. Bevan, A.J. Manninen, J.B. Cook, J.R. Hook, H.E. Hall, T. Vachaspati, G.E. Volovik, Momentum creation by vortices in superfluid \(^{3}\)He as a model of primordial baryogenesis. Nature 386, 689 (1997)
E. Collin, T. Moutonet, J.S. Heron, O. Bourgeois, Y.M. Bunkov, H. Godfrin, A tunable hybrid electro-magnetomotive NEMS device for low temperature physics. J. Low Temp. Phys. 162, 653 (2011)
D. Schmoranzer, M. La Mantia, G. Sheshin, I. Gritsenko, A. Zadorozhko, M. Rotter, L. Skrbek, Acoustic emission by quartz tuning forks and other oscillating structures in cryogenic \(^{4}\)He fluids. J. Low Temp. Phys. 163(5), 317 (2011)
W. Fang, J.A. Wickert, Determining mean and gradient residual stresses in thin films using micromachined cantilevers. J. Micromech. Microeng. 6, 301 (1996)
A. Cleland, M. Roukes, External control of dissipation in a nanometer-scale radiofrequency mechanical resonator. Sens. Actuators A Phys. 72(3), 256 (1999)
S. Schmid, L.G. Villanueva, M.L. Roukes, Fundamentals of Nanomechanical Resonators (Springer, Berlin, 2016)
E. Collin, Y.M. Bunkov, H. Godfrin, Addressing geometric nonlinearities with cantilever microelectromechanical systems: beyond the duffing model. Phys. Rev. B 82, 235416 (2010)
M. Suijlen, J. Koning, M. van Gils, H. Beijerinck, Squeeze film damping in the free molecular flow regime with full thermal accommodation. Sens. Actuators A Phys. 156, 171 (2009)
M. Defoort, K.J. Lulla, T. Crozes, O. Maillet, O. Bourgeois, E. Collin, Slippage and boundary layer probed in an almost ideal gas by a nanomechanical oscillator. Phys. Rev. Lett. 113, 136101 (2014)
M. Boninsegni, On the existence of supersolid \(^{4}\)He monolayer films. J. Low Temp. Phys. 165, 67 (2011)
Acknowledgements
Open access funding provided by Aalto University. This work has been performed at the Low Temperature Laboratory, which is part of the OtaNano infrastructure, supported by Aalto University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kamppinen, T., Eltsov, V.B. Nanomechanical Resonators for Cryogenic Research. J Low Temp Phys 196, 283–292 (2019). https://doi.org/10.1007/s10909-018-02124-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10909-018-02124-z