Abstract
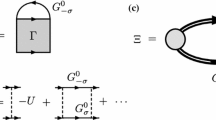
We investigate strong-coupling properties of a two-dimensional ultracold Fermi gas in the normal phase. In the three-dimensional case, it has been shown that the so-called pseudogap phenomena can be well described by a (non-self-consistent) T-matrix approximation (TMA). In the two-dimensional case, while this strong-coupling theory can explain the pseudogap phenomenon in the strong-coupling regime, it unphysically gives large pseudogap size in the crossover region, as well as in the weak-coupling regime. We show that this difficulty can be overcome when one improves TMA to include higher-order pairing fluctuations within the framework of a self-consistent T-matrix approximation (SCTMA). The essence of this improvement is also explained. Since the observation of the BKT transition has recently been reported in a two-dimensional \(^6\hbox {Li}\) Fermi gas, our results would be useful for the study of strong-coupling physics associated with this quasi-long-range order.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. Gurarie, L. Radzihovsky, Ann. Phys. 332, 2 (2007)
I. Bloch, J. Dalibard, W. Zwerger, Rev. Mod. Phys. 80, 885 (2008)
J.T. Stewart, J.P. Gaebler, D.S. Jin, Nature 454, 744 (2008)
J.P. Gaebler et al., Nat. Phys. 6, 569 (2010)
K. Martiyanov, V. Makhalov, A. Turlapov, Phys. Rev. Lett. 105, 030404 (2010)
M. Feld et al., Nature 480, 75 (2011)
B. Fröhlich et al., Phys. Rev. Lett. 106, 105301 (2011)
A.T. Sommer et al., Phys. Rev. Lett. 108, 045302 (2012)
V. Makhalov, K. Martiyanov, A. Turlapov, Phys. Rev. Lett. 112, 045301 (2014)
M.G. Ries et al., Phys. Rev. Lett. 114, 230401 (2015)
P.A. Murthy et al., Phys. Rev. Lett. 115, 010401 (2015)
K. Fenech et al., Phys. Rev. Lett. 116, 045302 (2016)
V.L. Berezinskii, Sov. Phys. JETP 32, 493 (1971)
J.M. Kosterlitz, D.J. Thouless, J. Phys. C 6, 1181 (1973)
S. Tsuchiya, R. Watanabe, Y. Ohashi, Phys. Rev. A 80, 033613 (2009)
Q.J. Chen, K. Levin, Phys. Rev. Lett. 102, 190402 (2009)
H. Hu, X.-J. Liu, P.D. Drummond, H. Dong, Phys. Rev. Lett. 104, 240407 (2010)
F. Marsiglio et al., Phys. Rev. B 91, 054509 (2015)
M. Matsumoto, D. Inotani, Y. Ohashi, Phys. Rev. A 93, 013619 (2016)
S.A. Morgan, M.D. Lee, K. Burnett, Phys. Rev. A 65, 022706 (2002)
R. Haussmann, Z. Phys. B: Condens. Matter 91, 291 (1993)
M. Bauer, M.M. Parish, T. Enss, Phys. Rev. Lett. 112, 135302 (2014)
B.C. Mulkerin et al., Phys. Rev. A 92, 063636 (2015)
N.D. Mermin, H. Wagner, Phys. Rev. Lett. 17, 1133 (1966)
P.C. Hohenberg, Phys. Rev. 158, 383 (1967)
D.J. Thouless, Ann. Phys. 10, 553 (1960)
J.R. Schrieffer, Theory of Superconductivity (Addison-Wesley, New York, 1964)
K. Miyake, Prog. Theor. Phys. 69, 6 (1983)
Acknowledgments
We thank H. Tajima, T. Yamaguchi, P. van Wyk , and D. Kagamihara for discussions. M. M. was supported by Graduate School Doctoral Student Aid Program from Keio University. R. H. was supported by a Grant-in-Aid for JSPS fellows. D. I. was supported by Grant-in-Aid for Young Scientists (B) (No. 16K17773) from JSPS in Japan. This work was supported by the KiPAS project in Keio university. Y.O was supported by Grant-in-Aid for Scientific Research from MEXT and JSPS in Japan (Nos. 15K00178, 15H00840, 16K05503).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Matsumoto, M., Hanai, R., Inotani, D. et al. Pseudogap Phenomena Near the BKT Transition of a Two-Dimensional Ultracold Fermi Gas in the Crossover Region. J Low Temp Phys 187, 668–676 (2017). https://doi.org/10.1007/s10909-016-1694-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10909-016-1694-6