1 Introduction

SPICA [1] is a Japanese-led mission to fly a 3.25 m diameter IR telescope with a cryogenically cooled mirror (∼5 K). Cooling the optics reduces the background radiation caused by the ambient temperature of the FIR space telescopes that limits the sensitivity. The loading is then dominated by astrophysical background sources. The SAFARI [2] instrument is an imaging Fourier Transform Spectrometer (FTS) on SPICA with three bands covering the wavelength ranges: 35–60 μm, 60–110 μm, and 110–210 μm. The background radiation in these bands is estimated by emission from the Zodiacal light at a level of 0.3–1 fW. [2] This gives a photon noise equivalent power (NEP) at the detectors of \({\sim} 2\mbox{--}3\times 10^{-19}~\mbox{W/}\sqrt{\mathrm{Hz}}\). Therefore, we require detectors with electrical NEPs at least lower than the photon noise limit, i.e. \({\leq} 3\times 10^{-19}~\mbox{W/}\sqrt{\mathrm{Hz}}\). This is about 2 orders of magnitude higher sensitivity than what is required for detectors on a ground based telescope and impose a great challenge on the detector technology.

Transition edge sensor (TES) is the chosen detector for the SAFARI instrument. In collaboration with several European institutes, SRON is developing low thermal conductance TES bolometers that are based on Ti/Au bilayer as the sensitive element on suspended silicon nitride (SiN) membranes. The measured dark NEPs in our original devices were typically a factor of 2–3 higher than what were expected from the measured thermal conductance [3]. Here we argue that part of the excess noise is due to the thermal fluctuation in the supporting legs and present a distributed leg model that provides a guideline for designing low noise devices. We then support the model by our latest measurement results.

2 Distributed Model

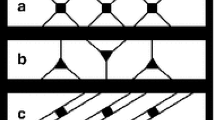
The simplest TES model consists of a heat capacity C TES connected to the bath with a heat conductance G TES . The electrical-thermal equations that follow from this model were introduced by M.A. Lindeman [4]. In the low-G devices as the legs are very long the mass and the heat capacity of the legs are considerable compared to that of the TES and the SiN island. The temperature along the legs also varies between the T C and the T bath . A way to model this would be to consider the legs as a series of bodies with certain heat capacities C′s at different temperature that are connected with series of G′s as shown in Fig. 1. The total heat conductance is then G TES =G/(n+1). Similarly, the total heat capacity of the legs is C LEG =nC, where n is the number the segments chosen for a SiN leg. A more comprehensive model would take into account the temperature dependence of C′s and G′s and assign different values to different bodies. Also we assume a linear temperature distribution between the bodies from T C to T bath , which further simplifies the model. Writing the small signal heat balance equations similar to the simple model leads us the following impedance matrix that can be used to calculate the noise, responsivity and the complex impedance of the TES.

Fig. 1
figure 1

(Color online) Distributed leg model with n bodies and the resulting impedance matrix from the small signal electrical-thermal equations

Full size image

In Fig. 1 R L is the loading resistance and L is the inductance in the bias circuit. T 0 is the temperature of the device, R 0 is the resistance of the TES, I 0 is the dc current that runs through the device and P 0 is the corresponding dc power. α and β are defined as:

$$\alpha =\frac{T_{0}}{R_{0}}\frac{\partial R}{\partial T}\bigg|_{I_{0}} ,\qquad\beta = \frac{I_{0}}{R_{0}}\frac{\partial R}{\partial I} \bigg|_{T_{0}}.$$

The total noise current consists of the phonon noise I PH , the Johnson noise I JO and the noise from the loading resistor I L .

where I JO and I L are:

In order to calculate the phonon noise we need to know the thermal fluctuation in each of the bodies in the model and the responsivity associated with them. The responsivity of the ith body is defined as SI i =dP i /dI with P i being the power applied to that body and I is the TES current. The responsivity and the phonon noise contribution of each of the bodies are as follows:

Here k B is the Boltzmann’s constant and γ n is a number between 0.5–1 that depends on the heat transport mechanism and can be estimated as γ n =((T n /T n+1)4+1)/2 for each section [5]. The total phonon noise is:

The impedance of the device Z TES can also be calculated using the matrix:

By setting n equal to 0, all equations above are reduced to that of the simple bolometer model. In that case M 0 will be a 2×2 matrix and there is only one responsivity (SI 0) and only one term for the phonon noise (I PH =I PH0) [6]. Figure 2 shows the measured and modeled impedance and the noise spectra using the simple TES model (n=0) and the distributed leg model (n=10). The bias point is at 30% low in the transition. The details of this device are reported elsewhere [3]. Note that in this calculation all device parameters are identical in both models. The bias point and the total G TES are known from the IV curves. α, β and C TES are extracted from the impedance curves. The only difference is that for the distributed leg model we estimate the C LEG by comparing the geometry of the legs and the island, distribute that into 10 bodies and insert it between the TES and the bath. The number 10 is chosen as an example and by no means is an optimal. We ran the model for up to 10 bodies and see that the results converge slowly. Increasing the number of bodies further has to be investigated but we do not expect a drastic change in results and the conclusions certainly remain the same. As we see in Fig. 2 (a) and (b), the measured noise is about a factor of two higher than the calculated noise at low frequencies. Besides, there is a bump in the measured noise spectra that cannot be explained by the simple model and there is a clear difference between the measured and modeled impedance curves at low frequencies. Although the distributed leg model cannot explain all the excess noise, it does predict the shape of the noise spectra and is in better agreement with the measured impedance. Overall our modeling effort indicates that the major part of our excess noise is due to the thermal fluctuations in the long supporting legs.

Fig. 2
figure 2

(Color online) Measured (red dots) noise and complex impedance compared with calculated (solid lines) values using (a) simple TES model (n=0) and (b) distributed leg model (n=10). The bias point is at 30% of the normal state resistance

Full size image

3 Low Noise Design Guidline

The measured NEP of the TES in Fig. 2 is \(2\times 10^{-18}~\mbox{W/}\sqrt{\mathrm{Hz}}\), which is about an order of magnitude higher than what is required for the SAFARI. In order to reduce the NEP we need to lower the G TES . Assuming that G TES scales with the leg geometry this can be realized by combination of increasing the length, decreasing the width and reducing the membrane thickness.

In principle we can achieve a certain G TES using different leg geometries and the distributed leg model enables us to calculate the noise for different designs. Figure 3 shows the calculated noise current spectra and the corresponding NEP for TES with the same G TES but different leg mass. A T C of 100 mK is used, which gives an NEP of about \(3\times 10^{-19}~\mbox{W/}\sqrt{\mathrm{Hz}}\). Here the C TES is set to 5 fJ/K but the total heat capacity of the legs (C LEG ) varies between 0.5 to 50 times smaller than C TES .

Fig. 3
figure 3

(Color online) Calculated noise and NEP using the distributed model (n=10) for different heat capacity in the legs. In all cases the heat capacity of TES (C TES ) is 5 fJ/K and total heat conductance is 0.3 pW/K. The bias point is at 30% of the normal state resistance

Full size image

It is clear that the lighter the legs, the lower the excess noise bump. The lower the total G TES , the slower the device and therefore the noise role-off frequency is lower. In case of very low-G devices with heavy legs, the low frequency tail of the noise bump can be stretched well below 10 Hz, where it merges with 1/f noise. As a result the measured dark NEP would be larger. To confirm this hypothesis we compare two devices one with heavy legs (TES #1) and the other one with light legs (TES #2). Table 1 summarized some of the important parameters of these two devices. As we see in Table 1, the T C , saturation power and the G of these two are very similar but note that the legs of the TES #1 are about 42 times heavier than TES #2 (shown in Fig. 4). Although the membranes and the TES sizes are not the same, we believe that the main difference between the two devices is the mass of the legs. Figure 5 shows the noise current spectra at different bias points.

Fig. 4
figure 4

(Color online) TES #2 fabricated on 0.5 μm thick 160×160 μm2 SiN island supported by 1 μm wide and 400 μm long SiN legs

Full size image
Fig. 5
figure 5

(Color online) Noise current spectra of devices with heavy legs (TES #1) and light legs (TES #2). TES #1 has 42 times heavier legs than the TES #2

Full size image
Table 1 Parameters of the devices
Full size table

It is evident that the excess noise bumps seen in TES #1 are substantially smaller in TES #2 as expected from the model. We measured lower dark NEP of \(4.2\times 10^{-19}~\mbox{W/}\sqrt{\mathrm{Hz}}\) for the latter. The conclusion is that in order to achieve low NEP it is essential to fabricate low-G TES devices with as light as possible supporting legs. This means that they should be made as narrow as possible on as thin as possible membrane and only as long as necessary.