1 Introduction

Polymer nanocomposite has received significant commercial interest. Polymer blends have long been used to improve the performance of materials rather than a single polymer in many device applications [1]. Among the nanocomposites currently being researched and manufactured are polymer embedded with inorganic metal particles, complexed organometallic polymer, polymer blend, metal/ceramic composite, and inorganic-within nanocomposites [2, 3]. Poly(vinyl alcohol) (PVA) and poly(vinyl pyrrolidone) (PVP) are synthetic polymers that are degradable, non-toxic, and easily scalable. These nanocomposites are employed in medical, engineering, and technological applications [4,5,6]. PVA is prepared via alcoholysis reaction of poly(vinyl acetate) because vinyl alcohol monomer doesn't really exist in free state. Moreover, it has hydroxyl functional groups connected to the backbone structure, which gives a hydrophilic polymer. As a result, PVA dissolves to a more significant or lower extent in water, depending on its hydrolysis [7, 8]. Indeed, PVP film is regularly too fragile to withstand industrial processors such as folding or extending. PVP polymer has interacting domains with nitrogen atom and C=O group which act as a barrier between other inorganic compound surfaces [9].

It should be noted that the solubility of polymer in water decreases as the degree of polymer hydrolysis increases and the treating temperature. This behavior is responsible for the enhanced crystallinity as well as the higher proportion of hydrogen bonding in totally hydrolyzed polymers [10, 11]. Blending, also known as a physical mixture of both PVA and PVP polymers in weight percentage of 1:1 results in a new novel unique polymeric blend with strong suitability due to hydrogen bond interaction [12, 13].

Metal nanoparticles (NPs) have been extensively studied over the last decade due to its critical role in applied nanoscience such as sensors, contamination of water and biomedicine [7, 14,15,16,17,18].

The combination of PVP and PVA forms a stable and flexible polymer film which have functional polar groups hydroxyl (–OH) and carbonyl (C=O) in their chain backbones which form strong interactions with different types of inorganic ingredients and nanofillers [12]. The blend of PVA and PVP polymers and its doping with broad bandgap composite semiconductor NPs is of tremendous optoelectronic importance because of the rich charge transport mechanism in the π-conjugate structure of PVP and the charge storage capacity of PVA [19]. The interactions between copolymer PVA and PVP network with presence of Zn NPs are depicted in Fig. 1. In this figure, zinc NPs are electrostatically stabilized through the carbonyl and hydroxyl groups from the pyrrolidone rings and PVA, respectively. Also, in Fig. 1 presence of hydrogen bonds between hydroxyl (–OH) and carbonyl (C=O) found in the chain backbone of PVA and PVP asset in the stabilization of zinc NPs.

Fig. 1
figure 1

Zinc nanoparticles capped in a co-polymer network (PVA/PVP)

Full size image

2 Formation Mechanism of PVA/PVP Doped with ZnO/ZnS Nanoparticles

Once ionizing radiation is absorbed in aqueous solutions it causes radiolysis. Some of the absorbed energy is used to form reactive intermediates, which are then used in a variety of activities [20,21,22]:

$$ {\text{H}}_{2} {\text{O}} \to {\text{e}}_{{{\text{aq}}}} ,\;{\text{H}}^{ \cdot } ,\;^{ \cdot } {\text{OH}},\;{\text{H}}_{2} ,\;{\text{H}}_{2} {\text{O}}_{2} ,\;{\text{H}}_{3} {\text{O}}^{ + } ,\;{\text{OH}}^{ - } ,\;{\text{HO}}_{2} . $$
(1)

The creation of transitory species such as radicals (H·, ·OH) and free electrons (eaq) comes from the radiolysis of water [as in Eq. (1)]. Most of these species are effective oxidizing (OH) or reducing (eaq) agents. Zinc NPs can be formed through reactions of intermediate species such as radicals (H·, ·OH) and free electrons (eaq) with a precursor (zinc sulfate) dissolved in irradiated aqueous solutions. In the present study glycerol was added during the synthesis of zinc NPs to generate hydroxyalkyl radicals which can also act as reducing agents:

$$ {\text{R}}_{2} {\text{CH}} \cdot {\text{H}} + {\text{H}}\left( {{\text{OH}}} \right) \to {\text{R}}_{2}^{ \cdot } {\text{COH}}. $$
(2)

During the preparation, acetic acid was also added to act as an OH and H radical scavenger commonly utilized to enhance the reducing effectiveness in irradiated solutions [22].

$$ {\text{HCOO}}^{ - } + {\text{OH}}/{\text{H}} \to {\text{COO}}^{ - } + {\text{H}}_{2} {\text{O}}/{\text{H}}_{2} . $$
(3)

Furthermore, hydroxyalkyl radicals react with OH/H via hydrogen elimination or removal, as seen in the following equation:

$$ {\text{R}}_{2}^{ \cdot } {\text{COH}} + {\text{OH}}/{\text{H}} \to \left( {{\text{CH}}_{3} } \right)_{2} {\text{COH}} + {\text{CH}}_{2} {\text{CH}} \cdot {\text{HCH}}_{3} + {\text{H}}_{2} {\text{O}}/{\text{H}}_{2} . $$
(4)

Moreover, the radicals generated in the previous reactions, eaq, COO−, and (CH3)2COH can reduce metal ions to lower valences [21,22,23,24] as follows:

$$ {\text{Zn}}^{2 + } + {\text{e}}^{ - } \to {\text{Zn}}^{ + } + {\text{e}}^{ - } \to {\text{Zn}}^{0} , $$
$$ {\text{Zn}}^{ + } + {\text{COO}}^{ - } \to \left[ {{\text{Zn}}^{ + } {\text{COO}}} \right]^{{\left( {{\text{n}} - 1} \right) + }} \to {\text{Zn}}^{{({\text{n}} - 1)}} + {\text{CO}}_{2} , $$
$$ {\text{Zn}}^{ + } + \left( {{\text{CH}}_{3} } \right)_{2} {\text{COH}} \to \left[ {{\text{Zn}}\left( {{\text{CH}}_{3} } \right)_{2} {\text{COH}}} \right]^{{{\text{n}} + }} \to {\text{Zn}}^{{({\text{n}} - 1)}} + \left( {{\text{CH}}_{3} } \right)_{2} {\text{C}} = {\text{O}} + {\text{H}}^{ + } , $$
(5)
$$ 2{\text{Zn}}^{{\left( {{\text{n}} - 1} \right) + }} \to {\text{Zn}}^{ + } + {\text{Zn}}^{{\left( {{\text{n}} - 2} \right) + }} , $$
$$ 2{\text{Zn}}^{ + } + 2{\text{OH}}^{ - } \to 2\left[ {{\text{ZnOH}}} \right] \to 2{\text{ZnO}} + {\text{H}}_{2} {\text{O}}. $$

The role of stabilizing agents or polymeric (such as PVA and PVP of the present case) is critical because they prevent aggregation caused by high surface energy. This can be done by interaction with different polymeric functional groups like –OH, –NH2, CONH2 and –COOH, that have a strong attraction for metallic atoms and metal ions. Indeed, the lone pair electrons of the polymer aids to the stability of metallic NP at their surface via covalent interaction [23]. Furthermore, steric hindrance in the polymer chain prevents metallic NPs from aggregation. Hence, by electrostatic and steric stabilization the repulsion forces equalize the attraction forces providing stability. The stabilizers can also vary the size of the NPs and thus act as a capping agent, avoiding agglomeration and oxidation that after preparation process owing to oxidant agents or pH medium changes. It should be noted that the stabilizers are selected before irradiation to reduce metallic ions [24].

In the present work, blended nanocomposite PVA/PVP polymer films doped with ZnO/ZnS are prepared. The structural changes due to irradiation of as-prepared samples with e-beam at a given doses are recorded using EDXS, XRD, SEM, and HR-TEM techniques. Furthermore, the impact of the structural changes on the linear optical parameters such as energy gap and width of localized states are evaluated. Indeed, the calculated dispersion energy, single oscillator energy and lattice oscillator strength are applied to estimate material dispersion and its zero-dispersion wavelength. The wavelength at zero dispersion is necessary parameter to show the suitability of the studied PVA/PVP polymer doped with ZnO/ZnS to apply as a fiber core to transmit optical data with minimum dispersion.

3 Experimental Details

3.1 Materials and Chemicals

PVA/PVP doped with ZnO/ZnS NPs are prepared with the following starting materials, PVA with molecular weight (M.Wt.) 115,000, (–C2H4O)n, purity 95%, hydrolysis (mole%) 98–99, and provided by Loba Chemie, India. PVP, M.Wt. 40,000, extra pure 99.18%, supplied by Alpha Chemika. Acetic acid glacial with purity 99.85%; M.Wt. 60.05 g/mol, delivered by Loba Chemie. Furthermore, zinc sulfate (ZnSO4·7H2O), M.Wt. 161.47 g/mol, purity 99% provided by El Gomhouria Co., Egypt. Glycerin (C3H8O3) with M.Wt. 92.094 g/mol, purity 99.5% (spectrophotometric grade), El Gomhouria Co., Egypt. It should be noted that in the previous work [25], a series of PVA/PVP copolymers are prepared at different compositions (0:100), (20:80), (40:60), (60:40), (80:20) and (100:0). The gelation (%) was determined to assist in the selection of the most suitable composition for the application part. The PVA/PVP composition at (40:60) was selected to be used as stabilizing agent or nanoreactors for NP preparation.

3.2 Preparation

To prepare a polymeric film from PVA/PVP blend with good optical and electro-conductive properties, PVA/PVP blend was functionalized with a carboxylic group (COOH) using acetic acid and glycerol then doped with zinc oxide and zinc sulfide NPs via following procedures: PVA (10 wt%) and PVP (10 wt%) were stirred in distilled water until dissolved at 85 °C and 45 °C. The two solutes were blended at a ratio of (PVA/PVP) (40:60). Furthermore, 14% (v/v) of acetic acid and 10% (v/v) of glycerol were added during stirring via a magnetic stirrer to be functionalized with the carboxylic group (COOH). Indeed, 6 wt% of ZnSO4·7H2O was added to the reaction mixture. After completely dissolving, the mixture was poured into Petri dishes and dried at room temperature. The as-prepared samples were irradiated with e-beam at irradiation doses 20, 25, 30, 35, and 40 kGy using a 3 MeV industrial linear accelerator beam 3 mA. Convyier speed 16 m/min. Here, it should be noted that an electron-beam is applied as an irradiation source in the present work because other irradiation sources such as gamma rays has un-controlled effect on some physical properties of irradiated samples such as mechanical and thermal properties than did e-beam [26]. The thickness of the films are determined to be ~ 1.8 mm using a digital micrometre screw gauge.

3.3 Measurements

The structure of the phases of non-irradiated and irradiated investigated samples are identified at room temperature using a computerised X-ray diffraction (XRD) system model Philips EXPERT-MPDUG PW-3040 diffractometer with a Cu Kα radiation source (λ = 0.15406 nm). The elemental analysis of the prepared films is tested using energy dispersive X-ray spectroscopy (EDXS). On the other hand, the surface morphology of the fresh samples is investigated by scanning electron microscope (SEM) model JEOL-JSM-5400. Indeed, the variations of the structure of the investigated films are probed by high resolution transmission electron microscope (HR-TEM) model JEOL, JEM 2100, Japan operating at 200 kV. The optical transmission (T) and reflection (R) spectra of the investigated PVA/PVP nanocomposite films are measured at room temperature in the spectral range 200–2500 nm using JASCO 670 UV–Vis–NIR dual beam spectrophotometer.

4 Results and Discussion

4.1 Structural Characteristics

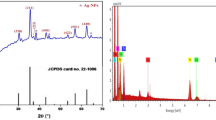
EDXS is a technique employed to investigate the elemental structural components of the studied samples. Spectra of EDXS shown in Fig. 2 are for the present 0.4PVA/0.6PVP Zinc Sulphate nanocomposite films irradiated with e-beam at doses 0.0 kGy (Fig. 2a), 20 kGy (Fig. 2b) and 35 kGy (Fig. 2c). Furthermore, the spectra revealed an oxygen peak positioned at 0.5 keV, Zn signals at approximately 1 keV and a signal between 8.5 and 9.5 keV, which refers to ZnO NPs molecule production with two phases. These two phases are ZnO and ZnS. Moreover, the EDXS spectra show Sulphur signal around 2.25 keV, indicating the production of zinc sulphide nanoparticles (ZnS NPs) [27]. As given in the inset tables of Fig. 2, the values of weight and atomicity percentage of Zn, O, and S are [4.74, 1.06], [47.93, 43.91], [2.75, 1.26] for zero irradiation dose, [6.59, 1.49], [43.59, 40.28], [3.61, 1.66] (irradiation dose 20 kGy) and [8.21, 1.87], [41.2, 38.42], [3.95, 1.67] for 35 kGy respectively [28]. As seen in Fig. 2, increasing the irradiation dose from 0 kGy up to 20 kGy strengthen sulphur peak by ratio ~ 31% and weaken the oxygen peak by ~ 9% accompanied by an increase in weight percent and atomicity of Zn. On the other hand, increasing the irradiation dose to 35 kGy increased the ratio of Zn by 39% accompanied by a little decrease of Sulphur and Oxygen peaks.

Fig. 2
figure 2

The EDXS pattern of the investigated PVA/PVP zinc sulphate nanocomposite films after being irradiated with e-beam at doses of 0.0 kGy (a), 20 kGy (b) and 35 kGy (c)

Full size image

4.2 X-Ray Diffraction

Figure 3 illustrates the XRD spectra of the studied 0.4PVA/0.6PVP (PP) films doped with zinc sulphate NPs for non-irradiated (0 kGy) and irradiated films with e-beam at doses 20, 25, 30, 35 and 40 kGy. Regarding non-irradiated sample absence of any diffraction peaks in XRD spectrum confirms the amorphous structure of the fresh films. Increasing the irradiation dose by 20 kGy leads to appearance of diffraction peaks at 2θ = 19.48° to 23.33°, which is attributed to the poly-crystalline nature between the functional groups (–OH and C=O) of PVA and PVP [29, 30]. Indeed, the peak position seen around ~ 10° represents the bond formed between OH of PVA with Zn metal and is called oxide phase molecule [30, 31]. Moreover, the identified XRD patterns show diffraction peaks at 2θ = 29.62°, 49.40°, and 57.67°, which correspond to the diffraction from planes (111), (220), and (311) and are related to ZnS nano-crystallites wurtzite structure (JCPDS card No. 36-1450) [32]. On the other hand, observed peaks at around angular positions 31.92°, 36.16°, 39°, 48.88°, 64.64°, 69.2° and 73.42° correspond to planes (100), (002), (101), (102), (103), (112) and (201) which refers to presence of ZnO. Zinc atoms occupy half of the tetrahedral sites in ZnO, which has a hexagonal wurtzite structure of closely packed lattice reported in JCPDS card No. 36-1451 [33, 34]. In addition, the intensity of the diffraction peaks becomes more pronounced with increasing electron beam dose which indicates more polycrystalline structure of the studied samples. This means that irradiation with e-beam assist to transform to polycrystalline structure of the investigated films. This behavior takes place because the electron beam provides enough energy to the crystallites of the studied samples to align in the proper equilibrium position.

Fig. 3
figure 3

XRD profile for non-irradiated, 0.0 kGy, and irradiated films at doses of 20, 25, 30, 35, and 40 kGy of PVA/PVP zinc sulphate nanocomposite films

Full size image

It is known that the measured X-ray spectrum of polycrystalline polymer consists of amorphous, crystalline, and background regions. The background spectrum is due to additives, and/or stabilizers in the studied polymer [35]. To distinct these three regions, a separation of the background from amorphous and crystalline regions is attained by applying the convolution process on the measured X-ray spectrum [35, 36]. It should be noted that the deconvolution process is used to separate amorphous hallow broad bands and crystalline peaks of X-ray spectrum into its several symmetrical Gaussian bands by considering area of each band related to a particular structural phase. The deconvolution process is applied on the investigated samples by sub-dividing the spectrum at each irradiation dose into different spectral regions and then fitting each band with Gaussian function. The area and the position of each Gaussian peak are recorded for quantitative analysis of the measured spectrum as shown in Fig. 4. The area under X-ray peak is considered to be proportional to the concentration of structural phase emerging it. If Aam is area under amorphous hollow region and Acr represent total area under crystalline peaks, the degree of crystallinity (Xc) is given by [35]:

Fig. 4
figure 4

Deconvolution for measured X-ray spectrum shown in Fig. 3 at different irradiation doses. Blue curve is the measured spectrum fitted with red line. Green hallows represents the amorphous hallows phase and orange peaks depicts for crystalline phase (Color figure online)

Full size image
$$\mathrm{Crsystallinity}\left({X}_{c}\right)\mathrm{\%}=\frac{ {A}_{cr}}{{A}_{am}+{A}_{cr}}.$$
(6)

The calculated crystallinity values of the studied PVA/PVP doped with ZnO/ZnS using deconvolution are listed in Table 1 as a function of irradiation doses. According to Table 1 the crystallinity value increases from 5.2% (dose = 0.0 kGy) up to 28% (dose = 40 kGy).

Table 1 Evaluated values of crystallinity %, mean crystalline size, D, microstrain ε, dislocation density δ calculated using XRD peaks, direct, \({E}_{g}^{dir}\), indirect, \({E}_{g}^{indir}\), energy gaps, Urbach energy Eu, single oscillator energy, \({E}_{0}\), dispersion energy, \({E}_{d}\), lattice oscillator strength, \({E}_{l}\), and wavelength at zero material dispersion, \({\lambda }_{WZMD}\), as function of irradiation dose
Full size table

The average crystalline size (D) of ZnO/ZnS NPs integrated in the functional network of 0.4PVA/0.6PVP could be determined by applying Scherrer formula on a peak with pronounced intensity at each irradiation dose. Scherrer equation has the form D = kλ/βcosθ, where k is a constant (= 0.94), λ symbolizes the used X-ray wavelength, β is the X-ray profile full width at half maximum (FWHM), and θ denotes the Bragg angle of the considered X-ray peak. Table 1 lists the determined particle size values of Zinc atoms as a function of irradiation dose. The calculated values of particle size (D) for the investigated films (Table 1) proves that irradiation increases the particle size from 30 nm (at 20 kGy) up to 42 nm (at 40 kGy), i.e. by increment ratio ~ 40% which means an aggregation of Zn NPs.

On the other hand, the microstrain (ε) generated within the PVA/PVP:ZnO/ZnS matrix is calculated using the following relation: ε = (βcosθ)/4 [37]. The evaluated microstrain values for the studied samples, is inserted in Table 1. Furthermore, changing atom displacement with respect to their reference-lattice positions causes the Lattice strain to decrease. A uniform compressive or microstrain causes diffraction line peak shift, whereas a non-uniform tensile and compressive strain causes diffraction line broadening (microstrain) [37].

The dislocation density (deformability) of a material is determined by the number and strength of dislocations per unit volume and is given by δ = 1/D2 [38]. The dislocation density established by the ZnO/ZnS nanofillers within the PVA/PVP matrix is listed in Table 1. The value of δ measures the agglomerations of crystalline clusters. The observed decrease of dislocation density (δ) meets an increase in crystallization and a massive reduction in vacancies as the irradiation dose increases [39].

4.3 High-Resolution Transmission Microscopy (HR-TEM)

HR-TEM is an enhanced technique that provides direct high-resolution images for the structure of the tested sample. HR-TEM provides a real image of NPs, allowing the internal morphology of nanocomposites to be identified. Furthermore, it is a useful supplement to XRD, especially when diffraction peaks are not easily visible in the pattern. Figure 5 depicts an HR-TEM image of the investigated zinc NPs embedded in a PVA/PVP polymer structural matrix and irradiated at irradiation doses of 0, 20, 35, and 40 kGy. In these images the bright area represents the PVA/PVP (40:60) hydrogel matrix while the dark areas denote zinc NPs and the areas between the dark shapes refer to interfacial spaces. However, it is observed that zinc NPs are well dispersed and capped inside the PVA/PVP network. Moreover, the detected NPs in Fig. 5 exhibit a variety of forms, including pyramidal, hexagonal, octahedron, cuboid, and rods [27]. Additionally, it was noticed that at an irradiation dose of 35 kGy, the PVA/PVP blend had branched out into several tiny dendritic subdivisions. In Fig. 5, the particle sizes are plotted against the number of counts in a histogram patterns. The Gaussian distribution function is used to fit the histogram, which revealed that the average particle size is around 58 nm for an unirradiated film. In addition, increasing irradiation dose the average particle size are 29 nm (20 kGy), 46 nm (35 kGy), and 47 nm (40 kGy). This is consistent with the value of particle size (D) calculated using XRD analysis for the investigated irradiated films. Furthermore, HR-TEM depicts the selected area electron diffraction (SAED) of the investigated samples as shown in Fig. 6 for irradiated samples at 20 kGy. In Fig. 6a SAED clearly reflects that the NPs are polycrystalline ZnO/ZnS, with viewable spots matching the pronounced four main reflection planes of (111), (100), (002), and (101), as seen in XRD in Fig. 3 [40]. The average distances of the ten clearly visible lattice fringes are used to calculate d-spacing as shown in Fig. 6b, c. The d-pacing value obtained is 0.35 nm, which corresponds to the interplanar spacing of (111) planes in ZnS [41].

Fig. 5
figure 5

High-resolution transmission electron microscope (HR-TEM) images and particle size histogram for investigated films at irradiation doses 0.0, 20, 35, and 40 kGy

Full size image
Fig. 6
figure 6

The selected area electron diffraction (SAED) profile a the lattice spacing, b the interplanar spacing, and c for a studied film irradiated at 20 kGy

Full size image

4.4 Scanning Electron Microscope (SEM)

SEM micrographs of PVA/PVP/zinc sulphate heptahydrate containing zinc NPs at different irradiation dose (0.0, 20, 25, 30, 35 and 40 kGy) are presented in Fig. 7. For all images of the investigated samples the smooth surface denotes the polymer (0.0 kGy), while at higher irradiation dose (20–40 kGy) the observed dark spot on the surface represents a composite material with a high mineral phase content (ZnO/ZnS) [42]. Furthermore, at a low irradiation dose of 0–25 kGy, crosslinked PVA/PVP/acetic acid/glycerin containing zinc NPs exhibited a homogeneous surface with a porous structure [33]. Throughout the polymerization reaction, the electrostatic repulsive forces between acetic acid carboxylate anions (COO−) cause the polymeric network to expand. Nonetheless, when the irradiation dose is increased to 30–40 kGy, the degree of crosslinking or polymerization increases because more free radicals and free electrons are formed, resulting in the formation of more bonds and a more precise network with fewer pores on the surface [43]. The uniform distribution of Zn NPs filler in PVA/PVP matrices resulted in high affinity, thermal stable properties, and enhanced activity in biological systems [44].

Fig. 7
figure 7

SEM images of investigated PVA/PVP films and doped with zinc nanoparticles at irradiation doses 0.0, 20, 25, 30, 35, and 40 kGy

Full size image

5 The Optical Spectra of PVA/PVP/Zinc Sulphate Nanocomposite Films

The measurement of optical properties in UV–Vis–IR spectral regions is considered as an essential tool for examining the electronic density of states, band structure, and electronic configuration of materials [12, 33].

5.1 Linear Optical Parameters

The dependence of the measured transmission (T) on wavelength (λ) for the investigated un-exposed and exposed films in the studied dose range is shown in Fig. 8. In this figure T shows an increase against λ up to a maximum value in the IR region at ~ 1320 nm. This trend is followed by a decrease of T accompanied by appearance of some transmission peaks with lower intensity at 1660, 1850 and 2005 nm. On the other hand, the dependence of T on irradiated dose shows a decrease more than 80% as the exposure dose increases with respect to non-irradiated sample (0.0 kGy). This trend could be explained as follows: The calculated values of particle size (D), for the investigated films (Table 1), proved an increase against irradiation dose from 30 nm (at 20 kGy) up to 42 nm (at 40 kGy), i.e. by increment ratio ~ 40% which means an aggregation of Zn NPs. The aggregation of Zn NPs increases the optical reflectance and decreases optical transmission which is argued to the metallic character of Zn.

Fig. 8
figure 8

The optical transmission spectra of non-irradiated and irradiated samples as a function of wavelength at various e-beam doses

Full size image

Opacity is an assessment of impenetrability to electromagnetic or any other types of radiation, particularly visible light, and may be employed to evaluate the spectral behavior of PVA/PVP/zinc sulphate nanocomposite films using the ASTM standard test procedure for plastic sheeting transparency [43]. The opacity is determined by using the measured transmission (T) spectra in the following relationship [43, 44]:

$$opacity=\frac{-\mathrm{log}({T}_{\lambda })}{x},$$
(7)

where Tλ represents the transmission at a given wavelength and x represents the thickness of the studied film. The calculated opacity values for the investigated samples in the visible spectral region at 600 nm and for the studied samples are shown in Fig. 9. It is observed that the opacity of all samples increases as irradiation doses and particle size increase.

Fig. 9
figure 9

The opacity at 600 nm of the investigated PVA/PVP/zinc sulphate nanocomposite films as a function of irradiation doses

Full size image

The linear optical dispersion coefficients index of refraction (n), extinction coefficient (k), and optical energy band gap (Eg) are essential parameters used to determine the optical applications of the studied material. The measured optical transmission T and reflection R against wavelength are applied to determine the linear optical constants (n) and (k) for PVA/PVP/zinc sulphate samples at different irradiation doses (0, 20, 25, 30, 35 and 40 kGy) of polymeric nanocomposite films using an analytical model [45]. The refractive index, n, is closely related to the electronic polarization of the ions as well as the local electric and lattice fields [39]. Figure 10 shows the calculated refractive index (n) versus wavelength of the studied non-irradiated and irradiated films. The obtained refractive index values decrease with increasing wavelength at any irradiation dose. From the figure it is seen that the n values decrease with increase of e-beam doses. This is due to changes in crystalline size and microstrain of samples, which cause changes in surface morphology and vacancies within the crystal structure. The trend of refractive index in Fig. 10 suggests a wide range of application for investigated samples such as optoelectronic applications, including enhanced visual functionalities of display screens such as LCDs, Organic light emitting, and quantum dot light emitting diode (QDLED) televisions [46, 47]. The intensity attenuation of electromagnetic waves passing through a thin film is described by the absorption coefficient (α) [48]. The absorption coefficient parameter can be calculated as α = 4πk/λ [48]. Figure 11 displays the calculated optical absorption coefficients (α) of the investigated samples as a function of photon energy at different e-beam doses. The observed increase of α against irradiation dose in Fig. 11 clarify that more photon energy are absorbed by PVA/PVP:ZnO/ZnS films due to an increase of particle size. Obviously, as Zn NPs size increases, the absorption edge shifts toward lower photon energy (red shift) which is argued to the formation of the conjugated bond system as a result of bond cleavage and reconstruction which is argued to the structural and chemical modifications of PVA/PVP combined with Zn NPs [49].

Fig. 10
figure 10

The variation of refractive index versus wavelength for non-irradiated and irradiated nanocomposite films

Full size image
Fig. 11
figure 11

The optical absorption coefficients (α) of non-irradiated and irradiated samples as a function of photon energy at various e-beam doses

Full size image

To specify the type of electronic transition, Tauc's method is used [50]. The optical absorption spectrum is useful for studying the physical properties of polymers, including band creation and electrical structures in pure and doped states. In actuality, the optical band gap could be calculated using Tauc's formula of the form [50]:

$$ (\alpha h\nu )^{m} = \alpha_{0} (h\nu - E_{g} ), $$
(8)

where α0 is an energy-independent constant associated with the size of the defect states of band tailing, hν is the photon energy, and m is an exponent that represents the type of optical transition. If m = 0.5, the indirect transition is supposed to allow, and m = 2 is direct transition. Figure 12 depicts the functional dependence of (αhν)0.5 and (αhν)2 at 0 kGy (as an example) on photon energy. The optical energy gap (Eg) could be calculated by extrapolating the linear portions of a plot to zero absorption values. Table 1 contains the values obtained of direct and indirect optical energy gaps for the investigated films as a function of irradiation dose. According to Table 1 the band gap decreased as irradiation increased which could be due to the formation of more free charge carriers/radicals. Based on these results, one can conclude that these samples can be used for a variety of optoelectronic devices [48, 49]. Urbach energy, also known as Eu factor, is used to efficiently detect the level of disorder in the optical energy gap of the studied films [51]. Absorption coefficient near the optical band edge is given by: ln (α) = constant + hν/Eu, where Eu is equal to the reverse of the slope of the ln (α) vs. photon energy. The calculated values of Urbach energy of non-irradiated and irradiated films as a function of irradiation doses are listed in Table 1. As seen in Table 1, the slightly reduced Urbach energy (Eu) versus radiation doses indicates that the irradiation process binds many ligands, resulting in binding in the carbon backbone in polymer system and a reduced degree of disorder of the film studied [30]. This is consistent with XRD results of the studied samples, which show that crystallinity increases with increasing irradiation (see Fig. 3).

Fig. 12
figure 12

Calculation method of both direct and indirect optical energy gap for investigated non-irradiated sample (as an example)

Full size image

5.2 Material Dispersion of PVA/PVP Doped with ZnO/ZnS (NPs)

Material dispersion is a phenomenon in which different optical wavelengths propagate at different velocities through a given medium, depending on the refractive index of the used material. To explore the optical dispersion behavior in the studied films, it is essential to determine some optical dispersion parameters such as single oscillator energy (E0), which represents the strength of optical transition between bands, dispersion energy (Ed) and lattice oscillator strength (El) for the investigated samples as follows: below the absorption edge the refractive index of the material could be expressed by Wemple–DiDominico [52] that has the following formula,

$${n}^{2}-1=\frac{{E}_{0}{E}_{d}}{{E}_{0}^{2}-{E}^{2}},$$
(9)

where E is the applied photon energy. Values of E0 and Ed could be evaluated from the slope and intercept of the straight part of the graphical plot of \({\left({n}^{2}-1\right)}^{-1}\) against \({E}^{2}\) in the high energy region of Eq. (9). On the other hand, in the spectral region when the resonance frequency is longer than the applied wavelength, the refractive index is given by [53]

$${n}^{2}-1=\frac{{E}_{d}}{{E}_{0}}-\frac{{E}_{l}^{2}}{{E}^{2}}.$$
(10)

The slope of the straight part of the graphical dependence of \({(n}^{2}-1)\) on \({E}^{-2}\) gives the value of El. The calculated values of E0, Ed and El are listed in Table 1. The material dispersion M(λ) could be expressed as follows:

$$M\left(\lambda \right)=-\frac{\lambda }{C}\frac{{d}^{2}n}{d{\lambda }^{2}},$$
(11)

where C is the speed of light in vacuum. According to Eq. (11), differentiating Eq. (10) twice with respect to wavelength yields the material dispersion in relations of E0, Ed, El and n as: [54, 55]:

$$\mathrm{M}\left(\lambda \right)=1.54\times {10}^{4}\left(\frac{{E}_{d}n{\lambda }^{3}}{{E}_{0}^{3}}\right)-2.17\times {10}^{3}\left(\frac{{E}_{l}^{2}\lambda }{n}\right).$$
(12)

5.2.1 Wavelength at Zero Material Dispersion

The WZMD is very special case of the optical dispersion where the wavelength of material dispersion and waveguide dispersion cancels each other. Furthermore, at this wavelength the minimum energy loss of transmitted data is attained through optical data transmission in fiber telecommunication. At M(λ) = 0 in Eq. (12), the calculated values of wavelengths at zero material dispersion, \({\lambda }_{WZMD}\), are shown graphically in Fig. 13.

Fig. 13
figure 13

Material dispersion curves versus wavelength, evaluated using Eq. (12) for investigated non-irradiated and irradiated samples at doses 20, 25, 30, 35, and 40 kGy with e-beam. Previously reported values of Silicates (SiO2) and Germinate (GeO2) (Wemple and DiDomenico, 1971) are introduced to the figure for the sake of comparison

Full size image

This figure shows that value of WZMD is 1.6842 μm for fresh non-irradiated sample and lie midway between the two best candidates used to manufacture data transmitters. These promised materials are silicate (SiO2) (WZMD = 1.56 μm) and germanate (GeO2) (WZMD = 1.87 μm). Irradiation of the studied blended PVA/PVP doped with ZnO/ZnS (NPs) decrease the WZMD against the increase of the e-beam irradiation dose from 1.6710 μm (at 20 kGy) down to 1.0351 μm (at 40 kGy), i.e. irradiation dose can tune the structure of the studied polymer to transmit data in a wide range of IR spectrum 1.6842–1.0351 μm.

6 Conclusions

The in situ chemical reduction method is used to prepare PVA/PVP blend doped with zinc sulphate NPs. Fresh samples are irradiated with an e-beam at doses ranging from 0 to 40 kGy. EDXS is used to verify the elemental composition of the fresh films, which revealed that the dominant phases in the explored peaks are zinc sulphide and zinc oxide. On the other hand, XRD measurements assured presence of ZnO and ZnS NPs in the PVA/PVP matrix and increasing the crystallinity against irradiation dose. Deconvolution of the measured X-ray showed that the \(\mathrm{crsystallinity}\) of the studied samples increases from 5.2% (for dose 0.0 kGy) to 28% (for dose 40 kGy) HR-TEM revealed formation of zinc NPs with a mean size of 29 nm within the polymeric network of the (PVA/PVP) blend. Furthermore, SEM images revealed a homogenous porous structure for the surface of (PVA/PVP) containing ZnO/ZnS NPs. The optical energy band gap (Eg) values decrease as the irradiation dose loading in the polymer matrix increases. Estimation of WZMD showed that e-beam irradiation could be used to tune the structure of the studied films to be used as a data transmitter in optical fiber telecommunication in the IR spectral range 1.6842–1.0351 μm.