Abstract
We use an annual household panel to conduct a comparative analysis of which decision theory explains life satisfaction better. We consider expected utility theory and prospect theory. We consider the effects of three domains on life satisfaction: income, health, and (un)employment. Using a fixed effects estimator we find that life satisfaction contains features of both expected utility theory and prospect theory. However, the elements of expected utility theory are stronger predictors of life satisfaction. Life satisfaction depends positively on income, good health, and employment. It also depends positively on income and employment improvements, however the reverse is true for health improvements. Life satisfaction is concave in income gains and convex in income losses, and it exhibits loss aversion in income and employment status, but not in health. The results suggest that life satisfaction is best described by expected utility theory, but also contains some aspects of prospect theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We investigate which decision theory best explains life satisfaction (henceforth LS) as reported in an annual household panel. We consider the two most prominent decision theories in economics: expected utility theory (EUT), and prospect theory (PT). We analyse their predictions by looking at three outcomes which have consistently been found to improve LS: income, health, and employment.
We consider the following properties of PT: First, whether individuals evaluate their LS against a reference point. Specifically, we test whether changes in an outcome can help explain LS levels. An affirmative answer would be consistent with individuals using their past outcome as a reference point in evaluating their current LS. Second, whether individuals exhibit loss aversion in outcomes, that is, whether the effect of a decrease in one of those variables reduces LS more than an equivalent increase improves it. Finally, whether individuals exhibit the reflection effect for income. That is, we test whether LS is concave in income gains and convex in income losses. In PT, these three features—a reference point, loss aversion and the reflection effect—are identified as the distinguishing elements of the value function. PT is a theory of “decision under risk” but these properties are relevant even in choices not involving chance (Kahneman & Tversky, 1979; Tversky & Kahneman, 1991).Footnote 1
The two theories considered in this paper need not be exclusive. For example, the literature has found support for both absolute and relative income effects (Blanchflower & Oswald, 2004; Clark et al., 2008b). Empirically, one theory is not nested within the other in explaining LS. This is reflected in our model which allows for absolute effects, relevant to EUT, and relative effects, relevant to PT. We find that LS is best described by an empirical model that incorporates features of both EUT and PT. However, EUT predicts LS more strongly than PT. In line with the literature on subjective well-being (SWB), we find that LS is increasing in income levels and in good health. Being employed implies higher LS than being unemployed, and LS is concave in income. In addition, many, but not all, of the features of PT are also supported. The marginal effect of income changes is asymmetric and supports loss aversion. The positive effect of income gains on LS is non-significant, but the negative effect of losses is highly significant. Similarly, LS concavity in income gains is not significant, but LS convexity in income losses is strong and highly significant, consistent with the reflection effect of PT. As expected, losing a job decreases LS while finding a job increases it. Maybe our most striking finding is that LS is decreasing in health improvements and increasing in health losses, when controlling for health status. While a person’s LS is strictly increasing in their health, it is also sensitive to whether they arrived at their current health status from better or from worse health. We also find a significant loss aversion effect in employment changes. The only domain for which we do not find evidence of loss aversion is health. Instead, in this domain we find that individuals have a loss preference.
Our paper is related to two areas of research in the literature: the (quasi-)experimental research on PT and related decision theories, and the LS research, which mainly builds on survey data. The main contribution of our paper to the literature is that we estimate a model which can nest elements of both EUT and PT in one empirical model. In contrast, the literature has typically focused on one aspect of a decision theory and sought to find evidence for or against it. For example, Boyce et al. (2013) test for loss aversion in income changes, but do not include income levels as an explanatory variable. While they support the notion of loss aversion, it is not clear whether income changes contribute more to life satisfaction than income levels, or indeed whether loss aversion would still hold once income levels are controlled for. The second contribution is that we consider life domains other than income. The importance of labour force status and of health on LS is well documented, and there is also a literature which looks at dynamic phenomena such as adaptation to certain health states (Oswald & Powdthavee, 2008) and to a lesser extent to employment states (Clark et al., 2008a, 2001). However, most of the research comparing EUT and PT focus on income. We are not aware of any research which compares the said theories with respect to health and employment. Since health is a good, and employment is by definition preferred to unemployment, we should expect LS to display characteristics of a value function with respect to those goods too. We use the individual’s past self as a reference point. We believe this to be a more natural choice for panel data than a peer group based definition, which is severely restricted by data constraints. However, the online appendix includes a discussion of alternative reference points.
2 Literature Review
Since the publication of “Prospect theory: An analysis of decision under risk” by Kahneman and Tversky (1979), non-expected utility theory has developed into a very active literature. Many authors have proposed alternatives to the classical expected-utility model,Footnote 2 and another strand of the literature has tested hypotheses related to PT and its extensions by means of laboratory or field experiments.Footnote 3 The strongest support for PT and other reference-dependent value models comes from such laboratory and field experiments (Abdellaoui et al., 2007; List, 2004).
In contrast, the literature on LS and SWB in general has relied on survey data and this is the approach followed in this paper. Dolan et al. (2008) and Clark (2018) provide good surveys of the literature. The work closest to ours is Boyce et al. (2013), Di Tella et al. (2010), Vendrik and Woltjer (2007), Ferrer-i Carbonell (2005), Fang and Niimi (2017), and De Neve et al. (2018). The listed papers, however, have different goals and differ in important aspects from ours. First, the modelling choices in the literature are such that only some feature of EUT or PT can be tested for at once, while our model contains the main features of both theories and leaves it to the data to retain or to reject them. Second, we extend the analysis of aspects of PT to life domains other than income. Specifically, we test whether reference point effects and loss aversion are present in health and employment status.Footnote 4
Boyce et al. (2013) consider the effect of income changes on well-being and find evidence for loss aversion. Their paper is closest in spirit to ours. While informative, the empirical model used is improper as a test of discriminating between PT and EUT, because it does not map to the value functions of either of those theories. In particular, they use previous-period LS as a control variable and allow for a discontinuity between negative and positive income changes. This feature makes it impossible to identify LS with any value function known in decision theory. EUT as an explanation for LS is ruled out ex-ante, as income levels are not included as an explanatory variable.
Di Tella et al. (2010) are mainly concerned with the long-run adaptation to income and social status of individuals where they measure status as the prestige of the respondent’s occupation. The prestige scores are based on survey results and reflect the ranking of occupations by respondents. They find that people adapt to income but not to social status. They consider a model with changes in income as independent variables. They also allow asymmetric effects from gains and losses, i.e., loss aversion, but these gains and losses are from the present to the next period (assuming that future income is closely related to anticipated income).Footnote 5 This approach assumes that individuals have realistic expectations about their future incomes. The model only accommodates a symmetric effect of the change in income from the previous period. By contrast, our choice of reference point can be interpreted as looking for the asymmetric effect of already-realised income changes on currently experienced utility. In addition, we also allow for diminishing marginal effects and look for differences in curvature over gains and losses.
Fang and Niimi (2017) look for loss aversion in a Japanese household panel. For loss aversion in income, they use a very similar specification to the one of Di Tella et al. (2010), discussed above. A similar discussion regarding the reference point can be made, but they enjoy an advantage over Di Tella et al. (2010) in that they have data for expected future income changes. This means they do not have to proxy expected future income by future income in the panel, which brings their empirical reference point closer to its theoretical counterpart. As Di Tella et al. (2010), they do not consider possible diminishing marginal effects of income changes. Their quantile regression approach shows that the loss aversion comes from the bottom quantiles, and no effects can be seen at the mean.
Vendrik and Woltjer (2007) have the same goal as us of testing the predictions of PT on the German Socio-Economic Panel — a widely used data set in life satisfaction research. However, they make a very different choice for the reference point. They use as reference point the average income of the social reference group of an individual. This group is defined to be a cell of individuals with similar education, similar age, from the same region and of the same gender. The social reference group specification has advantages and disadvantages over ours. Since PT has no clearly defined theory of reference point formation, one can see these results as being complementary to ours. They use a general specification to look for all features of PT, like loss aversion and asymmetries in the diminishing marginal effects of relative income. In addition, they look carefully at the robustness of the concavity results to distortions of the LS scale. One result is significant concavity for both positive and negative relative income. The concavity is stronger for losses and robust to distortions in the LS scale.
Ferrer-i Carbonell (2005) also looks at the importance of “comparison income”, that is, the income relative to a social group. She concludes that income relative to the reference group is as important as absolute income for individual happiness. Restricting the analysis to West Germany, she finds support for loss aversion. McBride (2001) also considers comparison income but does not allow for asymmetric effects of positive and negative differences. He finds stronger effects at lower levels of income, but does not consider features of prospect theory.
Using large survey datasets (Gallup World Poll, Behavioral Risk Factor Surveillance System, Eurobarometer), De Neve et al. (2018) find that measures of SWB are linked to growth, but individuals are more than twice as sensitive to negative as to positive economic growth, a sign of loss aversion. This has implications for the long term effect of economic growth with volatility, and is one of the proposed explanations to the Easterlin paradox. The Easterlin paradox describes the phenomenon that people with higher incomes enjoy higher levels of happiness in a cross-section, but that average happiness does not increase over time despite long-run economic growth. De Neve et al. (2018) propose that longer periods of economic growth could be offset by short recessions if people’s happiness is more sensitive to losses than to gains.
Table 1 summarises the most relevant literature and highlights our contribution. While most papers have considered loss aversion (and by extension reference points), only Vendrik and Woltjer (2007) is a comprehensive test of PT on LS. Our paper differs from theirs in two important respects: We consider income, but also health and employment, and we use individuals’ past values of those variables as reference points, instead of social peer groups.Footnote 6
3 Data
We use the German Socio-Economic Panel (2016), version 32 (henceforth SOEP), which is widely used in LS research and is described in detail in Goebel et al. (2019). We use survey years 1995–2015, as the health variable that we use is continually available from 1994 onwards. We consider individuals aged 18–85.Footnote 7
3.1 Outcomes
Current LS is measured with the question: (1) “How satisfied are you at present with your life as a whole?” The respondent can answer with an integer between 0 and 10, with 0 being the lowest and 10 the highest level of LS.Footnote 8 We treat LS as a cardinal variable. This is a choice of convenience, but supported by practice in the psychology literature for scales of at least 11 points (see Nunnally and Bernstein (1994), p. 115). It is also robust: We have also conducted all our estimations and tests based on the Blow-up and Cluster estimator in Baetschmann et al. (2015). The estimator treats the dependent variable as ordinal but not necessarily cardinal. The estimator allows for individual fixed effects and makes no assumption about their correlation with the independent variables. The results were only marginally different from our main results. Ferrer-i-Carbonell and Frijters (2004) also support the robustness of LS regression results to treating LS as cardinal or ordinal. The results for the Blow-up and Cluster estimator can be found in Table 6 in the appendix.
3.2 Main Independent Variables
Literature reviews of correlates of subjective well-being typically identify the following variables and domains: Social relationships, income and wealth, employment status, demographic characteristics, health, education, and religion (Argyle, 1999; Clark, 2018; Diener et al., 2018; Dolan et al., 2008). However, not all of those variables lend themselves to a ranking of values. More income ranks higher than less income, and someone preferring the latter would be very exceptional. However, having a partner might not be preferred over not having a partner, at least for some people, or some of the time. We therefore focus on three variables for which we can confidently establish a preference ranking.
For income we use equivalised net monthly real (CPI-adjusted) household income. Household income is typically used in LS research to account for the fact that resources are often pooled and distributed at the household level (Proto & Rustichini, 2015). We use the OECD equivalence scale: Total net monthly household income is divided by a weighted sum of household members, where the first adult household member is counted fully, any other person above the age of 13 as 0.7, and all younger household members as 0.5. To fit our model to a typical range of income changes we restrict the estimation sample to observations whose equivalised net monthly household income does not change by more than 500 Euros from one year to another, which comprise 88.8% of all person-year observations, with a sample mean of 1,414 Euros. Table 5 in the online appendix compares the main results for different sample restrictions based on income changes. The only result that is affected is the significance on the concavity of income gains.
Health is captured by individuals’ self-assessment. Survey participants are asked: “How would you describe your current health?” and can choose between the answers “Bad”, “Poor”, “Satisfactory”, “Good” and “Very good”. We create dummy variables for each category and use “Bad” as the omitted category in the regressions. Self-assessed health is far from ideal in our setting and is almost certain to be endogenous. Omitted variables which have an effect on self-assessed health are likely to affect LS in the same direction thus causing an upward bias in the estimated health effect. Unfortunately, the SOEP does not offer convincing alternatives. Since 2002 a health questionnaire based on the SF-12 is administered (Andersen et al., 2007) but this is done only every other year. We would thus have to assume that people use their health status from two years ago as a reference point, or have to interpolate the missing years. Omitting any health variable is equally problematic. Health certainly correlates with income and employment and by omitting it from the model we would only substitute one type of omitted variable bias for another one.
As an alternative we create a health index which is the sum of a dummy for not having visited a doctor in the previous three months, a dummy for not having any hospital visit in that year, and a variable categorising the extent to which health interferes with daily functions (0: substantially, 1: partially, 2: not at all). Our index ranges from 0 to 4, and we have used the same parametrisation as for our original health variable (dummies for all categories and transitions). We will discuss further implications of using self-assessed health in the next section.
Labour force status is captured by three dummy variables for being employed (E), being unemployed (U), and not being in the labour force (N, omitted category). Among the three categories only two can be ranked in terms of which is preferred by the respondent. For an employed person, unemployment is an available option, so employment is preferred to unemployment. For an unemployed person, employment is preferred by definition. We therefore treat employment as a status better than unemployment. For a pair-wise comparison between (un)employment and non-participation we cannot make any general assumptions in terms of their preference ranking.
3.3 Control Variables
The choice of the remaining explanatory variables is informed by the literature on happiness. We include the following characteristics: A dummy for males, a dummy for living with a partner, a dummy for having children, years of education, and six age categories (18–29, 30–39, 40–49, 50–59, 60–69, 70–85). Table 2 presents the summary statistics of our sample.
3.4 Choice of Reference Point
PT postulates that utility is derived from the value of a variable compared against a reference value. What that reference value in a given context should be is not always clear. Kőszegi and Rabin (2006) argue that “a person’s reference point is her probabilistic belief about the relevant consumption outcome held between the time she first focused on the decision determining the outcome and shortly before consumption occurs” (page 1,141), thus proposing expected consumption as the reference point. Others have argued that, in evaluating their LS, people compare themselves to a peer group (e.g., Vendrik and Woltjer (2007) and work cited within). Then the reference point is usually constructed as the average of the variable of interest within a subsample which share the demographic characteristics of the individual for whom the reference point is being calculated. A natural choice with panel data is to use the lagged value of the variable of interest as reference point. This means that the reference point is unique to the person, as it is based on the individual’s own past responses. This approach has been taken by many papers discussed above which, sometimes implicitly, use past income as reference point.
Whether people use their past self or a social comparison group as reference depends on a number of factors (Schwarz & Strack, 1999; Wilson & Ross, 2000): their goal in engaging in the comparison (an accurate self-assessment or increasing their self-esteem), what their attention is focused on (surroundings, people in the room), and their recent experiences or concerns (retirement, marriage, etc.). While social comparisons received more attention in the psychological literature, Wilson and Ross (2000) demonstrate that comparisons to one’s own self are at least as common as social comparisons, and Steffel and Oppenheimer (2009) show that individuals might be more likely to spontaneously adopt an intra- rather than inter-personal reference point. The main independent variables (income, health, and employment) lend themselves intuitively to intra-personal comparisons. A salary increase, a recovery from illness, and finding a job are all likely to be experienced as improvements or achievements, suggesting that the past self is a proper reference point, albeit maybe one of several.
Two more arguments support the past self as a reference point in our context. First, the fact that any respondent included in the estimation sample must have answered the survey in the previous year, and probably has done so over a number of years. Second, the LS question is the last question being asked during the interview so that an attention focus on any particular aspect of their lives induced by the interview itself is unlikely. Finally, the variables characterising the state of the past self are readily available. Using a social reference point requires a number of ad-hoc or data-driven choices: which social group to choose, over which spatial and temporal dimension, and which statistic to use as reference point. There is likely to be a considerable mismatch between such constructed reference groups (e.g., all of West Germany) and the true social reference points that people compare themselves against (e.g., one’s neighbours). Hence, we use the past self as reference point, but we return to social comparisons in the extensions section.
4 Model and Estimation
We test whether LS exhibits the properties of reference dependence, diminishing marginal utility, and loss aversion, all of which are discussed further below. To this end we estimate an equation which can accommodate and potentially reject all these properties:
where i indexes the person, and t the survey year. Line (1) includes the income variables, line (2) the health variables, line (3) the employment status variables, and the fourth line (4) includes other control variables, \({X_{it}}\), person fixed effects, \(u_i\), year fixed effects, \(v_t\), and the classical error term, \(\epsilon _{it}\).
In (1), \(\Delta y_{it} := y_{it}-y_{i,t-1}\), and \(\mathbbm {1}_{A}\) is an indicator variable which evaluates to 1 if statement A is true, and to 0 if A is false. The income specification allows for level (through \(\beta _1\) and \(\beta _2\)), and for change effects, differentiated by gain and loss effects (through \(\gamma _1\), \(\gamma _2\), \(\delta _1\) and \(\delta _2\)). Using a quadratic function allows for concavity and convexity. The quadratic function imposes an (inverted) U-shape on the LS-income relationship. However, this will not be a problem as long as most of the observed incomes fall into the domain for which LS is only increasing. The decreasing part of the function would be empirically irrelevant.
The model for income is parsimonious in the sense that it contains the minimum number of parameters that we need to test for the shape of LS with respect to income. We want to test for the direction and the curvature of the income effect and therefore require two parameters. If we included only the natural logarithm of income, then finding a positive effect of income on LS would also impose this effect to be concave. The same reasoning holds for estimating the shape of the LS function for income gains and for income losses. Note that the function employed by Vendrik and Woltjer (2007) achieves the same: it employs one parameter which governs the direction of income gains and losses and another which governs the concavity or convexity. However, their function is not linear in parameters and needs to be estimated by non-linear methods. This gives rise to the incidental parameters problem when combined with a large number of fixed effects, or otherwise complicates the estimation. We therefore decided to use the quadratic specification for levels, gains, and losses. We have also estimated the specification as in Vendrik and Woltjer (2007) to check robustness, and it did not substantially affect our main results. It resulted in a very strong convexity parameter for income losses and a negative coefficient for income gains. A graphical comparison between our model and the model in Vendrik & Woltjer is presented in Figs. 2 and 3 further below.
A limitation of our model is the linear dependence between current income, past income, and the difference between the two. In our specification a separate effect of past income is not identified in the linear model. However, under the assumption that past income has a positive independent effect on LS, its omission leads to an overestimation of the effect of current income and to an underestimation of the effect of income changes. To see this for example for income gains, consider that \(\beta _1 y_t + \gamma _1 \Delta y + \eta y_{t-1} = (\beta _1+\eta )y_t + (\gamma _1 - \eta )\Delta y = (\beta _1+\eta )y_t - (\gamma _1 - \eta ) y_{t-1}\).
Our estimate for current income thus combines the effect of current and past income, while the estimate for income change is biased downward by the value of \(\eta\). This problem is not unique to our paper. Any model which seeks to estimate the effect of a variable along with the effect of a reference point (or the difference) implicitly assumes that the difference (or the reference point) does not have an effect on the dependent variable. Clark and Oswald (1996) estimate the impact of current and past income on job satisfaction, and thus assume that income gains or losses have no effect. Ferrer-i Carbonell (2005) estimates the impact of own and reference income on LS and thus her parameters are combinations of the effect of own income, reference income, and the difference between the two. The difference matters since both reference income and the difference between own and reference income might have separate effects (e.g., the former through better local services, the latter through social comparison effects).
In (2) we include dummy variables for all but one of the different health categories, H2 to H5, as well as all genuine transitions TH from one health state to another, where J is the set of integers from one to five (one for each health state), and the indices j and k stand for the previous and current health status respectively. The current health state can be written as the sum of all transitions which lead to this state. We therefore omit the degenerate transitions (\(j=k\)). For example, \(TH^{23}\) is 1 if an individual reported the second health category in the previous year, and reports the third category in the current year. Finally, for labour force status, we also include dummies for being employed and unemployed, E, U, as well as all possible transitions TL from one labour force status to another, where L is the set \(L = \{E,U,N \}\) and N stands for not being in the labour force. The indices l and m stand for the previous and current employment status respectively. For example, \(TL^{EU}\) is 1 if an individual was employed in the previous year, but is unemployed in the current year.
The SOEP provides cross-sectional and longitudinal weights. However, we do not apply weights to our estimation. The longitudinal weight of an observation reflects their sampling probability when first interviewed combined with their attrition probability. Two households which joined the SOEP at different times but are otherwise equal would thus have different weights. Moreover, we exclude observations which have missing values for any of the variables included in our model, and we have no way of adjusting weights to account for this additional sample selection.
To gauge the sensitivity of our results to potential bias due to attrition we repeated our estimation including as control variable an indicator which equals 1 for the last interview of a respondent in the panel (see for example Yaman et al. (2022)). This did not substantially change our results.
In the following subsections we discuss our hypotheses and how we test them. Table 3 summarises the main hypotheses along with their results. To control the power of our tests we have formulated our hypotheses such that the features we are looking for are stated as alternative hypotheses.
4.1 Income, Health and Employment Improve LS
We first establish that the variables of interest are desirable in terms of LS – either as ends in themselves or because they are instrumental in achieving those ends. The literature has firmly established that income, health, and employment exert a positive influence on LS. We re-affirm these results for completeness before proceeding to tests regarding reference points and loss aversion.
For income to be desirable, it needs to increase LS. Holding fixed the change in income \(\Delta y\) (and omitting the individual subscript) we have the following condition for income to be desirable:
leading to the following hypothesis:
Hypotheses (G)
Income is desirable,
For health and labour force status we formulate the following hypotheses, assuming that a person has been in the same state in the previous year (all transition dummies are zero):
Hypotheses (G)
Better health increases LS,
Being employed is better than being unemployed,
4.2 Reference Point
The reference point test in the context of PT is straightforward. If LS is not evaluated against a reference point (or, more conservatively, if the past value of a variable is not a reference point) then the coefficients on changes and transitions are zero. Conversely, if LS is evaluated only against the reference point, then the coefficients on the current levels are zero. We test whether income changes and health and employment transitions have an influence on LS once income levels and health and employment states are controlled for. PT postulates a positive effect of “increases” of those goods. We therefore have for income gains:
Suppose two persons have the same income. If the first has had the same income in the previous year, while the second person has arrived at their current income from a lower level, then Eq. 6 implies that the second person enjoys higher levels of LS.
For income increases to be a good in the loss domain we have
Suppose two persons have the same income. If the first has had the same income in the previous year, while the second person has arrived at their current income from a higher level, then Eq. 7 implies that the second person enjoys lower levels of LS.
Similarly, for two people with the same health status, we should expect higher LS for the person who arrived at this status from a poorer health state, and lower LS for the person who arrived at this status from a better health state. Since someone whose health deteriorates is experiencing both a lower health state (estimated as \(\alpha _j\)) as well as a health loss (estimated as \(\alpha _{jk}\) with \(j>k\)) we would expect the two effects to result in lower LS than if the same health state had been experienced without a loss. An analogous argument holds for health gains. Note that with 5 health states we have 20 potential transitions between health states, half of which are health improvements, and the other half health deteriorations.
For employment status the reasoning is analogous. An employed person should enjoy more LS than an unemployed person. But an unemployed person who recently lost their job should report lower LS than if they had been unemployed in the past, and an employed person who recently was unemployed should report higher LS than if they had been employed in the past.
For small gains in income (\(\Delta y\) approaching zero) we test:
Hypotheses (RP1)
LS is increasing in changes in the gains domain,
Hypotheses (RP2)
LS is increasing in changes in the loss domain,
In the hypotheses above, only transitions between employment and unemployment are considered, since only these are unambiguously ranked in relation to each other.
4.3 Diminishing Marginal Utility
Testing for the presence of diminishing marginal utility in LS requires certain assumptions on the variables. If both LS and the independent variable are cardinal, testing for diminishing marginal utility is straightforward. If we relax the cardinality assumption for LS but retain its ordinal property, we can still apply a latent variable framework such as ordered logit and assume that the latent variable has cardinal properties. We have estimated our model under both assumptions. We used the fixed effects OLS estimator for the cardinal, and the fixed effects ordinal logit (Blow-up and cluster, Baetschmann et al., 2015) for the ordinal specification. The two specifications yielded almost identical results. We produce a table of results for the ordinal model in the appendix, and proceed here with the cardinal model.
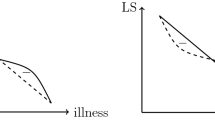
The respondent reports life satisfaction ‘x’ in satisfactory health, ‘x+1’ in good health, and ‘x+2’ in very good health. In the left figure the health gain between Satisfactory and Good is the same as between Good and Very good. Life satisfaction is therefore linear in health. In the right figure the health gain between Satisfactory and Good is less than the health gain between Good and Very good. Life satisfaction is concave in health
Cardinality in the independent variable however cannot be dispensed with. To see this consider a person who reports the same increase in LS when going from satisfactory to good and from good to very good health (see Fig. 1). If these two changes in health categories reflect an equivalent change in the person’s underlying “true” health we would conclude that marginal utility is constant (left sub-figure). But if the incremental gain in health between satisfactory and good is smaller than the gain in health between good and very good, the person would still exhibit diminishing marginal utility with respect to health (right sub-figure). Of our explanatory variables only income is cardinal, therefore it is the only variable for which we can test diminishing marginal LS. While health categories can be ordered, we do not assume that gains in health have ratio properties.
We test for diminishing marginal utility in levels and in changes. The two channels are not mutually exclusive but EUT supports the levels effect, while PT supports the changes effect. For income levels to have diminishing marginal effects on LS, the sufficient condition is \(\beta _2<0.\)
For income changes we can use Eqs. 6 and 7. Taking derivatives with respect to \(\Delta y\) we obtain
For LS to be concave in gains and convex in losses we require
The hypotheses are the following:
Hypotheses (DMU1)
LS is concave in income levels,
Hypotheses (DMU2)
LS is concave in income gains,
Hypotheses (DMU3)
LS is convex in income losses,
4.4 Loss Aversion
Loss aversion means that the decrease in utility due to a loss (of income, health, employment) is greater than the increase in utility due to the corresponding gain. To classify anything as a loss or a gain, a reference point must be defined. While marginal effects for health and employment status could not be estimated, the presence of loss aversion can, as individuals can go from good to bad health and vice versa, or from employment to unemployment and vice versa. For loss aversion in income we compare \(\frac{\partial ls}{\partial \Delta y}\) in the gain domain to the same derivative in the loss domain. Loss aversion requires that the rate of change of LS for a decrease in y be greater than the rate of change in LS for a corresponding increase. From Eqs. (6) and (7),
In particular, \(\lim _{\Delta y \rightarrow 0}\) implies \(\delta _1>\gamma _1\), giving the utility function with loss aversion its characteristic kink at the origin. For labour force status we compare only two states: employment and unemployment. The change in LS for someone who moves from unemployment to employment is \((\rho _E - \rho _U)+\rho _{UE}\), and the change in LS for someone who moves from employment to unemployment is \((\rho _U - \rho _E)+\rho _{EU}\). The former is expected to be positive, and the latter to be negative. If so, loss aversion will also imply:
For health, the same argument as for employment applies. However, as there are 5 (ordered) health categories, there are 10 comparisons that can be made.
The hypothesis on loss aversion is:
Hypothesis (LA)
LS exhibits loss aversion in income, health and employment,
4.5 Endogeneity of Self-Assessed Health
In Sect. 3.2 we mentioned the endogeneity of self-assessed health. We would expect an omitted variable to correlate with LS and self-assessed health in the same direction. Whatever drives respondents to report better health also drives them to report higher LS. The bias on health’s effect on LS is thus positive. But how would this affect our estimates for health state transitions? Consider a simplified measure of health gains constructed as \(\mathbbm {1}_{H_t > H_{t-1}}\) with \(H_t\) being current health, and \(H_{t-1}\) past health. If past health is exogenous or its endogeneity negligible compared to current health, then health gain effects will also be estimated with a positive bias since the omitted variable drives health and health gains in the same direction. On the other hand, health loss effects for health loss defined as \(\mathbbm {1}_{H_t < H_{t-1}}\) will be negatively biased.
Recall that our test for LS to increase in health gains is given by \(\alpha _{jk}>0\) for \(j<k\) (\({H_{RP1,h}}\)). Due to its positive bias estimated \(\alpha _{jk}\) will exceed its true value and we might erroneously conclude that it is positive. Rejecting the hypothesis however would be achieved despite the upward bias. The case for health losses is analogous. Accepting \(\alpha _{jk}<0\) for \(j>k\) can be driven by negative bias and need not imply that health loss truly negatively affects LS, but rejecting it is strong evidence that health loss does NOT negatively affect LS.
Unfortunately, the two biases do not combine to give us an unambiguous direction for the bias in testing loss aversion. Since both biases amplify the coefficients \(\alpha _{jk}\) and \(\alpha _{kj}\) in absolute value we would need to know which of the two coefficients is affected more. The loss aversion test is therefore not conclusive but only suggestive.
5 Results
The exact results for our main econometric model from Eqs. (1–4) can be found in Table 4 in the appendix. All models use standard errors clustered at the person level. The results are generally in line with what is known about LS. Having a partner, having children, not being unemployed, being in good health, and income are associated with higher levels of LS. The differences between the OLS and fixed effects coefficients demonstrate the importance of unobserved individual characteristics. Our preferred specification is therefore the fixed effects estimator.Footnote 9 Table 3 summarizes the hypotheses and test results on reference points, diminishing marginal utility, and loss aversion. We find that all our outcome variables (income, health, employment) are goods in term of LS (panel A). The hypothesis of no income effect (G,y) is rejected at the 1% level for a wide range of income levels \(y_{t}\) in favour of the alternative hypothesis of positive income effects. Hypothesis G,h (no health effects) is strongly rejected for all possible health states. G,l (no employment effect) is also strongly rejected. Our estimates imply that a person enjoys 0.27 more ‘units’ of LS with an income of 2,000 Euros than they do with an income of 1000 Euros.Footnote 10 Better health implies higher LS by between 0.35 (between very good and good) and 1.26 units (between not so good and bad), and a person enjoys half a unit of LS more when they are employed rather than unemployed.
5.1 Reference Point
Panel B of Table 3 shows that none of the hypotheses in RP1 (gains relative to the reference point have no effect) can be rejected. For income, there is no statistical evidence that a gain has any effect on LS over and above the level effects. For employment, a transition from unemployment to employment actually carries a significant (for a one-sided test) negative sign. However, the results for the loss domain are in agreement with the properties of PT. An income increase in the loss domain—making the loss smaller—increases LS. The transition from employment to unemployment reduces LS, controlling for employment status. A person who just became unemployed has lower LS than a person who was unemployed in the previous period and is still unemployed. Thus, the evidence is that losses hurt but gains do not help. The magnitudes of these relative effects are quite small. Removing a loss of 100 Euros increases LS by 0.03 points, adding a gain of the same amount leaves LS virtually unchanged. The transition effect from employment to unemployment is a reduction in LS by 0.05, only a tenth of the level effect difference between employment and unemployment.
For health we get a completely reversed, and unexpected, result. Since there are many different health improvement transitions we test each of them. To see whether health gains improve LS, we test the null hypothesis that a health gain coefficient is \(\le\) 0 against the alternative that it is positive. For health losses, we test the null hypothesis that a health loss coefficient is \(\ge\) 0 against the alternative that it is negative. The p-value in the table is the smallest out of all p-values for those tests, that is, all tests for health gains had a p-value of at least 0.517. There is thus no support for the claim that health gains increase LS. Indeed, the results mask the fact that all but one of the tests supported a negative coefficient, despite the likely positive bias as explained in section 4.5. Someone whose health state is x as a result of a health improvement still enjoys lower LS than someone whose health state is and was x. The reverse is true for health losses: A person whose health is x as a result of a health decrease still enjoys higher LS than someone whose health is and was x.
Taken together, the results reported in panels A and B do not lend exclusive support for or against EUT or PT. Rather, LS seems to be best described by an EUT model which also incorporates elements from PT, albeit not always in expected ways.
5.2 Diminishing Marginal Life Satisfaction
Panel C presents the results for hypotheses DMU1 to DMU3. LS is concave in income levels. While it is clearly convex in the loss domain of income, the support for concavity in the gains domain is not strong. We cannot reject that it is flat or convex at the 10% significance level.
5.3 Loss Aversion
The gradient for income losses close to the reference point is 0.26 while for income gains it is only 0.01. Loss aversion (panel D) is thus present at the 5% significance level for income. Loss aversion is also present for employment status. Given our results for reference points for health transitions, it makes no sense to test for loss aversion in health. Rather, if we test for “loss preference”, that is, the LS increase after a drop in health exceeding the LS decrease after a symmetric health improvement, we find significant support at the 5% level for this phenomenon for six out of the ten possible health transitions.
5.4 Shape of LS Function
The LS function for changes in income in a range of -200 to +200 Euros is depicted in Figs. 2 and 3. Figure 2 depicts the effect of income changes when current income is fixed (the change thus occurs through past income). This corresponds to a pure change effect (e.g., is driven by \(\Delta y\) only). The left panel shows the resulting LS function from our quadratic model, and the right panel from a LS specification as in Vendrik and Woltjer (2007). Standard errors for the latter specification do not have a closed form. We therefore did not produce confidence bands. The models have the same properties in the loss domain (increasing and convex), even though the LS function as implied by the quadratic model is much smoother. The two models look distinct in the gains domain. Our model implies more of a flat profile (we cannot reject that it is flat on statistical grounds, see Sect. 5.2), whereas the Vendrik & Woltjer specification results in decreasing LS in income gains. Figure 3 shows the combined level and change effects (varying current income while holding past income fixed). Here, as the effect of current income dominates the loss and gain effects, the two profiles resemble each other. They have most of the characteristic features of Prospect Theory: the kink at the origin, a slight concavity in gains, convexity in losses, and a general stronger effect of losses than gains.
Life satisfaction as a function of income changes, with current income held fixed. The left-hand figure is our benchmark model. Dashed line is the 95% confidence interval for the change in life satisfaction. The right-hand figure is based on the power function specification as in Vendrik and Woltjer (2007). For the power function we did not compute confidence bands. Income changes are in 1,000s of Euro. The vertical axis is LS relative to no income change
Life satisfaction as a function of income changes, with past income held fixed. The left-hand figure is our benchmark model. Dashed line is the 95% confidence interval for the change in life satisfaction. The right-hand figure is based on the power function specification as in Vendrik and Woltjer (2007). For the power function we did not compute confidence bands. Income changes are in 1,000s of Euro. The vertical axis is LS relative to no income change
6 Discussion
Our findings suggest that LS can be best described by EUT but also contains some features associated with PT. LS follows EUT in that higher income and better health are associated with higher LS. Individuals enjoy higher LS when employed rather than unemployed. Furthermore, LS is concave in income levels and thus exhibits diminishing marginal LS. In this section we discuss threats to the validity of our results and interpretations. We discuss the issue of measurement error, and other potential mechanisms that link self-assessed health with LS and to what extent they can explain our findings. We also offer some thoughts on the difference between reported and ‘true’ LS and their implications for our findings.
6.1 Measurement Error
It is well known that measurement error in independent variables results in inconsistency of OLS and typically biases the concerned coefficient towards zero. Fixed effects estimators can exacerbate this attenuation bias and a number of methods have been proposed to deal with measurement error in panel data (Griliches & Hausman, 1986; Meijer et al., 2017).
In the present case measurement error enters in a number of ways. First, we have classical measurement error in all our variables: People might inaccurately report their incomes, their health, and their employment status. Bound et al. (1994) show that earned incomes are fairly accurately reported in the Panel Study of Income Dynamics, but biases are amplified by using income changes, which is a key variable in our model. Second and relatedly, ours is a dynamic panel model since the key variables enter both contemporaneously as well as with a one-period lag, further complicating the analysis of measurement error. Third, recall that our income variable is real equivalised household income, which almost certainly misspecifies how income and household composition interact in determining LS. We are likely to misclassify some losses as gains and vice versa by assuming that individuals care about real income changes and have knowledge about year-on-year inflation. Forth, we have continuous measurement error in income, and measurement error in the form of misclassification for health and for employment. Card (1996) proposes an estimator which takes account of misclassification but relies on external information on misclassification probabilities.
The literature on subjective well-being seems to have largely ignored the problem of measurement error, and given the complexity of it in the present context we do not pursue a strategy to tackle this problem.
6.2 Health Transitions and Life Satisfaction
The results for the effects of health transitions on LS run against our expectations. The relationship between self-assessed health and life satisfaction is complex and perhaps our results are driven by a mechanism which we did not model. One possibility is that our results are driven by the endogeneity of self-assessed health and health state transitions. We have discussed this in Sect. 4.5 and have argued that the resulting bias might explain positive effects of health gains and negative effects of health losses. However, we find the opposite despite the direction of the bias.
We also explored whether health effects might be dependent on age and that this might account for our results. However, including all interaction effects between health and age categories yielded very similar results on health transition effects. In the online appendix we offer some further thoughts on the relationship between health and adaptation, and how the subjectivity of our health variable might affect our results.
6.3 Further Considerations
The validity of our findings could be compromised under certain conditions. Vendrik and Woltjer (2007) discuss the possibility that people might under-report LS for high values and over-report for low values. They argue that the shape of the “true” LS function might be different from the shape of the reported LS function. The validity of these objections hinge on how one interprets LS. While some studies have used LS and other SWB variables as utility measures, they have not discussed what exactly they mean by utility. Kahneman et al. (1997) provide a useful taxonomy. They distinguish utility by how it is inferred—decision utility vs. experienced utility—and by when and over what time period it is measured—instant, total, and recalled utility—with important consequences for decision making (Dolan & Kahneman, 2008). Decision utility is the utility concept underlying modern economics, according to which utility is that theoretical construct that individuals maximise with their choices under a set of constraints. If LS is a measure of decision utility, then any distinction between reported and true LS is not meaningful, as long as reported LS can rationalise and in turn explain individuals’ choices, just as different utility functions can rationalise observed choices. If however one wishes to use LS as a measure of experienced utility then issues of measurement, inter- and intra-personal comparability, and reporting behaviour become paramount.
The experienced utility interpretation can be supported by the view that LS is a global evaluation of one’s life. Schwarz and Strack (1999) argue that subjective well-being measures suffer from a myriad of context effects, however the LS question is asked to survey participants at the end of a lengthy interview and asks about life in general. This should minimise the probability that their answers will be biased due to attention focus or context effects. Perhaps a more serious argument against the experienced utility interpretation is that LS is evaluated based on past and current, but also prospective experiences (Dolan & Kahneman, 2008).
Given that EUT and PT are theories of choice, the relevant utility concept in the current context is decision utility. However, LS is unlikely to perfectly overlap with decision utility. Benjamin et al. (2014) show that choices do not always correspond to the options with the highest anticipated happiness. Even if realised choices would correspond to the highest anticipated LS, phenomena like adaptation (Loewenstein & Ubel, 2008) and projection bias (Loewenstein et al., 2003) will induce systematic differences between anticipated and realised LS.
7 Alternatives and Extensions
In the online appendix we discuss in detail extensions to our analysis. We consider social rather than intra-personal reference points, reference points in the more distant past, and a more careful analysis of the income effects.
Some of the literature discussed previously construct socio-demographic or geographic reference groups. We follow this approach and construct reference values for our outcomes in four alternative specifications. The first three specifications segment the population and calculate cell averages to serve as reference values. For the first specification, we calculate reference values for each of the 16 German states, and separately for urban and rural locations. For the second specification we segment the population into age, education, and East-West cells as in Ferrer-i Carbonell (2005). The third specification uses only observations who are in full-time employment and segments this population by occupation code and by East and West Germany. For the last specification we use full-time employees to estimate a Mincer equation. We use the predicted values from those regressions as reference values. The results are presented and discussed in the online appendix.
When evaluating one’s LS, people might consider their experiences and achievements over longer periods of time, and perhaps different domains of life might affect one’s LS over different time spans. We therefore re-estimated our model after replacing previous year’s reference points with reference points from two and three years ago. Our findings on level effects are unchanged. Income transitions are attenuated, while the association between LS and employment transitions remains strong even after three years.
Recall that our income variable is real equivalised household income (y). It can thus change due to a number of reasons: changes in nominal income, inflation, and changes in household composition. Since the effect of changes in y on LS is likely to depend on the underlying cause we have estimated our model differentiating changes in y by whether they were accompanied by changes in nominal household income. The results are presented and discussed in the online appendix.
8 Conclusion
We have analysed which characteristics of expected utility theory and prospect theory can be found in life satisfaction in an annual household panel. We found that LS exhibits features of both theories, in particular: LS resembles utility in EUT in that it increases in levels of income, health, and employment status, but it also shows features of utility in PT as it also increases in positive changes of those variables (except for health). Furthermore, LS exhibits loss aversion in income and in employment, but not in health. The main caveat is our choice of reference point: the value of the variable of interest for the same person, at the time of the previous interview. Different reference points might result in a rejection of EUT in favour of PT or vice versa. However, this is also true for the other reference point models in the literature. Finding the correct model, or the best model for a specific type of data available, is an important goal for future work.
Data Availability
This research has used survey data collected by the German Institute for Economic Research. No further data has been collected from human participants and/or animals.
Notes
We do not test for the presence of probability weighting in this paper, another important assumption in PT, because our data do not provide a good source of identification of probability weighting.
Kőszegi and Rabin (2006) propose a model with reference-dependent utility where the reference-point is defined to be expected consumption shortly before consumption occurs. Bénabou (2012), Brunnermeier and Parker (2005), Gollier (2011), and Gottlieb (2014) all build models in which agents choose what to believe in order to enjoy anticipatory utility.
See DellaVigna (2009) for an overview of this literature.
Interestingly, the idea of state dependence in explaining labour market outcomes has a history. For example, Heckman (1981) explores the idea of past unemployment spells affecting the probability of future unemployment. We are not aware of any attempt to connect this line of research to prospect theory.
For example, a person might expect to be promoted or receive a pay rise, leading to satisfaction from this anticipated gain. Or, they might fear that their earnings will not keep up with increases in the cost of living, leading to dissatisfaction from anticipated loss.
Vendrik and Woltjer (2007) include employment as a control variable. They do not include health: “A control variable for health status was not included since this may represent an important intermediate variable between absolute income and life satisfaction. Moreover, one third or more of the observations are missing” (page 1,434, footnote 15).
Our results are not sensitive to this choice. Results for a sample restricted to individuals aged 18–64 are very similar.
The question clarifies that “0 means completely dissatisfied and 10 means completely satisfied”, but no labels (“excellent”, “good”, etc.) are attached to the values.
A Hausman test rejects the equality of coefficients from the random effects and fixed effects estimators.
The within person standard deviation of LS is 1.14, so the LS difference between 2,000 and 1000 Euros corresponds to a quarter of an LS standard deviation.
References
Abdellaoui, M., Bleichrodt, H., & Paraschiv, C. (2007). Loss aversion under prospect theory: A parameter-free measurement. Management Science, 53, 1659–1674.
Andersen, H. H., Mühlbacher, A., Nübling, M., Schupp, J., & Wagner, G. G. (2007). Computation of standard values for physical and mental health scale scores using the SOEP version of SF-12v2. Schmollers Jahrbuch, 127, 171–182.
Argyle, M. (1999). Causes and correlates of happiness. In Well-Being: The foundations of hedonic psychology (Daniel Kahneman, Edward Diener, and Norbert Schwarz, eds.), pp. 353–373, Russell Sage Foundation.
Baetschmann, G., Staub, K. E., & Winkelmann, R. (2015). Consistent estimation of the fixed effects ordered logit model. Journal of the Royal Statistical Society: Series A (Statistics in Society), 178, 685–703.
Bénabou, R. (2012). Groupthink: Collective delusions in organizations and markets. The Review of Economic Studies, 80, 429–462.
Benjamin, D. J., Heffetz, O., Kimball, M. S., & Rees-Jones, A. (2014). Can marginal rates of substitution be inferred from happiness data? Evidence from residency choices. American Economic Review, 104, 3498–3528.
Blanchflower, D. G., & Oswald, A. J. (2004). Well-being over time in Britain and the USA. Journal of Public Economics, 88, 1359–1386.
Bound, J., Brown, C., Duncan, G. J., & Rodgers, W. L. (1994). Evidence on the validity of cross-sectional and longitudinal labor market data. Journal of Labor Economics, 12, 345–368.
Boyce, C. J., Wood, A. M., Banks, J., Clark, A. E., & Brown, G. D. A. (2013). Money, well-being, and loss aversion: Does an income loss have a greater effect on well-being than an equivalent income gain? Psychological Science, 24, 2557–2562.
Brunnermeier, M. K., & Parker, J. A. (2005). Optimal expectations. American Economic Review, 95, 1092–1118.
Card, D. (1996). The effect of unions on the structure of wages: A longitudinal analysis. Econometrica, 957–979.
Clark, A., Georgellis, Y., & Sanfey, P. (2001). Scarring: The psychological impact of past unemployment. Economica, 68, 221–241.
Clark, A. E. (2018). Four decades of the economics of happiness: Where next? Review of Income and Wealth, 64, 245–269.
Clark, A. E., Diener, E., Georgellis, Y., & Lucas, R. E. (2008). Lags and leads in life satisfaction: A test of the baseline hypothesis. The Economic Journal, 118, F222–F243.
Clark, A. E., Frijters, P., & Shields, M. A. (2008). Relative income, happiness, and utility: An explanation for the Easterlin paradox and other puzzles. Journal of Economic Literature, 46, 95–144.
Clark, A. E., & Oswald, A. J. (1996). Satisfaction and comparison income. Journal of Public Economics, 61, 359–381.
DellaVigna, S. (2009). Psychology and economics: Evidence from the field. Journal of Economic Literature, 47, 315–372.
Di Tella, R., Haisken-De New, J., & MacCulloch, R. (2010). Happiness adaptation to income and to status in an individual panel. Journal of Economic Behavior & Organization, 76, 834–852.
Diener, E., Lucas, R. E., Oishi, S., Hall, N., Brent D. M. (2018). Advances and open questions in the science of subjective well-being. Collabra: Psychology, 4.
Dolan, P., & Kahneman, D. (2008). Interpretations of utility and their implications for the valuation of health. The Economic Journal, 118, 215–234.
Dolan, P., Peasgood, T., & White, M. (2008). Do we really know what makes us happy? A review of the economic literature on the factors associated with subjective well-being. Journal of Economic Psychology, 29, 94–122.
Fang, Z., & Niimi, Y. (2017). Does everyone exhibit loss aversion? Evidence from a panel quantile regression analysis of subjective well-being in Japan. Journal of the Japanese and International Economies, 46, 79–90.
Ferrer-iCarbonell, A. (2005). Income and well-being: An empirical analysis of the comparison income effect. Journal of Public Economics, 89, 997–1019.
Ferrer-i-Carbonell, A., & Frijters, P. (2004). How important is methodology for the estimates of the determinants of happiness? The Economic Journal, 114, 641–659.
Goebel, J., Grabka, M. M., Liebig, S., Kroh, M., Richter, D., Schröder, C., & Schupp, J. (2019). The German socio-economic panel study (SOEP). Jahrbücher für Nationalökonomie und Statistik, 239, 345–360.
Gollier, C. (2011). Optimal illusions and the simplification of beliefs. Working Paper, University of Toulouse.
Gottlieb, D. (2014). Imperfect memory and choice under risk. Games and Economic Behavior, 85, 127–158.
Griliches, Z., & Hausman, J. A. (1986). Errors in variables in panel data. Journal of Econometrics, 31, 93–118.
Heckman, James J. (1981). Heterogeneity and state dependence. Studies in labor markets. University of Chicago Press.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291.
Kahneman, D., Wakker, P. P., & Sarin, R. (1997). Back to Bentham? Explorations of experienced utility. The Quarterly Journal of Economics, 112, 375–406.
Kőszegi, B., & Rabin, M. (2006). A model of reference-dependent preferences. The Quarterly Journal of Economics, 121, 1133–1165.
List, J. A. (2004). Neoclassical theory versus prospect theory: Evidence from the marketplace. Econometrica, 72, 615–625.
Loewenstein, G., O’Donoghue, T., & Rabin, M. (2003). Projection bias in predicting future utility. The Quarterly Journal of Economics, 118, 1209–1248.
Loewenstein, G., & Ubel, P. A. (2008). Hedonic adaptation and the role of decision and experience utility in public policy. Journal of Public Economics, 92, 1795–1810.
McBride, M. (2001). Relative-income effects on subjective well-being in the cross-section. Journal of Economic Behavior & Organization, 45, 251–278.
Meijer, E., Spierdijk, L., & Wansbeek, T. (2017). Consistent estimation of linear panel data models with measurement error. Journal of Econometrics, 200, 169–180.
Neve, D., Jan-Emmanuel, G. W., De Keulenaer, F., Van Landeghem, B., Kavetsos, G., & Norton, M. I. (2018). The asymmetric experience of positive and negative economic growth: Global evidence using subjective well-being data. Review of Economics and Statistics, 100, 362–375.
Nunnally, J. C., & Bernstein, I. H. (1994). Psychometric Theory (3rd ed.). McGraw-Hill.
Oswald, A. J., & Powdthavee, N. (2008). Does happiness adapt? A longitudinal study of disability with implications for economists and judges. Journal of Public Economics, 92, 1061–1077.
Proto, E., & Rustichini, A. (2015). Life satisfaction, income and personality. Journal of Economic Psychology, 48, 17–32.
Schwarz, N., & Strack, F. (1999). Reports of subjective well-being: Judgmental processes and their methodological implications. Well-being: The foundations of hedonic psychology, 7, 61–84.
Socio-Economic Panel (2016). Data for years 1984-2015, version 32, https://doi.org/10.5684/soep.v32.
Steffel, M., & Oppenheimer, D. M. (2009). Happy by what standard? The role of interpersonal and intrapersonal comparisons in ratings of happiness. Social Indicators Research, 92, 69–79.
Tversky, A., & Kahneman, D. (1991). Loss aversion in riskless choice: A reference-dependent model. The Quarterly Journal of Economics, 106, 1039–1061. https://doi.org/10.2307/2937956.
Vendrik, M. C. M., & Woltjer, G. B. (2007). Happiness and loss aversion: Is utility concave or convex in relative income? Journal of Public Economics, 91, 1423–1448.
Wilson, A. E., & Ross, M. (2000). The frequency of temporal-self and social comparisons in people’s personal appraisals. Journal of Personality and Social Psychology, 78, 928–942.
Yaman, F., Cubi-Molla, P., & Plagnol, A. C. (2022). Why do immigrants become less happy? Explanations for the decrease in life satisfaction of immigrants in Germany over time. Migration Studies, 10, 670–702.
Funding
This research has not received any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Any views and opinions in this article are the author's alone and do not represent the views of Ofcom.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yaman, F., Cubí-Mollá, P. & Ungureanu, S. Which Decision Theory Describes Life Satisfaction Best? Evidence from Annual Panel Data. J Happiness Stud 24, 893–916 (2023). https://doi.org/10.1007/s10902-023-00627-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10902-023-00627-5