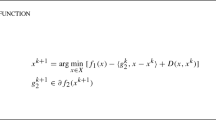A bundle-type method for nonsmooth DC programs

Abstract

A bundle method for minimizing the difference of convex (DC) and possibly nonsmooth functions is developed. The method may be viewed as an inexact version of the DC algorithm, where each subproblem is solved only approximately by a bundle method. We always terminate the bundle method after the first serious step. This yields a descent direction for the original objective function, and it is shown that a stepsize of at least one is accepted in this way. Using a line search, even larger stepsizes are possible. The overall method is shown to be globally convergent to critical points of DC programs. The new algorithm is tested and compared to some other solution methods on several examples and realistic applications.

1 Introduction

The problem under consideration, called a DC program, is the minimization problem

$$\begin{aligned} \min _{\varvec{x} \in \mathbb {R}^n} \ f(\varvec{x}):= g(\varvec{x})-h(\varvec{x}), \end{aligned}$$

(1.1)

where the objective function $f: \mathbb {R}^n \rightarrow \mathbb {R}$ is a difference of two convex and possibly nonsmooth functions $g,h: \mathbb {R}^n \rightarrow \mathbb {R}$. Therefore, f is referred to as a DC function, whereas g and h are the corresponding DC components of f (these DC components are, of course, not unique).

A versatile consideration of DC programs, both in terms of theory and implementation, can be found in [8]. These DC programs occur frequently in a variety of applications. Among them are the detection of edges in digital images [17], techniques utilized in data mining [2], like the minimum sum-of-squares clustering [25] or the multidimensional scaling problem [19], and the modeling of biochemical reaction networks [1], to name only a few.

The cornerstones for numerically tackling DC programs have already been placed some time ago (see [20] for an extensive treatment of the history of DC programs). The classical approach for solving (1.1) is the DC Algorithm (DCA) (see e.g. [21]) which can be applied to DC programs with both DC components being nonsmooth. Provided that the first DC component g is continuously differentiable, the convergence of DCA can often be accelerated by applying a boosted version of the classical DC Algorithm, the so called Boosted DCA (BDCA). The crucial point thereby is that the iterates computed by DCA can be used to derive descent directions for the objective function, which allows to add a line search to the algorithm (see [2]).

The idea of using bundle methods to solve DC programs is also not new. In [16], gathering the subgradient information for each of the DC components in two separate bundles, leads to a nonconvex cutting plane model of the objective function which incorporates both the convex and the concave behavior of the DC function. The resulting proximal bundle method (PBDC) keeps in the bundles only information related to points close to the current iterate. Another algorithm presented in [10] is also based on a cutting plane approach. But this time just the bundle with respect to the first DC component is restricted to local information, whereas the one with respect to the second DC component keeps information related to distant points. Once again, a nonconvex DC piecewise-affine model is derived, which gives rise to the name DC Piecewise-Concave algorithm (DCPCA) of the resulting method. Yet another bundle method was derived in [15] as an improved variation of the previously mentioned PBDC. The major novelty of this proximal Double Bundle method for DC problems (DBDC) is the procedure to escape from critical points which are not approximate Clarke stationary. Within this procedure it is assured that the difference of subgradients of the DC components lies in the Clarke subdifferential of the objective function itself, which is usually not the case. In that way convergence to an approximate Clarke stationary point is achieved under the assumption that the subdifferentials of the DC components are polytopes. The notion of a Clarke stationary point is, in general, stronger than the frequently used notion of a critical point.

Moreover, bundle methods for the minimization of DC functions subject to some constraints have also been developed during the last few years. However, these algorithms usually are restricted to a certain structure of the constraints (see e.g. [7, 28]).

In contrast to these bundle methods, our approach utilizes the standard subproblem from the classical DC algorithm. This results in a convex subproblem which is then solved inexactly by a simple bundle method. We terminate this bundle method after its first serious step, meaning that we do not require to solve these subproblems exactly or almost exactly, not even close to a solution. Nevertheless, the resulting inexact solution is shown to yield a descent direction. Hence, a line search can be applied to globalize the overall method. This line search is shown to accept at least the full step, that is a stepsize of at least one, and it even allows to take larger stepsizes. However, it is known from the boosted DCA that it may not share the improved descent property of the boosted DCA in case both DC components are nonsmooth. On the other hand, the new bundle-type DC method is shown to have nice global convergence properties when both DC components g and h are nondifferentiable, whereas the boosted DCA requires g to be smooth.

The paper is organized as follows. In Sect. 2 we first recall some basic concepts and definitions as well as the elementary bundle method which forms the basis of the new algorithm. We then present the new bundle-type DC algorithm in Sect. 3, together with a convergence theory and an additional discussion of some descent properties. The results of an extensive numerical testing are provided in Sect. 4. We close with some final remarks in Sect. 5.

2 Preliminaries

This section first recalls some basic definitions and results from nonsmooth and convex analysis (see e.g. [13, 27]). We then provide some details concerning a basic bundle method like it is outlined for example in [11, 18, 22].

2.1 Tools from nonsmooth and convex analysis

A function $f:\mathbb {R}^n \rightarrow \mathbb {R}$ is said to be convex if

$$\begin{aligned} f(\lambda \varvec{x}+(1-\lambda ) \varvec{y}) \le \lambda f(\varvec{x})+ (1-\lambda )f(\varvec{y}) \quad \forall \varvec{x}, \varvec{y} \in \mathbb {R}^n, \ \forall \lambda \in (0,1). \end{aligned}$$

It is called uniformly convex with modulus $\mu > 0$ if is convex, where denotes the Euclidean norm on $\mathbb {R}^n$. Recall that uniformly convex functions always attain a unique global minimum. The (one-sided) directional derivative of a function $f:\mathbb {R}^n \rightarrow \mathbb {R}$ at a point $\varvec{x} \in \mathbb {R}^n$ in a direction $\varvec{d} \in \mathbb {R}^n$ is defined as

$$\begin{aligned} f'(\varvec{x};\varvec{d}):= \lim _{t \downarrow 0} \frac{f(\varvec{x}+t\varvec{d})-f(\varvec{x})}{t} \end{aligned}$$

provided that the limit on the right-hand side exists. The latter holds, in particular, for convex functions f.

Given a convex function $f:\mathbb {R}^n \rightarrow \mathbb {R}$ and a parameter $\epsilon \ge 0$, the $\epsilon$-subdifferential at a point $\varvec{x} \in \mathbb {R}^n$ is the set

$$\begin{aligned} \partial _{\epsilon } f(\varvec{x}):= \left\{ \varvec{s} \in \mathbb {R}^n \ | \ f(\varvec{y}) \ge f(\varvec{x})+\varvec{s}^T (\varvec{y}-\varvec{x}) - \epsilon \quad \forall \varvec{y} \in \mathbb {R}^n \right\} . \end{aligned}$$

The special case $\partial f(\varvec{x}):= \partial _0f(\varvec{x})$ is known as the (convex) subdifferential of f at $\varvec{x}$ and each element of this set is called a subgradient of f at $\varvec{x}$. For arbitrary $\epsilon \ge 0$, the $\epsilon$-subdifferential $\partial _{\epsilon } f(\varvec{x})$ is a nonempty, convex and compact set for every $\varvec{x} \in \mathbb {R}^n$. The directional derivative of a convex function f can be calculated using its subdifferential via the formula

$$\begin{aligned} f'(\varvec{x};\varvec{d})=\max _{\varvec{s} \in \partial f(\varvec{x})} \varvec{s}^T \varvec{d}. \end{aligned}$$

(2.1)

For a locally Lipschitz continuous function $f: \mathbb {R}^n \rightarrow \mathbb {R}$ (recall that every convex function is locally Lipschitz), we denote the Clarke subdifferential of f at $\varvec{x}$ by $\partial _C f \left( \varvec{x} \right)$. For a precise definition and some basic properties of the Clarke subdifferential, we refer to [5]. Note that for convex functions f the Clarke subdifferential coincides with the convex one. Furthermore, $\varvec{0} \in \partial _C f(\varvec{x}^*)$ is a necessary optimality condition for some point $\varvec{x}^*$ to be a local minimum of f. Any point meeting this requirement is named a Clarke stationary point. Applying this optimality condition to the DC function $f:=g-h$ and using some calculus rules of the Clarke subdifferential leads to the stationarity condition

$$\begin{aligned} \partial g\left( \varvec{x}^* \right) \cap \partial h \left( \varvec{x}^* \right) \ne \emptyset . \end{aligned}$$

(2.2)

Each point $\varvec{x}^* \in \mathbb {R}^n$ satisfying (2.2) is called a critical point of the DC function f (see also [12] for characterizations of a minimizer of DC functions). Due to the derivation each Clarke stationary point is a critical point. But the opposite needs not to be necessarily true. Hence, criticality is a weaker optimality condition than Clarke stationarity. For a convex function $f:\mathbb {R}^n \rightarrow \mathbb {R}$, the optimality condition $\varvec{0} \in \partial f \left( \varvec{x}^* \right)$ becomes even sufficient for having a (global) minimum at $\varvec{x}^* \in \mathbb {R}^n$.

Given a function $f:\mathbb {R}^n \rightarrow \mathbb {R}$, we say that some vector $\varvec{d} \in \mathbb {R}^n$ is a descent direction of f at $\varvec{x}$ if there exists some $t^*> 0$ such that $f(\varvec{x}+t\varvec{d}) < f(\varvec{x})$ for all $t \in ( 0,t^* ]$. Note that in case f is directionally differentiable at $\varvec{x}$ in a direction $\varvec{d}$, the descent property $f'(\varvec{x};\varvec{d})<0$ is a sufficient criterion for $\varvec{d}$ being a descent direction.

Finally, we define the (Euclidean) distance between two sets $A, \ B \subseteq \mathbb {R}^n$ by

In particular, the projection of a point $\varvec{y} \in \mathbb {R}^n$ onto a nonempty, closed, and convex set $X \subseteq \mathbb {R}^n$ is determined as the (unique) point in X having the least distance towards $\varvec{y}$. We write

for this projection.

2.2 A bundle method for convex optimization

This section gives a short introduction to a (simple) bundle method for minimizing a convex function, mainly following the references [11, 18, 22]. Note that there exist more involved bundle schemes. However, the aim is to keep the presentation as simple as possible within this section. The bundle method and its convergence theory will later be used to solve the (convex, but nonsmooth) subproblems resulting in our algorithm for solving DC programs.

Therefore, consider the minimization problem

$$\begin{aligned} \min _{\varvec{x} \in \mathbb {R}^n } f(\varvec{x}) \end{aligned}$$

(2.3)

for a convex function $f: \mathbb {R}^n \rightarrow \mathbb {R}$. Similar to the classical steepest descent method, the first idea is to compute a descent direction $\varvec{d}^k \in \mathbb {R}^n$ of f at the current iterate $\varvec{x}^k \in \mathbb {R}^n$ by solving the subproblem

$$\begin{aligned} \min _{\varvec{d} \in \mathbb {R}^n} f'(\varvec{x}^k;\varvec{d}) \quad \text {s.t.} \quad \Vert \varvec{d} \Vert \le 1. \end{aligned}$$

Using the relation (2.1), it is not difficult to see that

is the unique solution of this subproblem. This suggests to choose $\varvec{d}^k=-\varvec{g}^k$ as a search direction. Although $\varvec{d}^k$ can indeed be verified to be a descent direction of f at $\varvec{x}^k$, simple examples show that the resulting method may not converge to a minimum, and that a successful version should include information of some neighboring subgradients. This idea leads to the search direction

$$\begin{aligned} \varvec{d}^k=-\varvec{g}^k \quad \text {with} \quad \varvec{g}^k=P_{\partial _{\epsilon }f(\varvec{x}^k)}(\varvec{0}). \end{aligned}$$

Unfortunately, the $\epsilon$-subdifferential is difficult to compute and projections onto this set might not be easy to calculate. The idea is then to replace the $\epsilon$-subdifferential by an inner approximation $G_{\epsilon }^k$ which has a simpler structure (like being polyhedral) and therefore allows the calculation of the projection

$$\begin{aligned} \varvec{g}^k:=P_{G_{\epsilon }^k}(\varvec{0}) \end{aligned}$$

(2.4)

with a significantly reduced effort. A suitable approximation $G_{\epsilon }^k$ can be obtained by using previously computed subgradients $\varvec{s}^j \in \partial f(\varvec{x}^j), \ j \in \{0,1,\ldots ,k\}$. More precisely, denoting the respective (nonnegative) linearization errors of f by

$$\begin{aligned} \alpha _j^k:=f(\varvec{x}^k)-f(\varvec{x}^j)-(\varvec{s}^j)^T(\varvec{x}^k-\varvec{x}^j) \quad \forall j=0,1,\ldots ,k, \end{aligned}$$

(2.5)

the set $G_{\epsilon }^k$ is defined by

$$\begin{aligned} G_{\epsilon }^k:= \bigg \{ \sum _{j=0}^k \lambda _j \varvec{s}^j \ \bigg | \ \sum _{j=0}^k \lambda _j \alpha _j^k \le \epsilon , \ \sum _{j=0}^k \lambda _j =1, \ \lambda _j \ge 0 \ \forall j=0,1,\ldots ,k \bigg \}. \end{aligned}$$

One can verify that this set has indeed the property that $G_{\epsilon }^k \subseteq \partial _{\epsilon } f(\varvec{x}^k)$ holds, which justifies to call it an inner approximation. Since $G_{\epsilon }^k$ is a nonempty, convex, and compact set, the projections (2.4) do exist. Numerically, these projections require the solution of the quadratic program

$$\begin{aligned} \min \ \frac{1}{2} \Big \Vert \sum _{j=0}^k \lambda _j \varvec{s}^j \Big \Vert ^2 \quad \text {s.t.} \quad \sum _{j=0}^k \lambda _j \alpha _j^k \le \epsilon , \quad \sum _{j=0}^k \lambda _j =1, \quad \lambda _j \ge 0 \quad \forall j=0,1,\ldots ,k.\nonumber \\ \end{aligned}$$

(2.6)

If $\varvec{\lambda }^k:=(\lambda _0^k, \lambda _1^k,\ldots ,\lambda _k^k)$ denotes a solution of this quadratic program, then the projection $\varvec{g}^k:=P_{G_{\epsilon }^k}(\textbf{0})$ is given by

$$\begin{aligned} \varvec{g}^k=\sum _{j=0}^k \lambda _j^k \varvec{s}^j. \end{aligned}$$

In practice, the coefficients gathered in $\varvec{\lambda }^k$ are often computed by considering the closely related quadratic program

$$\begin{aligned} \min \ \frac{1}{2} \Big \Vert \sum _{j=0}^k \lambda _j \varvec{s}^j \Big \Vert ^2 + \sum _{j=0}^k \lambda _j \alpha _j^k \quad \text {s.t.} \quad \sum _{j=0}^k \lambda _j =1, \ \lambda _j \ge 0 \quad \forall j=0,1,\ldots ,k. \end{aligned}$$

(2.7)

Altogether, this (almost) motivates the following algorithm.

Algorithm 2.1

(Bundle method)

(S.0):

Choose $\varvec{x}^0 \in \mathbb {R}^n, \ \varvec{s}^0 \in \partial f(\varvec{x}^0), \ m \in (0,1)$, set $k:=0, \ \varvec{y}^0:=\varvec{x}^0, \ \alpha _0^0:= 0, \ J_0:= \{0\}$.

(S.1):

Compute $\lambda _j^k, \ j \in J_k$, as a solution of the quadratic program

$$\begin{aligned} \min \ \frac{1}{2} \Big \Vert \sum _{j\in J_k} \lambda _j \varvec{s}^j \Big \Vert ^2 + \sum _{j \in J_k} \lambda _j \alpha _j^k \quad \text {s.t.} \quad \sum _{j \in J_k} \lambda _j =1, \ \lambda _j \ge 0 \qquad \forall j \in J_k. \end{aligned}$$

(S.2):

Set

$$\begin{aligned} \varvec{g}^k:= \sum _{j \in J_k} \lambda _j^k \varvec{s}^j, \quad \epsilon _k:= \sum _{j \in J_k} \lambda _j^k \alpha _j^k, \quad \varvec{d}^k:= -\varvec{g}^k, \quad \zeta _k:= - \Vert \varvec{g}^k \Vert ^2 - \epsilon _k. \end{aligned}$$

(S.3):

If $\zeta _k=0$: STOP.

(S.4):

Set $\varvec{y}^{k+1}=\varvec{x}^k+\varvec{d}^k$, choose $\varvec{s}^{k+1} \in \partial f(\varvec{y}^{k+1})$. If

$$\begin{aligned} f(\varvec{x}^k+\varvec{d}^k) \le f(\varvec{x}^k) + m \zeta _k, \end{aligned}$$

set (“serious step”)

$$\begin{aligned} t_k:=1, \quad \varvec{x}^{k+1}:= \varvec{x}^k+\varvec{d}^k, \end{aligned}$$

otherwise set (“null step”)

$$\begin{aligned} t_k:= 0, \quad \varvec{x}^{k+1}:= \varvec{x}^k. \end{aligned}$$

(S.5):

Set

$$\begin{aligned} J_k^p&:= \{ j \in J_k \ | \ \lambda _j^k > 0 \}, \quad J_{k+1} \ :=J_k^p \cup \{k+1\}, \\ \alpha _j^{k+1}&:= f(\varvec{x}^{k+1})-f(\varvec{y}^j)-(\varvec{s}^j)^T(\varvec{x}^{k+1}-\varvec{y}^j) \quad \forall j \in J_{k+1}. \end{aligned}$$

(S.6):

Set $k \leftarrow k+1$, and go to (S.1).

In order to restrict the number of constraints in (2.7) and to limit the amount of subgradients and linearization errors to be stored, the index set in the algorithm is reduced to a suitable subset $J_k \subseteq \{0,\ldots ,k\}$. Moreover, the linearization errors in (S.5) are slightly modified in comparison to (2.5), since the intermediate points $\varvec{y}^j, \ j \in J_k$, are also taken into account. The underlying principle is very simple: If the search direction $\varvec{d}^k$ provides a sufficient decrease in the function value, one proceeds in this direction (with stepsize $t_k=1$). Otherwise one sticks with the current iterate, but adds some further information to the bundle in order to get a better search direction during the next iteration. Furthermore, the termination criterion in (S.3) gets motivated by the subsequent observation.

Lemma 2.2

If $\zeta _k=0$ holds for some $k \in \mathbb {N}_0$, then the corresponding iterate $\varvec{x}^k$ is already a minimizer of the convex objective function f.

This last assertion comes from the elementary observation that

$$\begin{aligned} \varvec{g}^k \in \partial _{\epsilon _k} f(\varvec{x}^k) \quad \forall k \ge 0. \end{aligned}$$

(2.8)

In case a solution of the convex optimization problem (2.3) exists, one gets the following global convergence result for Algorithm 2.1.

Theorem 2.3

Assume that the solution set $\mathcal {S}:= \left\{ \varvec{x}^* \in \mathbb {R}^n \ \big | \ f(\varvec{x}^*) = \inf _{\varvec{x} \in \mathbb {R}^n} f(\varvec{x}) \right\}$ is nonempty. Then every sequence $\{\varvec{x}^k\}$ generated by Algorithm 2.1 converges towards a minimizer $\varvec{x}^* \in \mathcal {S}$ of the convex objective function f.

3 A bundle method for DC optimization

This section introduces the new algorithm for DC optimization using the approach of the classical DC Algorithm in combination with the previously presented bundle method. The precise statement together with a convergence theory is given in Sect. 3.1, whereas some additional descent properties are discussed in Sect. 3.2.

3.1 Algorithm and convergence properties

The aim of our approach is to develop an algorithm which, similar to the Boosted DCA (BDCA), computes descent directions of the objective function using the subproblems arising in the classical DC Algorithm (DCA) (see [2, 21]). This allows a line search to determine the subsequent iterate. In contrast to BDCA, however, the new algorithm is applicable to DC functions with both DC components being nonsmooth. To gain a suitable descent direction from the convex subproblems, we allow an inexact solution of these subproblems by the previous bundle technique.

Having a DC function f as defined in (1.1) to be minimized, the classical DCA approach replaces, in each step $l \in \mathbb {N}_0$, the second DC component h by some linear minorization

$$\begin{aligned} h_l(\varvec{x}):= h(\varvec{x}^l)+ (\varvec{s}^l)^T (\varvec{x}-\varvec{x}^l) \end{aligned}$$

with some subgradient $\varvec{s}^l \in \partial h(\varvec{x}^l)$. That way, a convex majorization of the objective function f is obtained. Minimizing this model function is then equivalent to minimizing

$$\begin{aligned} \phi _l (\varvec{x}):= g(\varvec{x})-(\varvec{s}^l)^T \varvec{x}. \end{aligned}$$

(3.1)

To guarantee the existence of a minimizer one usually assumes g to be uniformly convex. This can be done without loss of generality by adding a uniformly convex term, for example with $\rho > 0$, to each convex DC component, if necessary. In contrast to the BDCA, the new algorithm does not require the exact minimization of the convex function $\phi _l$ in order to obtain a descent direction of the objective function. Instead, the bundle method from Sect. 2.2 is applied until a serious step is carried out. It turns out that the search direction of this step is a descent direction of f at the current iterate $\varvec{x}^l$. A subsequent line search is then used to compute the next iterate. The convergence theory shows that this line search always accepts the full step, which means a stepsize of one. Even larger stepsizes are possible.

Algorithm 3.1

(DCBA–DC Bundle Algorithm)

(S.0):

Choose $\varvec{x}^0 \in \mathbb {R}^n, \ \beta \in (0,1), \ m \in (0,1), \ \mu \in (0,m]$, set $l:= 0$.

(S.1):

Choose $\varvec{s}^l \in \partial h(\varvec{x}^l)$, and define $\phi _l$ as in (3.1).

(S.2):

Apply the bundle method from Algorithm 2.1 to minimize $\phi _l(\varvec{x})$ until a serious step is carried out or until it terminates. Retain $(\varvec{d}^l,\epsilon _l, \zeta _l)$ from the corresponding quantities of the serious step or the termination step, respectively. In case of termination of the bundle method: STOP.

(S.3):

Choose $\bar{\tau }_l \ge 1$, compute $\tau _l = \max \left( \left\{ \bar{\tau }_l \beta ^j \ \big | \ j \in \mathbb {N}_0 \right\} \cup \{1\} \right)$ such that

$$\begin{aligned} f(\varvec{x}^l+\tau _l \varvec{d}^l) \le f(\varvec{x}^l) + \mu \tau _l^2 \zeta _l. \end{aligned}$$

(S.4):

Set $\varvec{x}^{l+1}:= \varvec{x}^l + \tau _l \varvec{d}^l, \ l \leftarrow l+1$, and go to (S.1).

To guarantee that (S.2) always terminates, we have to make sure that the function $\phi _l$ attains a minimum (cf. Theorem 2.3). Recall that this automatically holds if g is uniformly convex. Hence, we state this assumption explicitly in the following, which is implicitly supposed to hold throughout our convergence analysis. We stress once more, however, that this assumption is not at all restrictive since we can always add and subtract a uniformly convex function to the DC decomposition of f.

Assumption 3.2

The DC component g is a uniformly convex function.

Some comments are in order regarding Algorithm 3.1. First note that l denotes the iteration counter for the (outer) DC-type method, whereas we will use the letter k to denote the iterations of the inner (bundle) method. Hence, $J_{k,l}$ denotes the index set that occurs in iteration k of the bundle method, called in iteration l of Algorithm 3.1. The notation $\varvec{d}^{k,l}$ is defined similarly.

Note that the bundle method executes null steps only except possibly in the last iteration. This, in particular, allows a simplified calculation of the linearization errors. Since the iterate $\varvec{x}^l$ does not change in such a situation, only the computation of the linearization error corresponding to the new intermediate point is required, but not the computation for each index $j \in J_{k,l}$. Hence, in the kth sub-iteration with the search direction $\varvec{d}^{k,l}$ and corresponding subgradient $\varvec{v}^{k+1,l} \in \partial \phi _l(\varvec{x}^l+\varvec{d}^{k,l})$, the required linearization error can be obtained by

$$\begin{aligned} \alpha ^{k+1}_l:= \phi _l (\varvec{x}^l) - \phi _l (\varvec{x}^l+\varvec{d}^{k,l}) + (\varvec{v}^{k+1,l})^T \varvec{d}^{k,l}. \end{aligned}$$

(3.2)

Furthermore, a subgradient $\varvec{v}^{k+1,l} \in \partial \phi _l(\varvec{x}^l+\varvec{d}^{k,l})$ can be computed by selecting some element $\varvec{t}^{k+1,l} \in \partial g(\varvec{x}^l+\varvec{d}^{k,l})$ and setting $\varvec{v}^{k+1,l}:=\varvec{t}^{k+1,l}-\varvec{s}^l$.

The line search is an Armijo-type one but with two modifications. First, a quadratic stepsize is considered. This idea already occurs in [6] but with a more involved procedure for determining a suitable stepsize. Second, we look for a decrease in the function value of at least $\mu \tau ^2_l (-\zeta _l)$. At first glance, one might expect $\Vert \varvec{d}^{l} \Vert ^2$ instead of the enlarged value $- \zeta _l= \Vert \varvec{d}^{l} \Vert ^2 + \epsilon _l$. This adjustment is motivated by Lemma 3.4 below. In addition, the initial stepsize $\bar{\tau }_l$ can be determined as a self-adaptive trial stepsize like the one suggested in [2]. One only needs to ensure $\bar{\tau }_l \ge 1$.

Before proving a global convergence result for Algorithm 3.1, we begin with some preliminary observations. To this end, we first justify the termination criterion in (S.2).

Lemma 3.3

Suppose $\zeta _{l} = 0$ holds for some l. Then the current iterate $\varvec{x}^l$ is a critical point of the objective function f.

Proof

As the iterate does not change during the bundle process, having $\zeta _{l} = 0$ for some l together with Lemma 2.2 implies that $\varvec{x}^l$ minimizes $\phi _l$. Hence, we have $\varvec{0} \in \partial \phi _l (\varvec{x}^l) = \partial g(\varvec{x}^l) -\varvec{s}^l$. On the other hand, $\varvec{s}^l \in \partial h(\varvec{x}^l)$ by our choice. Consequently, $\partial g(\varvec{x}^l) \cap \partial h(\varvec{x}^l) \ne \emptyset$ follows, showing that $\varvec{x}^l$ is indeed a critical point of the DC function f. $\square$

Motivated by Lemma 3.3, we assume, from now on, that $\zeta _l < 0$ holds for all l, which means Algorithm 3.1 does not stop after finitely many iterations. The following result then shows that the Armijo-type line search is always well-defined (together with Assumption 3.2 this implies that the entire Algorithm 3.1 is well-defined), and that the full step satisfies the line search criterion.

Lemma 3.4

At each iteration l, there exists a stepsize $\tau _l, \ \tau _l = 1$ or $\tau _l = \bar{\tau }_l \beta ^j \ge 1$ with some $j \in \mathbb {N}_0$, such that

$$\begin{aligned} f(\varvec{x}^l+\tau _l \varvec{d}^l) \le f(\varvec{x}^l) + \mu \tau _l^2 \zeta _l \end{aligned}$$

(3.3)

holds.

Proof

Let l be arbitrarily chosen. Then

$$\begin{aligned} {\begin{matrix} f(\varvec{x}^l+\varvec{d}^l)-f(\varvec{x}^l) &{} = g(\varvec{x}^l+\varvec{d}^l)-g(\varvec{x}^l)-h(\varvec{x}^l+\varvec{d}^l)+h(\varvec{x}^l)\\ &{} \le g(\varvec{x}^l+\varvec{d}^l)-g(\varvec{x}^l)-(\varvec{s}^l)^T\varvec{d}^l \\ &{} = \phi _l (\varvec{x}^l+\varvec{d}^l) - \phi _l (\varvec{x}^l) \\ &{} \le m \zeta _l \le \mu \zeta _l, \end{matrix}} \end{aligned}$$

where the first inequality exploits the fact that $\varvec{s}^l \in \partial h(\varvec{x}^l)$, the penultimate inequality comes from the serious step termination of the bundle method, and the last estimate uses $\mu \in (0,m]$ as well as $\zeta _l < 0$ (see the previous discussion). This shows that at least $\tau _l=1$ has the desired property. Taking into account the construction of the stepsize yields the desired claim. $\square$

Finally, we need the following auxiliary result for proving global convergence of Algorithm 3.1.

Lemma 3.5

Assume that Algorithm 3.1 generates an infinite sequence $\{\varvec{x}^l\}$. Then the sequence $\{f(\varvec{x}^l)\}$ is monotonically decreasing. If, in addition, there exists a lower bound $f^* \in \mathbb {R}$ such that $f(\varvec{x}^l) \ge f^*$ holds for all l, then the estimate

$$\begin{aligned} \sum _{l=0}^{\infty } \left( \Vert \varvec{d}^l \Vert ^2+ \epsilon _l \right) \le \frac{f(\varvec{x}^0)-f^*}{\mu } \end{aligned}$$

holds. In particular, we then have $\varvec{d}^l \rightarrow 0$ and $\epsilon _l \rightarrow 0$ for $l \rightarrow \infty$.

Proof

The monotonicity of the function values follows directly from $\zeta _l$ being negative and the line search in (S.3).

To establish the second assertion, note that (S.3) can be written as $- \mu \tau _l^2 \zeta _l \le f(\varvec{x}^l)-f(\varvec{x}^{l+1})$ for all l. Taking the sum over $l=0,\ldots ,j-1$, we get

$$\begin{aligned} \mu \sum _{l=0}^{j-1} \tau _l^2 (-\zeta _l) \le f(\varvec{x}^0)-f(\varvec{x}^j) \le f(\varvec{x}^0)-f^* \qquad \forall j \in \mathbb {N} \end{aligned}$$

by the boundedness assumption. Letting $j \rightarrow \infty$ therefore gives

$$\begin{aligned} \sum _{l=0}^{\infty } \tau _l^2 (- \zeta _l) \le \frac{f(\varvec{x}^0)-f^*}{\mu }. \end{aligned}$$

Using $\tau _l \ge 1$ and inserting the definition of $\zeta _l$ gives the desired inequality. $\square$

The following is the main global convergence result for Algorithm 3.1.

Theorem 3.6

Every accumulation point of a sequence $\{\varvec{x}^l\}$ generated by Algorithm 3.1 is a critical point of the objective function f.

Proof

Let $\varvec{x}^*$ be an accumulation point of the sequence $\{\varvec{x}^l\}$ and $\{\varvec{x}^l\}_{L}$ be a corresponding subsequence converging to $\varvec{x}^*$. Since $\varvec{s}^l \in \partial h(\varvec{x}^l)$ for all l, the convergence of $\{\varvec{x}^l\}_{L}$ implies the boundedness of the sequence $\{\varvec{s}^l\}_{L}$. Hence, without loss of generality, we may assume that $\{\varvec{s}^l\}_{L}$ converges to some limit $\varvec{s}^*$. Due to the closedness property of the convex subdifferential, it follows that $\varvec{s}^* \in \partial h(\varvec{x}^*)$.

By continuity of f, we have $f(\varvec{x}^l) \rightarrow _L f(\varvec{x}^*)$. Hence, the monotonicity of the entire sequence $\{f(\varvec{x}^l)\}$ yields convergence of the entire sequence $\{f(\varvec{x}^l)\}$ to $f(\varvec{x}^*)$. The monotonicity also implies $f(\varvec{x}^l) \ge f(\varvec{x}^*)$ for all l. Thus, the previous lemma can be applied to obtain $\varvec{d}^l \rightarrow 0$ and $\epsilon _l \rightarrow 0$ for $l \rightarrow \infty$.

Furthermore, since we have $-\varvec{d}^l \in \partial _{\epsilon _l} \phi _l (\varvec{x}^l)$ in view of (2.8), we get

$$\begin{aligned} \phi _l(\varvec{x}) \ge \phi _l (\varvec{x}^l) - (\varvec{d}^l)^T(\varvec{x}-\varvec{x}^l) - \epsilon _l \qquad \forall \varvec{x} \in \mathbb {R}^n \ \forall l \in \mathbb {N}_0. \end{aligned}$$

Using the definition of $\phi _l$, this can be rewritten as

$$\begin{aligned} g(\varvec{x})-(\varvec{s}^l)^T \varvec{x} \ge g(\varvec{x}^l)-(\varvec{s}^l)^T \varvec{x}^l -(\varvec{d}^l)^T(\varvec{x}-\varvec{x}^l) - \epsilon _ l \qquad \forall \varvec{x} \in \mathbb {R}^n \ \forall l \in \mathbb {N}_0. \end{aligned}$$

Taking $l \rightarrow _L \infty$ and exploiting the continuity of g therefore yields

$$\begin{aligned} g(\varvec{x}) - (\varvec{s}^*)^T \varvec{x} \ge g(\varvec{x}^*) - (\varvec{s}^*)^T \varvec{x}^* \qquad \forall \varvec{x} \in \mathbb {R}^n \end{aligned}$$

or, equivalently,

$$\begin{aligned} g(\varvec{x}) \ge g(\varvec{x}^*) + (\varvec{s}^*)^T(\varvec{x}-\varvec{x}^*) \qquad \forall \varvec{x} \in \mathbb {R}^n. \end{aligned}$$

Consequently, we have $\varvec{s}^* \in \partial g(\varvec{x}^*)$. Together with $\varvec{s}^* \in \partial h(\varvec{x}^*)$, this shows that $\partial g(\varvec{x}^*) \cap \partial h(\varvec{x}^*) \ne \emptyset$. Hence, $\varvec{x}^*$ is a critical point of the DC function f. $\square$

Recall that we terminate our method(s), for our theoretical considerations, only if $\zeta _l = 0$. Numerically, one should replace this condition in (S.3) of the bundle method 2.1 by a more practical condition like

(3.4)

with some given tolerance $\delta > 0$. The following result then shows that Algorithm 3.1 terminates after finitely many iterations in a point which approximately satisfies the condition of being a critical point of the DC function f.

Theorem 3.7

Assume that f is bounded from below. Then Algorithm 3.1, with the modified termination criterion (3.4), terminates after finitely many iterations in a point $\varvec{x}^L$ satisfying

$$\begin{aligned} {\text {dist}} \left( \partial _{\epsilon _L} g(\varvec{x}^L), \partial h(\varvec{x}^L) \right)< \sqrt{\delta } \quad \text {with} \quad \epsilon _L < \delta . \end{aligned}$$

(3.5)

Proof

First recall that, in each outer iteration l, due to Assumption 3.2, the bundle step (3.2) terminates after a finite number of inner iterations either meeting the termination criterion or detecting a descent direction $\varvec{d}^l$. This is based on the fact that carrying out only null steps within the bundle iteration leads to $\{\zeta _{k}\}$ tending to zero (see e.g. [11]). Hence, the condition (3.4) eventually holds.

We next show that Algorithm 3.1 terminates after finitely many iterations. Assume, by contradiction, that an infinite sequence $\{\varvec{x}^l\}$ is generated. Then each call of the bundle method ends with a serious step and hence the computation of a descent direction $\varvec{d}^l$. The subsequent line search then yields

$$\begin{aligned} f(\varvec{x}^{l+1}) \le f(\varvec{x}^l) + \mu \tau _l^2 \zeta _l \le f(\varvec{x}^l) + \mu \zeta _l \qquad \forall l \in \mathbb {N}_0, \end{aligned}$$

where the final inequality results from $\tau _l \ge 1$ and $\zeta _l$ being negative. Summation over $l= 0,\ldots ,j-1$ gives

$$\begin{aligned} f(\varvec{x}^j)-f(\varvec{x}^0) \le \mu \sum _{l=0}^{j-1} \zeta _l \le - \mu \delta j \qquad \forall j \in \mathbb {N}, \end{aligned}$$

since $\zeta _l \le -\delta$ for all l by assumption (the inexact termination criterion never holds). Letting $j \rightarrow \infty$, the right-hand side tends to $- \infty$, whereas the left-hand side is bounded from below by assumption. This contradiction shows that Algorithm 3.1 terminates within a finite number of iterations.

Let $\varvec{x}^L$ denote the point of termination. It remains to show that $\varvec{x}^L$ satisfies the properties from (3.5). To this end, we first note that a simple calculation shows that $\partial _{\epsilon } \phi _l (\varvec{x}) = \partial _{\epsilon } g(\varvec{x}) -\varvec{s}^l$ holds for all $l \in \mathbb {N}_0, \ \epsilon \ge 0$, and $\varvec{x} \in \mathbb {R}^n$. Since $-\varvec{d}^l \in \partial _{\epsilon _l} \phi _l (\varvec{x}^l)$ by (2.8), we therefore obtain the existence of an element $\tilde{\varvec{t}}^l \in \partial _{\epsilon _l} g(\varvec{x}^l)$ such that $-\varvec{d}^l = \tilde{\varvec{t}}^l - \varvec{s}^l$. Together with the fact that $\varvec{s}^l \in \partial h(\varvec{x}^l)$, we get

$$\begin{aligned} {\text {dist}} \big ( \partial _{\epsilon _l} g(\varvec{x}^l), \partial h(\varvec{x}^l) \big )&= \inf \big \{ \Vert \varvec{t}-\varvec{s} \Vert \ \big | \ \varvec{t} \in \partial _{\epsilon _l} g(\varvec{x}^l), \ \varvec{s} \in \partial h(\varvec{x}^l) \big \} \\&\le \big \Vert \tilde{\varvec{t}}^l - \varvec{s}^l \big \Vert = \Vert \varvec{d}^l \Vert \le \sqrt{| \zeta _l |}, \end{aligned}$$

where the last inequality just exploits the definition of $\zeta _l$. This definition also implies $\epsilon _l \le | \zeta _l |$. Since, upon termination, we have $| \zeta _L | < \delta$, the two estimates (3.5) follow. $\square$

Note that (3.5) can be seen as an approximation of

$$\begin{aligned} {\text {dist}} \left( \partial g(\varvec{x}^*), \partial h(\varvec{x}^*) \right) = 0. \end{aligned}$$

(3.6)

Due to the closedness of the subdifferential, (3.6) is equivalent to $\partial g(\varvec{x}^*) \cap \partial h(\varvec{x}^*) \ne \emptyset$, which means that $\varvec{x}^*$ is a critical point of the DC function f. We may therefore view the point of termination as an approximate critical point of the objective function.

3.2 Descent properties of search directions

The subject of this section is to discuss some additional properties of the search direction $\varvec{d}^l$. We will see that $\varvec{d}^l$ is indeed a descent direction of the objective function f at the current iterate $\varvec{x}^l$, but, in general, not in the point $\varvec{x}^l+ \varvec{d}^l$. Note that this latter property holds for the boosted DCA method from [2] if g is smooth. We also discuss a modified version for determining a suitable stepsize in (S.3).

Note that the convergence theory in Sect. 3.1 is completely independent of any descent properties of $\varvec{d}^l$. In particular, the line search in (S.3) makes no explicit use of this feature (see also Lemma 3.4). Nevertheless, it is interesting to see that $\varvec{d}^l$ is indeed a descent direction of f in $\varvec{x}^l$.

Proposition 3.8

The directional derivative of the objective function satisfies

$$\begin{aligned} f'(\varvec{x}^l;\varvec{d}^l) \le \phi _l ' (\varvec{x}^l;\varvec{d}^l) < 0 \quad \forall l \in \mathbb {N}_0. \end{aligned}$$

Hence, $\varvec{d}^l$ is a descent direction of f in $\varvec{x}^l$.

Proof

Let l be fixed. We then obtain

$$\begin{aligned} f'(\varvec{x}^l;\varvec{d}^l)&= g'(\varvec{x}^l;\varvec{d}^l)-h'(\varvec{x}^l;\varvec{d}^l)\\&= g'(\varvec{x}^l;\varvec{d}^l)- \max _{\varvec{s} \in \partial h(\varvec{x}^l)} \varvec{s}^T \varvec{d}^l \\&\le g'(\varvec{x}^l;\varvec{d}^l)- (\varvec{s}^l)^T \varvec{d}^l \\&= \phi _l ' (\varvec{x}^l;\varvec{d}^l), \end{aligned}$$

where the relation (2.1) together with $\varvec{s}^l \in \partial h(\varvec{x}^l)$ was exploited. By construction, $\varvec{d}^l$ results from a serious step of the bundle method, hence $\phi _l(\varvec{x}^l + \varvec{d}^l) < \phi _l(\varvec{x}^l)$ holds. A standard characterization of the directional derivative for convex functions therefore yields

$$\begin{aligned} \phi _l ' (\varvec{x}^l;\varvec{d}^l) = \inf _{t>0} \frac{\phi _l (\varvec{x}^l+t \varvec{d}^l)- \phi _l (\varvec{x}^l)}{t} \le \frac{\phi _l (\varvec{x}^l+\varvec{d}^l)-\phi _l(\varvec{x}^l)}{1} < 0. \end{aligned}$$

Putting both estimates together completes the proof. $\square$

Recall that Lemma 3.4 shows that a full step in the direction $\varvec{d}^l$ is always accepted by the line search criterion (S.3). Using a minor modification in the bundle procedure ensures that DCBA even allows to take a stepsize $\tau _l$ strictly larger than one. The details are given in the subsequent proposition.

Proposition 3.9

Assume that we replace the inequality in (S.4) of the Bundle Algorithm 2.1 by a strict one. Then there exists a stepsize $\tau _l > 1$ such that (3.3) holds.

Proof

For arbitrary l, one can follow the proof of Lemma 3.4 to see that the sharp estimate

$$\begin{aligned} f(\varvec{x}^l+ \varvec{d}^l) < f(\varvec{x}^l) + \mu \zeta _l \end{aligned}$$

holds. Consequently, (3.3) is satisfied for $\tau _l=1$, but with a strict inequality. Since the mapping $\tau \mapsto f(\varvec{x}^l+\tau \varvec{d}^l) - f(\varvec{x}^l) - \mu \tau ^2 \zeta _l$ is continuous, (3.3) holds on an interval $[1, \tau _*)$ for some $\tau _*> 1$ (depending on l). This completes the proof. $\square$

The previous result motivates to search for a suitable stepsize by using a strategy like

$$\begin{aligned} \tau _l = \max \left\{ 1+ \bar{\tau }_l \beta ^j \ \big | \ j \in \mathbb {N}_0 \right\} \quad \text {such that} \quad f(\varvec{x}^l+\tau _l \varvec{d}^l) \le f(\varvec{x}^l) + \mu \tau _l^2 \zeta _l \end{aligned}$$

for some $\beta \in (0,1)$, where $\bar{\tau }_l$ can be determined by the self-adaptive trial stepsize strategy introduced in [2]. In this way, our approach shares some properties of the boosted version of DCA, but for general nonsmooth functions g and h.

At first glance, this modified stepsize seems to be rather promising, and is more likely to yield a stepsize larger than one than the original stepsize rule from (S.3). However, numerical tests indicate that the overall results are often better for the original stepsize rule, at least for most applications considered in this work. The computation of stepsizes larger than one by the modified rule sometimes leads to the situation where the method crosses a valley with a one-dimensional minimizer, ending up in a region of ascent again. Therefore, the progress in the function value of the objective is often less than accepting a stepsize of one. As this behavior accumulates, one keeps jumping from one side of the valley to the other, sometimes even on a straight line. We illustrate this behavior in Fig. 1 where Example 3.10 (see below) is used, with the standard choice of parameters given in Sect. 4.1 and initial point $(x^0,y^0)^T:=(2.5,1)^T$. It is remarkable that the vector provided by the bundle method often seems to be a pretty good choice for updating the iterate without any scaling.

Fig. 1

Variants of stepsize strategies

Recall that Lemma 3.4 and Proposition 3.9 show that the full step in the direction $\varvec{d}^l$ is always accepted by our line search rule(s). Similar to [2], one may therefore ask whether $\varvec{d}^l$ is also a direction of descent at the point $\varvec{x}^l + \varvec{d}^l$. Note, however, that this cannot be expected for nonsmooth functions g since it was already shown in [2] that this property does not hold, in general, even if the convex subproblems are solved exactly. It is therefore not surprising to see that this descent property is also violated for our inexact solution $\varvec{d}^l$ of the convex subproblem. This is shown by the following counterexample taken from [2].

Example 3.10

(Failure of a boosted version of DCBA) Consider the function

with uniformly convex DC components $g, h: \mathbb {R}^2 \rightarrow \mathbb {R}$ chosen as

Taking $(x^0,y^0)^T:=(0.5,0.1)^T$ as a starting point, the bundle method applied to $\min _{(x,y) \in \mathbb {R}^2} \phi _0(x,y)$ with $m=0.1$ stops after two iterations with the detection of the descent direction

$$\begin{aligned} \varvec{d}^0 = \frac{1}{{10,820}} ({6610}, {-3061})^T \approx (0.61091,-0.28290)^T. \end{aligned}$$

Let us note, for the sake of completeness, that selecting m in a different way would not open the door for gaining a descent direction in the first iteration, as the first search direction $(d^{0,0}_1,d^{0,0}_2)^T$ satisfies $\phi _0(x^0+d^{0,0}_1,y^0+d^{0,0}_2)-\phi _0(x^0,y^0)=2>0$.

Before verifying analytically that $\varvec{d}^0$ is indeed not a descent direction of f at the intermediate point

$$\begin{aligned} (x^0,y^0)^T+\varvec{d}^0=\frac{1}{{10,820}} ({12,020}, {-1979})^T \approx (1.11091, -0.18290)^T, \end{aligned}$$

let us have a look at Fig. 2, which contains a contour plot of the function f, revealing the basic situation. Starting at $(x^0,y^0)^T=(0.5,0.1)^T$ and heading in the direction $\varvec{d}^0$, one initially achieves a decrease in the function value. This was expectable as $\varvec{d}^0$ is known to be a descent direction of f at $(x^0,y^0)^T$. But proceeding further (below the line $y=0$ to be more precise), one leaves the region of descent, entering a region of ascent. Accepting a full step $\tau _0=1$, one touches the region of ascent. Therefore, moving further in the direction $\varvec{d}^0$ from $(x^0,y^0)^T+\varvec{d}^0$ would result in a continuing increase of the function value. Consequently, $\varvec{d}^0$ is not a descent direction of f at the point $(x^0,y^0)^T+\varvec{d}^0$. Analytically this claim is confirmed by the corresponding scalar product

$$\begin{aligned} \nabla f (x^0+d^0_1,y^0+d^0_2)^T \varvec{d}^0 \approx 0.09695 \end{aligned}$$

being positive (note that one can indeed consider the gradient of the objective, as the considered point is located in a region where f is differentiable). In addition, this instance shows that the search direction $\varvec{d}^0$ is not running tangential towards the contour line through $(x^0+d^0_1,y^0+d^0_2)^T$, which is marked pink in Fig. 2, although it might seem to be the case at first glance.

Fig. 2

Change of the function value in the direction $\varvec{d}^0$ starting at $(0.5,0.1)^T$

Recall that in [2] (making use of the notation therein) it is proven that for continuously differentiable functions g computing the exact solution $\varvec{y}^l$ of the convex subproblem arising in DCA leads to $\bar{\varvec{d}}^l:=\varvec{y}^l-\varvec{x}^l$ being a descent direction of f at the optimal point $\varvec{y}^l=\varvec{x}^l+\bar{\varvec{d}}^l$. The boosted version of the DC Algorithm, BDCA, is based on this observation. But this descent property does not necessarily hold for our approach where $\varvec{d}^l$ is only computed by means of an inexact solution of the convex subproblem. This is illustrated in the following smooth example which results from the previous one by replacing the absolute value function using a scaled and shifted version of Huber’s loss (see [14]).

Example 3.11

(Failure of a boosted version of DCBA in case of smooth DC components) Consider the smoothed function

$$\begin{aligned} \tilde{f}: \mathbb {R}^2 \rightarrow \mathbb {R}, \quad \tilde{f}(x,y):=-\frac{5}{2}x +\frac{1}{2} ( x^2+y^2) + \psi _{\epsilon }(x)+ \psi _{\epsilon }(y) \end{aligned}$$

with

being the described smooth adaption of the absolute value function for sufficiently small $\epsilon > 0$, for example $\epsilon =10^{-3}$. Similarly to the previous example the uniformly convex DC components $\tilde{g},\tilde{h}: \mathbb {R}^2 \rightarrow \mathbb {R}$ are chosen as

$$\begin{aligned} \tilde{g}(x,y):=-\frac{5}{2}x +x^2+y^2 + \psi _{\epsilon }(x) + \psi _{\epsilon }(y), \quad \tilde{h}(x,y):=\frac{1}{2}(x^2+y^2). \end{aligned}$$

Note that the smooth modification $\tilde{f}$ coincides with the function f from the previous example on the set $Q_{\epsilon }:= \left\{ (x,y) \in \mathbb {R}^2 \ \big | \ \vert x \vert \ge \epsilon , \ \vert y \vert \ge \epsilon \right\}$. Therefore, taking $\epsilon > 0$ sufficiently small, and starting again in $(x^0,y^0)^T=(0.5,0.1)^T$, the approximation function $\tilde{\phi }_0$ matches the corresponding one from Example 3.10 at least on the relevant part of the domain of definition, namely $Q_{\epsilon }$. Thus, all calculations from Example 3.10 remain valid, as we stay inside $Q_{\epsilon }$ during the whole computation. Consequently, also in case of a smooth first DC component the accepted search direction turns out not to be a descent direction of the smooth objective $\tilde{f}$ at the intermediate point $(x^0+d^0_1,y^0+d^0_2)^T$.

The previous example, of course, shows that our approach has a drawback compared to the boosted DCA. Recall, however, that our primary aim was to develop a method for solving DC programs where both DC components g and h are nonsmooth. In this situation, the descent property of $\varvec{d}^l$ cannot be expected at the point $\varvec{x}^l + \varvec{d}^l$ even for the exact solution of the convex subproblem.

4 Numerical experiments and applications

This section presents some numerical experiments of the new algorithm DCBA and gives a comparison with some existing solvers for DC programs. In particular, our method is compared with the solvers DCA [21], BDCA [2], PBDC [16], and DCPCA [10] which are briefly reviewed in Sect. 4.1, together with some details of our implementations. The numerical experiments are then carried out using a broad class of academic test problems [2, 16] as well as some examples arising from applications, namely minimum sum-of-squares clustering [2, 25], multidimensional scaling [2, 19], and edge detection by means of a clustering technique [17].

4.1 Methods and implementation

This section first provides some details of the DC solvers that are used in our numerical studies. The standard method for solving DC problems is the DCA [21, 26], which can be accelerated to a boosted version, namely the BDCA [2], in suitable cases. In addition, we use two bundle methods, PBDC [16] and DCPCA [10]. A brief overview of these algorithms is given in Table 1.

As already noted, DCA derives, in each iteration, a convex majorization of the objective function by approximating the second DC component by some linear minorization. The minimizer of this model function yields the next iterate, which means DCA solves the subproblems exactly and uses no line search globalization (see [21]).

BDCA is introduced in [2]. It is an accelerated version of DCA being motivated by the observation that, in case of a smooth first DC component, the solution of the convex subproblem occurring in DCA gives rise to a descent direction at the point that is accepted by DCA as the next iterate. The latter detection allows to add a line search right after solving the very same convex subproblem as in DCA. This often speeds up the convergence.

PBDC is described in [16]. This bundle method constructs two separate cutting plane models, one for each DC component. Combining both leads to a piecewise linear, nonconvex model of the objective function which incorporates the convex behavior of the DC function as well as its concave one. The computation of the search direction uses a stabilizing term which includes a proximity parameter. Thus, a line search is superfluous. The termination criterion directly refers to the definition of a critical point of the DC function (see (2.2)) and estimates the distance between the respective two subdifferentials.

DCPCA originates from [10]. Similar to PBDC, it develops two separate cutting plane models, one for each DC component. This initially leads to a nonconvex piecewise linear approximation. The two DC components, however, are not treated equally. The bundle related to the first DC component is restricted to local information only, whereas the bundle concerning the second DC component is not. The resulting model, a pointwise maximum of concave functions, is then approximated by a local quadratic program which, in turn, is used to compute a (candidate) search direction. In case no satisfactory solution can be found, the method switches to an auxiliary (also quadratic) program. Having found an appropriate search direction, a line search follows.

Table 1 Summary of the methods used in our numerical experiments

In order to achieve a better comparability of the numerical results, the termination criteria of the different algorithms are adapted to some extent. While BDCA stops whenever the computed descent direction $\varvec{d}^l$ is (close to) zero, for DCBA the sum of the squared norm of the search direction and the $\epsilon$-tolerance of the current approximation of the subdifferential is checked to be (close to) zero. This motivates to split the termination criterion for DCBA into two parts, namely

$$\begin{aligned} \Vert \varvec{d}^{l} \Vert< \bar{\varepsilon }_1 \quad \text {and} \quad \epsilon _{l} < \bar{\varepsilon }_2 \end{aligned}$$

with some given tolerances $\bar{\varepsilon }_1, \ \bar{\varepsilon }_2 > 0$. Note that suppressing the square of the norm in the first condition is not essential. Accordingly, the termination criterion for BDCA is inherited as $\Vert \varvec{d}^l \Vert < \bar{\varepsilon }_1$. As the stopping condition for DCA and BDCA coincides, it is clear how to choose the respective one for DCA.

Comparing the convergence theorems for PBDC (see Theorem 6 in [16]) with the corresponding Theorem 3.7 for DCBA, one realizes an immediate similarity. The first result ensures that at the point $\varvec{x}^L$ of termination the approximate criticality condition ${\text {dist}} \left( \partial _{\bar{\varepsilon }_2}g(\varvec{x}^L), \partial _{\bar{\varepsilon }_2}h(\varvec{x}^L) \right) \le \bar{\varepsilon }_1$ is satisfied whenever the termination criterion

is met (the notation is taken from [16]). The second one proves the final estimate ${\text {dist}} \left( \partial _{\epsilon _L} g(\varvec{x}^L), \partial h(\varvec{x}^L) \right) < \bar{\varepsilon }_1$ with $\epsilon _L < \bar{\varepsilon }_2$. This suggests to stuck with the termination criterion for PBDC as it is stated in the cited work. In addition, it indicates in which range the second termination tolerance $\bar{\varepsilon }_2$ should be taken.

Having in mind Remark 2 of [10], one gets a direct connection of the termination criterion for DCPCA to the one for DCBA, which gives rise to adapt the stopping condition of DCPCA in the same manner as the one for DCBA towards

$$\begin{aligned} \Vert \bar{\varvec{d}} \Vert< \bar{\varepsilon }_1 \quad \text {and} \quad -\Vert \bar{\varvec{d}} \Vert ^2 - \bar{v} = \sum _{i \in I} \bar{\lambda }_i \alpha _{i}^{(1)} < \bar{\varepsilon }_2 \end{aligned}$$

(the notation is taken from [10]). Note that both, $\alpha _{i}^{(1)}$ in terms of DCPCA and $\alpha ^{k+1}_l$ in terms of DCBA, denote linearization errors corresponding to the first DC component. Indeed the latter one was defined as a linearization error of the approximation $\phi _l$ in (3.2), but, as this function differs from the first DC component g only by a linear function, $\alpha ^{k+1}_l$ in fact yields the linearization error with respect to g. This last modification ensures that for DCPCA in the point of termination $\varvec{x}^L$, the estimate ${\text {dist}} \left( \partial _{\bar{\varepsilon }_2} g(\varvec{x}^L), h(\varvec{x}^L) \right) \le \bar{\varepsilon }_1$ holds, similar to the previous ones for PBDC and DCBA.

Note that even though choosing $\bar{\varepsilon }_1 \ll \bar{\varepsilon }_2$ in the presented examples, in case of DCBA as well as DCPCA, the second termination quantity related to the linearization errors undershoots even the lower critical tolerance $\bar{\varepsilon }_1$ in the point of termination with only two exceptions. The first one is the reproduction of the Bavarian map by means of multidimensional scaling in Sect. 4.4. For this special instance, DCBA ended with a precision of 0.089 and DCPCA with 0.062, while having a comparatively large $\bar{\varepsilon }_1=10^{-2}$. The second exception is Problem 7 of the academic test collection in Sect. 4.6. Here DCBA terminates with an accuracy of 0.009 for the (combined) linearization errors and DCPCA with 0.012 while having $\bar{\varepsilon }_1=10^{-3}$.

To be able to consider the running time for comparison at least in most applications all algorithms are implemented from scratch using the same computer language. The codes used in Sects. 4.2–4.6 are implemented in Matlab version 2022b and executed on a 8xIntel®$\text {Core}^{\text {TM}}$i7-7700 CPU @ 3.60 GHz computer with 31.1 GiB RAM under an open SUSE Leap 15.4 (64-bit) system. The only exceptions are the test runs of DCBA for the multidimensional scaling problem in Sect. 4.4 which are run in GNU Octave 5.1.0 on a Radeon Vega Mobile Gfx 2.00 GHz computer with AMD Ryzen 5 2500U CPU and 8.00 GB RAM under Windows 10 (64-bit). The simple reason for this exception is that the quadratic programming solver of Matlab claims for quite some instances to converge to the solution although it does verifiably not.

In all numerical experiments, the initial stepsize of every line search procedure contained in BDCA as well as DCBA gets computed by means of a self-adaptive trial stepsize strategy introduced in [2]. For the remaining part of the line search within DCBA a standard backtracking approach as described in [4] is used. With our choice of parameters $\gamma$, the enlargement factor within the self-adaptive trial stepsize, and $\beta$, the reduction factor within the actual line search, we ensure that, unless the line search does not terminate beforehand, at least $\tau =1$ gets tested and hence approved.

Furthermore, the proximity parameter t for PBDC is chosen as $t=0.8 \left( t_{min}+t_{max}\right)$, as suggested in [16], though it is not consistent with the request $t \in [t_{min},t_{max}]$. But numerical experiments confirm that this choice is to be preferred. In addition, we adopt the proposed modifications from [16] while implementing PBDC.¹ On the one hand, we add a subgradient aggregation technique for the first bundle which is based on [18]. On the other hand, we restrict the size of the first bundle to $\min \{n+5, 1000 \}$, where n is the number of variables.

Moreover, the quadratic programs occurring in the bundle methods DCBA, PBDC and DCPCA are solved using the quadprog² command. Thereby, in case of the academic testproblems we switch from the default option interior-point-convex for the algorithm to active-set in case of the dimension n being at most 10 as the latter method performs better for problems with a small number of variables. The solution methods applied to the convex subproblems of DCA differ depending on the smoothness property of the first DC component. Whenever it is nonsmooth the bundle method from Algorithm 2.1 following [11] gets executed. Whenever the first DC component is smooth and hence, BDCA can be applied as well, we use a Limited-Memory BFGS method (see [23, 24]).

For most of the numerical tests, a similar parameter setting is used. Unless said otherwise, the termination tolerances are set to $\bar{\varepsilon }_1 = 10^{-3}$ and $\bar{\varepsilon }_2=10^{-1}$. The remaining parameters are chosen as follows, referring once again to the notation in the respective papers from Table 1: In terms of BDCA we take $\alpha =0.1, \ \beta = 0.5, \gamma = 4$, and $\bar{\lambda }_1=4$. The last two parameters concerning the self-adaptive trial stepsize strategy are also used for DCBA. In addition, the remaining parameters for this algorithm are set to $\beta =0.5, \ m = 0.5$ and $\mu =0.1$. The missing parameters for PBDC are chosen as $m=0.5, \ R=10^7, \ L_1=L_2=1000$ as well as the maximum size of the second bundle as 3 and $r= 0.75$ whenever the spatial dimension n is less than 10, $r= 0.99$ in case of $n \ge 300$, and $r = \lfloor \frac{ n}{ n +5}\cdot 100 \rfloor / 100$ else. This last bunch of selections corresponds to the default values from [16]. Moreover, for DCPCA the still missing parameters are also taken as the default values from [10], namely $\eta =0.7, \ m=0.5, \ \sigma =0.5$ and $\rho =0.95$.

4.2 An academic test problem

The essential aim of examining the subsequent academic test problem is to investigate how often the algorithms under consideration converge to the known global minimum of the objective function and not just to a critical point. This test setting is inspired by Example 3.1 in [2].

For the objective function $f: \mathbb {R}^2 \rightarrow \mathbb {R}$ with

the DC composition $f:=g-h$ to be examined is chosen as

so that the DC components g, h are uniformly convex. The global minimum is at $(-1,-1)$. But there exist three additional critical and non-optimal points $(-1,0), (0,-1)$ and (0, 0) . In fact, these three points are not even local minimizers.

To investigate the ability of the different solvers to find the optimal point, 10,000 test runs for minimizing f are considered. Thereby, all five algorithms start at the same initial points which are chosen quasi-randomly from the rectangle $[-1.5,1.5]^2$. In the end, the sequences converging to each of the critical points are counted.

The result is shown in Table 2. BDCA and DCBA are both able to find the minimizer in every single instance. After all, PBDC succeeds in 99.9% of the test cases and DCPCA in 97.7%. However, DCA converges to each of the four critical points more or less the same number of times and determines the optimum in only 24.4% of instances.

Table 2 Absolute frequency of sequences converging to the respective critical point by the different DC algorithms

4.3 The minimum sum-of-squares clustering problem

We first provide a short introduction of the minimum sum-of-squares clustering problem. Then we present two test settings that are examined afterwards, one related to randomly generated data and another one referring to real data in the form of geographic coordinates of Bavarian cities.

Clustering describes the separation of a data set into disjoint subsets, so called clusters, by gathering points of similarity. The method is used in data mining for the analysis of huge data sets to get a better (or condensed) overview of the information actually contained in the given data. Thereby, the measure of similarity may differ depending on the application. In the following, each cluster gets characterized by its centroid and the classification gets done by considering the (minimal) squared Euclidean distance of each data point towards these centroids. Hence, denoting with $A:=\{\varvec{a}^1,\ldots ,\varvec{a}^k\}$ the set of points $\varvec{a}^i \in \mathbb {R}^n, \ i=1,\ldots ,k$, to be partitioned, and letting p be the desired number of clusters, the aim is to determine p centroids $\varvec{x}^j \in \mathbb {R}^n, \ j=1,\ldots ,p$, such that the (averaged) sum over the squared distance of each data point towards the corresponding centroid gets minimal. Thus, using the notation $\varvec{X}:=(\varvec{x}^1,\ldots ,\varvec{x}^p) \in \mathbb {R}^{n \times p}$, the problem under consideration is

In [25], a DC composition of f is derived. Adding a quadratic term to each DC component $g,h:\mathbb {R}^{n \times p} \rightarrow \mathbb {R}$ like suggested in [2], one obtains

Thereby, a modulus $\rho > 0$ ensures uniform convexity and denotes the Frobenius norm of the matrix $\varvec{X}$. The following tests are carried out using $\rho =0.1$.

In the first numerical experiment for a varying combination of parameters, k quasi-randomly generated vectors in $\mathbb {R}^n$ with normally distributed entries having a mean of zero and a standard deviation of ten get to be clustered in p groups. For that matter, $k \in \{500,750,1000,2500,5000\}, \ n \in \{2,5,10,15\}$, and $p \in \{5,10,20,50,75\}$ are considered. For each triple of parameters, ten test runs with all algorithms listed at the beginning of this section are passed. We start with p centroid candidates in $\mathbb {R}^n$ which get generated according to the same rules as the points to be clustered. During the ten test runs the set of points to be partitioned remains identical, whereas the initial centroid candidates vary with each run. However, all algorithms start from the same initial situation.

In the process, methods are rated successful whenever they reach the smallest function value in comparison. We call such a value an optimum although it may not connect to a global solution of the underlying optimization problem. To cope with the nature of numerics, we further call a method successful whenever it yields a function value deviating from the declared optimal function value less than 0.1 in case of $n=2$ and 1 in case of $n \in \{5,10,15\}$. Throughout this experiment, the number of iterations, the running time as well as the number of evaluations of the DC components and their (sub-)gradients are reported and evaluated by means of the performance profiles introduced in [9]. Thereby, for the bundle methods an iteration gets identified with a change of the iterate, which means null steps are not counted as such. Though the iterations of the respective methods, of course, are not directly comparable in view of computational effort, the related information is added to the resulting diagrams shown in Fig. 3. Note that DCA does not require evaluation of the second DC component h and thus does not appear in the corresponding profile.

While DCA, DCPCA and PBDC are able to solve the problem with nearly the same probability, BDCA and DCBA are both slightly ahead. DCBA even has a minor lead over BDCA. But in terms of efficiency, that is requiring the least running time and number of diverse evaluations, BDCA clearly outperforms all other algorithms. This might not be surprising as BDCA is specifically designed for DC problems with smooth first DC component. Comparing the bundle methods, PBDC and DCBA show on average similar profiles, whereas DCPCA drops behind. In particular, DCPCA usually has the longest running time.

Fig. 3

Performance profiles of the minimum sum-of-squares clustering problem with random data

With regard to DCBA additional analysis reveals that during all test runs the part of the number of function evaluations of the first DC component g in context with the bundle procedure remains pretty stable around $66\%$. The remaining $34\%$ of the function evaluations of g are allotted to the line search. Note that the latter percentage gives also the ratio of the number of function evaluations of the second DC component h and the first DC component g.

Moreover, further plots show some minor differences in the performance profiles with respect to varying values of the spatial dimension n or number of clusters p. Considering distinction with n first, the ability of solving a problem sinks with growing n, starting with $80-90\%$, ending up with slightly less than $45\%$ in terms of BDCA and DCBA and concerning DCA, PBDC and DCPCA $30-40\%$. While for $n=2$ PBDC is, with some minor advance, the most likely algorithm to solve the problem, for $n=5$ hardly any and for $n=10$ only small differences between the methods are visible. Surprisingly, for $n=15$ the picture changes noticeably. BDCA and DCBA are now clearly ahead of DCPCA which still outgoes PBDC and DCA. The latter two perform nearly identical in this matter.

The distinctions with varying number of clusters p are more diffuse. Increasing p initially results in a diminished ability of solving a problem. But in the end, further rising leads to the methods being more likely to find the optimum again. The value of p for which the algorithm performs worst varies from method to method. All algorithms start at $p=5$ with a probability to solve the problem of about $70\%$ with BDCA being slightly on top. For DCA, DCPCA and PBDC, $p=20$ is the value for which they perform worst with having a probability of solving the problem around $50\%$ in terms of DCA as well as DCPCA and $55\%$ with regard to PBDC. The latter percentage corresponds also to the worst performance of BDCA, which is, however, met at $p=50$. DCBA remains on a level about $60\%$ for $p=10$ to $p=50$. In the end, for $p=75$ the ability of finding the optimum lies for each algorithm in the range of $60-70\%$ with DCPCA falling slightly behind.

In the second illustrative example, we investigate how the administrative districts of Bavaria would look like if their cities got grouped by the minimum sum-of-squares clustering method. To this end, a data set of geographic coordinates of $k={2073}$ Bavarian cities and towns is considered,³ which consequently get to be separated in $p=7$ clusters. As initial guess, seven vectors with quasi-random entries in the range $[9.06,13.80] \times [47.41,50.52]$ of the geographic coordinates of the considered data set are selected.

All five algorithms determine (approximately) the same seven centroids, but differ in convergence speed. In Fig. 4, the resulting clusters are shown with their centroids marked as pentagrams. Additionally, the first ten iterations of each method beside the ones of DCBA are drawn. Moreover, in Fig. 5 the evolution of the function value with proceeding iterations is plotted for each algorithm. Essentially, the differences in convergence speed are similar to the experiment with random data, with the exception that, in this special instance, PBDC is the most promising solution method. BDCA is still ahead of DCBA which, in turn, beats DCPCA as well as DCA.

Fig. 4

Division of Bavarian cities into administrative districts by means of minimum sum-of-squares clustering

Fig. 5

Evolution of the function value with proceeding iterations while applying minimum sum-of-squares clustering towards Bavarian cities

4.4 The multidimensional scaling problem

Similar to the organization of the previous section, we first give a brief introduction of the problem under consideration (see [2, 19]) and then use two different test settings, one based on random data and the other one with real data based on the geographic problem from the previous section.

Multidimensional scaling is also a method from data mining. This time, the preprocessing of large data sets for further analysis happens by summarizing data through reduction. To be more precise, having a data set consisting of k points, each of dimension n, the aim is to replace the data set by the same number of points with dimension $p \le n$. Of course, one tries to keep the relevant information in the best possible way. To this end, the differences within the data set are considered by means of the dissimilarity matrix $\varvec{\delta } \in \mathbb {R}^{k \times k}$ with entries

where $\tilde{\varvec{X}}:=(\tilde{\varvec{x}}^1,\tilde{\varvec{x}}^2,\ldots ,\tilde{\varvec{x}}^k) \in \mathbb {R}^{ n \times k }$ contains the data points to be analyzed. Now, the goal is to find a matrix $\hat{\varvec{X}} \in \mathbb {R}^{p \times k }$ whose dissimilarity matrix approximates the one of the original data (i.e. $\varvec{\delta }$) in an optimal way, and hence reflects the existing differences in the data. Therefore, the underlying optimization problem is

$$\begin{aligned} \min _{\varvec{X} \in \mathbb {R}^{p \times k}} \tilde{f}(\varvec{X}):= \frac{1}{2} \sum _{i<j} \omega _{ij} \left( d_{ij}(\varvec{X})-\delta _{ij} \right) ^2, \end{aligned}$$

where $\varvec{\omega } \in \mathbb {R}^{k \times k}$ is a symmetric matrix consisting of nonnegative weights with zeros on its diagonal. In the following experiments, it is taken as

$$\begin{aligned} \omega _{ij} = {\left\{ \begin{array}{ll} 1 &{} \text {if} \ i \ne j, \\ 0 &{} \text {if} \ i=j. \end{array}\right. } \end{aligned}$$

Obviously, the case $p = n$ does not yield a reduction in the data set, but leads towards the question whether the original data set can be reproduced by its dissimilarity matrix. Consequently, the optimal function value for this special instance is known to be zero.

Neglecting constant terms, the primary optimization problem can be rewritten as a DC problem with the adapted objective function $f: \mathbb {R}^{p \times k} \rightarrow \mathbb {R}$ given by its DC components $g, \ h: \mathbb {R}^{p \times k} \rightarrow \mathbb {R}$,

Thereby, a modulus $\rho > 0$ ensures the uniform convexity of g and h and $\Vert \varvec{X} \Vert$ denotes the Frobenius norm of the matrix $\varvec{X}$. In the subsequent experiments, $\rho = \frac{1}{kp}$ is chosen depending on the size of the data set and the dimension of the destination space.

The first numerical experiment uses quasi-randomly generated data $\tilde{\varvec{X}} \in \mathbb {R}^{n \times k}$ consisting of normally distributed entries, having a mean of zero and a standard deviation of ten. Reproducing the data as well as reducing each data point to half its size is tested. For that matter, the parameters are taken as $k \in \{25,50,75,100,125,150\}$ and $p \in \{2,3\}$ (and, consequently, $n \in \{p,2p\}$). For each parameter combination, ten test runs with all algorithms from the beginning of this section are executed.

To construct a suitable initial guess $\varvec{X}^0 \in \mathbb {R}^{ p \times k }$, we follow the suggestion in [2]. Thus, we first create a matrix $\tilde{\varvec{X}}^0$ of the same size as $\varvec{X}^0$ with quasi-random entries drawn from the same normal distribution as the data set itself. Afterwards,

$$\begin{aligned} \varvec{X}^0:=\tilde{\varvec{X}^0} \Big ( \textbf{I}_{k \times k}-\frac{1}{k} \textbf{E}_{k \times k} \Big ) \end{aligned}$$

(4.1)

is set, with $\textbf{I}_{k \times k}$ denoting the identity matrix and $\textbf{E}_{k \times k}$ the matrix consisting of ones only. Both, this initial guesses as well as the data to be approximated, change with each test run. Nevertheless, all algorithms have to deal with the very same data.

This time, some parameters are adopted, namely in case of BDCA $\alpha = 0.05$ and $\beta = 0.1$. In addition, the quantities related to the self-adaptive trial stepsize strategy are set to $\gamma =10$ and $\bar{\lambda }_1=10$. The latter two are also used for DCBA, for which $\beta = 0.1, \ m = 0.2$ and $\mu =0.05$ are selected. Comparably, $m= 0.2$ is also set for the bundle methods PBDC and DCPCA together with $\sigma = 0.1$ for the latter method.

During the overall process, in the case of $p=n$, a method gets rated successful whenever approaching the (a priori known) optimal function value. In the case of $p < n$ for each test run we identify the algorithm among the five considered ones which yields the lowest objective function value. (Note that, in general, there will be more than one method yielding the lowest objective value.) It seems likely to classify this method as successful. Once again, also methods obtaining function values which deviate less than a given tolerance, namely 1, from the optimal or the lowest function value are graded successful.

Reporting for each test run the number of iterations and the running time as well as the number of function and (sub-)gradient evaluations for each DC component leads to the performance profiles shown (in extracts) in the Figs. 6 and 7. The evaluation is done separately for the cases of data reproduction (the case $p=n$) and data reduction (the case $p<n$). Whenever necessary to make the differences between the most efficient algorithms visible, performance profiles are only drawn partially. To get still an impression of the extent of the respective performance profiles, at least the factor allowing even the most inefficient method to reach its maximum probability for solving the problem should be reported. For Figs. 6a and 6f the factor is 63, for 6b as well as 6c 290, for 6d 354, for 7b 2900, for 7c 171 and for 7d 199. In any case, DCPCA is the method with the highest values of the measured quantities. Besides, for Fig. 6b the factor at which the curve of DCBA flattens is 234. Once again, note that DCA never evaluates the second DC component h during iterations as only linearizations of this function are considered. In specific, no line search is performed. Note further that due to using different computers (see Sect. 4.1) the running time is not comparable for this problem, at least not with respect to DCBA.

Fig. 6

Performance profiles (partly extracts) of reconstructing (case $p=n$) random data by means of multidimensional scaling

Fig. 7

Performance profiles (partly extracts) of data reduction (case $p<n$) of random data by means of multidimensional scaling

While considering the performance profiles, the first thing to be mentioned is that for each algorithm the probability of being able to solve a problem is lower when reducing the data in comparison to reconstructing the data. But in both cases the probabilities are nearly identical for all algorithms. Further, it is noticeable that PBDC usually requires less function and gradient evaluations of g than BDCA and DCBA, but having a look at the corresponding figures for the function h the relationship reverses nearly completely.

Let us note, in addition, that for DCBA $74-81\%$ of the function evaluations of the first DC component fall upon the bundle procedure and the remaining ones upon the line search. There is a clear tendency that the higher the number k of data points to be considered, the higher the percentage of function evaluations in conjunction with the bundle method. Keep in mind that function evaluations of the second DC component only occur during the line search procedure.

The second example deals, once again, with geographic coordinates of Bavarian cities. Taking the identical set of data as in Sect. 4.3, the task is to reproduce the geographic coordinates on the basis of the dissimilarity matrix related to the raw data. Thereby, the initial guess is constructed similarly as in the previous example. For this purpose, the columns of the auxiliary matrix $\tilde{\varvec{X}}^0 \in \mathbb {R}^{2 \times {2073}}$ take quasi-random values ranging in $[0,4.74]\times [0,3.12]$, motivated by the east–west as well as the north–south extension of Bavaria, determined on the basis of the underlying data set. To each column of the resulting matrix $\varvec{X}^0$ from (4.1), the geographic mean of Bavaria $(11.43,48.93)^T$ (once again calculated with respect to the cities under consideration) is added. We use the standard parameter settings from the beginning of this subsection, with the only exception that $\bar{\varepsilon }_1=10^{-2}$.

All algorithms manage to restore the map of Bavarian cities, but with differences in the speed of convergence. This distinction gets already foreshadowed in Fig. 8, in which next to the map to be reproduced and the initial guess also, for each method, the current standing at iteration 25 as well as the final result is pictured (note that the slight rotation is due to the formulation of the problem, estimating only the distances between cities). Further plots reveal that the major progress happens during the first 60% of iterations, whereas the changes following afterwards can hardly be seen in corresponding images. All methods yield satisfying results although BDCA and PBDC come out on top in terms of iterations.

Fig. 8

Reproducing the map of Bavaria by means of multidimensional scaling

4.5 Edge detection by means of a DC optimization based clustering technique

Edge detection is a well known method in image segmentation for carving out certain objects in an image. It is based on the idea of determining contours of objects marked by discontinuities and erratic changes in the brightness values of the grey scale image. The technique presented in the following, using a DC optimization based clustering approach, was developed in [17]. To each pixel, a vector representing the differences in the grey scale values with respect to nearby pixels gets assigned. Subsequently, the norms of these vectors are split into two groups yielding a differentiation into pixels belonging to an edge and the ones which do not.

Consider a grey scale image consisting of $(n+2) \times (m+2)$ pixels with coordinates $(k,l) \in \{1,\dots ,n+2\} \times \{1,\dots , m+2\}$. To each pixel of the interior of the image with coordinates $(k,l) \in \{2,\dots ,n+1\} \times \{2,\dots ,m+1\}$ a vector $\varvec{v}_i \in \mathbb {R}^4, i=1,\ldots ,N$ with $N=nm$, containing the differences in the brightness values of the pixel under consideration and the four vertical and horizontal immediately adjacent pixels gets assigned. For obvious reasons, marginal pixels are neglected and also will not get classified in the progress. Taking the norm , of each such vector, one attains a measure of change in the grey scale values in relation to the neighborhood of the central pixel. A high value indicates an affiliation towards an edge, whereas a low value does not. This motivates to separate the set $\{a_i\}_{i=1,\ldots ,N}$ into two groups. To this end, the well known K-means clustering method gets applied with $K=2$. Denoting with $z_1,z_2 \in \mathbb {R}$ the variables for determining the centroids, the resulting optimization problem is given by

$$\begin{aligned} \min _{z_1,z_2 \in \mathbb {R}} f(z_1,z_2):= \sum _{i=1}^N \min \left\{ | a_i-z_1|,|a_i-z_2| \right\} . \end{aligned}$$

Similar to the clustering method introduced in Sect. 4.3, the objective function f can be written as a DC function with (uniformly) convex DC components $g,h: \mathbb {R}^2 \rightarrow \mathbb {R}$,

with modulus $\rho \ge 0$. In the following, $\rho$ is chosen to be 0.1.

On the basis of [17], the starting point is selected as

$$\begin{aligned} \begin{pmatrix} z_1^0 \\ z_2^0 \end{pmatrix}:= \kappa \left( a_{max}-a_{min}\right) \begin{pmatrix} 1 \\ 2 \end{pmatrix} \end{aligned}$$

with $a_{max}=\max _{i=1,\ldots ,N}a_i$ and $a_{min}=\min _{i=1,\ldots ,N}a_i$. However, $\kappa$ varies in our experiments with the image under consideration, as not only but especially DCBA turns out to be pretty sensitive regarding the initial choice.

Moreover, in contrast to many other applications, the minimization of this clustering problem does not need to be carried out with a high precision in order to yield a satisfactory classification of edges. Therefore, for our subsequent numerical experiments with some classical test images for edge detection, the termination tolerance $\bar{\varepsilon }_1$ is reduced to 0.1. In addition, the maximum number of iterations is limited to five. It turns out that these adaptions still allow acceptably good approximations of the centroids leading to satisfactory classification of edges.

The parameter m for all three bundle methods is adapted to 0.1. Note that, this time, BDCA cannot be applied to solve the optimization problem, as the corresponding first DC component g is nonsmooth. Three classical test images for edge detection are considered. Thereby, both, the cameraman as well as the house, contain $256 \times 256$ pixels whereas the moon spans $537 \times 358$ pixels. For determining the initial point we choose $\kappa = \frac{1}{3}$ in terms of the cameraman, $\kappa = 0.3$ with regard to the house and $\kappa =0.25$ for the moon.

The results are shown in Fig. 9, in which also the input images are displayed in the first column. While for the cameraman the output seems apparently identical, differences can be seen for the moon. Here, DCPCA and PBDC detect the fading edge of the moon more clearly than DCA and DCBA. For the house, differences only get visible while considering DCBA. This method recognizes the top end of the chimney slightly better than the remaining algorithms, and also identifies, in a better way, some less pronounced edges as dotted lines.

Let us note that, in connection with the house, the sensitivity of DCBA regarding the initial value gets particularly clear, especially when adapting the parameter m at the same time. Only slight modifications lead from recognizing hardly any edges over a result comparable to the ones from the other methods to detection of every brick stone (see Fig. 10 for which $m=0.5$ and $\kappa =0.25$ is chosen). In contrast, the output of the remaining algorithms stays pretty stable.

Although the number of iterations is not reported here in detail, it is worth mentioning that, in many instances, the desired accuracy of $\bar{\varepsilon }_1=0.1$ is often reached within less than the maximum of five iterations. Only DCPCA exploits the full number of iterations for each image. Altogether all remaining methods yield pretty similar results for this application, detecting sharp edges quite reliably.

Fig. 9

Edge detection by means of a DC optimization based clustering technique

Fig. 10

Detecting brick stones with DCBA

4.6 A collection of academic benchmark problems

In this section, a set of ten academic DC test problems from [16], which in parts originate from [3], is considered to further assess the performance of the newly introduced algorithm in comparison to the methods mentioned at the beginning of this overall section. Some of the problems have a variable dimension n, so that a range of $n=2$ to $n={50{,}000}$ is covered by a total of 46 test instances. All functions are nonsmooth, which is why BDCA, requiring the first DC component to be smooth, can only be applied to the Problems 9 and 10. Besides, the initial guesses proposed in the cited paper are used as starting points.

Above all, we add to the respective termination criteria of the algorithms a further escape procedure which is independent of the used method. Since in the paper [16] for each test instance a known best value is reported, we also terminate a method whenever it approaches the corresponding function value within a tolerance of $\min \{10^{-3}n,0.1\}$ where n denotes the number of variables. Moreover, some parameters have to be adapted. For DCBA, we set $m=0.2, \mu = 0.05$ as well as $\beta =0.05$ whenever $n<10$, and $\beta =0.6$ whenever $n\ge 10$. In addition, for the self-adaptive trial stepsize strategy used for DCBA and BDCA, the parameters are chosen as $\bar{\lambda }_1= \gamma =20$ whenever $n<10$, and $\bar{\lambda }_1 =\gamma = \left( \frac{10}{6} \right) ^3$ whenever $n\ge 10$. Besides, for BDCA $\beta$ is selected in the same way as for DCBA and $\alpha$ is set to 0.05. For PBDC as well as DCPCA m is changed to 0.2 and in terms of DCPCA, $\sigma$ is chosen in the same way as $\beta$ for DCBA and BDCA, respectively.

For each instance of the academic DC test problems, we report the value of the objective function at the point of termination, the running time, the number of iterations, as well as the number of evaluations of the first and second DC component itself and their (sub)gradients. The detailed listing of the results can be found in the “Appendix”. For the sake of completeness, we tabulate the respective outcomes from the academic test problem (see Sect. 4.2), clustering of the Bavarian cities by the minimum sum-of-squares approach (see Sect. 4.3), reproducing the Bavarian map (see Sect. 4.4), and edge detection for the cameraman, the brick house and the moon (see Sect. 4.5).

For each instance of the academic DC test problems, an algorithm is considered as failed if the running time exceeds a limit of one hour which only happens with the two bundle methods PBDC and DCPCA. Moreover, in a few cases, some of the algorithms terminate in a point for which the corresponding function value is worse than the best known one. A quick overview of how often these instances occur with each algorithm within the 46 problem instances, is given in Table 3. Note that BDCA can merely be applied to ten of the test problem instances. It is worth mentioning that DCBA together with DCA is the method with the (relatively) least instances of not detecting the known best function value $f^*$.

Table 3 Instance of termination for each method applied to the collection of 46 academic test problems

Let us note some distinctive features in the detailed results. Having a look at the problems with variable dimensions that finally cover large scales, clearly DCA, DCBA and, for Problem 10, also BDCA come out on top. The two bundle methods PBDC and DCPCA suffer from rapidly increasing running times with growing dimensions in Problem 4, finally exceeding the time limit. For Problem 10 in case of higher number of variables both methods end up with function values deviating heavily from the known best ones. The results obtained by DCA for Problem 4 are standing out. For every single test instance it requires only one single iteration which favors quite low numbers of evaluations compared to DCBA. Though also Problem 5 covers large dimensions, the situation here is a bit different. Following [16], the starting point is selected in such a way that, with increasing dimension, one already has a pretty good estimate for the optimum. This may explain, to some extent, the unexpected and heterogeneous behavior of the algorithms. While for some methods a few measured quantities hardly change with growing dimension, other measures show a rather continuing but quite low increase and yet others reveal a fairly erratic behavior. At this point, we want to thank an anonymous referee for drawing our attention to the special structure of Problem 5.

Furthermore, there are also some visible differences in the small-scale problems whose number of variables are at most four. First of all, PBDC is the only algorithm to solve Problem 9. Though the both bundle methods, PBDC as well as DCPCA, are able to find the optimum for Problem 2 DCPCA requires much less evaluations than PBDC. Similarly, for Problem 7 next to PBDC it is DCBA which succeeds and, once again, PBDC is the one with the noticeably higher number of evaluations. Nevertheless, in case of convergence PBDC fails to reach the known best function value only for some instances of one single problem class, namely Problem 10.

5 Concluding remarks

In this article, a bundle method to solve unconstrained DC optimization problems (DCBA) was introduced. In contrast to various existing bundle methods designed for this topic, the bundles are not directly constructed with respect to the DC components of the objective function. Instead, a convex approximation of the function to be minimized, which is already known from the classical DC Algorithm (DCA, see [21]), gets constructed first. Applying the bundle method towards the model function yields a descent direction for the original objective function which allows to add a line search afterwards. Hence, the concept of DCBA is pretty similar to the one of the Boosted DCA (BDCA) which is introduced in [2]. The latter one considers the same convex approximation known from the DCA and constructs a descent direction by minimizing this model function. Contrary to BDCA, the bundle method in DCBA is not carried out until a minimizer of the approximation is found, but only until a serious step is executed the very first time. An advantage of DCBA against BDCA is that the new method can be applied to DC problems with both DC components being nonsmooth, whereas the convergence theory of BDCA requires the first DC component to be smooth.

The algorithm was shown to be well-defined for functions being bounded from below. In addition, the method was proven to be globally convergent in the sense that every accumulation point is a critical point of the objective function. Moreover, termination of the algorithm (with numerically implementable termination criterion) occurs within a finite number of iterations in a point satisfying an approximate criticality measure.

The performance of the algorithm was tested by means of diversified nonsmooth DC problems and compared to four other DC methods, DCA, BDCA and two bundle methods, namely the Proximal Bundle method for DC optimization (PBDC, see [16]) and the DC Piecewise-Concave Algorithm (DCPCA, see [10]). In specific, DCBA together with DCA are the algorithms succeeding most frequently while considering a bunch of various academic test problems. Clearly, DCA falls behind by far performing even worse than most of the other methods while considering the applications of minimum sum-of-squares clustering and multidimensional scaling. With these problems DCBA visibly gets outperformed by BDCA which still has the disadvantage of only being applicable to a restricted class of DC problems. But none of the two remaining bundle methods has proven to be apparent advantageous over DCBA. In addition, the results for detecting edges with the new algorithm are rather encouraging.

So far, this method is applicable to unconstrained DC programs only. Our future work will concentrate on suitable extensions to constrained problems, first to DC programs with convex constraints, and then also to DC programs with general DC-type constraints.

Appendix: Detailed results for the collection of academic test problems

A quick overview over the test instances taken from [16] is given in Table 4, which is inspired by [10]. Thereby, ID is an instance identifier, n gives the spatial dimension and $f^*$ the known best value of the objective function. Note that in [10] for Problem $10.03 \ f^*$ has been adapted to a newly detected better function value. In addition, the problems AP, C_BY, R_BY, ED_C, ED_H and ED_M refer to the academic test problem from Sect. 4.2, the clustering of the Bavarian cities, the reproduction of the Bavarian map and edge detection for the cameraman, the house and the moon.

The detailed results are then shown in Tables 5, 6, 7, 8 and 9. Here the value of the objective function at the point of termination f, the running time, the number of iterations it, as well as the number of evaluations of the first and second DC component itself and their (sub)gradients, in sequence denoted by $n_{f_1}, \ n_{f_2}, \ n_{\xi _1}, \ n_{\xi _2}$, gets reported. Note that in case of the problem AP the average quantities over all 10,000 test runs are tabulated. Besides, for the problems related to edge detection the function value f at the point of termination is not listed, as no minimization of the objective function is aspired in the first place. Instead, the algorithms may terminate after a preset number of iterations. Furthermore, DCA does not require an evaluation of the second DC component h during the iterations. Moreover, for DCA, BDCA, DCBA and DCPCA one has $it=n_{\xi _2}$ and for PBDC $n_{f_1}=n_{f_2}$. See the references in Table 1 for clarification. Correspondingly, the respective columns are combined or neglected. Besides, in case a method fails within a test class not only once but for all subsequent instances, only the first fail gets reported in Tables 5, 6, 7, 8 and 9. Furthermore, an instance is marked with $^\dagger$ if for an algorithm the function value at the point of termination differs significantly from the known best one $f^*$.

Table 4 An overview of the benchmark problems

Table 5 Computational results for DCA being applied to the benchmark problems

Table 6 Computational results for DCBA being applied to the benchmark problems

Table 7 Computational results for PBDC being applied to the benchmark problems

Table 8 Computational results for DCPCA being applied to the benchmark problems

Table 9 Computational results for BDCA being applied to the benchmark problems