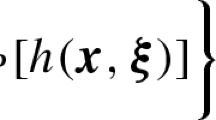Abstract
We discuss stochastic optimization problems under distributional ambiguity. The distributional uncertainty is captured by considering an entire family of distributions. Because we assume the existence of data, we can consider confidence regions for the different estimators of the parameters of the distributions. Based on the definition of an appropriate estimator in the interior of the resulting confidence region, we propose a new data-driven stochastic optimization problem. This new approach applies the idea of a-posteriori Bayesian methods to the confidence region. We are able to prove that the expected value, over all observations and all possible distributions, of the optimal objective function of the proposed stochastic optimization problem is bounded by a constant. This constant is small for a sufficiently large i.i.d. sample size and depends on the chosen confidence level and the size of the confidence region. We demonstrate the utility of the new optimization approach on a Newsvendor and a reliability problem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the seminal work by Dantzig [16] and Beale [4], the stochastic (linear) optimization problem has been well-studied by assuming the knowledge of the involved probability distribution [11, 34, 38, 39, 52]. However, in practical applications, the distribution is rarely known with sufficient accuracy, even if good estimators are at hand. Stability studies of stochastic optimization problems can yield important insights about the sensitivity of the computed optimal solutions if the assumed distribution does not mature [37, 44, 47, 48]. To explicitly take the uncertainty around the involved distribution into account, the field of stochastic optimization under distributional ambiguity has emerged, which assumes that the underlying distribution is part of a family of distributions [35, chapter 7]. This paper proposes a new data-driven stochastic optimization approach under distributional ambiguity.
The key idea of all stochastic optimization approaches under distributional ambiguity is to optimize some objective function over an entire family of distributions. Such an optimization problem is well-defined as soon as an appropriate metric has been chosen. To this end, two different methods have emerged: Bayesian and minimax approaches—minimax is also known as distributionally robust stochastic optimization in the context of our paper. The Bayesian approach assumes the knowledge of some a-priori distribution; if such an a-priori distribution is known, then the problem reduces to classical stochastic optimization. Minimax approaches take only the worst case distribution into account, instead of the entire family of distributions. This may result in over-conservative solutions [51, 53]; careful construction of the family of distributions can mitigate this conservatism [9].
In this paper, we follow the recent trend of data-driven optimization [2, 10, 14, 45]. We use observations to construct confidence regions. Specifically, we assume the parametric case, i.e., the family of distributions is parametrized by \(\theta \). A confidence region at level \((1-\alpha )\) is then constructed from the observations for the parameter \(\theta \). Therefore, we assume that the set of parameter vectors is compact and that we know a safe region which contains the true parameter, i.e., \(\theta \) is a vector that lies in some compact multidimensional set. For such a situation, minimax approaches typically optimize against the worst case distribution in either the safe region or some kind of confidence region taking the observations into account. In contrast, the Bayesian approach assumes the knowledge of a distribution of the parameter \(\theta \). This distribution is then typically estimated by a uniform distribution or a conditional uniform distribution taking the observations into account, for the safe region. The resulting optimization problem is then obtained by taking the expected value, where the parameter \(\theta \) is treated as a random vector of the associated stochastic optimization problem (which is a function of \(\theta \)).
In our proposed approach, we combine the idea of the Bayesian method with a confidence region in a unique way. First, we define an appropriate estimator inside the calculated confidence region. In a second step, a new confidence region around this estimator is constructed. Then, a Bayesian-type optimization model is set up for the resulting confidence region. The careful construction of the new stochastic optimization problem allows us to study the quality of the optimal solutions obtained. Because this data-driven stochastic optimization approach takes only the available observations into account, the solution quality analysis needs to consider all possible observations and all possible distributions of the parameter \(\theta \), in the Bayesian sense. Therefore, we build the expectation with respect to all possible observations. This allows us to bound the optimal objective function in the expected value sense.
The derived bound is valid not only for the parameters contained in the confidence region, but for all parameters of the distribution in the safe region. Furthermore, it holds for any finite number of observations. This bound depends on the user-specified confidence level and three terms characterizing the quality of the estimation methods and the set of parameters for the distributions chosen. We are able to show that the derived bound converges to zero with an increase in the number of observations.
This paper contributes to the body of literature on stochastic optimization under distributional ambiguity in the following unique ways:
-
We propose a new data-driven stochastic optimization model for stochastic optimization under distributional ambiguity (Definition 6).
-
We analyze optimal solutions of the proposed model to provide optimality bounds (Theorem 1). We further show that the proposed data-driven stochastic optimization model reduces to stochastic optimization in case of a known parameter (Corollary 1) and that the optimality bound converges to zero for an infinite number of observations (Corollary 2); two desired properties which show the consistency of the proposed model. We show that our approach contains the Bayesian approach as a special case, yielding a new bound for the Bayesian approach (Corollary 3). Further, we use the same proof technique to yield a classical result for the naïve case, where only an estimator is used for \(\theta \) instead of a confidence region (Corollary 4).
-
We provide computational results for two different problems: a Newsvendor and a reliability problem.
The remainder of the paper is organized as follows. We present the mathematical foundations and notation of stochastic optimization under distributional ambiguity and review the literature on both Bayesian and distributionally robust stochastic optimization approaches in Sect. 2. In Sect. 3, we define confidence regions and how they can be computed by combining different estimators. Then, the main contributions are presented in Sect. 4. We suggest a new data-driven methodology towards stochastic optimization under distributional ambiguity and analyze its solution quality with respect to the expected value of all observations and all a-priori distributions. Further, we study the behavior of the optimal solutions for an increase in the number of available observations, i.e., the asymptotic case. We also discuss the complexity of the proposed model. In Sect. 5, we apply the proof ideas towards the Bayesian approach and an naïve approach using only one estimator. We then present computational results in Sect. 6 for two different problems, before we conclude with Sect. 7.
We denote the decision variables by vector \(\mathbf {x}\) and the decision function by \(d(\cdot )\) or simply d. Observations are denoted by a capital \(\mathbf {X}\).
2 Stochastic optimization problem under distributional ambiguity
Let there be l (unknown) parameters which build a random vector denoted by \(\xi \), i.e., the function \(\xi : \Omega \rightarrow \mathbb {R}^{l}\) is measurable w.r.t. a \(\sigma \)-algebra \(\mathcal {A}\) on \(\Omega \). Then, \(\mathbb {E}_P\) denotes the expectation, given the distribution P of this random vector \(\xi \).
We are interested in solving the following stochastic optimization problem
for a continuous loss function \(L : \mathbb {R}^{n} \times \mathbb {R}^l \rightarrow \mathbb {R}\) and a feasible region \(\mathbb {X} \subset \mathbb {R}^{n}\). The feasible region, \(\mathbb {X}\), is assumed to be non-empty and compact. It might be given by a collection of constraints
with function \(H : \mathbb {R}^n \rightarrow \mathbb {R}^{m}\). As such, the m constraints are all deterministic. The optimization problem (1) has n here-and-now decision variables, collected in vector \(\mathbf {x}\).
We follow the spirit of stochastic optimization under distributional ambiguity and assume that the distribution P, the “true” distribution of \(\xi \), is not known, but instead an element of a non-empty set \(\mathcal {P}\). The set \(\mathcal {P}\) can contain all kinds of probability distributions. However, we make the following assumptions:
Assumption 1
The set of distributions of the random vector \(\xi \) has the form
with \(\Theta \) being compact. \(\square \)
The non-emptiness and compactness of \(\mathbb {X}\) together with the continuity of \(L(\cdot ,\cdot )\) imply that the optimization problems \(\min _{\mathbf {x} \in \mathbb {X}} \mathbb {E}_{P} \big [ L(x,\xi ) \big ]\) and \(\max _{\mathbf {x} \in \mathbb {X}} \mathbb {E}_{P} \big [ L(x,\xi ) \big ]\) admit a finite extremum. Together with the compactness assumption of \(\Theta \), the corresponding minimization and maximization problems over \(P \in \mathcal {P}\) are finite as well; we exclude the trivial case that the minimum equals the maximum. This allows us to present the main theoretical results of this paper as absolute bounds, rather than relative bounds, by considering the normalized function
and the corresponding stochastic optimization problem
This normalization is constructed such that \(0 \le \mathbb {E}_{P} \big [ Q( \mathbf {x}, \xi ) \big ] \le 1\) for all \(\mathbf {x} \in \mathbb {X}\); note that this does not necessarily hold for \(Q( \mathbf {x}, \xi )\).
Assumption 1 assumes the parametric case with an unknown \(\tilde{d}\)-dimensional parameter \(\theta \). With other words, the form of the distribution is known but its coefficients or parameters are unknown. Then,
is a discretization of (2) and therefore
is a discretization of \(\Theta \), for some \(K \in \mathbb {N}\). The set of all distributions on the discrete set \(\widetilde{\mathcal {P}}\), as defined in (4) and (5), creates the \((K-1)\)-dimensional standard simplex \(\Delta ^{K-1} \subset \mathbb {R}^K\). With other words, assuming that \(\theta \) is a random vector, then the discretizations (4) and (5) yield a discrete random vector with K possible realizations. The collection of all possible distributions with K realizations is then given by \(\Delta ^{K-1}\).
To avoid notational ambiguity, we distinguish between an element of \(\theta \in \Theta \) and the true parameter, which we denote by \(\tilde{\theta }\). Given the situation that the “true” distribution P is unknown, we cannot expect to solve problem \((\mathcal {SP})\). In fact, we call the stochastic optimization problem \((\mathcal {SP})\) the baseline problem for
Our methodology assumes the availability of R data points in \(\mathbb {R}^{l}\).
Assumption 2
We have R realizations \(\mathbf {X}_1, \ldots , \mathbf {X}_R\) with \(\mathbf {X}_r \in \mathbb {R}^{l}\), \(r=1, \ldots ,\) R, of the random vector \(\xi \) and assume that the corresponding random vectors \(\xi _1, \ldots , \xi _R\) are i.i.d. random vectors. We denote \(\zeta = (\xi _1, \ldots , \xi _R)\) and assume that the distribution of \(\xi _i\) is discrete or has density \(f(\cdot )\) with respect to the Lebesgue measure in \(\mathbb {R}^l\).\(\square \)
Note that we do not require the independence (nor the identical distribution) of the l coordinates of \(\xi _r\), \(r=1, \ldots , R\), in Assumption 2.
We also refer to realizations as observations or data throughout the paper. For our discussions of data-driven Bayesian approaches, we require
Definition 1
Let \(s \in \Delta ^{K-1}\). As in the Bayesian approach, \(s = (s_1, \ldots , s_K)\) is called a-priori distribution, i.e., \(s_k\) is the probability that \(\theta \) as a random vector has value \(\theta _k\) for \(k=1, \ldots , K\). For a given a-priori distribution s, \(s_k(\mathbf {X})\) is defined as the conditional probability that \(\theta \) as a random vector has value \(\theta _k\), under the condition that \(\zeta \) has realization \(\mathbf {X}\). This conditional distribution \(s(\mathbf {X})\) is called the a-posteriori distribution and can be calculated by
where \(f(\cdot |\theta _k)\) is the density of \(\zeta \), if \(\theta = \theta _k\). \(\square \)
Two main streams of research have emerged to solve stochastic optimization problems under distributional ambiguity, where \(P \in \mathcal {P}\): Bayes and Minimax.
2.1 Bayesian approach
Assuming the discrete case \(\Theta _0\), in the Bayesian approach, the unknown distribution P (or parameter \(\theta \)) is interpreted as a realization of a discrete random vector. Therefore, we assume an a-priori distribution \(s = (s_1, \ldots , s_K)\) on the discrete set of distributions \(\widetilde{\mathcal {P}}\). In the Bayesian approach, typically the discrete uniform distribution is chosen by default on \(\widetilde{\mathcal {P}}\), i.e., \(s_i = \frac{1}{K}, i \in \{ 1, \ldots , K \}\), if no special a-priori distribution is given. We obtain the a-priori Bayesian problem, also called the mean-risk stochastic optimization problem
where we write \(\mathbb {E}_{\theta _k}[\cdot ]\) for ease of notation, instead of \(\mathbb {E}_{P_{\theta _k}}[\cdot ]\) stating that the expected value is taken for random vector \(\xi \) following the distribution \(P_{\theta _k}\) with parameter \(\theta _k\). Any optimal solution to \((\mathcal {B})\) is called the Bayesian solution to the stochastic optimization problem under distributional ambiguity.
We can define an analogous a-posteriori Bayesian approach, by taking the data \(\mathbf {X}\) into account to yield
We observe that the optimal solution of \(\big (\mathcal {B}(\mathbf {X})\big )\) depends on the data \(\mathbf {X}\), i.e., a different set of realizations of the observation \(\zeta \) may lead to a different optimal solution.
Recently, Wu et al. [57] proposed a data-driven Bayesian optimization approach. The authors apply a risk functional towards the expected value \(\mathbb {E}_{\theta _k}\big [ Q( \mathbf {x}, \xi ) \big ]\). This risk functional contains the a-posteriori distribution, as a mapping from the random vector to the real numbers. Mean, mean-variance, value-at-risk (VaR) and conditional value-at-risk (CVaR) are considered as four different risk measures. This Bayesian risk optimization framework was already proposed before [60], whereas tailored solution strategies were first presented in [61]. For the case of an infinite number of observations, Wu et al. [57] prove several consistency and asymptotic results. This is the main theoretical difference to our work, where we establish bounds for a finite number of observations; cf. Theorem 1.
2.2 Minimax: distributionally robust stochastic optimization
Robust optimization approaches typically do not require probabilistic information but rely solely on the range (support) of the parameters. Then, robust optimization seeks a solution which optimizes against the worst among all possible realizations of the parameters [6].
If a set of distributions \(\widetilde{\mathcal {P}}\) is given instead of a single one, recent work has applied robust approaches for stochastic optimization problems under distributional ambiguity in the following minimax sense [59]:
This line of research is called distributionally robust stochastic optimization. In this context, the set of distributions \(\widetilde{\mathcal {P}}\) is called the ambiguity set.
An a-posteriori approach is obtained when taking the observations \(\mathbf {X}\) into account to yield a new ambiguity set \(\widetilde{\mathcal {P}}(\mathbf {X})\); see Sect. 3.3. More precisely, the data are used to construct a probability model with an associated “confidence region” which then yields the ambiguity set (as a subset of \(\widetilde{\mathcal {P}}\)). Chapter 7 in the book by Pflug and Pichler [35] explains this concept very clearly. However, using an a-posteriori ambiguity set, constructed in such a way, is “dangerous” in the sense that we lose control over the error in the set of distributions “outside” \(\widetilde{\mathcal {P}}(\mathbf {X})\); see Sect. 4.
Because there is a growing body of literature in the area of distributionally robust stochastic optimization [49], we restrict our discussions on a few truly outstanding papers. The papers on distributionally robust stochastic optimization can be classified by the way the ambiguity sets are constructed. There are several papers which restrict the set of probability distributions by limiting its maximal deviation to a reference distribution, the baseline model [13, 27]. Others restrict the set of probability distributions by some conical constraint [17] or derive bounds via two measurable sets [50]. Also, methods have been proposed which restrict the moments of the probability distributions considered [24, 26, 28]. Finally, one can also restrict the set of possible distributions by some ball in the Wasserstein distance sense [36]. A general class of ambiguity sets was also proposed which contains most published ambiguity sets as special cases [56].
Data-driven distributionally robust stochastic optimization approaches considering confidence regions have been proposed by various groups. Delage and Ye [17] construct ambiguity sets from data for mean and covariance matrices to yield distributionally robust stochastic optimization problems which allow for probabilistic performance guarantees. Bertsimas et al. [8] connect sample average approximation, distributionally robust optimization and hypothesis testing of goodness-of-fit. The resulting robust sample average approximation makes use of a refined ambiguity set construction and confidence regions to establish necessary and sufficient conditions on the hypothesis test to ensure that the resulting solution satisfies certain (probabilistic) finite-sample and asymptotic performance guarantees in a variety of parametric, and non-parametric settings. This idea has been extended to so-called Wasserstein sets establishing statistical guarantees on distributionally robust policies [19]. Ambiguity sets, composed of all distributions within a certain Wassertein distance with respect to an empirical distribution (for given observations) were also proposed and analyzed [21]. In an earlier work, Wang et al. [55] construct ambiguity sets by considering distributions which achieve a certain level of likelihood, given the set of observations. Gupta [25] uses Bayesian techniques to construct ambiguity sets which have very desirable features—they are optimal in some sense. In addition, the constructed ambiguity sets outperform many popular ambiguity sets previously proposed in the literature. The tutorial by Bayraksan [3] discusses the construction of data-driven ambiguity sets by limiting the phi-divergence of all considered distributions with respect to some nominal distribution. Agrawal et al. [1] quantify the maximal loss incurred when correlations among data are ignored via distributionally robust stochastic optimization problems. All papers in the stream of research on data-driven distributionally robust stochastic optimization approaches have the following two main differences to the proposed approach in this paper: (1) these approaches are worst-case approaches in the minimax-sense, while we are proposing the optimization of an expected value, and (2) the performance guarantees are either probabilistic (i.e., with a high probability) or asymptotic (i.e., for an infinite number of observations), while our guarantees are deterministic and hold for any number of observations in the entire parameter space.
Van Parys et al. [54] also deal with data-driven distribution optimization and make a special kind of asymptotic optimal decision. Similar to our work, they also provide a series of finite sample size results. There are, however, some fundamental differences to the present paper. First, the approach is robust and not Bayesian-like softened robust. Second, the data are used for a predictor (and prescriptor) of the cost function. In contrast, we have chosen an estimator (as a function of the data) for the parameter that defines the distribution of the random parameter vector. Thirdly, we can bound the expected value, over all observations and all possible distributions, of the optimal objective function of the proposed stochastic optimization problem for a finite number of observations by a constant, and accordingly the asymptotic analysis yields the convergence of this constant to zero. This stands in contrast to the finite sample size results from Van Parys et al. [54], for example their Theorem 8, in that they assume the asymptotic distribution \(P^\infty \) (i.e., the sample path distribution) while our results hold for all a-priori distributions, cf. Theorem 1.
Soft robust optimization [5] and light robustness [20] have been suggested, for instance, to overcome the conservativeness of robust optimization under distributional ambiguity. Robust stochastic optimization approaches under ambiguity have received special attention in financial applications by considering ambiguous risk and utility functions [22, 62].
3 Application of estimation methods
Per construction, \(\tilde{\theta }\) is included in the set \(\Theta \). However, in many applications, it is sufficient that this condition is met with probability less then 1, say equal to \((1 - \alpha )\) with \(0< \alpha < 1\), for a subset of \(\Theta \). The value \(\alpha \) is a user input and should be chosen as a good compromise between the level \((1-\alpha )\) and the size of the corresponding subset (i.e., confidence region). Loosely speaking, the level \((1-\alpha )\) allows the application of confidence regions instead of \(\Theta \).
3.1 Confidence region
We are seeking a confidence region, determined for an estimator \(T= T(\zeta )\), where we rely on the usual definition of a (point) estimator, i.e., a measurable function \(T = T(\zeta ) : \Xi \rightarrow \Theta \subset \mathbb {R}^d\), according to the following
Definition 2
Let \(\zeta (\Omega ) =: \Xi \subset \mathbb {R}^{l \cdot R}\). For \(\alpha \in (0,1)\), we denote a subset \(R( \alpha , T )\) of \(\Xi \times \Theta \) as confidence region to T at the level \((1 - \alpha )\), if
In Definition 2, (a) requires that any estimator T is, for all realizations of \(\zeta \), contained in the confidence region \(R( \alpha , T )\) as a subset of \(\Theta \). (b) and (c) ensure that the confidence region \(R( \alpha , T )\) contains the true parameter \(\tilde{\theta }\) with probability \(\ge (1-\alpha )\). We remark that in the literature, confidence regions are also defined without any estimator.
For the following, we are given the realization \(\mathbf {X}\) of \(\zeta \).
Definition 3
We call
the a-posteriori confidence region to \(T(\mathbf {X})\) at the level \((1 - \alpha )\). \(\square \)
3.2 Integrated confidence region
3.2.1 Integration of confidence regions
If more than one estimation procedure is at hand, say V estimators \(T_1, \ldots ,\) \(T_V\), we can intersect their corresponding a-posteriori confidence regions \(R\big ( \alpha _{\nu }, T_{\nu }(\mathbf {X})\big )\) at the level \((1-\alpha _{\nu })\), \({\nu } = 1, \ldots , V\).
The idea is to choose, for every \(T_{\nu }\), \((1 - \alpha / V)\) as the level of the corresponding confidence region and to intersect all a-posteriori confidence regions as follows
Note that \(I(\alpha , \mathbf {X})\) is in general not an a-posteriori confidence region according to Defintion 3, as an appropriate estimator T is missing. However, if only one estimator is at hand, i.e., \(V=1\), then we denote the appropriate a-posteriori confidence region by \(I(\alpha ,\mathbf {X})\) as well.
Remark 1
The choice of the \(\alpha _\nu \) values as \(\frac{\alpha }{V}\) is arbitrary. Any other assignment is fine as well, as long as \(\alpha _\nu \in [0,1]\) and condition \(\alpha = \sum _{\nu =1}^V \alpha _\nu \) holds. \(\square \)
Remark 1 holds because the probability that \(\bigcap _{\nu =1}^V R\big ( \alpha _\nu , T_{\nu }(\mathbf {X}) \big )\) does not contain \(\tilde{\theta }\) is the probability that either of the confidence regions \(R\big ( \alpha _\nu , T_{\nu }(\mathbf {X}) \big )\) does not contain \(\tilde{\theta }\), which is less than or equal to \(\sum _{\nu =1}^V \alpha _\nu = \alpha \).
Figure 1 illustrates the resulting region \(I\big (\alpha ,\mathbf {X}\big )\) when two a-posteriori confidence regions are integrated, i.e., intersected.
3.2.2 Integrated confidence region with a new estimator
To transform \(I(\alpha , \mathbf {X})\) into an a-posteriori confidence region, we require a suitable estimator \(T_o\). Such an estimator is defined in the following, together with the resulting a-posteriori confidence region.
For any given \(\alpha \), with \(0< \alpha < 1\), we define an estimator \(T_o(\alpha ,\mathbf {X})\) of \(\theta \) as an element of \(I(\alpha , \mathbf {X})\) which minimizes the squared maximal Euclidean distance, i.e.,
The motivation of definition (8) is to obtain a parameter which has the minimal distance to the “true” parameter \(\tilde{\theta }\) at the level \((1-\alpha )\), i.e., with a great probability. This is an a-posteriori-like result. The mathematical reason for this particular choice of \(T_o\) becomes clear with the proof of Theorem 1 on page 13.
Remark 2
The set
with
is also a confidence region at the level \((1-\alpha )\). \(\square \)
We define the expected maximal Euclidean distance of all elements in \(I(\alpha ,\mathbf {X})\) as
Note that \(\epsilon (\alpha ) \ge 0\) because \(\varepsilon (\alpha ,\zeta ) \ge 0\).
Remark 3
The set
is an a-posteriori confidence region to estimator \(T_o\) at level \((1-\alpha )\) and, with that, also a subset of \(\Theta \) . \(\square \)
In the remainder of the paper, we mostly use \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\). Figure 2 illustrates the estimator \(T_o(\alpha ,\mathbf {X})\) and \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\), corresponding to Fig. 1.
3.3 A-posteriori minimax using confidence region
Any (a-posteriori) region \(I(\alpha ,\mathbf {X})\) can be readily applied towards the minimax approach. The idea is to replace the ambiguity set \(\widetilde{\mathcal {P}}\) by \(I(\alpha ,\mathbf {X}) \cap \Theta _0\).
We obtain the DRSP problem at level \((1-\alpha )\)
For any realization \(\mathbf {X}\) of observation \(\zeta \), \(I(\alpha ,\mathbf {X})\) is a subset of \(\Theta \), and hence the robustness of (\(\mathcal {DRSP}_{\alpha }\)) is somewhat “softened.”
4 Stochastic optimization with confidence level for continuum \(\Theta \)
Based on the a-posteriori confidence region \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\) to estimator \(T_o\), we propose a new stochastic optimization problem in an effort to solve stochastic optimization problems under distributional ambiguity. The key idea is the combination of the a-posteriori Bayesian approach with our (integrated) confidence region.
4.1 Decision functions and mean-risk
Additionally to the new estimator \(T_o(\mathbf {X})\) and its corresponding confidence region, we propose a novel solution for the stochastic optimization problem with distribution ambiguity minimizing the mean-risk. For that we require the following definitions.
Definition 4
A measurable function \(d = d(\zeta ) : \Xi \rightarrow \mathbb {X}\) is called a feasible decision function for \((\mathcal {SP})\). We collect all such feasible decision functions d in the set \(\mathcal {D}\). \(\square \)
The decision function formalizes the concept that any solution of an a-posteriori optimization problem depends on the data \(\mathbf {X}\). With that, any solution is a function of the observation \(\zeta \).
Definition 5
We define the risk function in \(\theta \in \Theta \) for decision function \(d \in \mathcal {D}\) as
For any distribution W on \(\Theta \) (in the a-priori sense) with Lipschitz-continuous density \(w(\theta )\), the mean-risk for decision function \(d \in \mathcal {D}\) is then defined as
The mean-risk for \(d \in \mathcal {D}\) is also called the Bayes risk for d. \(\square \)
Because \(\Theta \) is compact, it is especially a Lebesgue-measurable set. The risk is defined as the expected value of the function \(\mathbb {E}_{\theta } \big [ Q( d(\zeta ), \xi ) \big ]\) of random vector \(\zeta \). As such, the risk is an average of the objective function value for the decision function d of the stochastic optimization problem \((\mathcal {SP})\). The mean-risk is then the average risk\((d,\theta )\) over all parameters \(\theta \in \Theta \). The risk function is of interest because the true value of the parameter \(\theta \) is unknown.
4.2 The proposed solution
We propose a new kind of “softened robustness” in an effort to avoid the often criticized “over-conservatism” of the minimax criterion. This proposed alternative is a Bayesian-like approach. In this context, “robust” means that the Bayesian solution remains approximately optimal in a neighborhood (of some appropriate metric space of a-priori distributions) around the given a-priori distribution, or around the a-priori uniform distribution (if none is specified). While the Bayesian approach can overcome the aforementioned “over-conservatism”, it is sensitive to the choice of the a-priori distribution and thus, robustness with respect to this distribution is of interest, cf. [7] and [23, chapters 3.6 and 3.7]. This is what we propose in this paper.
This new kind of robustness is intuitively successful, if, for the computation of the a-posteriori-Bayes solution, instead of the entire parameter space \(\Theta \), a confidence region around an efficient estimator \(T_o\) is chosen, whose diameter is small—in the sense that the resulting a-posteriori confidence region is smaller than \(\Theta \)—with a high confidence level (i.e., small \(\alpha \)). This is the motivation for us to define the a-posteriori confidence region \(\widetilde{H}(T_o\big (\alpha ,\mathbf {X})\big )\) for the estimator \(T_o\).
Definition 6
For any given data \(\mathbf {X}\) and level \((1-\alpha )\), consider the data-driven stochastic optimization problem \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) within our best confidence region \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\)
with constant
We denote a solution of the data-driven stochastic optimization problem \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) as \(B^*(\alpha , \mathbf {X})\). \(\square \)
The proposed new optimization model \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) represents a Bayes-like solution. Therefore, the appropriate optimality criterion is the Bayesian risk. The Bayesian risk, as defined in Definition 5, is an average with respect to the posterior distribution of the mean risk as a function of \(\theta \).
Remark 4
Solutions \(B^*(\alpha , \mathbf {X})\) are well-defined because \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) optimizes a continuous function of \(\mathbf {x}\) over a compact set \(\mathbb {X}\); we assume that Q is a continuous function.
4.2.1 The main property of \(B^*(\alpha , \mathbf {X})\)
Theorem 1 provides the main properties of solutions \(B^*(\alpha , \mathbf {X})\) on the continuum \(\Theta \) for any finite number of observations. We utilize this Theorem do derive similar bounds for the Bayesian approach and the naïve approach.
First, for fixed \(\alpha \), we define
with \(\epsilon (\alpha )\) as defined in (9) and the standard deviation \(\text {std}(T_o)\) of \(T_o\). Especially if only one estimator is used, then it is particularly easy to check whether or not \(T_o\) is unbiased. The main result is then stated as:
Theorem 1
Let \(\Theta \) be continuous, non-empty and compact; \(L(\cdot ,\cdot )\) be continuous and non-constant on the non-empty compactum \(\mathbb {X}\) and let Assumption 2 hold. For any data \(\mathbf {X}\) and level \((1-\alpha )\), let \(B^*(\alpha , \mathbf {X})\) be a solution of \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\). Then, for any distribution W on \(\Theta \) (in the a-priori sense) with Lipschitz-continuous density \(w(\theta )\) and Lipschitz constant \(l_\mathrm{W}\) as well as \(\eta ^*(\alpha )\) as defined in (12) and Lebesgue measure \(\lambda (\Theta )\) of \(\Theta \), it holds that
Proof
For any feasible decision function \(d \in \mathcal {D}\), \(\theta \in \Theta \) and \(y \in \Xi \), we define for notational convenience
Then
1. Case: \(T_o\) not unbiased:
In this case, \(\eta ^*(\alpha ) = \epsilon (\alpha )\). By definition and using the Lebesgue integral
The first term, (15a), is re-written as
For any \(y \in \Xi \), according to the definition of \(B^*(\alpha ,y)\),
Therefore (16a) is also \(\le 0\).
By using the Lipschitz constant \(l_\mathrm{W}\), (16b) can be estimated by
We have used Hölder’s inequality (with parameter \(p=1\)) by re-writing \(\Vert \theta - T_o(\alpha ,y) \Vert _2 = \Vert \theta - T_o(\alpha ,y) \Vert _2 \cdot 1\) and by identifying \(\prod _{r=1}^R f( y_r | \theta ) dy_1 \ldots dy_R\) as the (probability) measure.
Hence, for (15a), we obtain
The second term, (15b), is estimated by
as \(w(\cdot )\) is a probability density and therefore \(\int _{\Theta } w(\theta ) d\theta =1\) and \(\overline{H}\big (T_o(\alpha ,\zeta )\big )\) is a confidence region at level \((1-\alpha )\), cf. Remark 2.
2. Case: \(T_o\) unbiased:
In this case, all estimations for the 1. case until (17) remain valid. But then, we change the estimation of the term (16b) as follows:
We have used Hölder’s inequality by re-writing \(\Vert \theta - T_o(\alpha ,y) \Vert _2 = \Vert \theta - T_o(\alpha ,y) \Vert _2\cdot 1\) and by identifying \(\prod _{r=1}^R f( y_r | \theta ) dy_1 \ldots dy_R\) as the (probability) measure. Also we remember (14).
Because the term (15b) is \(\le \alpha \) and the term (16a) is \(\le 0\),
holds. \(\square \)
We use the normalization (3) of the function \(Q(\cdot ,\cdot )\) in inequality (14). This is the motivation of the normalization of function \(Q(\cdot ,\cdot )\).
We make the following comments on Theorem 1 for our data-driven approach towards stochastic optimization under distributional ambiguity and solutions \(B^*(\alpha , \mathbf {X})\):
-
(i)
Theorem 1 is a Bayesian-type result because the bound \(\alpha + \eta ^*(\alpha ) \cdot \lambda (\Theta ) \cdot l_\mathrm{W}\) assumes an a-priori distribution W on \(\Theta \).
-
(ii)
The bound \(\alpha + \eta ^*(\alpha ) \cdot \lambda (\Theta ) \cdot l_\mathrm{W}\) is averaged over all possible observations (this is a unique result).
-
(iii)
The bound depends on four constants: \(\alpha \), \(\eta (\alpha )\), \(\lambda (\Theta )\) and \(l_\mathrm{W}\). \(\alpha \) is a user-controlled parameter; \(\eta (\alpha )\) depends on the quality of the estimator, see (12); \(\lambda (\Theta )\) is the size of the parameter space; \(l_\mathrm{W}\) depends on the chosen a-priori distribution W and is controlled by the user as well.
-
(iv)
The bound improves with smaller \(\alpha \) values. This is consistent with our intuition in that smaller \(\alpha \) values yield confidence regions of higher level.
-
(v)
Better estimator(s) also yield(s) smaller bounds because \(\eta (\alpha )\) gets smaller.
-
(vi)
Increasing the “sharpness” of the a-priori distribution yields to a larger bound as the slope \(l_W\) of the density increases. This is explained because a sharper distribution puts more “weight” on a smaller number of parameters \(\theta \in \Theta \), making it harder for solutions \(B^*(\alpha , \mathbf {X})\) to yield good results for this sharper a-priori distribution.
Next, we draw a connection to classical stochastic optimization where the distribution function is known, i.e., \(|\mathcal {P}|=1\).
Corollary 1
If only one distribution function is given, i.e., \(K=1\), then \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) reduces to the baseline stochastic optimization problem \((\mathcal {SP})\). Hence, the (optimality deviation) bound \((\alpha + \eta ^*(\alpha ) \cdot \lambda (\Theta ) \cdot l_\mathrm{W}) = 0\) holds.
Proof
For \(K=1\), the estimator \(T_o(\alpha ,\mathbf {X}) = \tilde{\theta }\) and \(\eta ^*(\alpha ) \equiv 0\). The confidence level \((1-\alpha ) = 1\). The quantities \(\lambda (\Theta )\) and \(l_\mathrm{W}\) are bounded; as the dimension of the parameter \(\theta \), \(\tilde{d}\) is fixed. The solution of \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) solves \((\mathcal {SP})\) to optimality since the Lebesgue integral in \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) with respect to the unique trivial (probability) measure, which gives the singleton \(\tilde{\theta }\) mass 1, yields the optimization problem
\(\square \)
4.2.2 Asymptotic analysis
The idea of the asymptotic analysis is to show that the optimality deviation \((\alpha + \eta ^*(\alpha ) \cdot \lambda (\Theta ) \cdot l_\mathrm{W})\) converges to zero with the number of observations R.
We have defined \(R \in \mathbb {N}\) as the finite number of i.i.d. observations and \(\zeta = ( \xi _1, \ldots , \xi _R )\) as the corresponding random vector. In the asymptotic case, there is an infinite (and countable) set of i.i.d. observations \((\mathbf {X}_1, \mathbf {X}_2, \ldots )\) and \((\xi _1, \xi _2, \ldots )\) is the corresponding infinite dimensional random vector. Therefore, we have a sequence
of n-dimensional decision variable vectors.
We also must require the sequence of estimators \((T_R)_{R \in \mathbb {N}}\) to be asymptotically efficient in the sense that \(\lim _{R \rightarrow \infty } \alpha _R = 0\), with
for some positive null sequence \((\eta _R)_{R \in \mathbb {N}}\). We denote the set in (19) by
Clearly, \(T_R\) corresponds with \(T_o\), \(\alpha _R\) with \(\alpha \) and \(\eta _R\) with \(\eta ^*\).
In many cases, one can choose as the sequence \((\eta _R)_{R \in \mathbb {N}}\) any null sequence \((\eta _R)_{R \in \mathbb {N}} = \big (O(\frac{1}{\sqrt{R}}) \big )_{R \in \mathbb {N}}\), i.e., the sequence \((\eta _R)_{R \in \mathbb {N}}\) divided by the sequence \((\frac{1}{\sqrt{R}})_{R \in \mathbb {N}}\) diverges to infinity. For example, one may choose
If the parameter is the expected value (i.e., the \(\xi _i\) are random variables) and \((T_R)_{R \in \mathbb {N}}\) the sample mean, then, under the corresponding assumptions, the inequality of Chebyshev provides the convergence of \((\alpha _R)_{R \in \mathbb {N}}\) to zero. This can be seen as follows. According to the Chebyshev inequality
which shows the converges to zero if R tends to infinity.
Corollary 2
We assume that the sequence \((l_R)_{R \in \mathbb {N}}\) of Lipschitz-constants, corresponding with \(l_W\), is bounded. Normally it converges to zero, as the corresponding calculation for the case of normal distribution with the mean as parameter shows.
For any given data \(\mathbf {X}\) and \(R \in \mathbb {N}\), consider the stochastic optimization problem \((\mathcal {BP^*}_{\alpha }(\mathbf {X}))_R\) for confidence region \(C\big (T_R\big )\)
with constant
and solution \((B^*(\alpha _R, \mathbf {X}))_R\). Then the sequence of solutions \((B^*(\alpha _R, \mathbf {X}))_{R \in \mathbb {N}}\) is asymptotically optimal for all \(\theta \in \Theta \) (Theorem 1), i.e.,
\(\square \)
4.2.3 The complexity of \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\)
The complexity of optimization problem \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) depends (i) on the shape of the function \(\mathbb {E}_\theta \big [Q(\mathbf {x},\xi ) \big ]\), (ii) the shape of the feasible region \(\mathbb {X}\) and (iii) the dimension of \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\).
We start by recognizing that the optimization problem \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) preserves the convexity of the original problem, i.e., if the stochastic optimization problem (1) is a convex optimization problem (for known probability distribution, i.e., given \(\theta \)), then \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) is also a convex optimization problem. This holds, because for \(\lambda \in [0,1]\) and \(\mathbf {x}_1, \mathbf {x}_2 \in \mathbb {X}\)
with density \(f(\cdot | \theta )\) of \(\zeta \) for parameter \(\theta \), implying that \(\prod _{r=1}^R f(\mathbf {X}_r | \theta ) \ge 0\) for all \(\mathbf {X}_1, \ldots , \mathbf {X}_R\) and \(\theta \).
Problem \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) can be solved, for instance, by using a numerical approximation method for the integral over \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\). The resulting optimization problem falls then in one of the standard classes, for example, convex nonlinear programming (as in the computational examples in Sect. 6) or, more generally, mixed-integer nonlinear nonconvex programming (MINLP) problems. If the resulting optimization problem, after using some numerical approximation for the integral, is a (non-convex) MINLP, then one can resort to available off-the-shelf global optimization solvers. Alternatively, the resulting MINLP problem can be approximated using piecewise linear constructs to yield MILP problems, subject to any approximation quality [12, 29, 40,41,42,43].
For the optimization problem \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\) to be computationally tractable, it is not sufficient that the stochastic optimization problem (1) is tractable. The reason is that numerical integration (e.g., when using a cubature formula for dimension \(\ge 2\)) gets hard with increasing dimension of \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\). One is trapped by a curse-of-dimensionality [15].
5 Bounding the standard Bayesian and the Naïve approach
We next apply the idea of the proof of Theorem 1 towards the Bayesian and the Naïve Approach.
5.1 The standard Bayesian approach
We start with the definition of the standard Bayesian approach.
Definition 7
For any given data \(\mathbf {X}\), consider the data-driven stochastic optimization problem \(\big (\mathcal {BP^*}(\mathbf {X})\big )\)
with constant
The chosen a-posteriori distribution is the uniform distribution on \(\Theta \), i.e., standard Bayesian. We denote a solution as \(B(\mathbf {X})\), called standard Bayesian solution; see also Sect. 2.1 about the Bayesian approach.
For the standard Bayesian solution \(B(\mathbf {X})\), as defined in Definition 7, we derive from Theorem 1 the following
Corollary 3
We propose the same assumptions and notations as in Theorem 1 and the unbiasedness of \(T_o\). Then, for any distribution W on \(\Theta \) with Lipschitz-continuous density \(w(\theta )\) and Lipschitz constant \(l_\mathrm{W}\), it holds that
Proof
The proof, especially the second part, is analogous to that of Theorem 1.
By definition and using the Lebesgue integral
Now we estimate the term (24) as follows:
We have used Hölder’s inequality by re-writing \(\Vert \theta - T_o(\alpha ,y) \Vert _2 = \Vert \theta - T_o(\alpha ,y) \Vert _2 \cdot 1\) and by identifying \(\prod _{r=1}^R f( y_r | \theta ) dy_1 \ldots dy_R\) as the (probability) measure. Also we remember (14).
Because the term (23) is \(\le 0\) ,
holds. \(\square \)
Remark 5
Theorem 1 and Corollary 3 establish the optimization of the mean-risk up to the bound \((\alpha + \eta ^* \cdot \lambda (\Theta ) \cdot l_\mathrm{W} )\) in (13) resp. up to \((\eta \cdot \lambda (\Theta ) \cdot l_\mathrm{W} )\) in (22) for an entire class of a-priori distributions. With other words, \(B^*(\alpha , \mathbf {X})\) is the solution of the stochastic optimization problem under distributional ambiguity, minimizing the mean-risk (up to a constant and for all a-priori distributions with Lipschitz-continuous density).
The difference of Theorem 1 to the Bayesian approach (as described in Sect. 2.1) is twofold. First, in the Bayesian approach, the parameter set \(\Theta \) is used instead of \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\), as mentioned above. Second, Bayesian approaches do not involve an estimator \(T_o(\alpha ,\mathbf {X})\).
5.2 Optimality bound for the risk
The key idea of our new approach, \(\big (\mathcal {BP^*}_{\alpha }(\mathbf {X})\big )\), is the combination of an a-posteriori Bayesian-like approach with a confidence region around a special estimator. Therefore the derived optimality bound relates to the mean risks.
In order to obtain also a similar result in the classical sense, i.e., an optimality bound for the risk with respect to the true parameter, we take now the estimator itself instead of a confidence region around it. This is the naïve approach, where the uncertainty around the distribution P is ignored and the best estimator for \(\theta \) is chosen.
We assume that we have an estimator \(T_d = T_d(\zeta )\) for the (true) parameter \(\theta \in \Theta \), where we rely on the usual definition of an estimator, i.e., a measurable function \(T_d = T_d(\zeta ) : \Xi \rightarrow \Theta \). We then solve the stochastic optimization problem \((\mathcal {SP})\) for \(T_d(\mathbf {X})\) instead of \(\theta \), which we call the naïve approach.
Definition 8
For any given data \(\mathbf {X}\), consider the data-driven stochastic optimization problem \(\big (\mathcal {DP^*}(\mathbf {X})\big )\)
We denote a solution of the data-driven stochastic optimization problem \(\big (\mathcal {DP^*}_{T_d}(\mathbf {X})\big )\) as \(D^*_{T_d}(\mathbf {X})\) . \(\square \)
For our analysis, we require the confidence region for estimator \(T_d\)
to any confidence level \((1-\alpha )\). For any \(\theta \in \Theta \), we set for abbreviation
We assume the Lipschitz continuity of \(f( y_0 | \theta )\) as a function of \(\theta \), with Lipschitz-constant \(l(y_0)\) for every \(y_0 \in \xi (\Omega )\) and assume that
exists. With this notation in place, we can derive the bound for the naïve approach.
Corollary 4
Let \(L(\cdot ,\cdot )\) be continuous and non-constant on the non-empty compactum \(\mathbb {X}\) and let Assumption 2 hold. For any data \(\mathbf {X}\), let \(D_{T_d}^*(\mathbf {X})\) be a solution of \(\big (\mathcal {DP}^*_{T_d}(\mathbf {X})\big )\). Then, for any \(\theta \in \Theta \) and any \(\alpha \) with \(0< \alpha < 1\), it holds that
Proof
Let any \(\theta \in \Theta \) be given. For any feasible decision function \(d \in \mathcal {D}\) and \(y = (y_1, \ldots , y_R) \in \Xi \), we define for notational convenience
Then
By definition and using the Lebesgue integral
The first term, (32a), is re-written as
According to the definition of \(D^*(y)\),
holds for all y \(\in \Xi \). Therefore (33a) is also \(\le 0\).
According to (31) and by using the Lipschitz constant \(l_d\), (33b) can be estimated by
Hence, for (32a), we obtain (because the probability is less or equal to one)
The second term, (32b), is estimated by
first estimation respecting (31) and the last as \(I_{\alpha }(\theta ) := \{ ||T_d(\zeta ) - \theta ||_2 \le \eta (\alpha ) \}\) is a confidence region at level \((1-\alpha )\). \(\square \)
Corollary 4 is a classical result, in contrast to the Bayesian-type results in Theorem 1 and Corollary 3, in the sense that it holds for all \(\theta \in \Theta \). With other words, the bound in (30) holds for the risk and not the mean-risk.
6 Computational results
The computational results are obtained with GAMS version 24.4.6, where we use LINDOGLOBAL and BARON to solve the resulting non-linear programming (NLP) problems in Sect. 6.1 and Sect. 6.2, respectively [33, 46]. For the sake of simplicity in the discussions, we optimize the loss function \(L(\cdot ,\cdot )\) directly, instead of the normalized and standardized expected function \(\mathbb {E} \big [Q(\cdot ,\cdot )\big ]\). We approximate the integrals in the optimization problem \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) via the trapezoidal rule. Together with the convexity of the considered functions \(L(\cdot ,\cdot )\), the resulting optimization problem for \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) is convex. Note that solving the new optimization model \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) is computationally more expensive than the Bayesian approaches, which are in turn more computational expensive than the distributionally robust optimization approaches, for our tested instances.
6.1 Production planning & control (PPC): newsvendor problem
Given is the following simplified and stylized production planning & control (PPC) problem, in this special form also known as the Newsvendor problem, with a single consumer product to be produced for a single time horizon [18, 32, 58]. The demand is random and follows a normal distribution with unknown mean \(\mu \) and known standard deviation of 10; i.e.,
6.1.1 Illustrative example
We assume that the true mean \(\tilde{\mu } = 50\) is unknown. However, we assume knowledge that \(\tilde{\mu }\) is contained in the interval \([a,b] = [40,55] := \Theta \) which we discretize with step 0.1, for computational reasons. This yields a family of 151 normal distributions, i.e.,
Overproduction leads to inventory cost of \(c_1=2\) [$/item]; underproduction is allowed but imposes a penalty of \(c_2=10\) [$/item]. The cost (or loss) function is then given by
with \([y]_+ = \max \{0,y\}\). There is no initial inventory and between \([l,u]=[25,100]\) items can be produced. For some known random variable \(\xi \sim P = \mathcal {N}(\mu , \sigma ^2)\), the expected value of (35) is evaluated as
with standard normal CDF \(F^\mathrm{SN}(x)\). Notice that \(\mathbb {E}_P \big [ L( \mathbf {x}, \xi ) \big ]\) is a convex function in x and that both \(\min _{x \in \mathbb {X}, P \in \mathcal {P}} \mathbb {E}_P \big [ L( \mathbf {x}, \xi ) \big ] \) and \(\max _{x \in \mathbb {X}, P \in \mathcal {P}} \mathbb {E}_P \big [ L( \mathbf {x}, \xi ) \big ] \) exist, i.e., they are finite.
To evaluate the computed solutions for the true objective function, we define
The optimal solution \(\mathbf {x}^*\) as a function of \(\theta \) is shown in Fig. 3. The corresponding function values for the true parameter \(\tilde{\theta } = 50\) are shown in Fig. 4.
Table 1 summarizes the results of the different stochastic optimization models, as listed in the first column. The second column reports on their optimal solution; the third column lists their corresponding objective function value; the fourth column shows their true objective function value (36), i.e., the computed solution is evaluated by the model with the true but unknown parameter \(\tilde{\theta }\); the last column presents the gap between the optimal objective function value and the true objective function value, i.e., gap = (true objective function value − 29.982)/29.982. The a-posteriori approaches (S2), (S4), (S5), (T1) and (T2) utilize \(R=20\) realizationsFootnote 1 of \(\zeta \). These values are given in the footnote below so that an interested reader can re-compute all quantities of the illustrative example.
The baseline model is the true model (therefore, the values in column three and four are identical and the gap in column five is 0%). Thus, the baseline model (B) serves as the benchmark for the 7 different tested stochastic optimization models (S1)-(S5) and (T1)-(T2). The performance of each tested model is then given by the closeness of their solution to the true solution \(\mathbf {x}^* \approx 59.674\) (second column) and the true objective function value \(z^* = z(\mathbf {x}^*) \approx 29.982\) (fourth column).
For the a-priori Bayesian model (S1), we use the (discrete) uniform distribution for the a-priori distribution, i.e., \(s_k=1/151\) for \(k \in \{ 1,\ldots , 151 \}\). The corresponding results are shown in Table 1. The obtained solution is worse than the three a-posteriori approaches but slightly better than the other a-priori approach (S3), which is an expected result (but does not hold in general for any random draw of the realizations) as the a-posteriori approaches take additional information into account compared to the a-priori approaches; the \((\mathcal {DRSP})\) is a worst-case approach and, thus, is typically outperformed if the worst-case distribution does not mature.
In our example, \(\zeta \) is a continuous random vector. Because \(\xi _1, \ldots , \xi _R\) are i.i.d. random vectors, we obtain the a-posteriori Bayesian problem \((\mathcal {B}(\mathbf {X}))\)
Its optimal solution and the function values are reported in row (S2) in Table 1. We observe that the a-posteriori Bayesian approach outperforms both a-priori approaches: the a-priori Bayesian and the a-priori distributionally robust stochastic optimization model, whose results are reported in row (S3).
We choose the sample mean, as our first estimator \(T_1\), i.e.,
Because the standard deviation is known, the sample mean follows the normal distribution \(\mathcal {N}(\hat{\mu }_1, \frac{10^2}{R})\). This yields the \((1-\alpha )\) confidence interval
for the true mean \(\tilde{\mu }\), with the critical value \(z_{\alpha }\) of the standard normal distribution. Because we know that \(\tilde{\mu } \in [a,b] \subset \mathbb {R}\), we may truncate the confidence interval (37) to obtain the \((1-\alpha )\) confidence interval
For a second estimator \(T_2\), we choose the weighted-moving average method. Its estimator for \(\tilde{\mu }\) is given by
with weights or parameters \(g_r \in \mathbb {R}^+\), \(r=1, \ldots , R\). Choosing \(g_r=1\) for all \(r = 1, \ldots , R\) reveals that the weighted-moving average method is a generalization of the sample mean. Estimator \(\hat{\mu }_2\) is unbiased and follows the normal distribution
This yields another \((1-\alpha )\) confidence interval for \(\tilde{\mu }\), similar to (38).
We choose as confidence level \((1-\alpha ) = 0.95\). The weights \(g_r\) are chosen as a null-sequence with \(g_r = \frac{1}{ \lceil r / 5 \rceil }\). The 20 data points lead to the following confidence regions
The first confidence interval contains 83 parameters for the mean, while the second contains 77 parameters. For example, when choosing \(\alpha _1 = 0.0178\) and \(\alpha _2 = 0.0322\), we obtain the region
containing 73 distributional parameters. The solution of \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\) for \(I(\alpha ,\mathbf {X})\subset \Theta \) is reported in row (S4) in Table 1. We observe that \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\) yields a slightly better solution than the a-posteriori Bayesian model (S2). This might be unexpected because of the worst-case nature of \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\) but is explained by the incorporation of the additional information of the estimators \(T_1\) and \(T_2\).
We obtain as estimator \(T_o(\alpha ,\mathbf {X}) = 50.6\). This yields
We approximate the integral over \(\widetilde{H}\big (T_o(\alpha ,\mathbf {X})\big )\), in optimization problem \((\mathcal {BP^*}_{\alpha }(\mathbf {X}))\), via the trapezoid rule with 73 trapezoids. This yields a box-constrained NLP. The obtained solution is shown in row (S5) in Table 1. We observe that the solution \(x^*\) and the true objective function value is the best among the seven different stochastic optimization models (S1)-(S5) and (T1)-(T2) with a gap of 0.02%.
We also compute the results for the naïve approach, using the two estimators \(T_1\) and \(T_2\). The sample average yields \(T_1(\mathbf {X}) \approx 49.0004\) and for the second estimator \(T_2(\mathbf {X}) \approx 51.1941\). The resulting solutions are then shown in columns (T1) and (T2) in Table 1. Note that the naïve approach is outperformed by all other a-posteriori approaches (S2), (S4) and (S5).
Next, we study the error bounds from Theorem 1 and Corollaries 3-4. Note that the derived bounds apply for the normalized expected function \(\mathbb {E}\big [ Q(\cdot ,\cdot ) \big ]\). For the error bound \(\alpha + \eta ^*(\alpha ) \cdot \lambda (\Theta ) \cdot l_\mathrm{W}\) in (13), we restrict the discussions to the sample average as estimator \(T_0 = T_1\) alone. Because the half-width of the confidence interval (37) is independent of the observations (as we assume a known standard deviation), we obtain
The sample average is an unbiased estimator of \(\tilde{\theta }\) with standard deviation
Thus,
for \(\alpha \le 0.317\). The Lebesgue measure \(\lambda (\Theta ) = 55-40=15\) is the interval length. This yields
for the Lipschitz constant \(l_\mathrm{W}\) of the density \(w(\theta )\). Thus, \(l_\mathrm{W}\) is a user input and depends on the “sharpness” of the imposed measure. For example, for the uniform distribution
for the triangular distribution with lower limit 40, upper limit 55 and mode 47.5:
and the truncated normal with lower limit 40, upper limit 55, mean \(\mu _W\) and standard deviation \(\sigma _W\)
For example, for choices \(\mu _W = 47.5\) and \(\sigma _W= 15\), we obtain \(l_W \approx 0.0001872\) for the truncated normal. With \(R=20\) and assuming this truncated normal, we obtain for the bound in Theorem 1
This yields the bound (22)
for the Bayesian approach, as analyzed in Corollary 3. Both bounds (39) and (40) are for the mean-risk.
The bound \(\alpha + l_d \cdot \eta (\alpha ) \) of Corollary 4 is estimated as follows. The Lipschitz constant \(l_d\) is bounded by
because \(R=20\) and \(\sigma =10\) for our illustrative example; see above. Because \(\eta (\alpha )\) is bounded and not “too large,” we obtain
Note that (41) bounds the risk (instead of the mean-risk for the other two approaches).
6.1.2 Varying the number of observations and the confidence level
We continue our Newsvendor example by making the following changes: the cost \(c_2\) is reduced from 10 to 7, we choose only one estimator \(T_1\) to compute the confidence intervals around the single parameter \(\tilde{\mu } = \tilde{\theta } = 50\). This yields a true optimal objective function value of approx. 26.802. Further, we assume the knowledge of \(\tilde{\theta } \in [40,80]\), and the parameter discretization is set to be 0.5, leading to 81 parameters in \(\Theta _0\).
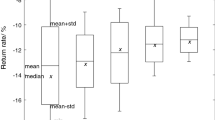
We test \(\alpha =0.10, 0.05, 0.04\) and 0.03 for \(R=10, 15, 20, 25, 50, 75, 100, 150\) and 200 observations. For each combination, we solve 100 instances. All computed \(x^*\) are then evaluated by the true objective function (36); this is an out-of-sample performance test. For \(\alpha = 0.05\), the results are plotted in Fig. 5. Specifically, Fig. 5 plots the objective function values for the 100 samples for different values of R in decreasing order. These function values are obtained by the optimal solution \(x^*\) of \((\mathcal {BP^*}_{0.05}(\mathbf {X}))\), evaluated with the true objective function. For example, for \(R = 25\) observations, 100 random test instances are drawn and the resulting true objective function values are plotted in decreasing order. Note that the x-axis shows the sample number after sorting in decreasing order for each different value of R individually.
True objective function value for \((\mathcal {BP^*}_{0.05}(\mathbf {X}))\) for different numbers of observations R, as evaluated by (36). The plot shows the results for 100 samples, sorted in decreasing order, of the true objective function values. Thus, the x-axis shows the (sorted) sample number
For our experiments, the solution plots for \((\mathcal {B}(\mathbf {X}))\) and \((\mathcal {DRSP}_{0.05}(\mathbf {X}))\) look very similar and largely overlap with the one produced by \((\mathcal {BP^*}_{0.05}(\mathbf {X}))\). We observe in Fig. 5 that the worst solutions computed among the 100 instances improve with the increase in the number of observations. This is a very desirable and is the expected behavior of the model \((\mathcal {BP^*}_{0.05}(\mathbf {X}))\). Further, we note a convergence towards the optimal true objective function value of approximately 26.802.
The solution of the two a-priori approaches \((\mathcal {B})\) and \((\mathcal {DRSP})\) lead to true objective function values of approx. 45.3913901 and 45.1890283, respectively. They are far worse than any of the solutions computed by \((\mathcal {B}(\mathbf {X}))\), \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\) and \((\mathcal {BP^*_{\alpha }(\mathbf {X})})\) for all 3600 instancesFootnote 2. This comes as no surprise, since the interval for \(\tilde{\theta } \in [40,80]\) is quite large and, consequently, the value of this information is quite limited.
Table 2 summarizes the computational results for all instances on the three different a-posteriori approaches \((\mathcal {B}(\mathbf {X}))\), \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\) and \((\mathcal {BP^*_{\alpha }(\mathbf {X})})\). Specifically, columns 3-5 report the number of instances where each single approach yields a smaller true objective function value than the other two methods, for the computed solutions. Columns 6-8 state the standard deviation of the 100 computed true objective function values. Note that the a-posteriori Bayesian model \((\mathcal {B}(\mathbf {X}))\) does not depend on our choice of \(\alpha \); while the observations are taken into account via the a-posteriori distribution, the confidence interval is not.
The computational results, as shown in columns 3-5, reveal that none of the three approaches always dominates any other method. Actually, we argue that each of the three approaches are valuable and are particularly strong in specific cases.
The a-posteriori Bayesian model \((\mathcal {B}(\mathbf {X}))\) performs very well when many i.i.d observations are available (e.g., 150 or more). For these cases, all three approaches yield similar results (while recognizing that the standard deviation between the 100 objective function values is very small if many observations are available, leading also to small differences between the three approaches). A big advantage of \((\mathcal {B}(\mathbf {X}))\) is that no confidence level and no estimator has to be chosen. Also, the computational burden in solving \((\mathcal {B}(\mathbf {X}))\) is lower compared to \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\).
The a-posteriori distributionally robust stochastic optimization model \((\mathcal {DRSP}_{\alpha }(\mathbf {X}))\) is particularly strong for the cases where a significant number of i.i.d. observations are given (e.g., between 100 and 150).
Finally, the new approach \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) yields strong results when relatively few observations are given (e.g., between 10 and 75). The computational effort required in solving \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) is similar to \((\mathcal {B}(\mathbf {X}))\) if the trapezoidal rule is used.
The results of columns 6–8 in Table 2 quantify the tendency shown in Fig. 5 that the standard deviation decreases with an increase in the number of observations.
6.2 Reliability: two-dimensional parameter space \(\Theta \)
As a second test bed, we consider a reliability problem. Replacing a part in time, i.e., before it is broken, costs \(p_1 > 0\). Once it is broken, the replacement costs increase to \(p_2 > p_1\). The goal is to find the optimal time \(t > 0\) to replace the part, minimizing the expected replacement cost.
The corresponding loss function for the continuous random variable \(\xi \), measuring the time until failure, is then given by
with indicator function \(\mathbb {I}_A(\cdot ): \mathbb {R}^1 \rightarrow \mathbb {R}^1\). Our goal is to minimize the expected losses
as a function of \(t>0\).
For an exponentially distributed random variable \(\xi \sim P=\)EXP(\(\alpha ,\lambda \)) with mean \(\alpha +\lambda \) and density
we obtain for \(t \ge \alpha \)
An optimal replacement time t is obtained at
to yield the minimum
which is independent of \(\alpha \).
We assume that both parameters \(\alpha \) and \(\lambda \) are unknown. This yields the two-dimensional parameter \(\theta = (\alpha , \lambda )\). To obtain a common estimator \(\hat{\theta } = (\hat{\alpha },\hat{\lambda })\), we use the maximum likelihood estimates
which makes use of our (i.i.d.) realizations \(\mathbf {X}_1, \ldots , \mathbf {X}_R\) having distribution EXP(\(\alpha ,\lambda )\) with unknown \(\alpha \) and \(\lambda \).
Because \(\hat{\alpha }\) and \(\hat{\lambda }\) are independent [31], we can use the following confidence regions at levels \((1-\alpha _1)\) and \((1-\alpha _2)\) for \(\alpha \) and \(\lambda \), respectively,
with critical values \(r_{1,R,\alpha _1}\) and \(r_{2,R,\alpha _2}\). The distributions, of which the critical values \(r_{1,R,\alpha _1}\) and \(r_{2,R,\alpha _2}\) are derived, can be taken from the literature [30]. The non-negativity of the exponential distribution implies that \(\alpha \le \hat{\alpha }\) which explains the one-sided confidence interval for \(\alpha \). An exact confidence region at level \((1- \alpha _1) \cdot (1-\alpha _2)\) for both parameters \(\alpha \) and \(\lambda \) jointly, is then obtained by
6.2.1 Varying the number of observations and the confidence level
For our computational experiments, we choose \(\tilde{\theta }=(\tilde{\alpha },\tilde{\lambda }) = (25, 100)\) with cost \(p_1 = 61.6575\) and \(p_2 = 123.315\) to yield \(t^* \approx 65.5\) and \(\min _{t > 0} \; \mathbb {E}_{\tilde{\theta }}\big [L(t,\xi )\big ] \approx \) 5000.0. The integral in (11), to obtain \((\mathcal {BP^*}_{\alpha }(\mathbf {X}))\), is solved using the two-dimensional trapezoidal rule. For our first computational tests, we further assume
which we discretize using 40 and 100 parameter values to obtain \(\Theta _0\). The confidence interval (42) is then updated to
It is theoretically possible, that the \((1- \alpha _1) \cdot (1-\alpha _2)\) confidence interval (44) is empty; that did not occur in our tests of over 42,000 instances (as reported in Tables 3 and 4, see below).
Figures 6 and 7 plot the expected loss functions for different parameter configurations of \(\lambda \) and \(\alpha \) within the safe interval (43). The horizontally dotted lines show the optimal \(t^*\) values for each parameter configurations. The graphs for \(\lambda =100\) and \(\alpha =25\) in Figs. 6 and 7 show the true expected loss function, against which we compare the computed t values (for the three different a-posteriori approaches tested). The figures show that (i) the loss functions are smooth in t for different parameter configurations \(\lambda \) and \(\alpha \), (ii) the optimal values for t vary quite significantly for the different parameter values shown in the two figures, ranging from approx. 49.33 to 80.55. Even though the true objective function (yellow curve in Fig. 6 and red curve in Figure 7) is smooth, the true objective function values differ quite significantly when evaluating different values of t.
Table 3 shows the results for the different computational tests performed for the reliability example. The setup of the experiments is similar to the ones reported in Table 2, while we use 1000 instances in Table 3 compared to 100 instances of Table 2. Column 1 shows the number of draws, R. The values of \(\alpha _1\) and \(\alpha _2\) are reported in column 2, while columns 3-5 report the number of instances where each approach yielded a better expected loss, i.e., the computed t was inserted in the true objective function value with the true parameters \(\tilde{\theta }\). The last three columns show the standard deviation of the true objective function values for the 1000 different runs.
Most notably, the proposed solution \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) outperforms both the a-posteriori distributionally robust and Bayesian approaches consistently and considerably. The new approach yielded the best true objective function values among the three approaches in over 87% of the 36000 instances. In general, \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \) does particularly well for 50, 75 and 100 i.i.d. data points. We observe that the standard deviation of the true objective function values evaluated at the computed solutions for all approaches tends to decrease with the number of available data points, i.e., with increasing R. This behavior is expected as more realizations leads to smaller confidence regions which in turn should lead to smaller variations in the computed optimal time t.
The a-posteriori Bayesian approach has a much lower standard deviation (column 6 in Table 3) compared to the two other a-posteriori approaches. In general, a lower standard deviation is a desired property, but only when it comes together with better objective function values. This is not the case for the a-posteriori Bayesian approach. In contrast, the standard deviation for the new approach (column 8) is always smaller compared to the a-posteriori distributionally robust optimization approach, while having better objective function values—a desirable property.
One might expect that the a-posteriori distributionally robust approach is better for such cases, where one of the true parameters \(\tilde{\alpha }\) and \(\tilde{\lambda }\) lies outside the confidence interval. This is the case with probability \(\alpha _1 + \alpha _2 - \alpha _1 \cdot \alpha _2\). For example, for \(\alpha _1 = \alpha _2 = 0.075\) and \(\alpha _1 = \alpha _2 = 0.100\) this leads to probabilities of 0.9375 and 0.81, respectively. Thus, for 1000 independent instances, we expect that the a-posteriori distributionally robust approach outperforms the other two approaches at about 73 and 190 instances, for \(\alpha _1 = \alpha _2 = 0.075\) and \(\alpha _1 = \alpha _2 = 0.100\), respectively. As the results in Table 3 reveal, this is only rarely the case. That the solution of the new approach, \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \), tends to outperform the a-posteriori distributionally robust approach even in such cases where at least one of the true parameters lies outside of the confidence interval further illustrates the strengths of the new approach.
6.2.2 Varying the safe interval
Next, we study the computational effects when varying the safe interval (43) as
Therefore, consider Table 4 which shows experiments for \(R=20\) data points. The results indicate that the particular choice of the safe interval influences the relative results of the three approaches; this comes at no surprise as the \((1- \alpha _1) \cdot (1-\alpha _2)\) confidence interval (44) directly depends on the safe interval. With smaller safe intervals (43), both the a-posteriori Bayesian and the a-posteriori distributionally robust approaches tend to improve. Despite that trend, even for as small intervals as \([20,30] \times [80,110]\), the new approach does considerably and consistently better. The relative improvement of both the a-posteriori Bayesian and a-posteriori distributionally robust optimization approaches is explained by the decreasing leeway. Very small safe intervals favors a-posteriori Bayesian approaches as their solutions get closer to \(\left( \mathcal {BP}^*_{\alpha }(\mathbf {X})\right) \); this can also be observed by comparing the results of \(\alpha _1 =\alpha _2=0.075\) with the smaller confidence intervals resulting from \(\alpha _1 =\alpha _2=0.100\).
7 Conclusions
We present a new data-driven approach towards stochastic optimization under distributional uncertainty. The proposed approach uses observations to construct confidence regions. We then apply an a-posteriori Bayesian approach towards this confidence region. This yields a new data-driven stochastic optimization problem.
The careful construction of the confidence region around an appropriate estimator allows us to analyze the quality of the solutions obtained when taking the expected values of all observations and all a-priori distributions. The derived optimality bound provides various insights on the quality of the obtained solutions. For example, this bound improves with better estimators and the bound converges to zero in the number of observations. If the distribution is known, i.e., the family of distributions reduces to a singleton, then the proposed approach is identical to the standard stochastic optimization problem. In this case, the aforementioned constant is zero. Our computational results shows that solutions of the proposed data-driven stochastic optimization problems can be superior to solutions of data-driven Bayesian and data-driven distributionally robust stochastic optimization approaches.
Future research might attempt to derive data-driven stochastic optimization problems which minimize the derived bound, though it remains unclear how this can be achieved. Another research direction is to search for a novel type of robustness. Robustness is then understood as the criterion that optimality holds for an entire environment of a-posteriori distributions, for a suitable distance-measure in the space of probability distributions. Then, the new model can be designed with the aim to produce the best compromise between the maximal distance and the resulting bound.
Notes
61.0457983, 61.9744177, 67.7895157, 56.7949099, 48.7586821, 40.4456203, 55.4598745, 39.1465527, 47.8671564, 49.5706960, 35.9694537, 32.0929183, 57.2161088, 67.8262998, 53.1509340, 48.3931528, 42.9176131, 38.3446179, 44.4684806, 30.7752857.
There are 4 different parameter values for \(\alpha \) and 9 different values for R, each with 100 instances, yielding a total of 3600 instances tested.
References
Agrawal, S., Ding, Y., Saberi, A., Ye, Y.: Price of correlations in stochastic optimization. Oper. Res. 60(1), 150–162 (2012)
Basciftci, B., Ahmed, S., Gebraeel, N.: Data-driven maintenance and operations scheduling in power systems under decision-dependent uncertainty. IISE Trans. 1–14 (2019)
Bayraksan, G.: Data-driven stochastic programming using phi-divergences. In: The operations research revolution—tutorials in operations research. INFORMS (2015)
Beale, E.: On minimizing a convex function subject to linear inequalities. J. Roy. Stat. Soc. 17, 173–184 (1955)
Ben-Tal, A., Bertsimas, D., Brown, D.: A soft robust model for optimization under ambiguity. Oper. Res. 58, 1220–1234 (2010)
Ben-Tal, A., Nemirovski, A.: Robust convex optimization. Math. Oper. Res. 23(4), 769–805 (1998)
Berger, J.O., Moreno, E., Pericchi, L.R., Bayarri, M.J., Bernardo, J.M., Cano, J.A., De la Horra, J., Martín, J., Ríos-Insúa, D., Betrò, B., et al.: An overview of robust Bayesian analysis. TEST 3(1), 5–124 (1994)
Bertsimas, D., Gupta, V., Kallus, N.: Robust sample average approximation. Math. Program. 171, 217–282 (2018)
Bertsimas, D., Sim, M.: The price of robustness. Oper. Res. 52(1), 35–53 (2004)
Beykal, B., Avraamidou, S., Pistikopoulos, I.P., Onel, M., Pistikopoulos, E.N.: Domino: Data-driven optimization of bi-level mixed-integer nonlinear problems. J. Global Optim. 1–36 (2020)
Birge, J., Louveaux, F.: Introduction to Stochastic Programming, 2nd edn. Operations Research and Financial Engineering. Springer (2011)
Burlacu, R., Geißler, B., Schewe, L.: Solving mixed-integer nonlinear programmes using adaptively refined mixed-integer linear programmes. Optim. Methods Softw. 1–28 (2019)
Calafiore, G.: Ambiguous risk measures and optimal robust portfolios. SIAM J. Optim. 18(3), 853–877 (2007)
Chen, B., Chao, X.: Parametric demand learning with limited price explorations in a backlog stochastic inventory system. IISE Trans. 51(6), 605–613 (2019)
Cools, R.: Advances in multidimensional integration. J. Comput. Appl. Math. 149(1), 1–12 (2002)
Dantzig, G.: Linear programming under uncertainty. Manage. Sci. 1, 197–206 (1955)
Delage, E., Ye, Y.: Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 58(3), 595–612 (2010)
Edgeworth, F.: The mathematical theory of banking. Roy. Stat. Soc. 51, 113–127 (1888)
Esfahani, P., Kuhn, D.: Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Math. Program. 171, 115–166 (2018)
Fischetti, M., Monaci, M.: Light robustness. In: Robust and Online Large-scale Optimization, Lecture Notes in Computer Science, pp. 61–84. Springer (2009)
Gao, R., Kleywegt, A.J.: Distributionally robust stochastic optimization with wasserstein distance. Technical report. arXiv:1604.02199v2 (2018)
Ghaoui, L.E., Oks, M., Oustry, F.: Worst-case value-at-risk and robust portfolio optimization: a conic programming approach. Oper. Res. 51(4), 543–556 (2003)
Ghosh, J.K., Delampady, M., Samanta, T.: An Introduction to Bayesian Analysis: Theory and Methods. Springer Science & Business Media (2007)
Goh, J., Sim, M.: Distributionally robust optimization and its tractable approximations. Oper. Res. 58, 902–917 (2010)
Gupta, V.: Near-optimal bayesian ambiguity sets for distributionally robust optimization. Manage. Sci. 65(9), 4242–4260 (2019)
Hanasusanto, G., Kuhn, D., Wallace, S., Zymler, S.: Distributionally robust multi-item newsvendor problems with multimodal demand distributions. Math. Program. 152(1–2), 1–32 (2015)
Hansen, L., Sargent, T.: Robustness. Princeton University Press, Princeton (2007)
Jagannathan, R.: Minimax procedure for a class of linear programs under uncertainty. Oper. Res. 25(1), 173–177 (1977)
Kallrath, J., Rebennack, S.: Computing area-tight piecewise linear overestimators, underestimators and tubes for univariate functions. In: Optimization in Science and Engineering, pp. 273–292. Springer (2014)
Krishnamoorthy, K., Xia, Y.: Confidence intervals for a two-parameter exponential distribution: one- and two-sample problems. Commun. Stat. Theory Methods 47(4), 935–952 (2018)
Lawless, J.F.: Statistical Models and Methods for Lifetime Data, 2nd edn. Wiley, NewYork (2003)
Levi, R., Perakis, G., Uichanco, J.: The data-driven newsvendor problem: new bounds and insights. Oper. Res. 63(6), 1294–1306 (2015)
Lin, Y., Schrage, L.: The global solver in the LINDO API. Optim. Methods Softw. 24, 657–668 (2009)
Lohmann, T., Hering, A., Rebennack, S.: Spatio-temporal hydro forecasting of multireservoir inflows for hydro-thermal scheduling. Eur. J. Oper. Res. 255(1), 243–258 (2016)
Pflug, G., Pichler, A.: Multistage Stochastic Optimization. Springer, Heidelberg, New York, Dordrecht, London (2014)
Pflug, G., Wozabal, D.: Ambiguity in portfolio selection. Quant. Finance 7(4), 435–442 (2007)
Rachev, S., Römisch, W.: Quantitative stability in stochastic programming: the method of probability metrics. Math. Oper. Res. 27(4), 792–818 (2002)
Rebennack, S.: Generation expansion planning under uncertainty with emissions quotas. Electric Power Syst. Res. 114, 78–85 (2014)
Rebennack, S.: Combining sampling-based and scenario-based nested Benders decomposition methods: application to stochastic dual dynamic programming. Math. Program. 156(1), 343–389 (2016)
Rebennack, S.: Computing tight bounds via piecewise linear functions through the example of circle cutting problems. Math. Methods Oper. Res. 84(1), 3–57 (2016)
Rebennack, S., Kallrath, J.: Continuous piecewise linear delta-approximations for bivariate and multivariate functions. J. Optim. Theory Appl. 167(1), 102–117 (2015)
Rebennack, S., Kallrath, J.: Continuous piecewise linear delta-approximations for univariate functions: computing minimal breakpoint systems. J. Optim. Theory Appl. 167(2), 617–643 (2015)
Rebennack, S., Krasko, V.: Piecewise linear function fitting via mixed-integer linear programming. Inform. J. Comput. 32(2), 507–530 (2020)
Römisch, W., Schultz, R.: Distribution sensitivity in stochastic programming. Math. Program. 50, 197–226 (1991)
Sadeghzadeh, S., Bish, E.K., Bish, D.R.: Optimal data-driven policies for disease screening under noisy biomarker measurement. IISE Trans. 52(2), 166–180 (2020)
Sahinidis, N.V.: BARON: a general purpose global optimization software package. J. Global Optim. 8(2), 201–205 (1996)
Schultz, R.: Some aspects of stability in stochastic programming. Ann. Oper. Res. 100(1–4), 55–84 (2000)
Shapiro, A.: Quantitative stability in stochastic programming. Math. Program. 67(1–3), 99–108 (1994)
Shapiro, A.: Distributionally robust stochastic programming. SIAM J. Optim. 27(4), 2258–2275 (2017)
Shapiro, A., Ahmed, S.: On a class of minimax stochastic programs. SIAM J. Optim. 14(4), 1237–1249 (2004)
Soyster, A.: Convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 21, 1154–1157 (1973)
Steeger, G., Lohmann, T., Rebennack, S.: Strategic bidding for a price-maker hydroelectric producer: stochastic dual dynamic programming and Lagrangian relaxation. IISE Trans. 50(11), 929–942 (2018)
Thiele, A.: A note on issues of over-conservatism in robust optimization with cost uncertainty. Optimization 59(7), 1033–1040 (2010)
Van Parys, B.P., Esfahani, P.M., Kuhn, D.: From data to decisions: Distributionally robust optimization is optimal. Manage. Sci. (2020)
Wang, Z., Glynn, P.W., Ye, Y.: Likelihood robust optimization for data-driven problems. CMS 13(2), 241–261 (2016)
Wiesemann, W., Kuhn, D., Sim, M.: Distributionally robust convex optimization. Oper. Res. 62(6), 1358–1376 (2014)
Wu, D., Zhu, H., Zhou, E.: A bayesian risk approach to data-driven stochastic optimization: formulations and asymptotics. SIAM J. Optim. 28(2), 1588–1612 (2018)
Yue, J., Chen, B., Wang, M.C.: Expected value of distribution information for the newsvendor problem. Oper. Res. 54(6), 1128–1136 (2006)
Žáčková, J.: On minimax solutions of stochastic linear programming. Časopis pro pěstování matematiky 91, 423–430 (1966)
Zhou, E., Xie, W.: Simulation optimization when facing input uncertainty. In: Proceedings of the 2015 Winter Simulation Conference (2015)
Zhu, H., Hale, J., Zhou, E.: Simulation optimization of risk measures with adaptive risk levels. J. Global Optim. 70(4), 783–809 (2018)
Zhu, S., Fukushima, M.: Worst-case conditional value-at-risk with application to robust portfolio management. Oper. Res. 57(5), 1155–1168 (2009)
Acknowledgements
I would like to thank the two anonymous reviewers for their detailed and constructive comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rebennack, S. Data-driven stochastic optimization for distributional ambiguity with integrated confidence region. J Glob Optim 84, 255–293 (2022). https://doi.org/10.1007/s10898-022-01146-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-022-01146-y