The supporting hyperplane optimization toolkit for convex MINLP

Abstract

In this paper, an open-source solver for mixed-integer nonlinear programming (MINLP) problems is presented. The Supporting Hyperplane Optimization Toolkit (SHOT) combines a dual strategy based on polyhedral outer approximations (POA) with primal heuristics. The POA is achieved by expressing the nonlinear feasible set of the MINLP problem with linearizations obtained with the extended supporting hyperplane (ESH) and extended cutting plane (ECP) algorithms. The dual strategy can be tightly integrated with the mixed-integer programming (MIP) subsolver in a so-called single-tree manner, i.e., only a single MIP optimization problem is solved, where the polyhedral linearizations are added as lazy constraints through callbacks in the MIP solver. This enables the MIP solver to reuse the branching tree in each iteration, in contrast to most other POA-based methods. SHOT is available as a COIN-OR open-source project, and it utilizes a flexible task-based structure making it easy to extend and modify. It is currently available in GAMS, and can be utilized in AMPL, Pyomo and JuMP as well through its ASL interface. The main functionality and solution strategies implemented in SHOT are described in this paper, and their impact on the performance are illustrated through numerical benchmarks on 406 convex MINLP problems from the MINLPLib problem library. Many of the features introduced in SHOT can be utilized in other POA-based solvers as well. To show the overall effectiveness of SHOT, it is also compared to other state-of-the-art solvers on the same benchmark set.

Introduction

The Supporting Hyperplane Optimization Toolkit (SHOT) is an open-source solver for mixed-integer nonlinear programming (MINLP). It is based on a combination of a dual and a primal strategy that, when considering a minimization problem, gives lower and upper bounds on the objective function value of an optimization problem; the terms primal and dual should not here be mixed up with duality of optimization problems, rather these are terms with special meaning in the context of MINLP. The dual strategy is based on polyhedral outer approximation (POA) by supporting hyperplanes or cutting planes of the integer-relaxed feasible set defined by the nonlinear constraints in the problem. The primal strategy consists of several deterministic primal heuristics based on, e.g., solving problems with fixed integer variables, root searches or utilizing solutions provided by the MIP solver in the dual strategy. Here the term ‘heuristic’ does not indicate that the procedures are stochastic, only that they are not guaranteed to succeed in finding a new better solution in each iteration. Although SHOT can be used on nonconvex problems as well without a guarantee of finding a solution, the convex functionality is the main focus of this paper.

Convex MINLP is a subclass of the more general nonconvex MINLP problem class. MINLP combines the nonlinearity aspect from nonlinear programming (NLP) with the discreteness of mixed-integer programming (MIP). This increases the flexibility when used as a modeling tool, since nonlinear phenomena and relations can be expressed in the same framework as discrete choices. Due to its generality, the solution process for problems in the MINLP class is computationally demanding, in fact NP-hard, and even small problem instances may pose difficulties for the available solvers. This is one of the motivations behind considering the more specific convex MINLP problem type separately. The convexity assumption of the functions in the problem (either by manual determination or by automatic means) provide certain properties that can be utilized to make the solution procedure more tractable. For example, the property that a linearization of a convex function in any point always give an underestimation of its value in all points forms the theoretical foundation for many solution methods including those utilizing POA, e.g., Outer Approximation (OA) [18, 19], Extended Cutting Plane (ECP) [77] and Extended Supporting Hyperplane (ESH) [38] algorithms. Other algorithms for convex MINLP include generalized Bender’s decomposition [26], quadratic OA [36, 66], decomposition-based OA [57], and nonlinear branch-and-bound [15, 30].

Due to the discrete nature of the MINLP problems, convexity alone is not enough to guarantee an efficient solution process. The discreteness is normally handled by considering a so-called branch-and-bound tree that in its nodes considers smaller and easier subproblems where the discrete possibilities are gradually reduced [30]. Handling such a tree is difficult in itself as the number of nodes required are often large, and creating an efficient MINLP solver-based on the branch-and-bound methodology requires a significant development effort solely for managing the tree structure. MIP solvers such as CPLEX and Gurobi have, during their development phase, also faced the problem of efficiently handling a large tree structure. The main motivation during the development of SHOT has been to utilize the MIP subsolver as much as possible. For example, SHOT takes direct advantage of their parallelism capabilities, preprocessing, heuristics, integer cuts, etc. This makes the future performance of SHOT increase in line with that of the MIP solvers.

There are currently many software solutions for solving convex MINLP problems available to end-users; examples include AlphaECP [75], BONMIN [8], AOA [34], DICOPT [28], Juniper [35], Minotaur [52], Muriqui [53], Pajarito [45] and SBB [24]. Nonconvex global MINLP solvers include Alpine [58], ANTIGONE [56], BARON [62], Couenne [4], LINDOGlobal [44], and SCIP [71]. MINLP solvers are often integrated with one or more of the mathematical modeling systems AIMMS [7], AMPL [21], GAMS [10] JuMP [17] or Pyomo [31]. Recent reviews of methods and solvers for convex MINLP are provided in [37, 70]; in [37] an extensive benchmark between convex MINLP solvers is also provided. Overviews over MINLP methods and software are also given in [13] and [27], while an older benchmark of MINLP solvers was conducted in [41]. Of the mentioned MINLP solvers, AlphaECP, AOA, BARON, BONMIN, DICOPT, SBB and SCIP are compared to SHOT in a numerical benchmark given in Sect. 7.1.

In addition to presenting the SHOT solver, this paper can be seen as an explanation on how to efficiently implement a POA-based algorithm with tight integration with its underlying MIP solver and primal heuristics. In Sect. 2, a dual/primal POA-algorithm based on the ECP and ESH cut-generation techniques, is presented. It is also discussed how this type of algorithm can be implemented as a so-called single-tree manner utilizing callback-functionality in the MIP solver. The major accomplishments presented in this paper can be summarized as:

• A thorough description of the different techniques (both primal and dual) implemented in the SHOT solver (Sects. 3–5). Most of these features are also applicable to other POA-based solvers.

• A step-wise algorithmic overview of how SHOT is implemented (Sect. 6).

• An extensive benchmark of SHOT versus other state-of-the art free and commercial solvers for convex MINLP (Sect. 7.1).

• Numerical comparisons of the impact of the different features developed for SHOT (Sects. 7.2).

A dual/primal POA-based method for convex MINLP

In this paper, we assume that we are dealing with a minimization problem to avoid confusion regarding the upper and lower objective bounds, even though SHOT naturally solves both maximization and minimization problems. Therefore, the problem type considered is a convex MINLP problem of the form

$$\begin{aligned} \begin{aligned}&\text {minimize}&f({{\mathbf {x}}}),&\\&\text {subject to}&\mathrm A{{\mathbf {x}}}\le \mathbf {a},\ \mathrm B{{\mathbf {x}}}= \mathbf{b},&\\&g_k({{\mathbf {x}}}) \le 0&\forall k \in K, \\&\underline{x}_i \le x_i \le \overline{x}_i&\forall i \in I = \{1,2,\ldots ,n\}, \\&x_i \in \mathbf {Z}&\forall i \in I_{Z}, \\&x_i \in \mathbf {R}&\forall i \in I \setminus I_{Z}. \\ \end{aligned} \end{aligned}$$

(P)

The objective function f can be either affine, quadratic or general nonlinear. It is furthermore assumed that the objective function and all nonlinear functions $g_k$ (indexed by the set K) are convex and at least once differentiable. (Note that some NLP subsolvers may have other requirements.) It is assumed that the intersection of the linear constraints is a bounded polytope, i.e., all variables (indexed by the set I) are bounded. The ESH strategy in SHOT requires that a continuous relaxation of Prob. (P) satisfies Slater’s condition [65] for finding an interior point; however in the absence of an interior point SHOT falls back on the ECP strategy. In theory, SHOT would work even if the functions are nonalgebraic but convex, and more generally as long as the implicit feasible region and the objective function is convex, however as of version 1.0 this is not implemented; therefore, in this paper, all functions are assumed to be compositions of standard mathematical functions expressible in the Optimization Services instance Language (OSiL) syntax as discussed in Sect. 3.2.

Primal and dual bounds

Often in MINLP, the terms ‘primal and dual solutions’ and ‘primal and dual bounds’ have specific meanings differing somewhat from those normally used in continuous optimization. A primal solution is here considered to be a solution that satisfies all the constraints in Prob. (P), including linear, nonlinear and integer constraints, to given user-specified numerical tolerances. The incumbent solution is the currently best know primal solution by the algorithm and its objective value is the current primal bound. Since we are considering minimization problems this is the one with the lowest objective value. Whenever a primal solution with a lower objective value is found, the incumbent is updated. In SHOT the primal solutions are found by a number of heuristics described in Sect. 5.

A solution point not satisfying all constraints, for example an integer-relaxed solution, but whose objective function value provides a valid lower bound of the optimum of Prob. (P), is here referred to as a dual solution. In SHOT, the dual solutions are obtained by solving relaxed subproblems where the feasible region of the nonlinear constraints in problem (P) is replaced with a POA. The subproblems are of the mixed-integer linear programming (MILP) class if the objective function is affine, and of the mixed-integer quadratic programming (MIQP) class if the objective function is quadratic. Note that if the MILP/MIQP subsolver supports quadratic constraints these can be extracted from the general nonlinear constraints in $g_k({{\mathbf {x}}}) \le 0$ and handled directly in the subsolver; then the POA is only generated as a linearization of the feasible set of the nonquadratic, nonlinear constraints. In this case, mixed-integer quadratically constrained quadratic programming (MIQCQP) problems are solved in SHOT’s dual strategy. This is further discussed in Sect. 4.7. To simplify the notation of the rest of the paper, we will in the context of the types of subproblems solved in the dual strategy in SHOT use the term MIP problem, where MIP is an acronym for mixed integer programming, instead of the longer, but more descriptive MILP, MIQP or MIQCQP problem.

The dual bounds are the best possible objective value returned by the MIP solver. Thus, all dual solutions provide a dual bound, but not all dual bounds give a dual solution. This ensures that a valid bound is obtained from the MIP solver even if the subproblem is not solved to optimality. Depending on the type of the original MINLP problem, dual bounds can also be found by solving integer-relaxed problems such as linear programming (LP), nonlinear programming (NLP), quadratic programming (QP) or quadratically constrained quadratic programming (QCQP) problems.

The primal and dual bounds can be utilized as quality measures of a solution and hence for determining when to terminate the solver. Since we always consider a minimization problem, the absolute and relative primal/dual objective gaps in SHOT are defined as

$$\begin{aligned} {{{\,\mathrm{GAP}\,}}_{\text {abs}}}= {\text {PB}}- {\text {DB}}\qquad \text {and} \qquad {{{\,\mathrm{GAP}\,}}_{\text {rel}}}= \frac{{\text {PB}}- {\text {DB}}}{|{\text {PB}}| +10^{-10}}, \end{aligned}$$

(1)

where ${\text {PB}}$ and ${\text {DB}}$ are the current primal and dual bounds respectively. There are other alternative ways to calculate the gaps, however this mimics the behavior of the MIP solvers CPLEX and Gurobi, a necessity due to the tight integration with these solvers. The value of $10^{-10}$ in the denominator is used to avoid issues when ${\text {PB}}= 0$. Initially PB is defined as an infinitely large positive number and DB as an infinitely large negative number, while the gaps are initialized to plus infinity.

A combined dual/primal approach for solving MINLP problems

SHOT is based on a technique for generating tight POAs closely integrated with the MIP solver in combination with efficient primal heuristics. In [38] the ESH algorithm, forming the basis of the dual strategy in SHOT, was introduced. In the ESH algorithm (and similarly in the older ECP algorithm [77]), the POA of the original MINLP problems are solved and improved iteratively in the form of MIP problems. If the MIP solution does not satisfy the nonlinear constraints, a linear constraint is added that removes the invalid solution from the MIP subproblem and, in the process, tightens the POA. This cut can either be a supporting hyperplane (ESH) or a cutting plane (ECP). This procedure gives an increasing lower bound that, by its own, can solve a convex MINLP problem to a given tolerance of the nonlinear constraints. Note however, that an integer-feasible solution is not guaranteed until the final MIP iteration; this can be circumvented by introducing an upper bound strategy based on primal heuristics. These so-called primal strategies fulfill a very important role in SHOT since they can provide integer-feasible solutions during the entire solution process.

By combining the dual and primal strategies and their resulting bounds, termination based on absolute and relative objective function gaps, cf., Eq. (1), can be performed. This significantly increases the performance of the solver as well as returns valuable quality information about the solution during the iterative solution process. A general overview of the algorithm for efficiently solving convex MINLP problems utilized in SHOT is provide in Alg. 1. The convergence for this algorithm follows naturally from the fact that its dual strategy (either ECP or ESH) is convergent, while the algorithm’s performance is increased due to the inclusion of the primal strategies. The dual and primal parts of this strategy is described in Sects. 2.2.1 and 2.2.2.

Dual bound based on polyhedral outer approximation

To improve the dual bound, a POA of the feasible set of the nonlinear constraints is iteratively improved by adding additional linear inequality constraints to the linear part of Prob. (P). We denote these linear constraints with $c_j({{\mathbf {x}}}) \le 0$, and can thus write the POA as:

$$\begin{aligned} \begin{aligned}&\text {minimize}&\mu ,&\\&\text {subject to}&\mathrm A{{\mathbf {x}}}\le \mathbf {a},\ \mathrm B{{\mathbf {x}}}= {\mathbf {b}}, f({{\mathbf {x}}}) - \mu \le 0&\\&c_j({{\mathbf {x}}}) \le 0&\forall j \in {K_\text {CUTS}},\\&{\underline{x}}_i \le x_i \le {\overline{x}}_i&\forall i \in I = \{1,2,\ldots ,n\},\\&x_i \in \mathbf {Z}&\forall i \in I_{Z}, \\&x_i \in \mathbf {R}&\forall i \in I \setminus I_{Z}. \\ \end{aligned} \end{aligned}$$

(POA)

Here we assume that the objective function is linear as the epigraph-reformulation can be used if it is nonlinear; that is, a new objective variable $\mu$ is minimized and an auxiliary nonlinear constraint $f({{\mathbf {x}}}) - \mu \le 0$ is introduced into Prob. (P).

To improve the POA, we initially solve Prob. (POA) with ${K_\text {CUTS}}= \emptyset$ using a MILP solver to obtain the solution ${{\mathbf {x}}}_0$. Using the cut-generation technique of the ECP algorithm, we can then directly generate a cutting plane that, when added to the POA, excludes this solution. This procedure is iteratively repeated to remove solution points that do not belong to the feasible set of the original Prob. (P). In general, the solution point ${{\mathbf {x}}}_n$, in the current (n-th) iteration, is directly used to generate the cutting plane

$$\begin{aligned} g_m({{\mathbf {x}}}_n) + \nabla g_m({{\mathbf {x}}}_n) ({{\mathbf {x}}}-{{\mathbf {x}}}_n) \le 0, \end{aligned}$$

(2)

that excludes the solution point ${{\mathbf {x}}}_n$. Normally, $g_m$ is the constraint function with the largest (positive) value when evaluated in the point ${{\mathbf {x}}}_n$. It is also possible to generate additional cuts in each iteration, e.g., for all violated constraints with $g_k({{\mathbf {x}}}_n) > 0$ or a fraction of these.

In the ESH algorithm, a one-dimensional root search is instead utilized to approximately project ${{\mathbf {x}}}_n$ onto the integer-relaxed feasible set. This root search is performed on the line segment connecting ${{\mathbf {x}}}_n$ and an interior point ${{{\mathbf {x}}}_{\text {int}}}$ to find the point where the line intersects with the boundary of the integer-relaxed feasible set of the MINLP problem. The points on this line can be expressed as

$$\begin{aligned} {{\mathbf {x}}}' = \lambda {{{\mathbf {x}}}_{\text {int}}}+ (1-\lambda ) {{\mathbf {x}}}_n,\quad \lambda \in [0,1]. \end{aligned}$$

Thus, we want to find $\lambda$ such that the maximum value of all constraint functions, $G({{\mathbf {x}}}'):= \max _{k\in K} g_k({{\mathbf {x}}}')$, is equal to zero, i.e., 

$$\begin{aligned} \max _{k\in K} g_k \left( \lambda {{{\mathbf {x}}}_{\text {int}}}+ (1-\lambda ) {{\mathbf {x}}}_n\right) = 0. \end{aligned}$$

This is a standard one-dimensional root search in the variable $\lambda$ (the individual functions $g_k$ can be evaluated in $\lambda$ after which the maximum value of the constraint functions $g_k$ is selected) and can be solved using bisection or a more elaborate method, cf., Sect. 3.5.3. Assuming that the nonlinear constraint function with the largest positive value is $g_m$, a supporting hyperplane to the integer-relaxed nonlinear feasible region of Prob. (P) can now be generated in this point as

$$\begin{aligned} \nabla g_m({{\mathbf {x}}}_n) ({{\mathbf {x}}}-{{\mathbf {x}}}_n) \le 0. \end{aligned}$$

(3)

The interior point ${{{\mathbf {x}}}_{\text {int}}}$ must satisfy the nonlinear inequality constraints in Prob. (P) in a strict sense, i.e., < instead of $\le$. It should also satisfy the linear constraints in Prob. (P), but satisfying the integer requirements is not necessary. Note that the root search is a computationally cheap operation as long as evaluating all nonlinear constraint functions is computationally cheap. To find an interior point to use as end point in the root searches, the following minimax formulation of Prob. (P) can be solved

$$\begin{aligned} \begin{aligned}&\text {minimize}&\nu ,&\\&\text {subject to}&A{{\mathbf {x}}}\le \mathbf {a},\ B{{\mathbf {x}}}= \mathbf {b},&\\&g_k({{\mathbf {x}}}) - \nu \le 0&\forall k \in K, \\&{\underline{x}}_i \le x_i \le {\overline{x}}_i, \ \ x_i \in \mathbf {R}\quad&\forall i \in I, \\&\nu \in \mathbf {R},&\\ \end{aligned} \end{aligned}$$

(MM)

Note that a possible nonlinear objective function $f({{\mathbf {x}}})$ can be ignored (as it does not affect the interior point), or it can be included as an auxiliary constraint as in Prob. (POA). Using a standard NLP solver such as IPOPT to solve the convex minimax problem to optimality is in most cases the most efficient option. However, within the SHOT solver it is not necessary to solve the minimax problem to optimality as any solution satisfying the linear constraints in Prob. (MM) with a strictly negative objective value is sufficient. Therefore, the simple cutting-plane-based method described in App. A is a good alternatives within SHOT as it fits directly within the solver framework and provides full control of the solution procedure. This enables the search to be terminated as soon as possible, in many cases after only a fraction of the number of iterations needed to solve the problem to optimality. Alternatively, the method from [74] can also be used to find an interior point.

Primal strategy based on heuristics

Any solution that satisfies all the constraints in Prob. (P) is a candidate to become the new incumbent, and thus it does not matter how a primal solution is obtained; this enables the usage of heuristic strategies. Since primal solutions affect when the solution process is terminated, cf., Eq. (1), they have a significant impact on the efficiency of the solver implementation as well as the quality of the solutions returned. There are a number of such strategies implemented in SHOT, cf., Sect. 5.

One primal strategy, which in principle adds little computational overhead, is to utilize alternative but nonoptimal solutions to Prob. (POA) found by the MIP solver, i.e., the so-called solution pool. Even though these are often nonoptimal for Prob. (POA) in the current iteration, they are primal solutions to Prob. (P) as long as they also satisfy the nonlinear constraints; one of them could even be an optimal solution.

Another possible strategy is to fix the discrete variables to a specific integer combination, e.g., obtained from the MIP solution point, and solve the resulting convex NLP problem with an external solver. Solving this continuous problem is often much easier than the original discrete one and can provide solutions difficult to locate by only considering the linearized POA-version of the problem. This strategy mimics the usage of NLP calls in the OA-method, but here they are not required in each iteration, but can be used more sparingly.

In addition to these strategies, there are many other primal heuristics that can be used for MINLP problems, including the center-cut algorithm [39] and feasibility pumps [6, 9].

Single- and multi-tree POA

The standard strategy of implementing a POA-based algorithm, as the one described previously in this section, is to solve several separate MIP instances in a sequence. This provides a flexible and easily implementable strategy since no deep integration with the MIP solver is required, and a basic implementation can simply write a MIP subproblem to a file and call the subsolver on this problem. The solution can then be read back into the main solver where linearizations based on cutting planes or supporting hyperplanes are created and added to the MIP problem file before resolving the problem. At a certain point some termination tolerance is met and the final solution to the MINLP problem has been found. This type of strategy is called a multi-tree POA algorithm because a new branch-and-bound tree is built in each call of the MIP solver.

In a single-tree POA algorithm, only one master MIP problem is solved and so-called lazy constraints are added through callbacks to cut away integer-feasible solutions that violate the nonlinear constraints in the MINLP problem. Callbacks are methods provided by the MIP solver that activate at certain parts of the solution process, e.g., when a new integer feasible solution has been found or a new node is created in the branching tree. This provides increased flexibility for the user to implement custom strategies affecting the behavior of the MIP solver in a way not possible through normal solver parameters. It is also possible to affect the node generation in the MIP solvers using callbacks, but this is not considered in this paper, nor is it implemented in the SHOT solver.

To understand how a single-tree POA algorithm works, one can imagine that supporting hyperplanes expressed as linear constraints have been generated in every point on the boundary of the feasible region given by the nonlinear constraints in the MINLP problem. The optimal solution to this MIP subproblem would then provide the optimal solution also to the original MINLP problem. However, it is neither possible nor often required to add all of these linear constraints to obtain the optimal MINLP solution. In contrast, when utilizing lazy constraints, the supporting hyperplanes are only added as needed to cut away MIP solutions encountered by the MIP solver, but not feasible in the nonlinear model. Thus, it can be imagined that the model has all the constraints required to find the optimal solution to the MINLP problem, but only those that are actually needed are currently included explicitly.

As soon as a new integer-feasible solution is found by the MIP solver, the callback is activated, and it is possible for the MINLP solver to determine whether a lazy constraint removing this integer-feasible point or not should be generated. Note that no constraints are generated for solutions that satisfy also the nonlinear constraints. In the callback primal heuristics can be executed and obtained primal solutions provided back to the MIP solver. Since we are not required to restart the MIP solution procedure as when adding normal constraints in multi-tree algorithms, the same branch-and-bound tree can be utilized after adding a new linearization as a lazy constraint. Finally, when the POA of the original MINLP problem, as expressed in the MIP solvers internal model of the problem, is tight enough, i.e., Eq. (1) is satisfied, the MIP solver will terminate with the optimal solution for the original MINLP problem.

SHOT implements both a multi- and single-tree strategy based on the MINLP algorithm in Alg. 1. Another solution method utilizing a single-tree approach is the LP/NLP-based branch-and-bound algorithm [61], which integrates OA and BB to reduce the amount of work spent on solving MILP subproblems in OA. This technique is implemented in the MINLP solvers BONMIN [8], AOA [34], FilMINT [1] and Minotaur [52], and has previously been shown to significantly reduce the number of total nodes required in the branching trees [42].

The SHOT solver implementation

SHOT is available as an open-source COIN-OR project,¹ and is also included in GAMS (as of version 31). A simplified version is also available for Wolfram Mathematica [48], however, this version lacks many of the features described in this paper and its performance is not comparable to the main SHOT solver.

The SHOT solver is based on the primal/dual methodology for solving convex MINLP problems presented in the previous section. To make a stable solver that can be used efficiently on a wide range of problems, there are however several components missing from Alg. 1. Details on the implementation is discussed in this section (preprocessing and input/output), in Sect. 4 (the dual strategy) and in Sect. 5 (the primal strategy). Finally, in Sect. 6 we present what we call the SHOT algorithm, i.e., a detailed overview of the individual steps implemented in the SHOT solver. These sections together provide a ‘recipe’ for creating a solver based on the method described in the previous section.

SHOT is programmed in C++ 17 and released as a COIN-OR open-source project [49]. Its external dependencies include Cbc [20] for solving MILP subproblems and IPOPT [72] for solving NLP subproblems. SHOT can also interface with commercial MIP and NLP solvers, as described later on in this section, in which case Cbc and IPOPT are not required. In addition to these external dependencies, SHOT also utilizes functionality in the Boost libraries [63] for root and line search functionality and CppAD [3] for gradient calculations. A full list of utilized third party libraries are available on the project web site.

The SHOT solver is itself very modular and is based on a system where most of the functionality is contained in specific tasks. This makes it easy to change the behavior of the solver by defining solution strategies that contain a list of specific tasks to perform in sequence. Since there are also if- and goto-tasks, iterative algorithms can easily be implemented without modifying the underlying tasks. The tasks are executed in a sequence defined by the solution strategy, but the order of execution can also be modified at runtime. Currently four main solution strategies are implemented: the single-tree and multi-tree strategies, a strategy for solving MI(QC)QP problems directly with the MIP solver, as well as one for solving problems without discrete variables, i.e., NLP problems.

Solver options

Options are provided in a text-based pair-value format (option = value); alternatively, options can be given using the XML-based OSoL-format, which is part of the COIN-OR OS project [25]. The options are organized in categories, e.g., Termination.TimeLimit is part of the termination category and controls the time limit and can thus be given a numeric value in seconds. Other possible option types are strings, booleans and integer-valued options (sometimes also indicating logical choices). The settings are documented in the options file and in the solver documentation on the project web site. The most important options and option categories are also indicated in the text below.

Problem representation

SHOT can read problems in the XML-based OSiL-format [23] through its own parser, and AMPL-format [22] through the AMPL solver library (ASL). Through an interface to GAMS, it can also read problems in GAMS-format [12]. In all cases however, the model is translated into an internal representation.

The internal problem representation consists of three different entities: an objective function (linear, quadratic or general nonlinear), constraints (linear, quadratic or general nonlinear) and variables (continuous, binary or integer). In addition to linear and quadratic terms, the nonlinear objective function and constraints consists of monomial and signomial terms, as well as general nonlinear expressions internally represented by expression trees.

Convexity detection

SHOT automatically determines the convexity of the objective function and constraints, and utilizes this information when selecting whether the convex strategy should be employed or not; the user can also force SHOT to assume a given problem is convex with the switch Model.Convexity.AssumeConvex; this is especially useful if the automatic convexity procedure cannot correctly identify a problem instance as convex. The convexity of quadratic terms can easily be decided by determining if the corresponding Hessian matrix is positive semidefinite or not utilizing the Eigen library [29]. Monomials are always nonconvex and the convexity of signomials can easily be determined using predetermined rules [46]. For nonlinear expressions, SHOT utilizes automatic rule-based convexity identification inspired by [14].

Bound tightening

Although bound tightening is, to some extent, performed in the underlying MIP solvers, these are only aware of the linear (and quadratic, if supported) parts of the problem. Therefore, SHOT also performs feasibility-based bound tightening (FBBT; [54, 64]) on both the linear and nonlinear part of the MINLP problem. For special terms (linear and quadratic), SHOT has specialized logic for obtaining the bounds of the expressions; for general nonlinear expressions, FBBT is performed using interval arithmetic on the expression tree. Bound tightening is activated by default, but can be disabled with the switch Model.BoundTightening. FeasibilityBased.Use.

Since FBBT is a relatively cheap operation, it is by default performed on both the original and reformulated model, the reason for the former being that this might enable more automated reformulations that are dependent on the bounds or convexity of the underlying variables. Bound tightening on the reformulated problem might further reduce the bounds of auxiliary variables introduced in automated reformulations. SHOT also performs implicit bound tightening based on the allowed domain of functions, e.g., if $\sqrt{f(x)}$ occurs in the problem, it is assumed that $f(x) \ge 0$, which can then be utilized to further tighten the variable bounds. The FBBT procedure is terminated when progress is no longer made or a time-limit is hit.

Subsolvers and auxiliary functionality

SHOT relies heavily on subsolvers in its main algorithm, with the main workload passed on to the MIP and NLP solvers. Being able to perform root and line searches efficiently is also very important for the overall performance and stability of SHOT, and therefore, efficient external libraries are utilized for this purpose. These integrations with third party software are described in this section.

MIP solvers

SHOT currently interfaces with the commercial solvers CPLEX and Gurobi, as well as the open-source solver Cbc. The MIP solver is selected with the option Dual.MIP.Solver. Note that Cbc does not support quadratic objective functions so these are considered to be general nonlinear if Cbc is used. The interface to Cbc also does not support callbacks so the single-tree strategy is disabled.

By default, most MIP solvers work in parallel utilizing support for multiple concurrent threads on modern CPUs. This, however means that a fully deterministic algorithm is difficult, if not impossible, to achieve without hampering the performance too much. Therefore, the solution times, and even e.g., the number of iterations, in SHOT may vary slightly between different runs. Some of the MIP solvers have parameters that try to force the behavior of the solver to be more deterministic, but total deterministic behavior is not possible to achieve in most cases when using more than one thread. The number of threads made available to the MIP solver in SHOT is controlled by the user (with option Dual.MIP.NumberOfThreads), with the default that the choice is made by the MIP solver.

Some relevant algorithmic options are automatically passed on to the MIP solvers, including absolute and relative gap termination values and time limits. There are also a number of additional solver-specific parameters that can be specified; these parameters are documented in the solver manual.

NLP solvers

SHOT currently supports either IPOPT or any licensed NLP solver in GAMS. The NLP solver is selected using the option Primal.FixedInteger.Solver. For IPOPT, which implements an interior point line search filter method [73], it is recommended to utilize one of the HSL subsolvers [33] if available for maximum performance and stability. A comparison of the performance of different subsolvers in IPOPT, especially with regards to parallelism, can be found in [68]. Note that for GAMS NLP solvers to be used, the problem must be given in GAMS-syntax, cf., Sect. 3.2, or SHOT must be called from GAMS. If available, CONOPT is the default overall NLP solver in GAMS because it has been found to be very stable in combination with SHOT. CONOPT is a feasible path solver based on the generalized reduced gradient (GRG) method [16].

Root and line search functionality

Since root searches are extensively utilized in SHOT, both for finding the point to generate supporting hyperplanes and in primal heuristics, cf., Sect. 5.3, an efficient and numerically stable root search implementation is required. The roots package in the Boost library [63], more specifically its implementations of the TOMS 748 algorithm [2] and a bisection-based method, are provided. TOMS 748 implements cubic, quadratic and linear (secant) interpolation. Functionality for minimizing a function along a line is also provided by Boost through the minima library. This functionality is used in the minimax solver for obtaining an interior point of the nonlinear feasible set described in App. A. There are several parameters (in the option category Subsolver.Rootsearch) controlling the root and line search functionality in SHOT. However, in most cases these can be left to their default values. If a root search fails when generating a supporting hyperplane because of numerical issues a cutting plane generated by the ECP method, i.e., directly from the MIP solution point, is always added; this significantly improves the stability of SHOT in case the original problem is, e.g., badly scaled.

Note that when performing a root search on a max function $G({{\mathbf {x}}}):= \max _j g_j({{\mathbf {x}}})$, with convex component functions $g_j$ on a line between an interior point ${{{\mathbf {x}}}_{\text {int}}}$ and an exterior point ${{{\mathbf {x}}}_{\text {ext}}}$, often not all constraint functions $g_j$ need to be evaluated in each point. All functions that get a negative value in both endpoints of the current interval containing the root during subsequent evaluations can be disregarded in the rest of the current root search iterations, as they will not be active in the final point due to the convexity of the functions $g_j$. This reduces the number of function evaluations needed in case there are many inactive nonlinear constraints.

Termination

The SHOT solver is normally terminated based on the relative and absolute objective gaps, cf., Eq. (1), which are given as the options Termination.ObjectiveGap.Relative and Termination.ObjectiveGap.Absolute, respectively; also time and iteration limits can be specified (Termination.TimeLimit and Termination.IterationLimit). The iteration limit behaves differently depending on whether the single- or multi-tree methodology is used. In the multi-tree case, the iterations are counted as number of LP, QP, QCQP, MILP, MIQP or MIQCQP iterations performed, and thus correspond to the number of dual subproblems solved. In the single-tree case, whenever the lazy callback has been activated, i.e., a new integer-feasible solution is found, is regarded as an iteration. Note that for the same problem, the number of iterations are often much higher in the single-tree case, but the solution time per iteration is often less. Solving NLP problems are not counted as main iterations.

In the multi-tree case, there is also an option, which is normally disabled, to terminate when the maximum constraint deviation in the MIP solution point ${{\mathbf {x}}}_k$ is satisfied, i.e., $G({{\mathbf {x}}}_k) \le \epsilon _g$, and the solution of the current subproblem is flagged optimal by the MIP solver. This termination criterion is the normal one in the standard ESH and ECP algorithms, motivating its inclusion in the SHOT solver. Note however, that a primal solution need not be found in this case, and therefore the solution status of the solver may indicate a failure.

Solver results and output

The obtained solution results and statistics are returned as an XML-file in the OSrL-format. Also, a GAMS trace file can be created. The trace file does not contain the variable solution vector, only the dual and primal bounds on the objective value in addition to statistics about the solution process. The trace files are mainly provided for benchmarking purposes as these can be directly read by PAVER [11], the tool used in the benchmarks provided in Sect. 7.

For debugging purposes there is an option (Output.Debug.Enable), which when enabled makes SHOT output intermediate files in a user-specified or temporary directory. These include subproblems in text format, solution points, etc. The amount of output shown on screen or written to the log file during the solution process is also user-controllable.

Details on the dual strategy implemented in SHOT

In this section, we consider the dual strategies available in SHOT, i.e., strategies for updating the POA, and techniques to efficiently integrate these strategies with the MIP solver. We also describe how to efficiently implement the multi-tree approach by, e.g., using early termination of the MIP solver and utilizing the MIP solution pool, as well as, how to implement the single-tree approach with its MIP callbacks and lazy constraints. Many of the strategies detailed here are new and unique to the SHOT solver when compared to other similar POA-based solvers such as AlphaECP, BONMIN (with its OA-strategy) and DICOPT.

In SHOT, a POA is created mainly by the ESH algorithm to represent the nonlinear feasible region of the MINLP problem. It is, however, possible for the user to select the ECP algorithm, and the ECP algorithm is also the fallback method if no interior point is known in the ESH algorithm. The selection between ESH and ECP is done with the option Dual.CutStrategy. Regardless of how the linear approximation is generated, it is updated iteratively to remove at least the previous solution point(s) to the MIP problem, thus improving the POA. What differentiates ECP and ESH is how the linearizations are generated.

In the following sections, some enhancements to the standard dual strategy in SHOT are described that help to improve its efficiency. Many of these enhancements are not unique to SHOT, but may be integrated into other solvers based on POA, such as the OA algorithm, as well.

Single- and multi-tree dual strategies

In many POA-based solvers, such as AlphaECP and DICOPT, additional hyperplane cuts in the form of linear constraints are added in each iteration, and this requires a new branch-and-bound tree to be created in each iteration as well. As described in Sect. 2.3, it is however possible to enhance the performance by tightening the integration by utilizing so-called lazy constraints in combination with MIP solver callbacks [47].

In SHOT, both multi- and single-tree strategies are implemented, and the strategy can be selected by the user with the option Dual.TreeStrategy. In the multi-tree strategy additional linear constraints are added in each iteration to the MIP model, and thus the branch-and-bound tree must also be recreated by the MIP solver. Information about previously found solutions can by retained by the MIP solver (if supported), otherwise, e.g., the primal solution, must be communicated to the MIP solver between iterations. Since many dual iterations are often required, this can lead to a significant reduction in performance. After the MIP solver has solved the current iteration, SHOT can then execute its primal strategies, cf., Sect. 5, as well as check if the current solution satisfies the termination criteria.

In the single-tree strategy, the integration between SHOT and its MIP subsolver is tightened by utilizing so-called lazy constraints in combination with MIP solver callbacks [47]. In this strategy, instead of iteratively solving individual MIP problems, only one main MIP problem is considered, and whenever a new integer-feasible solution is found by the MIP solver, the callback is activated and control returned to SHOT. SHOT can now execute its primal strategies and perform the termination checks. If the solution satisfies the termination criteria we can terminate SHOT with this solution. Otherwise we must generate supporting hyperplanes or cutting planes based on this solution, and add the cuts as lazy constraints to the MIP model. The lazy constraints do not invalidate the branching tree, and the MIP solver can continue until the next integer-feasible solution has been found.

The functionality in both the multi- and single-tree strategies in SHOT are otherwise similar, except for some specialized steps that cannot be implemented in one or the other. The multi-tree strategy is available with all supported MIP solvers, i.e., Cbc, Gurobi and CPLEX, while the single-tree strategy is currently only available with Gurobi and CPLEX, as Cbc lacks (stable) support for lazy-constraint callbacks.

Handling problems with a nonlinear objective function

In addition to adding linearizations of the nonlinear constraints, a nonlinear objective must also be represented in the MIP problem. This can be accomplished by rewriting Prob. (P) into the so-called epigraph form by introducing an auxiliary variable $\mu$, i.e., the variable vector is replaced with ${{\mathbf {x}}}:= ({{\mathbf {x}}}, \mu )$ and replacing the objective function with $\mu$. The original nonlinear objective function, from now on denoted as $\tilde{f}$, can then be moved into an objective function constraint $\tilde{f}({{\mathbf {x}}})- \mu \le 0$, which is included in the set of nonlinear constraints. This reformulated problem is now equivalent to the original one in the sense that they have the same solution in the original variables.

If all nonlinearities in the reformulated MINLP problem are ignored to get the initial dual MIP problem, the auxiliary variable $\mu$ is not present in any constraints. As the MIP solver will try to minimize the value of the $\mu$ variable that constitutes the objective function in the subproblems, initially a very low or unbounded solution value for this variable is returned. However, as linearizations are performed for the added objective constraint function $\tilde{f}({{\mathbf {x}}})- \mu$ in the same manner as described above for the normal constraints functions $g_j$, the solution value for $\mu$ will eventually increase. Note also that a constraint such as $\tilde{f}({{\mathbf {x}}})- \mu \le 0$ has the property that if a cutting plane is generated for it, the cutting plane will automatically become a supporting hyperplane [74].

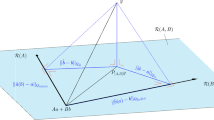
When utilizing the epigraph reformulation, it is possible to get to a situation where all other constraints but the auxiliary objective function constraint are satisfied. So, although the strategy to treat the nonlinear objective constraint in the same manner as all other nonlinear constraints will work, it is often beneficial to treat a nonlinear objective function differently. Thus, by performing a one-dimensional root search in the $\mu$-direction for a given ${{\mathbf {x}}}$, an interval $[{\underline{\mu }},\overline{\mu }]$, containing the root of $\tilde{f}({{\mathbf {x}}})-\mu = 0$ can be found. Then a supporting hyperplane is generated in the exterior point $({{\mathbf {x}}}, {\underline{\mu }})$ to avoid numerical difficulties, while the interior point $({{\mathbf {x}}}, \overline{\mu })$ is a good primal candidate since it satisfies all constraints in the current MIP problem. This is described in more detail in Sect. 6.4 and illustrated in Fig. 1. By default, a nonlinear objective function is treated in this way is SHOT, but the epigraph reformulation can be activated using the switch Model.Reformulation.ObjectiveFunction.Epigraph.Use.

An objective linearization does not necessarily need to be added in each MIP iteration if not all the nonlinear constraints are satisfied. However, it is often best to get a tight linear representation of the objective function as early as possible, so by default this procedure is performed in each iteration in SHOT, and on all available MIP solutions. Otherwise, several iterations might be wasted on improving the POA in regions with a poor objective value.

Utilizing convexity-preserving reformulations

In [40] it was shown that POA-based methods can benefit significantly from the optimization problem being written in a specific form. This was also studied in [32, 69]. As a rule of thumb, nonlinear expressions with fewer variables are normally more suitable for POA-methods. Therefore, partitioning or disaggregating nonlinear objective functions

$$\begin{aligned} \text {minimize} \ \ f_1({{\mathbf {x}}}) + \cdots + f_n({{\mathbf {x}}}) \quad \longrightarrow \quad \left\{ \begin{aligned}&\text {minimize} \ \&\mu _1 + \cdots + \mu _n,&\\&\text {subject to}&f_i({{\mathbf {x}}}) \le \mu _i,\ i=1,\ldots ,n,&\end{aligned}\right. \end{aligned}$$

or nonlinear constraints

$$\begin{aligned} f_1({{\mathbf {x}}}) + \cdots + f_n({{\mathbf {x}}}) \le 0 \quad \longrightarrow \quad \left\{ \begin{aligned}&\mu _1 + \cdots + \mu _n \le 0,&\\&f_i({{\mathbf {x}}}) \le \mu _i,\ i=1,\ldots ,n,&\end{aligned}\right. \end{aligned}$$

can have a significant impact on the solution performance on problems with this kind of structure. Naturally, for this transformation to guarantee to preserve the convexity of the problem, the individual functions $f_i$ need to be convex. However, as many users are not directly aware of the benefits of these reformulations, and since performing them manually are time-consuming and error-prone, this should preferably be done either in the modeling system used or by the solver. A general overview of reformulations in mathematical programming is given in [43].

As of version 1.0 SHOT performs the following reformulations automatically:

• Nonlinear sum reformulation: Partition sums of convex quadratic or nonlinear terms into auxiliary convex constraints.

• Logarithmic transform of signomial terms combined with term partitioning into convex constraints [40].

• Epigraph reformulation, i.e., rewrite a nonlinear objective function as an auxiliary constraint.

Whereas the first two reformulations give a significant impact on the performance on SHOT on certain problems, normally there is no benefits with an epigraph reformulation. The reason for this is that we then lose the possibilities of handling a nonlinear objective function in a special way, e.g., with regards to hyperplane generation; rather the objective function constraint would then be considered as any other nonlinear constraint in the ESH and ECP strategy, cf., Sect. 4.2. The reformulations in SHOT are controlled by a number of user-modifiable options in the Model.Reformulation group. Note that bounds on the auxiliary variables utilized in the reformulations are important; in SHOT these are obtained through evaluating the bounds on the corresponding reformulated expressions using interval arithmetic.

Obtaining an interior point for the ESH algorithm

Prob. (MM) could be solved with a standard NLP solver such as IPOPT to obtain the interior point needed for the ESH cut-generation. However, since the problem does not need to be solved to optimality, the specialized cutting plane-based method described in App. A is used instead in SHOT. Since the method solves a sequence of LP problems, we can check for a feasible solution after each iteration and terminate as soon as a valid interior point has been found. The method also has the good property that some of the cutting planes can also be reused when creating the POA in dual strategy in SHOT. Utilizing a builtin method also removes the dependency on an external NLP solver.

If the ESH algorithm has been selected in SHOT, but no interior point is found within a fixed number of iterations or within a specified time limit, SHOT will utilize the ECP algorithm until an interior point is found, e.g., by the primal heuristics, and then switch back to the ESH algorithm. The interior point can also be updated during the solution process, e.g., it can be replaced with the current primal solution point, or it can be set as an average between the current interior point and the solution point. Furthermore, multiple interior points can be utilized to perform several root searches with different interior end points. This will decrease the impact of having one ‘bad’ interior point, however it will increase the number of supporting hyperplanes generated, and thus, the complexity of the MIP subproblem(s). The options in SHOT controlling the behavior of the interior point are contained within the Dual.ESH.InteriorPoint category, and we refer to the solver manual for more details on these.

Generating multiple hyperplanes per iteration

In the ECP algorithm additional cutting planes can easily be generated for more than one of the nonlinear constraints not satisfied by the point ${{\mathbf {x}}}_k$. In theory, a cutting plane can be generated for all violated constraints, but in practice this may result in a too steep increase in the size of the MIP subproblems reducing the overall performance. In the ESH algorithm, the root search with respect to the max function G will often only give one active constraint in the found root, and thus only one supporting hyperplane will be obtained. However, it is also possible to do root searches on the individual constraint functions $g_j$ instead of the max function. This is the default strategy in SHOT, and the fraction of violated constraints a root search is performed against is controlled with the option Dual.HyperplaneCuts.ConstraintSelectionFactor. Performing individual root searches is feasible as long as the function evaluations of $g_j$ are computationally cheap, which is often the case whenever the functions are defined as compositions of standard mathematical functions. If function evaluations are expensive, or it is not possible to evaluate functions in certain points (e.g., only at some discrete values), the ECP method is preferable as it only requires function and gradient evaluations in the MIP solution point ${{\mathbf {x}}}_k$.

In SHOT, the MIP solution pool is also utilized to generate more hyperplane cuts by using solutions that do not satisfy the nonlinear constraints as either starting points for the root search in the ESH algorithm, or as generation points for the cutting planes in the ECP algorithm. In fact, the optimal solution to next MIP iteration can actually be present already in the solution pool, and utilizing these alternative solutions to generate additional linearizations can, therefore, greatly reduce the number of MIP subproblems. The maximal number of cutting planes or supporting hyperplanes added per iteration is controlled by the option Dual.HyperplaneCuts.MaxPerIteration. Utilizing the solution pool for generating multiple constraints has also been used in [67] for an OA-type algorithm and in [38] for the ESH algorithm.

As normally more integer-feasible solutions are found in the single-tree than in the multi-tree strategy, the cut-generation pace should be more moderate in the former. This can be controlled, e.g., by reducing the number of individual constraints the root search is performed against. If supported, it is also possible to allow the MIP solver to remove lazy constraints that it deems are unnecessary to reduce the number of constraints in the model.

Early termination of MIP problems in the multi-tree strategy

An important aspect for obtaining good performance in the multi-tree strategy is to initially solve the MIP subproblems to feasibility instead of optimality, and in principle, only the final iteration need to be solved to optimality. In this way, we quickly obtain points to generate new hyperplanes in, while in the process rapidly getting a tight initial POA. In SHOT this strategy is accomplished by utilizing the solution limit termination criterion of the MIP solvers. When enough integer-feasible solutions are found, the MIP solver terminates, regardless of the MIP objective gap and other termination criteria.

The solution limit parameter is initially set to the value one, i.e., the MIP solver terminates as soon as a solution satisfying all linear and integer constraints in the MIP problem is found. It is can also be set as the user-specified value Dual.MIP.SolutionLimit.Initial. If the solution status returned from the MIP solver is that the solution limit parameter has been reached and the first solution in the solution pool does not satisfy one or more of the nonlinear constraints to a given tolerance Dual.MIP.SolutionLimit.UpdateTolerance, linearizations are generated by the ESH or ECP methods and the solver proceeds to the next iteration. However, if the best solution in the solution pool satisfies also the nonlinear constraints to the specified tolerance, the solution limit parameter is increased, and, if the MIP solver supports it, will continue without rebuilding the tree to find additional solutions. The rebuilding can be avoided since no new hyperplane cuts are added to the MIP model in these iterations. (Cuts are still generated for the solution points in the solution pool that do not satisfy the nonlinear constraints, but these are added in the next iteration without solution limit update.) To help improve the efficiency, limits on how many iterations can be solved before forcing a solution limit update are also set (option Dual.MIP.SolutionLimit.IncreaseIterations).

Such a strategy was originally described in [78] and implemented in the GAECP solver [76]. In the AlphaECP solver in GAMS [75], instead of the solution limit, the relative MIP gap termination is iteratively reduced in steps to initially solve the subproblems to feasibility rather than optimality.

Solving quadratic subproblems

As described in [38] it is also possible to solve MIQP subproblems in the dual strategy in SHOT if the original problem contains a quadratic objective function and the MIP subsolver supports it. In this case, the strategies for handling a nonlinear objective function described in Sect. 4.2 are not needed as the objective function is by construction exact in the subproblems. Of the MIP solvers available in SHOT, CPLEX and Gurobi can solve MIQP problems, while Cbc does not currently provide this functionality. Thus, with Cbc as subsolver, all quadratic expressions are considered to be general nonlinear and linearized as part of the POA.

CPLEX and Gurobi also support convex quadratic constraints, i.e., solving (convex) MIQCQP problems, and SHOT has the functionality to directly pass such constraints on to these subsolvers. In this case, a POA is only generated for the feasible set of the nonquadratic nonlinear constraints, while the MIQCQP subsolver makes sure that the quadratic constraints are fulfilled.

For CPLEX and Gurobi, the behavior of whether to regard quadratic terms in the objective function and constraints as quadratic or general nonlinear is controlled with the option Model.Reformulation.Quadratics.Strategy.

Solving integer-relaxed subproblems

Since integer-relaxed problems are normally solved much faster than corresponding MIP problems, solving problems with their integer-constraints removed can be exploited to enhance the performance of SHOT. The first technique, based on solving LP, QP or QCQP problems, is to be used as a presolve strategy and can be utilized in both the single- or multi-tree strategies, while the second and third strategy are for the multi-tree and single-tree strategies respectively.

It is possible to initially ignore the integer constraints of the problem and rapidly solve a sequence of integer-relaxed subproblems to obtain a tight POA as a presolve step. Since each subproblem is normally solved to optimality in this case, the solution always provides a dual bound that can be utilized by SHOT. As soon as a maximum number of relaxed subproblems have been solved, or the progress of the dual bound has stagnated, i.e., the integer-relaxed solution to the MINLP problem has been obtained, the integer constraints are activated. After this, MIP subproblems are solved that include all the hyperplane cuts generated when solving the integer-relaxed problems. If SHOT is tasked to solve a MINLP problem without integer variables, i.e., a NLP problem, no additional iterations are required after this step. The initial integer-relaxation step is controlled with the option Dual.Relaxation.Use.

Another relaxation strategy can be used whenever the same integer combination is obtained repeatedly in several subsequent iterations. Here, the integer variables are fixed to these values and a sequence of integer-relaxed LP or QP problems are solved. The idea in this strategy is similar to fixing the integer variables in the MINLP problem and instead solving NLP problems as described in Sect. 5.2. However, it can be more efficient to solve LP, QP or QCQP problems instead of NLP problems, and we can utilize the generated hyperplane cuts in the main POA afterwards as well. Note that the solutions to these subproblems cannot be used to update the dual bound since it is not known whether the selected integer combination is the optimal one. Primal candidates found, are however, still valid for the main problem. In practice, using this strategy is similar to using SHOT as a NLP subsolver in the primal strategy, cf., Sect. 5.2; this functionality is, however, not yet available in the version of SHOT considered in this paper.

The previous strategy cannot be used in the single-tree strategy as it would require that the branching tree is rebuilt when fixing the integer variables and restoring the original integer variable bounds. However, an alternative method can be implemented in the single-tree strategy if the MIP solver also provides callbacks that activate on relaxed solutions. Then linearizations can be generated also in these points. This strategy will most often give rise to a significant increase in the number of lazy constraints in the model, and should be used moderately. This functionality is also not implemented in the SHOT version considered in this paper.

Details on the primal strategy implemented in SHOT

In this section, three primal heuristics utilized in SHOT are discussed. These strategies are executed after the current MIP problem has been solved in the multi-tree strategy and in the lazy constraint callback in the single-tree strategy. If they return a primal candidate, it is then checked if it satisfies all constraints of Prob. (P) and is an improvement to the current incumbent solution. If the solution is either better than the incumbent, or better than the worst solution in SHOT’s solution pool, it is saved. The maximal number of primal solutions stored in SHOT is controlled with the option Output.SaveNumberOfSolutions.

Utilizing the MIP solution pool

The simplest primal heuristic implemented in SHOT is to utilize valid alternative solutions to the MIP problem that also satisfy the nonlinear constraints. If the single-tree strategy is used, such solutions may be found during the MIP search and these can be utilized as primal candidates. In the multi-tree strategy, the so-called solution pool, containing nonoptimal integer-valid solutions found during the solution process, can be checked for solutions satisfying the nonlinear constraints. Also, as described in Sect. 4.6, there is normally no need to solve all MIP problems to optimality, and in this case the MIP solver may terminate with a feasible MIP solution satisfying also the nonlinear constraints. The maximum numbers of solutions stored in the solution pool in the MIP solvers is controlled with the option Dual.MIP.SolutionPool.Capacity.

The methods described above do not cost anything extra performance-wise for SHOT. However, some MIP solvers also provide the functionality to more actively search for additional solutions; this functionality is controlled by several solver specific options in SHOT. More actively searching for alternative solutions will, of course, require more effort by the MIP solver, which may have negative effects on the overall solution time for some problem instances.

Solving fixed NLP problems

When an integer solution has been found by, e.g., the MIP solver in SHOT, it is possible to fix the integer variables to their corresponding solution values and to solve the resulting NLP problem considering only the continuous variables. If a feasible solution to this problem is found, a new primal solution candidate has been obtained. It is possible to control the fixed NLP strategy, e.g., if and when fixed NLP problems should be solved and which NLP solver to use, using the options in the Primal.FixedInteger category. Note that if fixed NLP problems are solved after each MIP iteration, SHOT will behave similarly to an OA-type algorithm. As of SHOT version 1.0, IPOPT is available as NLP solver. However, if SHOT is integrated with GAMS, all licensed NLP solvers in GAMS can additionally be used.

After a NLP problem for a combination of the values of the integer variables in the problem has been solved, an integer cut can be added to filter out this combination from future MIP iterations, a so-called no-good cut. If all discrete variables are binary, such a cut can be added both in the single- and multi-tree strategies. However, if there are general integer variables in the problem, this would require adding additional variables [5], which is not possible without rebuilding the branch-and-bound tree. Therefore, integer cuts for problems with nonbinary discrete variables are not added in the single-tree strategy. Integer cuts have mostly been implemented to enhance SHOT’s nonconvex capabilities, but can optionally be activated for convex problems as well with the option Dual.HyperplaneCuts.UseIntegerCuts.

Utilizing information from root searches

As mentioned in Sect. 4.2, if the objective function of the MINLP problem is nonlinear, a root search on the added nonlinear objective constraint can be utilized to find an interior point. This point satisfies all linear constraints in the problem and is integer-feasible, and is thus, a good candidate for a primal solution. Generally, whenever a root search is performed in SHOT, a point on the interior of the integer-relaxed feasible set is obtained, and this point is tested to see if it may be a primal solution, i.e., if it satisfies all constraints in the original problem. Most often, these points do not satisfy the integer requirements for one or more variables, which naturally invalidates them. One possibility, still not implemented in SHOT, is to utilize some rounding and projection heuristics on these partial primal solutions.

Detailed description of the SHOT algorithm

The basic steps in the integrated primal/dual method implemented in SHOT is presented in this section as the SHOT algorithm. To make the step-wise explanation easier to follow, and to avoid repetition, some of the functionality, e.g., the main steps in the single- and multi-tree algorithms, is extracted into Sects. 6.2–6.4.

The main steps of the SHOT algorithm

Define the values for the following parameters:

${\epsilon _{\text {abs}}}$:

Absolute objective termination tolerance (Termination.ObjectiveGap.Absolute)

${\epsilon _{\text {rel}}}$:

Relative objective termination tolerance (Termination.ObjectiveGap.Relative)

$K_{\max }$:

Main iteration limit (Termination.IterationLimit)

$T_{\max }$:

Main time limit (Termination.TimeLimit)

${\epsilon _{\text {LP}}}$:

Integer-relaxation step tolerance limit (Dual.Relaxation.TerminationTolerance)

$K_{\max }^{\text {LP}}$:

Integer-relaxation iteration limit (Dual.Relaxation.IterationLimit)

${\epsilon _{\text {SL}}}$:

Solution limit update tolerance (Dual.MIP.SolutionLimit.UpdateTolerance)

${\text {SL}}$:

Initial solution limit (Dual.MIP.SolutionLimit.Initial)

${{\text {SL}}_{\max }}$:

Max iterations without solution limit update (Dual.MIP.SolutionLimit.IncreaseIterations).

Initialize best-known dual (${\text {DB}}= -\infty$) and primal (${\text {PB}}= +\infty$) bounds.

• 1. MIQP or MIQCQP strategy: If the MIP solver supports solving MIQP or MIQCQP problems, and the problem is of this type, solve the problem directly with the MIP solver and set MIPstatus to the value optimal, feasible, unbounded, timelimit or infeasible depending on the return status of the subsolver. Set ${\text {DB}}$ as the dual bound obtained from the MIP solver. If a solution ${{\mathbf {x}}}$ is found, set ${{{\mathbf {x}}}^*}= {{\mathbf {x}}}$, ${\text {PB}}= f({{{\mathbf {x}}}^*})$ and update ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$ according to Eq. (1). Then go to Step 8.

• 2. Bound tightening: Perform FBBT on the problem to reduce the variable bounds.

• 3. Reformulation step: Reformulate Prob. (P) by, e.g., partitioning quadratic or nonlinear sums of convex terms in the objective and nonlinear constraints into new auxiliary constraints as explained in Sect. 4.3. Call the new problem (RP).

• 4. Interior point step: If the ESH method is to be used for generating cuts, find an interior feasible point ${{{\mathbf {x}}}_{\text {int}}}$ to Prob. (RP) using the minimax strategy in App. A. If no interior point is found, use the ECP algorithm until a primal solution on the interior of the integer-relaxed feasible set has been found.

• 5. Initialize the MIP problem and solver:

  • (a) Create a MIP problem based on Prob. (RP) containing all variables and all constraints except for the nonlinear ones. If the objective is linear or quadratic (and the MIP solver supports quadratic objective functions), use it directly. Otherwise denote the nonlinear objective function with ${\tilde{f}} ({{\mathbf {x}}})$, introduce an auxiliary variable $\mu$, i.e., ${{\mathbf {x}}}:= ({{\mathbf {x}}}, \mu )$, and set the MIP objective to minimize this variable, i.e., $f({{\mathbf {x}}}) := \mu$.

  • (b) Add the valid cutting planes generated while solving the minimax problem in Step 4 to the dual problem.

  • (c) Set the time limit in the MIP solver to the time remaining of $T_{\max }$ and the MIP solver’s relative and absolute MIP gaps to ${\epsilon _{\text {rel}}}$ and ${\epsilon _{\text {abs}}}$.

• 6. Integer-relaxation step: Set the iteration counter $k:=0$ and relax the integer-variables in the MIP problem, i.e., we now have a LP, QP or QCQP problem. Repeat while $k < K_{\max }^{\text {LP}}$:

  • (a) Solve the relaxed problem to obtain the solution ${{\mathbf {x}}}_k$ and dual bound ${\text {DB}_{\text {MIP}}}$ from the subsolver. If no solution is obtained, set MIPstatus:=infeasible and go to Step 8.

  • (b) If $G({{\mathbf {x}}}_k) < {\epsilon _{\text {LP}}}$, terminate the integer-relaxation step and go to Step 7. If $G({{\mathbf {x}}}_k) \ge {\epsilon _{\text {LP}}}$ generate linearizations according to Sect. 6.4 and increase the counter $k:=k+1$.

• 7. Main iteration: Activate the integer constraints in the MIP problem and update the time limit in the MIP solver. Select one of the following:

  • (a) Single-tree strategy: Enable a callback in the MIP solver performing the steps in Sect. 6.2 whenever a new integer-feasible solution ${{\mathbf {x}}}_k$ is found. Solve the subproblem until the MIP solver terminates, e.g., when its relative or absolute gaps have been met or the time limit has been reached. Set MIPstatus to either optimal, feasible, timelimit or infeasible depending on the return status. Go to Step 8.

  • (b) Multi-tree strategy: Set the iteration counter $k:=0$. Denote with HPS a list of hyperplane linearizations not added. Repeat while $k<K_{\max }$:

    • i Solve the current MIP problem and set MIPstatus to the termination status of the MIP solver.

    • ii If MIPStatus is timelimit or iterlimit go to Step 8.

    • iii If MIPstatus is infeasible go to Step 8. Otherwise, denote the solution point with the best objective value in the solution pool as ${{\mathbf {x}}}_k$.

    • iv If MIPstatus is solutionlimit:

      • A Perform the steps in Sect. 6.3 to generate the hyperplane cuts and add them to the list HPS instead of the MIP problem.

      • B If the solution limit has not been updated in ${{\text {SL}}_{\max }}$ iterations or if $G({{\mathbf {x}}}_k) < {\epsilon _{\text {SL}}}$, increase the limit ${\text {SL}}:={\text {SL}}+1$. Otherwise, add all linearizations in the list HPS to the MIP model and empty the list.

    • v If MIPstatus is optimal, perform the steps in Sect. 6.3.

    • vi Set the time limit in the MIP solver to the time remaining of $T_{\max }$.

    • vii Increase the iteration counter $k:=k+1$.

• 8. Termination: Remove the variable solutions in the solution vector ${{{\mathbf {x}}}^*}$ corresponding to auxiliary variables originating from the reformulations, so that only the the solution in the original variables in Prob. (P) remain.

  • (a) If ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}< {\epsilon _{\text {abs}}}$ or ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}<{\epsilon _{\text {rel}}}$, terminate with the status optimal and the solution ${{{\mathbf {x}}}^*}$.

  • (b) If ${\text {PB}}< \infty$, i.e., a primal solution is found but the algorithm has been unable to verify optimality to the given tolerances, return with the status feasible and the solution ${{{\mathbf {x}}}^*}$.

  • (c) If MIPStatus is timelimit, iterlimit, unbounded or infeasible, return this status.

Steps performed by the MIP callback

The following steps are performed by the callback function whenever a new integer-feasible solution is found in the single-tree strategy.

Denote the MIP feasible solution found with ${{\mathbf {x}}}$, and the current dual bound provided by the MIP solver by ${\text {DB}_{\text {MIP}}}$.

• 1. Update dual bound: If ${\text {DB}_{\text {MIP}}}> {\text {DB}}$, set ${\text {DB}}:= {\text {DB}_{\text {MIP}}}$ and update ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$.

• 2. Update incumbent: If $G({{\mathbf {x}}}) \le 0$ and $f({{\mathbf {x}}}) < {\text {PB}}$, set ${\text {PB}}:= f({{\mathbf {x}}})$ and ${{{\mathbf {x}}}^*}:= {{\mathbf {x}}}$; update ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$.

• 3. Check termination criteria: If ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}< {\epsilon _{\text {abs}}}$ or ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}<{\epsilon _{\text {rel}}}$ exit the callback without excluding the current solution ${{\mathbf {x}}}$ with a lazy constraint since we already have found a solution to the provided tolerance.

• 4. Update interior point: If $G({{\mathbf {x}}}) < 0$ and the ESH method is used but no point ${{{\mathbf {x}}}_{\text {int}}}$ is yet available, set ${{{\mathbf {x}}}_{\text {int}}}:= {{\mathbf {x}}}$.

• 5. Generate linearizations: If $G({{\mathbf {x}}}) > 0$ generate one or more linearizations according to Sect. 6.4 and add these to the MIP model as lazy constraints.

• 6. Primal search: Perform one or more of the primal heuristics mentioned in Sect. 5 to reduce ${\text {PB}}$. If ${\text {PB}}$ is updated pass it on to the MIP solver as the new incumbent and recalculate ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$.

• 7. If the time limit has been reached, set MIPstatus to timelimit and go to Step 8 in the SHOT algorithm (Sect. 6.1).

• 8. Increase the iteration counter $k:=k+1$. If $k = K_{\max }$ set MIPstatus to iterlimit and go to Step 8 in the SHOT algorithm (Sect. 6.1).

Main iterative step in the multi-tree strategy

Denote the j-th integer feasible solution in the current MIP solution pool with ${{\mathbf {x}}}_j$, and the dual bound provided by the MIP solver with ${\text {DB}_{\text {MIP}}}$. It is assumed that the solutions in the MIP solution pool are ordered in ascending order depending on their objective value.

• 1. Update dual bound: If ${\text {DB}_{\text {MIP}}}> {\text {DB}}$, set ${\text {DB}}:= {\text {DB}_{\text {MIP}}}$; update ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$.

• 2. Repeat for each point in the solution pool:

  • (a) Update incumbent: If $G({{\mathbf {x}}}_j) \le 0$ and $f({{\mathbf {x}}}_j) < {\text {PB}}$, set ${\text {PB}}:= f({{\mathbf {x}}}_j)$ and ${{{\mathbf {x}}}^*}:= {{\mathbf {x}}}_j$; update ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$.

  • (b) Update interior point: If $G({{\mathbf {x}}}_j) < 0$ and the ESH method is used but no interior point is yet known, set ${{{\mathbf {x}}}_{\text {int}}}:={{\mathbf {x}}}_j$.

  • (c) Generate linearizations: If $G({{\mathbf {x}}}_j) > 0$ generate one or more linearizations according to Sect. 6.4. Add them to the list HPS if MIPstatus is solutionlimit, otherwise directly to the model in the MIP solver.

• 3. Primal search: Perform one or more of the primal heuristics mentioned in Sect. 5 to reduce ${\text {PB}}$. If ${\text {PB}}$ is updated, recalculate ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}$ and ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}$ and pass the new primal solution on to the MIP solver.

• 4. If ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}< {\epsilon _{\text {abs}}}$ or ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}<{\epsilon _{\text {rel}}}$ or if $k = K_{\max }$ set MIPstatus to optimal or iterlimit respectively, and go to Step 8 in the SHOT algorithm (Sect. 6.1). Otherwise increase the iteration counter $k=k+1$.

Steps for generating cuts for nonlinearities

Assume that a point ${{{\mathbf {x}}}_{\text {ext}}}$ is given that lies on the exterior of the integer-relaxed feasible region of Prob. (RP).

• 1. If there are nonlinear constraints, the ESH dual strategy is used, and an interior point ${{{\mathbf {x}}}_{\text {int}}}$ is known:

  • (a) Perform a root search on the line between ${{{\mathbf {x}}}_{\text {int}}}$ and ${{{\mathbf {x}}}_{\text {ext}}}$ with respect to the max function $G({{\mathbf {x}}})$ as described in Sect. 2.2.1 using the functionality described in Sect. 3.5.3. This gives an interval $[{\underline{t}},{\overline{t}}] \subset {\mathbf {R}},$ so that for $\tilde{t} \in [{\underline{t}},{\overline{t}}]$, $G({{\mathbf {p}}}(\tilde{t})) = 0$, and thus, ${{\mathbf {p}}}({\underline{t}})$ and ${{\mathbf {p}}}({\overline{t}})$ are on the exterior and interior of the integer-relaxed feasible set $G({{\mathbf {x}}}) \le 0$ respectively. It is also possible to perform root searches with respect to the individual constraints with $g_j({{{\mathbf {x}}}_{\text {ext}}}) > 0$ instead of the max function G. In this case several points ${{\mathbf {p}}}_j({\underline{t}})$ are obtained. The interior points found, i.e., ${{\mathbf {p}}}({\overline{t}})$ or ${{\mathbf {p}}}_j({\overline{t}})$ can be used as the starting point in a primal heuristic.

  • (b) Generate a supporting hyperplane in ${{\mathbf {p}}}({\underline{t}})$ for the constraint function $g_j$ with $j={{\,\mathrm{argmax}\,}}_j g_j({{\mathbf {p}}}({\underline{t}}))$, i.e., the function with the largest value evaluated in this point:

    $$\begin{aligned} g_j({{\mathbf {p}}}({\underline{t}})) + \nabla g_j\left( {{\mathbf {p}}}({\underline{t}})\right) ^T ({{\mathbf {x}}}-{{\mathbf {p}}}({\underline{t}})) \le 0, \end{aligned}$$

    or if individual root searches were performed for all constraints $g_j({{\mathbf {p}}}_j({\underline{t}})) > 0$:

    $$\begin{aligned} g_j({{\mathbf {p}}}_j({\underline{t}})) + \nabla g_j\left( {{\mathbf {p}}}_j({\underline{t}})\right) ^T ({{\mathbf {x}}}-{{\mathbf {p}}}_j({\underline{t}})) \le 0. \end{aligned}$$

• 2. If there are nonlinear constraints and the ECP dual strategy is used (or the ESH dual strategy is used, but no interior point is known): Generate cutting planes in ${{{\mathbf {x}}}_{\text {ext}}}$ for one or more of the violated constraints $g_j$, e.g., at least for $j= {{\,\mathrm{argmax}\,}}_j g_j({{{\mathbf {x}}}_{\text {ext}}})$:

  $$\begin{aligned} g_j({{{\mathbf {x}}}_{\text {ext}}}) + \nabla g_j\left( {{{\mathbf {x}}}_{\text {ext}}}\right) ^T ({{\mathbf {x}}}-{{{\mathbf {x}}}_{\text {ext}}}) \le 0. \end{aligned}$$

• 3. If the objective function is considered as generally nonlinear: A root search is performed on the line segment connecting the points ${{{\mathbf {x}}}_{\text {ext}}}$ and ${{{\mathbf {x}}}'_{\text {ext}}}$ with respect to the auxiliary objective expression ${\tilde{f}} ({{{\mathbf {x}}}}) - \mu = 0$ using the functionality described in Sect. 3.5.3. Here ${{{\mathbf {x}}}'_{\text {ext}}}$ is a vector that satisfies the objective constraint ${\tilde{f}} ({{{\mathbf {x}}}}) - \mu < 0$, e.g., 

  $$\begin{aligned} \big (\underbrace{x_1,\ \ x_2, \ldots ,\ \ x_n}_{{{\mathbf {x}}}},\ \ \underbrace{{\tilde{f}} ({{{\mathbf {x}}}_{\text {ext}}}) + \epsilon }_{\mu }\big ),\quad \epsilon > 0. \end{aligned}$$

  Through the root search both an exterior point ${{\mathbf {p}}}({\underline{t}})$ and an interior point ${{\mathbf {p}}}({\overline{t}})$ are obtained. The interior point is a candidate for a new primal solution, and a supporting hyperplane for the nonlinear objective function is generated in the point ${{\mathbf {p}}}({\underline{t}})$:

  $$\begin{aligned} {\tilde{f}} ({{\mathbf {p}}}({\underline{t}})) + \nabla {\tilde{f}} \left( {{\mathbf {p}}}({\underline{t}})\right) ^T ({{\mathbf {x}}}-{{\mathbf {p}}}({\underline{t}})) \le 0. \end{aligned}$$

  This is illustrated in Fig. 1 for a objective function of one variable. Note that, if the multi-tree strategy is used and the MIP solver has flagged the current solution ${{{\mathbf {x}}}_{\text {ext}}}$ as optimal, ${{{\mathbf {x}}}'_{\text {ext}}}$ will no longer be optimal if the value for the variable $\mu$ has been updated in the solution, since there is no guarantee (and most often is not the case) that the updated solution point is the optimal one for the current MIP problem.

Fig. 1

Illustration of the procedure to perform a root search on the objective function as described in Sect. 6.4. The original objective function in the MINLP problem (P) is $\tilde{f}(x)$, where x is a scalar variable, and the variable vector is thus ${{\mathbf {x}}}=(x,\mu )$. The thick boundary of the shaded region is where $\tilde{f}(x)-\mu =0$, i.e., the exact values of the original nonlinear objective function. The linearization $l_1$ of the objective function is the result of a previously generated objective linearization. In the figure to the right, the objective function linearization $l_2$, generated in the point ${{\mathbf {p}}}({\underline{t}})$, is illustrated. Note that, for the purpose of illustration, the interval between the two interval endpoints obtained through the root search is quite large, and therefore, the linearization in the figure is not an exact supporting hyperplane

Numerical comparisons

In this section, SHOT is compared to some state-of-the-art MINLP solvers to illustrate its performance. There are both free versions and commercial solvers included, and although SHOT is open-source and can be used freely by all, some of the subsolvers have different licenses. Therefore, a fully noncommercial version of SHOT with Cbc and IPOPT is also included in the comparison, as is a version with CPLEX and CONOPT. It should be noted though, that the MIP solvers CPLEX and Gurobi both have fully working academic versions that can be directly used in SHOT. To analyze a few of the different strategy choices in SHOT, some internal benchmarks are also presented. The benchmark set is all the 406 convex problems in MINLPLib [55] having at least one binary or integer variable; the problems are listed in App. B. The performance of the solvers was analyzed using PAVER 2.0 [11], and the generated PAVER reports are available at www.andreaslundell.github.io/minlpbenchmarks.

All comparisons were performed on a computer with an Intel Xeon 3.6 GHz processor with four physical cores (with the possibility to process eight threads) and 32 GB memory. The MIP solvers utilized in SHOT 1.0 was CPLEX 12.10, Gurobi 9.0 and Cbc 2.10. The NLP subsolver selected in SHOT was CONOPT 3.17L and IPOPT 3.13.2 (with MUMPS linear solver) for the commercial version and noncommercial version respectively. The termination criteria used was ${{{\,\mathrm{GAP}\,}}_{\text {rel}}}= 0.1\%$, ${{{\,\mathrm{GAP}\,}}_{\text {abs}}}= 0$ and a time limit of 900 seconds.

Comparisons to other MINLP solvers

In [37], it was shown that a prerelease version of the SHOT solver (0.9.3) was very competitive when comparing to other convex MINLP solvers. The functionality of SHOT has been significantly extended since the publication of that paper, e.g., the entire problem handling has been rewritten, and the automated reformulations, bound tightening and convexity identification steps are new. Therefore, a new comparison is conducted in this paper. The solvers included in the comparison are the GAMS solvers AlphaECP (2.10.06), BARON (20.4.14), BONMIN (1.8), DICOPT (2), SBB (31.1.0) and SCIP (7.0). The AIMMS solver AOA (4.72.3.2) was also considered. For the solvers with multiple main strategies we selected one: in BONMIN the outer-approximation strategy, and for AOA the LP/NLP-based branch-and-bound strategy; the reason being that these strategies performed best in the benchmark provided in [37]. SCIP, which is technically open-source and free for noncommercial use, does have a more restrictive license than both BONMIN and SHOT, and cannot be used for commercial purposes without additional licensing. However for the sake of this comparison we classified SCIP as a noncommercial solver. Note that for academic use, SHOT can also be used freely with CPLEX and Gurobi as MIP solvers. The commercial GAMS solvers utilized CPLEX 12.10 and CONOPT 3.17L as subsolvers, while BONMIN used Cbc 2.10 and IPOPT 3.13.2 (with the MUMPS linear solver). The AOA solver is implemented in AIMMS 4.72.3 and utilized CPLEX 12.10 and CONOPT 3.14V. If the solvers had a convex strategy, or recommended parameters for convex problems, these were used; in addition, some parameters were modified to prevent the solvers to terminate prematurely. The modified parameters are listed in App. C.

Fig. 2

Solution profiles indicating the number of solved problem instances in the solver benchmark in Sect. 7.1 with a relative objective gap $\le 0.1\%$. In the plots, the area between the virtual worst and virtual best solvers in each group is shaded. Also, to make it easier to compare the two plots, thin gray lines representing the performance of the solver in the other category (noncommercial/commercial) are shown

Fig. 3

Solution profiles indicating the number of solved problem instances in the solver benchmark in Sect. 7.1 with a primal gap, i.e., the relative difference to the optimal solution in MINLPLib, $\le 0.1\%$. The dashed line indicates the number of problems with a solution classified as optimal (318). In the plots, the area between the virtual worst and virtual best solvers in each group is shaded. Also, to make it easier to compare the two plots, thin gray lines representing the performance of the solver in the other category (noncommercial/commercial) are shown

Table 1 Some statistics from the comparison described in Sect. 7.1

The comparisons are shown as a solution profile in Fig. 2 when considering the number of instances solved to a relative objective gap of $0.1\%$, and Fig. 3 when considering the number of instances where he found primal solution is less than $0.1\%$ from the solution classified as optimal in MINLPLib; note that the solution to only 318 of the 406 problems in this benchmark set are flagged as optimal in MINLPLib. Additionally, some statistics are provided in Table 1. Two versions of SHOT is included, one with commercial subsolvers (CPLEX and CONOPT) and one with open-source subsolvers (Cbc and IPOPT). This provides not only a comparison of how the choice of subsolvers affect SHOT’s performance, but also what performance can be expected of a state-of-the-art open-source solver today.

Commercial solvers

Of the commercial solvers, It is clear that SHOT (with CPLEX and CONOPT) is very competitive on the whole test set, as is AOA and BARON. AOA is an implementation in AIMMS of an LP/NLP based branch-and-bound strategy. Both SHOT and AOA thus utilize a single-tree strategy with tight MIP solver integration through lazy constraint callbacks, and this clearly illustrates the benefits of such an implementation.

BARON is a global solver, and can therefore solve problems of the more general nonconvex MINLP class. However, as the results show, it is also a very good convex MINLP solver. The convex setting for AlphaECP is used here but although the basic methods are similar (dual bounds by ECP and ESH, respectively, together with primal heuristics based on solving integer-fixed NLP problems), the performance of AlphaECP is not on par with SHOT in this comparison. Some of the reasons include that AlphaECP does not currently support solving MIQP subproblems, nor does it have automated reformulations, bound tightening, etc.

Noncommercial solvers

Of the open-source solvers SHOT and BONMIN, both with Cbc and IPOPT as subsolvers, it can clearly be seen that SHOT is more efficient. In fact, the noncommercial version of SHOT is overall more efficient than some commercial alternatives. This clearly shows that it is possible to implement an efficient, completely free solver for convex MINLP. SCIP is a global solver, but in this comparison its convex strategy has been used since we know all problems are convex. It is obvious that SCIP is much faster than both BONMIN and the noncommercial version of SHOT. Also, note that the performance profile is for the entire test set, so with parameter tuning, it is possible to reduce the solution times for specific problems. Recently, there has been significant development on Cbc as well, and it can be expected that the performance and stability of SHOT with Cbc will increase in future versions. Another option, not yet investigated, is how a single-tree version implementation of SHOT with Cbc would work. While the choice between single- or multi-tree strategies does not seem to impact the overall performance of SHOT as much when using CPLEX, cf., Sect. 7.2.4, it can be assumed that the single-tree strategy will be relatively more efficient than the multi-tree strategy in the case of Cbc, since the interface between SHOT and Cbc is such that it does not reuse as much information between MIP iterations as SHOT’s multi-tree interface to CPLEX and Gurobi.

Benchmarks of a selection of functionality in SHOT

As SHOT heavily depends on the underlying MIP solver, changing it, or its behavior significantly affects the performance of SHOT. In this section, some of the MIP related features are benchmarked. Also, the impact of the automated reformulations is examined. In these comparisons, if nothing is specified, CPLEX and CONOPT are used as MIP and NLP solver respectively.

Fig. 4

Comparison of using SHOT with different MIP subsolvers

Performance of different MIP subsolvers

SHOT can currently be used with Cbc, CPLEX or Gurobi as MIP subsolver, and in Fig. 4 their solution profiles are compared. This comparison tries to catch the best performance that can be obtained with the commercial and free alternatives, so CPLEX and Gurobi uses the single-tree strategy and CONOPT as NLP solver, while Cbc uses the multi-tree strategy and IPOPT (with MUMPS as its linear solver).

As can be expected, the two commercial solvers CPLEX and Gurobi have the best performance, and the difference between them is quite small on the entire benchmark set. For a specific problem, however, the differences can be significant. These differences are probably due to default parameter choices done in the MIP solver, e.g., how well an automatic setting for a parameter can adapt to different characteristics of a problem. Note that the results in this paper should not be seen as a comparison of the performances of CPLEX and Gurobi, rather how well they work integrated in SHOT.

Cbc trails the commercial solvers, but still manages to solve many of the problems within the 900 s time limit. A reason for the reduced performance for Cbc is that quadratic objective functions and constraints are currently not supported.

Fig. 5

The impact of solving MIQP or MIQCQP subproblems instead of MILP subproblems in SHOT as described in Sect. 4.7. CPLEX was used as MIP solver

Utilizing quadratic functions in MIP subsolvers

Out of the 406 convex MINLP instances currently in MINLPLib, there are 67 pure MIQP problems (a quadratic objective function and no other nonlinearities). As stated in Sect. 4.7, such problems can be directly solved by CPLEX and Gurobi. This is normally much more efficient than utilizing iterative linearizations of the objective function to approximate its nonlinearity since a quadratic objective can now be expressed exactly. There are also instances with a quadratic objective function and quadratic constraints in addition to general nonlinear constraints. In this case, it is possible to handle the nonlinear constraints with the ESH or ECP methods, while passing the quadratic objective function and/or constraints on to the MIP solver. Thus, MIQP or MIQCQP subproblems are solved instead of MILP subproblems. In Fig. 5, the impact of utilizing a MIQCQP subsolver with the multi-tree strategy has been illustrated. CPLEX was used in this comparison, but the results are similar with Gurobi as well. Also, using the single-tree strategy does not normally affect the performance significantly when considering all the 67 problems, but for individual problems the solution times may of course vary. As can be seen from the figure, the impact of utilizing a MIQCQP subsolver is quite significant, and it is clear that a dedicated MI(QC)QP solver performs better for these kind of problems than SHOT with its POA strategy.

Fig. 6

The impact of multi-threading on CPLEX with the single-tree strategy. It is clear that utilizing more than one thread is beneficial for more difficult problems

Impact of multi-threading in the MIP solver

In Fig. 6, the impact of utilizing several threads in CPLEX is shown. The number of threads are set at one, four and seven (the maximum number supported simultaneously by the CPU minus one). As can be expected, using more than one thread has a significant influence on the solution time required to solve certain problem instances. For example, it takes about 74 seconds to solve 350 problems with only one thread, while it takes only about 14 s and 10 s of that time to solve the same number with four and seven threads respectively. It is however well-known that the performance does not normally grow linearly with the number of used MIP solver threads and the difference between the overall performance when using four and seven threads is with regards to this benchmark negligible. However, for a newer CPU with more cores than the one used in this comparison, the differences may be more significant.

Fig. 7

A comparison of the performance of the single and multi-tree strategies in SHOT when using CPLEX as MIP solver

Impact of MIP solution strategies on SHOT

In Fig. 7, the multi-tree and single-tree strategies in SHOT are compared using CPLEX as the MIP solver. The multi-tree strategy performs somewhat better when considering how many instances were solved to an objective gap below $0.1\%$. For simpler problems however, the single-tree strategy is significantly more efficient. A reason that the single-tree strategy is less efficient for more difficult problems is because utilizing MIP solver callbacks in CPLEX disables functionality such as dynamic search, which might have more effect on solving more difficult problems. Therefore, if the problem is expected to be difficult, the multi-tree strategy might be the best choice.

The results support the assumption that a multi-tree strategy can also be very competitive if implemented efficiently. A multi-tree implementation like the one in SHOT communicates information to the MIP solver, including the current primal solution point, as well as a cut-off value from this solution point’s objective value for pruning the branching tree. The cut-off value is also provided as a cut-off constraint if the objective function is linear, but this is mostly used in SHOT’s nonconvex strategy. Also the technique to only solve some subproblems to feasibility (cf., Sect. 4.6) and utilizing the solution pool to add multiple linearizations per iteration (cf., Sect. 4.5) impact the performance of the multi-tree implementation. Another important aspect why the multi-tree strategy is so efficient is the usage of the MIP presolver in each iteration in the subsolver: Due to the fact that many of the MIP subproblems are not solved to optimality when utilizing the MIP solution limit strategy, often no branching is needed, and the subproblems are solved during the presolving phase.

Fig. 8

The impact of not utilizing the solution limit strategy described in Sect. 4.6 and the MIP solution pool described in Sect. 4.5

In Fig. 8, the impact of disabling these strategies are illustrated. To make the differences clearer, the functionality to solve quadratic subproblems (MIQP or MIQCQP) were disabled, i.e., all subproblems are now linear. Differences are noticeable, e.g., disabling both the solution pool functionality and solving the problems to optimality changes the time for solving 350 instances from about 43 s to 253 s. However for simple problems, the results indicate that it is beneficial to solve the subproblems to optimality, which can be expected as fewer but better linearizations are created.

Impact of automated reformulations

To test the impact of the automated convexity-preserving reformulations described in Sect. 4.3, these are now disabled. Also here the quadratic functionality of the MIP subsolver is disabled, i.e., only LP and MILP subproblems are solved. The solution profile compared to standard strategy is shown in Fig. 9, and the difference is significant. This can clearly be seen as an indication that the reformulations are beneficial for a POA-based MINLP solver.

Fig. 9

The impact of disabling the automatic reformulations in SHOT. Note that solving quadratic subproblems in SHOT has been disabled

Conclusions and future work

In this paper, the SHOT solver was described in detail and its performance was thoroughly benchmarked. The internal numerical benchmarks of the solver-specific functionality indicate that the performance of SHOT is not due to a single feature, but a combination of many different strategies that together result in a well-performing solver. Thus, it can be summarized that SHOT builds on and extends 30 years worth of research on POA methods for MINLP. One of the main features of POA-based solvers is that they rely heavily on the subsolvers utilized, and this is especially true for the single-tree strategy in SHOT. Although the numerical comparison between the single- and multi-tree strategies did not result in a clear winner, it should be mentioned, that a large part of the convex problems in MINLPLib are very easy to solve with both strategies as long as an efficient MIP solver is utilized. For the multi-tree implementation, there is not much more possibilities for further enhancing the performance by tighter integration with the MIP solver. However, for the single-tree implementation, there are still many aspects to consider including generating hyperplane cuts also in relaxed solution points, and to only add cuts locally in the search tree.

For SHOT, the next major development steps are to implement more primal heuristics and to include more automated convexity preserving reformulations. These improvements are meant to enhance the performance especially for more demanding problems. Although SHOT 1.0 has some basic, mainly heuristic, nonconvex capabilities, we plan to add more functionality, based on lifting reformulations, for nonconvex MINLP in the feature. In addition to being important in itself, convex MINLP can also then be used as a tool for solving nonconvex problems by reformulating such problems into convex MINLP problems [50, 51, 59, 60]. In certain aspects, this mimics how MIP problems can be used in POA to solve convex MINLP problems. Of course, this is much more difficult in practice due to the fact that several convex MINLP problems are solved in sequence to find the optimal solution to a nonconvex MINLP problems. Also, the reformulated problems grow not only in the number of additional linear constraints as in POA, but also in the number of auxiliary variables needed for the reformulations. However, since a tight integration of these reformulations with SHOT is possible, we assume this will be an efficient way to solve certain classes of nonconvex MINLP problems.

Appendices

Appendix A: A cutting plane-based algorithm for locating an interior point

To find the interior point to use as end point in the root searches in the ESH algorithm implemented in SHOT, cf., Sect. 4.4, the minimax problem Prob. (MM) is considered. An optimal or feasible interior point can be obtained with the tailor-made minimax solver described below:

Specify a maximum number of iterations and a relative (${\epsilon _{\text {rel}}^{\text {MM}}}$) and absolute (${\epsilon _{\text {abs}}^{\text {MM}}}$) termination tolerance for the objective function. Set ${{{\,\mathrm{GAP}\,}}_{\text {rel}}^{\text {MM}}}:= \infty$ and ${{{\,\mathrm{GAP}\,}}_{\text {abs}}^{\text {MM}}}:= \infty$, and determine a maximal number of iterations $K_{\max }^{\text {MM}}\ge 2$. Set the iteration index $k:=1$.

• 1. Reformulate the original MINLP problem, Prob. (P), into a minimax problem of the type in Prob. (MM). Denote the function $G({{\mathbf {x}}}) = \max _j g_j({{\mathbf {x}}})$, i.e., the maximum error of all nonlinear constraints functions in the original problem.

• 2. Create a copy of the minimax problem without the nonlinear constraints, i.e., an LP problem.

• 3. Solve the LP problem. If the subproblem can not be solved to optimality, set the flag MinimaxStatus to failure and go to Step 5; otherwise obtain the solution $({{\mathbf {x}}}_1, \nu _1)$, and denote ${{\text {OBJ}}_{\text {LP}}}= \nu _1$.

• 4. Repeat while $k < K_{\max }^{\text {MM}}$.

  • (a) Increase the iteration counter, i.e., set $k:=k+1$.

  • (b) Solve the LP problem. If the subproblem could not be solved to optimality, set MinimaxStatus to failure and go to Step 5; otherwise, obtain the solution $({{\mathbf {x}}}_k, \nu _k)$ and set ${{\text {OBJ}}_{\text {LP}}}= \nu _k$.

  • (c) Solve the following one-dimensional minimization problem:

    $$\begin{aligned} \lambda _k = {{\,\mathrm{argmin}\,}}_{\lambda \in [0,1]} G\left( \lambda {{\mathbf {x}}}_k + (1-\lambda ){{\mathbf {x}}}_{k-1}\right) \end{aligned}$$

    and calculate the solution point as ${{{\mathbf {x}}}_{\text {LS}}}= \lambda _k {{\mathbf {x}}}_k + (1-\lambda _k){{\mathbf {x}}}_{k-1}$. Calculate ${{\text {OBJ}}_{\text {LS}}}= G({{{\mathbf {x}}}_{\text {LS}}})$.

  • (d) Calculate the absolute and relative difference in objective values between the LP and line search:

    $$\begin{aligned} {{{\,\mathrm{GAP}\,}}_{\text {abs}}^{\text {MM}}}= |{{\text {OBJ}}_{\text {LP}}}-{{\text {OBJ}}_{\text {LS}}}|, \qquad \text {and} \qquad {{{\,\mathrm{GAP}\,}}_{\text {rel}}^{\text {MM}}}= \frac{|{{\text {OBJ}}_{\text {LP}}}-{{\text {OBJ}}_{\text {LS}}}|}{|{{\text {OBJ}}_{\text {LP}}}| + 10^{-10}}. \end{aligned}$$

    If ${{\text {OBJ}}_{\text {LP}}}< 0$, and ${{{\,\mathrm{GAP}\,}}_{\text {rel}}^{\text {MM}}}< {\epsilon _{\text {rel}}^{\text {MM}}}$ or ${{{\,\mathrm{GAP}\,}}_{\text {abs}}^{\text {MM}}}< {\epsilon _{\text {abs}}^{\text {MM}}}$, set MinimaxStatus to success and go to Step 5.

  • (e) Select the constraint function with the largest error in the point ${{{\mathbf {x}}}_{\text {LS}}}$, i.e., find

    $$\begin{aligned} j' = {{\,\mathrm{argmax}\,}}_{j} g_j({{{\mathbf {x}}}_{\text {LS}}}) \end{aligned}$$

    and add the following cutting plane to the LP problem

    $$\begin{aligned} g_{j'}({{{\mathbf {x}}}_{\text {LS}}}) + \nabla g_{j'}\left( {{{\mathbf {x}}}_{\text {LS}}})\right) ^T ({{\mathbf {x}}}-{{{\mathbf {x}}}_{\text {LS}}}) \le 0. \end{aligned}$$

    Note that it is also possible to generate cutting planes for more than one of the violated constraints.

• 5. Termination: If MinimaxStatus is success, return with the status success and the interior point ${{{\mathbf {x}}}_{\text {LS}}}$, otherwise with status failure.

Appendix B: Included problems in the benchmark

The following 406 problems were used in the benchmark in Sect. 7. They are the instances that are identified as convex in MINLPLib, with at least one nonlinearity (in the objective function or constraints), and at least one discrete (binary or integer) variable. Of these, the 67 problems marked with an $^*$ have only a quadratic objective function and no further nonlinearities in the constraints, i.e., they are MIQP problems.

alan$^*$, ball_mk2_10, ball_mk2_30, ball_mk3_10, ball_mk3_20, ball_mk3_30, ball_mk4_05, ball_mk4_10, ball_mk4_15, batch, batch0812, batchdes, batchs101006m, batchs121208m, batchs151208m, batchs201210m, clay0203h, clay0203hfsg, clay0203m, clay0204h, clay0204hfsg, clay0204m, clay0205h, clay0205hfsg, clay0205m, clay0303h, clay0303hfsg, clay0303m, clay0304h, clay0304hfsg, clay0304m, clay0305h, clay0305hfsg, clay0305m, color_lab2_4x0$^*$, color_lab6b_4x20$^*$, cvxnonsep_normcon20, cvxnonsep_normcon20r, cvxnonsep_normcon30, cvxnonsep_normcon30r, cvxnonsep_normcon40, cvxnonsep_normcon40r, cvxnonsep_nsig20, cvxnonsep_nsig20r, cvxnonsep_nsig30, cvxnonsep_nsig30r, cvxnonsep_nsig40, cvxnonsep_nsig40r, cvxnonsep_pcon20, cvxnonsep_pcon20r, cvxnonsep_pcon30, cvxnonsep_pcon30r, cvxnonsep_pcon40, cvxnonsep_pcon40r, cvxnonsep_psig20, cvxnonsep_psig20r, cvxnonsep_psig30, cvxnonsep_psig30r, cvxnonsep_psig40, cvxnonsep_psig40r, du-opt$^*$, du-opt5$^*$, enpro48pb, enpro56pb, ex1223, ex1223a$^*$, ex1223b, ex4$^*$, fac1, fac2, fac3$^*$, flay02h, flay02m, flay03h, flay03m, flay04h, flay04m, flay05h, flay05m, flay06h, flay06m, fo7, fo7_2, fo7_ar25_1, fo7_ar2_1, fo7_ar3_1, fo7_ar4_1, fo7_ar5_1, fo8, fo8_ar25_1, fo8_ar2_1, fo8_ar3_1, fo8_ar4_1, fo8_ar5_1, fo9, fo9_ar25_1, fo9_ar2_1, fo9_ar3_1, fo9_ar4_1, fo9_ar5_1, gams01, gbd$^*$, hybriddynamic_fixed$^*$, ibs2, jit1, m3, m6, m7, m7_ar25_1, m7_ar2_1, m7_ar3_1, m7_ar4_1, m7_ar5_1, meanvar-orl400_05_e_8$^*$, meanvarx$^*$, meanvarxsc$^*$, netmod_dol1$^*$, netmod_dol2$^*$, netmod_kar1$^*$, netmod_kar2$^*$, no7_ar25_1, no7_ar2_1, no7_ar3_1, no7_ar4_1, no7_ar5_1, nvs03, nvs10, nvs11, nvs12, nvs15$^*$, o7, o7_2, o7_ar25_1, o7_ar2_1, o7_ar3_1, o7_ar4_1, o7_ar5_1, o8_ar4_1, o9_ar4_1, pedigree_ex1058, pedigree_ex485, pedigree_ex485_2, pedigree_sim2000, pedigree_sim400, pedigree_sp_top4_250, pedigree_sp_top4_300, pedigree_sp_top4_350tr, pedigree_sp_top5_200, pedigree_sp_top5_250, portfol_buyin, portfol_card, portfol_classical050_1, portfol_classical200_2, portfol_roundlot, procurement2mot, ravempb, risk2bpb, rsyn0805h, rsyn0805hfsg, rsyn0805m, rsyn0805m02h, rsyn0805m02hfsg, rsyn0805m02m, rsyn0805m03h, rsyn0805m03hfsg, rsyn0805m03m, rsyn0805m04h, rsyn0805m04hfsg, rsyn0805m04m, rsyn0810h, rsyn0810hfsg, rsyn0810m, rsyn0810m02h, rsyn0810m02hfsg, rsyn0810m02m, rsyn0810m03h, rsyn0810m03hfsg, rsyn0810m03m, rsyn0810m04h, rsyn0810m04hfsg, rsyn0810m04m, rsyn0815h, rsyn0815hfsg, rsyn0815m, rsyn0815m02h, rsyn0815m02hfsg, rsyn0815m02m, rsyn0815m03h, rsyn0815m03hfsg, rsyn0815m03m, rsyn0815m04h, rsyn0815m04hfsg, rsyn0815m04m, rsyn0820h, rsyn0820hfsg, rsyn0820m, rsyn0820m02h, rsyn0820m02hfsg, rsyn0820m02m, rsyn0820m03h, rsyn0820m03hfsg, rsyn0820m03m, rsyn0820m04h, rsyn0820m04hfsg, rsyn0820m04m, rsyn0830h, rsyn0830hfsg, rsyn0830m, rsyn0830m02h, rsyn0830m02hfsg, rsyn0830m02m, rsyn0830m03h, rsyn0830m03hfsg, rsyn0830m03m, rsyn0830m04h, rsyn0830m04hfsg, rsyn0830m04m, rsyn0840h, rsyn0840hfsg, rsyn0840m, rsyn0840m02h, rsyn0840m02hfsg, rsyn0840m02m, rsyn0840m03h, rsyn0840m03hfsg, rsyn0840m03m, rsyn0840m04h, rsyn0840m04hfsg, rsyn0840m04m, slay04h$^*$, slay04m$^*$, slay05h$^*$, slay05m$^*$, slay06h$^*$, slay06m$^*$, slay07h$^*$, slay07m$^*$, slay08h$^*$, slay08m$^*$, slay09h$^*$, slay09m$^*$, slay10h$^*$, slay10m$^*$, smallinvDAXr1b010-011, smallinvDAXr1b020-022, smallinvDAXr1b050-055, smallinvDAXr1b100-110, smallinvDAXr1b150-165, smallinvDAXr1b200-220, smallinvDAXr2b010-011, smallinvDAXr2b020-022, smallinvDAXr2b050-055, smallinvDAXr2b100-110, smallinvDAXr2b150-165, smallinvDAXr2b200-220, smallinvDAXr3b010-011, smallinvDAXr3b020-022, smallinvDAXr3b050-055, smallinvDAXr3b100-110, smallinvDAXr3b150-165, smallinvDAXr3b200-220, smallinvDAXr4b010-011, smallinvDAXr4b020-022, smallinvDAXr4b050-055, smallinvDAXr4b100-110, smallinvDAXr4b150-165, smallinvDAXr4b200-220, smallinvDAXr5b010-011, smallinvDAXr5b020-022, smallinvDAXr5b050-055, smallinvDAXr5b100-110, smallinvDAXr5b150-165, smallinvDAXr5b200-220, squfl010-025$^*$, squfl010-040$^*$, squfl010-080$^*$, squfl015-060$^*$, squfl015-080$^*$, squfl020-040$^*$, squfl020-050$^*$, squfl020-150$^*$, squfl025-025$^*$, squfl025-030$^*$, squfl025-040$^*$, squfl030-100$^*$, squfl030-150$^*$, squfl040-080$^*$, sssd08-04, sssd12-05, sssd15-04, sssd15-06, sssd15-08, sssd16-07, sssd18-06, sssd18-08, sssd20-04, sssd20-08, sssd22-08, sssd25-04, sssd25-08, st_e14, st_miqp1$^*$, st_miqp2$^*$, st_miqp3$^*$, st_miqp4$^*$, st_miqp5$^*$, st_test1$^*$, st_test2$^*$, st_test3$^*$, st_test4$^*$, st_test5$^*$, st_test6$^*$, st_test8$^*$, st_testgr1$^*$, st_testgr3$^*$, st_testph4$^*$, stockcycle, syn05h, syn05hfsg, syn05m, syn05m02h, syn05m02hfsg, syn05m02m, syn05m03h, syn05m03hfsg, syn05m03m, syn05m04h, syn05m04hfsg, syn05m04m, syn10h, syn10hfsg, syn10m, syn10m02h, syn10m02hfsg, syn10m02m, syn10m03h, syn10m03hfsg, syn10m03m, syn10m04h, syn10m04hfsg, syn10m04m, syn15h, syn15hfsg, syn15m, syn15m02h, syn15m02hfsg, syn15m02m, syn15m03h, syn15m03hfsg, syn15m03m, syn15m04h, syn15m04hfsg, syn15m04m, syn20h, syn20hfsg, syn20m, syn20m02h, syn20m02hfsg, syn20m02m, syn20m03h, syn20m03hfsg, syn20m03m, syn20m04h, syn20m04hfsg, syn20m04m, syn30h, syn30hfsg, syn30m, syn30m02h, syn30m02hfsg, syn30m02m, syn30m03h, syn30m03hfsg, syn30m03m, syn30m04h, syn30m04hfsg, syn30m04m, syn40h, syn40hfsg, syn40m, syn40m02h, syn40m02hfsg, syn40m02m, syn40m03h, syn40m03hfsg, syn40m03m, syn40m04h, syn40m04hfsg, syn40m04m, synthes1, synthes2, synthes3, tls12, tls2, tls4, tls5, tls6, tls7, unitcommit1$^*$, unitcommit_200_100_1_mod_8$^*$, unitcommit_200_100_2_mod_8$^*$, unitcommit_50_20_2_mod_8$^*$, watercontamination0202$^*$, watercontamination0202r$^*$, watercontamination0303$^*$, watercontamination0303r$^*$

Appendix C: Used solver options in the benchmark

In the comparison in Sect. 7.1, the goal was to use the default solver options as much as possible. However, several of the solvers have certain default parameter values that makes them terminate prematurely, and these were then increased to avoid this behavior. Also convex strategies are activated for solvers supporting this, and if the solver has recommended parameters for convex problems, these were used. The used parameters listed in Table 2 are more or less the same as in [37], and are explained further there.

Table 2 The used parameters for the solvers in the benchmark