Global optimization for the multilevel European gas market system with nonlinear flow models on trees

Abstract

The European gas market is implemented as an entry-exit system, which aims to decouple transport and trading of gas. It has been modeled in the literature as a multilevel problem, which contains a nonlinear flow model of gas physics. Besides the multilevel structure and the nonlinear flow model, the computation of so-called technical capacities is another major challenge. These lead to nonlinear adjustable robust constraints that are computationally intractable in general. We provide techniques to equivalently reformulate these nonlinear adjustable constraints as finitely many convex constraints including integer variables in the case that the underlying network is tree-shaped. We further derive additional combinatorial constraints that significantly speed up the solution process. Using our results, we can recast the multilevel model as a single-level nonconvex mixed-integer nonlinear problem, which we then solve on a real-world network, namely the Greek gas network, to global optimality. Overall, this is the first time that the considered multilevel entry-exit system can be solved for a real-world sized network and a nonlinear flow model.

1 Introduction

The European gas market is organized as a so-called entry-exit system. This market structure was introduced as a result of the European gas market liberalization [7, 8] with the main goal to decouple transport and trading of natural gas. To this end, the market system is split into multiple levels, in which the transmission system operator (TSO) and gas traders interact with each other. The traders book capacities at nodes in the network, typically for a longer time period, e.g., months. They then nominate every day the amount of gas they want to trade at this node. To determine the capacity that can be booked at a point, the TSO allocates technical capacities in advance. These technical capacities are the main tool to decouple the transport and trading of gas. To achieve this goal, the TSO has to guarantee that every nomination below these technical capacities—i.e., infinitely many balanced load flows—can be transported through the network. As a consequence, gas trading within these technical capacities is no longer explicitly restricted by the actual transport of gas. The advantage of this setup is that the traders can completely ignore the physical network and that they only have to know the technical capacities that have been announced by the TSO.

The main goal that the entry-exit-system is meant to achieve is the “effective separation of supply and production activities from network operations” [7]. On the other hand, the entry-exit-system has some obvious drawbacks. By decoupling the different steps it is expected that economic inefficiencies arise. It is, however, very difficult to quantify the welfare losses of this system, which is the goal of the multilevel model studied in this paper. From a mathematical point of view, the allocation of technical capacities leads to a highly challenging nonlinear adjustable robust problem, which is one of the major computational challenges of the entry-exit market organization. For a general overview about adjustable robust optimization, we refer to [1, 36] and the references therein. We will show how one can overcome these mathematical difficulties to analyze an entry-exit-system for a tree-shaped network with a nonlinear gas flow model. A multilevel mathematical model of an entry-exit-system has been proposed in [14], where it is also shown that it can be reformulated as an equivalent bilevel model under suitable assumptions. In a stylized way, the considered entry-exit system can be described along four subsequent and interconnected levels. First, the TSO has to allocate technical capacities to all nodes of the network. Afterward, the TSO and the gas traders sign mid- to long-term booking contracts in which the traders buy node-specific capacity-rights for the maximal injection or withdrawal of gas. The sum of these bookings at every node of the network is bounded from above by the previously allocated technical capacities. On the day-ahead market, the traders then nominate the amount of gas that they feed in or withdraw under the condition that these amounts are below their booked quantities. Lastly, the TSO operates the network such that the requested amount of gas is transported through the network.

The model in [14] does not prescribe the physical model underlying the gas flow. For simplified linear flow models, this model can be solved on stylized small and passive (but cyclic) networks, i.e., networks without active elements such as compressor stations or (control) valves; see [2]. Unfortunately, the techniques exploited in [2] cannot be applied to nonlinear flow models. In this paper, we focus on solving the multilevel problem for a nonlinear flow model. Since switching from a linear to a nonlinear flow model makes the computation of technical capacities much more challenging, we need to restrict ourselves to only considering tree-shaped networks. Our results allow for the first time to solve a multilevel entry-exit gas market model in a real-world sized network, namely a passive version of the Greek gas network.

Since even linear multilevel problems are highly challenging in general, see [17, 20], and since we additionally consider nonlinear flow models on top of the multilevel structure, we need to make the following assumptions. First, the considered multilevel market model in [14] is based on the assumption of perfect competition among gas traders. Including strategic interaction is out of scope of this paper since strategic interaction alone leads to computationally challenging models in this context; see, e.g., [13]. Second, many different approaches exist for modeling gas physics. For a comprehensive overview see, e.g., the book [26] and the survey article [28] as well as the many references therein. We assume that our gas flow model represents a stationary potential-based flow and that the network does not contain active elements such as compressor stations or control valves. These assumptions allow us to consider the classic Weymouth equation for gas flows, which we formally introduce in Sect. 2. However, our findings hold for any nonlinear potential-based flow model under mild assumptions.

Let us note that the choice of modeling the gas physics directly influences the computational complexity of computing technical capacities, bookings, and nominations. For capacitated linear and linear potential-based flows, deciding the feasibility of a nomination is in P; see [5, 19, 24]. However, it is NP-hard in case of active elements; see [34]. Deciding the feasibility of a booking can be done in polynomial time for linear potential-based flows as well as in tree-shaped and single-cycle networks in case of nonlinear potential-based flows; see [21, 22, 29]. On the contrary, it is coNP-complete for capacitated linear flows, see [19], and it is coNP-hard for nonlinear potential-based flows; see [35]. In [32], structural properties such as (non-)convexity regarding the sets of feasible nominations and bookings are proven w.r.t. different models of gas transport. Finally, the computation of maximal technical capacities is NP-hard for capacitated linear and nonlinear potential-based flows even on trees; see [31]. Consequently, solving the considered multilevel entry-exit model including nonlinear flows poses a big challenge.

Our contribution is the following. We use the bilevel reformulation of the multilevel entry-exit gas market model presented in [14] and derive, as in [2], an exact single-level reformulation. In contrast to [2], we consider a nonlinear flow model of gas transport. The obtained single-level reformulation is still computationally intractable since it contains infinitely many nonlinear adjustable robust constraints that model technical capacities. We then derive for these constraints an equivalent finite-dimensional reformulation for the case of tree-shaped networks. This reformulation provides nice properties such that it consists of finitely many convex constraints including newly introduced integer variables. We further derive additional combinatorial constraints using the tree-shaped network structure that significantly speed up the solution process. Overall, we obtain a finite-dimensional nonconvex mixed-integer nonlinear single-level reformulation of the multilevel entry-exit gas market system. We then apply our results to solve the entry-exit model for a real-world network, namely the Greek gas network without active elements, to global optimality. Our computational results demonstrate the effectiveness of our techniques since the majority of the instances can be solved within 1 h. We further show that the additional combinatorial constraints are of great importance to achieve these short running times.

The remainder of this paper is structured as follows. In Sect. 2, we review the multilevel model and its bilevel reformulation as given in [14]. We then present the single-level reformulation in line with [2] and derive further model improvements in Sect. 3. Afterward, we handle the nonlinear adjustable robust constraints regarding the technical capacities in tree-shaped networks; see Sect. 4. In Sect. 5, we derive additional combinatorial constraints for the computation of technical capacities that significantly speed up the solution process. Finally, we apply our findings to solve the entry-exit model for the real-world Greek gas network without active elements in Sect. 6.

2 A multilevel model of the entry-exit gas market system

In this section, we briefly review the optimization model of the European entry-exit gas market developed in [14]. Its structure is given by the European directive [7] and the subsequent regulation [8] as a result of the European market liberalization. As in [14], we informally describe the four decision steps that correspond to the timing of the considered entry-exit market. We then go into more detail for the bilevel model that is the basis for our further investigations. The four steps of the entry-exit gas market system can be briefly outlined as follows:

• (i) Allocation of technical capacities and specification of booking price floors by the TSO.

• (ii) Booking of capacity rights by gas traders.

• (iii) Nomination of gas within the booked capacities by gas traders at the day-ahead market.

• (iv) Transport of the nominations by the TSO at minimum costs.

In Section 3 of [14], it is shown that the gas market model can be formulated as a bilevel model. The upper level (4) represents the first and fourth step, in which the TSO takes action. The lower level (5) corresponds to the second and third step, in which the gas traders interact with each other. We note that for this model, the assumption of perfect competition is essential. Otherwise, combining step 2 and 3 leads to a multi-leader multi-follower game, which can be modeled as an equilibrium problem with equilibrium constraints; see, e.g., the recent paper [13] in which the strategic setting is studied in detail. A visualization of this bilevel reformulation is given in Figure 3 of [14].

In the following, we discuss the notation and motivate the objective functions and constraints of the bilevel model.

We first introduce some basic notation regarding the considered gas networks. We model a gas network as a directed and weakly connected graph $G =(V, A)$ with nodes $V$ and arcs $A$. The set of nodes is partitioned into the set of entry nodes $V_+$, at which gas is injected, the set of exit nodes $V_-$, at which gas is withdrawn, and the remaining inner nodes$~V_0$. We note that the model allows for multiple gas traders $i$ at any single node of the network, i.e., $i\in {\mathcal {P}}_{u}$ for $u \in V_+ \cup V_-$. Moreover, we consider multiple time periods $t\in T$ of gas trading and transport with $\mathchoice{\left|T \right|}{|T|}{|T|}{|T|} < \infty$. Due to the general hardness of the multilevel model, we consider stationary gas flow without active, i.e., controllable, elements such as valves or compressors. In the upper level (4), the TSO allocates technical capacities $q^{\text {TC}}$, specifies booking price floors ${\underline{\pi }}^\mathrm {book}_{}$, and is responsible to transport the gas in accordance with the nominations to maximize the total social welfare in the considered market. The decision variables of the first level are the technical capacities $q^{\text {TC}}$, the booking price floors ${\underline{\pi }}^\mathrm {book}_{}$, and the pressure and flow variables ($p_{}$ and $q$, respectively) to express the state of the network for each time period $t\in T$. Throughout this paper, we consider the optimistic notion of bilevel optimization. Thus, the leader also optimizes over the optimal solutions of the lower-level problem, which makes the bookings $q ^{\mathrm {book}}_{}$ and the nominations $q ^{\mathrm {nom}}_{}$ variables of the upper-level problem as well.

The objective function (4a) represents the total social welfare aggregated over the considered time periods $T$. Further, $c^{\mathrm {var}}_{i}$ are the variable production costs of a gas seller $i\in {\mathcal {P}}_{u}$ at node $u \in V_+$. For a gas buyer $i\in {\mathcal {P}}_{u}$ at node $u \in V_-$, elastic demand is modeled by the inverse demand function $P_{i, t}$. This function models the marginal price tolerance as a function of the demand. Using inverse demand functions is standard in such micro-economic settings; see, e.g., the seminal textbook [23]. There it is also justified that these functions $P_{i, t}$ are continuous and strictly decreasing, which we assume in the following for all $i\in {\mathcal {P}}_{u}, u \in V_-,$ and $t\in T$. We discuss the transportation costs after we have introduced the physical modeling of the gas transport.

Next, we discuss the core regulatory constraint. Constraint (4d) ensures that all balanced nominations that comply with the technical capacities, i.e.,

$$\begin{aligned} {\mathcal {N}}(q^{\text {TC}}) \mathrel {{\mathop :}{=}}\left\{ q ^{\mathrm {nom}}_{}\in \mathbb {R} ^{V_+ \cup V_-} \,:\, 0 \le q ^{\mathrm {nom}}_{}\le q^{\text {TC}}, \sum _{u \in V_+}q ^{\mathrm {nom}}_{u} = \sum _{u \in V_-}q ^{\mathrm {nom}}_{u}\right\} , \end{aligned}$$

can be transported through the considered network. This is formalized by ${\mathcal {F}}({\hat{q}}^{\mathrm {nom}}_{})$, which consists of the feasible transport solutions for ${\hat{q}}^{\mathrm {nom}}_{}$. Many different approaches for modeling the set ${\mathcal {F}}(q ^{\mathrm {nom}}_{})$ exist. As mentioned earlier, we consider stationary gas flow without active elements such as (control) valves or compressor stations. We further focus on a nonlinear gas transport model that is based on the Weymouth pressure loss equation. Note that our results also hold for the general case of nonlinear potential-based flows, which we further explain in Remark 2.1.

For every node $u \in V$ of the gas network and time period $t\in T$, we denote the pressure level at node $u$ by $p_{u, t}$ with corresponding bounds

$$\begin{aligned} 0< p^{-}_u \le p_{{u, t}} \le p^{+}_u < \infty . \end{aligned}$$

(1)

We further denote the flow on arc $a \in A$ by $q _{a, t}$. Note that arc flow $q _{a, t}$ can be negative if it flows in the opposite direction w.r.t. the orientation of the arc. For every time period $t\in T$, the flows have to satisfy flow conservation at every node of the network, which is modeled by

$$\begin{aligned} \sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a, t} - \sum _{a \in \delta ^{\mathrm {in}}(u)}q _{a, t}&= \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{u, t}, \quad&u \in V_+, \ t\in T, \nonumber \\ \sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a, t} - \sum _{a \in \delta ^{\mathrm {in}}(u)}q _{a, t}&= - \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{u, t}, \quad&u \in V_-, \ t\in T, \\ \sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a, t} - \sum _{a \in \delta ^{\mathrm {in}}(u)}q _{a, t}&= 0, \quad&u \in V_0, \ t\in T.\nonumber \end{aligned}$$

(2)

Here, $\delta ^{\mathrm {out}}(u)$ represents the set of outgoing arcs and $\delta ^{\mathrm {in}}(u)$ the set of incoming arcs at node $u$. We note that we need to impose different signs for the nominations of entries $V_+$ and exits $V_-$ in (2) to model that gas is injected or withdrawn since a nomination is a nonnegative vector. For an arc $a \in A$ and a time period $t\in T$, the corresponding flow $q _{a, t}$ links the pressure levels at the incident nodes of arc $a$. This link is given by the following Weymouth-like pressure loss law

$$\begin{aligned} p^2_{u, t} - p^2_{v, t} = \Lambda _{a} q _{a, t} \mathchoice{\left|q _{a, t} \right|}{|q _{a, t}|}{|q _{a, t}|}{|q _{a, t}|}, \quad a = (u,v) \in A, \ t\in T, \end{aligned}$$

(3)

where ${\Lambda _{a}}>0$ is an arc specific constant.

We finally turn to the modeling of the transportation costs $c_{t}$ for $t\in T$. Here, we model transportation costs as proposed in [2]. As in the latter paper, we consider a passive network without active elements. However, the majority of transportation costs consist of the operating costs of active elements such as compressors. Usually, these transportation costs are driven by the pressure losses in the network. In order to mimic cost-optimal transport in a passive network, the costs are given by the absolute squared pressure losses in the entire network

$$\begin{aligned} \sum _{t\in T} c_{t}({p_{,} q; }q ^{\mathrm {nom}}_{}) = \sum _{t\in T} \sum _{a =(u, v)} c^{\mathrm {trans}}_{t} \mathchoice{\left|p^2_{u, t} - p^2_{v, t} \right|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|}, \end{aligned}$$

where $c^{\mathrm {trans}}_{t}>0$ holds for $t\in T$. We note that using Constraints (3), we can equivalently reformulate the transport costs as follows:

$$\begin{aligned} \sum _{t\in T} c_{t}({p_{,} q; }q ^{\mathrm {nom}}_{}) = \sum _{t\in T} \sum _{a =(u, v)} c^{\mathrm {trans}}_{t} \mathchoice{\left|p^2_{u, t} - p^2_{v, t} \right|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|} = \sum _{t\in T} \sum _{a =(u, v)} c^{\mathrm {trans}}_{t} \Lambda _{a} q ^2_{a, t}. \end{aligned}$$

The transportation costs also appear in Constraint (4c). This constraint ensures that the booking price floors are chosen such that they recover transportation costs and additional investment costs $C$. Finally, the coupling between the upper and lower level is expressed in Constraint (4f).

In the lower level (5), gas traders buy capacity rights, so-called bookings $q ^{\mathrm {book}}_{}$, that determine the maximum amount of gas that can be nominated. All traders then nominate their individual load of gas that is only bounded above by the chosen booking. The goal of every trader is to maximize its own profit, i.e., the trader books a capacity right that later leads to a surplus maximizing nomination. In doing so, the traders are only restricted by the technical capacities and booking price floors determined by the TSO in the first level. Note that the gas buyers and sellers do not take into account flow balance equations as well as any other physical or technical restrictions of the transport network. This is a defining aspect of the entry-exit system. It is touted as one of its features that buyers and sellers of gas do not have to care about the state of the network when making their trading decisions—except for the bookings that limit the nominations.

The interplay of booking and nominating can be modeled as a multi-leader multi-follower game. This game is difficult to analyze (see [13]) and, hence, is not usable in our context. Under a number of assumptions (as discussed in [14]), however, the solution of the game can be expressed as the solution of an optimization problem. We use the strongest assumption considered in [14], i.e., we assume perfect competition both in the booking and the nomination process on the day-ahead markets for both buyers and sellers. This allows to rewrite both the model of the booking and the day-ahead markets as mixed nonlinear complementarity problems (MNCP). These MNCPs are equivalent to optimization problems and can then be aggregated into a single optimization problem.

The single optimization problem can be interpreted as follows: The objective (5a) maximizes the welfare of all traders, that is, the surplus of the buyers minus the generation costs of the sellers, and minus the booking costs of all traders. The constraints make sure that bookings stay within the technical capacities (5b), nominations stay within the bookings (5c), and that all nominations are balanced (5d).

In summary, we obtain the bilevel model

$$\begin{aligned} \max _{\begin{array}{c} q^{\text {TC}}, {\underline{\pi }}^\mathrm {book}_{}, p_{,} q, \\ q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{}\end{array}}&\ \varphi (q ^{\mathrm {nom}}_{}, p_{}) = \sum _{t\in T} \left( \sum _{u \in V_-} \sum _{i\in {\mathcal {P}}_{u}} \int _0^{q ^{\mathrm {nom}}_{i, t}} P_{i, t}(s) \mathrm {d} s - \sum _{u \in V_+} \sum _{i\in {\mathcal {P}}_{u}} c^{\mathrm {var}}_{i} q ^{\mathrm {nom}}_{i, t} \right) \end{aligned}$$

(4a)

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \quad - \sum _{t\in T} \sum _{a =(u, v) \in A} c^{\mathrm {trans}}_{t} \mathchoice{\left|p^2_{u, t} - p^2_{v, t} \right|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|} - C\nonumber \\ \text {s.t.} \quad&0 \le q^{\text {TC}}_u, \ 0 \le {\underline{\pi }}^\mathrm {book}_{u}, \quad \quad u \in V_+ \cup V_-, \end{aligned}$$

(4b)

$$\begin{aligned}&\sum _{u \in V_+ \cup V_-} \sum _{i\in {\mathcal {P}}_{u}} {\underline{\pi }}^\mathrm {book}_{u} q ^{\mathrm {book}}_{i} = \sum _{t\in T} \sum _{a =(u, v) \in A} c^{\mathrm {trans}}_{t} \mathchoice{\left|p^2_{u, t} - p^2_{v, t} \right|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|}{|p^2_{u, t} - p^2_{v, t}|} + C, \end{aligned}$$

(4c)

$$\begin{aligned}&\forall {\hat{q}}^{\mathrm {nom}}_{}\in {\mathcal {N}}(q^{\text {TC}}) : {\mathcal {F}}({\hat{q}}^{\mathrm {nom}}_{}) \ne \emptyset , \end{aligned}$$

(4d)

$$\begin{aligned}&(p_{,} q) \in {\mathcal {F}}(q ^{\mathrm {nom}}_{}), \text {i.e.,} \ (p_{,} q) \text { satisfies } \text {(1)--(3)}, \end{aligned}$$

(4e)

$$\begin{aligned}&(q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{}) \in \mathrm {arg} \max (5), \end{aligned}$$

(4f)

where the lower level is given by

$$\begin{aligned} \max _{q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{}}&\sum _{t\in T} \left( \sum _{u \in V_-} \sum _{i\in {\mathcal {P}}_{u}} \int _0^{q ^{\mathrm {nom}}_{i, t}} P_{i, t}(s) \mathrm {d} s - \sum _{u \in V_+} \sum _{i\in {\mathcal {P}}_{u}} c^{\mathrm {var}}_{i} q ^{\mathrm {nom}}_{i, t} \right) \end{aligned}$$

(5a)

$$\begin{aligned}&\quad - \sum _{u \in V_+ \cup V_-} \sum _{i\in {\mathcal {P}}_{u}} {\underline{\pi }}^\mathrm {book}_{u} q ^{\mathrm {book}}_{i} \nonumber \\ \text {s.t.} \quad&\ \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {book}}_{i} \le q^{\text {TC}}_u, \quad u \in V_+ \cup V_-, \end{aligned}$$

(5b)

$$\begin{aligned}&0 \le q ^{\mathrm {nom}}_{i, t} \le q ^{\mathrm {book}}_{i}, \quad i\in {\mathcal {P}}_{u}, \ u \in V_+ \cup V_-, \ t\in T, \end{aligned}$$

(5c)

$$\begin{aligned}&\sum _{u \in V_-} \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{i, t} - \sum _{u \in V_+} \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{i, t} = 0, \quad t\in T. \end{aligned}$$

(5d)

In general, bilevel problems are nonconvex. Further, they are strongly NP-hard even in case of linear bilevel problems; see [17, 20]. In addition, the upper level of the considered problem is very challenging itself as we briefly outline in the following. First, the upper level contains nonsmooth terms in the objective function, which also appear in (4c). Moreover, Constraint (4c) contains nonconvex bilinear terms ${\underline{\pi }}^\mathrm {book}_{u} {q ^{\mathrm {book}}_{i}}$. Additionally, considering a nonlinear flow model for gas transport leads to nonconvex constraints in (4e). Finally, and most critical, (4d) is a nonlinear adjustable robust constraint, which, in general, is computationally intractable. From the point of view of robust optimization, Constraint (4d) is an adjustable robust constraint with uncertainty set ${\mathcal {N}}(q^{\text {TC}})$. For a detailed explanation regarding the connection of computing technical capacities, respectively deciding the feasibility of a booking, and adjustable robustness, we refer to Remark 2.6 in [22]. For the considered nonlinear flow model, already deciding its feasibility is coNP-hard; see [35]. Due to the inherent difficulty of the problem, we focus on tree-shaped networks. This allows us to obtain a finite-dimensional reformulation of the nonlinear adjustable robust constraint (4d) in Sect. 4. Moreover, this reformulation has some nice properties such that it is a convex mixed-integer model.

Remark 2.1

We note that our results, especially the computation of the technical capacities in Sect. 4, are also valid for the general case of potential-based flows. This means that we can generally replace Constraints (1) and (3) by the potential-based flow model

$$\begin{aligned}&0< {\pi }^-_{u} \le \pi _{u, t} \le {\pi }^+_{u} < \infty ,&u \in V, \ t\in T, \\&\pi _{u, t} - \pi _{v, t} = \phi _{a}(q _{a, t}),&a =(u, v) \in A, \ t\in T, \end{aligned}$$

where $\phi _a$ is a continuous, strictly increasing, and odd (i.e., $\phi _{a}(-q _{a, t}) = -\phi _{a}(q _{a, t})$) function. The latter is rather natural in the context of utility networks. We note that the freedom of modeling $\phi _a$ is large and it ranges from simple linear models to sophisticated nonlinear ones. On the one hand, this allows to apply our results to many different gas transport models. In particular, this includes the case of non-horizontal pipes; see [26]. On the other hand, we can also apply our results to many other different network types such as water, hydrogen, or lossless DC power flow networks, if the physics is appropriately modeled; see [15].

In the next section, we reformulate the presented bilevel as a single-level problem and present further model improvements.

3 Reduction to a single level problem

Since the bilevel model (4) with lower level (5) contains nonlinearities in the upper and lower level and since the linking variables $q^{\text {TC}}$ and ${\underline{\pi }}^\mathrm {book}_{}$ are continuous, we replace the convex lower level by its necessary and sufficient first-order optimality conditions to obtain a single-level problem. This is in line with [2], where the multilevel problem is considered for a linear potential-based flow model. We can adapt the single-level reformulation of [2] since the lower level is independent of the considered gas flow model.

To obtain concave-quadratic upper- and lower-level objective functions w.r.t. the upper- or lower-level variables, we make the following assumption.

Assumption 1

All inverse market demand functions are linear and strictly decreasing, i.e., $P_{i, t} (q ^{\mathrm {nom}}_{i, t}) = b_{i, t} q ^{\mathrm {nom}}_{i, t} + a_{i, t}$ with $a_{i, t} > 0$ and $b_{i, t} < 0$ for all $i\in {\mathcal {P}}_{u}, u \in V_-, t\in T$.

This assumption is rather standard in multilevel modeling of energy markets; see, e.g., [2, 11, 12] and the many references therein. Since the lower-level (5) then is a concave-quadratic maximization problem with a linearly constrained feasible region, its KKT conditions are both necessary and sufficient; see, e.g., [3]. We now replace the lower level (5) by its KKT conditions, i.e., the stationarity conditions

$$\begin{aligned} - {\underline{\pi }}^\mathrm {book}_{u} - \beta _{u} + \sum _{t\in T} \gamma ^+_{i, t}&= 0,&i\in {\mathcal {P}}_{u}, \ u \in V_+ \cup V_-, \end{aligned}$$

(6a)

$$\begin{aligned} a_{i, t} + b_{i, t} q ^{\mathrm {nom}}_{i, t} + \gamma ^-_{i, t} - \gamma ^+_{i, t} - \delta _{ t}&= 0,&i\in {\mathcal {P}}_{u}, \ u \in V_-, \ t\in T, \end{aligned}$$

(6b)

$$\begin{aligned} -c^{\mathrm {var}}_{i} + \gamma ^-_{i, t} - \gamma ^+_{i, t} + \delta _{t}&= 0,&i\in {\mathcal {P}}_{u}, \ u \in V_+, \ t\in T, \end{aligned}$$

(6c)

primal feasibility (5b)–(5d), nonnegativity

$$\begin{aligned} \beta _{u}&\ge 0,&u \in V_+ \cup V_-, \end{aligned}$$

(7a)

$$\begin{aligned} \gamma ^-_{i, t}, \gamma ^+_{i, t}&\ge 0,&i\in {\mathcal {P}}_{u}, \ u \in V_+ \cup V_-, \ t\in T, \end{aligned}$$

(7b)

of inequality multipliers, and complementary slackness conditions

$$\begin{aligned} \beta _{u} \left( q^{\text {TC}}_{u} - \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {book}}_{i}\right)&= 0,&u \in V_+ \cup V_-, \end{aligned}$$

(8a)

$$\begin{aligned} \gamma ^-_{i, t} q ^{\mathrm {nom}}_{i, t}&= 0,&i\in {\mathcal {P}}_{u}, \ u \in V_+ \cup V_-, \ t\in T, \end{aligned}$$

(8b)

$$\begin{aligned} \gamma ^+_{i, t} \left( q ^{\mathrm {book}}_{i} - q ^{\mathrm {nom}}_{i, t}\right)&= 0,&i\in {\mathcal {P}}_{u}, \ u \in V_+ \cup V_-, \ t\in T. \end{aligned}$$

(8c)

Then, the bilevel problem (4) can be reformulated as the single-level problem

$$\begin{aligned} \max _s \quad&{\varphi (q ^{\mathrm {nom}}_{}, p)} \end{aligned}$$

(9a)

$$\begin{aligned} \text {s.t.} \quad&\text { upper-level feasibility: } \text {(4b)--(4e), } \end{aligned}$$

(9b)

$$\begin{aligned}&\text { lower level: } \text {(5b)--(5d), (6)--(8),} \end{aligned}$$

(9c)

where $s=(q^{\text {TC}}, {\underline{\pi }}^\mathrm {book}_{}, q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{}, p_{,} q, \beta _{}, \gamma ^-_{}, \gamma ^+_{}, \delta _{})$.¹

3.1 Linearization of KKT complementarity conditions

Using the standard big-$M$ method, see [9], we now linearize the nonconvex complementarity constraints (8). To this end, bounds for the primal and dual variables are necessary.

For the dual variables, we adopt the values of [2], which are independent from the chosen gas flow model. To this end, we introduce the following notation:

$$\begin{aligned} a_{t}^{\mathrm {min}}&\mathrel {{\mathop :}{=}}\min \{a_{i, t} : i\in {\mathcal {P}}_{u}, u \in V_- \}, \\ a_{t}^{\mathrm {max}}&\mathrel {{\mathop :}{=}}\max \{a_{i, t} : i\in {\mathcal {P}}_{u}, u \in V_- \}, \\ c^{\mathrm {var}}_{\mathrm {min}}&\mathrel {{\mathop :}{=}}\min \{c^{\mathrm {var}}_{i} : i\in {\mathcal {P}}_{u}, u \in V_+ \}, \\ c^{\mathrm {var}}_{\mathrm {max}}&\mathrel {{\mathop :}{=}}\max \{c^{\mathrm {var}}_{i} : i\in {\mathcal {P}}_{u}, u \in V_+ \}. \end{aligned}$$

Furthermore, we need the following assumptions.

Assumption 2

For every $t\in T$, it holds $a_{t}^{\mathrm {min}} \ge c^{\mathrm {var}}_{\mathrm {min}}$ and $a_{t}^{\mathrm {max}} \ge c^{\mathrm {var}}_{\mathrm {max}}$.

The intuition behind this assumption is that every player can participate in the market in every time period: The gas buyer with smallest willingness to pay can still receive gas from the seller with the smallest variable costs. The assumption can be easily checked a priori. Furthermore, we assume that the network is designed in such a way that trading takes place in every time period.

Assumption 3

For every time period $t\in T$, there exists a node $u \in V_+ \cup V_-$ with $i\in {\mathcal {P}}_{u}$ so that $q ^{\mathrm {nom}}_{i, t} > 0$ holds.

A violation of this assumption in reality would mean that there is no gas trading in the entire market at all for a certain time period. That this takes place is very unrealistic—thus, the assumption itself should always hold in practice.

For the following we use Lemmas 2–4 of [2], by which we obtain upper bounds for the booking price floors and bounds for the dual variables.

Lemma 3.1

([2], Lemmas 2–4) There exists an optimal solution of (9) with

$$\begin{aligned}&0 \le \gamma ^-_{i, t} \le 2 (a_{t}^{\mathrm {max}} - c^{\mathrm {var}}_{\mathrm {min}}), \quad&i\in {\mathcal {P}}_{u}, \ u \in V_+ \cup V_-, \ t\in T, \end{aligned}$$

(10a)

$$\begin{aligned}&0 \le \gamma ^+_{i, t} \le a_{t}^{\mathrm {max}} - c^{\mathrm {var}}_{\mathrm {min}}, \quad&i\in {\mathcal {P}}_{u}, \ u \in V_+ \in V_-, \ t\in T, \end{aligned}$$

(10b)

$$\begin{aligned}&0 \le \beta _{u} \le \sum _{t\in T} (a_{t}^{\mathrm {max}} - c^{\mathrm {var}}_{\mathrm {min}}), \quad&u \in V_+ \cup V_-, \end{aligned}$$

(10c)

$$\begin{aligned}&{\underline{\pi }}^\mathrm {book}_{u} \le \sum _{t\in T} (a_{t}^{\mathrm {max}} - c^{\mathrm {var}}_{\mathrm {min}}),&u \in V_+ \cup V_-. \end{aligned}$$

(10d)

We now provide bounds for certain primal variables of the bilevel problem (4), respectively its single-level reformulation (9). We further present additional feasible constraints that tighten these bounds. As previously mentioned, these bounds are necessary for the linearization of the complementarity conditions (8). To this end, we first prove properties regarding nominations, bookings, and technical capacities in an optimal solution, see Lemmas 3.2–3.4, that enable us to a priori bound the technical capacities; see Lemma 3.5.

From Lemma 3.1 and Corollary 1 in [2], we obtain that an optimal solution exists in which the booking of a player equals its maximum nomination.

Lemma 3.2

(Corollary 1 of [2]) There exists an optimal solution of the bilevel problem (4) satisfying (10) and

$$\begin{aligned} \max _{t\in T} \left\{ {q ^{\mathrm {nom}}_{i, t}} \right\} = q ^{\mathrm {book}}_{i} \end{aligned}$$

(11)

for all $i\in {\mathcal {P}}_{u}, u \in V_+ \cup V_-$.

Using this result, we now prove that an optimal solution exists in which the bookings equal the technical capacities.

Lemma 3.3

There exists an optimal solution of the bilevel problem (4) satisfying (10), (11), and

$$\begin{aligned} q^{\text {TC}}_u = \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {book}}_{i} \end{aligned}$$

(12)

for all $u \in V_+ \cup V_-$.

Proof

From Lemma 3.2 it follows that a solution $z=(q^{\text {TC}}, {\underline{\pi }}^\mathrm {book}_{}, q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{}, p_{,} q)$ of (4) satisfying (10) and (11) exists. We now set ${\tilde{z}} = ({\tilde{q}}^{\text {TC}}, {\underline{\pi }}^\mathrm {book}_{}, q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{}, p_{,} q)$ with ${\tilde{q}}^{\text {TC}}_u = \sum _{i\in {\mathcal {P}}_{u}}q ^{\mathrm {book}}_{i}$ for $u \in V_+ \cup V_-$.

The feasible region of the lower level (5) w.r.t. z is a relaxation of the feasible region of (5) w.r.t. ${\tilde{z}}$ since

$$\begin{aligned} 0 \le \sum _{i\in {\mathcal {P}}_{u}}q ^{\mathrm {book}}_{i} = {\tilde{q}}^{\text {TC}}_u \le q^{\text {TC}}_u, \quad u \in V_+ \cup V_-, \end{aligned}$$

holds. However, due to the latter inequalities, $(q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{})$ is feasible for (5) w.r.t. ${\tilde{z}}$. We further note that the corresponding lower-level objective functions are equal. Consequently, the optimal solution $(q ^{\mathrm {book}}_{}, q ^{\mathrm {nom}}_{})$ of the lower-level (5) w.r.t. z is also optimal for (5) w.r.t. ${\tilde{z}}$.

Furthermore, ${\tilde{z}}$ satisfies the upper level constraints (4b)–(4f). We note that (4d) is valid due to ${\hat{q}}^{\mathrm {nom}}_{}\in {\mathcal {N}}({\tilde{q}}^{\text {TC}}) \subseteq {\mathcal {N}}(q^{\text {TC}})$. Thus, ${\tilde{z}}$ is a bilevel feasible point of (4). Moreover, $q^{\text {TC}}$ is not present in the upper-level objective function and hence, the optimal values corresponding to z and to ${\tilde{z}}$ are equal. Consequently, ${\tilde{z}}$ is an optimal solution of (4). $\square$

Note that, despite the two last results, it is not possible to eliminate nominations, bookings, or technical capacities from the model since they are decided on at different levels of our multilevel model.

Using the latter result, we now introduce additional constraints that bound the technical capacity of a node.

Lemma 3.4

There exists an optimal solution of the bilevel problem (4) that satisfies (10)–(12) as well as the inequalities

$$\begin{aligned}&q^{\text {TC}}_u \le \mathchoice{\left|{\mathcal {P}}_{u} \right|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|} \sum _{v \in V_-} q^{\text {TC}}_{v}, \quad u \in V_+ \end{aligned}$$

(13a)

$$\begin{aligned}&q^{\text {TC}}_u \le \mathchoice{\left|{\mathcal {P}}_{u} \right|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|} \sum _{v \in V_+} q^{\text {TC}}_{v}, \quad u \in V_-. \end{aligned}$$

(13b)

Proof

From Lemma 3.3 it follows that an optimal solution of (4) exists that satisfies (10)–(12). Let $t\in T$ be an arbitrary time period and $i\in {\mathcal {P}}_{u}$ an arbitrary player at node $u \in V_+ \cup V_-$. From Constraint (5c), we obtain $q ^{\mathrm {nom}}_{i, t} \le q ^{\mathrm {book}}_{i}$. Furthermore, from Constraint (5d) it follows

$$\begin{aligned} q ^{\mathrm {nom}}_{i, t} \le \sum _{v \in V_-} \sum _{j \in {\mathcal {P}}_{v}} q ^{\mathrm {nom}}_{j, t} \end{aligned}$$

in case of a gas seller at $u \in V_+$ and

$$\begin{aligned} q ^{\mathrm {nom}}_{i, t} \le \sum _{v \in V_+} \sum _{j \in {\mathcal {P}}_{v}} q ^{\mathrm {nom}}_{j, t} \end{aligned}$$

in case of a gas buyer at $u \in V_-$. Moreover, a time period $l \in T$ with $q ^{\mathrm {nom}}_{i, l} = q ^{\mathrm {book}}_{i}$ exists due to Lemma 3.2. From this and Lemma 3.3, we obtain

$$\begin{aligned} q ^{\mathrm {nom}}_{i, t} \le q ^{\mathrm {nom}}_{i, l} = q ^{\mathrm {book}}_{i} \le \sum _{v \in V_-} \sum _{j \in {\mathcal {P}}_{v}} q ^{\mathrm {nom}}_{j, l} \le \sum _{v \in V_-} \sum _{j \in {\mathcal {P}}_{v}} q ^{\mathrm {book}}_{j} = \sum _{v \in V_-} q^{\text {TC}}_{v} \end{aligned}$$

in case of $u \in V_+$ and

$$\begin{aligned} q ^{\mathrm {nom}}_{i, t} \le q ^{\mathrm {nom}}_{i, l} = q ^{\mathrm {book}}_{i} \le \sum _{v \in V_+} \sum _{j \in {\mathcal {P}}_{v}} q ^{\mathrm {nom}}_{j, l} \le \sum _{v \in V_+} \sum _{j \in {\mathcal {P}}_{v}} q ^{\mathrm {book}}_{j} = \sum _{v \in V_+} q^{\text {TC}}_{v} \end{aligned}$$

in case of $u \in V_-$. Consequently, the claim follows from summing up the previous inequalities w.r.t. $i\in {\mathcal {P}}_{u}$ and again using Lemma 3.3. $\square$

We note that the Constraints (13) can be valuable for finding good upper bounds of the technical capacities since gas networks usually contain a small number of entry nodes and very few single players at the nodes. We finally introduce upper bounds for the technical capacity of a node, which depend on the pressure bounds and which can be computed a priori.

Lemma 3.5

There exists an optimal solution of the bilevel problem (4) satisfying (10)–(13) as well as the constraints

$$\begin{aligned} q^{\text {TC}}_u&\le \mathchoice{\left|{\mathcal {P}}_{u} \right|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|} \left( \sum _{(u,v) \in \delta ^{\mathrm {out}}(u)} \sqrt{ \frac{ (p^{+}_u)^2 - (p^{-}_{v})^2}{\Lambda _{(u,v)}} } + \sum _{(v, u) \in \delta ^{\mathrm {in}}(u)} \sqrt{ \frac{(p^{+}_{u})^2 - (p^{-}_{v})^2}{\Lambda _{(v, u)}} } \right) \end{aligned}$$

(14a)

$$\begin{aligned}&{\mathrel {{=}{\mathop :}}} \ M^+_u, \quad u \in V_+, \nonumber \\ q^{\text {TC}}_u&\le \mathchoice{\left|{\mathcal {P}}_{u} \right|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|} \left( \sum _{(u,v) \in \delta ^{\mathrm {out}}(u)} \sqrt{ \frac{(p^{+}_v)^2 - (p^{-}_{u})^2}{\Lambda _{(u,v)}} } + \sum _{(v, u) \in \delta ^{\mathrm {in}}(u)} \sqrt{ \frac{(p^{+}_v)^2 - (p^{-}_{u})^2}{\Lambda _{(v, u)}} } \right) \\&{\mathrel {{=}{\mathop :}}} \ M^-_u, \quad u \in V_-. \nonumber \end{aligned}$$

(14b)

Proof

From Lemma 3.4, it follows that an optimal solution of (4) exists that satisfies (10)–(13). Let $u \in V_+$. Then, for any feasible point $(q ^{\mathrm {nom}}_{}, q, p_{})$ of (1)–(3) and time period $t\in T$, it follows

$$\begin{aligned} q _{(u, v),t}&\le \sqrt{({(p^{+}_u)^2 - (p^{-}_{v})^2})/{\Lambda _{(u,v)}}}, \quad (u, v) \in \delta ^{\mathrm {out}}(u), \\ - q _{(v, u), t}&\le \sqrt{ ((p^{+}_u)^2 - (p^{-}_{v})^2)/\Lambda _{(v, u)}} , \quad (v, u) \in \delta ^{\mathrm {in}}(u). \end{aligned}$$

Due to this and (2), it follows

$$\begin{aligned} \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{i, t} = \sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a, t} - \sum _{a \in \delta ^\mathrm {in}(u)} {q _{a, t}} \le \frac{1}{\mathchoice{\left|{\mathcal {P}}_{u} \right|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|}{|{\mathcal {P}}_{u}|}} M^+_u. \end{aligned}$$

Consequently, from this, (11), and (12), it follows

$$\begin{aligned} q^{\text {TC}}_u = \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {book}}_{i} = \sum _{i\in {\mathcal {P}}_{u}} \max _{t\in T} \left\{ {q ^{\mathrm {nom}}_{i, t}} \right\} \le M^+_u. \end{aligned}$$

Analogously, one can show (14b). $\square$

Now, we have derived bounds for the booking price floors, see Lemma 3.1, as well as for the bookings, respectively technical capacities, see Lemma 3.5. These bounds are very important for handling the bilinear terms ${\underline{\pi }}^\mathrm {book}_{u} q ^{\mathrm {book}}_{u}$ in Constraint (4c). Later on, we handle these bilinear terms with the help of Gurobi [16], which uses McCormick envelopes [25] and spatial branching. For the latter, bounds for ${\underline{\pi }}^\mathrm {book}_{u}$ and $q ^{\mathrm {book}}_{u}$ are necessary.

Moreover, we now can equivalently replace the complementarity constraints (8) by using the standard big-$M$ method. Consequently, we obtain a single-level problem that is larger than the bilevel problem (4) with additional continuous and binary variables and constraints. We note that this single-level problem contains nonsmooth and nonconvex terms in the objective function as well as in Constraint (4c).

We emphasize that the obtained single-level reformulation is still computationally intractable since it contains the infinitely many nonlinear adjustable robust constraints (4d) that model technical capacities. We now tackle these constraints in the next section and show that we can model their feasible region by finitely many convex constraints including integer variables.

4 Handling technical capacities in trees

In this section, we provide a finite-dimensional model for the infinitely many nonlinear adjustable robust constraints (4d) for the case of tree-shaped networks. Since these adjustable robust constraints are very challenging, especially for the considered nonlinear gas transport model (1)–(3), we assume that the graph $G$ is a tree throughout this section.

We first introduce some necessary notation, which is mainly taken from [31]. Using directed graphs to represent gas networks is a modeling choice that allows to interpret the direction of flows. However, the flow in a gas network is not influenced by the direction of the arcs. Thus, for $u,v \in V$, we introduce so-called flow-paths in which contains the nodes of the path from u to v in the undirected version of the graph $G$ and contains the corresponding arcs of this path. Consequently, a flow-path can be interpreted as an undirected path that additionally contains for each arc its direction in the original network $G =(V, A)$. The latter allows us to determine the flow direction for an arc. For another pair of nodes $u ',v ' \in V$, we say that is a flow-subpath of if , i.e., and , holds and if is itself a flow-path.

We now focus on tree-shaped networks and thus, the flow-path between two nodes is unique. For modeling reasons, we partition the arcs of a given flow-path into $A ^{\rightarrow }{(u,v)}$ and $A ^{\leftarrow }{(u,v)}$. The set $A ^{\rightarrow }{(u,v)}$ contains all arcs of that are directed from $u$ to $v$, i.e., an arc $({u '}, {v '}) \in A ^{\rightarrow }{(u,v)}$ satisfies . The remaining arcs of the flow-path  are contained in $A ^{\leftarrow }{(u,v)}$. We note that for a fixed node pair these arc sets are unique due to the tree structure of the graph. We can also compute them for every flow-path a priori by depth-first search.

Finally, for a tree-shaped network and arc $a = (u,v) \in A$, we now introduce two sub-graphs that are later used to determine the maximal flow on an arc. If we delete arc $a$ in $G$, then the tree decomposes into two sub-trees. We define the sub-tree including node $u$ as and the other sub-tree, which contains $v$, as . Due to this construction, holds.

The outline to derive a finite-dimensional reformulation of the computational intractable nonlinear adjustable constraint (4d) is as follows. We first state a known characterization for technical capacities that enables us to verify the feasibility of technical capacities by solving, for each pair of nodes, a nonlinear optimization problem to global optimality. We then exploit monotonicity properties of these nonlinear problems together with certain flow properties in tree-shaped networks to model the corresponding optimal value functions by finitely many convex constraints including newly introduced binary variables.

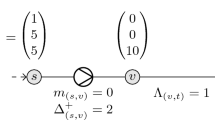
From Theorem 10 in [21], it follows that we can verify the feasibility of given technical capacities by solving a nonlinear optimization problem for each pair of nodes $({w_1}, {w_2}) \in V ^2$. One of these nonlinear problems computes the maximal pressure difference between the considered nodes ${w_1}$ and ${w_2}$ within the given technical capacities and is composed of

$$\begin{aligned} \triangle _{({w_1},{w_2})}(q^{\text {TC}}) \mathrel {{\mathop :}{=}}\max _{ q ^{\mathrm {nom}}_{}, q, p}&\quad p_{{w_1}}^2 - p_{{w_2}}^2 \end{aligned}$$

(15a)

$$\begin{aligned} \text {s.t.} \quad&\sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a} - \sum _{a \in \delta ^{\mathrm {in}}(u)}q _{a} = \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{{i} }, \quad u \in V_+, \end{aligned}$$

(15b)

$$\begin{aligned}&\sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a} - \sum _{a \in \delta ^{\mathrm {in}}(u)}q _{a} = - \sum _{i\in {\mathcal {P}}_{u}} q ^{\mathrm {nom}}_{{i} }, \quad u \in V_-, \end{aligned}$$

(15c)

$$\begin{aligned}&\sum _{a \in \delta ^{\mathrm {out}}(u)} q _{a} - \sum _{a \in \delta ^{\mathrm {in}}(u)}q _{a} = 0, \quad u \in V_0, \end{aligned}$$

(15d)

$$\begin{aligned}&p^2_{u} - p^2_{v} = \Lambda _{a} q _{a} \mathchoice{\left|q _{a} \right|}{|q _{a}|}{|q _{a}|}{|q _{a}|}, \quad a = (u,v) \in A, \end{aligned}$$

(15e)

$$\begin{aligned}&q ^{\mathrm {nom}}_{}\in {\mathcal {N}}(q^{\text {TC}}). \end{aligned}$$

(15f)

We note that Constraints (15b)–(15e) are the same as Constraints (2) and (3) except that they do not depend on the specific time step anymore since the technical capacities are determined once for all time steps.

It is shown in Theorem 10 of [21] that feasible technical capacities can be characterized by constraints on the maximum pressure difference between all pairs of nodes, i.e., by constraints on the objective value of (15).

Lemma 4.1

(Theorem 10 in [21]) Let $G =(V, A)$ be a graph and $q^{\text {TC}}\in \mathbb {R} _{\ge 0}^{V_+ \cup V_-}$. Then, $q^{\text {TC}}$ satisfies Constraint (4d) if and only if for each node pair $({w_1},{w_2}) \in V ^2$ the corresponding optimal value of (15) satisfies

$$\begin{aligned} \triangle _{({w_1},{w_2})}(q^{\text {TC}}) \le (p^{+}_{{w_1}})^2 - (p^{-}_{{w_2}})^2. \end{aligned}$$

(16)

We note that this characterization allows us to replace the nonlinear adjustable robust constraint (4d) by (16). For tree-shaped networks, it is further proven in [21] that the optimal value function  $\triangle _{{w_1}, {w_2}}(q^{\text {TC}})$ can be modeled by exploiting the following flow bounds that depend on given technical capacities.

Lemma 4.2

(Lemma 3.2 in [31]) Let $G =(V,A)$ be a tree, $q^{\text {TC}}\in \mathbb {R} ^{V_+ \cup V_-}$ technical capacities, $q ^{\mathrm {nom}}_{}\in \mathcal {N}(q^{\text {TC}})$ a nomination, and $q$ its unique flow given by (2). Then, for every arc $a = (u,v) \in A$, the flow $q _{a}$ is bounded by

(17)

Moreover, it is shown in [21], respectively in Lemmas 3.4 and 3.5 of [31] by using an alternative proof technique, that these flow bounds are tight for all arcs of a given flow-path. Consequently, the optimal value function $\triangle _{{w_1}, {w_2}}(q^{\text {TC}})$ can be explicitly expressed as follows, which has been shown in Corollary 19 in [21] in a slightly modified setting.

Lemma 4.3

(Corollary 19 in [21]) Let $G =(V,A)$ be a tree, $q^{\text {TC}}\in \mathbb {R} ^{V_+ \cup V_-}$ technical capacities, and ${w_1}, {w_2}\in V$. Then,

$$\begin{aligned} \triangle _{{w_1}, {w_2}}(q^{\text {TC}}) = \sum _{a \in A ^{\rightarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^+_{a}({q^{\text {TC}}})}^2 + \sum _{a \in A ^{\leftarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^-_{a}({q^{\text {TC}}})}^2 \end{aligned}$$

(18)

holds, where $\xi ^+_{a}({q^{\text {TC}}})$ and $\xi ^-_{a}({q^{\text {TC}}})$ are the upper and lower arc flow bounds given by (17).

This explicit representation of the optimal value function $\triangle _{{w_1}, {w_2}}(q^{\text {TC}})$ allows us to simplify the characterization for technical capacities of Lemma 4.1.

Corollary 4.4

Let $G =(V, A)$ be a graph and $q^{\text {TC}}\in \mathbb {R} _{\ge 0}^{V_+ \cup V_-}$. Then, $q^{\text {TC}}$ satisfies Constraint (4d) if and only if for each node pair $({w_1},{w_2}) \in V ^2$ the constraint

$$\begin{aligned} \sum _{a \in A ^{\rightarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^+_{a}({q^{\text {TC}}})}^2 + \sum _{a \in A ^{\leftarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^-_{a}({q^{\text {TC}}})}^2 \le (p^{+}_{{w_1}})^2 - (p^{-}_{{w_2}})^2 \end{aligned}$$

(19)

is fulfilled, where $\xi ^+_{a}({q^{\text {TC}}})$ and $\xi ^-_{a}({q^{\text {TC}}})$ are the upper and lower arc flow bounds given by (17).

We now can replace the nonlinear adjustable robust constraint (4d) that models feasible technical capacities by our simplified characterization (19). To do so, we present a model for this simplified characterization (19) that consists of finitely-many convex constraints including newly introduced integer variables. For stating the model, we first need to bound the technical capacities. From Lemma 3.5, it follows that an optimal solution of the bilevel problem (4) exists such that the technical capacity of a node is bounded above by $M^+_u$ for all $u \in V_+$ and by $M^-_u$ for all $u \in V_-$. Consequently, we can bound the aggregated technical capacities of all entries, respectively exits, by

$$\begin{aligned}&M^+\mathrel {{\mathop :}{=}}\sum _{u \in V_+} M^+_u \ge \sum _{u \in V_+} q^{\text {TC}}_u, \end{aligned}$$

(20a)

$$\begin{aligned}&M^-\mathrel {{\mathop :}{=}}\sum _{u \in V_-} M^-_u \ge \sum _{u \in V_-} q^{\text {TC}}_u. \end{aligned}$$

(20b)

We note that the bilinear terms of the following model can be reformulated by using big-$M$s, which we describe later. Our convex mixed-integer model of (19) is given as follows:

(21a)

(21b)

(21c)

(21d)

(21e)

(21f)

(21g)

(21h)

(21i)

(21j)

(21k)

(21l)

Constraints (21a)–(21d) and (21e)–(21h) ensure that ${\bar{q}}_{}$ is at least as large as the upper flow bound $\xi ^+_{a}({q^{\text {TC}}})$ and ${\underline{q}}_{}$ is at least the absolute value of the lower flow bound $\xi ^-_{a}({q^{\text {TC}}})$; see Lemma 4.2. The negative sign of the lower flow bound is directly modeled in Constraints (21k). Constraints (21i) and (21j) result from a modeling choice. They allow to model the flow linearly in Constraints (21k), which reduces the number of convex constraints.

We now show the correctness of (21). To this end, we first prove that any feasible point of the original bilevel problem (4) satisfying Lemma 3.5 can be extended to a feasible point of (21). Afterward, we prove that every feasible point of (21) is also feasible for the adjustable robust constraint (4d) of the bilevel problem (4). We abbreviate a feasible point of (21) by $z$, i.e.,

$$\begin{aligned} z= \left( {\bar{f}}, {\underline{f}}, {\bar{q}}_{,} {\underline{q}}_{,} {\underline{h}}^{-}_{,} {\bar{h}}^{-}_{,} {\underline{h}}^{+}_{,} {\bar{h}}^{+}_{,} {\underline{x}}_{,} {\bar{x}}_{,} q^{\text {TC}}\right) . \end{aligned}$$

Lemma 4.5

Let $G =(V,A)$ be a tree and $q^{\text {TC}}\in \mathbb {R} _{\ge 0}^{V_+ \cup V_-}$ be part of an optimal solution of (4) satisfying Lemma 3.5. Then, $q^{\text {TC}}$ can be extended to a feasible point $z$ of (21).

Proof

Constraints (21a), (21b), (21e), and (21f) are uniquely determined by $q^{\text {TC}}$. Further, they are feasible because the corresponding variables are not bounded. Due to the construction of $M^+$ by (20a) and (20b), we can set for $a \in A$ the variable ${\bar{x}}_{a}$, respectively ${\underline{x}}_{a}$, to 1 if the left-hand side of (21c), respectively (21g), is positive and otherwise to 0. Due to this assignment, ${\bar{q}}_{a}$ is uniquely determined and equals the upper flow bound $\xi ^+_{a}({q^{\text {TC}}})$; see (17). Further, ${\underline{q}}_{a}$ is unique and equals the absolute value of the lower flow bound $\xi ^-_{a}({q^{\text {TC}}})$; see (17). We now set ${\bar{f}}_a = {\bar{q}}_{a}^2$, respectively ${\underline{f}}_a = {\underline{q}}_{a}^2$, for $a \in A$ and thus, Constraints (21i) and (21j) are satisfied.

Finally, we have to check the feasibility of Constraints (21k). For doing so, we consider an arbitrary node pair $(u, v) \in V ^2$. From the previous construction it follows that (21k) simplifies to

$$\begin{aligned} \sum _{a \in A ^{\rightarrow }{(u,v)}} \Lambda _{a} {{\bar{f}}_a} + \sum _{a \in A ^{\leftarrow }{(u,v)}} \Lambda _{a} {{\underline{f}}_a}&= \sum _{a \in A ^{\rightarrow }{(u,v)}} \Lambda _{a} {\xi ^+_{a}({q^{\text {TC}}})}^2 + \sum _{a \in A ^{\leftarrow }{(u,v)}} \Lambda _{a} {\xi ^-_{a}({q^{\text {TC}}})}^2 \\&\le (p^{+}_{u})^2 - (p^{-}_{v})^2. \end{aligned}$$

The feasibility of the last inequality follows from Corollary 4.4 and the feasibility of the considered technical capacities $q^{\text {TC}}$ for (4d). Consequently, the constructed point is feasible for (21). $\square$

We now prove that a feasible point of (21) is also feasible to the adjustable robust constraint (4d).

Lemma 4.6

Let $G =(V,A)$ be a tree and let $z$ be a feasible point of (21). Then, $q^{\text {TC}}$ satisfies (4d).

Proof

We contrarily assume that $q^{\text {TC}}$ does not satisfy Constraint (4d). Thus, from Corollary 4.4 it follows that there is a node pair $({w_1}, {w_2}) \in V ^2$ violating (19), i.e.,

$$\begin{aligned} \sum _{a \in A ^{\rightarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^+_{a}({q^{\text {TC}}})}^2 + \sum _{a \in A ^{\leftarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^-_{a}({q^{\text {TC}}})}^2 > (p^{+}_{{w_1}})^2 - (p^{-}_{{w_2}})^2. \end{aligned}$$

(22)

Due to Constraints (21a)–(21d), it follows

$$\begin{aligned} \xi ^+_{a}({q^{\text {TC}}})^2 \le {\bar{q}}_{a}^2 \le {\bar{f}}_a, \ a \in A ^{\rightarrow }{(u,v)}, \quad \xi ^-_{a}({q^{\text {TC}}})^2 \le {\underline{q}}_{a}^2 \le {\bar{f}}_a, \ a \in A ^{\leftarrow }{(u,v)}. \end{aligned}$$

Consequently, from this and the feasibility of (21k) for $z$, it follows

$$\begin{aligned}&\sum _{a \in A ^{\rightarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^+_{a}({q^{\text {TC}}})}^2 + \sum _{a \in A ^{\leftarrow }{({w_1},{w_2})}} \Lambda _{a} {\xi ^-_{a}({q^{\text {TC}}})}^2 \\&\quad \le \sum _{a \in A ^{\rightarrow }{({w_1},{w_2})}} \Lambda _{a} {{\bar{f}}} + \sum _{a \in A ^{\leftarrow }{({w_1},{w_2})}} \Lambda _{a} {{\underline{f}}} \le (p^{+}_{{w_1}})^2 - (p^{-}_{{w_2}})^2, \end{aligned}$$

which is a contradiction to (22). $\square$

Combining the previous results proves that we can model the infinitely many adjustable robust constraints (4d) by the finitely many Constraints (21).

Theorem 4.7

Let $G =(V,A)$ be a tree. Then, every optimal solution of the bilevel problem (4), where we replaced (4d) by (21), is an optimal solution of the bilevel problem (4). Moreover, every optimal solution of (4) that additional satisfies the conditions of Lemma 3.5 can be extended to an optimal solution of (4), where we replaced (4d) by (21).

Proof

The claim follows from Lemmas 3.5, 4.5, and 4.6 . $\square$

Remark 4.8

We note that we can easily include lower $q^-_a$ and upper $q^+_a$ arc flow bounds for all arcs $a \in A$ by

$$\begin{aligned} q^-_a \le -{\underline{q}}_{a} \le q^+_a, \quad q^-_a \le {\bar{q}}_{a} \le q^+_a. \end{aligned}$$

Since in Model (21) the variable ${\underline{q}}_{a}$ equals the absolute value of the lower arc flow bound $\xi ^-_{a}({q^{\text {TC}}})$ and since ${\bar{q}}_{a}$ equals the upper arc flow bound $\xi ^+_{a}({q^{\text {TC}}})$ given by Lemma 4.2, this ensures that the flow stays in the a priori given flow bounds. We abstract from flow bounds in our model, since the consideration of pressure levels allows to bound the flow by Constraints (21k).

Model (21) contains bilinear terms in Constraints (21d) and (21h). Since these bilinear terms are products of a binary variable and a nonnegative and bounded variable, we can reformulate them using big-$M$s. We note that the upper bounds for ${\underline{h}}^{+}_{(u,v)}$ and ${\bar{h}}^{+}_{(u,v)}$ are given by (20a) and for ${\bar{h}}^{-}_{(u,v)}$ and ${\underline{h}}^{-}_{(u,v)}$ by (20b). The bilinear constraints (21d) can thus be reformulated as

$$\begin{aligned}&{\bar{q}}_{(u,v)} = {\bar{y}}^+_{(u, v)} + {\bar{y}}^-_{(u, v)}, \end{aligned}$$

(23a)

$$\begin{aligned}&{\bar{y}}^+_{(u, v)} \ge 0, \quad {\bar{y}}^+_{(u, v)} \le M^+(1-{\bar{x}}_{(u, v)}), \quad {\bar{y}}^+_{(u, v)} \ge {\bar{h}}^{+}_{(u, v)} - M^+{\bar{x}}_{(u, v)}, \end{aligned}$$

(23b)

$$\begin{aligned}&{\bar{y}}^-_{(u, v)} \ge 0, \quad {\bar{y}}^-_{(u, v)} \le M^-{\bar{x}}_{(u, v)}, \quad {\bar{y}}^-_{(u, v)} \ge {\bar{h}}^{-}_{(u, v)} - M^-(1 - {\bar{x}}_{(u, v)}). \end{aligned}$$

(23c)

In analogy, we can reformulate the bilinear constraints (21h) by

$$\begin{aligned}&{\underline{q}}_{(u,v)} = {\underline{y}}^+_{(u, v)} + {\underline{y}}^-_{(u, v)}, \end{aligned}$$

(24a)

$$\begin{aligned}&{\underline{y}}^+_{(u, v)} \ge 0, \quad {\underline{y}}^+_{(u, v)} \le M^+(1-{\underline{x}}_{(u, v)}), \quad {\underline{y}}^+_{(u, v)} \ge {\underline{h}}^{+}_{(u, v)} - M^+{\underline{x}}_{(u, v)}, \end{aligned}$$

(24b)

$$\begin{aligned}&{\underline{y}}^-_{(u, v)} \ge 0, \quad {\underline{y}}^-_{(u, v)} \le M^-{\underline{x}}_{(u, v)}, \quad {\underline{y}}^-_{(u, v)} \ge {\underline{h}}^{-}_{(u, v)} - M^-(1 - {\underline{x}}_{(u, v)}). \end{aligned}$$

(24c)

For ease of notation in the following lemma, (21*) denotes (21) where we replaced Constraints (21d) and (21h) by (23) and (24).

Lemma 4.9

A vector $q^{\text {TC}}\in \mathbb {R} _{\ge 0}^{V_+ \cup V_-}$ is feasible for (21) if and only if it is feasible for (21*).

Proof

We can extend every feasible solution of (21) to satisfy (23) and (24). To do so, we choose ${\bar{y}}^+, {\bar{y}}^-, {\underline{y}}^+,$ and ${\underline{y}}^+$ as small as possible. Consequently, (23a) and (24a) equal Constraints (21d) and (21h). Thus, the extended solution satisfies (21*).

From the construction of (23) and (24) it follows that the flows ${\bar{q}}_{}$ and ${\underline{q}}_{}$ obtained in (23a) and (24a) are at least as large as the flows obtained in (21d) and (21h). From this and the fact that $\Lambda _a q _a \mathchoice{\left|q _a \right|}{|q _a |}{|q _a |}{|q _a |}$ is increasing for all $a \in A$, it follows that every feasible point of (21*), is also feasible for (21). $\square$

After reformulating the bilinear terms in (21) by the discussed linearizations, we can model the adjustable robust Constraint (4d) by the finitely many constraints

$$\begin{aligned} \text {(21a)--(21c), (21e)--(21g), (21i)--(21l), (23), (24)}. \end{aligned}$$

(25)

For the considered nonlinear flow model, which is based on the Weymouth pressure loss equation, the presented model of the technical capacities is a convex mixed-integer model. This is surprising since the Weymouth pressure drop model is itself nonconvex. The convex mixed-integer reformulation is obtained by using additional binary variables to model the maximum flow in a pipe and by exploiting that, for the considered gas transport model, the pressure drop $\Lambda _{a} q _{a} \mathchoice{\left|q _{a} \right|}{|q _{a}|}{|q _{a}|}{|q _{a}|}$ is quadratic for every pipe $a \in A$ if the direction of the arc flow $q _{a}$ is known. The model further consists only of polynomially many (in the number of nodes of the network) constraints and variables. Finally, we note that this model can also be generalized to potential-based flow models as explained in Remark 2.1. To do so, we only have to replace (21k) by

$$\begin{aligned} \sum _{a \in A ^{\rightarrow }{(u,v)}} \phi _{a}({{\bar{q}}_{a}}) + \sum _{a \in A ^{\leftarrow }{(u,v)}} \phi _{a}({{\underline{q}}_{a}}) \le {\pi }^+_{u} - {\pi }^-_{v}, \quad (u, v) \in V ^2, \end{aligned}$$

where $\phi$ is the potential loss function as introduced in Remark 2.1. We further can neglect Constraints (21i) and (21j), which result from a modeling choice to reduce the number of convex constraints. For general potential-based flows, the obtained model is not necessarily convex anymore since general potential loss functions may not depend quadratically on the arc flow, e.g., in case of water networks.

5 Additional combinatorial constraints

In this section, we present valid combinatorial constraints for (21), respectively (25), that speed up the solution process, which we will analyze later in Sect. 6. We prove the results w.r.t. Model (21), but they can be shown in analogy for Model (25). We note that these additional constraints do not influence the set of feasible technical capacities modeled by (21).

We first prove that for every feasible point $z$ of (21), a feasible point with the same technical capacities $q^{\text {TC}}$ always exists such that the right-hand sides of Constraints (21c) and (21g) are minimal, i.e., a binary variable is zero if the corresponding left-hand side is non-positive. Here, $\lceil x \rceil$ denotes rounding up the value x.

Lemma 5.1

Let $G =(V,A)$ be a tree and let $z$ be a feasible point of (21) with technical capacities $q^{\text {TC}}$. Then, a feasible point ${\tilde{z}}$ with the same technical capacities $q^{\text {TC}}$ exists such that for arc $(u, v) \in A$ the corresponding binaries are given by

$$\begin{aligned}&\tilde{{\bar{x}}}_{(u, v)} = \max \left\{ {0, \left\lceil \frac{1}{M^+} ({\bar{h}}^{+}_{(u, v)} - {\bar{h}}^{-}_{(u, v)}) \right\rceil } \right\} , \end{aligned}$$

(26a)

$$\begin{aligned}&\tilde{{\underline{x}}}_{(u, v)} = \max \left\{ {0, \left\lceil \frac{1}{M^+} ({\underline{h}}^{+}_{(u, v)} - {\underline{h}}^{-}_{(u, v)}) \right\rceil } \right\} . \end{aligned}$$

(26b)

Proof

Let be $z= ({\bar{f}}, {\underline{f}}, {\bar{q}}_{,} {\underline{q}}_{,} {\underline{h}}^{-}_{,} {\bar{h}}^{-}_{,} {\underline{h}}^{+}_{,} {\bar{h}}^{+}_{,} {\underline{x}}_{,} {\bar{x}}_{,} q^{\text {TC}})$ a feasible point of (21). We assume that an arc $(u, v) \in A$ exists such that, w.l.o.g.,

$$\begin{aligned} 1 = {\bar{x}}_{(u, v)} > 0 = \max \left\{ {0, \left\lceil \frac{1}{M^+} ({\bar{h}}^{+}_{(u, v)} - {\bar{h}}^{-}_{(u, v)}) \right\rceil } \right\} \end{aligned}$$

holds. We now set ${\bar{x}}_{(u, v)}=0$. Consequently, ${\bar{q}}_{(u, v)}$ possibly decreases according to Constraint (21d). The remaining point stays feasible since Constraints (21a), (21b), (21e)–(21h), (21j), and (21l) are not affected by this modification. Furthermore, Constraint (21i) is still fulfilled since we only possibly decreased ${\bar{q}}_{(u, v)}$ and thus, (21k) is satisfied. We also note that Constraint (21c) is satisfied due to the choice of $M^+\ge 0$.

Repeating the previous procedure for ${\bar{x}}_{}$ and ${\underline{x}}_{}$ shows the claim. $\square$

With the help of the latter result, we now present additional combinatorial constraints regarding the binary variables that explicitly use the network structure. The intuition behind these constraints can be sketched as follows: From Lemma 5.1 it follows that an optimal solution for model (21) exists such that for an arc $a =(u, v) \in A$, the variable ${\bar{q}}_{a}$ represents the maximal arc flow of $a$, i.e.,

This means that ${\bar{q}}_{a}$ equals the minimum flow that can be sent via $(u, v)$ by entries in , which is the sub-tree that includes node $u$ and is obtained by removing arc $(u,v)$, and of the flow that can be received by exits in . If the entries in  can supply more flow than the exits in  can receive, i.e.,

then ${\bar{x}}_{(u,v)}=1$ holds. Considering now for an outgoing arc $(v, l)$ the variable ${\bar{q}}_{(v, l)}$ only possibly increases the number of entries that can supply flow via $(v, l)$, i.e., , and possibly reduces the number of exits that can receive flow via arc $(v, l)$, i.e., . Consequently, the value of ${\bar{q}}_{(v,l)}$ is again determined by the exits, i.e., ${\bar{q}}_{(v,l)} = {\bar{h}}^{-}_{(v,l)}$, and, thus, ${\bar{x}}_{(v,l)}=1$ holds. This shows a correspondence between the binary variables using the given network structure and is the key for the following combinatorial constraints. In analogy to the above, we can derive further constraints for the binaries ${\underline{x}}_{}$ corresponding to the lower flow variables ${\underline{q}}_{}$.

Lemma 5.2

Let $G =(V,A)$ be a tree and $z$ a feasible point of (21) that satisfies (26). Then, the inequalities

$$\begin{aligned} {\bar{x}}_{(u, v)}&\le {\bar{x}}_{(v,l)},\quad \,(v, l) \in \delta ^{\mathrm {out}}(v), \end{aligned}$$

(27a)

$$\begin{aligned} {\underline{x}}_{(v, l)}&\le {\underline{x}}_{(u,v)},\quad \!\,(v, l) \in \delta ^{\mathrm {out}}(v), \end{aligned}$$

(27b)

$$\begin{aligned} {\bar{x}}_{(u, v)}&\le {\underline{x}}_{(l,v)},\quad \,(l, v) \in \delta ^{\mathrm {in}}(v), \end{aligned}$$

(27c)

are satisfied for $a =(u, v)$.

Proof

Applying Lemma 5.1, a feasible point $({\bar{f}}, {\underline{f}}, {\bar{q}}_{,} {\underline{q}}_{,} {\underline{h}}^{-}_{,} {\bar{h}}^{-}_{,} {\underline{h}}^{+}_{,} {\bar{h}}^{+}_{,} {\underline{x}}_{,} {\bar{x}}_{,} q^{\text {TC}})$ for (21) exists that satisfies (26).

We first consider Inequality (27a). If ${\bar{x}}_{(u, v)} = 0$ holds, then (27a) is redundant since ${\bar{x}}_{(v, l)} \in \left\{ {0,1} \right\}$. We now assume that ${\bar{x}}_{(u, v)} = 1$ holds. Consequently,

$$\begin{aligned} 1 = {\bar{x}}_{(u, v)} = \left\lceil \frac{1}{M^+} ({\bar{h}}^{+}_{(u, v)} - {\bar{h}}^{-}_{(u, v)}) \right\rceil \end{aligned}$$

holds and thus,

$$\begin{aligned} {\bar{h}}^{+}_{(u, v)} > {\bar{h}}^{-}_{(u, v)} \ge 0 \end{aligned}$$

is satisfied. From $(v, l ) \in \delta ^{\mathrm {out}}(v)$ it follows

(28)

where , respectively , contains the nodes of the connected component that includes $u$, respectively $v$, and is created by removing arc $(u, v)$, respectively $(v, l)$. From this as well as Constraints (21a) and (21b), it follows

$$\begin{aligned} {\bar{h}}^{+}_{(v, l)} \ge {\bar{h}}^{+}_{(u, v)} > {\bar{h}}^{-}_{(u, v)} \ge {\bar{h}}^{-}_{(v, l)} \ge 0, \end{aligned}$$

and consequently, ${\bar{x}}_{(v, l)} = 1$ is satisfied due to (21c).

We now consider (27b). If ${\underline{x}}_{(v, l)} = 0$ holds, then (27b) is redundant since ${\underline{x}}_{(u, v)} \in \left\{ {0,1} \right\}$. Thus, we now assume that ${\underline{x}}_{(v, l)} = 1$ holds. Due to (26),

$$\begin{aligned} 1 = {\underline{x}}_{(v, l)} = \left\lceil \frac{1}{M^+} ({\underline{h}}^{+}_{(v, l)} - {\underline{h}}^{-}_{(v, l)}) \right\rceil \end{aligned}$$

holds and, thus,

$$\begin{aligned} {\underline{h}}^{+}_{(v, l)} > {\underline{h}}^{-}_{(v, l)} \ge 0 \end{aligned}$$

is satisfied. From $(v, l ) \in \delta ^{\mathrm {out}}(v)$ it again follows (28). This, as well as Constraints (21e) and (21f), lead to

$$\begin{aligned} {\underline{h}}^{+}_{(u, v)} \ge {\underline{h}}^{+}_{(v, l)} > {\underline{h}}^{-}_{(v, l)} \ge {\underline{h}}^{-}_{(u, v)} \ge 0, \end{aligned}$$

and consequently, ${\underline{x}}_{(u, v)} = 1$ is satisfied due to (21g).

We finally consider (27c). If ${\bar{x}}_{(u, v)} = 0$ holds, then (27c) is redundant since ${\underline{x}}_{(l, v)} \in \left\{ {0,1} \right\}$. Thus, we now assume that ${\bar{x}}_{(u, v)} = 1$ holds. Due to (26),

$$\begin{aligned} 1 = {\bar{x}}_{(u, v)} = \left\lceil \frac{1}{M} ({\bar{h}}^{+}_{(u, v)} - {\bar{h}}^{-}_{(u, v)}) \right\rceil \end{aligned}$$

holds and, thus,

$$\begin{aligned} {\bar{h}}^{+}_{(u, v)} > {\bar{h}}^{-}_{(u, v)} \ge 0 \end{aligned}$$

is satisfied.

From $(l, v) \in \delta ^{\mathrm {in}}(v)$, it follows

and thus, from (21a), (21b), (21e), and (21f) it follows

$$\begin{aligned} {\underline{h}}^{+}_{(l, v)} \ge {\bar{h}}^{+}_{(u, v)} > {\bar{h}}^{-}_{(u, v)} \ge {\underline{h}}^{-}_{(l, v)} \ge 0. \end{aligned}$$

From this and Constraint (21g) it follows ${\underline{x}}_{(l, v)} = 1$. $\square$

Consequently, the adjustable robust constraint (4d) can be modeled by (21), respectively (25), and the additional Constraints (27a)–(27c). In the following computational study, we demonstrate the impact of the presented combinatorial constraints w.r.t. running times.

6 Computational results

We now apply our results to solve the considered multilevel model of the European entry-exit gas market system with a nonlinear flow model in tree-shaped networks. To this end, we solve the model for a passive version of the Greek gas network, i.e., the network corresponds to the Greek gas network excluding its single compressor station and its single control valve. This is the first time that the considered entry-exit gas market model can be solved for a real-world sized network. For our computations, we consider the single-level reformulation (9) with linearized complementarity constraints, the additional constraints (12) and (13), the handling of the technical capacities (25), and the additional combinatorial constraints (5.2). For the latter, we also analyze their explicit effect on the running times. We further note that we can a priori exclude Constraints (1) and (3) since the flow is uniquely determined by (2) in tree-shaped networks.

6.1 Physical and economic data

For our computational analysis, we consider the GasLib 134 (version 2) network; see [33]. The GasLib 134 represents the Greek gas network, with more than 7000 km of pipes. It further is the largest publicly available tree-shaped gas network and, thus, we focus on this network in our computational study. Since the integration of active elements is currently out of scope, we bypass the single compressor station and single control valve of the GasLib 134 network. Moreover, we slightly adapt the lower pressure bounds of the GasLib 134 network by setting all lower pressure bounds of at least 37.5 bar to 32.5 bar. This ensures that the intersection of the lower and the upper pressure bound intervals is non-empty, i.e., $\bigcap _{u \in V_+ \cup V_-} [p^{-}_u, p^{+}_u ] \ne \emptyset$. The latter is a necessary condition for the existence of a feasible nomination in a passive network. In total, the network consists of 134 nodes, which contain 3 entries, 45 exits, and 86 inner nodes, and 133 pipes, which contain 47 short pipes² and 86 pipes. Each pipe $a \in A$ is characterized by its length $L_a$, diameter $D_a$, and roughness $k_a$. Further, we assume that all pipes are horizontal. For each pipe $a \in A$, we compute the pressure loss coefficient $\Lambda _a$ of the considered Weymouth model (1)–(3) according to (2.25) in [10], i.e.,

$$\begin{aligned} \Lambda _a = \left( \frac{4}{\pi } \right) ^2 \lambda _a \frac{R_{\mathrm {s}} T_{\mathrm {m}} L_a z_{\mathrm {m}, a}}{D^5_a}. \end{aligned}$$

Here, $R_{\mathrm {s}}$ is the specific gas constant, $T_{\mathrm {m}}$ a constant mean temperature, $\lambda _a$ is the friction factor of pipe $a \in A$ computed using the formula of Nikarudse, and $z_{\mathrm {m}, a}$ is the mean compressibility factor of a pipe $a \in A$ computed by the formula of Papay and an a priori estimation of the mean pressure; see Chapters [10, 30] for the explicit formulas and additional explanations.

We now turn to the modeling of the economic data. The considered time horizon consists of four time periods $t\in T$ that model the seasons summer ($t=0$), autumn ($t=1$), winter ($t=2$), and spring ($t=3$). In line with [2], we assume a single player per node. We model the variable production costs $c^{\mathrm {var}}_{i}$ of the three existing entries as follows. For entry node_80, we set  and then increase this value by 5% for production costs of the remaining entries. In a simplified way, this roughly represents the current situation regarding production costs in the Greek gas network. For the linear demand functions of the exit nodes, we assume

$$\begin{aligned} P_{i, t} (q ^{\mathrm {nom}}_{i, t}) = b_{i} q ^{\mathrm {nom}}_{i, t} + a_{i, t} \quad \text {with} \quad a_{i, t} = \max _{j \in {\mathcal {P}}_{u}, u \in V_+} \left\{ c^{\mathrm {var}}_{j} \right\} + h_{i, t}, \end{aligned}$$

where the integer $h_{i, t}$ is uniformly sampled in certain intervals; see Table 1. This construction explicitly ensures that Assumption 2 is satisfied. We note that $a_{i, t}$ is lowest in the summer $(t=0)$ and highest in the winter $(t=2)$. After fixing the previous values, we consider exogenous network costs  and the transport costs $c^{\mathrm {trans}}_{t} \in \left\{ {0.1,0.2,\ldots , 1.0} \right\}$ . Additionally, for the instances with , we vary the intercepts $a_{i, t}$ by adding a “shift” in $\left\{ {-10,-5,0,5,10} \right\}$ . In total, we obtain 110 instances.

Table 1 Economic data for exit demands functions $P_{i, t} (q ^{\mathrm {nom}}_{i, t}) = b_{i} q ^{\mathrm {nom}}_{i, t} + a_{i, t}$ with $a_{i, t} = \max _{j \in {\mathcal {P}}_{u}, u \in V_+} \{c^{\mathrm {var}}_{j} \} + h_{i, t}$, where the integer $h_{i, t}$ (in ) is uniformly sampled in the given intervals and $b_{i}$ is given in

We note that all these values have to be seen w.r.t. the considered time horizon of 1 h per time period. Moreover, extrapolating the results for the time horizon of a whole year shows that the total gas consumption of the base case, i.e., and  deviates by less than 1.4% from the total gas consumption of approximately 5.1 billion $\hbox {m}^3$ in Greece for 2019; see [4]. Additionally, the investment costs and variable costs are chosen such that the sum of the latter corresponds to 6.5% of the market volume.

6.2 Computational setup

All optimization problems have been implemented in Python 3 using Pyomo 5.6.8, see [18], and have been solved with Gurobi 9.0.1, see [16]. In doing so, we used Gurobi with standard settings except for the following adaptions. We set the parameter NumericFocus to 3 and the parameter NonConvex to 2. Thus, Gurobi tackles the nonlinear bilinear terms of Constraint (4c) by spatial branching. For the computations, we used the Kaby Lake nodes with Xeon E3-1240 v6 CPUs and 32 GB RAM of the computer cluster [27] and set a time limit of 24 h. The necessary big-$M$s are computed as presented in Sects. 3.1 and 4. Additionally, we used the upper flow bounds of the GasLib 134 network to tighten these big-$M$s.

We now briefly discuss some statistics of the considered model. Our single-level model consists of 3599 variables, which contain 698 binary variables, and of 22 085 constraints, which contain 267 quadratic constraints. The presolve of Gurobi roughly halves the number of constraints but hardly influences the other statistics including the number of quadratic constraints. We note that before presolve we have 266 combinatorial constraints (5.2). In the next section, we discuss the numerical results in detail and explicitly analyze the computational speed up of the combinatorial constraints.

6.3 Discussion of numerical results

The scope of this section is twofold: We first discuss the numerical results w.r.t. running times. Here, we focus on the computational benefit of the combinatorial constraints (5.2) of Sect. 5. Afterward, we exemplarily show the effects of modifying the economic data on the output of the four-level gas market model for the Greek gas network to shed some light on the sensitivity of the model and the solution approach.

For our discussion of the computational results, we consider 110 instances as described in Sect. 6.1. The running times are summarized in Table 2. Overall, we can solve 107 out of 110 instances to global optimality for the considered four-level gas market model within the time limit. More specifically, we solve 90 of the 110 instances within 1 h. One of the key components to achieve this performance is our modeling of the adjustable robust constraints (4d) and the additional combinatorial constraints (5.2). The running times significantly increase if these combinatorial constraints are excluded; see Table 2. This leads to the results that 23 instances could not be solved in the time limit of 24 h if the additional combinatorial constraints are neglected. The significant computational speed up of these constraints is underlined by the fact that the minimum running times without them is larger than the median, receptively nearly equal to the third quartile, of the running times including these constraints. Moreover, only 4 of the 110 instances can be solved in 1 h if the additional constraints are excluded.

Table 2 Number of solved instances (out of 110 instances) and statistics for the running times (always taken only for all instances solved to optimality)

We further analyze the computational benefit of the combinatorial constraints with the help of log-scaled performance profiles as proposed in [6]. Figure 1 shows the log-scaled performance profiles w.r.t. running times (left) and w.r.t. nodes explored in the branch-and-bound algorithm of Gurobi (right) for all 110 instances. To do so, we separately solved the considered model with the combinatorial constraints (5.2) and without them. In line with Table 2, the left profile shows that including the combinatorial constraints clearly dominates w.r.t. running times. This is mainly explained by the right performance profile in Fig. 1, which compares the number of nodes that are explored during the branch-and-bound solution process. Including the combinatorial constraints significantly reduces the number of explored nodes, which leads to the observed speed up of the solution process.

Fig. 1

Log-scaled performance profiles of running times (left) and of nodes explored in the branch and bound algorithm (right) for all 110 instances

Finally, we now turn to the analysis of the sensitivity of the approach w.r.t. changes in the economic input data. To this end, we consider a base instance with fixed exogenous investment costs  and variable transport costs . Then, we adjust the intercepts of the demand functions $a_{i, t}$ for all $i\in {\mathcal {P}}_{u}, \ u \in V, \ t\in T$, by adding a constant, which we call “shift”. Table 3 shows that increasing, respectively decreasing, the demand mainly affects the nominated amount of gas in the summer period $(t=0)$. The remaining time periods are only slightly affected by demand changes. Moreover, a decrease of the demand affects the nominations more than an increase of the demand. On the one hand, this indicates that for time periods $t\in \left\{ {1,2,3} \right\}$ the network already operates near to its maximal capacity since an increased demand only slightly leads to higher nominations. On the other hand, the demand in time periods $t\in \left\{ {1,2,3} \right\}$, especially the winter period $t=2$, is nearly inelastic since an decrease of the demand only leads to a small decrease of the nominated amount of gas. Moreover, the sum of all booked capacities is nearly the same. This can be explained by the almost inelastic demand of the winter period since, usually, the booking is determined by the period with highest demand, i.e., it is determined in winter. Although the total booked capacity is almost not affected by the change of the demand, the booked capacity at the single nodes clearly differs; see third column of Table 3. Thus, the overall solution of the four-level optimization problem is clearly affected by demand changes; see Table 3. We illustrate these changes w.r.t. the bookings in Fig. 2. The figure shows that uniformly increasing the demand of all exits decreases the booked capacities in the south and leads to larger booked capacities in the middle, respectively north, of the network. This is possibly based on a combination of the larger willingness to pay of the exits and the transport capacity of the network. There are more exits in the south than in the north and, thus, the network probably already operates at its maximum especially in the south. Consequently, an increased willingness to pay at the demand nodes makes it more attractive for the TSO to reduce the technical capacities in the south and increase them in the north. This results in larger bookings in the north and smaller bookings in the south.

Table 3 For all $i\in {\mathcal {P}}_{u}, \ u, \ t\in T$, the intercepts $a_{i, t}$ vary by adding “shift” in . The remaining values denote the corresponding relative changes of the bookings $q ^{\mathrm {book}}_{}$, and nominations $q ^{\mathrm {nom}}_{}$ w.r.t. the base case marked in bold

Fig. 2

Relative changes of the bookings, i.e., $q^\mathrm {book}_v / q^\mathrm {book}_{\mathrm {base},v}$, for the case $\text {shift} = 10$ and the base case ($\text {shift} = 0$) in the Greek gas network. Entries are denoted by blue squares, inner nodes by small black diamonds, exits with positive relative change by green circles, and exits with negative relative change by orange circles

7 Conclusion

This paper provides optimization techniques that enable us to solve a multilevel model of the European entry-exit gas market system, see [14], with a nonlinear flow model for real-world sized and tree-shaped networks. In line with the literature [2, 14], this multilevel model can be equivalently reformulated to a bilevel problem and, on top of that, to a nonconvex and nonsmooth mixed-integer nonlinear single-level problem. This reformulation is independent of the considered flow model. The core difficulty of this single-level reformulation are the nonlinear adjustable robust constraints, by which the TSO computes the technical capacities of the network. These constraints alone make the considered problem computationally intractable in general. However, under the assumption of passive networks, i.e., no active elements such as compressor stations are considered, we derived a finite-dimensional reformulation of these nonlinear adjustable robust constraints for the case of tree-shaped networks. Moreover, we strengthened this reformulation by additional combinatorial constraints. The latter significantly increase the performance of our model as demonstrated by the numerical results. Further, the presented reformulation can also be generalized to other potential-based flow models under very mild assumptions. The reformulation has some nice properties such that it only uses convex constraints including newly introduced integer variables. This enables us to solve the multilevel model of the European entry-exit gas market system with a nonlinear flow model for a real-world sized network, namely the Greek gas network without active elements, to global optimality. This is the first time that this multilevel model can be solved for a real-world sized network since even for simplified linear flow models the latter can only be solved for stylized small (but cyclic) networks so far in the literature. The computational tractability of our approach is demonstrated by our computational study, in which the majority of the instances can be solved within 1 h.

Nevertheless, there still are many possibilities for future research. Both from a mathematical as well as application point of view, it would be of interest to see if the results can be further developed so that one can also cope with active elements or general, i.e., cyclic, networks. From an economic point of view, our results can be directly applied to analyze economic effects such as social welfare losses for real-world sized networks and nonlinear flow models.