Multi-objective dynamic programming with limited precision

Abstract

This paper addresses the problem of approximating the set of all solutions for Multi-objective Markov Decision Processes. We show that in the vast majority of interesting cases, the number of solutions is exponential or even infinite. In order to overcome this difficulty we propose to approximate the set of all solutions by means of a limited precision approach based on White’s multi-objective value-iteration dynamic programming algorithm. We prove that the number of calculated solutions is tractable and show experimentally that the solutions obtained are a good approximation of the true Pareto front.

1 Introduction

Markov decision processes (MDPs) are a well-known conceptual tool useful for modelling the operation of systems as sequential decision processes. To solve a MDP is to find a policy (a rule for making decisions) that causes the system to perform optimally with respect to some criterion (see Puterman [10]).

Usual optimization procedures take into account just a scalar value to be maximized. However, as stated in Miettinen and Ruiz [8], many real-world optimization applications deal with making decisions in the presence of several conflicting objectives. Different methodologies must be developed to solve these multi-objective problems.

By merging both concepts (MDPs and multi-objective optimization) we are led to consider Multi-objective Markov decision processes (MOMDPs), that are Markov decision processes in which rewards given to the agent consist of two or more independent values, i. e., rewards are numerical vectors. In recent years there has been a growing interest in considering theory and applications of multi-objective Markov decision processes and multi-objective Reinforcement Learning, e.g. see Roijers and Whiteson [11], and Drugan et al. [2].

In standard scalar optimization problems the solution is usually a singleton. In particular, for MDPs a deterministic stationary policy can be found that attains the optimal value. However, in a multi-objective setting we are usually faced with a set of incomparable nondominated solutions that is called the Pareto front. The computation of the Pareto front must face a difficulty: since the number of values in the front is usually huge (in fact, it can be infinite), the computation can be infeasible.

Decision makers eventually take just one solution from the Pareto front. However, there are different possible ways to reach such decision. In this sense, Roijers et al. [12] explore the concept of solution to a MOMDP, and provide a taxonomy based on three different factors: whether one or multiple policies are required, whether mixtures of stationary policies are allowed, and whether a linear scalarization of the rewards can be a faithful model for user preferences.

When it is possible to explicitly state the decision maker’s preferences prior to problem solving as a scalar function to be optimized, we are lead to single-policy approaches ( Perny and Weng [9], Wray et al. [19]). These compute a single optimal policy according to some scalarization of preferences, usually expressed as a vector of weights. Of course, the process can be repeated as many times as desired in order to find different solutions.

On the other hand, multi-policy approaches try to compute simultaneously all the values in the Pareto front (Van Moffaert and Nowé[17], Ruiz-Montiel et al. [13]). Roijers et al. [12] (Sect. 3) describe three different motivating scenarios for MOMDPs in which calculating the whole or part of the Pareto front is advisable before the final choice for a particular policy is made. The first scenario occurs when the vector of weights is unknown in advance. The second one occurs when the vector of weights is not well defined. The underlying idea in these two scenarios is to present choices before asking for preferences. Finally, when preferences are known but the decision function is nonlinear (e.g. nonadditive rewards), thus leading to a nonstationary or stochastic optimal policy, scalarization may be undesirable.

Even if we are interested in the full Pareto front, sometimes the problem is simplified by the fact that the solution is delimited by the convex coverage of the subset of deterministic stationary policies (see Vamplew et al. [16]). That is the case when a linear scalarization is an acceptable preference model, or when mixtures of stationary policies are allowed. Several practical contributions have been made in this setting. For example Etessami et al. [4] and Forejt et al. [5] formalize model-checking problems as MOMDPs where mixture policies are allowed. The exact solution to these problems can be achieved finding only the set of nondominated deterministic stationary policies. Since there can still be an exponentially large number of such policies, the authors also provide fully polynomial-time approximation schemes for the convex coverage of the solution set.

In the general case, with more general preference models where mixture policies are not acceptable (e.g. for ethical reasons, see Lizotte et al. [7]), Pareto-optimal non-stationary policies need also to be taken into consideration. This case was theoretically solved by White [18], but the exact solution is not possible in practice due to the infeasible (or even infinite) size of the Pareto front. Therefore, recent multi-objective reinforcement learning techniques avoid approximating the full Pareto front, or are tested on limited problem instances, like deterministic domains (see Drugan et al. [2] Drugan [3]). The main focus of our work is then to provide a general procedure that, while being feasible, provides a “good” approximation of the complete Pareto front.

The structure of this paper is as follows: first we define formally the concepts related to MOMDPs and prove that under a very restrictive set of assumtions the number of solutions of a MOMDP is tractable (Proposition 1); but we show that if any of these assumptions does not hold, then that number becomes intractable or even infinite. In the following section we present the basic value-iteration algorithm for solving a MOMDP (Algorithm 1) and the modification that we propose (Algorithm $W_{LP}$, given by equation 1), and prove that algorithm $W_{LP}$ computes a tractable number of approximate solutions. Algorithm $W_{LP}$ is then applied to benchmark problems to check if it can provide a good approximation of the true Pareto front. Finally some conclusions are drawn.

2 Multi-objective Markov decision processes

This section defines multi-objective Markov decision processes (MOMDPs) and their solutions. When possible, notation is consistent with that of Sutton and Barto [14].

A MOMDP is defined by at least the elements in the tuple $({\mathcal {S}}, {\mathcal {A}}, p, \mathbf {r}, \gamma )$, where: ${\mathcal {S}}$ is a finite set of states; ${\mathcal {A}}(s)$ is the finite set of actions available at state $s \in {\mathcal {S}}$; p is a probability distribution such that $p(s,a,s')$ is the probability of reaching state $s'$ immediately after taking action a in state s; $\mathbf {r}$ is a function such that $\mathbf {r}(s,a,s') \in \mathrm{I\!R}^q$ is the reward obtained after taking action a in state s and immediately transitioning to state $s'$; and $\gamma \in (0,1]$ denotes the current value of future rewards. We will denote $S= |{\mathcal {S}}|$ and $\mathbf {r}(s,a)=\sum _{s'} p(s,a,s') \mathbf {r}(s,a,s')$. The only apparent difference with scalar finite Markov decision processes (MDPs) (e.g., see Sutton and Barto [14]) is the use of a vector reward function.

A MOMDP can be episodic, if the process always starts at a start state $s_o \in {\mathcal {S}}$, terminates when reaching any of a set of terminal states $\Gamma \subseteq {\mathcal {S}}$, and before termination there is always a non-zero probability of eventually reaching some terminal state. Otherwise, the process is continuing. A MOMDP can be of finite-horizon, if the process terminates after at most a given finite number of actions n. We say that such process is n-step bounded. Otherwise, it is of infinite-horizon.

MDPs are frequently used to model the interaction of an agent with an environment at discrete time steps. We define the goal of the agent as the maximization of the expected accumulated (additive) discounted reward over time.

Let us now define the concepts related to solving a MOMDP. A decision rule $\delta$ is a function that associates each state to an available action. A policy $\pi = (\delta _1, \delta _2, \ldots \delta _i, \ldots )$ is a sequence of decision rules, such that $\delta _i(s)$ determines the action to take if the process is in state s at time step i. If there is some decision rule $\delta$ such that for all i, $\delta _i = \delta$, then the policy is stationary. Otherwise, it is non-stationary. We denote by $\pi ^n = (\delta _1, \ldots , \delta _n), \ n \ge 1$ the finite n-step subsequence of policy $\pi$.

Let $S_t, R_t$ be two random variables denoting the state, and the vector reward received at time step t respectively. The value $\mathbf {v}_{\pi }$ is defined as the expected accumulated discounted reward obtained starting at state s and applying policy $\pi$ (analogously to the scalar case Sutton and Barto [14]),

$$\begin{aligned} \mathbf {v}_{\pi }(s) = {\mathbb {E}}\Big [\sum _{k=0}^{\infty }{\gamma ^k R_{t+k+1}} \ | \ S_t = s \Big ] \end{aligned}$$

For any given policy $\pi$, we denote the values of its n-step subpolicies $\pi ^n$ as $\mathbf {v}_{\pi }^n$.

Vector values define only a partial order dominance relation. Given two vectors $\mathbf {u} = (u_1, \ldots u_q), \mathbf {v} = (v_1, \ldots , v_q)$, we define the following relations: (a) Dominates or equals, $\mathbf {u} \succeq \mathbf {v}$ if and only if for all i, $u_i \ge v_i$; (b) Dominates, $\mathbf {u} \succ \mathbf {v}$ if and only if $\mathbf {u} \succeq \mathbf {v}$ and $\mathbf {u} \ne \mathbf {v}$; (c) Indifference, $\mathbf {u} \sim \mathbf {v}$ if and only if $\mathbf {u} \not \succeq \mathbf {v}$ and $\mathbf {v} \not \succeq \mathbf {u}$.

Given a set of vectors $X \subset \mathrm{I\!R}^q$, we define the subset of nondominated, or Pareto-optimal, vectors as ${{\,\mathrm{{\mathcal {N}}}\,}}(X) = \{\mathbf {u} \in X \ | \ \not \exists \mathbf {v} \in X, \ \mathbf {v} \succ \mathbf {u} \}$.

We denote by ${\mathbb {V}}^n(s)$ and ${\mathbb {V}}(s)$ the set of nondominated values of all possible n-step policies, and of all possible policies at state s respectively. For an n-step bounded process, ${\mathbb {V}}^n(s) = {\mathbb {V}}(s)$ for all $s \in {\mathcal {S}}$. The solution to a MOMDP is given by the ${\mathbb {V}}(s)$ sets of all states.

2.1 Combinatorial explosion

In this section we analyze some computational difficulties related to solving MOMDPs.

Proposition 1

Let us consider an episodic q-objective MDP with initial state $s_0$ satisfying the following assumptions:

• 1. The length of every episode is at most d.

• 2. Immediate rewards $\mathbf {r}(s,a,s')$ are integer in every component and every component is bounded by $r_{min}$, $r_{max}$.

• 3. The MDP is deterministic.

• 4. Discount rate is $\gamma = 1$.

Then $|{\mathbb {V}}(s_0)| \le (R\times d + 1)^{q-1}$, where $R=r_{max}-r_{min}$.

Proof

given assumptions 2, 3 and 4 the value of a policy is a vector with integer components. Given assumptions 1 and 2 these components lie in the interval $\left[ d\times r_{min}, d\times r_{max}\right]$. The interval can contain at most $R\times d + 1$ integers. So there can be at most $(R\times d + 1)^q$ different vectors for the values; however, not all of them can be nondominated. Consider the $q-1$ first components $1,\ldots , q-1$ of the vector. There are at most $(R\times d + 1)^{q-1}$ different possibilities for them. For each one, just one vector is nondominated: the one having the greatest value for the q-th component. Hence there are at most $(R\times d + 1)^{q-1}$ nondominated policy values.

$\square$

Notice that nothing has been assumed about the number of policies (except that it is finite, by assumption 1). So in general there are many more policies (an exponential number of them) than values.

Let us consider the graph of Fig. 1 (adapted from Hansen [6]) with rewards $\mathbf {r}(s_i, a_1, s_{i+1}) = (0, 1)$ and $\mathbf {r}(s_i, a_2, s_{i+1}) = (1, 0)$. It represents an instance (for $d=3$) of a family of deterministic MDPs. Assume $\gamma = 1$. All episodes are of length d and all the assumptions of Proposition 1 hold. And ${\mathbb {V}}(s_0) =$ ${{\,\mathrm{{\mathcal {N}}}\,}}({\mathbb {V}}(s_0)) =$ $\{(d,0), (d-1, 1),\ldots ,(0,d)\}$ and $|{\mathbb {V}}(s_0)| = d + 1$. Notice that the number of policies is $2^d$.

Fig. 1

Hansen’s graph

We will show now that if any of the assumptions is not satisfied, then the number of different nondominated values $| {\mathbb {V}}(s_0) |$ can be also exponential in d.

Nonbounded or noninteger immediate rewards Let us consider a case where rewards are not bounded and assumption 2 does not hold. Consider for example for all i, $\mathbf {r}(s_i, a_1, s_{i+1}) = (0, 2^i)$ and $\mathbf {r}(s_i, a_2, s_{i+1}) = (2^i, 0)$. Then, for depth d, for all subset $I \subseteq \left[ 1, d\right]$ and all vector ${\mathbf {v}}= (\sum _{i \in I} 2^i, \sum _{i \notin I} 2^i )$ there exists a policy with value $\mathbf {v}$ for $s_0$, namely the policy that for all state $s_i$ selects $a_1$ if $i\notin I$ and $a_2$ if $i\in I$. Notice that all these values ${\mathbf {v}}$ are nondominated. So the number of nondominated values grows exponentially with d.

Let us consider now a case with noninteger rewards, for example for all i, $\mathbf {r}(s_i, a_1, s_{i+1})$ = $(0, 1/2^i)$ and $\mathbf {r}(s_i, a_2, s_{i+1})$ = $(1/2^i, 0)$. Let b be a bit (0 or 1) and ${\bar{b}}$ its negation (1 or 0). Consider numbers in binary notation. Then, for depth d and for all $\mathbf {v}= (0.b_1b_2\ldots b_d, 0.{\bar{b}}_1{\bar{b}}_2\ldots {\bar{b}}_d)$ there exists a policy with value $\mathbf {v}$ for $s_0$, namely the policy that for all state $s_i$ selects $a_1$ if $b_i = 0$ and $a_2$ if $b_i= 1$. Notice that all these values ${\mathbf {v}}$ are nondominated. So the number of nondominated values grows exponentially with d.

Discount rate Assume rewards are for all i $\mathbf {r}(s_i, a_1, s_{i+1}) = (0, 1)$ and $\mathbf {r}(s_i, a_2, s_{i+1}) = (1, 0)$, so integer and bounded. But consider a discount rate $\gamma < 1$, for example $\gamma = 1/2$. Then, for depth d and for all $\mathbf {v}= (0.b_1b_2\ldots b_d, 0.{\bar{b}}_1{\bar{b}}_2\ldots {\bar{b}}_d)$ there exists again a policy (the same defined for noninteger rewards) with value $\mathbf {v}$ for $s_0$. So the number of nondominated values grows exponentially with d.

Nondeterministic actions Assume rewards are $\mathbf {r}(s_i, a_1, s_{i+1}) = (0, 1)$ and $\mathbf {r}(s_i, a_2, s_{i+1}) = (1, 0)$, so integer and bounded. Assume also $\gamma = 1$. It is well known that every discounted MDP can be transformed into an equivalent non-discounted probabilistic MDP (see for instance Puterman [10], Sect. 5.3). Let us add a final state g to the previous model, and for all i let $p(s_i, a_1, s_{i+1})= p(s_i, a_2, s_{i+1}) = 1/2$, $p(s_i, a_1, g)= p(s_i, a_2, g) = 1/2$. Then again for depth d, for all $\mathbf {v}= (0.b_1b_2\ldots b_d, 0.{\bar{b}}_1{\bar{b}}_2\ldots {\bar{b}}_d)$ there exists a policy (again the same defined for noninteger rewards) with value $\mathbf {v}$ for $s_0$, and the number of nondominated values grows exponentially with d.

Fig. 2

Unbounded episodes

Cyclical graphs Let us now withhold assumption 1 (i. e., let us assume that episodes are finite but can be of unbounded length). To avoid the divergence of $\mathbf {v}$, we must consider that the model is probabilistic, i. e., also abandon assumption 3. Then the situation is even worse: there are MDPs with a finite number of states and an infinite number of nondominated values. This is due to the existence of nonstationary nondominated policies, i. e., policies that take a different action every time a state is reached. For example, let us consider the graph in Fig. 2. Let $\mathbf {r}(s_0, a_1, s_0) = (0, 1)$, $\mathbf {r}(s_0, a_2, s_0) = (1, 0)$, $\mathbf {r}(s_0, a_1, s_1) = \mathbf {r}(s_0, a_2, s_1) = (0, 0)$. Let $p(s_0, a_1, s_0)= p(s_0, a_1, s_1) = p(s_0, a_2, s_0)= p(s_0, a_2, s_1)= 1/2$. Then, for all ${\mathbf {v}}= (0.b_1b_2\ldots b_i\ldots , 0.{\bar{b}}_1{\bar{b}}_2\ldots {\bar{b}}_i\ldots )$ there exists a nonstationary policy with value $\mathbf {v}$ for $s_0$. That policy selects for the i-th visit to $s_0$ $a_1$ if $b_i=0$ and $a_2$ if $b_i=1$. So the number of nondominated values is infinite.

If we consider continuing MDPs -even deterministic- with $\gamma < 1$ the same situation appears: there are nonstationary nondominated policies and an infinite number of values can be obtained. For example, let us consider the graph of Fig. 3, $\mathbf {r}(s_0, a_1, s_0) = (0, 1)$, $\mathbf {r}(s_0, a_2, s_0) = (1, 0)$, $\gamma = 1/2$. Again for all ${\mathbf {v}}= (0.b_1b_2\ldots b_i\ldots , , 0.{\bar{b}}_1{\bar{b}}_2\ldots {\bar{b}}_i\ldots )$ the same policy above defined yields the value $\mathbf {v}$.

Fig. 3

Continuing task

3 Algorithms

This section describes two previous multi-objective dynamic programming algorithms, and proposes a tractable modification.

3.1 Recursive backwards algorithm

An early extension of dynamic programming to the multi-objective case was described by Daellenbach and De Kluyver [1]. The authors showed that the standard backwards recursive dynamic programming procedure can be applied straightforwardly to problems with directed acyclic networks and additive positive vector costs. The idea easily extends to other decision problems, including stochastic networks. We denote this first basic multi-objective extension of dynamic programming as algorithm B.

3.2 Vector value iteration algorithm

The work of White [18] considered the general case, applicable to stochastic cyclic networks, and extended the scalar value-iteration method to multi-objective problems.

Algorithm 1 displays a reformulation of the algorithm described by White. The original formulation considers a single reward associated to a transition (s, a), while we consider that rewards $\mathbf {r}(s,a,s_i)$ may depend on the reached state $s_i$ as well. Otherwise, both procedures are equivalent.

The procedure is as follows. Initially, the set of nondominated values $V_0(s)$ for each state s is $\{\mathbf {0}\}$. Line 9 calculates a vector $\mathbf {s2} = (s_1, s_2, \ldots s_i, \ldots s_m)$ with all reachable states for the state-action pair (s, a). Let $s2(l) = s_l$ be the l-th element in that vector. Then, lines 11 to 13 calculate a list lv with all the sets $V_{i-1}(s_l)$ for each state in $\mathbf {s2}$, i.e. $lv = [V_{i-1}(s_1),\ldots V_{i-1}(s_l), \ldots V_{i-1}(s_m)]$. Function len(s2) returns the length of vector $\mathbf {s2}$. Next, the cartesian product P of all sets in lv is calculated. Each element in P is of the form $\mathbf {p} = (\mathbf {v_1}, \ldots \mathbf {v_l}, \ldots \mathbf {v_m}) \ | \ \forall l \ \mathbf {v_l} \in V_{i-1}(s_l)$.

Line 15 calculates a temporal set of updated vector value estimates T(a) for action a. Each new estimate is calculated according to the dynamic programming update rule. The calculation takes one vector estimate for each reachable state, and adds the immediate reward and discounted value for each reachable state, weighted by the probability of transition to each such state. All possible estimates are stored in set T(a). Finally, in line 18, the estimates calculated for each action are joined and the non-dominated set is used to update the new value for $V_i(s)$. Maximum memory requirements are determined by the size of $V_i$, $V_{i-1}$ and T.

Some new difficulties arise in algorithm W, when compared to standard scalar value iteration White [18]:

• After n iterations, algorithm W provides ${\mathbb {V}}^n(s)$, i.e. the sets of nondominated values for the set of n-step policies (see White [18], theorem 2). However, for infinite-horizon problems these are only approximations of the ${\mathbb {V}}(s)$ sets. Let us consider two infinite-horizon policies $\pi _1$, and $\pi _2$ with values $\mathbf {v}_{\pi _1}(s), \mathbf {v}_{\pi _2}(s)$ respectively at a given state, and all their n-step sub-policies $\pi _1^n$, and $\pi _2^n$ with values $\mathbf {v}_{\pi _1}^n(s), \mathbf {v}_{\pi _2}^n(s)$. It is possible to have $\mathbf {v}_{\pi _1}(s) \prec \mathbf {v}_{\pi _2}(s)$, and at the same time $\mathbf {v}_{\pi _1}^n(s) \sim \mathbf {v}_{\pi _2}^n(s)$ for all n. In other words, given two infinite-horizon policies that dominate each other, their n-step approximations may not dominate each other for any finite value of n. So, as $n \rightarrow \infty$, the values returned by algorithm W converge to ${\mathbb {V}}(s)$, but with a proviso: it would be necessary to perform an additional test of dominance “at the infinity” (see White [18], theorem 1).

• Nonstationary policies may be nondominated. This is also an important departure from the scalar case, where under reasonable assumptions there is always a stationary optimal policy. White’s algorithm converges to the values of nondominated policies, either stationary or nonstationary.

• Finally, if policies with probability mixtures over actions are allowed, these policies may also be nondominated. Therefore, if allowed, these must also be covered in the calculations of the W algorithm.

Despite its theoretical importance, we are not aware of any practical application of White’s algorithm to general MOMDPs. This is not surprising, given the result presented in proposition 1.

3.3 Vector value iteration with limited precision

In order to overcome some of the computational difficulties imposed by proposition 1, we propose a simple modification of algorithm 1. This involves the use of limited precision in the values of vector components calculated by the algorithm. We consider a maximum precision factor $\epsilon$. More precisely, for a given $\epsilon$ we consider the set of rational numbers ${\mathcal {E}} = \{ x \, | \, \exists n \in {\mathbb {Z}} \quad x = n \times \epsilon \}$. We round vector components to the nearest number in ${\mathcal {E}}$ in step 18. Notice that vectors in the T(a) sets are rounded before being joined. Therefore, all vectors in $V_i$ will be of limited precision.

We denote the W algorithm limited to $\epsilon$ precision by $W_{LP}(\epsilon )$. The new algorithm has a new parameter $\epsilon$, and line 18 is replaced by,

$$\begin{aligned} V_i(s) \leftarrow {{\,\mathrm{{\mathcal {N}}}\,}}[ \ \cup _a \ round(T(a), \epsilon )] \end{aligned}$$

(1)

where $round(X,\epsilon )$ returns a set with all vectors in set X rounded to $\epsilon$ precision.

Proposition 2

Let us consider an episodic q-objective MDP with initial state $s_0$ satisfying the following assumption:

• 1. Immediate rewards $\mathbf {r}(s,a,s')$ are bounded by $r_{min}$, $r_{max}$.

Then the size of the $V_n(s)$ sets for all states s calculated by $W_{LP}(\epsilon )$ after n iterations, is bounded by $[(R\times n + 1)/\epsilon ]^{q-1}$, where $R=r_{max}-r_{min}$.

The proof is straightforward from the considerations in the proof of proposition 1, since regardless of the number of possible policies, that is the maximum number of different limited precision vectors that can be possibly generated by the algorithm in n iterations.

$\square$

Now let us define recursively the operation of algorithms W and $W_{LP}(\epsilon )$. We will use ${\mathbb {V}}_i(s)$ to denote the vector $V_i(s)$ computed by W at step i and ${\mathbb {W}}_i(s)$ to denote the vector $V_i(s)$ computed by $W_{LP}(\epsilon )$ at step i. Obviously the following recursions hold:

${\mathbb {V}}_0(s) = \{\mathbf {0}\}$

${\mathbb {V}}_{i+1}(s) = {{\,\mathrm{{\mathcal {N}}}\,}}(\{ \mathbf {v}\in \mathrm{I\!R}^q | \,\exists a \in {\mathcal {A}}\, \exists \mathbf {v_1}\in {\mathbb {V}}_i(s_1) \ldots \exists \mathbf {v_S}\in {\mathbb {V}}_i(s_S)$

            $\text {such that}\,\mathbf {v} = \mathbf {r}(s,a)+\gamma \sum _j p(s,a,s_j)\mathbf {v}_j\})$

and

${\mathbb {W}}_0(s) = \{\mathbf {0}\}$

${\mathbb {W}}_{i+1}(s) = {{\,\mathrm{{\mathcal {N}}}\,}}(\{ \mathbf {w}\in \mathrm{I\!R}^q | \,\exists a \in {\mathcal {A}}\, \exists \mathbf {w_1}\in {\mathbb {W}}_i(s_1) \ldots \exists \mathbf {w_S}\in {\mathbb {W}}_i(s_S)$

            $\text {such that}\, \mathbf {w} = round(\mathbf {r}(s,a)+\gamma \sum _j p(s,a,s_j)\mathbf {w}_j, \epsilon )\})$

We will show that for every step i, and every state s both sets do not differ “too much”. To this end we will define the known (additive) concept of $\epsilon$-dominance. Given two vectors $\mathbf {u}, \mathbf {v}$, we say that $\mathbf {u}$ $\epsilon$-dominates $\mathbf {v}$ if, for some $\epsilon > 0$ and all i, $u_i + \epsilon \ge v_i$. The binary additive indicator that measures the proximity between two frontiers R, A is defined then as

$$\begin{aligned} I_{\epsilon ^+}(R, A) = \max _{\mathbf {v} \in R}{ \min _{\mathbf {u} \in A}{\max _{i} (v_i - u_i)}} \end{aligned}$$

(2)

In other words, the indicator provides the minimum value of $\epsilon$ such that every point in R is $\epsilon$-dominated by some point in A.

Proposition 3

Assume $\gamma <1$. Let $\eta _i = \epsilon (1-\gamma ^i)/2(1-\gamma )$. Then for every step i of algorithm $W_{LP}(\epsilon )$ and every state $s\in {\mathcal {S}}$, $I_{\epsilon ^+}({\mathbb {V}}_i(s), {\mathbb {W}}_i(s)) \le \eta _i$ and $I_{\epsilon ^+}({\mathbb {W}}_i(s), {\mathbb {V}}_i(s)) \le \eta _i$.

Proof

by induction on the number i of steps of the algorithm $W_{LP}(\epsilon )$.

In the following, given any scalar x, we will denote $\mathbf {x} = (x, \ldots x)$.

Base case: $i=0$. Since for every state s ${\mathbb {V}}_0(s) = {\mathbb {W}}_0(s) = \{\mathbf {0}\}$, the proposition trivially holds.

Induction step. Let us assume the proposition holds for step i of the algorithm. We will prove that it also holds for step $i+1$.

First consider $s\in {\mathcal {S}}$, step $i+1$ and any $\mathbf {v}\in {\mathbb {V}}_{i+1}(s)$. We will show a $\mathbf {w}$ such that $\mathbf {w}\in {\mathbb {W}}_{i+1}(s)$ and $\mathbf {w} + \eta _{i+1} \succ \mathbf {v}$. By definition of ${\mathbb {V}}_{i+1}(s)$, $\mathbf {v} = \mathbf {r}(s,a) + \gamma \sum _j p(s,a,s_j)\mathbf {v_j}$ with $\mathbf {v_j} \in {\mathbb {V}}_{i}(s_j)$ for some action $a\in {\mathcal {A}}$ and some subset $\{s_1, \ldots , s_k\} \subseteq {\mathcal {S}}$. By the induction hypothesis, for every $s_j$ there exists $\mathbf {w_j}\in {\mathbb {W}}_{i}(s_j)$ such that $\mathbf {w_j} + \eta _i \succeq \mathbf {v_j}$. Now consider $\mathbf {w'} = \mathbf {r}(s,a) + \gamma \sum _j p(s,a,s_j)\mathbf {w_j}$. Then we know that $\mathbf {w'} \succeq \mathbf {r}(s,a) + \gamma \sum _j p(s,a,s_j)(\mathbf {v_j} - {\eta _i}) = \mathbf {v} - \gamma {\eta _i}$. But $\mathbf {w'}$ does not belong necessarily to ${\mathbb {W}}_{i+1}(s)$; first it must be rounded giving $\mathbf {w''} = round(\mathbf {w'}, \epsilon )$. However, $\mathbf {w''} + \varvec{\epsilon }/2 \succeq \mathbf {w'}$, hence $\mathbf {w''} \succeq \mathbf {v} - (\epsilon /2 + \gamma {\eta _i})$. We have also $\epsilon /2 + \gamma {\eta _i} = \epsilon /2 + \epsilon (1-\gamma ^i)/2(1-\gamma ) = \epsilon (1-\gamma ^{i+1})/2(1-\gamma ) = \eta _{i+1}$ so $\mathbf {w''} \succeq \mathbf {v} - {\eta _{i+1}}$. Now, either $\mathbf {w''}\in {\mathbb {W}}_{i+1}(s)$ or there is a $\mathbf {w'''}\in {\mathbb {W}}_{i+1}(s)$ such that $\mathbf {w'''} \succ \mathbf {w''}$, and in any case $\mathbf {w''}$ or $\mathbf {w'''}$ is an element in ${\mathbb {W}}_{i+1}(s)$ that satisfies the proposition.

Now consider any $\mathbf {w}\in {\mathbb {W}}_{i+1}(s)$. We will show a $\mathbf {v}$ such that $\mathbf {v}\in {\mathbb {V}}_{i+1}(s)$ and $\mathbf {v} + \eta _{i+1} \succeq \mathbf {w}$. By definition of ${\mathbb {W}}_{i+1}(s)$, $\mathbf {w} = round(\mathbf {w'}, \epsilon )$, $\mathbf {w'} = \mathbf {r}(s,a) + \gamma \sum _j p(s,a,s_j)\mathbf {w_j}$ with $\mathbf {w_j} \in {\mathbb {W}}_{i}(s_j)$ for some action $a\in {\mathcal {A}}$ and some subset $\{s_1, \ldots , s_k\} \subseteq {\mathcal {S}}$. Notice also that $\mathbf {w} \succeq \mathbf {w'} - \varvec{\epsilon }/2$. By the induction hypothesis, for every $s_j$ there exists $\mathbf {v_j}\in {\mathbb {V}}_{i}(s_j)$ such that $\mathbf {v_j} + \eta _i \succeq \mathbf {w_j}$. Now consider $\mathbf {v} = \mathbf {r}(s,a) + \gamma \sum _j p(s,a,s_j)\mathbf {v_j}$. Then we know that $\mathbf {v} \succeq \mathbf {r}(s,a) + \gamma \sum _j p(s,a,s_j)(\mathbf {w_j} - \varvec{\eta _i}) = \mathbf {w'} - \gamma \varvec{\eta _i}$ and $\mathbf {v} \succeq \mathbf {w'} - \gamma \varvec{\eta _i} - \varvec{\epsilon }/2$ so $\mathbf {v} \succeq \mathbf {w'} - \varvec{\eta _{i+1}}$. Now, by definition of ${\mathbb {V}}_{i+1}(s)$, either $\mathbf {v}\in {\mathbb {V}}_{i+1}(s)$ or there is a $\mathbf {v'}\in {\mathbb {V}}_{i+1}(s)$ such that $\mathbf {v'} \succ \mathbf {v}$; and in any case $\mathbf {v}$ or $\mathbf {v'}$ is an element in ${\mathbb {V}}_{i+1}(s)$ that satisfies the proposition. $\square$

The following proposition is now trivial:

Proposition 4

Assume $\gamma <1$. Then for every $\delta >0$ there exists a version of the algorithm $W_{LP}(\epsilon )$ with precision $\epsilon$ such that for every state $s\in {\mathcal {S}}$ and step i, $I_{\epsilon ^+}({\mathbb {V}}_i(s), {\mathbb {W}}_i(s)) \le \delta$ and $I_{\epsilon ^+}({\mathbb {W}}_i(s), {\mathbb {V}}_i(s)) \le \delta$.

For the proof, it suffices to notice that for every i, $\eta _i = \epsilon (1-\gamma ^i)/2(1-\gamma ) < \epsilon /2(1-\gamma )$. Take then $\epsilon = 2\delta (1-\gamma )$ and the proposition follows immediately from Proposition 3. $\square$

Since ${\mathbb {V}}_i(s)$ approximates in the limit ${\mathbb {V}}(s)$, then by selecting an adequate precision $\epsilon$ and using the algorithm $W_{LP}(\epsilon )$ we can approximate ${\mathbb {V}}(s)$ (in the sense of $\epsilon ^+$-dominance) as much as needed. Notice, however, that for a fixed precision $\epsilon$ of the algorithm we cannot guarantee an approximation better than $\epsilon /2(1-\gamma )$.

In infinite-horizon problems, in general we must set $\gamma <1$ in order to ensure convergence. However, if it is known that for every state s all optimal solutions are reached in at most K steps, it is possible to set $\gamma =1$. Then, by a reasoning enterily analogous to the proof of Proposition 3, we obtain the following:

Proposition 5

Assume $\gamma =1$. Let $\eta _i = i\epsilon /2$. Then for every step i of algorithm $W_{LP}(\epsilon )$ and every state $s\in {\mathcal {S}}$, $I_{\epsilon ^+}({\mathbb {V}}_i(s), {\mathbb {W}}_i(s)) \le \eta _i$ and $I_{\epsilon ^+}({\mathbb {W}}_i(s), {\mathbb {V}}_i(s)) \le \eta _i$.

This result allows to bound the error for these cases, as shown in the following proposition.

Proposition 6

Assume $\gamma =1$. Assume that for every state $s\in {\mathcal {S}}$ all optimal values ${\mathbb {V}}(s)$ are reached in at most K steps. Further assume that there also exists some N such for every state $s\in {\mathcal {S}}$, ${\mathbb {W}}_N(s)= {\mathbb {W}}_{N+1}(s)$. Let $M = \max (K,N)$. Then for every state $s\in {\mathcal {S}}$, $I_{\epsilon ^+}({\mathbb {V}}(s), {\mathbb {W}}_M(s)) \le M\epsilon /2$ and $I_{\epsilon ^+}({\mathbb {W}}_M(s), {\mathbb {V}}(s)) \le M\epsilon /2$.

Proof

Since all optimal values ${\mathbb {V}}(s)$ are reached in K steps, for $i \ge K$ and every state s we have ${\mathbb {V}}_i(s) = {\mathbb {V}}_{K}(s) = {\mathbb {V}}(s)$. Also, for $j \ge N$, and every s we have ${\mathbb {W}}_j(s) = {\mathbb {W}}_N(s)$, and since $M = \max (K,N)$, for all $k \ge M, I_{\epsilon ^+}({\mathbb {V}}_k(s), {\mathbb {W}}_k(s)) = I_{\epsilon ^+}({\mathbb {V}}(s), {\mathbb {W}}_N(s)) \le M\epsilon /2$. Analogously, $I_{\epsilon ^+}({\mathbb {W}}_k(s), {\mathbb {V}}_k(s)) = I_{\epsilon ^+}({\mathbb {W}}_N(s), {\mathbb {V}}(s)) \le M\epsilon /2$ $\square$

However, notice that the bound given by Proposition 6 depends on K, which is generally unknown.

4 Experimental evaluation

This section analyzes the performance of $W_{LP}(\epsilon )$ on two different MOMDPs: the Stochastic Deep Sea Treasure environment; and the N-pyramid environment. First, we describe the quality indicators used to evaluate the relative performance of the algorithms. Then, results obtained for each environment are presented.

4.1 Comparing Pareto front approximations

According to the recommendations of Zitzler et al. [20], we use a combination of two standard indicators to assess the quality of the approximations of the true Pareto front calculated by our algorithms: the hypervolume, and the above defined binary additive $\epsilon$-indicator.

The hypervolume $H(P,\mathbf {r})$ measures the volume of space dominated by a given Pareto front P, in the subspace delimited by a specified (nadir) reference point $\mathbf {r}$. This measure is monotone with dominance, in the sense that given two Pareto fronts $P_1, P_2$, then if $P_1$ strictly dominates $P_2$, then $H(P_1, \mathbf {r}) > H(P_2, \mathbf {r})$. Generally, a front with a larger hypervolume is regarded as a better approximation. However, the hypervolume is not a good indicator of how well the points of an approximation are distributed along the true Pareto front, i.e. there can be situations where an approximation with large gaps with respect to the true Pareto front still achieves near optimal hypervolume value (see Zitzler et al. [20]). On the contrary, the additive $\epsilon$-indicator is more sensitive to the presence of these gaps.

On the other hand, when the true Pareto front is not available for comparison, the non-dominated set of the results provided by all algorithms considered can still be used as a reference. In our experiments, we shall use this approach, even in the cases where the true front is known, since our limited precision approximations can occasionally slightly dominate the true values due to the rounding errors.

4.2 Stochastic deep sea treasure

We first analyze the performance of $W_{LP}(\epsilon )$ on a modified version of the Deep Sea Treasure (DST) environment Vamplew et al. [15]. The DST is a deterministic MOMDP defined over a $11 \times 10$ grid environment, as depicted in Fig. 4. The true Pareto front for this problem is straightforward. In any case, the environment satisfies all the simplifying assumptions of proposition 1, and therefore can easily be solved with reasonable resources by multi-policy methods.

We introduce the Stochastic DST environment with right-down moves (SDST-RD), as a modified version of the DST task. Our aim is to provide a test environment where the approximations of the Pareto front calculated by multi-policy approaches like $W_{LP}(\epsilon )$ can be evaluated over a truly stochastic MOMDP. We consider the same grid environment depicted in Fig. 4. The agent controls a submarine that is placed in the top left cell at the beginning of each episode. The agent can move to adjacent neighboring cells situated down or to its right. Moves outside the grid are not allowed (i.e. the state space has no cycles). When two moves are allowed, the agent actually moves in the specified direction 80% of the time, and in the other allowed direction the remaining 20%. Episodes terminate when the submarine reaches one of the bottom cells. Each bottom cell contains a treasure, whose value is indicated in the cell. The agent has two objectives: maximizing a penalty score (a reward of -1 is received after each move), and maximizing treasure value (the reward value of the treasure is received after reaching a treasure cell).

The state space of the SDST-RD is a directed acyclic graph. Therefore, the exact Pareto front of the start state can be potentially calculated using the recursive backwards algorithm discussed above (we denote this as algorithm B).

This provides a reference for the approximations calculated by $W_{LP}(\epsilon )$. We are interested in analyzing the performance of the algorithms as a function of problem size. Therefore, we actually consider a set of subproblems obtained form the SDST-RD. The state space of subproblem i comprises all 11 rows, but only the i leftmost columns of the grid shown in Fig. 4.

Fig. 4

Deep Sea Treasure environment Vamplew et al. [15]. Start cell is denoted by ’S’

The subproblems were solved with algorithm B, and with $W_{LP}(\epsilon )$ with precision $\epsilon \in \{0.1, 0.05, 0.02, 0.01, 0.001\}$. Smaller values provide higher precision and better approximations. The discount rate was set to $\gamma = 1.0$. With $W_{LP}$, the number of iterations for each subproblem was set to the distance of the most distant treasure.

Figure 5 displays the exact Pareto front for subproblems 1–6 as calculated by algorithm B. All experiments on this environment were run with a 96 hour time limit, except for the exact solution of subproblem 6, which took 10 days to complete. In general, the Pareto fronts present a non-convex nature, like in the standard deterministic DST. However, the number of nondominated vectors in $V(s_0)$ is much larger (in the standard DST, subproblem i has just i nondominated solution vectors). Only precisions of $\epsilon \ge 0.02$ were able to solve all 10 subproblems within the time limit. Figure 6 shows the best Pareto frontier approximation obtained for subproblems 7–10 by $W_{LP}$ within the time limit.

Fig. 5

Exact Pareto front for subproblems 1–6 of the SDST-RD task calculated with algorithm B

Fig. 6

Best approximation of the Pareto frontier obtained for subproblems 7–10 of the SDST-RD task with algorithm $W_{LP}$. The exact frontier of subproblem 6 is included as reference

The cardinality of $V(s_0)$ for each subproblem is shown in Table 1. These figures illustrate the combinatorial explosion frequently experienced in stochastic MOMDP even for acyclic state spaces.

Figure 7 shows the maximum number of vectors stored for each subproblem by each algorithm (in logarithmic scale). As expected, the requirements of the exact algorithm grow much faster than any of the approximations. $W_{LP}$ achieves better approximations, and in consequence larger vector sets, with increasing precision (smaller values of $\epsilon$).

Table 1 Cardinality of $V(s_0)$ for the SDST-RD subproblems

Fig. 7

Memory requirements (# of vectors) of each algorithm for the different subproblems of the SDST-RD task (log scale)

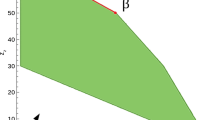
Finally, we briefly examine the quality of the approximations. Figure 8 shows the exact Pareto front and the approximations obtained for subproblem 6. In general, all approximations lie very close, and are difficult to distinguish visually from each other in objective space. Results for other subproblems (omitted for brevity) show a similar pattern. Figure 9 zooms into a particular region of the Pareto front, to display values obtained by different precisions. In general, the approximations are evenly distributed across the true Pareto front, and reasonably close according to the precision values. Table 2 shows the hypervolume of the $V(s_0)$ sets returned by each algorithm for each subproblem. These are calculated relative to the standard reference point $(-25, 0)$ used for DST. Differences with the exact Pareto front are almost negligible for $\epsilon \le 0.02$. Finally, the values of the $\epsilon$-indicator are displayed in Table 3. The small values obtained indicate that the points in each approximated Pareto front are all evenly distributed in all cases, as already suggested by the results of Fig. 8.

Fig. 8

Pareto fronts obtained for SDST-RD subproblem 6. The area in the rectangle is shown magnified in Fig. 9

Fig. 9

Enlarged portion of objective space from Fig. 8 (SDST-RD subproblem 6)

Table 2 Hypervolumes of $V(s_0)$ for the SDST-RD task

Table 3 $\epsilon$-indicator for the values of $V(s_0)$ for the SDST-RD task. Reference is the non-dominated set of all considered fronts for each subproblem

4.3 N-pyramid

The N-pyramid environment presented here is inspired in the pyramid MOMDP described by Van Moffaert and Nowé [17]. More precisely, we define a family of problems of variable size over $N \times N$ grid environments. Each cell in the grid is a different state. Each episode starts always at the start node, situated in the bottom left corner (with coordinates $(x,y) = (1,1)$). The agent can move in any of the four cardinal directions to an adjacent cell, except for moves that would lead the agent outside of the grid, which are not allowed. Transitions are stochastic, with the agent moving in the selected direction with probability 0.95. With probability 0.05 the agent actually moves in a random direction from those available at the state. The episode terminates when the agent reaches one of the cells in the diagonal facing the start state. Figure 10 displays a sample grid environment for $N = 5$. The agent wants to maximize two objectives. For each transition to a non-terminal state, the agent receives a vector reward of $(-1, -1)$. When a transition reaches a terminal cell with coordinates (x, y), the agent receives a vector reward of (10x, 10y). This environment defines a cyclic state space. Therefore, its solution cannot be calculated using the B algorithm.

Fig. 10

An N-pyramid environment for $N = 5$. The start state is denoted by ’S’. Terminal states are indicated in light grey

The N-pyramid environment was solved with $W_{LP}(\epsilon )$ using $\epsilon \in \{1.0, 0.1, 0.05, 0.01, 0.005 \}$. The discount rate was set to $\gamma = 1.0$, and the number of iterations to $3 \times N$. A twelve hour runtime limit was imposed for all experiments. The largest subproblem solved was $N = 5$, for $\epsilon = 1.0$.

Figure 11 displays the best frontier approximation for each problem instance, and the corresponding $\epsilon$ value. Smaller $\epsilon$ values could not solve the problem within the time limit.

Fig. 11

Best approximations obtained for the Pareto fronts for the N-pyramid problem instances

Figure 12 displays the frontiers calculated by the different precision values for the 3-pyramid. This was the largest problem instance solved by all precision values. Figure 13 displays an enlargement of a portion of this frontier. This illustrates the size and shape of the different approximations. As expected, smaller values of $\epsilon$ produce more densely populated policy values.

Fig. 12

Approximated Pareto fronts for the 3-pyramid instance. An enlarged portion is displayed in Fig. 13

Fig. 13

Enlarged portion of objective space from Fig. 12 (3-pyramid instance)

Finally, we summarize the quality indicators for the approximated frontiers. Table 4 summarizes the cardinality of the $V(s_0)$ sets calculated for each problem instance by the different precision values, and Table 5 the corresponding hypervolumes using the original reference point $(-20,-20)$. Table 6 includes the values of the $\epsilon$-indicator for the approximated fronts. Once again, the small values achieved indicate that the points in each front are evenly distributed in all cases, as already suggested by Fig. 13.

Table 4 Cardinality of $V(s_0)$ for the N-pyramid instances

Table 5 Hypervolumes of $V(s_0)$ for the N-pyramid task

Table 6 Values of the $\epsilon$-indicator for $V(s_0)$ in the N-pyramid task. Reference is the non-dominated set of all considered frontiers

5 Conclusions and future work

This paper analyzes some practical difficulties that arise in the solution of MOMDPs. We show that the number of nondominated policy values is tractable (for a fixed number of objectives q) only under a number of limiting assumptions. If any of these assumptions is violated, then the number of nondominated values becomes intractable or even infinite with problem size in the worst case.

Multi-policy methods for MOMDPs try to approximate the set of all nondominated policy values simultaneously. Previous works have addressed mostly deterministic tasks satisfying the limiting assumptions that guarantee tractability.

We show that, if policy values are restricted to vectors with limited precision, the number of such values becomes tractable. This idea is applied to a variant of the algorithm proposed by White [18]. This new variant has been analyzed over a set of stochastic benchmark problems. Results show that good approximations of the Pareto front can be obtained both in terms of the hypervolume and the $\epsilon$-indicator. These corroborate the presence of consistently good evenly distributed approximation fronts, even as precision is progressively limited. To our knowledge, the results reported in this work deal with the hardest stochastic problems solved to date by multi-policy multi-objective dynamic programming algorithms.

Future work includes the application of the limited precision idea to more general value iteration algorithms, and the generation of additional benchmark problems for stochastic MOMDPs. This should support the exploration and evaluation of other approximate solution strategies, like multi-policy multi-objective evolutionary techniques.