Abstract
A real symmetric matrix A is copositive if \(x^\top Ax\ge 0\) for all \(x\ge 0\). As A is copositive if and only if it is copositive on the standard simplex, algorithms to determine copositivity, such as those in Sponsel et al. (J Glob Optim 52:537–551, 2012) and Tanaka and Yoshise (Pac J Optim 11:101–120, 2015), are based upon the creation of increasingly fine simplicial partitions of simplices, testing for copositivity on each. We present a variant that decomposes a simplex \(\bigtriangleup \), say with n vertices, into a simplex \(\bigtriangleup _1\) and a polyhedron \(\varOmega _1\); and then partitions \(\varOmega _1\) into a set of at most \((n-1)\) simplices. We show that if A is copositive on \(\varOmega _1\) then A is copositive on \(\bigtriangleup _1\), allowing us to remove \(\bigtriangleup _1\) from further consideration. Numerical results from examples that arise from the maximum clique problem show a significant reduction in the time needed to establish copositivity of matrices.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let A be a real symmetric matrix of order n. If \(x^\top Ax\ge 0\) for all \(x\in {\mathbb {R}}^n_+=\{x\in {\mathbb {R}}^n\,|\, x\ge 0\}\) then A is called copositive [7]. If \(x^\top Ax>0\) for all \(x\in {\mathbb {R}}^n_+\setminus \{0\}\) then A is strictly copositive. The set of all order n copositive matrices \(\mathcal {COP}\) is a closed, convex, and full-dimensional pointed cone whose interior is the set of strictly copositive matrices.
Methods to determine copositivity are important because of their role in algorithms for the solution of copositive optimization problems [2, 5], a class of problems that include, for example, the maximum clique problem [1]. The challenge is that Murty and Kabadi [8] have shown that given a square integer matrix A the decision problem “is A not copositive?" is NP-complete.
This algorithm has the same branch-and-bound design as Bundfuss and Dür’s [4] BD algorithm, which was improved by Sponsel et al. [9], and then generalized by Tanaka and Yoshise’s [10] TY algorithm. All four methods depend on partitions of the standard simplex. Ours is uniquely different in that we decompose a simplex \(\bigtriangleup \) into a simplex \(\bigtriangleup _1\) and a polyhedron \(\varOmega _1\), and then partition \(\varOmega _1\) into a set of at most \((n-1)\) simplices, each of which is subsequently decomposed into a simplex and a polyhedron, with the process continuing until copositivity is determined. We will show that if A is copositive on \(\varOmega _1\), then A is copositive on \(\bigtriangleup _1\), allowing us to remove \(\bigtriangleup _1\) from further consideration. As our selection of \(\bigtriangleup _1\) is done in a maximal way, the number of required partitions is, hopefully, significantly reduced.
Similar to the algorithms in [4, 9, 10], our new algorithm determines copositivity of A by checking whether \(M_\bigtriangleup ^\top A M_\bigtriangleup \in {\mathcal {M}}\), where \(M_\bigtriangleup \) is a matrix whose columns are the vertices of \(\bigtriangleup \), and where \({\mathcal {M}} \subset \mathcal {COP}\). In [4], \({\mathcal {M}} = {\mathcal {N}}\), the set of all nonnegative \(n\times n\) matrices. Sponsel et al. [9] comment that while checking \(M_\bigtriangleup ^\top A M_\bigtriangleup \in {\mathcal {N}}\) is relatively easy, the set \({\mathcal {N}}\) is too small and they suggest sets \({\mathcal {M}}\subset \mathcal {COP}\) with \({\mathcal {M}}\supset {\mathcal {N}}\). While this results in fewer iterations (simplices) the iterations are more time consuming as they require either the calculation of eigenvectors or the solution of semidefinite programs. They reported that in all instances, the BD algorithm with \({\mathcal {M}} = {\mathcal {N}}\) was fastest. It is to the BD algorithm that we compare the algorithm introduced in this paper where we also use \({\mathcal {M}} = {\mathcal {N}}\).
Tanaka and Yoshise’s [10] generalization is based on more sophisticated selections for \({\mathcal {M}}\). They consider \({\mathcal {M}} = {\mathcal {N}} + {\mathcal {S}}^+\), where \({\mathcal {S}}^+\) is the set of all positive semidefinite matrices. The consequence is that a linear program, rather than a semidefinite program, is to be solved to determine whether \(M_\bigtriangleup ^\top A M_\bigtriangleup \in {\mathcal {M}}\). However, the formulation of the linear program requires a singular value decomposition, and the decomposition is not unique even though the result depends on that decomposition. Tanaka and Yoshise suggest that the TY algorithm is promising for the determination of upper bounds for the maximum clique problem.
Our limited numerical experiments show that for the instances examined there is a significant reduction in the time needed to establish copositivity of matrices that arise in the determination of the clique number of an undirected graph. Further, the experimental results show that for the instances examined there is an advantage to our algorithm when A is near the copositive cone boundary.
2 Simplicial partition algorithms
We begin with the standard simplex
where \(\Vert \,\cdot \Vert _1\) is the 1-norm. The matrix A is copositive if and only if it is copositive on \(\bigtriangleup ^s\), that is, \(x^\top Ax \ge 0\) for all \(x\in \bigtriangleup ^s\). Let P be a simplicial partition of \(\bigtriangleup ^s\) as defined in [4]. That is, \(\bigtriangleup ^s\) is the union of all simplices in P; and the intersection of the interior of any two simplices in P is empty. For any \(\bigtriangleup \in P\) denote by \(V_\bigtriangleup \) the vertices \(v_1,\ldots ,v_n\) of \(\bigtriangleup \). Thus, the columns of \(M_\bigtriangleup \) are the elements of \(V_\bigtriangleup \). Lemma 1, which follows from the work in [9], gives conditions for copositivity. In fact, it shows that if \(M_\bigtriangleup ^\top A M_\bigtriangleup \in {\mathcal {N}}\), then A is copositive on \(\bigtriangleup \in P\). Lemma 2, which follows from the work in [4], gives a condition for non-copositivity; and, if non-copositivity is not determined, it establishes the existence of a vertex \(v_\ell \in V_\bigtriangleup \) with \(v_{\ell }^\top A v_{\ell }> 0\), needed for the new partitioning process presented in Sect. 3.
Lemma 1
If \(M^\top _\bigtriangleup A M_\bigtriangleup \ge 0\), i.e., \(M^\top _\bigtriangleup A M_\bigtriangleup \in {\mathcal {N}}\), then A is copositive on \(\bigtriangleup \in P\). If A is copositive on all \(\bigtriangleup \in P\) then A is copositive on \(\bigtriangleup ^s\), and is therefore copositive.
Lemma 2
For \(\bigtriangleup \in P\) suppose that \(M^\top _\bigtriangleup A M_\bigtriangleup \not \ge 0\) and that \(v^\top A v \ge 0\) for all \(v\in V_\bigtriangleup \). Either there exist \(v_i,\ v_j\in V_\bigtriangleup \), \(v_i\ne v_j\), with \(v_{i}^\top A v_{j}< 0\) and \(v_{i}^\top A v_{i}= v_{j}^\top A v_{j}= 0\) so that A is not copositive; or there exists a \(v_\ell \in V_\bigtriangleup \) with \(v_{\ell }^\top A v_{\ell }> 0\).
Theorem 1, which is Lemma 2.3 in [9], gives a criterion for termination. Suppose that it has been determined that A is copositive on all \(\bigtriangleup \in {{\tilde{P}}}\subset P\). Let \({{\hat{P}}} = P\backslash {{\tilde{P}}}\) and define the diameter of \({\hat{P}}\) by
Theorem 1
If the real symmetric matrix A is not copositive, then there exists an \(\epsilon >0\) such that if \(\delta ({{\hat{P}}})< \epsilon \) there exists a \(\bigtriangleup \in {{\hat{P}}}\) with \(v^\top Av<0\) for some \(v\in V_\bigtriangleup \).
The BD and TY simplicial partitioning algorithms are branch and bound algorithms that proceed as follows. Start with a partition P of \(\bigtriangleup ^s\). This is the first branch step. If Lemma 2 determines that A is not copositive then the algorithm terminates.
If Lemma 1 determines that A is copositive on \(\bigtriangleup \in P\), then \(\bigtriangleup \) can be removed from further consideration. That is, we do not need to create a partition of \(\bigtriangleup \). This is the bound step.
The branch step is to find simplicial partitions for each of the simplices in the original partition that have not been removed in the bound step. That is, the partitions are further refined. The process continues until it is either determined that A is not copositive (\(v^\top A v < 0\) for some simplex vertex v), that A is copositive on all remaining simplices, in which case A is copositive, or until the remaining simplices are sufficiently small so that the copositivity of A can be determined by the vertices of the remaining simplices.
3 A new method of partitions
Our new method differs in how the simplicial partitions are created. Consider a simplex \({\hat{\bigtriangleup }}\in P\). If \(M^\top _{{\hat{\bigtriangleup }}} A M_{{\hat{\bigtriangleup }}} \ge 0\) then, by Lemma 1, A is copositive on \({\hat{\bigtriangleup }}\) and we can then consider copositivity on the next \(\bigtriangleup \in P\). Let \(D(M_\bigtriangleup )\) be the vector of diagonal elements of \(M^\top _\bigtriangleup A M_\bigtriangleup \). If \(D(M_\bigtriangleup )\) has at least one negative element, then A is not copositive and we are done. If \(M^\top _\bigtriangleup A M_\bigtriangleup \not \ge 0\) and if \(D(M_\bigtriangleup )\ge 0\), then \(M^\top _\bigtriangleup A M_\bigtriangleup \) has a negative off-diagonal, say the entry in row i and column j. If both the i-th and j-th diagonal entries are zero, then, by Lemma 2, A is not copositive and we are done. Otherwise, there is at least one strictly positive element in \(D(M_\bigtriangleup )\), say, \(v_{\ell }^\top A v_{\ell }\), that we will use to create a simplex \(\bigtriangleup _1\) which can be sliced off \(\bigtriangleup \) and eliminated from further consideration.
Theorem 2
If \(D(M_\bigtriangleup )\ge 0\) and if there exists a \(v_{\ell }\in V_\bigtriangleup \) with \(v_{\ell }^\top A v_{\ell }> 0\), then for each \(j\ne \ell \) there exists a scalar \(\lambda _j\in (0,1]\), with \({\hat{v}}_{j}^\top A v_{\ell }\ge 0\) where \({\hat{v}}_{j}=(1-\lambda _j)v_{\ell }+\lambda _jv_{j}\).
Proof
If \(v_{j}^\top A v_{\ell }\ge 0\) then \({\hat{v}}_{j}^\top Av_{\ell }= (1-\lambda _j)v_{\ell }^\top Av_{\ell }+ \lambda _jv_{j}^\top Av_{\ell }\ge 0\) for all \(\lambda _j\in (0,1]\). Otherwise, \(v_{j}^\top A v_{\ell }< 0\) and we have that
\(\square \)
Let \(\bigtriangleup _1\) be the simplex with vertices \(v_\ell \) and \({\hat{v}}_{j}\), \(1\le j\le n\), \(j\ne \ell \), where the \({\hat{v}}_{j}\) are as described in Theorem 2 using the largest value possible for \(\lambda _j\). We have the partition
where
the convex hull of the points \((V_{\bigtriangleup _1}\ \cup \ V_\bigtriangleup )\setminus \{v_{\ell }\}\). In Fig. 1 we see a slice of a simplex \(\bigtriangleup \) in \({\mathbb {R}}^4\) and the partition into \(\bigtriangleup _1\) and \(\varOmega _1\) that it creates. In this example, \(\ell = 1\).
Theorem 3 shows that we can remove \(\bigtriangleup _1\) from further consideration as copositivity on \(\varOmega _1\) implies copositivity on \(\bigtriangleup _1\).
Theorem 3
If A is copositive on \(\varOmega _1\), then A is copositive on \(\bigtriangleup _1\).
Proof
For \(x=v_{\ell }\in \bigtriangleup _1\), where \(v_{\ell }\) is as described in Theorem 2, we have \(x^\top Ax > 0\). For every \(x \in \bigtriangleup _1\backslash v_{\ell }\) there exist scalars \(\alpha _j \ge 0\), \(j = 1,\ldots ,n\), summing to unity, such that
where
In this case, \(x\ne v_{\ell }\) so that \(\alpha _\ell \ne 1\). Since the scalars \(\alpha _j/(1-\alpha _\ell )\) are nonnegative and sum to unity it follows that \({\hat{v}}\in \varOmega _1\). By assumption, A is copositive on \(\varOmega _1\) so that \({\hat{v}}^\top A{\hat{v}}\ge 0\). Since \(v_{\ell }^\top A {\hat{v}}_{j}\ge 0\) for all \(j\ne \ell \), we have \(v_{\ell }^\top A{\hat{v}}\ge 0\). Thus,
and A is copositive on \(\bigtriangleup _1\). \(\square \)
If \(\varOmega _1\) has n vertices then it is a simplex from which we either determine copositivity or partition \(\varOmega _1\) into a simplex and a polyhedron as above. If \(\varOmega _1\) has more than n vertices we create the partition \(\varOmega _1= \bigtriangleup _2\cup \varOmega _2\) as follows.
Let \(J^\ell = \{\,1,2,\ldots ,n\,\}\backslash \{\ell \}\). Set \(J_1=\{\, j\in J^\ell \,|\, \lambda _j=1\,\}\) and \(J_2 = J^\ell \backslash J_1\), that is \(J_2 =\{\, j\in J^\ell \,|\, 0<\lambda _j<1\,\}\). For \(j\in J_1\) we have \({\hat{v}}_{j}= v_{j}\) and for \(j\in J_2\) we have \({\hat{v}}_{j}=(1-\lambda _j)v_\ell +\lambda _jv_j\). We then choose any index \(\mu \in J_2\). In Fig. 2 we begin with the \(\varOmega _1\) from Fig. 1. We have \(J_1 = \emptyset \), \(J_2 = \{2,3,4\}\) and we selected \(\mu =2\) giving the simplex \(\bigtriangleup _2\) with vertices \(v_2, {\hat{v}}_2, {\hat{v}}_3\) and \({\hat{v}}_4\). Lemma 3 shows that these vectors are linearly independent.
Lemma 3
The vectors \({{\hat{v}}}_j, 1\le j\le n, j\ne \ell \) together with \(v_\mu \) are linearly independent.
Proof
Consider
Since the vectors in \(V_\bigtriangleup \) are linearly independent, and since \(0<\lambda _j< 1\), for all \(j\in J_2\), we can conclude that \(\alpha _j = 0\), for all \(j\ne \ell \) and that \(\alpha _\mu = 0\).\(\square \)
By Lemma 3 we conclude that the convex hull of the vectors \({{\hat{v}}}_j, 1\le j\le n, j\ne \ell \) together with \(v_\mu \) is a simplex which we denote by \(\bigtriangleup _2\). We denote by \(\varOmega _2\) the convex hull of the set of vectors \(V_{\varOmega _1}\setminus \{{\hat{v}}_\mu \}\), which is a polyhedron with one vertex less than \(\varOmega _1\). The proposed algorithm will then slice a simplex off \(\varOmega _2\) creating \(\bigtriangleup _3\) and \(\varOmega _3\), with \(\varOmega _3\) having one less vertex than \(\varOmega _2\), continuing in this way until the \(\varOmega \) polyhedron is itself a simplex. The set of simplices created by this process is denoted by \(SL(\bigtriangleup )\), where SL represents the slicing process. Since \(\bigtriangleup _1\) need not be considered further, it is not included in \(SL(\bigtriangleup )\). The algorithm would continue by restarting the process for each simplex in \(SL(\bigtriangleup )\). In Fig. 3 we see a graphic of this process with the \(p\le n\) simplices, labeled \(\bigtriangleup _2\) to \(\bigtriangleup _{p+1}\), in \(SL(\bigtriangleup )\) down the right-hand side.
This, of course, depends on \(\varOmega _2\) and \(\bigtriangleup _2\) being a partition of \(\varOmega _1\). This is shown in Lemma 4 by showing that the hyperplane passing through \(v_\mu \), \({\hat{v}}_{j}\), \(\forall j\ne \mu , \ell \) is a separating hyperplane for \(\bigtriangleup _2\) and \(\varOmega _2\). Denote the hyperplane by H and represent it by \(w^\top x = b\).
Without loss of generality, assume that \(w^\top {\hat{v}}_\mu < b\). Since \(v_\mu \), \({\hat{v}}_{j}\), \(\forall j\ne \mu , \ell \) are on H, and since \({\hat{v}}_\mu \), \(v_\mu \), \({\hat{v}}_{j}\), \(\forall j\ne \mu , \ell \) are linearly independent, it follows that \(w^\top {\hat{v}}_\mu \ne b\). If \(w^\top {\hat{v}}_\mu > b\), replace w with \(-w\).
Lemma 4
For all \(x\in \bigtriangleup _2\setminus H\), we have \(w^\top x < b\) and for all \(x\in \varOmega _2\setminus H\), we have \(w^\top x > b\).
Proof
By assumption we have \(w^\top x < b\) when \(x = {\hat{v}}_\mu \). For \(x\in \bigtriangleup _2\setminus H\), \(x\ne {\hat{v}}_\mu \), we can write x as the convex combination
with \(t_\mu >0\) (since \(x\notin H\).) Thus
Since \(w^\top {\hat{v}}_j = b\) for all \(j\ne \ell \), which includes \(j=\mu \), we have
As we have a convex combination it follows that
giving
since \(t\ge 0\) and \(w^\top v_\mu < b\) (by assumption). That \(w^\top x > b\) for all \(x\in \varOmega _2\setminus H\) is proved in a similar manner.\(\square \)
4 The algorithm
We now present the algorithm. We use P to represent the set of simplices that have not yet been fathomed. For any \(\bigtriangleup \in P\) the center and width of \(\bigtriangleup \) are given by
respectively. Let
where \(||A||_1\) is the element-wise norm that is the sum of the absolute values of the entries in A.
Lemma 5
Let \(\bigtriangleup \in P\), and let \({\bar{v}}\), \(\delta \) and \({{\bar{\delta }}}\) be as given in (4) and (5). If \({\bar{v}}^\top A{\bar{v}}> 0\) and \(\delta \le {{\bar{\delta }}}\), then A is copositive on \(\bigtriangleup \).
Proof
Let \(x\in \bigtriangleup \) and consider
where the last inequality follows since \({\bar{v}}\in \bigtriangleup \) implies that \(||{\bar{v}}||_1=1\) and \(x\in \bigtriangleup \) implies that \(||x-{\bar{v}}||_1\le \delta \). The positive root of \(||A||_1 \delta ^2 + 2||A||_1\delta -{\bar{v}}^\top A{\bar{v}}\) is \({{\bar{\delta }}}\) as given in (5). It follows that for \(0\le \delta \le {{\bar{\delta }}}\),
Combining (6) and (7) we have that for \(0\le \delta \le {{\bar{\delta }}}\),
Since \({\bar{v}}^\top A{\bar{v}}>0\), this implies that \(x^\top Ax\ge 0\) for all \(x\in \bigtriangleup \). Thus, A is copositive on \(\bigtriangleup \).\(\square \)

In the statement of the algorithm, we use the notation \({\bar{V}}= M^\top _\bigtriangleup A M_\bigtriangleup \) and \({\bar{V}}_{ij} = v_i^\top Av_j\). Line 6 of the algorithm follows from the definition of copositivity (\({\bar{v}}^\top A{\bar{v}}< 0\)) and from Lemma 2; and Lemma 5 validates the line 5 of the algorithm.
Intuitively, we expect \(\delta (P)\), the diameter of P, to converge to zero, that is, that the sequence of partitions is exhaustive. In [6], Dickinson tells us that whether a sequence of partitions is exhaustive can “often defy our intuition". Fortunately, he provides two methods, that can be adapted to our method, to ensure exhaustion.
Under the assumption that \(\delta (P)\) converges to zero, if A is strictly copositive or A is not copositive, then the algorithm terminates, but if A is copositive but not strictly copositive, it may or may not terminate [4]. As in [4], we could modify the algorithm by choosing a small tolerance \(\epsilon >0\) and terminate when \(M^\top _\bigtriangleup A M_\bigtriangleup > -\epsilon \text{ for } \text{ all } \bigtriangleup .\) In this case, we say that A is \(\epsilon \)-copositive and Theorem 6 in [4] guarantees the termination of the algorithm.
5 Examples
The first three examples come from graph theory. Let E be the matrix of ones and let \(A_G\) be the adjacency matrix of a given undirected graph G and define \(B_{\gamma } = \gamma (E-A_G) - E\). From [1] we know that the clique number of G is
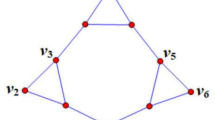
Consider the graphs \(G_8\), \(G_{10}\) and \(G_{12}\) shown in Fig. 4 by way of definition. The figures for \(G_8\) and \(G_{12}\) are from [9]. We have \(w(G_8) = 3\), \(w(G_{10}) = 3\) and \(w(G_{12})=4\).
We will determine the copositivity of \(A = B_\gamma \) for various values of \(\gamma \).
For the remaining nine examples we check copositivity of A, where A is created as follows. We choose the order n and a \(\gamma > 2\). Choose \({\hat{A}}\) to be symmetric with zeros on the diagonal and with the upper off-diagonal elements to be zero or one with equal probability. We can think of A as being the adjacency matrix of a randomly generated graph. Then \(A = \gamma (E-{{\hat{A}}}) - E\).
We test the proposed algorithm, called SNC, against the BD algorithm. Both algorithms were programmed by the second author and were run on a 2.70 GHz Dual Core Processor machine with 4 GB of RAM.
Table 1 shows the results for the graph \(G_8\). We see that both algorithms correctly determine that \(w(G_8) = 3\). For every value of \(\gamma \), the time taken by SNC is at least an order of magnitude less than for BD. The number of simplices considered by SNC is at most half the number considered by BD. Also, when \(\gamma =w(G_8)\), BD failed while SNC correctly determined copositivity. The time taken to determine non-copositivity is two orders of magnitude less for SNC and the number simplices considered an order of magnitude less.
Table 2 shows the results for the graph \(G_{10}\). We see that both algorithms correctly determine that \(w(G_{10}) = 3\). Both algorithms are able to determine copositivity when \(\gamma =w(G_{10})\). The number of simplices considered by SNC is an order of magnitude less than for BD when \(\gamma > 3.2\), and considerably less than BD for \(\gamma \le 3\).
Table 3 shows the results for the graph \(G_{12}\). For \(\gamma \ge 4 = w(G_{12})\) BD is unable to determine copositivity. While SNC is successful, the number of simplices considered is at least three orders of magnitude larger than for \(G_{8}\) and \(G_{10}\). For \(\gamma < 4\), SNC outperforms BD.
For the three graph theory (clique number) examples, SNC outperforms BD, especially in the determination of non-copositivity.
In Table 4 we see the results for the remaining nine examples. In all cases SNC takes less time and considers fewer simplices than BD.
6 Conclusion
We have presented a novel method to decompose the standard simplex in order to determine copositivity of real symmetric matrices. Thus, every algorithm that is based on simplicial partitioning in order to test for copositivity can be modified using our method. This includes the algorithms in, for example, [3, 4, 9,10,11], and others.
At each major iteration of our algorithm we are able to remove a maximal simplex from future consideration. After removal of the simplex, we are left with a polyhedron, which is then decomposed into at most n simplices. This gives a significant reduction to the number of simplices that need to be considered, and possibly decomposed, making the algorithm run more quickly.
Our algorithm works well with the set \({\mathcal {N}}\) so that we need not consider more sophisticated choices for \({\mathcal {M}}\subset \mathcal {COP}\) and hence avoid the need to solve a semidefinite programming problem or linear program. These claims, of fewer simplices and less time, are evidenced by the test results.
The purpose of our limited numerical testing is to validate the new method. As max-clique instances have a very particular structure they are perhaps not sufficient to fully establish a copositivity detection algorithm. Full numerical testing should include instances from the DIMACS challenge as in [4, 9]. Rigorous numerical testing and application to other algorithms is the next step.
Data availability statement
This paper has no associated data sets.
References
Bomze, I.M.: Evolution towards the maximum clique. J. Glob. Optim. 10(2), 143–164 (1997). https://doi.org/10.1023/A:1008230200610
Bomze, I.M., Dür, M., de Klerk, E., Roos, C., Quist, A.J., Terlaky, T.: On copositive programming and standard quadratic optimization problems. J. Glob. Optim. 18(4), 301–320 (2000). https://doi.org/10.1023/A:1026583532263
Bomze, I.M., Eichfelder, G.: Copositivity detection by difference-of-convex decomposition and \(\omega \) -subdivision. Math. Program. 138, 365–400 (2013)
Bundfuss, S., Dür, M.: Algorithmic copositivity detection by simplicial partition. Lin. Algebra Appl. 428, 1511–1523 (2008)
Burer, S.: On the copositive representation of binary and continuous nonconvex quadratic programs. Math. Program. 120(2), 479–495 (2009). https://doi.org/10.1007/s10107-008-0223-z
Dickinson, P.: On the exhaustivity of simplicial partitioning. J. Glob. Optim. 58(1), 189–203 (2014). https://doi.org/10.1007/s10898-013-0040-7
Motzkin, T.: Copositive quadratic forms. National Bureau of Standards, Tech. rep. (1952)
Murty, K.G., Kabadi, S.N.: Some NP-complete problems in quadratic and nonlinear programming. Math. Program. 39(2), 117–129 (1987). https://doi.org/10.1007/BF02592948
Sponsel, J., Bundfuss, S., Dür, M.: An improved algorithm to test copositivity. J. Glob. Optim. 52(3), 537–551 (2012). https://doi.org/10.1007/s10898-011-9766-2
Tanaka, A., Yoshise, A.: An lp-based algorithm to test copositivity. Pac. J. Optim. 11, 101–120 (2015)
Zilinskas, J., Dür, M.: Depth-first simplicial partition for copositivity detection, with an application to maxclique. Optim. Methods Softw. 26(3), 499–510 (2011). https://doi.org/10.1080/10556788.2010.544310
Acknowledgements
We thank the two referees for their very detailed review of this paper. Their comments improved our document in many ways.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Safi, M., Nabavi, S.S. & Caron, R.J. A modified simplex partition algorithm to test copositivity. J Glob Optim 81, 645–658 (2021). https://doi.org/10.1007/s10898-021-01092-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-021-01092-1