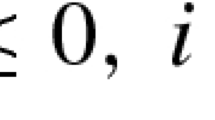A note on completely positive relaxations of quadratic problems in a multiobjective framework

Abstract

In a single-objective setting, nonconvex quadratic problems can equivalently be reformulated as convex problems over the cone of completely positive matrices. In small dimensions this cone equals the cone of matrices which are entrywise nonnegative and positive semidefinite, so the convex reformulation can be solved via SDP solvers. Considering multiobjective nonconvex quadratic problems, naturally the question arises, whether the advantage of convex reformulations extends to the multicriteria framework. In this note, we show that this approach only finds the supported nondominated points, which can already be found by using the weighted sum scalarization of the multiobjective quadratic problem, i.e. it is not suitable for multiobjective nonconvex problems.

1 Introduction

Many nonconvex, even combinatorial optimization problems can equivalently be reformulated as convex problems over the so-called completely positive matrix cone. Here the reader is referred to [3, 7, 9] for more details. This reformulation is possible since the whole complexity is moved to the cone constraint. Checking membership to the cone is known to be NP hard, cf. [8]. Nevertheless, especially in small dimensions, an optimal solutions for the nonconvex problem can be obtained by solving the convex reformulation. For larger dimensions, approximations of the cone or its dual can be used for deriving lower and upper bounds of the optimal value of the problems, cf. [4, 14, 16]. In this paper, we consider such a class of nonconvex quadratic problems including binary constraints which can, in the single-objective case, equivalently be reformulated. Thus we especially focus on quadratic objectives and linear constraints as motivated by Burer, cf. [5]. However, we will study the multiobjective case. Multiobjective quadratic problems are of importance in the field of data mining and especially in the context of classification, see for example [6, 18]. Classical portfolio optimization, where risk should be minimized and return should be maximized simultaneously, see for example [17], gives rise to another important field of application.

As we will see throughout this note, shifting the complexity of the original problem to the cone constraint comes along with the advantage of a linear objective. Since operating in a convex environment is also a big advantage in a multiobjective framework, naturally the question arises whether convexifying multiobjective nonconvex quadratic binary problems via completely positive reformulations is again a useful tool. In this note, we will show that considering multiobjective completely positive reformulations for this problem returns just a subset of the optimal solution set: only those efficient solutions which can already be found by using a weighted sum scalarization.

Thereby, it is known that the weighted sum scalarization is not an appropriate tool for scalarizing nonconvex problems: only in the case of convexity all efficient solutions of a multiobjective optimization problem can be found by this approach (and by varying the weights), cf. [10, Section 3]. It might even happen that one only finds the individual minima of the individual objective functions, as we will also illustrate with an example in this note. With our results we show that first applying the weighted sum method and then studying its completely positive reformulation, as proposed by [1], finds exactly the same efficient solutions as solving the direct multiobjective completely positive reformulation. Thus this convexifying approach using the cone of completely positive matrices seems not to be a suitable tool for nonconvex problems with multiple objectives.

The paper is organized as follows: In Sect. 2, we give the theoretical background based on the results by Burer [5] on how to convexify binary quadratic problems, followed by some basic properties in multiobjective optimization in Sect. 3. In Sect. 4, we give our main results in Theorems 4.3 and 4.5 followed by a short illustrative example.

2 Convex reformulations of nonconvex quadratic problems

Throughout the paper, for given matrices $X,Y\in {\mathbb {R}}^{m\times n}$, let $\langle X,Y\rangle :={{\,\mathrm{trace}\,}}(X^TY)$ denote the Frobenius matrix inner product. Moreover, for a given square matrix X, we understand the inequality $X\ge 0$ entrywise, and $X\succeq 0$ indicates X to be positive semidefinite. We denote by ${\mathbb {R}}^n_+=\{x\in {\mathbb {R}}^n\mid x_i\ge 0,\ i=1,\ldots ,n\}$ the nonnegative orthant and by ${{\,\mathrm{conv}\,}}(\cdot )$ the convex hull of a set. For vectors $x,y\in {\mathbb {R}}^n$ we write $x\le y$ in case $x_i\le y_i$ for $i=1,\ldots ,n$.

In the following, let $Q\in {\mathbb {R}}^{n\times n}$, $c\in {\mathbb {R}}^n$, $a^i\in {\mathbb {R}}^{n}$, $b_i\in {\mathbb {R}}$ for every $i=1,\dots ,l$ and $B\subseteq \{1,\dots ,n\}$. We consider the optimization problem

To obtain a convex reformulation of this problem, we make use of the cone of completely positive matrices.

Definition 2.1

A symmetric matrix X of order n is called completely positive if there exists a rank-1 representation of the following type: There exists $r\in {\mathbb {N}}$ such that

$$\begin{aligned} X=\sum \limits _{i=1}^r x^i({x^i})^T,\text { where }x^i\in {\mathbb {R}}^n_+~\text { for every } i=1,\ldots ,r. \end{aligned}$$

The smallest number $r\in {\mathbb {N}}$ for which such a factorization of X exists is called cp-rank of X. We denote by $\mathcal {CP}_n$ the set of all completely positive matrices of order n.

We have the following properties, cf. [2, Proposition 1.24] and [13]:

Lemma 2.2

 

• (a) $\mathcal {CP}_n$ is a closed, pointed, convex matrix cone with nonempty interior.

• (b) If $n\le 4$, then $\mathcal {CP}_n=\{X\in {\mathbb {R}}^{n\times n}\mid X=X^T,\ X\ge 0,\ X\succeq 0\}$.

In higher dimensions, i.e., for $n\ge 5$, to show that a matrix is completely positive is known to be NP-hard, cf. [8]. Nevertheless, any rank-1 representation defined as in Definition 2.1 gives a certificate for the matrix to be completely positive. For a projection-type approach to obtain completely positive factorizations, the reader is referred to [11].

Due to [5], Problem ($QP_1$) can equivalently be reformulated as

For showing this equivalence, Burer in [5] makes the following key assumption

$$\begin{aligned} x\ge 0\text { and } (a^i)^Tx=b_i \text { for every } i=1,\dots , l~ \ \Rightarrow \ 0\le x_j\le 1 \text { for every } j\in B \end{aligned}$$

and shows that this assumption holds without loss of generality. Thus, we assume this assumption to hold for the forthcoming results. The relation of Problem ($CP_1$) to Problem ($QP_1$) is now summarized in the following theorem, cf. [5, Theorem 2.6]:

Theorem 2.3

Problems ($QP_1$) and ($CP_1$) are equivalent in the following sense:

• (a) Assume one of the Problems ($QP_1$) or ($CP_1$) to have an optimal solution, then so has the other and the corresponding optimal objective function values coincide.

• (b) Let $(x^*,X^*)$ be optimal for ($CP_1$), then $x^*$ is in the convex hull of optimal solutions for ($QP_1$).

Moreover, we have the following useful results:

Lemma 2.4

If Problem ($CP_1$) is solvable, there always exists an optimal solution of the form $(x,xx^T)$.

Proof

Assume ($CP_1$) is solvable with optimal solution $(x^*,X^*)$. By Theorem 2.3(a) there exists an optimal solution $\bar{v}$ for ($QP_1$) with $f_1(\bar{v})= \bar{v}^TQ\bar{v}+2c^T\bar{v}=F_1(x^*,X^*)$. Since $\bar{v}_j=(\bar{v}\bar{v}^T)_{jj}$ for every $j\in B$ as well as

$$\begin{aligned} \begin{pmatrix}1&{}\bar{v}^T\\ \bar{v}&{}\bar{v}\bar{v}^T\end{pmatrix} =\begin{pmatrix}1\\ \bar{v}\end{pmatrix}\begin{pmatrix}1\\ \bar{v}\end{pmatrix}^T\in \mathcal {CP}_{n+1} \end{aligned}$$

holds by construction, we have that $(\bar{v},\bar{v}\bar{v}^T)$ is feasible for ($CP_1$). As $f_1(\bar{v})=F_1(\bar{v},\bar{v}\bar{v}^T)$ and thus $F_1(x^*,X^*)=F_1(\bar{v},\bar{v}\bar{v}^T)$, we derive that $(\bar{v},\bar{v}\bar{v}^T)$ is an optimal solution for ($CP_1$).

$\square$

Lemma 2.5

Let $(x,xx^T)$ be an optimal solution for ($CP_1$). Then x is an optimal solution for ($QP_1$).

Proof

We have that x is also feasible for  ($QP_1$). By Theorem 2.3(a) together with $f_1(x)=F_1(x,xx^T)$ it is also optimal for ($QP_1$). $\square$

Lemma 2.6

Let x be optimal for ($QP_1$), then $(x,xx^T)$ is optimal for ($CP_1$).

Proof

First, observe that x feasible for ($QP_1$) implies $(x,xx^T)$ feasible for ($CP_1$). Moreover, again by Theorem 2.3(a), the optimal values coincide and with $f_1(x)=F_1(x,xx^T)$ we derive that $(x,xx^T)$ is also optimal for ($CP_1$). $\square$

To sum up, we have the following relations between ($QP_1$) and ($CP_1$):

Corollary 2.7

It holds that:

$$\begin{aligned} \{x\in {\mathbb {R}}^n \mid x \text { optimal for}~ (QP_1)\}&\subseteq \{x\in {\mathbb {R}}^n \mid \exists X\in {\mathbb {R}}^{n\times n} : (x,X) \text { optimal for }~ (CP_1)\} \\ {{\,\mathrm{conv}\,}}\left( \{x\in {\mathbb {R}}^n \mid x \text { optimal for}~ (QP_1)\}\right)&\supseteq \{x\in {\mathbb {R}}^n \mid \exists X\in {\mathbb {R}}^{n\times n} : (x,X) \text { optimal for }~ (CP_1) \} \\ \{x\in {\mathbb {R}}^n\mid x\text { optimal for}~ (QP_1)\}&= \{x\in {\mathbb {R}}^n\mid (x,xx^T) \text { optimal for}~ (CP_1)\} \\ \{f_1(x)\mid x \text { optimal for}~ (QP_1) \}&= \{F_1(x,X)\mid (x,X)\text { optimal for}~ (CP_1)\}. \end{aligned}$$

3 Multiobjective optimization: efficiency and supported points

In the following, let ${\mathbb {R}}^m_+:=\{x\in {\mathbb {R}}^m\mid x\ge 0\}$, as well as $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$ and $M\subseteq {\mathbb {R}}^{n}$, $M\not =\emptyset$. We consider the multiobjective optimization problem

Definition 3.1

• (a) We call a feasible solution $x^*\in M$ of Problem (MOP) efficient if there exists no $x\in M$ such that $f_i(x)\le f_i(x^*)$ for all $i=1,\dots ,m$ and $f_j(x)<f_j(x^*)$ for at least one $j\in \{1,\dots ,m\}$.

• (b) We call a feasible solution $x^*\in M$ of Problem (MOP) weakly efficient if there exists no $x\in M$ such that $f_i(x)<f_i(x^*)$ for all $i=1,\dots ,m$.

• (c) We call a feasible solution $x^*\in M$ of Problem (MOP) supported if there exists $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^m w_i=1$ such that for every $x\in M$ it holds that $w^T f(x^*)\le w^T f(x)$, i.e., $x^*\in \text{ argmin }\{w^Tf(x)\mid x\in M\}$.

Thus, supported solutions of (MOP) are those which can be obtained by applying the weighted sum scalarization and by solving the resulting single-objective problem. Note that we can equivalently replace the assumption $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^m w_i=1$ in the definition above by $w\in {\mathbb {R}}^m_+\setminus \{0\}$. By [10, Proposition 3.9] any supported solution is also weakly efficient. In a convex setting, we have the following result, cf. [10, Section 3]:

Lemma 3.2

Let $f(M)+{\mathbb {R}}^m_+$ be convex. Then $x^*\in M$ is a weakly efficient solution for (MOP) if and only if $x^*$ is a supported solution for (MOP).

In case $f_i,\ i=1,\ldots ,m$ and M are convex, then $f(M)+{\mathbb {R}}^m_+$ is convex.

In the context of efficiency, we further introduce the following definition, see also [15, Definition 3.2.6], where this property is also named external stability.

Definition 3.3

We say that (MOP) fulfills the domination property if for every $x\in M$ there exists an efficient solution $x^*$ for (MOP) such that $f(x^*)\le f(x)$.

According to [15], (MOP) fulfills the domination property if f(M) is nonempty, $f(M)+{\mathbb {R}}^m_+$ is closed and there exists $y\in {\mathbb {R}}^m$ with $f(M)\subseteq \{y\}+{\mathbb {R}}^m_+$.

In the following, we pick up the convex inclusion condition as introduced in [1] and show its relation to the set of supported solutions.

Definition 3.4

[1, Def. 3.2] Let $x\in M$. We say that f(M) satisfies the convex inclusion condition at f(x) if there exists a convex set $K\subseteq {\mathbb {R}}^m$ with $f(M)\subseteq K$ such that $K\cap \left( \{f(x)\}- \text{ int }({\mathbb {R}}^m_+)\right) =\emptyset$.

Proposition 3.5

Let $x^*\in M$. Then f(M) satisfies the convex inclusion condition at $f(x^*)$ if and only if $x^*$ is supported.

Proof

First, let $x^*\in M$ be a supported solution. Thus, there exists $w\in {\mathbb {R}}^m_+\setminus \{0\}$ with $w^T f(x^*)\le w^Tf(x)$ for every $x\in M$. Now let $K:=\{y\in {\mathbb {R}}^m\mid w^Tf(x^*)\le w^Ty\}$. Then K is convex and $f(M)\subseteq K$ holds by definition. Moreover, for any $y\in \{f(x^*)\}-\text{ int }({\mathbb {R}}^m_+)$ it holds $w^Ty<w^Tf(x^*)$ and thus $y\not \in K$. Hence, f(M) satisfies the convex inclusion condition at $f(x^*)$.

For the reverse direction, let f(M) satisfy the convex inclusion condition at $f(x^*)$. Thus, there exists a convex set $K\supseteq f(M)$ such that $K\cap (\{f(x^*)\}-\text{ int }({\mathbb {R}}^m_+))=\emptyset$. Then, by Eidelheit’s separation theorem (see, for example, [12, Theorem 3.16]), there exists a vector $d\in {\mathbb {R}}^m\setminus \{0\}$ and a scalar $\gamma \in {\mathbb {R}}$ with

$$\begin{aligned} \forall \ k\in K,\ \forall \ r\in {\mathbb {R}}^m_+:\qquad d^Tk\le \gamma \le d^T(f(x^*)-r). \end{aligned}$$

(1)

As the assumption $d^T(-r)<0$ for some $r\in {\mathbb {R}}^m_+$ would contradict $\gamma \le d^T(f(x^*)-r)$ due to $\lambda r\in {\mathbb {R}}^m_+$ for any $\lambda >0$, we derive $d\in -{\mathbb {R}}^m_+$. For $w:=-d/\Vert d\Vert _1\in {\mathbb {R}}^m_+$ we obtain from (1) with $r=0$ and together with $f(M)\subseteq K$ that

$$\begin{aligned} \forall \ x\in M:\qquad w^Tf(x)\ge w^Tf(x^*) \end{aligned}$$

and thus $x^*$ is a supported solution. $\square$

In [1, Theorem 3.3] it was already stated for quadratic problems with linear constraints that if f(M) satisfies the convex inclusion condition at $f(x^*)$ with $x^*$ being weakly efficient for (MOP), then $x^*$ is a supported solution for (MOP). Above we have shown that there is an if and only if characterization between supported solutions and points $x^*$ for which the convex inclusion condition at $f(x^*)$ is satisfied. The further examinations in [1] have only been done for supported solutions by using the weighted sum approach.

4 Extension of the completely positive reformulation to the multiobjective framework

Let $Q^i\in {\mathbb {R}}^{n\times n}$ and $c^i\in {\mathbb {R}}^n$ for every $i=1,\dots ,m$. A multiobjective extension of Problem ($QP_1$) now reads as:

Following the steps from the single-objective reformulation one obtains the completely positive problem

In the following, we will show that only one of the relations in Corollary 2.7 does extend to the multicriteria framework. As will be shown in Theorems 4.3 and 4.5, as well as Corollary 4.6, similar results only hold for supported solutions for ($QP_m$). As a first step to obtain these results, we mention the following convexity property, which follows from the convexity of the cone $\mathcal {CP}_{n+1}$, see Lemma 2.2:

Lemma 4.1

The set $\{F(x,X)\in {\mathbb {R}}^m\mid (x,X)\ \text{ feasible } \text{ for }$  ($CP_m$)$\}$ is convex.

Following Lemma 3.2, we immediately obtain:

Lemma 4.2

A pair $(x^*,X^*)$ which is feasible for ($CP_m$) is a weakly efficient solution for ($CP_m$) if and only if it is a supported solution for ($CP_m$).

Thus, any weakly efficient solution (and, therefore, every efficient solution) $(x^*,X^*)$ for ($CP_m$) can be obtained by solving a problem of the following type, where $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^m w_i=1$:

Based on Lemmas 2.4, 2.5 and 2.6 we obtain the following main results:

Theorem 4.3

• (a) If there exists a weakly efficient solution for ($CP_m$), then there exists a weakly efficient solution of the form $(x,xx^T)$ for ($CP_m$).

• (b) If $(x,xx^T)$ is a weakly efficient solution for ($CP_m$), then x is a supported solution for ($QP_m$).

• (c) Let x be a supported solution for ($QP_m$), then $(x,xx^T)$ is weakly efficient for ($CP_m$).

Proof

• (a) Assume there exists a weakly efficient solution $(x',X')$ for Problem ($CP_m$). Lemma 4.2 implies that there exists $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^mw_i=1$ such that $(x',X')$ is an optimal solution for ($CP_m^w$). This problem is with $Q=\sum _{i=1}^m w_iQ^i$ and $c=\sum _{i=1}^m w_ic^i$ of the form ($CP_1$), so by Lemma 2.4 there exists an optimal solution of the form $(x,xx^T)$ for ($CP_m^w$). Again, by Lemma 4.2, $(x,xx^T)$ is weakly efficient for ($CP_m$).

• (b) By Lemma 4.2 there exists $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^mw_i=1$ such that $(x,xx^T)$ is also an optimal solution for ($CP_m^w$). Lemma 2.5 implies x to be an optimal solution for the problem:

  

  Thus, x is a supported solution for ($QP_m$).

• (c) Let x be a supported solution for ($QP_m$). Thus, there exists $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^mw_i=1$ such that x is an optimal solution for ($QP_m^w$). Due to Lemma 2.6, we know that $(x,xx^T)$ is optimal for ($CP_m^w$). Hence, $(x,xx^T)$ is a supported solution for ($CP_m$) and by Lemma 4.2 weakly efficient for ($CP_m$).

$\square$

Note that the weakly efficient solutions in Theorem 4.3(a), i.e., $(x',X')$ and $(x,xx^T)$, do not necessarily have the same objective function value w.r.t. the vector-valued objective function from ($CP_m$), i.e., w.r.t. F. They only have the same objective function value w.r.t. the objective function from ($CP_m^w$), i.e., $w^TF$, for some $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^mw_i=1$, see the proof.

Theorem 4.3 shows that extending the convex reformulation of quadratic binary problems to a multiobjective framework does only return those (weakly) efficient solutions as rank-1 solutions, which are supported. In contrast to the single-objective case, under the assumption that not every efficient solution for ($QP_m$) is supported, we have in general:

$$\begin{aligned}&\{x\mid x \text{(weakly) } \text{ efficient } \text{ for }~ (QP_m)\}&\ne \{x\mid (x,xx^T) \text{(weakly) } \text{ efficient } \text{ for }~ (CP_m)\} \end{aligned}$$

(2)

$$\begin{aligned}&\{f(x)\mid x \text{(weakly) } \text{ efficient } \text{ for }~ (QP_m)\}&\ne \{F(x,X)\mid (x,X) \text{(weakly) } \text{ efficient } \text{ for }~ (CP_m)\} \end{aligned}$$

(3)

Statement (2) will be discussed in Corollary 4.6. Recall that only under the assumption that $f(M)+{\mathbb {R}}^m_+$ is convex we have the guarantee that all weakly efficient solutions for ($QP_m$) are supported. Statement (3) will be shown in the forthcoming Example 4.8.

The only result which transfers from Corollary 2.7 to the multiobjective setting is the following:

Lemma 4.4

It holds that

$$\begin{aligned} {{\,\mathrm{conv}\,}}\left( \{x\mid x \text{ weakly } \text{ efficient } \text{ for }~ (QP_m)\}\right) \supseteq \{x\mid \exists X:~(x,X) \text { weakly efficient for}~ (CP_m)\}. \end{aligned}$$

Proof

Let (x, X) be weakly efficient for ($CP_m$). Then, by Lemma 4.2 there exists $w\in {\mathbb {R}}^m_+$ with $\sum _{i=1}^mw_i=1$ such that (x, X) is an optimal solution for ($CP_m^w$). By Theorem 2.3(b), x is then in the convex hull of optimal solutions for ($QP_m^w$). Any optimal solution for ($QP_m^w$) is a supported and thus, by [10, Proposition 3.9], a weakly efficient solution for ($QP_m$) and the proof is complete. $\square$

From the proof even the following main characterization follows:

Theorem 4.5

It holds that

$$\begin{aligned} {{\,\mathrm{conv}\,}}\{x\mid x \text{ supported } \text{ for }~ (QP_m)\}\supseteq \{x\mid \exists X:~(x,X) \text { weakly efficient for}~ (CP_m)\}. \end{aligned}$$

This is an important result, as it shows that by looking at weakly efficient solutions (x, X) for ($CP_m$), we can only find those weakly efficient solutions x for ($QP_m$) which are in the convex hull of supported solutions for ($QP_m$). Clearly, in general for a nonconvex problem ($QP_m$), not all weakly efficient solutions are in the convex hull of the supported solutions. Here the forthcoming Example 4.8 will provide a concrete instance.

Next to that, we only have the following results, which we collect similarly to Corollary 2.7:

Corollary 4.6

Concerning the relation between ($QP_m$) and ($CP_m$), it holds that

$$\begin{aligned} \{x\mid x \text{ supported } \text{ for }~ (QP_m)\}&=\{x\mid (x,xx^T) \text{ weakly } \text{ efficient } \text{ for }~(CP_m)\}\\&\subseteq \{x\mid \exists X:~(x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\}\\ \{f(x)\mid x \text{ supported } \text{ for }~ (QP_m)\}&\subseteq \{F(x,X)\mid (x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\} \end{aligned}$$

As we will also illustrate in the forthcoming Example 4.8, we have in general

$$\begin{aligned} \{f(x)\mid x \text{ supported } \text{ for }~ (QP_m)\}\not \supseteq \{F(x,X)\mid (x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\}. \end{aligned}$$

Instead, we have as a direct consequence of Corollary 2.7 for all $w\in {\mathbb {R}}^m_+\setminus \{0\}$

$$\begin{aligned} \{w^Tf(x)\mid x \text{ optimal } \text{ for }~ (QP_m^w)\} = \{w^TF(x,X)\mid (x,X) \text{ optimal } \text{ for }~ (CP_m^w)\}. \end{aligned}$$

The following proposition allows to characterize not only the supported but also the other weakly efficient solutions for ($QP_m$) and thus adds insights to (3):

Proposition 4.7

Let x be a weakly efficient solution for ($QP_m$) which is not supported. Further, assume $Y:=\{F(x,X)\mid (x,X) \text { feasible for}~ (CP_m)\}$ to be compact. Then there exists $({\bar{x}},{\bar{X}})$ efficient for ($CP_m$) such that $F({\bar{x}},{\bar{X}})\le F(x,xx^T)=f(x)$ and $F({\bar{x}},{\bar{X}})\not =f(x)$.

Proof

Let x be a weakly efficient solution for ($QP_m$) which is not supported. Then $(x,xx^T)$ is feasible for ($CP_m$). Due to Theorem 4.3(b), we get that $(x,xx^T)$ is not weakly efficient for ($CP_m$). To close the proof, it suffices to note that ($CP_m$) satisfies the domination property, cf. [15, Theorem 3.2.9]. $\square$

This proposition together with Corollary 4.6 now shows that if Y is compact, it holds that:

$$\begin{aligned} \{f(x)\mid x \text{ weakly } \text{ efficient } \text{ for }~ (QP_m)\}\subseteq \{F(x,X)\mid (x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\}+{\mathbb {R}}^m_+. \end{aligned}$$

The following example illustrates our results:

Example 4.8

Let $l=1$ and $B=\emptyset$ , as well as

$$\begin{aligned} Q^1:=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} 8 &{} 0\\ 0 &{} 0 &{} 0\end{pmatrix},~ c^1:=\begin{pmatrix} 0\\ 0\\ 0\end{pmatrix} \text{ and } \ Q^2:=\begin{pmatrix} 20 &{} 0 &{} 5\\ 0 &{} -8 &{} 8\\ 5 &{} 8 &{} -2\end{pmatrix},~ c^2:=\begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}. \end{aligned}$$

We consider the following instance of ($QP_m$):

For the completely positive reformulation of (EQP), we obtain:

At first, we will have a closer look at the decision space of (EQP) illustrated in Fig. 1. There, the set $\{x\in {\mathbb {R}}^3\mid x \text{ feasible } \text{ for }~ ($EQP$)\}$ is illustrated in dark blue and the set $\{x\mid x \text{ weakly } \text{ efficient } \text{ for }~ ($EQP$)\}$ is shown in red. In addition, all weakly efficient solutions which are as well supported for (EQP) are highlighted as green diamonds.

As Fig. 1 substantiates, there exist weakly efficient solutions of (EQP) which are not an element of ${{\,\mathrm{conv}\,}}\{x\mid x \text{ supported } \text{ for }~ ($EQP$)\}$. Thus, not all weakly efficient solutions x for (EQP) can be identified, using weakly efficient solutions (x, X) for (ECP), as Theorem 4.5 shows. The set $\{x\mid \exists X:~(x,X) \text { weakly efficient for ({ECP}{} )}\}$ equals the convex hull of the supported solutions for (EQP).

Fig. 1

Illustrations in the decision space of (EQP) in Example 4.8

In order to solve (ECP) and since $n\le 4$ holds, we can make use of Lemma 2.2, and thus replace the completely positive cone by the doubly nonnegative cone, which is the cone of symmetric $(4\times 4)$ matrices which are componentwise nonnegative and positive semidefinite in this concrete setting. Note that due to Lemma 4.2, all weakly efficient solutions of Problem (ECP) are supported. Thus, it is sufficient to apply the weighted sum scalarization with varying weights and to solve the corresponding individual scalar problem of type

via semidefinite programming in order to find all weakly efficient solutions for (ECP).

Fig. 2

Illustrations in the objective space of Problems (EQP) and (ECP)

Figure 2 visualizes the objective space of both problems (EQP) and (ECP). To be more precise, the set $\{f(x)\mid x \text { feasible for}~($EQP$)\}$ is illustrated in dark blue, the set $\{f(x)\mid x \text { weakly efficient for}~($EQP$)\}$ is shown in red, and the two green diamonds represent the set $\{f(x)\mid x \text { supported for}~($EQP$)\}$. Furthermore, the teal dots represent discrete points of the set $\{F(x,X)\mid (x,X) \text { feasible for}~($ECP$)\}$ and the set $\{F(x,X)\mid (x,X)\text { weakly efficient for}~($ECP$)\}$ is highlighted in orange. We first note that indeed every weakly efficient solution for (ECP) is as well supported.

Moreover, Fig. 2 indicates the images of three weakly efficient solutions for (ECP) in black, which can be obtained by solving ($ECP_w$) for different values of w. For instance, by taking $w=(0.42857142,0.57142858)$, we obtain a weakly efficient solution $(x^*,X^*)$ for (ECP) which corresponds to the center black circle in Fig. 2. Here especially ${{\,\mathrm{rank}\,}}(X^*)= 2$ holds. Thus, Fig. 2 further substantiates the fact that there does not exists $(x,xx^T)$ feasible for (ECP) such that $F(x,xx^T)=F(x^*,X^*)$. Nevertheless, since $(x^*,X^*)$ is optimal for ($ECP_w$) and with the help of Lemma 2.4, there exists a rank-1 optimal solution $(x',x'x'^T)$ for ($ECP_w$) such that $F_w(x^*,X^*)=F_w(x',x'x'^T)$ holds. This very rank-1 optimal solution corresponds to one of the outer black dots in Fig. 2. The outer black dots both correspond to so called individual minimizers, i.e., to images of points ${{\bar{x}}}^i$ with ${{\bar{x}}}^i\in \text{ argmin }\{f_i(x)\mid x \text{ feasible } \text{ for }~ ($EQP$)\}$. Also due to Theorem 4.3(b), $x'$ is supported for (EQP). Thus, the green diamonds in Fig. 2 correspond to the two supported solutions for (EQP): $(x_1,x_2,x_3)=(0,0,100)$ with $f(x)=(0,-20000)^T$, and $(x_1,x_2,x_3)=(0,100,0)$ with $f(x)=(80000,-80000)^T$. This especially shows

$$\begin{aligned} \{f(x)\mid x \text{ supported } \text{ for }~ (QP_m)\}\subseteq \{F(x,X)\mid (x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\}, \end{aligned}$$

as in Corollary 4.6. In addition, $F(x^*,X^*)\not \in \{f(x)\mid x \text{ feasible } \text{ for }~ (QP_m)\}$ holds, such that $\{f(x)\mid x \text{ supported } \text{ for }~ (QP_m)\}\not \supseteq \{F(x,X)\mid (x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\}$, and also

$$\begin{aligned} \{f(x)\mid x \text{ weakly } \text{ efficient } \text{ for }~ (QP_m)\}\not \supseteq \{F(x,X)\mid (x,X) \text{ weakly } \text{ efficient } \text{ for }~ (CP_m)\}, \end{aligned}$$

showing (3) as promised.

5 Conclusion

In this note, we proved that the advantages of convexifying quadratic problems via completely positive reformulations do not extend to a multicriteria framework. To be more precise, in the multiobjective completely positive reformulation ($CP_m$), every weakly efficient solution is already supported. To recover weakly efficient solutions for the multiobjective quadratic problem ($QP_m$), we need to consider rank-1 weakly efficient solutions for ($CP_m$). But here we saw that they can only recover the weakly efficient solutions for ($QP_m$) which are supported. Thus, to obtain these weakly efficient solutions for ($QP_m$), it would be sufficient to solve the single-objective problem ($QP_m^w$) and to leave the multiobjective framework. Further, a concrete example illustrated the results of this note.