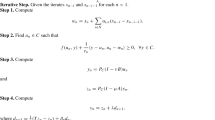Partially distributed outer approximation

Abstract

This paper presents a novel partially distributed outer approximation algorithm, named PaDOA, for solving a class of structured mixed integer convex programming problems to global optimality. The proposed scheme uses an iterative outer approximation method for coupled mixed integer optimization problems with separable convex objective functions, affine coupling constraints, and compact domain. PaDOA proceeds by alternating between solving large-scale structured mixed-integer linear programming problems and partially decoupled mixed-integer nonlinear programming subproblems that comprise much fewer integer variables. We establish conditions under which PaDOA converges to global minimizers after a finite number of iterations and verify these properties with an application to thermostatically controlled loads and to mixed-integer regression.

1 Introduction

A Mixed Integer Convex Program (MICP) is an optimization problem with convex objective and constraint functions, where the only non-convex constraint is that a subset of the optimization variables need to be integer-valued [8, 36]. MICPs arise in a plethora of application areas ranging from AC transmission expansion planning and robust power flow problems [1, 30], via thermal unit design and control [12], a variety of scheduling and layout design problems [53], design of multi-product batch plants [50], to obstacle avoidance and robotic motion planning problems [34].

Although MICPs are NP-hard in general, there exist a variety of algorithms for solving MICPs to global optimality [8]. State-of-the-art MICP solvers are based on tailored methods that exploit the fact that the integrality constraints are discrete while all other constraints are convex. Early attempts to develop tailored Branch and Bound (B&B) methods for MICP have been proposed in [24], mostly focussing on computational experiments and heuristics for selecting the branching variables and nodes. Improved versions of these early B&B methods for MICP can be found in [9, 35]. Other early methods for solving MICP include generalized Benders decomposition methods [5, 23], which are, however, less frequently used in state-of-the-art MICP solvers.¹

Modern MICP implementations are often based on or related to Outer Approximation (OA), which goes back to Duran and Grossmann [16]. In contrast to B&B, OA alternates between solving Nonlinear Programs (NLP) with fixed integer values as well as Mixed Integer Linear Programs (MILP), which are constructed by linearizing the objective and constraint functions at the solutions of the NLP and which are used to update the integer variables. A notable extension of OA has been developed by Fletcher and Leyffer [20], who suggest to include curvature information in the relaxed integer program leading to a quadratic outer approximation method. A more recent approach to second order outer approximation is that of Kronqvist et al. [32]. Moreover, Kesavan and co-workers [28] have studied variants of OA for solving non-convex mixed integer problems. Another class of MICP methods are based on (extended) cutting plane methods [59] or combination of OA and branch-and-cut [49]; see also [56] for a general overview of polyhedral branch-and-cut methods. In recent years, there has been considerable progress in lift-and-project methods for MICP. An excellent overview and discussion of the state-of-the-art of such lift-and-project methods can be found in a recent article by Kilinç, Linderoth, and Luedtke [29].

Another recent trend in MICP solver development is the exploitation of separable structures by so-called extended formulations [25]. Here, the main idea is to introduce auxiliary variables in order to bound decoupled summands in additive expressions separately [58], which can lead to tighter polyhedral outer approximations. Such extended formulations have not only found their way into OA methods, as discussed in [25] and [33], but they can also be used to increase the performance of lift-and-project methods for MICP [29]. Also of note are several algorithms that exploit separability to decompose large-scale MINLP problems into MINLP subproblems based on block separability [41, 42, 45, 46]. However, extended formulations only exploit separability to construct tighter outer approximations, but neither existing OA methods nor state-of-the-art lift-and-project methods ever attempt to break a large-scale MICP into decoupled MICPs with fewer integer variables. This is in contrast to distributed continuous convex optimization methods, such as dual decomposition [19, 43], Alternating Direction Method of Multipliers (ADMM) [10, 17, 21], or Augmented Lagrangian based Alternating Direction Inexact Newton (ALADIN) methods [26], which can all be used to solve large-scale convex optimization problems to global optimality by alternating between solving small-scale convex optimization problems and sparse linear algebra operations. These methods typically require communication of the solutions of the decoupled problems between neighbours or to a central coordinator [10]. Although some researchers, [39, 55], have attempted to apply these distributed local optimization methods in a heuristic manner, these methods cannot find global minimizers of non-convex problems reliably. This is due to the fact that ADMM, ALADIN, or similar distributed convex optimization method typically rely on strong duality results for augmented Lagrangians [52, 54], which fail to hold in the presence of integrality constraints.

After reviewing extended formulations and related existing outer approximation methods in Sect. 2, the main contribution of this paper is presented in Sect. 3, which introduces a Partially Distributed Outer Approximation (PaDOA) method for MICPs with separable objective functions. In contrast to existing algorithms for structured MICP, PaDOA alternates between solving MICPs with fewer integer variables and large-scale MILPs. Section 3.5 discusses the global convergence properties of PaDOA, as summarized in Theorem 3. In this context, we additionally establish the fact that global optimality of a given feasible point of an MICP with N separable objectives and Nn optimization variables can be computationally verified by solving N partially-decoupled MICPs, each comprising at most n local integer variables, and one MILP with Nn integer variables. This result is summarized in Theorem 2, which analyzes one-step convergence conditions for PaDOA. In the sense that both MICPs as well as MILPs are NP hard in general [22, 40], this result is not in conflict with existing complexity results for mixed integer optimization problems. However, there are solvers such as CPLEX [27], Gurobi [47], and many others [13], which are specifically designed for MIQPs and MILPs. Thus, the fact that one can reduce the task of verifying global optimality of a feasible point of a separable MICP with coupled affine constraints to the task of solving one MILP of a comparable size and several smaller subproblems, is—at least from a computational perspective—an important contribution. Notice that Sects. 2 and 3 focus on the theoretical properties of PaDOA, and consequently, a high level abstract notation is used to present these theoretical, yet, at this stage, conceptual ideas. These derivations lead to a formal prove of convergence, but, in general, the performance of PaDOA is problem dependent and a partial distribution of operations can only possibly lead to practical improvements if the problems are sufficiently structured. This aspect is illustrated by applying the method two MICP benchmark case studies in Sect. 4. The developments in this paper are not of pure theoretical interest only, but actually lead to a practical framework that has potential for future investigation, as outlined in our conclusions in Sect. 5.

1.1 Problem formulation

The present paper is concerned with mixed integer optimization problems of the form

$$\begin{aligned} \begin{array}{rccl} V^\star &{}=&{} \underset{x \in X, z \in Z}{\min }&{} f(x,z) \\ &{} &{} \text {s.t.}&{} A x = b \end{array} \end{aligned}$$

(1)

with separable objective function $f(x,z) = \sum _{i=1}^N f_i(x_i,z_i)$ and separable constraint sets

$$\begin{aligned} \begin{array}{rclcrcl} X &{}=&{} X_1 \times \ldots \times X_N \quad &{}\text {with}&{} \quad X_i&{}\subseteq &{} {\mathbb {R}}^{n_i} \\ \text {and} \quad Z &{}=&{} Z_1 \times \ldots \times Z_N \quad &{}\text {with}&{} \quad Z_i &{}\subseteq &{} {\mathbb {Z}}^{m_i} \; . \end{array} \end{aligned}$$

(2)

The coupling matrix A and the vector b are assumed to be given. In this context, the following blanket assumption is used.

Assumption 1

The sets $X_1, X_2, \ldots , X_N$ are non-empty convex polytopes, the sets $Z_1, Z_2, \ldots , Z_N$ are non-empty and compact, and the functions $f_i$ are convex on the convex hull of $X_i \times Z_i$.

The goal of this paper is to develop an efficient algorithm that finds $\varepsilon$-suboptimal points of (1), which are defined as follows:

Definition 1

A feasible point $(x^\star ,z^\star ) \in X \times Z$ with $A x^\star = b$ is said to be an $\varepsilon$-suboptimal point of (1), with $\varepsilon > 0$, if

$$\begin{aligned} f(x^\star ,z^\star ) \le f(x,z) + \varepsilon \,. \end{aligned}$$

for all $(x,z) \in X \times Z$ with $A x = b$.

Remark 1

The theoretical developments in this paper assume—for simplicity of presentation—that all coupled constraints are linear equations in x. This is not restrictive in the sense that coupled convex inequalities can always be reformulated by introducing slack variables [4, 11, 38].

Remark 2

Instead of (1), one could also consider more general optimization problems of the form

$$\begin{aligned} \begin{array}{cl} \underset{x \in X, z \in Z}{\min }&{} f(x,z) \\ \text {s.t.}&{} A x + B z = b \; . \end{array} \end{aligned}$$

(3)

However, under mild regularity assumptions [44], this problem is equivalent to

$$\begin{aligned} \begin{array}{cl} \underset{x \in X, y \in \mathrm {conv}\left( Z \right) , z \in Z}{\min }&{} \sum \limits _{i=1}^N \{ f_i(x_i,z_i) + {\bar{\lambda }}_i \Vert y_i - z_i \Vert _1 \} \\ \text {s.t.}&{} A x + B y = b \; . \end{array} \end{aligned}$$

(4)

with real-valued auxiliary variables y and $L_1$-penalty parameters ${\overline{\lambda }}_i \gg 0$. Here, $\mathrm {conv}\left( Z \right)$ denotes the convex hull of Z. Thus, for all theoretical purposes, it is sufficient to analyze problems of the form (1), where only the real-valued variables are coupled.

Remark 3

Modern MICP formulations, algorithms, and software can deal with rather general convex conic constraints [36]. Such constraints are left out for simplicity of presentation. Nevertheless all results in this paper can be easily extended for general conic constraints, as long as they are separable. From a purely theoretical perspective, one might argue that this can always be achieved by adding suitable convex penalty functions to the functions $f_i$, because this paper makes no assumptions on the differentiability properties of f. However, more tailored, practical algorithms that could exploit the structures of particular conic constraints are beyond the scope of this paper.

1.2 Notation

We use the notation

$$\begin{aligned} \partial _x g(x) = \left\{ a \in {\mathbb {R}}^n \mid \forall y \in {\mathbb {R}}^{n}, \; g(y) \ge g(x) + a^\mathsf {T}( y - x ) \right\} \end{aligned}$$

to denote the set of subgradients of a convex function $g: \mathbb R^{n} \rightarrow {\mathbb {R}}$ with respect to the variable x.

2 Outer approximation

The following section reviews OA by using a slightly more abstract viewpoint that is based on modern convex analysis notation. As mentioned in the introduction, OA has been introduced in the 1980s by Duran and Grossmann [16] using different notation, but the following section presents the method in a more general setting—also including Hijazi’s variants and extentions of OA—in order to prepare the developments in Sect. 3.

2.1 Polyhedral relaxations

In order to construct polyhedral outer approximations of the epigraph of the objective function f of (1), we consider the auxiliary optimization problem

$$\begin{aligned} f^\star (z) = \min _{x,y} \; f(x,z) \quad \mathrm {s.t.} \quad \left\{ \begin{array}{ll} x = y &{} \mid \; \lambda \\ A y = b \\ y \in X \; . \end{array} \right. \end{aligned}$$

(5)

for a fixed integer parameter $z \in Z$. Here, x and y are real valued primal optimization variables and the notation “$x = y \; \mid \lambda$” is used to say that $\lambda$ denotes the dual variable associated with the constraint $x=y$.

Proposition 1

If Assumption 1 is satisfied, strong duality holds for (5), i.e., we have

$$\begin{aligned} f^\star (z) = \max _{\lambda } \; \min _{x,y} \; f(x,z) + \lambda ^\mathsf {T}(y-x) \quad \mathrm {s.t.} \quad \left\{ \begin{array}{l} A y = b \\ y \in X \end{array} \right. \end{aligned}$$

(6)

for all $z \in Z$.

Proof

See “Appendix 1”. $\square$

Let $x^\star (z),y^\star (z),\lambda ^\star (z)$ denote any primal-dual solution of (5) in dependence on z. By writing out the optimality condition of (5) with respect to x, we find that

$$\begin{aligned} \lambda ^\star (z) \in \partial _x f( x^\star (z), z ) , \end{aligned}$$

i.e., $\lambda ^\star (z)$ must be a subgradient of f at the optimal solution of (5). For the developments given below it is helpful to keep in mind that the reverse statement is not correct, i.e., a subgradient of f at $(x^\star (z), z)$ is not necessarily a dual solution of (5).

In contrast to the particular choice of the subgradient $\lambda ^\star$ of f with respect to x, the construction of a subgradient of f with respect to z is less critical for the construction of outer approximation methods.² In the following, we assume that a function

$$\begin{aligned} \mu ^\star (z) \in \partial _z f( x^\star (z), z ) , \end{aligned}$$

is given, which returns a subgradient of f with respect to z at the optimal solution of (5). Because $f(x,z) = \sum _{i=1}^N f_i(x_i,z_i)$ is separable, the ith block components, $\lambda _i^\star (z)$ and $\mu _i^\star (z)$, of the subgradients of f are subgradients of $f_i$. Thus, the inequality

$$\begin{aligned} f_i(x_i, z_i) \ge f_i^\star ( {\hat{z}} ) + \left[ \lambda _i^\star ({\hat{z}}) \right] ^\mathsf {T}( x_i - x_i^\star ({\hat{z}}) ) + \left[ \mu _i^\star ({\hat{z}}) \right] ^\mathsf {T}( z_i - {\hat{z}}_i ) \end{aligned}$$

holds for all $x_i \in X_i$, and $z_i \in Z_i$ and all ${\hat{z}} \in Z$. Here, the shorthand

$$\begin{aligned} f_i^\star ( {\hat{z}} ) = f_i(x_i^\star ( {\hat{z}}), {\hat{z}}_i) \end{aligned}$$

is used. In this context, it is important to notice that the function $f_i^\star ({\hat{z}})$ depends on the whole vector ${\hat{z}}$, not only on its ith component, ${\hat{z}}_i$, because the equality constraints in (6) introduce a non-trivial coupling.

More generally, if $\varPi \subseteq Z_i$ denotes finite set of points in Z, we associate with $\varPi$ a set of hyperplane coefficients

$$\begin{aligned} {\mathcal {H}}_i( \varPi ) = \left\{ (\alpha ,\beta ,\gamma ) \left| \begin{array}{l} z \in \varPi \\ \alpha = \lambda _i^\star (z) \\ \beta = \mu _i^\star (z) \\ \gamma = f_i^\star (z) - \alpha ^\mathsf {T}x_i^\star (z) - \beta ^\mathsf {T}z_i \end{array} \right. \right\} \; . \end{aligned}$$

(7)

Notice that this set of hyperplane coefficients defines a polyhedral outer approximation of the epigraph of $f_i$. Thus, these coefficients can be used to construct a piecewise affine lower bound on $f_i$, which is for all $(x_i,z_i) \in X_i \times Z_i$ given by

$$\begin{aligned} \varPhi _{i}(x_i,z_i,\varPi ) = \max _{(\alpha ,\beta ,\gamma ) \in H_{i}(\varPi )} \left\{ \alpha ^\mathsf {T}x_i + \beta ^\mathsf {T}z_i + \gamma \right\} \; . \end{aligned}$$

(8)

Finally, we can construct the function

$$\begin{aligned} \varPhi (x,z,\varPi ) = \sum _{i=1}^N \varPhi _{i}(x_i,z_i,\varPi )\;. \end{aligned}$$

This function is—by construction—a piecewise affine lower bound on f,

$$\begin{aligned} \forall (x,z) \in X \times Z, \qquad \varPhi (x,z,\varPi ) \le f(x,z) \; . \end{aligned}$$

(9)

Next, our particular choice of the subgradient $\lambda ^\star (z)$ of f as the dual solution of (5) enables us to establish the following tightness property of the affine lower bound $\varPhi$.

Lemma 1

Let $\varPi \subseteq Z$ be any finite set of points. If Assumption 1 holds, then

$$\begin{aligned} f^\star (z) = \min _{x \in X} \; \varPhi (x,z,\varPi ) \quad \mathrm {s.t.} \quad A x = b \; . \end{aligned}$$

(10)

holds for all $z \in \varPi$.

Proof

See “Appendix 2”. $\square$

Note that Lemma 1 can be viewed as a special case of Theorem 2.3 in [23].

Remark 4

If the set $\varPi$ consists of m points, the computational cost for constructing the lower bound (9) of f has order $\mathbf {O}(m N)$. Notice that if we would have ignored the separable structure of f, the computational cost of computing the same lower bounding function would have been of order $\mathbf {O}(m^N)$. Thus, the construction of (9) as a sum of the lower bounds of the separable objective function is much cheaper than a direct construction of lower bounds of f. This reduction in complexity has for the first time been observed and exploited by Hijazi and co-workers [25]. By now, the expoitation of separability via extended formulations can be considered as a standard that has been adopted in many modern MICP algorithms and software tools [29, 36, 37].

2.2 Outer approximation algorithm

Algorithm 1 outlines the main steps of the outer approximation algorithm. Notice that this algorithm basically coincides with the original outer approximation algorithm that has been proposed in [16]. The only notable differences of Algorithm 1 compared to traditional OA are that the MILP in Step 3 uses the extended formulation based outer approximation variant from [25]. Moreover, because we do not assume that f is differentiable, we have to use the particular choice, $\lambda ^\star (z)$, of the subgradient, which is found as the dual solution³ of (5).

Notice that Step 1 of Algorithm 1 solves (1) under the additional constraint that the integer z is fixed. This implies that

$$\begin{aligned} f(x^\star ,z) \ge V^\star \end{aligned}$$

is an upper bound on the optimal objective value $V^\star$ of (1). Thus, the current upper bound U can be updated in Step 2. Moreover, the MILP (20) is by construction a relaxation of (1) which implies that the solution of Step 3, $\sum _{i=1}^N y_i^+$, is a lower bound on the optimal objective value $V^\star$. Thus, the difference, $U - \sum _{i=1}^N y_i^+$, between the current upper and lower bounds can be used as a termination criterion, which is implemented in Step 3 of Algorithm 1. The following finite termination result for outer approximation is (at least in very similar versions) well-known in the literature [16, 36].

Theorem 1

If Assumption 1 is satisfied, then Algorithm 1 terminates after a finite number of iterations.

Proof

See “Appendix 3”. $\square$

Remark 5

Algorithm 1 uses Hijazi’s extended formulation [25] for constructing the MILPs (20), which arguably exploits separability of the objective function to some extent. However, Algorithm 1 is not a fully distributed algorithm. In fact, a major disadvantage of Algorithm 1 becomes apparent, if one considers the special case that $A=0$ and $b=0$. In this case, the optimal solution of (1) could have been found with much less effort by solving the separable MICPs,

$$\begin{aligned} \min _{x_i \in X_i,z_i \in Z_i} f_i(x_i,z_i) \end{aligned}$$

which have much fewer integer variables. However, if Algorithm 1 is applied to such a problem with redundant equality constraint, this property is not detected and a large number of large-scale NLPs and large scale MILPs might have to be solved instead, until convergence is achieved. The goal of this paper is to mitigate this limitation of Algorithm 1 by proposing a partially distributed outer approximation algorithm that exploits the structure of the separable objective in a better way.

3 Partially distributed outer approximation algorithm

This section introduces a partially distributed outer approximation optimization algorithm for finding $\varepsilon$-suboptimal solutions of (1).

3.1 Partially decoupled upper bounds

The main idea of many distributed convex and local optimization methods is to solve a set of smaller-scale decoupled optimization problems in place of a single large one [5, 10, 14]. Similarly, consider partially decoupled optimization problems of the form

$$\begin{aligned} V_k(z) =&\underset{x,y,\zeta _k}{\min }&f_k(x_k,\zeta _k) + \varPsi _k(x,z) \nonumber \\&\text {s.t.}&\left\{ \begin{array}{ll} x = y &{} \mid \; \lambda \\ A y = b \\ y \in X \\ \zeta _k \in Z_k \end{array} \right. \end{aligned}$$

(13)

for $k \in \{ 1, \ldots , N \}$. Note that Problem (13) regards only the local integer variables $\zeta _k \in Z_k$ as optimization variables, while all other integers are fixed. However, concerning the real-valued variables, the whole vector $x \in X$ is kept as an optimization variable. In this context, the shorthands

$$\begin{aligned} \forall (x,z) \in X \times Z, \qquad \varPsi _k(x,z) = \underset{j \ne k}{\sum } f_j(x_j,z_j) \end{aligned}$$

are introduced in order to keep the x-dependence of the remaining summands, i.e., all objective terms whose index is not equal to k. As in the previous section, $\lambda$ denotes the dual solution that is associated with the consensus constraint “$x = y$”. Because the constraint $\zeta _k \in Z_k$ enforces integrality, strong duality of (13) does not hold in general. However, if $\zeta _k^\star (z)$ denotes an optimal solution of (13) for the integer variable and if Assumption 1 holds, we still have

$$\begin{aligned} V_k(z) = \max _{\lambda }&\underset{x,y}{\min }&\; \; f_k(x_k,\zeta _k^\star (z)) + \varPsi _k(x,z) + \lambda ^\mathsf {T}(y-x) \nonumber \\&\text {s.t.}&\; \; \left\{ \begin{array}{l} A y = b \\ y \in X \; . \end{array} \right. \end{aligned}$$

(14)

The proof of this statement is completely analogous to Proposition 1, i.e., if the linear coupling constraint $Ax =b$ has a solution in X, a maximizer of (14) exists and can be used to define a suitable subgradient. Also note that the functions $V_k$ yield upper bounds on the objective value of (1),

$$\begin{aligned} \forall z \in Z, \qquad \min _{k} \, V_k(z) \ge V^\star \end{aligned}$$

(15)

At this point, it should be mentioned that one basic assumption of the algorithmic developments in this paper is that the complexity of the mixed integer optimization problems of interest depends mostly on the number of integer variables. This is in contrast to the number of real-valued variables, which may be assumed to have a negligible influence on the overall complexity of the mixed-integer optimization problem. In other words, we assume that (13) is much easier to solve than (1) in the sense that it contains much fewer integer variables, although both problems have the same number of real-valued variables. Here, it is important to keep in mind that, although the algorithmic developments in this paper are inspired by the field of distributed optimization, the algorithm in this paper is (at least in the form in which we present and analyze it) not fully distributed. This is because solving (13) requires the evaluation of the function $\varPsi _k$, which, in turn, requires the evaluation of all functions $f_j$ with $j \ne k$.

3.2 Partially decoupled lower bounds

In this paper, we suggest to solve the decoupled MICPs (13) by lower level solvers that implement the traditional outer approximation algorithm that has been reviewed in Sect. 2.2. Notice that if Assumption 1 is satisfied, strong duality holds, i.e., these lower level solvers will return piecewise affine models

$$\begin{aligned} \varTheta _k^\star : X \times Z_k \rightarrow {\mathbb {R}} , \end{aligned}$$

which must satisfy the condition

$$\begin{aligned} V_k(z) - \epsilon _{\mathrm {L}}\; \le \min _{x \in X,\zeta \in Z_k} \varTheta _k^\star (x,\zeta ) \quad \mathrm {s.t.} \quad A x = b \end{aligned}$$

(16)

upon termination. Here, $\epsilon _{\mathrm {L}}\ge 0$ denotes the numerical tolerance of the lower level OA solvers. Notice that the optimization problem on the right hand of (16) corresponds to the last MILP relaxation that is solved by the lower level OA solver. In practice the function $\varTheta _k^\star$ can be stored by maintaining a set of hyperplane coefficients as explained in detail in the previous section.

The main idea of partially distributed outer approximation is to communicate the piecewise lower bounding functions $\varTheta _k^\star$ to a central coordinator, who constructs a piecewise affine lower bound on the function f, solves a master MILP problem, and updates z. Here, one option is use the maximum over the function $\varTheta _k^\star$ in order to obtain the lower bound

$$\begin{aligned} \forall x \in X, \; \forall z \in Z, \qquad \max _{k} \; \varTheta _k^\star (x,z_k) \; \le \; f(x,z) \; . \end{aligned}$$

(17)

However, in order to arrive at a practical implementation, it is recommendable to further refine this bound. This can be done by maintaining a collection of integers, $\varPi \subseteq Z$, such that the function

$$\begin{aligned} \varTheta (x,z) = \max \left\{ \; \varPhi (x,z,\varPi ) , \; \max _{k} \; \varTheta _k^\star (x,z_k) \; \right\} , \end{aligned}$$

(18)

can be used as a piecewise affine lower bound on f. Recall that the function $\varPhi$, which has been introduced in the previous section, exploits the separability properties of f. The integer collection $\varPi$ is then maintained by updating

$$\begin{aligned} \varPi \leftarrow \varPi \cup \{ \zeta ^\star \} , \end{aligned}$$

where $\zeta ^\star = [ \zeta _1^\star , \zeta _2^\star , \ldots , \zeta _N^\star ]$ is an integer vector, whose components are optimal solutions for the integer variables of the partially decoupled problems (13).

3.3 Partially distributed outer approximation (PaDOA)

Algorithm 2 outlines a partially distributed algorithm for solving (1). There are four main steps. In the first step, the partially decoupled MICPs of the form (13) are solved by using a traditional outer approximation method. Under the assumption that the original MICP (1) is feasible, the partially decoupled MICPs are feasible, too. Thus, the outer approximation solvers will return optimal integer solutions $\zeta _k^\star$ and associated piecewise affine lower bounds $\varTheta _k^\star$ such that (16) is satisfied. The second step of Algorithm 2 updates the associated upper bound U based on the inequality (15) as well as the piecewise affine lower bound. In practice, this step is implemented by storing the union of all supporting hyperplane coefficients that are needed to represent $\varTheta$. Finally, the third step of Algorithm 2 solves a large scale MILP problem. This MILP is constructed in analogy to the corresponding step in the traditional outer approximation algorithm. It yields a lower bound,

$$\begin{aligned} \varTheta (x^+,z^+) \le V^\star , \end{aligned}$$

on the objective value $V^\star$ of (1). Thus, the difference between the current upper and lower bounds,

$$\begin{aligned} U - \varTheta (x^+,z^+) , \end{aligned}$$

can be used as a termination criterion, which is implemented in the fourth step of Algorithm 2. If the termination is not successful, the integer variables z are updated, and the algorithm subsequently proceeds to the next iteration.

Notice that the main difference between Algorithms 1 and 2 is the introduction of partially decoupled MICP problems that can be solved separately and which contain much fewer integer variables than the original MICP (1). The theoretical results in Sect. 3.5 will elaborate further on the benefits of this alternation strategy. Moreover, in Sect. 4 a numerical case study is examined, which illustrates the practical advantages of Algorithm 2.

Remark 6

For the special case that the functions $f_i$ are convex and piecewise affine, the original optimization problem is an MILP, which could also be solved directly by using an MILP solver. If one uses Algorithm 2 instead, this algorithms solves an MILP by solving a sequence of MILPs—a strategy that may seem rather counter-intuitive on the first view. However, one interesting observation of this paper is that Algorithm 2 can even for (sufficiently structured) MILPs help to speed up the convergence process, because the complexity of the MILPs in Step 4 of Algorithm 2 depends on the complexity of the current lower bound $\varTheta$ and eventually is much easier to solve than the original MILP. This effect is illustrated by numerical experiments in Sect. 4.2.

3.4 Relation to distributed local optimization methods

The idea to “augment” the local objective functions $f_i$ with a suitable function $\varPsi _i$ is frequently used in the context of distributed local optimization algorithms. For example, in the context of dual decomposition [19, 43], one augments the separable functions $f_i$ with linear functions of the form⁴

$$\begin{aligned} \varPsi _i(x) = \sigma ^\mathsf {T}A x , \end{aligned}$$

where $\sigma$ is the current dual iterate. Similarly, in the context of ADMM or ALADIN, one uses augmented Lagrangians [3, 48], as in

$$\begin{aligned} \varPsi _i(x,y) = \sigma ^\mathsf {T}A x + \frac{\rho }{2} \Vert x - y \Vert ^2 \;, \end{aligned}$$

(21)

where z and $\sigma$ are the current primal and dual iterates; see [10, 17, 26]. In fact, the construction of Algorithm 2 is inspired by the distributed local nonlinear programming method ALADIN. Here, we recall that ALADIN alternates between solving small-scale decoupled NLPs that are augmented by terms of the form (21) and large scale equality constrained quadratic programming problems that update $\sigma$ and y [26]. This is in analogy to Algorithm 2, which alternates between solving decoupled MICPs (Step 1) and large-scale coupled MILPs (Step 3). However, unlike ALADIN, augmented Lagrangians are not used in Algorithm 2 as Lagrange multipliers in integer programming are not related to sensitivity and generally not applicable.

Also note that the construction of the functions $\varPsi _i$ in Algorithm 2 also has similarities with Gauss-Seidel or more general block-coordinate descent methods [57, 60] in the sense that a partial decoupling is obtained by fixing some of the integer variables while others are optimized. However, despite all these analogies and similarities of Algorithm 2 with methods from the field of local and convex optimization, we would like to highlight that all these existing distributed optimization methods are not reliably applicable to Problem (1) [55].

3.5 Convergence analysis

In this section we provide a concise overview of the convergence properties of Algorithm 2. The following theorem establishes one of the main results of this paper, namely, that Algorithm 2 converges after one iteration if the integer iterate, z, is initialized with an optimal solution of (1). This is in contrast to Algorithm 1, which does not necessarily terminate after a small number of steps—not even if it is initialized at an optimal solution.

Theorem 2

Let Assumption 1 be satisfied and let $(x^\star ,z^\star )$ be a minimizer of (1). If Algorithm 2 is initialized with $z = z^\star$ and if the termination tolerances of the lower level solvers satisfy $\epsilon _{\mathrm {L}}\le \epsilon$, then the termination criterion in Step 4 is satisfied. In other words, the algorithm terminates after one step.

Proof

See “Appendix 4”. $\square$

Notice that the statement of the above theorem is of fundamental relevance and a very favorable property of PaDOA. If we work with other global optimization methods, say branch-and-bound, an empirical observation is that such existing global optimization algorithm often find a global solution early on but then keep on iterating until the lower bound is accurate enough to prove global optimality. In contrast to this, PaDOA terminates as soon as a global minimizer is added to the collection $\varPi$. In fact, Theorem 2 implies that global optimality of a point $z^\star \in Z$ can be verified by solving the N instances of the partially decoupled MICPs and the master MILP (20). Notice that this result is not in conflict with existing results from the field of complexity theory, because the master MILP (20) remains NP-hard [22, 40].

Remark 7

The result of Theorem 2 relies heavily on the convexity of the functions $f_i$ on the convex hull of $X_i \times Z_i$, although this fact is not highlighted explicitly in the proof. This convexity assumption is first of all required implicitly by our assumption that the lower level solvers return piecewise level models $\varTheta _k$, which satisfy the termination condition (16) (this assumption is only reasonable if strong duality holds) and which need to be global lower bounds on f. These properties are in general all not satisfied if one considers more general non-convex MINLPs.

The following theorem establishes the fact that Algorithm 2 converges after a finite number of iterations under exactly the same conditions under which convergence of Algorithm 1 can be established.

Theorem 3

Let Assumption 1 be satisfied. If the termination tolerances of the lower level solvers satisfy $\epsilon _{\mathrm {L}}\le \epsilon$, then Algorithm 2 terminates after a finite number of steps (independently of the initialization).

Proof

See “Appendix 5”. $\square$

4 Implementation and case study

This section presents two benchmark problems to assess the computational performance of Algorithm 2. The first aims to provide a cost-optimal heater/cooler activation scheme such that a set of temperatures remain within pre-set limits. The objective is formulatable as an MILP, MIQP, or higher order MICP allowing for testing on a broad class of problems. Furthermore, each problem instance is scalable both vertically (in time horizon/subproblem size) and horizontally (number of regions/number of subproblems), which allows for an examination of the benefit which may come from the parallelizable Step 1 of Algorithm 2.

A second benchmark example comes in the form of a mixed-integer lasso problem. This is used to demonstrate the versatility of Algorithm 2 and verify the results of the first benchmark problem given the presence of an $L_1$-norm. Like the first benchmark problem, it is also scalable both vertically and horizontally, and the results for ten unique instances of the problem are given. The Partially Distributed Outer Approximation method is implemented in MATLAB R2017b. The optimization subproblems are solved using Gurobi [47] implemented via CasADi v1.9.0 [2]. All numerical experiments were run on a 2.9 GHz Intel Core i5-4460S CPU with 8 GB of RAM.

4.1 Thermostatically controlled loads

An important problem in the planning and operation of a heating and/or cooling system is the scheduling of so-called Thermostatically Controlled Loads (TCLs) [31]. These are devices that are used to regulate the temperature of a room/building within a certain user-defined interval known as a “deadband”. The optimal operation strategy is especially difficult to determine when a non-constant cost function is introduced for a population of heterogeneous TCLs [61]. The cost function may represent the cost of electricity or user-discomfort from noise generation. Regardless, such devices typically only have an “on” and an “off” setting and thus the resulting scheduling problem can be formulated as a binary MIP for R regions with a discretized time horizon H, consisting of hour-long time steps.

$$\begin{aligned}&\min \limits _{T(\cdot ),u(\cdot )} \sum \limits _{i=1}^R\sum \limits _{t=0}^{H-1} c(t)u(t) + \gamma (T_i(t) - T_{i,ref}(t))^2, \end{aligned}$$

(22a)

$$\begin{aligned}&\text {subject to} \forall i\in \{1,\ldots ,R\}, \nonumber \\&\underline{T}_i \le T_i(t) \le \overline{T}_i, \quad \forall t\in \{0,\ldots ,H\} \end{aligned}$$

(22b)

$$\begin{aligned}&u_i(t)\in \{0,1\}, \forall t\in \{0,\ldots ,H-1\} \end{aligned}$$

(22c)

$$\begin{aligned}&\forall t\in \{0,\ldots ,H\},\nonumber \\&T_i(t+1)=T_i(t)+b_i u_i(t)+a_i\left( \frac{T_i(t)+T_{amb}(t)+\sum _{j \in N(i)}T_j(t)}{|N(i)|+2} - T_i(t)\right) , \end{aligned}$$

(22d)

where c(t) is the vector of device costs at time t, $\gamma$ is a comfort parameter, $\underline{T}_i$ and $\overline{T}_i$ are the deadband temperature limits of device i, $a_i$ and $b_i$ are heat transfer parameters, $T_{amb}(t)$ is the ambient temperature at time t and N(i) are the number of regions neighbouring i. Equation (22d) models the thermodynamics of each room in a simplified manner, i.e., it takes an average of the current and surrounding temperatures to update the temperature of the next time step. This formulation results in $H+1$ real-valued and H binary variables per region. Figure 1 shows two possible initial configurations of (22). The ambient temperature is taken from [15] for two days in June 2017 in the Karlsruhe (Germany) area, with a reference temperature $T_{i,ref} = 20^{\deg }$ for each room. High prices of 25.67 cents/kWh are set from 2pm to 8pm (time steps 6 to 12 and 29 to 35) with low and medium prices of 2.46 cents/kWh and 4.62 cents/kWh in all other time steps. Each region is initialized at 20 degrees with $a_i=0.2$ and $b_i=-2$. As the temperature for each room is more influenced by past temperatures than neighbouring rooms, Problem (22) is partitioned spatially for Algorithm 2, with each room in its own partition.

Fig. 1

Two room configurations with controlled cooling elements $u_i$, ambient temperature $T_{amb}$ and initial temperatures $T_i(0)$

4.2 Results for MILP

If the comfort parameter $\gamma$ is taken to be zero then Problem (22) is linear and separable but coupled in both its discrete and real-valued variables. Shown in Tables 1 and 2 are the simulation results for each configuration, respectively. The results of Algorithm 2 are compared with results obtained from the MIP solver Bonmin with the Branch and Bound (B-BB) and Outer Approximation (B-OA) algorithm settings [7] as well as the commercial MIQP solvers Gurobi and CPLEX [27]. An example solution for the 3 room case is depicted in Fig. 2.⁵

Fig. 2

The red dotted line is the ambient temperature, the blue dotted lines are the limits of the temperature deadzone and the solid lines are the temperature trajectories of each region in the three room scenario. Highlighted on the trajectories are points where the coolers are activated. (Color figure online)

Table 1 Results obtained for the TCL problem with a 3-room configuration

Table 2 Results obtained for the TCL problem with a 4-room configuration

Table 3 Results obtained for the TCL problem with a linear room configuration

At first glance, the results from Tables 1 and 2 may seem surprising since the 4 room case has more space to keep cool but nonetheless is able to do so at a lower cost than the 3 room case. This is due to an insulation effect that the 4 room configuration enjoys. With the activation of two coolers in the first six time steps, the room temperatures can stay within their deadbands for the entire 48 h period. In contrast, the 3 room configuration is more susceptible to the ambient temperature and requires more use of the coolers. This also seems to have increased the computational complexity of the problem and requires more time for the 3 room case to be solved than the 4 room case. It should be noted that several initializations were tested and the solution times were not significantly affected, implying that this was not the cause of the runtime differences in the two cases.

One of the advantages of using a distributed method is the ability to solve problems that would be otherwise intractable for a centralized solver. Tables 1 and 2 show results for cases containing up to 496 variables, but even larger problems may be considered. Table 3 shows results for a variety of time horizons and rooms. Here, the room configuration is instead arranged such that the rooms are in a line. While unrealistic for most buildings, this setup is realistic for the temperature control of a train or rooms next to a corridor. Mathematically, this example differs somewhat from the other two. While the other problems have a significant amount of coupling between the control variables, this is not the case for the linear room configuration. The sparsity induced by this problem structure allows Algorithm 2 to outperform both Gurobi and CPLEX (applied to the centralized problem).

4.3 Results for MIQP

If the comfort parameter $\gamma$ is larger than zero then Problem (22) becomes a convex MIQP.⁶ As in Sect. 4.2, the results of Algorithm 2 for each room configuration are compared with those obtained from Bonmin, Gurobi, and CPLEX. The value of $\gamma$ was chosen to be one to allow for an equal weighting of comfort and cost. These results are displayed in Tables 4, 5, and 6.

Table 4 Results obtained for Problem (22) with a 3-room configuration

Table 5 Results obtained for Problem (22) with a 4-room configuration

Table 6 Results obtained for Problem (22) with a linear 7 room configuration

Shown in Fig. 3 are the trajectories obtained for the three-room scenario with a temperature deviation penalization. In contrast to Fig. 2, a quadratic penalty term is used to model discomfort caused by deviations from the set temperature. Indeed, the solution with $\gamma =1$ yields a trajectory with a similar number of activations as when $\gamma =0$ but with temperature trajectories that stay much closer to the middle of the deadband.

Fig. 3

The three room scenario, with the comfort parameter $\gamma =1$. The red dotted line is the ambient temperature, the blue dotted lines are the limits of the temperature deadzone and the solid lines are the temperature trajectories of each region in the three room scenario. Highlighted on the trajectories are points where the coolers are activated. (Color figure online)

4.4 Higher Order Convex Problems

One of the advantages of the proposed algorithm is that it is applicable to a relatively large class of problems (namely, MICPs). While Sect. 4.3 shows favourable results for both Gurobi and CPLEX, if the problem were adjusted slightly such that it were no longer an MIQP then these solvers would no longer be applicable. For example, if the objective function of Problem (22) became

$$\begin{aligned} \min \limits _{T(\cdot ),u(\cdot )} \sum \limits _{t=0}^{H-1} c(t)u(t) + \gamma (T_i(t) - T_{ref}(t))^4, \end{aligned}$$

then this would still be solvable via PaDOA, but not Gurobi or CPLEX. However, Bonmin can still be applied.⁷ The results for a variety of such problem configurations are shown below in Table 7. Therein it can be observed that Algorithm 2 returns the same, global solution as Bonmin with the B&B sub-algorithm, and does so in less time. The runtime difference is particularly striking for the 7 room scenarios as these contain the most variables and have the greatest potential for parallelization.

Table 7 Results obtained for Problem (22), but with a 4th order objective function

4.5 Discussion of TCL Benchmark Results

Algorithm 2 is able to converge quite quickly for the MILP instance of (22) since it is underapproximating a linear problem with linear functions and thus can prove optimality quickly and with few iterations. More supporting hyperplanes are needed in the MIQP case and thus we see a couple more iterations and a slightly longer runtime for Algorithm 2. As shown in Figs. 4 and 5, the upper and lower bound converge quite quickly for the MIQP and MINLP cases, but require several iterations to refine the solution.

Fig. 4

Progression of the upper and lower bounds during each iteration while solving the 2nd-order version of Problem (22) with 7 rooms and 48 time steps. The blue line depicts the progression of the upper bound and the red line shows that of the lower bound. (Color figure online)

Fig. 5

Progression of the upper and lower bounds during each iteration while solving the 4th-order version of Problem (22) with 4 rooms and 8 time steps. The blue line depicts the progression of the upper bound and the red shows that of the lower bound. (Color figure online)

Interestingly, the MIQP cases is generally obtained more quickly than the MILP case, even though one might expect the higher order problem to be more difficult to solve. The quadratic term should make the MIQP instance of Problem (22) more computationally difficult than the MILP instance, but in some cases both Gurobi and CPLEX actually require less time. It may be the case that the MILP instance of (22) is more poorly conditioned than the MIQP instance, and thus the centralized solvers require much more effort to guarantee the optimality of a given solution. This may imply that quadratic underapproximating functions and an MIQP coupling step could be more efficient than the current affine implementation. This would also allow for Algorithm 2 to be applicable to a wider class of problems.

It is also worth noting that the majority of the runtime used by Algorithm 2 for the MIQP problem instance is spent in the MILP coupling step. In contrast, the majority of the time spent solving the 4th-order problem is in the MINLP subproblems, and the MILP coupling problems are solved relatively quickly. A breakdown of the runtime per iteration for both of these cases is reported in Tables 8 and 9.

Table 8 Runtime breakdown of Algorithm 2 applied to the 2nd-order version of Problem 22 with 7 room TCL problem with 48 time steps

Table 9 Runtime breakdown of Algorithm 2 applied to the 4th-order version of Problem 22 with 4 rooms and 8 time steps

4.6 Mixed-Integer Lasso

As a second benchmark example we consider a mixed-integer lasso problem based on Problem (11.1) from [10]. The details of this problem are summarized below for $n+N$ features and M training samples:

$$\begin{aligned}&\min \limits _{w,v} \sum _{j=1}^M e^{(-a_j^{\top }w-b_j^{\top }z-c_ijv)} + \lambda (||w||_1 + ||z||_1), \end{aligned}$$

(23a)

$$\begin{aligned}&\text {subject to:} \nonumber \\&\underline{w}\le w,v \le \overline{w}, \end{aligned}$$

(23b)

$$\begin{aligned}&z \in \mathcal {Z} \subset \mathbb {Z}^N, \end{aligned}$$

(23c)

where $w\in \mathbb {R}^n$, $v\in \mathbb {R}$. As in [10], the features consist of the tuple $(a_j,b_j,c_j)$ where $a_j\in \mathbb {R}^n$, $b_j\in \mathbb {R}^N$, and $c_j\in \{-1,1\}$. The regularization parameter $\lambda$ is chosen as described in [10]. Assuming that $M\gg N$, Problem (23) can be decomposed into a collection of smaller problems of the form (23) with appropriate consensus constraints. Given the structure of Algorithm 2, it is logical to decompose (23) such that only one integer variable is present per subproblem:

$$\begin{aligned}&\min \limits _{w,v} \sum _{i=1}^N\sum _{j=1}^{M_i} e^{(-a_j^{\top }w_i-b_jz_i-c_jv_i)} + \lambda (||w_i||_1 + ||z_i||_1), \end{aligned}$$

(24a)

$$\begin{aligned}&\text {subject to } \forall i \in \{1,\ldots ,N\}:\nonumber \\&\underline{w}_i\le w_i,v_i \le \overline{w}_i, \end{aligned}$$

(24b)

$$\begin{aligned}&z_i \in \mathcal {Z}_i \subset \mathbb {Z}, \end{aligned}$$

(24c)

$$\begin{aligned}&w_i=w_k, z_i=z_k, \text { and } v_i =v_k, \; \forall k \in \{1,\ldots ,N\}. \end{aligned}$$

(24d)

That is, the collection of $M=\sum _{i=1}^N M_i$ training samples is decomposed into N (evenly sized) parts, all of which must be in consensus.

4.7 Numerical Results for Mixed-Integer Lasso

To test Algorithm 2 on Problem (24) the results for a variety of problem and partition sizes are presented, with features generated according to [10]. These are displayed in Table 10 with the results of Bonmin used for comparison.

Table 10 Results obtained for Problem (24) using Algorithm 2 and Bonmin

Note that Bonmin with standard settings fails for most of the benchmark problems. Nonetheless, the time spent by Bonmin to attempt a solution is still recorded in Table 10. Overall, Algorithm 2 tends to perform much better with a highly partitioned problem (large N), where each partition contains relatively few decision variables (low n).

Much like the 4th order instance of the TCL problem, the mixed-integer lasso problem requires many iterations until PaDOA converges. Likewise, the upper and lower bounds converge in a similar manner as shown in Fig. 6. That is, the lower bound increases much more quickly than the upper bound decreases.

Fig. 6

Progression of the upper and lower bounds during each iteration while solving the Problem (24) with $n=40$, $M=100$, and $N=10$. The blue line depicts the progression of the upper bound and the red shows that of the lower bound. (Color figure online)

One interesting difference between the results for the mixed-integer lasso and TCL problems is that the runtime for the TCL problem is much more balanced between the MILP and MINLP steps, as shown in Table 11. This may be due to the chosen problem partitioning, wherein each MINLP subproblem only requires the solution to a collection of continuous variables and a single integer variable.

Table 11 Runtime breakdown of Algorithm 2 applied to Problem (24) with $n=40$, $M=100$, and $N=10$

5 Conclusions

This paper has introduces a new method (PaDOA) for partially distributing MICP solvers to find $\epsilon$-suboptimal points of the structured MICP (1). PaDOA proceeds by alternating between solving partially decoupled MICPs that comprise m integer variables and large scale MILPs with nN variables. Finite termination conditions for PaDOA are established in Theorem 3. Moreover, we discuss the major theoretical and practical advantages of PaDOA compared to exising extended formulation based OA solvers. In particular, Theorem 2 states that PaDOA terminates after the first iteration, if it is initialized at a global minimizer—an important property that is neither shared by existing OA nor by existing branch-and-bound based methods for MICP.

In Sect. 4, first, second and fourth order mixed integer problems are used to demonstrate the practical performance of PaDOA compared to other state of the art solvers by application to a scheduling problem of thermostatically controlled loads. While the solution and runtime are competitive for each of the case studies considered, the best performance occurs for problems with sparse Hessians and coupling constraints. Furthermore, it is observed that PaDOA is able to return a solution in several cases where the centralized approach fails due to memory constraints. These results are confirmed with a second benchmark example in Sect. 4.6. It remains to be seen what the specific limitations of this method for distributing MICP solvers are, and a full investigation of PaDOA and a more mature software implementation is still subject to future work.

As shown in Sect. 4, the MIQP implementation of Problem (22) is solved more efficiently than the MILP implementation. Thus, it may be the case that quadratic underapproximating functions and an MIQP coupling step could actually be more efficient for certain problems than the current implementation with affine supporting hyperplanes. This would also have the added benefit of allowing for applicability to a larger problem class. Future work will investigate the use of other under-approximating functions and an extension of Algorithm 2 to non-convex MINLPs. Furthermore, Step 4 requires full constraint information in order to return a feasible solution. This restricts the applicability in terms of fully distributed settings and future work will focus on sidestepping this restriction.

Proofs

1.1 Proof of Proposition 1

If there is no $x \in X$ with $Ax = b$, both sides of (6) are equal to infinity and the statement of the proposition holds in the extended value sense. Thus, we may assume that the constraints in (6) are feasible. Consequently, Assumption 1 implies that (5) is a convex optimization problem with compact and non-empty feasible set. Moreover, since X is a polytope, all constraints in (5) are linear. It is well-known [6, 51] that strong duality holds under these conditions. $\square$

1.2 Proof of Lemma 1

If there is no $x \in X$ with $A x = b$, both sides of (10) are equal to infinity and the statement of the lemma holds in the extended value sense. Thus, we may assume that the equation $Ax = b$ has a solution in X. Next, because we have $z \in \varPi$, our particular construction of $\varPhi$ implies that

$$\begin{aligned} \varPhi (x,z,\varPi )\ge & {} f^\star (z) + \left[ \lambda ^\star (z) \right] ^\mathsf {T}( x - x^\star (z) ) + \underbrace{\left[ \mu ^\star (z) \right] ^\mathsf {T}( z - z )}_{=0} \end{aligned}$$

(25)

Thus, we have

$$\begin{aligned} \min _{x \in X, Ax = b} \; \varPhi (x,z,\varPi )= & {} \min _{y \in X, Ay = b} \; f^\star (z) + \left[ \lambda ^\star (z) \right] ^\mathsf {T}( y - x^\star (z) ) \\= & {} \min _{x,y} \; f(x,z) + \left[ \lambda ^\star (z) \right] ^\mathsf {T}( y - x ) \quad \mathrm {s.t.} \quad \left\{ \begin{array}{l} A y = b \\ y \in X \end{array} \right. \\= & {} \max _{\lambda } \; \min _{x,y} \; f(x,z) + \lambda ^\mathsf {T}(y-x) \quad \mathrm {s.t.} \quad \left\{ \begin{array}{l} A y = b \\ y \in X \end{array} \right. \; . \end{aligned}$$

Since Assumption 1 holds, we may substitute (6) (see Proposition 1), which yields the equation

$$\begin{aligned} \forall z \in \varPi , \qquad \min _{x \in X, Ax = b} \; \varPhi (x,z,\varPi ) = f^\star (z) \; . \end{aligned}$$

$\square$

1.3 Proof of Theorem 1

Notice that if the equation $Ax = b$ has no solution in X, this will be detected immediately by Step 2 of Algorithm 1, which causes termination. Thus, we may assume that all optimization problems are feasible. Now, the main idea of the proof is to show that the cardinality of the set $\varPi$ is strictly increasing in every iteration, if the algorithm does not terminate. For this aim, we first notice that any solution $(x^+,y^+,z^+)$ of the MILP (12) satisfies the equation

$$\begin{aligned} \varPhi (x^+,z^+,\varPi ) = \sum _{i=1}^N y_i^+ \end{aligned}$$

(26)

by construction. Moreover, because we have $A x^+ = b$, the inequality

$$\begin{aligned} \min _{x,Ax = b} \; \varPhi (x,z^+,\varPi ) \le \varPhi (x^+,z^+,\varPi ) \end{aligned}$$

(27)

holds. If we further assume that the termination criterion is not satisfied, we must have

$$\begin{aligned} \sum _{i=1}^N y_i^+ < U - \epsilon \end{aligned}$$

(28)

Thus, if we had $z^+ \in \varPi$, then the result of Lemma 1 would imply that

$$\begin{aligned} f^\star (z^+) \overset{(10)}{=} \min _{x,Ax = b} \; \varPhi (x,z^+,\varPi ) \end{aligned}$$

(29)

as well as $U \le f(z^+)$, since $z^+$ has already been added to the collection $\varPi$. By substituting all the above relations we would then find that

$$\begin{aligned} f^\star (z^+) \, \overset{(29),(27)}{\le } \, \varPhi (x^+,z^+,\varPi ) \, \overset{(26),(28)}{<} \, U - \epsilon \, \le \, f(z^+) - \epsilon , \end{aligned}$$

which is a contraction. Thus, either our assumption that the algorithm does not terminate or our assumption $z^+ \in \varPi$ must be wrong. In other words, if the algorithm does not terminate in the current step, then the cardinality of the set $\varPi$ increases by 1 in the next step, because $z^+$ is added to the collection $\varPi \subseteq Z$. But this is only possible for a finite number of steps, because the set Z contains only a finite number of points. Thus, Algorithm 1 must terminate after a finite number of iterations. $\square$

1.4 Proof of Theorem 2

Let $V^\star = \sum _{i=1}^N f_i(x_i^\star ,z_i^\star )$ denote the optimal value of (1). Because we assume that such an optimal solution exists while Assumption 1 is satisfied, the partially decoupled optimization problems are all feasible and return piecewise affine lower bounds that satisfy the termination condition (16) with $V_k(z^\star ) = V^\star$, i.e., we have

$$\begin{aligned} V^\star - \epsilon _{\mathrm {L}}\; \le \min _{x \in X,\zeta \in Z_k} \varTheta _k^\star (x,\zeta ) \quad \mathrm {s.t.} \quad A x = b \end{aligned}$$

(30)

for all $k \in \{ 1, \ldots , N \}$. Because the function $\varTheta$ is by construction an upper bound on $\varTheta _k$ (for any k), we further have

$$\begin{aligned} \min _{x \in X,\zeta \in Z_k,Ax = b} \varTheta _k^\star (x,\zeta ) \le \min _{x \in X,z \in Z,Ax = b} \varTheta (x,z) = \varTheta (x^+,z^+) , \end{aligned}$$

where $(x^+,z^+)$ denotes the solution of the master MILP (20). By substituting the above inequalities we find that

$$\begin{aligned} V^\star - \epsilon _{\mathrm {L}}\le \varTheta (x^+,z^+) \; . \end{aligned}$$

Because we assume that $\epsilon _{\mathrm {L}}\le \epsilon$, this implies that

$$\begin{aligned} U - \varTheta (x^+,z^+) = V^\star - \varTheta (x^+,z^+) \le \epsilon _{\mathrm {L}}\le \epsilon \; . \end{aligned}$$

Thus, the termination condition is satisfied and Algorithm 2 terminates after the first step. $\square$

1.5 Proof of Theorem 3

We may assume that the coupled equality constraint is feasible, as infeasibility would be detected immediately in Step 1 of Algorithm 2. Similar to the proof of Theorem 1, we need to keep track of the integer solutions of the master MILPs. For this aim, we introduce the following “artificial” additional step:

Step $3'$): After solving (20), update ${\tilde{\varPi }} = {\tilde{\varPi }} \cup \{ z^+ \}$.

If the set ${\tilde{\varPi }}$ is initialized with the empty set and if Step $3'$ is inserted in Algorithm 2 immediately after Step 3, the iterates of this algorithm remain unaffected. The main idea of the proof is now to show that the cardinality of the set ${\tilde{\varPi }}$ increases in every iteration of Algorithm 1 under the assumption that the termination criterion is not satisfied. Let us assume that the solution $z^+$ satisfies $z^+ \in {\tilde{\varPi }}$ (before ${\tilde{\varPi }}$ is updated in Step $3'$). Then we have

$$\begin{aligned} U \le V_k(z^+) \overset{(16)}{\le } \epsilon _{\mathrm {L}}+ \min _{x \in X,\zeta \in Z_k, Ax = b} \varTheta _k^\star (x,\zeta ) , \end{aligned}$$

Because $\varTheta$ is an upper bound on $\varTheta _k$, this implies that we also have

$$\begin{aligned} \min _{x \in X,\zeta \in Z_k, Ax = b} \varTheta _k^\star (x,\zeta ) \le \min _{x \in X,z \in Z, Ax = b} \varTheta ^\star (x,\zeta ) = \varPhi (x^+,z^+) , \end{aligned}$$

which yields $U - \varPhi (x^+,z^+) \le \epsilon _{\mathrm {L}}\le \epsilon$. Thus, either the termination criterion is satisfied or we have $z^+ \notin {\tilde{\varPi }}$. In the latter case, the cardinality of $\varPi$ increases by 1 in the current iteration. As this is only possible for a finite number of steps, Algorithm 2 must terminate. $\square$