Abstract
Solving mixed-integer nonlinear optimization problems (MINLPs) to global optimality is extremely challenging. An important step for enabling their solution consists in the design of convex relaxations of the feasible set. Known solution approaches based on spatial branch-and-bound become more effective the tighter the used relaxations are. Relaxations are commonly established by convex underestimators, where each constraint function is considered separately. Instead, a considerably tighter relaxation can be found via so-called simultaneous convexification, where convex underestimators are derived for more than one constraint function at a time. In this work, we present a global solution approach for solving mixed-integer nonlinear problems that uses simultaneous convexification. We introduce a separation method that relies on determining the convex envelope of linear combinations of the constraint functions and on solving a nonsmooth convex problem. In particular, we apply the method to quadratic absolute value functions and derive their convex envelopes. The practicality of the proposed solution approach is demonstrated on several test instances from gas network optimization, where the method outperforms standard approaches that use separate convex relaxations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this work, we develop a global solution approach for solving mixed-integer nonlinear Problems (MINLPs). Such optimization problems belong to the most challenging optimization tasks, due to the fact that they combine integral decision variables as well as nonlinear and nonconvex constraint functions. In this work, we focus on handling the latter property. MINLPs abound in many real-world applications such as energy and distribution networks, for example gas networks (e.g. [18]), and chemical process design (e.g. [9]). See [3] for a detailed overview.
The most commonly used solution strategy for general MINLPs consists in a Branch and Bound algorithm (see, e.g., the textbook [16]). It is implemented and enhanced in several state-of-the-art software packages like Antigone [22], Baron [30] or SCIP [8]. We refer to [5] for an extensive survey on MINLP solvers.
The main idea of the Branch and Bound algorithm is to generate a tree structure of subproblems that arise from a subdivision of the feasible set. For each subproblem, a convex relaxation of the feasible set is generated, providing lower bounds for the original subproblem, where the quality of these bounds depends on the tightness of the relaxation.
As weak relaxations usually result in a huge number of subproblems and, hence, create branch and bound trees of extremely large sizes, one is interested in constructing the tightest possible convex relaxations leading to smaller branch and bound trees and allowing to find faster good feasible solutions and appropriate branching rules. In a common approach to derive convex relaxations for MINLPs, the nonlinear functions appearing in the model description are replaced by convex under- and/or concave overestimators. Hence, a broad field of research is devoted to finding the tightest possible convex under- and concave overestimators (the so-called convex and concave envelopes) for different types of relevant functions. A description of the convex envelope was obtained explicitly for several specific classes of functions, e.g. for multilinear functions [23], for fractional terms [28] or for odd monomials [15]. Further results handle functions with specific curvature properties such as edge-convexity/concavity and indefiniteness [10, 12, 17, 21]. See also [4] for a list of publications on this subject.
Most of these results have in common that they analyze the convex envelope of a single real-valued function. However, the convex hull of a feasible set defined by multiple constraint functions is not completely described by the convex envelope of every single constraint. As a consequence, the standard relaxation of the feasible set can be significantly tightened by considering the interaction between multiple constraint functions. This interaction was already studied in [27]. In the following, we use the authors’ nomination and refer to the convex hull of a set given by multiple constraints as simultaneous convexification. The Reformulation-Linearization Technique (RLT, e. g. see [26]) and approaches based on semidefinite programming (SDP) techniques, e.g. see [14], can be interpreted as early results in this context. In particular, for the special case of quadratic bivariate functions, a simultaneous convexification is derived in [1], combining RLT and SDP techniques. In [2] a more general characterization is given. The convex hull of certain feasible sets defined by a vector-valued function can be described by the convex envelopes of all linear combinations of constraint functions.
In this work, we make use of that result to derive a refinement of the standard relaxation of relatively general MINLPs. We present a global optimization method that includes the refinement into an algorithmic framework by using a cutting plane approach. See [11] for an early publication on this strategy, or [6] for an extension to the nonsmooth mixed-integer case. The solution of a relaxed problem is separated by a linear inequality in order to iteratively converge to the optimum of the original problem. In our case, we separate from the convex hull of the feasible set by solving a convex optimization problem. The problem is not continuously differentiable. It relies on an algorithmically utilizable representation of the convex envelope of linear combinations of the constraint functions.
The solution of general MINLPs is often beyond what is currently possible in practice due to their computational difficulty. Therefore, the abstract framework presented here is rolled out for a general class of bivariate quadratic absolute value functions. We first derive the simultaneous convexifications and explain the details of the solution algorithm. We then show experimental results for an application in the operation of gas networks. The results indicate that the developed separation strategy is able to derive significantly tighter bounds than the standard relaxation.
The remainder of this paper is structured as follows. In Sect. 2 we briefly discuss the considered problem class and solution strategy. We motivate how standard relaxations of the feasible set are obtained and why there is room for improvements. In Sect. 3 we recap the main result on simultaneous convexification and use it to derive a separation problem and cutting planes for the convex envelope of the feasible set based on the solution of this problem. We further present some definitions and basic results concerning the convex envelope, generating sets and minimizing simplices. Section 4 introduces quadratic absolute value functions in the way they are used in gas network optimization. For these specific functions, we derive the convex envelopes of their linear combinations in order to apply our optimization method. The practical impact of our work is exemplarily evaluated in Sect. 5.
The results presented in this paper are also given in the dissertation by Mertens [20]. Preliminary considerations and computations are already introduced in the dissertation by Merkert [19].
2 Solving mixed-integer nonlinear optimization problems
We assume mixed-integer nonlinear optimization problems (MINLPs) given in the form
with cost vector \(c\in \mathbb {R}^{n+m}\), set \(D \subseteq \mathbb {R}^n\) and a continuous function \(g:D \rightarrow \mathbb {R}^m\). In general, the constraint function g is nonconvex, the feasible set X is nonconvex and Problem (OP) has multiple locally optimal solutions. Potential integrality constraints on certain entries of x are implied by D.
As this work aims on tackling the problems arising from nonlinearities in MINLPs, we omit the integrality restrictions in the following and assume that D is compact and convex. This assumption is usually satisfied by considering the continuous relaxation of a given mixed-integer problem. However, even without the integrality constraints, not all MINLPs can be formulated as Problem (OP). Only certain types of dependencies are allowed and bounds on z are only given implicitly by x. This is a relevant restriction for general MINLPs. Nevertheless, the proposed structure is well suited for demonstrating the effect of simultaneous convexification. Furthermore, at least a substructure of the form X is given in almost any MINLP. The developed strategies may therefore still be applied on more general feasible sets.
A common strategy for solving Problem (OP) is the so-called Spatial Branch and Bound Method. Therein, a convex superset \(\bar{X} \supseteq X\) of the feasible set and the corresponding relaxed problem
are considered. Problem (RP) is convex and yields a lower bound for Problem (OP). It may therefore be used as a tool to evaluate the quality of solutions and, by integrating this approach into a branch and bound framework, to achieve convergence to global optimality under certain assumptions. For a detailed introduction on global mixed-integer nonlinear optimization, we refer to [16] and [3].
We briefly discuss different approaches of constructing a relaxed feasible set \(\bar{X}\). Obviously, the choice of \(\bar{X}\) is crucial for the quality of the resulting lower bound given by Problem (RP). Problem (RP) gives the best lower bound of Problem (OP), if \(\bar{X}\) is chosen as small as possible. The smallest possible convex superset of X is \({{\,\mathrm{conv}\,}}(X)\). In fact, the objective value of both problems is equal in this case because of their identical linear objective function.
As \({{\,\mathrm{conv}\,}}(X)\) is hard to determine in general, it is common to make use of convex underestimators.
Definition 1
Let \(D \subseteq \mathbb {R}^n\) convex and \(g:D \rightarrow \mathbb {R}^m\) continuous.
-
1.
A convex function \(g^\text {lo}:D \rightarrow \mathbb {R}^m\) with \(g^\text {lo}(x) \le g(x)\) for all \(x\in D\) is called a convex underestimator of g on D. Correspondingly, a concave function \(g^\text {up}:D \rightarrow \mathbb {R}^m\) with \(g^\text {up}(x) \ge g(x)\) for all \(x\in D\) is called a concave overestimator of g on D.
-
2.
The convex envelope of g on D is defined by
$$\begin{aligned} {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{g}](x) := \sup \{h(x) \mid h(\bar{x}) \le g(\bar{x}) ~\forall ~ \bar{x} \in D,~h \text { convex}\}. \end{aligned}$$
A standard approach is now given by \(\bar{X} = X^0\) with
a convex underestimator \(g^\text {lo}\) and a concave overestimator \(g^\text {up}\) of g. Tighter estimators in general lead to a tighter relaxed feasible set \(X^0\). The tightest possible estimators are the convex/concave envelopes, so we define
Note that \({{\,\mathrm{conv}\,}}(X) \subsetneq X^* \subsetneq X^0\) holds in general. Hence, the resulting lower bound obtained by the respective Problem (RP) with \(\bar{X} = X^0\), or even \(\bar{X} = X^*\), is sub-optimal.
This observation motivates the remainder of this work. In the next section, we introduce a strategy that generates additional constraints in order to tighten the relaxed feasible set \(\bar{X}\), if it is not equal to \({{\,\mathrm{conv}\,}}(X)\). Afterwards, we exemplarily evaluate this strategy for a special type of constraint functions.
3 A separation method using simultaneous convexification
As motivated above, the convex envelopes of the single constraint functions are not sufficient to describe the convex hull of the feasible set of Problem (OP). Instead, a result in [2] gives an exact characterization. We aim to integrate this result into an algorithmic framework by a separation strategy.
For a given point \(x \in \bar{X}\), we either confirm that \( x \in {{\,\mathrm{conv}\,}}(X)\) holds, or compute a linear inequality that is valid for \({{\,\mathrm{conv}\,}}(X)\) but not for x. This allows us to design a cutting plane method [11]. First, the relaxed Problem (RP) is solved with an arbitrary \(\bar{X} \supseteq {{\,\mathrm{conv}\,}}(X)\). Second, a linear inequality, that separates the optimal solution from \({{\,\mathrm{conv}\,}}(X)\), is added to the description of \(\bar{X}\). This procedure can be iterated in order to reduce the size of the relaxed feasible set in every step. It can also be integrated into a Branch and Bound framework as an additional step. This combination is often called Branch and Cut.
In the first part of this section, we present the result in [2] that characterizes the convex hull of the feasible set as the intersection of inifinitely many sets. We further design an optimization problem that identifies one of the infinitely many sets that is suitable for separating a given point. Afterwards, we translate the solution of this problem into a linear inequality. The problem relies on the availability of the convex envelope of linear combinations of the constraint functions. We therefore discuss some well-known results on the structure of the convex envelope in the last part of this section.
3.1 Separation problem
We aim to derive a separation problem for the convex hull of the feasible set of Problem (OP). We denote it by
A result in [2] states that the convex hull of a vector of continuous functions on a compact, convex domain can be described using the convex envelopes of all possible linear combinations of the components.
Proposition 1
(Ballerstein, 2013 [2]) Given a compact, convex domain \(D\subseteq \mathbb {R}^n\) and a continuous function \(g:D\rightarrow \mathbb {R}^m\), \(x\mapsto g(x):=\big (g_1(x),\ldots ,g_m(x)\big )^\top \). Let \(Y_g\) be as defined in (1), i.e. the convex hull of the feasible set of Problem (OP). Then it is
with
In the following, we use this representation to derive a convex optimization problem that provides suitable \(\alpha \) for separating points from the convex hull of the feasible set of Problem (OP). To be more precise, we derive an algorithmic framework for the following separation task.
Separation Task 1
-
Input: A non-empty set \(D\subseteq \mathbb {R}^n\) compact and convex, a continuous function \(g:D \rightarrow \mathbb {R}^m\) and a point \((\bar{x}, \bar{z})\in D\times \mathbb {R}^{m}\).
-
Task: Decide whether \((\bar{x},\bar{z})\in Y_g\), and, if not, return a vector \(\alpha \in \mathbb {R}^{m}\) with
$$\begin{aligned} (\bar{x}, \bar{z}) \not \in M_g(\alpha ). \end{aligned}$$
Let a point \((\bar{x}, \bar{z})\in D\times \mathbb {R}^{m}\) be given. According to Proposition 1, we have
Observe that due to scaling, it suffices to consider only linear multipliers \(\alpha \in \mathbb {R}^m\) from the unit ball \(B^{m}:=\{\alpha \in \mathbb {R}^{m}\mid ||\alpha ||_2 \le 1\}\). Thus, we can check whether the given point \((\bar{x}, \bar{z})\in D\times \mathbb {R}^{m}\) is contained in \(Y_g\) by solving the optimization problem
Problem (SP) has the following properties.
Proposition 2
-
1.
For all \(\alpha \in \mathbb {R}^m\), \(h(\alpha ) < 0\) holds if and only if \((\bar{x}, \bar{z}) \notin M_g(\alpha ) \).
-
2.
Problem (SP) is convex and \(h:\mathbb {R}^m \rightarrow \mathbb {R}\) is continuous on \(B^m\). In particular, there exists an optimal solution to Problem (SP).
-
3.
Let \(\alpha ^\star \) be an optimal solution to Problem (SP). Then \(h(\alpha ^\star )\ge 0\) holds if and only if \((\bar{x},\bar{z}) \in Y_g\).
Proof
-
1/3.
By construction and Proposition 1.
-
2.
The feasible set \(B^m\) is non-empty, compact and convex, and \(\alpha ^\top \bar{z}\) is linear in \(\alpha \). We show that \(\text {vex}_D[\alpha ^\top g](\bar{x})\) is concave in \(\alpha \): Indeed, for arbitrary \(\alpha ,\beta \in \mathbb {R}^{m}\) and \(\lambda \in [0,1]\) we obtain
$$\begin{aligned}&\lambda {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{{\alpha }^\top g}](\bar{x}) + (1-\lambda ){{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\beta ^\top g}](\bar{x}) \\&\quad = {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\lambda \,{\alpha }^\top g}](\bar{x}) + {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{(1-\lambda )\beta ^\top g}](\bar{x}) \\&\quad \le {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\lambda \,\alpha ^\top g + (1-\lambda ) \beta ^\top g}](\bar{x}) \\&\quad ={{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{(\lambda \alpha + (1-\lambda ) \beta )^\top g}](\bar{x}) \end{aligned}$$The inequality holds, as \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{f_1}] + {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{f_2}]\) is a convex underestimator of \(f_1+f_2\) for arbitrary \(f_1,f_2:D \rightarrow \mathbb {R}\), which is a basic fact from convex analysis (see e.g. [16, p.157]).
Thus, the objective function h of Problem (SP) is convex on any open superset of \(B^m\) and therefore also continuous on \(B^m\).
\(\square \)
Note that, in the case of \((\bar{x},\bar{z})\not \in Y_g\), it is not necessary to solve Problem (SP) to optimality in order to fulfill Separation Task 1. In fact, it suffices to find a point \(\alpha \in B^{m}\) with objective value \(h(\alpha ) < 0\) to derive \((\bar{x}, \bar{z})\notin Y_g\).
From a practical point of view, it is important to mention that an efficient solvability of Problem (SP) heavily relies on the availability of an algorithmically utilizable representation of the convex envelope of \(\alpha ^\top g\) for every \(\alpha \in B^m\). Moreover, note that the function \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\alpha ^\top g}](x)\) is in general not continuously differentiable in \(\alpha \).
3.2 Deriving linear inequalities
We assume that a solution to Problem (SP) can be computed. In order to algorithmically utilize this solution in a cutting plane approach, we construct a linear inequality that separates the point \((\bar{x}, \bar{z})\) from \(Y_g\) based on this solution. We establish the following notation for our analysis.
Definition 2
Let \(Z\subseteq \mathbb {R}^n\) be a closed convex set. Furthermore, for \(\beta \in \mathbb {R}^n\) and \(\beta _0\in \mathbb {R}\), we consider the linear inequality \(\beta ^\top z\le \beta _0\) and the corresponding hyperplane \(\mathcal {H}(\beta ,\beta _0):=\{z\in \mathbb {R}^n\mid \beta ^\top z = \beta _0\}\).
-
1.
The inequality \(\beta ^\top z \le \beta _0\) is called a valid inequality for Z, if \(\beta ^\top z \le \beta _0\) holds for all \(z \in Z\).
-
2.
Let \(\bar{z} \in Z\). We call \(\mathcal {H}(\beta ,\beta _0)\) a supporting hyperplane of Z at \(\bar{z}\), if \(\beta ^\top z\le \beta _0\) is valid for Z and \(\bar{z}\in \mathcal {H}(\beta ,\beta _0)\).
-
3.
Let \(\bar{z} \notin Z\). We call \(\mathcal {H}(\beta ,\beta _0)\) a cutting plane of Z for \(\bar{z}\), if \(\beta ^\top z\le \beta _0\) is valid for Z but not valid for \(\{\bar{z}\}\).
The respective separation task using cutting planes is defined as
Separation Task 2
-
Input: A set \(D\subseteq \mathbb {R}^n\) compact and convex, a continuous function \(g:D \rightarrow \mathbb {R}^m\) and a point \((\bar{x}, \bar{z})\in D\times \mathbb {R}^{m}\).
-
Task: Decide whether \((\bar{x},\bar{z})\in Y_g= {{\,\mathrm{conv}\,}}\big (\{(x, g(x))\mid x\in D\}\big )\), and, if not, return a vector \((b,a,b_0)\in \mathbb {R}^{n+m+1}\), so that \(\mathcal {H}(b,a,b_0)=\{(x,z)\in \mathbb {R}^{n+m}\mid b^\top x + a^\top z = b_0\}\) is a cutting plane of \(Y_g\) for \((\bar{x}, \bar{z})\).
Our analysis and algorithmic results are summarized in the following proposition.
Proposition 3
Let \(D\subseteq \mathbb {R}^n\) be compact and convex and \(g:D \rightarrow \mathbb {R}^m\) continuous.
-
1.
Let \(\alpha \in \mathbb {R}^{m}\) and \(\bar{x} \in D\) be fixed. Let \((\beta ,\beta _0)\in \mathbb {R}^{(n+1)+1}\) with \({\beta _{n+1} = -1}\) define a supporting hyperplane \(\mathcal {H}(\beta ,\beta _0)\) of the epigraph \({{\,\mathrm{epi}\,}}\big ({{\,\mathrm{vex}\,}}_D[\alpha ^\top g], D\big )\) of the function \({{\,\mathrm{vex}\,}}_D[\alpha ^\top g]\) at the point \({\big (\bar{x}, {{\,\mathrm{vex}\,}}_D[\alpha ^\top g](\bar{x})\big )}\). Then, a valid linear inequality for \(Y_g\) is given by
$$\begin{aligned} (\beta _1,\dots ,\beta _n,-\alpha )^\top (x,z) \le \beta _0 \end{aligned}$$(4)We denote \(\mathcal {V}_{\alpha ,\bar{x}}[\beta ,\beta _0] := \mathcal {H}(\beta _1,\dots ,\beta _n,-\alpha ,\beta _0)\).
-
2.
Let \((\bar{x},\bar{z}) \notin Y_g\) and let \(\alpha ^\star \) be an optimal solution to Problem (SP). Let \((\beta ,\beta _0)\in \mathbb {R}^{(n+1)+1}\) with \(\beta _{n+1} = -1\) define a supporting hyperplane \(\mathcal {H}(\beta ,\beta _0)\) of \({{\,\mathrm{epi}\,}}\big ({{\,\mathrm{vex}\,}}_D[{\alpha ^\star }^\top g], D\big )\) at the point \(\big (\bar{x}, {{\,\mathrm{vex}\,}}_D[{\alpha ^\star }^\top g](\bar{x})\big )\). Then \(\mathcal {V}_{\alpha ^\star ,\bar{x}}[\beta ,\beta _0]\) is a cutting plane of \(Y_g\) for \((\bar{x}, \bar{z})\).
Proof
-
1.
First, we define the half-space given by (4) intersected with box D as
$$\begin{aligned} N_{ g,\bar{x}}(\alpha ,\beta ,\beta _0):= \big \{(x,z) \in \mathbb {R}^{n+m} \mid (\beta _1,\dots ,\beta _n,-\alpha )^\top (x,z) \le \beta _0,~x\in D\big \}. \end{aligned}$$\(\mathcal {H}(\beta ,\beta _0)\) is a supporting hyperplane of \({{\,\mathrm{epi}\,}}\big ({{\,\mathrm{vex}\,}}_D[\alpha ^\top g]\big )\) at the point \(\big (\bar{x}, {{\,\mathrm{vex}\,}}_D[\alpha ^\top g](\bar{x})\big )\). For every \((x,\hat{z}) \in \mathcal {H}(\beta ,\beta _0)\) it follows
$$\begin{aligned} \hat{z} \le {{\,\mathrm{vex}\,}}_D[\alpha ^\top g](x) \end{aligned}$$and
$$\begin{aligned} \hat{z} = \frac{\beta _0-\sum _{i=1}^n \beta _ix_i}{\beta _{n+1}} = \sum _{i=1}^n \beta _ix_i -\beta _0. \end{aligned}$$For any point \((x,z)\in M_ g(\alpha )\) we have
$$\begin{aligned} -\alpha ^\top z + {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\alpha ^\top g}](x)&\le 0 \\ \Leftrightarrow \quad -\alpha ^\top z + \sum _{i=1}^n \beta _ix_i -\beta _0&\le 0 \end{aligned}$$and therefore \((x,z)\in N_{ g,\bar{x}}(\alpha ,\beta ,\beta _0)\). This implies \(M_ g(\alpha )\subseteq N_{ g,\bar{x}}(\alpha ,\beta ,\beta _0)\), and that the linear inequality
$$\begin{aligned} (\beta _1,\dots ,\beta _n,-\alpha )^\top (x,z) \le \beta _0 \end{aligned}$$is valid for \(Y_g\).
-
2.
Let \((\bar{x},\bar{z}) \notin Y_g\). Using Proposition 2 we obtain
$$\begin{aligned} {\alpha ^\star }^\top \bar{z} < {{\,\mathrm{vex}\,}}_D[{\alpha ^\star }^\top g](\bar{x}). \end{aligned}$$As \(\mathcal {H}(\beta ,\beta _0)\) is a supporting hyperplane at \(\big (\bar{x}, {{\,\mathrm{vex}\,}}_D[{\alpha ^\star }^\top g](\bar{x})\big )\), we have
$$\begin{aligned} \big (\bar{x}, {{\,\mathrm{vex}\,}}_D[{\alpha ^\star }^\top g](\bar{x})\big ) \in \mathcal {H}(\beta ,\beta _0). \end{aligned}$$We follow the proof of 1. and derive
$$\begin{aligned} \sum _{i=1}^n \beta _i\bar{x}_i-\beta _0 = {{\,\mathrm{vex}\,}}_D[{\alpha ^\star }^\top g](\bar{x}). \end{aligned}$$Combining these equations, we have
$$\begin{aligned} {\alpha ^\star }^\top \bar{z} < \sum _{i=1}^n \beta _i\bar{x}_i-\beta _0. \end{aligned}$$This leads to \((\bar{x},\bar{z}) \notin N_{ g,\bar{x}}(\alpha ^\star ,\beta ,\beta _0)\) and to our statement.
\(\square \)
A direct consequence of Proposition 3 is that we can find an exact representation of \(Y_g\) based on supporting hyperplanes of the epigraph of the convex envelopes for different \(\alpha \). For this, let \((\beta (x,\alpha ),\beta _0(x,\alpha ))\in \mathbb {R}^{(n+1)+1}\) with \(\beta _{n+1}(x,\alpha )<0\) define an arbitrary supporting hyperplane \(\mathcal {H}(\beta (x,\alpha ),\beta _0(x,\alpha ))\) of \({{\,\mathrm{epi}\,}}\big ({{\,\mathrm{vex}\,}}_D[\alpha ^\top g]\big )\) at \(\big (x, {{\,\mathrm{vex}\,}}_D[\alpha ^\top g](x)\big )\). Then it is
Concluding these results, we are able to design cutting planes for the set \(Y_g\) by solving a convex nonlinear optimization problem. We further need to effectively construct \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\alpha ^\top g}](\bar{x})\) as well as a supporting hyperplane at a given point \(\bar{x}\) for arbitrary \(\alpha \in B^m\). The next subsection deals with the latter two parts.
3.3 Structure of the convex envelope
We present some well-known results concerning the structure of the convex envelope of a given function (e.g., see [16]). They are used in Sect. 4 in order to exemplarily apply the separation strategy developed above.
The value of the convex envelope of \(g:\mathbb {R}^n\rightarrow \mathbb {R}\) at a certain point \(x\in D\subseteq \mathbb {R}^n\) can be determined by the following nonconvex optimization problem.
with a suitably chosen \(G \subseteq D\). Note that k is bounded by \(n+1\), which is a consequence from Caratheodory’s theorem.
The most general choice for G in Problem (EP) is \(G=D\). We will, however, discuss some other valid choices that result in an equivalent problem in the following. For instance, the set G can be chosen as a real subset of D by using the concept of generating sets. Thereby, we can often strengthen the problem formulation significantly.
Definition 3
(Tawarmalani and Sahinidis, 2002 [29]) For a continuous function \(g:D\rightarrow \mathbb {R}\) on a compact convex domain \(D\subseteq \mathbb {R}^n\), we denote the generating set of g on D by
By definition of the generating set, we equivalently formulate Problem (EP) by setting \(G=\mathfrak {G}[{ g,D}]\). Next, we provide a necessary condition that allows us to exclude feasible points from the generating set.
Definition 4
Let a continuous function \(g:\mathbb {R}^n\rightarrow \mathbb {R}\) be given. The set of concave directions of g at \(\bar{x} \in \mathbb {R}^n\) is given by
In the case of g being twice continuously differentiable at \(\bar{x}\), the set of concave directions at \(\bar{x}\in \mathbb {R}^n\) is given by \(\delta [{g},{\bar{x}}] = \{d\in \mathbb {R}^n \mid d^\top H_g(\bar{x}) d < 0\},\) where \(H_g(x)\) denotes the Hessian Matrix of g at x.
A necessary condition for an interior point x of D to be an element of the generating set is that the function g must be strictly locally convex at x. This leads to the following observation.
Observation 1
(see [29, Cor. 5]) Let \(D\subseteq \mathbb {R}^n\) be convex and \(g:D\rightarrow \mathbb {R}\) continuous. Furthermore, let \({{\,\mathrm{int}\,}}(D)\) denote the interior of D. Then, for every \(\bar{x} \in {{\,\mathrm{int}\,}}(D)\) with \(\delta [{g},{\bar{x}}] \ne \emptyset \), we have that \(\bar{x} \notin \mathfrak {G}[{g,D}]\).
Throughout our analysis, it is often useful to not set G equal to \(\mathfrak {G}[{g,D}]\) in Problem (EP), but to choose a superset \(G \supseteq \mathfrak {G}[{g,D}]\) with \(G\subseteq D\). In certain cases, this will especially allow us to find an optimal solution \(\{\lambda ^\star ; x_1^\star ,\ldots ,x^\star _{n+1}\}\) of Problem (EP) with a reduced number of nonzero components of the vector \(\lambda ^\star \in \mathbb {R}^{n+1}\). To indicate nonzero components of vector \(\lambda ^\star \), we define \(I(\lambda ^\star ):=\{i\in \{1,\ldots ,n+1\}\mid \lambda _i^\star >0\}\).
Definition 5
For \(D \subseteq \mathbb {R}^n\), \(g:D\rightarrow \mathbb {R}\), \(\bar{x} \in D\) and some \(G\subseteq D\), let \(\{\lambda ^{\star }; x^\star _1,\ldots ,x^\star _{n+1}\}\) denote an optimal solution to Problem (EP) such that the cardinality \(|I(\lambda ^\star )|\) is minimal. Then, we call
a minimizing simplex for \(\bar{x}\) w.r.t. g and G. If \(|I(\lambda ^\star )|\le 2\), then we also use the term minimizing segment for \(\mathcal {S}_{g, G}\,({\bar{x}})\).
In order to determine the convex envelope of a specific function, it is advantageous to know the dimension of the minimizing simplices beforehand. If there exists, for some \(G\subseteq D\) and for every \(x \in D\), a minimizing segment w.r.t. g and G, then we say that the convex envelope of g (on D) consists of minimizing segments w.r.t. G. Note also that in this case the convex envelope of g also consists of minimizing segments with respect to every superset \(\bar{G} \supseteq G\).
Furthermore, we can exclude points and pairs of points from being part of minimizing simplices by again using the concept of concave directions.
Observation 2
Let \(D\subseteq \mathbb {R}^n\) be convex and \(g:D\rightarrow \mathbb {R}\) be continuous. Let \({{\,\mathrm{conv}\,}}(\{x^i \mid i \in \{1,\dots ,m\}\})\) be a minimizing simplex for a given \(\bar{x}\) w.r.t. g and D.
-
1.
If \(x^i \in {{\,\mathrm{int}\,}}(D)\) holds for some \(i \in \{1,\dots ,m\}\), then \(\delta [{g},{x^i}] = \emptyset \)
-
2.
For every pair \(x^i, x^j, i\ne j, i,j\in \{1,\dots ,m\}\) there exists \(x' \in {{\,\mathrm{conv}\,}}\big (\{x^i, x^j\}\big )\) with
$$\begin{aligned} (x^i-x^j) \in \delta [{g},{x'}] \end{aligned}$$
4 Convex envelope of quadratic absolute value functions
The proposed separation strategy relies on the availability of an algorithmic utilizable representation of the convex envelope of linear combinations of the constraint functions. As deriving the convex envelope of arbitrary functions is beyond the capability of the current state of research, it is common to only consider a specific function class. In the following, we exemplarily restrict ourselves to bivariate quadratic absolute value functions. We derive the convex envelope for these kind of functions, which allows us to apply the separation strategy on the corresponding constraint sets. As quadratic absolute value functions are used in the challenging field of gas network operation, we are also able to evaluate the impact of our strategy on a real world application. This is done in Sect. 5, where we derive stronger convex relaxations for some small examples of gas network optimization problems.
In this section, we briefly describe the gas network setting and the resulting constraint structure. We present some analytic tools and concepts that help to derive the convex envelope in general, and apply them to the given function class. The concrete representation of the envelopes is mostly moved to the appendix.
4.1 Constraint structure in gas networks
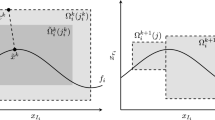
A gas network in its simplest form consists of a system of connected pipes. In our setting, we neglect all other components like compressor stations or control valves. We consider the stationary case without dependency on time. For more details on modeling optimization problems on gas networks, the reader is referred to [13]. Gas flows through the pipes based on the pressure differences at the respective endpoints. Mathematically, the network is modeled as a graph with arcs representing pipes and nodes representing coupling points. We focus on analyzing a single junction in a gas network consisting of four nodes and three arcs. Every node has a corresponding squared pressure variable \(\pi _i~(i=1,2,3,4)\) and every arc has a corresponding flow variable \(q_j ~(j=1,2,3)\). See Fig. 1 for a visualization. For a commonly used algebraic approximation of the underlying physics, the relevant constraints connecting these values are given by
with parameter \(c \in \mathbb {R}^3\), cf. [13].
Note that the direction of the flow is given by the sign of each flow variable. The respective flow is directed as shown in Fig. 1 for a positive sign and the other way around for a negative sign. We reformulate (5) into
As motivated in Sect. 3, we derive the convex envelope of \(\bar{\alpha }^\top \bar{g}\) for arbitrary \(\bar{\alpha }\in B^3\). Note that \(\bar{g}\) is separable and that parameter c is simply a scaling factor. Further, we identify \(x_1=q_1, x_2=q_2\) and reduce our analysis on the convex envelope of \(g_\alpha := \alpha ^\top g\) with
Deriving \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{g_\alpha }]\) in the general case is a challenging task. We assume \(D=[l_1,u_1]\times [l_2,u_2]\) and further reduce the complexity by fixing the direction of flow in the considered junction.
When all flow directions are fixed, we can assume that the variables \(x_1\) and \(x_2\) are nonnegative. This implies that the underlying functions reduce to quadratic ones and it is \(Y_g={{\,\mathrm{conv}\,}}(\{(x,x_1^2,x_2^2, (x_1+x_2)^2) \mid x \in [l_1,u_1]\times [l_2,u_2]\})\). In this case, a complete description of \(Y_g\) is given in [1].
The first case not covered by the literature is therefore defined by two fixed flow directions and one variable flow direction. Without loss of generality, the only variable with unfixed sign is \(x_1\). We assume that \(x_2 \ge 0\) and \(x_1+x_2 \ge 0\) holds, i.e. the single terms reduce to \( g_1(x)=|x_1|x_1\), \( g_2(x)=(x_1+x_2)^2\) and \( g_3(x)=x_2^2\). Thus, we are interested in determining the convex envelope of
on \(D= [l_1,u_1]\times [l_2,u_2]\) with \(l_2 \ge 0\) for all \(\alpha \in \mathbb {R}^3\). Function \(g_\alpha \) is twice continuously differentiable for \(x_1\ne 0\). The Hessian matrix of \(g_\alpha \) depends on the sign of \(x_1\) and is given by
with
Observe that due to scaling we can assume that \(\alpha _1\in \{-1,0,1\}\). In case of \(\alpha _1=0\), \(g_{\alpha }\) reduces to a quadratic function again. For the remainder of the section we restrict ourselves to \(\alpha _1=1\), as the case \(\alpha _1=-1\) is similar and can be obtained by symmetric considerations.
There are nine remaining cases that need to be discussed and that depend on the specific values of the parameters \(\alpha _2\) and \(\alpha _3\). They define the curvature properties of \(g_\alpha \). In order to distinguish the different cases, we use the following definition.
Definition 6
Let \(g:\mathbb {R}^n\rightarrow \mathbb {R}\) be continuous and \(D\subseteq \mathbb {R}^n\) convex.
-
1.
We call g direction-wise (strictly) convex/concave w.r.t. component i on D if, for every fixed \(\bar{x} \in D\), it is g (strictly) convex/concave on \(\bar{D}(\bar{x},i) := \{x\in D \mid x_j=\bar{x}_j ~\forall ~ i \ne j\}\).
-
2.
We call g indefinite on D, if, for every \(\bar{x} \in D\), it is \(\delta [{g},{\bar{x}}] \ne \emptyset \) and \(\xi [g,\bar{x}] \ne \emptyset \), with \(\xi [g,\bar{x}]\) being the set of convex directions of g at \(\bar{x}\), i.e.
$$\begin{aligned} \xi [g,\bar{x}] := \{d \in \mathbb {R}^n \mid \exists ~ \varepsilon > 0: \; h_{g,\bar{x},d}(\lambda ):=g(\bar{x} + \lambda d) \text { strictly convex on } [-\varepsilon ,\varepsilon ] \}. \end{aligned}$$
Using this notation, the nine different cases can be distinguished as listed in Table 1. The first column denotes the (sub)cases and the second one lists the conditions on \(\alpha \) for the respective case. Columns three to five give the curvature of \(g_\alpha \) with respect to both components and in general. Concave-convex means that \(g_\alpha \) is direction-wise concave for \(x<0\) and direction-wise convex for \(x\ge 0\) and indefinite-convex means that \(g_\alpha \) is indefinite for \(x<0\) and convex for \(x\ge 0\). Concave/indefinite indicates that \(g_\alpha \) is either concave or indefinite.
We do not elaborate on the analysis for all of these cases. Instead, we discuss interesting results and properties exemplarily on the two most complicated (sub)cases. The remaining ones are either trivial, are obtained by results in the literature, or can be derived using similar arguments as presented. For the sake of completeness, they can still be found in the appendix.
Section 4.2 considers Case (2.b.iii) and uses the concept of \((n-1)\)-convex functions (see [10]) in order to show that the convex envelope of \(g_\alpha \) consists of minimizing segments. In Sect. 4.3, we introduce the direction-wise convex envelope and reduce Case (3) to Case (2).
4.2 Reduction on minimizing segments
We consider Case (2.b.iii). The function \(g_\alpha \) is direction-wise convex w.r.t. components 1 and 2. Furthermore, it is convex for \(x_1\ge 0\) and indefinite for \(x_1<0\). We show that the convex envelope consists of minimizing segments and derive them for any given point \(\bar{x} \in D\).
For this, we make use of the concept of \((n-1)\)-convex functions as introduced in [10].
Definition 7
Let \(g : \mathbb {R}^n \rightarrow \mathbb {R}\) be a twice differentiable function. g is said to be (strictly) \((n-1)\)-convex if the function \(g|_{x_i=\bar{x}_i} : \mathbb {R}^{n-1} \rightarrow \mathbb {R}\) is (strictly) convex for each fixed value \(\bar{x}_i \in \mathbb {R}\) and for all \(i =1,\dots , n\).
For indefinite functions with this property, the authors give a statement on the structure of the concave directions.
Lemma 1
[10, Lemma 3.2] Let \(g : D = [l, u]\subseteq \mathbb {R}^n \rightarrow \mathbb {R}\) be a twice differentiable function, and let the collection \(\{\mathcal {O}_1,\dots ,\mathcal {O}_{2^n}\}\) be the system of open orthants of the space \(\mathbb {R}^n\). Then, the function g is \((n-1)\)-convex and indefinite if and only if \(\delta [{g},{x}]\) is nonempty for each \(x \in D\) and there exists an index \(i \in \{1,\dots , 2^n\}\), such that
holds for all \(x \in D\).
This statement can be extended to the function \(g_\alpha \) for Case (2.b.iii). \(g_\alpha \) can be divided into an indefinite \((n-1)\)-convex function for negative \(x_1\) and a convex function for positive \(x_1\). The property stated in Lemma 1 therefore also holds for \(g_\alpha \) as shown in the following Corollary.
Corollary 1
Let \(\alpha \) be as given in Case (2.b.iii). Then, there exists an index \(i \in \{1,\dots , 2^n\}\) such that
holds for all \(x \in D\).
Proof
We divide function \(g_\alpha \) into two parts and formulate it as
with
The function \(g_\alpha ^+\) is convex because of \(H_\alpha ^+ \succcurlyeq 0\), so we have
The concave directions at a point x with \(x_1 = 0\) need to be discussed separately. We consider the direction \(d = (d_1,d_2)\) and distinguish the two cases \(d_1 = 0\) and \(d_1 \ne 0\). For \(d_1 = 0\), the function
is convex in \(\lambda \) as \(g_\alpha \) is direction-wise convex w.r.t. component 2. Therefore, any d with \(d_1 = 0\) is not a concave direction. For \(d_1 \ne 0\), the function \(h_{g,x,d}(\lambda )\) with \(\lambda \in [-\varepsilon ,\varepsilon ]\) always has a domain that includes points whose first component attains values strictly greater zero for every \(\varepsilon >0\). As \(g_\alpha \) is convex for \(x_1 >0\), d is again not a concave direction.
Summarizing these results, we obtain
for every \(x\in D\). As \(g_\alpha ^-\) is an \((n-1)\)-convex and indefinite function, we can apply Lemma 1 to conclude that there exists an index \(i \in \{1,2,3,4\}\), such that for all \(x \in D\) the set of concave direction of \(g_\alpha \) at x is a subset of \(\mathcal {O}_i \cup -\mathcal {O}_i\). \(\square \)
This structure of the concave directions can be used to show the existence of minimizing segments for every point \(\bar{x}\in D\) w.r.t. a set G (see Definition 5). As the existence of minimizing segments depends on the choice of G, we first define \(G := G_1\cup G_2 \cup G_3 \cup G_4\) with
See Fig. 2a for a graphic representation of the subsets \(G_i\). Using Observation 1, it is easy to see that \(\mathfrak {G}[{g_\alpha ,D}] \subseteq G\) holds.
The existence of minimizing segments is then given by the following Corollary. A similar case and basic ideas of the proof are already provided in [10, Theorem 3.1].
Corollary 2
Let \(\alpha \) be as given in Case (2.b.iii), \(D = [l,u]\) with \(l_2 \ge 0\) and G as defined above. Then the convex envelope of \(g_\alpha \) on D consists of minimizing segments w.r.t. G.
Proof
Note the following preliminary considerations. Let
The proof of Corollary 1 already indicates that \(g_\alpha ^-\) is indefinite. The set of concave directions of \(g_\alpha \) at \(x \in E\) is therefore nonempty.
For the proof, we show that the convex envelope of g on D consists of minimizing segments w.r.t. D. Using Observation 2, it is easy to see that there are no extreme points of any minimizing segment inside E. We conclude that the convex envelope of g on D also consists of minimizing segments w.r.t. G.
Assume that there exists a point \(\bar{x} \in D\) with a minimizing simplex \(\mathcal {S}_{g_\alpha , D}\,({\bar{x}})\) consisting of at least three different extreme points, i.e.,
According to Observation 2, we have \(x^1,x^2,x^3 \notin E\), as \(\delta [{g_\alpha },{x}] \ne \emptyset \) holds for all points \(x\in E\). We conclude that \(x^1,x^2,x^3 \in G\) and we only need to distinguish two cases:
-
1.
Two of the points \(x^1,x^2,x^3\) are elements of the same subset \(G_i\) for some \(i \in \{1,\dots ,4\}\). Function \(g_\alpha \) is convex on \(G_i\) for every \(i\in \{1,\dots ,4\}\). This leads to a contradiction based on Observation 2.
-
2.
No two points are elements of the same subset \(G_i\) for all \(i \in \{1,\dots ,4\}\). For all possible combinations, one of the three vectors \((x^1-x^2)\), \((x^2-x^3)\) and \((x^3-x^1)\) is not an element of the same pair of open orthants \(\mathcal {O}_i \cup (-\mathcal {O}_i)\) for all \(i=1,\dots ,4\). According to Corollary 1, \(g_\alpha \) is convex on at least one of the three sets \({{\,\mathrm{conv}\,}}\big (\{x^1,x^2\}\big )\), \({{\,\mathrm{conv}\,}}\big (\{x^2,x^3\}\big )\) or \({{\,\mathrm{conv}\,}}\big (\{x^3,x^1\}\big )\). This contradicts Observation 2 again.
Hence, the convex envelope of g on D consists of minimizing segments w.r.t. D. We conclude our statement by using Observation 2 as described above. \(\square \)
Next, we construct a minimizing segment for any given point \(\bar{x}\in D\) w.r.t. \(g_\alpha \) and G. For this, we first analyze the structure of concave directions in order to apply Observation 2.
-
1.
For \(\alpha _2 > 1\) we show for each \(x \in D\) with \(x_1 < 0\) that
$$\begin{aligned} (-\alpha _2,\alpha _2-\alpha _1) \in \delta [{g_\alpha },{x}] \end{aligned}$$holds. In fact, we have
$$\begin{aligned}&(-\alpha _2,\alpha _2-\alpha _1)\, H_\alpha ^- (-\alpha _2,\alpha _2-\alpha _1)^\top \\&\quad = \alpha _2^2(\alpha _2-\alpha _1)-2\alpha _2^2(\alpha _2-\alpha _1) +(\alpha _2-\alpha _1)^2(\alpha _2+\alpha _3) \\&\quad = (\alpha _2-\alpha _1)\det (H_\alpha ^-). \end{aligned}$$With \(\alpha _2> 1=\alpha _1\) and \(H_\alpha ^- \not \succcurlyeq 0\), we obtain \(\det (H_\alpha ^-) <0\) and
$$\begin{aligned} (-\alpha _2,\alpha _2-\alpha _1) \in \delta [{g_\alpha },{x}]. \end{aligned}$$ -
2.
For \(\alpha _2 = 1\), it is easy to see that
$$\begin{aligned} (-\alpha _2+\alpha _3,1)\,H_\alpha ^- (-\alpha _2+\alpha _3,1)^\top < 0 \end{aligned}$$holds for all \(x \in D\) with \(x_1 < 0\). This leads to
$$\begin{aligned} (-\alpha _2+\alpha _3,1)\in \delta [{g_\alpha },{x}]. \end{aligned}$$ -
3.
\(\alpha _2 < 1\) does not occur in Case (2.b.iii).
Either way, there exists a vector \(v\in \mathbb {R}_-\times \mathbb {R}_+\) with \(v \in \delta [{g_\alpha },{x}].\) Using Corollary 1, we derive
for all \(x \in D\). This property of the structure of concave directions will be used together with Observation 2 in the following analysis.
By Corollary 2, there exists a minimizing segment \(\mathcal {S}_{g_\alpha , G}\,({\bar{x}})\) for any given point \(\bar{x} \in D\). We denote the two extreme points of \(\mathcal {S}_{g_\alpha , G}\,({\bar{x}})\) by \(p^1\) and \(p^2\), i.e.,
By definition of G, we have \(p^1 \in G_i\) and \(p^2 \in G_j\) for some \(i,j \in \{1,\dots ,4\}\). Next, we classify possible minimizing segments for all combinations of i and j (exploiting symmetry). For this, consider the following “easy” cases first.
-
\(i=j\): As \(g_\alpha \) is convex on \(G_k\) for \(k = 1,\dots ,4\), we have \(p^1 = p^2= \bar{x}\) in this case.
-
\((i,j) = (1,3)\): Using (8) and Observation 2, we derive that there are no minimizing segments with \(p^1 \in G_1\) and \(p^2 \in G_3\) except for \(p^1 =p^2 = \bar{x} = (l_1,u_2)\).
-
\((i,j) = (2,4)\): Using (8) and Observation 2 again, this leads to \(p^1 =p^2 = \bar{x} = (0,l_2)\).
-
\((i,j) = (2,3)\): See Case (2.a) in Appendix 7.1.
-
\((i,j) = (1,2)\): See Case (2.b.i) in Appendix 7.1.
The first interesting combination is \((i,j) = (1,4)\). For every given point \(\bar{x} \in D\) and every extreme point \(p^1 := (l_1,r) \in G_1\) of a possible minimizing segment of \(\bar{x}\), we consider the ray L starting at \(p^1\) into the direction of \(\bar{x}\) as
We determine the convex envelope of \(g_\alpha \) restricted to L, and thereby detect the second extreme point \(p^2 := (s,t) \in G_4\) (See Fig. 2b). The point \(p^2\) is given as the point with a directional derivative coinciding with the gradient of the line connecting \(\big (p^1,g_\alpha (p^1)\big )\) and \(\big (p^2,g_\alpha (p^2)\big )\), i.e.,
Note that \(s \ge 0\) holds because of \(p^2 \in G_4\). We further introduce a new variable \(\mu \) and set
Variable \(\mu \) can be interpreted as the distance between \(p^1\) and \(p^2\) relatively to the distance between \(p^1\) and \(\bar{x}\). We combine the equations above and derive
Each of the variables r, s, t and \(\mu \) now depends on r. We insert this information into the problem used to derive the value of the convex envelope at a given point \(\bar{x}\) (see (EP)). This results in the one-dimensional optimization problem
This problem has to be solved in order to determine the actual minimizing segment and the value of the convex envelope at \(\bar{x}\). Using basic transformation, we first reformulate the objective function into
with a constant c not depending on r, that can be omitted for sake of optimization. We aim to apply the first-order optimality condition and consider the derivative of h(r) (with \(\mu \) also depending on r), which reads as
In order to determine the optimal solution, the root of \((1-\mu )\) does not have to be considered as \(\mu = 1\) would result in \(p^2 = \bar{x}\). The remaining root of the derivative is given by
Hence, the optimal value of (9) is attained at \(r_1\) or at the boundary of the interval \([l_2,u_2]\), which can be efficiently tested by comparing the functional values of h at these positions. The minimum of (9) can not be attained at \(r = l_2\), because this would result in a minimizing segment not including a concave direction (see (8) and Observation 2). The two remaining possible optimal solutions are therefore \(r_1= \bar{x}_2+ \frac{\alpha _2}{\alpha _2+\alpha _3}(\bar{x}_1-l_1)\) and \(r_2 = u_2\), and their respective minimizing segments.
For \((i,j) = (3,4)\), the resulting possible minimizing segment can be derived in a similar way. Combining these results, we derive possible minimizing segments for several combinations of \(i,j \in \{1,\dots ,4\}\). As all combinations are considered, the actual minimizing segment for \(\bar{x}\) has to be one of them. In order to determine it, we compute the values of the convex combination induced by all different possible segments and take the lowest one.
Figure 3 exemplarily shows the resulting structure of the minimizing segments for different \(\bar{x} \in D\). We use green lines for segments with \((i,j) = (1,2)\), magenta and red lines for segments with \((i,j) = (1,4)\) and blue lines for segments with \((i,j) = (3,4)\). Yellow lines show intermediate segments with one extreme point at \((l_1,u_2)\). Black dots indicate minimizing segments of dimension zero inside set \(G_4\). This means that the function \(g_\alpha \) coincides with its convex envelope.
4.3 The direction-wise convex envelope
We consider Case (3) and all its subcases. In order to handle these cases, we introduce the concept of direction-wise convex envelopes and show how it can be used to reduce Case (3) on results from Case (2).
It is \(\alpha _2 \in (-1,1)\), so that, w.r.t. component 1, \(g_\alpha \) is direction-wise concave for \(x\le 0\) and direction-wise convex on \(x\ge 0\). For a function g that is not direction-wise convex w.r.t. to a certain coordinate \(i\in \{1,\dots ,n\}\) on the whole set D, we can design a function with this property by computing the convex envelope of g restricted to a line segment defined by fixing the value of \(x_j\) for all \(j\ne i\), \(i \in \{1,\dots ,n\}\).
Definition 8
The direction-wise convex envelope of g on D w.r.t. component i is defined as
In certain cases, this transformation preserves the direction-wise curvature with respect to other coordinates. To be more precise, we require that the entries of coordinate i of the generating set of \( \text {vex}_{\bar{D}(x,i)}[g](x)\) is the same for all \(x \in D\). We denote the respective entries by \(X_i\) in the following result. Note that the entries of the remaining coordinates are already given by x.
Lemma 2
Let \(g:\mathbb {R}^n\rightarrow \mathbb {R}\) continuous and direction-wise (strictly) convex/concave w.r.t. component \(k\in \{1,\dots n\}\). Let \(D\subseteq \mathbb {R}^n\) be a compact convex set and let \(i\in \{1,\dots ,n\}\), \(i \ne k\) be given. If there is a set \( X_i \subset \mathbb {R}\) such that for every \(x\in D\) it is
then it is \(\gamma _{\scriptscriptstyle {D,i}}[{g}]\) direction-wise (strictly) convex/concave w.r.t. component k.
Proof
We discuss the proof only for the statement on direction-wise convexity. The results for direction-wise concavity and strictness can be derived analogously.
Let \(\lambda \in [0,1]\), \(\bar{x} \in D\) and two points \(x^1,x^2\) with \(x^1_j = x^2_j = \bar{x}_j\) for every \(j=1,\dots ,n,~j\ne k\) be given. We denote \(x^\lambda = \lambda x^1 + (1-\lambda )x^2\). Due to (11), it is either
or
In the first case, it is \(\gamma _{\scriptscriptstyle {D,i}}[{g}](x) = g(x)\) for all \(x \in \{x^1,x^2,x^\lambda \}\) and
holds as g is direction-wise convex w.r.t. component k.
In the second case, the value \(\gamma _{\scriptscriptstyle {D,i}}[{g}](x)\) for \(x \in \{x^1,x^2,x^\lambda \}\) is given as a convex combination of two points respectively. This holds as the set \(\bar{D}\) in the definition of the direction-wise convex envelope is one-dimensional. Due to (11), the respective two points share the same value for every component but component k for all \(x \in \{x^1,x^2,x^\lambda \}\). To be more specific, there exists some \(\mu \in [0,1]\), and points \(x^{1,1}, x^{1,2}, x^{2,1}, x^{2,2}, x^{\lambda ,1},x^{\lambda ,2} \in D\) with \(x^{1,1}_j = x^{2,1}_j = x^{\lambda ,1}_j\) and \(x^{1,2}_j = x^{2,2}_j = x^{\lambda ,2}_j\) for every \(j = 1,\dots ,n, ~j\ne k\), such that
As \(\lambda g(x^{1,1}) + (1-\lambda )g(x^{2,1}) \ge g(x^{\lambda ,1})\) and \(\lambda g(x^{1,2}) + (1-\lambda )g(x^{2,2}) \ge g(x^{\lambda ,2})\) holds due to the direction-wise convexity of g, it is again
\(\square \)
Furthermore, the direction-wise convex envelope is a suitable intermediate step for determining the actual convex envelope.
Corollary 3
Let \(D \subseteq \mathbb {R}^n\) and \(g:D\rightarrow \mathbb {R}\). Let \(\gamma _{\scriptscriptstyle {D,i}}[{g}](x)\) be the direction-wise convex envelope of g on D w.r.t. some component \(i\in \{1,\dots ,n\}\). Then it is
Proof
The inequality \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{g}](x) \ge {{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\gamma _{\scriptscriptstyle {D,i}}[{g}]}](x)\) holds trivially. The direction-wise convex envelope is defined in a similar way as the actual convex envelope, using only a smaller subset \(\bar{D}(x,i) \subseteq D\). Since the value of the convex envelope is given by a minimization problem, this leads to
With \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{g}]\) being convex and an underestimator of \(\gamma _{\scriptscriptstyle {D,i}}[{g}]\), we derive our statement. \(\square \)
In order to make use of this result, we first derive the direction-wise convex envelope of \(g_\alpha \) w.r.t. component 1. It is
\(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }](x)\) restricted to \(x_1<s\) is twice differentiable, so we can derive the Hessian Matrix as
It is \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) direction-wise convex w.r.t. component 1 and indefinite for \(x_1 <s\). Note that, for all subcases, the direction-wise convexity/concavity w.r.t. component 2 is also preserved as stated in Lemma 2. This holds, as the value of s in the definition of \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is independent in \(x_2\).
By applying these results, the convex envelope of \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) for all subcases of Case (3) can be reduced to observations in previous cases. For Case (3.a), \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is indefinite, direction-wise convex w.r.t. component 1 and direction-wise concave w.r.t. component 2 (see Case (2.a)). For Case (3.b.i), \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is indefinite and direction-wise convex w.r.t. component 1 and 2 (see Case (2.b.i)). For Case (3.b.ii), \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is indefinite-convex and direction-wise convex w.r.t. component 1 and 2 (see Case (2.b.iii)).
Using the convex envelope of \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\), the convex envelope of \(g_\alpha \) can also be easily derived by translating the minimizing segments of \(\gamma _{\scriptscriptstyle {D,x}}[{g_\alpha }]\) into minimizing simplices of \(g_\alpha \). We refer to the appendix for more detailed information.
5 Computational results
In this section, we evaluate the proposed separation strategy from Sect. 3 exemplarily on the feasible set arising from two test networks. We aim to show that the resulting cutting planes are well suited to tighten the convex relaxation of the feasible set provided by state-of-the-art software packages. Additionally, we show that the computation of cutting planes is not very time consuming in comparison to their benefits. We present the test setting in Sect. 5.1, the strategy of our implementation in Sect. 5.2, and discuss the computational results in Sect. 5.3.
5.1 Test setting
We consider two test networks. The first one is artificially designed and denoted by “Net1” (see Fig. 4). It has 7 nodes, 4 of which are terminal nodes that may have nonzero demand. Furthermore, it has 9 arcs and 3 interior junctions. The topology of the second one is taken from a gas network library (GasLib-11, [25], see Fig. 5) and denoted by “Net2”. It has 11 nodes, 6 terminals, 11 arcs and 5 interior junctions.
For both networks we consider three different settings each, given by different bounds (box constraints) on the involved variables, including the demands at the terminal nodes. In order to work with reasonably tight variable bounds, all bounds have been tightened by applying the preprocessing routines implemented in the Lamatto++ software framework for gas network optimization, described in [7, Chapter 7].
In order to evaluate the relaxed feasible set in multiple “directions”, we further consider ten different objective functions respectively, which are formally all to be minimized in our computations. These objectives are given as linear combinations of the squared pressure and flow variables in the network. They are mostly inspired by applications and include finding minimum or maximum values for the demand of a specific terminal node (objectives 1, 2, 5 and 6), the (squared) pressure at a specific node (objectives 3 and 4), the squared pressure difference between two specific nodes (objective 10) and sparse linear combinations of flow variables (objectives 7, 8, and 9).
There are 30 different combinations of bound setting and objective function for both networks. We call each combination a scenario and denote it by the identifier i-j, where i specifies the bound setting and j the objective number.
The formulation of every interior junction in the considered networks is adapted according to Sect. 4.1, and has therefore the desired structure of Problem (OP). The bounds on the variables have been chosen in such a way that several flow directions are fixed automatically and at most one flow direction at every junction remains unfixed. This allows us to compute the convex envelope of all linear combinations of the constraint functions for every junction (see Sect. 4).
As a result, we are able to perform Separation Task 2 on the feasible set of every single junction. Note that not the whole network has the desired structure of Problem (OP), as additional constraints are needed to describe the coupling between the junctions. Therefore we are not able to separate from the convex hull of the feasible set of the whole network, but only from the convex hull of subsets. The design of the implementation is described in the next section.
5.2 Implementation
The strategy of our computations is the following: We design and solve a linear relaxation of the network. For each interior junction in the network, we perform Separation Task 2 by solving Separation Problem (SP). This way, we either confirm the solution of the relaxation or derive a cutting plane that is added to the description of the relaxation. We iterate this procedure until no further cutting planes are found, or until a maximum number of 100 iterations is reached.
The Separation Problem (SP) is implemented as a simple subgradient method. We use an arbitrary value \(\alpha \) from the unit sphere \(S^2 \subseteq \mathbb {R}^3\) as a starting point and compute value and subgradient according to Sect. 4. We make use of a diminishing step size and a stopping criterion based on iteration count and improvement of the objective function. We also apply several standard methods to avoid numerical issues, such as excluding cutting planes that are approximate conic combinations of other cutting planes, or safe rounding of coefficients. Note that this part of the implementation is not optimized in terms of computational efficiency, as the focus lies on the quality of the resulting cutting planes. We refer to Appendix 7.2 and 7.3 for a pseudo code of the cutting plane generation and the subgradient method, respectively.
If we only consider the progress of the objective value in the iterative linear relaxation outlined above, we simply confirm that the cutting planes hold additional information compared to the linear relaxation. However, our aim is to show that the cutting planes also tighten the “standard” relaxation provided by a state-of-the-art solver for MINLPs and are beneficial for its overall solution process. We chose BARON 18.5.8 ([30]) for this comparison. BARON does not allow the user to interfere with the solution process or to integrate custom optimization techniques. Therefore, we add the precomputed cutting planes to the model description and let BARON solve the problem with and without these additional constraints. We deactivate presolving routines and primal heuristics, and directly provide an optimal solution to the solver. This way, we are able to analyze the influence of our separation strategy on the quality of the convex relaxation and the resulting lower bounds. However, we would like to remark that in general also the primal bound may profit from the additional linear inequalities. It has been observed that even adding redundant constraints can help primal solution finding for nonconvex MINLPs, see e.g. [24].
We further deactivate the bound tightening strategies provided by BARON as they are also not available for the iterative linear relaxations used to derive the cutting planes. Note that this means slowing down the solver substantially, to the extend that very easy instances, solved in less than a second by BARON with standard parameter settings, now become challenging. Indeed, this is the case for most scenarios considered here. However, without this modification the cutting planes would be applied on a different relaxed feasible set than the one they were constructed for.
Except for the points above, we choose the default options for BARON. All computations are carried out on a 2.6 GHz Intel Xeon E5-2670 Processor with a limit of 32 GB memory space for each run.
5.3 Results
We first discuss the results of the iterative linear relaxation for both networks. Note that the iterative linear relaxation is in our setting only used to derive the cutting planes. We are not interested in comparing the quality of the linear relaxation with BARON, but in analyzing the influence of the generated cuts on the quality of the lower bounds obtained by BARON as a stand-alone solver. Therefore, we omit any further information on the solution process of the linear relaxation.
In a second step, we present the results obtained by BARON (see Tables 2 and 3). In column 2 and 3, we display the optimal value of the respective scenario and the lower bound at the root node obtained by BARON alone. Their difference is denoted as the gap. For all further settings, we display the respective lower bounds in terms of the percentage of this gap that was closed by the solver. Column 4 gives the lower bound at the root node obtained by BARON with the use of our cutting planes (w/ cuts). Column 5 and 6 show the lower bound after 10 minutes into the solving process. See column 5 for the results of BARON alone and column 6 for BARON with the additional use of our cutting planes. Percentages are rounded down to the first decimal. Whenever 100% of the gap has been closed, the time until successful termination is reported in the respective column instead. All cases in which using our cutting planes led to a strict improvement compared to not applying them have been highlighted.
Note that several of our 30 scenarios are already solved in the root node. The solution process of these scenarios does not offer any information in terms of improvement of lower bounds. They are therefore excluded from the presentation.
We discuss the artificially designed network Net1 first. 13 of our 30 scenarios are already solved in the root node and are not considered further. For the remaining scenarios our recursive linear relaxation generates between 14 and 57 cutting planes, with an average of 32 cutting planes per scenario. This also implies that the iteration limit of 100 was never hit for these instances. The computational effort needed for the construction of the cuts is negligible: For every scenario, the computation of all cuts together is done in less than a quarter of a second. The results obtained by BARON are given in Table 2. Our generated cuts clearly improve the quality of the lower bounds at the root node for almost all instances (see column 4). This improvement has a large range between 0 and 84%, and a mean value of approximately 35%. After 10 minutes into the solution process, the lower bounds obtained with the cuts are still significantly better than the ones obtained without them (see columns 5 and 6). The average values are 18% and 70% respectively, which is a difference of 52 percentage points. Note that Scenario 1-5 has been solved to optimality thanks to the cutting planes. Scenario 3-1 is solved to optimality with as well as without cuts, while the former version is significantly more efficient (5.87s vs. 106.14s until successful termination).
We also tested giving more time than 10 minutes to the solver. However, only extremely slow progress can be observed afterwards and, consequently, the key figures after 1h are very similar to the ones given in columns 5 and 6 of Table 2. In particular, the positive effect of our cutting planes on the lower bounds obtained does not seem to diminish for larger time limits.
Next, we discuss the library network Net2. 11 scenarios are already solved in the root node. The number of generated cuts ranges from 13 to 52 with an average of 27 per scenario. Furthermore, the construction of cuts is again performed in less than a quarter of a second. The results obtained by BARON are given in Table 3. Our observations for Net2 are similar to the ones for Net1. The improvement of the lower bounds at the root node has a large range and a mean value of 54% (see column 4). After 10 minutes into the solution process, the average amount of gap closed is 17% without the cuts and 69% with cuts (see columns 5 and 6). For three scenarios (3–2, 3–7 and 3–10) over 99% gap has been closed within 10 minutes thanks to the cutting planes.
Again, after more than 10 minutes very little solver progress can be observed and our observations stay valid also when considering the results after one hour of computation time. Is is worth noting, though, that the use of our cutting planes led to scenario 3-7 being solved to optimality within 1h.
We conclude that our separation method for this special application can be performed in a fraction of a second. This result is expected, as the value and a subgradient of our Separation Problem (SP) can be derived “mostly” analytically (see Sect. 4). Additionally, the designed cuts are well suited to improve the convex relaxation of the considered MINLP and the resulting lower bound. Furthermore, the amount of gap closed after 10 minutes is higher with the usage of the cuts for every single scenario. This indicates that the growth of the model formulation caused by the additional constraints is not significant compared to the provided benefits of the cuts. We assume that the separation strategy is even more efficient if it is integrated into a MINLP solver. In such a setting, cutting planes can not only be designed adaptively to cut off solutions of intermediate node relaxations, but can also profit from tightened variable bounds becoming available during the solution process, and be strengthened accordingly.
As argued above, our aim in this prototypical study cannot be to improve state-of-the-art solvers in the field. Instead, we show that indeed the new cutting planes obtained from simultaneous convexification help improving the quality of the bounds which is beneficial in a global optimizer. However, it is still of interest to study their impact if the solver can use its full potential, i.e., if default parameter settings are used. We thus include Table 4 in Appendix 7.4, showing corresponding results for the instances from Table 2. As already mentioned above, the instances are not difficult and can be solved in less than a second. They require up to 17 branch-and-bound nodes. Thus, the conclusions that can be derived from these results are limited. Still, we observe some benefit from using our cutting planes in terms of the number of explored branch-and-bound nodes. For such small total running times, the time for generating the cutting planes beforehand becomes significant, and so the benefit is not reflected in the total running times.
We want to point out that it is currently not possible to extend the computational results to larger instances with using default parameters in order to show the full potential of the novel methods. This is due to the fact that large passive gas networks essentially do not exist in practice since the pressure drop along pipes in a large network necessarily needs to be compensated by compressors. In addition, artificially created random instances are usually infeasible. Therefore, meaningful data for larger passive networks unfortunately is not available to us, and so we have to refrain from showing corresponding results for larger networks.
We note that our results from Sect. 4 could also be applied to junctions of degree \(d>3\), where \(d-1\) flow directions are fixed, by decomposing the junction into several auxiliary junctions with 3 fixed flow directions and a single junction of degree 3 of the type discussed in Sect. 4. This would, however, not be guaranteed to yield the simultaneous convex hull for the original junction but just a relaxation. Since junctions of high degree are quite uncommon in real-world gas networks, we did not include such cases in our test computations.
6 Conclusion
In this paper, we proposed an algorithmic framework for tightening convex relaxations of MINLPs as they are routinely constructed by MINLP solvers. The method is based on separating valid inequalities for the simultaneous convex hull of multiple constraint functions, which generally is much tighter than standard relaxations that are only based on convexifying individual constraint functions separately. A key ingredient for this strategy is having a suitable representation of the (lower-dimensional) convex hull of all linear combinations of the considered constraint functions. Under this assumption, we show that one can solve Separation Tasks 1 and 2 efficiently and thus determine a supporting hyperplane of the simultaneous convex hull cutting off any given point outside.
As an example application, we considered a constraint structure from gas network optimization, which can be modeled using quadratic absolute value functions. For this special case, we were able to determine the convex hull of arbitrary linear combinations of constraint functions belonging to a certain local substructure and successfully test the proposed approach. Indeed, the computational results suggest that already a small number of cutting planes derived from a standard relaxation can significantly improve the performance of a state-of-the-art MINLP solver. The positive effect on the dual bound when using our cutting planes also persists when looking deeper into the solution process. Furthermore, it clearly outweighs the time needed for the separation. In our tests, the separation routine neither had access to possible variable bound improvements after the root relaxation, nor was it given the opportunity to cut off optimal solutions from node relaxations after branching. We therefore expect that it would be even more effective when incorporated directly into a branch-and-branch solver.
It would be interesting to see the presented approach being applied to other function classes an/or application areas in the future. However, computing convex envelopes of arbitrary linear combinations of constraint functions is very difficult and cannot be expected to be feasible in each case. Therefore also techniques producing tight approximations that are consistent in the sense that (SP) remains a convex problem would be of great interest from a practical point of view.
Data Availability Statement
The instances used for the computational study in this article (see Sect. 5) will be made available on reasonable request.
References
Anstreicher, K.M., Burer, S.: Computable representations for convex hulls of low-dimensional quadratic forms. Math. Program. 124(1), 33–43 (2010). https://doi.org/10.1007/s10107-010-0355-9
Ballerstein, M.: Convex Relaxations for Mixed-Integer Nonlinear Programs. Ph.D. thesis, Eidgenössische Technische Hochschule Zürich (2013)
Belotti, P., Kirches, C., Leyffer, S., Linderoth, J., Luedtke, J., Mahajan, A.: Mixed-integer nonlinear optimization. Acta Numerica 22, 1–131 (2013). https://doi.org/10.1017/S0962492913000032
Boukouvala, F., Misener, R., Floudas, C.A.: Global optimization advances in Mixed-Integer Nonlinear Programming, MINLP, and Constrained Derivative-Free Optimization CDFO. Eur. J. Oper. Res. 252(3), 701–727 (2016). https://doi.org/10.1016/j.ejor.2015.12.018
Bussieck, M.R., Vigerske, S.: MINLP Solver Software (2014)
Eronen, V.P., Mäkelä, M.M., Westerlund, T.: On the generalization of ecp and oa methods to nonsmooth convex minlp problems. Optimization 63(7), 1057–1073 (2014). https://doi.org/10.1080/02331934.2012.712118
Geißler, B.: Towards globally optimal solutions for minlps by discretization techniques with applications in gas network optimization. Ph.D. thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (2011)
Gleixner, A., Eifler, L., Gally, T., Gamrath, G., Gemander, P., Gottwald, R.L., Hendel, G., Hojny, C., Koch, T., Miltenberger, M., Müller, B., Pfetsch, M.E., Puchert, C., Rehfeldt, D., Schlösser, F., Serrano, F., Shinano, Y., Viernickel, J.M., Vigerske, S., Weninger, D., Witt, J.T., Witzig, J.: The SCIP Optimization Suite 5.0. Technical Report, pp. 17-61, Zuse Institute Berlin (2017)
Grossmann, I.E., Caballero, J.A., Yeomans, H.: Mathematical Programming Approaches to the Synthesis of Chemical Process Systems. Korean J. Chem. Eng. 16(4), 407–426 (1999). https://doi.org/10.1007/BF02698263
Jach, M., Michaels, D., Weismantel, R.: The Convex Envelope of \((n-1)\)-Convex Functions. SIAM J. Optim. 19(3), 1451–1466 (2008). https://doi.org/10.1137/07069359X
Kelley Jr., J.E.: The cutting-plane method for solving convex programs. J. Soc. Ind. Appl. Math. 8(4), 703–712 (1960)
Khajavirad, A., Sahinidis, N.V.: Convex envelopes generated from finitely many compact convex sets. Math. Program. 137(1), 371–408 (2013). https://doi.org/10.1007/s10107-011-0496-5
Koch, T., Hiller, B., Pfetsch, M., Schewe, L. (eds.): Evaluating gas network capacities. MOS-SIAM Ser. Optim. (2015). https://doi.org/10.1137/1.9781611973693
Lasserre, J.B.: Global optimization with polynomials and the problem of moments. SIAM J. Optim. 11(3), 796–817 (2001). https://doi.org/10.1137/S1052623400366802
Liberti, L., Pantelides, C.C.: Convex envelopes of monomials of odd degree. J. Global Optim. 25(2), 157–168 (2003). https://doi.org/10.1023/A:1021924706467
Locatelli, M., Schoen, F.: Global optimization: theory, algorithms, and applications. Soc. Ind. Appl. Math. (2013). https://doi.org/10.1137/1.9781611972672
Locatelli, M., Schoen, F.: On convex envelopes for bivariate functions over polytopes. Math. Program. 144(1), 65–91 (2014). https://doi.org/10.1007/s10107-012-0616-x
Martin, A., Möller, M., Moritz, S.: Mixed integer models for the stationary case of gas network optimization. Math. Program. 105(2), 563–582 (2006). https://doi.org/10.1007/s10107-005-0665-5
Merkert, M.: Solving mixed-integer linear and nonlinear network optimization problems by local reformulations and relaxations. Ph.D. thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (2017)
Mertens, N.: Relaxation Refinement for Mixed Integer Nonlinear Programs with Applications in Engineering. Ph.D. thesis, Technische Universität Dortmund (2019)
Meyer, C.A., Floudas, C.A.: Convex envelopes for edge-concave functions. Math. Program. 103(2), 207–224 (2005). https://doi.org/10.1007/s10107-005-0580-9
Misener, R., Floudas, C.A.: ANTIGONE: Algorithms for coNTinuous integer global optimization of nonlinear equations. J. Global Optim. (2014). https://doi.org/10.1007/s10898-014-0166-2
Rikun, A.D.: A convex envelope formula for multilinear functions. J. Global Optim. 10(4), 425–437 (1997). https://doi.org/10.1023/A:1008217604285
Ruiz, J.P., Grossmann, I.E.: Using redundancy to strengthen the relaxation for the global optimization of minlp problems. Comput. Chem. Eng. 35(12), 2729–2740 (2011). https://doi.org/10.1016/j.compchemeng.2011.01.035
Schmidt, M., Aßmann, D., Burlacu, R., Humpola, J., Joormann, I., Kanelakis, N., Koch, T., Oucherif, D., Pfetsch, M.E., Schewe, L., Schwarz, R., Sirvent, M.: GasLib-a library of gas network instances. Data 2(4), 40 (2017). https://doi.org/10.3390/data2040040
Sherali, H.D., Alameddine, A.: A new reformulation-linearization technique for bilinear programming problems. J. Global Optim. 2(4), 379–410 (1992). https://doi.org/10.1007/BF00122429
Tawarmalani, M.: Inclusion certificates and simultaneous convexification of functions. Math. Program. 5, 94 (2010)
Tawarmalani, M., Sahinidis, N.V.: Semidefinite relaxations of fractional programs via novel convexification techniques. J. Global Optim. 20(2), 133–154 (2001). https://doi.org/10.1023/A:1011233805045
Tawarmalani, M., Sahinidis, N.V.: Convex extensions and envelopes of lower semi-continuous functions. Math. Program. 93(2), 247–263 (2002). https://doi.org/10.1007/s10107-002-0308-z
Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103, 225–249 (2005)
Acknowledgements
Open Access funding enabled and organized by Projekt DEAL. We thank Robert Weismantel for many fruitful discussions on different ideas connected with simultaneous convexification, and the anonymous reviewers for their constructive comments on this paper. The work of the first four authors is part of the Collaborative Research Center “Mathematical Modelling, Simulation and Optimization Using the Example of Gas Networks”. Financial support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) is gratefully acknowledged within Projects A05, B06, B07 and Z01 in CRC TRR 154. The work of the fourth and the fifth author is part of the Collaborative Research Center “Integrated Chemical Processes in Liquid Multiphase Systems”. Financial support by the DFG is gratefully acknowledged through TRR 63. The work of the third author is supported by the DFG within GRK 2297 “MathCoRe”. Furthermore, this research has been performed as part of the Energie Campus Nürnberg and is supported by funding of the Bavarian State Government.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Analysis of the remaining cases from Table 1
1.1.1 Case (1.a)
In this case, \(g_\alpha \) is direction-wise concave w.r.t. components 1 and 2. As our domain D is a box, \(g_\alpha (x)\) is also called edge-concave. Functions with this property and the respective convex envelopes are for example studied in [21].
The generating set of \(g_\alpha \) is given by the four extreme points of the box, i.e.,
The convex envelope is polyhedral and the minimizing simplices are induced by a certain triangulation of the box D. As we deal with a bivariate function, D can be triangulated in only two different ways:
-
1.
Triangulation \(T_1\) is given by the sets \(G_1:=\big \{(l_1,u_2),(l_1,l_2),(u_1,u_2)\big \}\) and
\(G_2:=\big \{(l_1,l_2),(u_1,u_2),(u_1,l_2)\big \}\).
-
2.
Triangulation \(T_2\) is given by the sets \(G_3:=\big \{(l_1,l_2),(l_1,u_2),(u_1,l_2)\big \}\) and
\(G_4:=\big \{(l_1,u_2),(u_1,l_2),(u_1,u_2)\big \}\).
In order to decide which of the two possible triangulations determines the convex envelope, we need to compare the respective values at the center point \(\tfrac{1}{2}(l_1+u_1,l_2+u_2)\) of D (e.g., see [21]). The corresponding possible minimizing segments for the center point are given by
It turns out that
holds for \(x_2 \ge 0\) and that, hence, triangulation \(T_1\) determines the convex envelope. The resulting minimizing simplices are given by \({{\,\mathrm{conv}\,}}(G_1)\) (green region in Fig. 6), \({{\,\mathrm{conv}\,}}(G_2)\) (blue region in Fig. 6) and \({{\,\mathrm{conv}\,}}\big (\{(l_1,l_2),\) \((u_1,u_2)\}\big )\) (red line in Fig. 6).
1.1.2 Case (1.b)
In this case, \(g_\alpha \) is direction-wise concave w.r.t. component 1 and direction-wise convex w.r.t. component 2. The generating set of \(g_\alpha \) is given as
As \(g_\alpha (x)\) is convex on \(\{l_1\} \times [l_2,u_2]\) and \(\{u_1\} \times [l_2,u_2]\) respectively, no minimizing simplex contains more than one point in each of both subsets. Hence, the convex envelope w.r.t. \(\mathfrak {G}[{g_\alpha ,D}]\) consists of minimizing segments of the form \({{\,\mathrm{conv}\,}}\big ((l_1,y_1), (u_1,y_2)\big )\), with \(y_1,y_2\in [l_2,u_2]\). Functions of this type are already studied in the literature (e.g., see [10, 28]).
For a given point \(\bar{x}\), the specific values of \(y_1\) and \(y_2\) are given as the unique minimizer of a univariate optimization problem. They need to satisfy
or either \(y_1\) or \(y_2\) need to lie at the boundary of the interval \([l_2,u_2]\).
Thus, a minimizing segment is either parallel to the vector \(v := \left( 1,-\frac{\alpha _2}{\alpha _2+\alpha _3}\right) \) (red lines in Fig. 7), or is determined by \(y_1 = l_2\) (blue lines in Fig. 7) or by \(y_2 = u_2\) (green lines in Fig. 7).
1.1.3 Case (2.a)
In this case, \(g_\alpha \) is direction-wise convex w.r.t. component 1 and direction-wise concave w.r.t. component 2. The generating set of \(g_\alpha \) is given as
In order to compute the minimizing segments, we use the same arguments as in Case (1.b) with inverted roles of the two coordinates (e.g., see [10]).
As the second derivative of \(g_\alpha \) differs among the two half-spaces \(x_1\le 0\) and \(x_1\ge 0\), we additionally distinguish three possibilities defined by the position of the minimizing segments with respect to these half-spaces. Minimizing segments containing only points with negative values of \(x_1\) are parallel to the vector \(v^1 := \left( \frac{\alpha _2}{\alpha 2-\alpha _1},-1\right) \) (yellow lines in Fig. 8), or defined by the extreme point \((l_1,u_2)\) (green lines in Fig. 8). Segments containing only points with a positive value of \(x_1\) are parallel to the vector \(v^2 := \left( \frac{\alpha _2}{\alpha 2+\alpha _1},-1\right) \) (red lines in Fig. 8) or defined by the extreme point \((u_1,l_2)\) (blue lines in Fig. 8). Minimizing segments containing points from both half spaces are not parallel to each other. For one extreme points \((y_1,u_2)\), the second one is given by \(\left( y_1+\frac{\alpha _2(u_2-l_2)-2\alpha _1y_1}{\alpha _1+\alpha _2},l_2\right) \) (magenta lines in Fig. 8).
1.1.4 Case (2.b.i)
In this case, \(g_\alpha \) is indefinite and direction-wise convex w.r.t. components 1 and 2. We derive a similar result as in Sect. 4.2 for Case (2.b.iii).
Corollary 4
([10]) Let \(\alpha \) be as defined in Case (2.b.i) and let \(G={{\,\mathrm{bd}\,}}(D)\) be the boundary of D. Then we have \(\mathfrak {G}[{g_\alpha ,D}] \subseteq G\) and the convex envelope of \(g_\alpha \) on D consists of minimizing segments w.r.t. G.
Proof
Analogous to Corollary 2. \(\square \)
We divide G into four sets given by
Again, every minimizing segment \(\mathcal {S}_{g_\alpha , G}\,({\bar{x}})\) is defined by its two extreme points \(p^1\) and \(p^2\) with \({p^1 \in G_i}\) and \(p^2 \in G_j\) for some \(i,j \in \{1,2,3,4\}\). We classify the minimizing segments for all possible combinations of i and j (with exploited symmetry). Similar to Sect. 4.2, we can exclude the following “easy” cases.
-
\(i=j\): As \(g_\alpha \) is convex on \(G_k\) for \(k = 1,\dots ,4\), we obtain \(p^1 = p^2 = \bar{x}\) in this case.
-
\((i,j) = (1,3)\): Leads to \(p^1=p^2=(l_1,u_2)\) by considering the concave directions and Observation 2.
-
\((i,j) = (2,4)\): Leads to \(p^1=p^2=(u_1,l_2)\) by considering the concave directions and Observation 2.
-
\((i,j) = (1,4)\): See Case (1.b).
-
\((i,j) = (2,3)\): See Case (2.a).
We consider the combination \((i,j) = (1,2)\) in more detail. Every minimizing segment is defined by two points \(p^1 := (l_1,t)\) and \(p^2 := (q,l_2)\). Furthermore, the following equation
must hold. For \(q<0\) we derive
and for \(q\ge 0\) we derive
Minimizing segments with \(p^1 \in G_3\) with \(p^2\in G_4\) are handled analogously. They are not shown in the figures below in order to keep the presentation clean. Again, we derive a possible minimizing segments for several combinations of \(i,j \in \{1,\dots ,4\}\) and choose the one with the lowest induced value (see Sect. 4.2).
This results in two possible options for the structure of the convex envelope. The first one consists of, roughly speaking, minimizing segments running from the left to the right side of the box D (see Fig. 9). Red and blue lines indicate minimizing segments with extreme points in \(G_1\) and \(G_4\), similar to Case (1.b). Green and magenta lines indicate minimizing segments with extreme points in \(G_1\) and \(G_2\), as distinguished above.
The second option instead consists of, roughly speaking, minimizing segments running from the top to the bottom side of the box (see Fig. 10). Magenta, red and blue lines indicate minimizing segments with extreme points in \(G_2\) and \(G_3\), as described in Case (2.a). Green lines again indicate minimizing segments with extreme points in \(G_1\) and \(G_2\).
1.1.5 Case (2.b.ii)
Function \(g_\alpha \) is convex on D. The convex envelope is given by \(g_\alpha \) itself.
1.1.6 Case (3.a)
As explained in Sect. 4.3, we first derive the convex envelope w.r.t. \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\). In this case, \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is direction-wise convex w.r.t. component 1 and direction-wise concave w.r.t. component 2. We apply a similar approach as in Case (2.a). We again derive the structure of minimizing segments by analyzing the derivatives of \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\).
As a second step, Fig. 11 displays the structure of the minimizing segments w.r.t. \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\gamma _{\scriptscriptstyle {D,i}}[{g_\alpha }]}]\). Green, yellow and blue lines indicate minimizing segments that are determined by the extreme points \((l_1,u_2), (q,l_2)\) and \((u_1,l_2)\) respectively. The red lines indicate minimizing segments parallel to the vector v.
It is
Note that the analysis and visualization only holds for \(\alpha _2 \ge 0\). However, the case of \(\alpha _2 < 0\) is mostly symmetric and can be handled analogously.
1.1.7 Case (3.b.i)
As explained in Sect. 4.3, we first derive the convex envelope w.r.t. \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\). The function \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is indefinite and direction-wise convex w.r.t. components 1 and 2. Hence, we can use the same arguments as in Case (2.b.i) to derive the structure of the of minimizing segments.
As a second step, Fig. 12 displays the structure of the minimizing segments w.r.t. \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\gamma _{\scriptscriptstyle {D,i}}[{g_\alpha }]}]\). Minimizing segments connecting opposite sides are colored in green, yellow and red (similar to Case (3.a)). Magenta and blue lines indicate segments that connect adjacent sides. Note that the analysis and visualization only holds for \(\alpha _2 \ge 0\). However, the case of \(\alpha _2 < 0\) is mostly symmetric and can be handled analogously.
1.1.8 Case (3.b.ii)
As explained in Sect. 4.3, we first derive the convex envelope w.r.t. \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\). The function \(\gamma _{\scriptscriptstyle {D,1}}[{g_\alpha }]\) is direction-wise convex w.r.t. components 1 and 2. Furthermore, it is indefinite for \(x<s\) as motivated in Sect. 4.3. We use the same strategy and the same subdivision of G as in Case (2.b.iii).
As a second step, Fig. 13 displays the structure of the minimizing segments w.r.t. \({{\,\mathrm{vex}\,}}_{\scriptscriptstyle {D}}[{\gamma _{\scriptscriptstyle {D,i}}[{g_\alpha }]}](x)\). Magenta and red lines show segments connecting \(G_1\) and \(G_4\) and yellow lines show segments defined by the extreme point \((l_1,u_2)\). Black dots indicate that the function \(g_\alpha \) coincides with its convex envelope. Note that the analysis and visualization only holds for \(\alpha _2 \ge 0\). However, the case of \(\alpha _2 < 0\) is mostly symmetric and can be handled analogously.
1.2 Cutting plane method
- INPUT: :
-
Box D, Point \(\bar{x} \in D\), Function g
- 1.:
-
Estimate Problem (SP) with Subgradient Method
- 2.:
-
If solution \(< 0\) holds:
- 3.:
-
Derive a supporting hyperplane of \({{\,\mathrm{epi}\,}}\big ({{\,\mathrm{vex}\,}}_D[\alpha ^\top g], D\big )\) at the point \({\big (\bar{x}, {{\,\mathrm{vex}\,}}_D[\alpha ^\top g](\bar{x})\big )}\) (see Sect. 4)
- 4.:
-
Construct a cutting plane (see Proposition 3)
- 5.:
-
Numeric rounding
- OUTPUT: :
-
Cutting Plane
1.3 Subgradient method
- INPUT: :
-
Box D, Point \(\bar{x} \in D\), Function g, Starting Point \(\alpha ^0\)
- 1.:
-
k = 0, iterate until k = n or until no more improvement than \(\mu \) for m iterations
- 2.:
-
Project \(\alpha ^k\) onto the boundary of \(B^3\)
- 3.:
-
Compute the convex envelope of \(g_{\alpha ^k}\), given by some \(\sum \lambda ^i g_{\alpha ^k}(x^i)\)
- 4.:
-
Derive a subgradient \(\nabla g_{\alpha ^k} \sum \lambda ^i \nabla g_{\alpha ^k}(x^i)\)
- 5.:
-
Make a step: \(\alpha ^{k+1} = \alpha ^k + \frac{1}{k} \nabla g_{\alpha ^k}\)
- OUTPUT: :
-
Estimated solution of Problem (SP)
- Parameters: :
-
\(n = 10000,~ \mu = 0.01,~ m = 10/20\) for negative/positive solutions of Problem (SP)
1.4 Computational results with BARON using default settings
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liers, F., Martin, A., Merkert, M. et al. Solving mixed-integer nonlinear optimization problems using simultaneous convexification: a case study for gas networks. J Glob Optim 80, 307–340 (2021). https://doi.org/10.1007/s10898-020-00974-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-020-00974-0