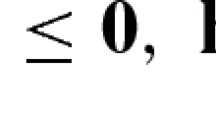Abstract
We present a global optimization algorithm, Branch-and-Sandwich, for optimistic bilevel programming problems that satisfy a regularity condition in the inner problem. The functions involved are assumed to be nonconvex and twice continuously differentiable. The proposed approach can be interpreted as the exploration of two solution spaces (corresponding to the inner and the outer problems) using a single branch-and-bound tree. A novel branching scheme is developed such that classical branch-and-bound is applied to both spaces without violating the hierarchy in the decisions and the requirement for (global) optimality in the inner problem. To achieve this, the well-known features of branch-and-bound algorithms are customized appropriately. For instance, two pairs of lower and upper bounds are computed: one for the outer optimal objective value and the other for the inner value function. The proposed bounding problems do not grow in size during the algorithm and are obtained from the corresponding problems at the parent node.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Real-life decisions are often made hierarchically. For instance, the allocation of resources by a federal government is a multilevel allocation process where one level of government distributes resources to several lower levels of government [20]. The overall objective of such a process is to achieve the goals of the federal government. However, each lower level of government will react independently according to best serving their own interests; these (rational) reactions may be gainful or detrimental to the overall objective. Hence, decision making within such a framework requires careful analysis in order to ensure the best possible outcome for all the decision makers.
The concept of hierarchical decision making, in the presence of two decision makers, namely one leader and one follower, dates back to 1952 when von Stackelberg introduced the basic leader/follower strategy in a duopoly setting. Since then, hierarchical decision making has found application to numerous practical problems across various disciplines, such as economics, management, agriculture, transportation and engineering [19, 39, 48, 53, 65]. Of particular interest are hierarchical systems in parameter estimation [59, 66], environmental policies in biofuel production [10] and chemical equilibria [21, 22].
In this work, we employ the well-known mathematical formulation of a two-level decision making process, known as the bilevel programming problem and propose a new solution strategy for finding global solution(s). Special cases of this problem have been studied extensively and many algorithms have been proposed in the literature [9, 33, 42]. However, the general nonconvex form is a very challenging problem for which only two algorithms exist to the best of our knowledge: the first method for general (nonconvex) bilevel problems developed by Mitsos et al. [60] and the approximation method introduced by Tsoukalas et al. [74].
The optimistic bilevel programming problem is defined as follows:
where \(X\!=\![x^\mathrm{L},x^\mathrm{U}]\subset \mathrm{I\!R}^n, Y=[y^\mathrm{L},y^\mathrm{U}]\subset \mathrm{I\!R}^m, F,f:\mathrm{I\!R}^n \times \mathrm{I\!R}^m \!\rightarrow \! \mathrm{I\!R}, G:\mathrm{I\!R}^n \!\times \! \mathrm{I\!R}^m \!\rightarrow \! \mathrm{I\!R}^o\) and \(g:\mathrm{I\!R}^n \times \mathrm{I\!R}^m \rightarrow \mathrm{I\!R}^r\). Variables \(x\ (y)\) are the outer (respectively inner) decision variables and functions \(G(x,y)\le 0\) \((g(x,y)\le 0)\) are the outer (inner) constraints. Inequality signs in both outer and inner constraints can be replaced by equalities; thus, problem (1) is a generalization of the bilevel problem tackled in [60] where equality constraints, that depend on \(x\) and \(y\), are allowed in the outer but not in the inner problem. Finally, function \(F(x,y)\) \((f(x,y))\) is the outer (inner) objective function. In a leader/follower game framework, the leader is associated with variables \(x\) and chooses his strategy first. The follower responds with a vector \(y\) optimizing his own objective (given \(x\)). Formulation (1) implies that if the follower has more than one global optimal solutions, the leader can choose the one that minimizes his own objective function; hence, the word optimistic applies.
Severe implications stem from the hierarchical structure of bilevel problems, such as nonconvex, disconnected or even empty feasible regions, especially in the presence of outer constraints and nonconvex inner problems. In this paper, we propose a deterministic global optimization algorithm, Branch-and-Sandwich (B&S), based on the refinement of two sets of convergent lower and upper bounds. Namely, valid lower and upper bounds are computed simultaneously for the outer and inner objective values. Their convergence to the corresponding optimal values is proved within a branch-and-bound framework.
The proposed approach makes use of an equivalent formulation of problem (1), where the outer and inner problems are not coupled by the set of optimal solutions of the inner problem but by the inner value function:
In particular, problem (1) can equivalently be written as [31, 80, 81]:
The benefit of the latter formulation is that a restriction of the inner problem (2) yields a relaxation of the overall problem (3) and vice-versa [60]. In view of this observation, we propose the solution of a series of restrictions and relaxations of the inner problem. In particular, in a branch-and-bound framework, we not only construct lower and upper bounding problems for the overall problem (3), but also lower and upper bounding problems for problem (2). Thus, the proposed approach can be interpreted as the exploration of two solution spaces (corresponding to the inner and the outer problems) using a single branch-and-bound tree. To achieve this, the well-known features of branch-and-bound algorithms need to be customised appropriately.
To this end, we first introduce a novel branching scheme such that the hierarchy in the decisions is maintained and the requirement for (global) optimality in the inner problem is not violated. As for the bounding, two pairs of lower and upper bounds are computed: one for the outer optimal objective value and the other for the inner value function. KKT-based relaxations are used to construct the inner upper bounding problem and the outer lower bounding problem. The inner upper bound serves as a constant bound cut in the outer lower bounding problem. These two problems result in convergent bounds on the inner and the outer optimal objective values; they are both nonconvex and must be solved globally, i.e., with classical global optimization techniques,Footnote 1 e.g., [37, 44, 63]. Well-known convexification techniques are employed to construct a convex inner lower bounding problem whose value is used in the selection operation and in fathoming. The outer upper bounding problem is motivated by Mitsos et al. [60], but flexibility is added in that convex relaxations of the original inner problem, i.e., problem (2), over refined subsets of the inner space can be solved. The proposed bounding problems do not grow in size during the course of the algorithm and are obtained from the corresponding problems of the parent node.
The paper is organized as follows: Sect. 2 is devoted to background theory and a discussion of the challenges that need to be addressed. Our bounding ideas are presented in Sect. 3 without considering any branching. Connections to relevant semi-infinite programming literature are also pointed out in this section. The branching scheme is introduced in Sect. 4 and the proposed bounding problems are modified to allow branching. The overall algorithm is presented in Sect. 5 and conclusions are presented in Sect. 6.
2 Background theory
2.1 Definitions, notations and properties
To start with, the expressions relaxation and restriction are briefly explained below.
Definition 1
A relaxation (restriction) of a minimization problem is another minimization problem with (i) an objective function always lower than or equal to (greater than or equal to) the original objective function,Footnote 2 and with (ii) a feasible region that is a superset (subset) of the original’s problem feasible region.
A well-known relaxed problem associated with the bilevel problem (1) is [77]:
In other words, the relaxed feasible regionFootnote 3 of the bilevel program (1) is:
and by solving relaxation (4) one can obtain a valid lower bound on the global optimal value of the bilevel program (1). However, such a lower bound is not convergent as pointed out in [60], i.e., it cannot lead to a globally convergent algorithm even if exhaustive space partitioning was performed. For each \(x \in X\), the lower level feasible set is:
Then, the reaction set of the follower, namely the set of optimal solutions to the inner optimization problem (2), parameterized on \(x\), is:
Using the notation above, the bilevel problem in its most general form is:
However, in formulation (8), there exists a certain ambiguity that concerns the minimization with respect to \(x\) when the reaction set \(O(x)\) is not reduced to a singleton for each \(x \in X\). Thus, in the presence of non-uniquely determined lower level solutions, two alternative formulations can be employed: (i) the optimistic or weak formulation, e.g., [9, 28], where the follower is assumed to choose the solution in \(O(x)\) that better serves the leader’s objective, and (ii) the pessimistic or strong formulation, e.g., [49–51, 75], where the leader has to consider the worst solution in \(O(x)\) with respect to his/her objective. Both approaches require the optimization with respect to \(x\) of a nonsmooth, often discontinuous, function [28]:
in the optimistic approach, and
in the pessimistic approach. The optimistic formulation always provides a lower (optimistic) bound for the pessimistic formulation, but when the reaction set of the follower is indeed a singleton, the two formulations are equivalent. This is the case for example, if \(f(x,\cdot )\) and \(g(x,\cdot )\) are strictly convex and quasi-convex in their second argument, respectively, for every \(x \in X\).
The limitation of the optimistic approach is that it violates the basic assumption of noncooperation. However, there are several applications where limited cooperation is permitted and \(\varepsilon \)-optimal solutions, using the optimistic approach, are appropriate, such as applications in the management of multi-divisional firms [6]. On the other hand, there exist instances for which cooperation is ruled out and the use of the pessimistic approach is more realistic, such as applications in production planning [8]. Alternatively, if one wishes to avoid using either approach, a regularization approach can be employed that bypasses the difficulties of non-uniquely determined lower-level solutions [27]. The problem of tackling the pessimistic or regularized approaches is outside the scope of this work. However, we briefly mention that the extension of B&S to the pessimistic approach does not appear to be straightforward due to two main reasons: (i) the use of the equivalent optimal value reformulation is no longer possible in the pessimistic approach; (ii) the proposed branching scheme that entails branching on \(y\) may have serious implications on the worst-case (\(\max \) with respect to \(y\)) outer objective and needs to be thoroughly investigated. On the other hand, it appears that B&S can trivially be applied to the regularized approach.
Finally, problem (8) is related to many well-known optimization problems, such as multi-objective optimization problems [53], max-min problems [4, 34, 35, 73, 74, 78], MPEC [25, 62], and (usual or generalized) semi-infinite optimization problems [14, 15, 38, 61, 67, 74]. Many of these problems are known to be \(\textit{NP}\)-hard which implies that the bilevel problem is also \(\textit{NP}\)-hard [32].
2.2 Optimistic bilevel programming problems
From this point onward, we focus on the optimistic approach and, for simplicity, the word “optimistic” will be omitted. Bilevel programming problems are then written as in problem (1) or, using the notation introduced in Sect. 2.1, as follows:
In order to write problem (1) as an equivalent single-level mathematical programming problem, most of the algorithms for bilevel problems, e.g., [5, 7, 79], have focused on cases where the inner problem is convex and has a unique optimal solution for all values of \(x\) such that it can be replaced by its KKT necessary and sufficient optimality conditions. This results in the well-known KKT reformulation:
The use of the KKT inner optimality conditions also assumes the satisfaction of an appropriate constraint qualification,Footnote 4 such as the Mangasarian-Fromowitz constraint qualification (MFCQ), the linear independence constraint qualification (LICQ), as well as the Cottle, Abadie, Kuhn-Tucker, Zangwill, Arrow-Hurwicz-Uzawa and Slater constraint qualifications [11, 12]. Reviews on methods that employ the equivalent KKT reformulation can be found in [23, 29, 77], as well as a plethora of references therein. On the other hand, when problem (2) has more than one solution for at least one value of \(x\), the KKT conditions are not sufficient. Replacing the inner problem by its KKT necessary optimality conditions, provided that an appropriate constraint qualification holds for all values of \(x\), results in reformulation (12) being only a relaxation of the original bilevel problem (1) [54, p. 13].
An alternative way to reformulate problem (1) as a one-level problem such that equivalence is retained without any regularityFootnote 5 or convexity assumptions whatsoever, is to employ the optimal value equivalent reformulation (3). This reformulation has several advantages that make it preferable to formulation (11). One is that it couples the outer and the inner problems via the value function \(w(x)\), as opposed to the set of optimal solutions \(O(x)\); this is useful because even in the presence of infinitely many global optima of the inner problem, the optimal objective value is unique [60]. Moreover, formulation (3) makes it possible to use standard analysis to derive conditions that guarantee the existence of optimal solutions in (1), such as [26]:
-
A1:
All the functions involved, i.e., \(F(\cdot ,\cdot )\), \(G(\cdot ,\cdot )\), \(f(\cdot ,\cdot )\), \(g(\cdot ,\cdot )\), are lower semicontinuous (l.s.c.) on \(X\times Y\); and,
-
A2:
the set \(\{(x,y) \in X \times Y \mid f(x,y) \le w(x)\}\) is compact.
Formulation (3) was employed in the first algorithm for optimistic bilevel optimization problems with a nonconvex inner problem [60]. In [60], Mitsos et al. first described a specific instance of their proposed algorithm where branching is not required and then extended this version to a generalized algorithm in a branching framework.Footnote 6 For the former, a bounding procedure for problem (3) was introduced based on the algorithm by Blankenship and Falk [16] for semi-infinite programs. In particular, they proposed a parametric upper bound on the value function such that iteratively tighter lower bounds are constructed with the addition of more and more parametric upper bound cuts until the relaxed problem converges to the original problem. For the upper bounding procedure, a feasible solution to problem (1) was derived by fixing \(x\) in (3) and by allowing an \(\varepsilon _f\) violation in the inner objective value. Similar ideas were discussed independently in [72]. In our paper, formulation (3) is also employed in developing the proposed algorithm.
Definition 2
(\({{\varepsilon }}\) -Optimal solution [60]) Let \(\varepsilon _F\) and \(\varepsilon _f\) be given and fixed optimality tolerances for the outer and the inner problems, respectively. Then, a pair \((x^*,y^*) \in X\times Y\) is called an \(\varepsilon \)-feasible solution of problem (1)—and of (3)—Footnote 7if it satisfies the constraints of the inner and outer problems, as well as \(\varepsilon _f\)-optimality in the inner problem:
An \(\varepsilon \)-feasible point is called \(\varepsilon \)-optimal if it satisfies \(\varepsilon _F\)-optimality in the outer problem:
where \(F^*\) denotes the outer optimal objective value, i.e., the optimal objective value of the bilevel problem (1) and of its equivalent single-level problem (3).
Remark 1
For an \(\varepsilon \)-optimal pair, as defined in Def. 2, we also use the notation \(f^*\) to refer to the corresponding inner optimal objective value, namely, \(f^* = w(x^*)\) in (15).
Remark 2
Notice that \(\varepsilon _f\) is an optimality tolerance from the perspective of the inner problem. However, it can also be interpreted as a feasibility tolerance (for one of the constraints) from the perspective of the overall problem (3).
Remark 3
In this paper, our aim is to compute \(\varepsilon \)-optimal solutions as defined in Def. 2. This implies that we apply \(\varepsilon _f\)-optimality in the inner problem throughout the paper.
The following assumptions are also made throughout the paper.
Assumption 1
All the functions involved, i.e., \(F(\cdot ,\cdot )\), \(G(\cdot ,\cdot )\), \(f(\cdot ,\cdot )\), \(g(\cdot ,\cdot )\), are continuous on \(X\times Y\).
Assumption 2
The sets \(X\) and \(Y\) are compact.
Assumption 3
All the functions involved, i.e., \(F(\cdot ,\cdot )\), \(G(\cdot ,\cdot )\), \(f(\cdot ,\cdot )\), \(g(\cdot ,\cdot )\), are twice continuously differentiable on \(X\times Y\).
Assumption 4
A constraint qualification holds for the inner problem (2) for all values of \(x\).
Observe that no convexity assumptions are made. Note also that Assumption 1 is implied by Assumption 3, but is given explicitly to highlight the role of each assumption. Assumptions 1–2 guarantee that there exists a pair \((x^*,y^*)\) satisfying \(\varepsilon \)-optimality based on Def. 2. Assumption 3 is needed to make it possible to apply convexification and semi-infinite programming techniques, as discussed in the next section. Finally, Assumption 4 ensures that the KKT conditions for problem (2) can be employed and are necessary [12]. Then, if we replace \(y \in Y\) by the corresponding bound constraints: \(y^\mathrm{L} \le y\le y^\mathrm{U}\), and assign Lagrange multipliers \(\mu \in \mathrm{I\!R}^r\) to the inner constraints and \(\lambda ,\nu \in \mathrm{I\!R}^m\) to the bound constraints, the first-order conditions of problem (2) define the set below:

where InKKT\(_{0}\) stands for Inner KKT conditions and the zero subscript is used to denote that the calculations are done over the whole \(X\times Y\) domain, i.e., at the root node.
Remark 4
With regards to Assumption 4, if, for instance, the MFCQ is assumed (without reference to a point), then we assume that it is valid at each local minimizer of problem (2). Then, \(y \in O(x)\) implies that there are vectors \(\mu ,\lambda ,\nu \) such that \((x,y,\mu ,\lambda ,\nu ) \in {\varOmega }_\mathrm{KKT}\) [28].
Remark 5
Assumption 4 is a mild but essential assumption. Violation of this assumption (a constraint qualification may not be satisfied for all values of \(x\)) may result in an undesirable outcome, such as an infeasible outer lower bounding problem (\(\mathrm{LB}_{0}\)) (cf. Sect. 3) whilst the original bilevel problem possesses an optimal solution [30]. The implications of lack of regularity are discussed in detail in [46].
In the present work and the companion paper [47], all test problems considered satisfy Assumption 4. In particular, either the Abadie or the linear/concave constraint qualification holds [12, 58].
2.3 Challenges
There are several important challenges one needs to overcome when considering bilevel optimization problems with a nonconvex inner problem. One challenge is related to the difficulty of creating convergent lower bounding problems since deriving an equivalent one-level formulation, as is possible with convex inner problems, is no longer feasible. The second important challenge stems from the need to identify correctly the global solution(s) of a nonconvex inner problem and thus derive valid bounds on its optimal objective value. For instance, solving a nonconvex inner problem locally or partitioning the inner space and treating each subdomain independently of one another may lead to invalid solutions/bounds. An analytical discussion on these issues can be found in [57]. Here, we consider an example from [58], to visualize these challenges.
Example 1
(Example 3.5 [58])
As can be verified in Fig. 1a, the global optimal solution of the inner problem is at \(y=0.5\). The inner problem also has two local optimal solutions: a local minimum at \(y=-0.5\) and a local maximum at \(y=-0.0938\). However, by the definition of the bilevel problem, only \(y=0.5\) is feasible in Example 1; hence, the example has a unique optimal solution at \(y^*=0.5\) with optimal objective value \(F^*=0.5\). Next, assume that we partition the inner space and deal with the two following inner subproblems independently in e.g., a branch-and-bound scheme.
As shown in Fig. 1b, c, the first subproblem would give \(y^{(1)}=-0.5\) with corresponding outer objective value \(F^{(1)}=-0.5\), while the solution of the second subproblem would be \(y^{(2)}=0.5\) with corresponding outer objective value \(F^{(2)}=0.5\). Comparing the outer objective values, \(F^{(1)}\) appears to be more promising and one could be drawn to the false conclusion that \(y^{(1)}=-0.5\) is the solution when it is not even feasible in the original problem. Similarly, if one applies a local algorithm on the inner problem of the example, again there exists the risk of reporting a false solution corresponding to a local optimal solution of the inner problem. Based on these observations, Mitsos et al. [60] and Tsoukalas [72] suggest that the inner problem should always be solved to global optimality and over the whole of \(Y\), i.e., that no partitioning of the inner space should be allowed in the construction of the overall lower bounding problem.
To explore the difficulties in constructing lower bounding problems that lead to convergent algorithms, let us write the well-known relaxed problem as shown in (4) for the example:
The relaxed problem has optimal objective value equal to \(-1\), i.e., strictly less than the actual optimal value \(F^*=0.5\), and this cannot be improved unless we either branch on \(y\) or add more constraints. In this vein, the authors in [60, 72] employed formulation (3), in which they relaxed the non-smooth constraint \(f(x,y)\le w(x)\) by introducing parametric-in-\(x\) upper bound cuts on the inner value function \(w(x)\). In line with the well-known algorithm by Blankenship and Falk [16], the progressive addition of these cuts makes the relaxed problem convergent [60].
In this work, with regards to the challenge of ensuring the global optimality of the inner problem solution, we pursue partitioning of the inner space by considering the “whole” inner space for successively refined subdomains of \(X\). With the use of quotes to refer to the “whole” inner space, we imply that either the whole of \(Y\) or a proper subdomain of \(Y\) is considered. The latter case occurs because some \(Y\) subdomains are eliminated at some point due to fathoming (cf. Sect. 4.6) with a guarantee not to miss any regions where inner global optimal solutions lie (cf. Lemma 2). As a result, the inner space \(Y\) is successively refined (for successively refined subdomains of \(X\), cf. Sect. 4.1) and flexibility is gained, since we can solve subproblems of the inner problem over the refined subsets of \(Y\), i.e., :

using one of the following three approaches: (i) solve globally, which is cheaper than solving globally over a large domain, e.g., over the whole \(Y\); (ii) convexify and solve with a local algorithm, which has low computational cost; (iii) solve globally to very loose convergence, which is relatively cheap and helps improve the bounds at relatively low cost. None of these three approaches compromise the ability of the algorithm to converge. Moreover, they can readily be combined in the form of a hybrid approach. The relative merit of these different approaches is not explored in this paper, as the focus is on the overall algorithmic framework rather than detailed computational performance.
To deal with the challenge of generating a convergent overall lower bounding problem, we introduce a constant upper bound cut on the inner value function \(w(x)\). The right hand side of the cut is tightened when appropriate, resulting in one cut only each time the lower bounding problem is solved. Such a formulation results in a significant simplification compared to the lower bounding problem presented in [60].
3 Bounding scheme: initial node
The proposed bounding scheme applies to formulation (3) and is based on the fact that a relaxed inner problem yields a restriction of the overall problem (3) and a restricted inner problem yields a relaxed overall problem. In view of the above, we create two auxiliary inner problems, i.e., the auxiliary relaxed and restricted inner problems, whose objective values are always lower and upper bounds, respectively, on the inner optimal value for the domain of interest. We then apply appropriate techniques to solve these problems efficiently. In particular, for the auxiliary relaxed inner problem we apply classical convexification techniques [36, 71] to construct and solve a convex problem. For the auxiliary restricted inner problem, we apply generalized semi-infinite programming techniques [41, 69] to reduce it to a finite problem. The resulting problem is nonconvex; hence, we can either solve a convex relaxation or solve it directly to global optimality.
The resulting bounds on the inner optimal objective value are employed in the classical sense to prune branches from the branch-and-bound tree. Furthermore, the inner upper bound is also used in the bounding scheme for the outer problem. Specifically, it is used to construct a constant upper bound cut to augment the overall lower bounding problem.
Remark 6
Recall that in this section, we develop our bounding ideas over the whole \(X\times Y\) space; hence, we use the zero subscript in the problem names to denote that the calculations are done over the whole \(X\times Y\) domain, i.e., at the root node. The proposed bounding problems of this section are employed in Step 1 of the B&S algorithm (cf. Sect. 5). To allow branching, modifications of these problems over subdomains of \(X \times Y\) are discussed in Sect. 4, after our branching scheme is introduced.
3.1 Inner problem bounding scheme
Inner lower bounding problem The auxiliary relaxed inner problem is:

which we tackle by following the ideas on constructing convex underestimators of nonconvex functions developed in [1, 3, 52], although any convex relaxation scheme can of course be used (e.g., [36, 71]). In particular, let \(\breve{f}_{X,Y}(x,y)\) and \(\breve{g}_{X,Y}(x,y)\) represent convex underestimators of functions \(f\) and \(g\) on \(X\times Y\), respectively. Then, we may construct a convex auxiliary problem whose optimal value is always a lower bound on the optimal value of (2) for all \(x \in X\):

since for any \(\bar{x} \in X\) the following holds:
where \(w(\bar{x})\) is the optimal value of (2) with \(x=\bar{x}\). Consequently, for \(x = x^*\), corresponding to the optimal solution for \(x\) of the bilevel problem, we have:
Remark 7
We support our choice of minimizing with respect to both the inner and outer variables in (\(\mathrm{ILB}_{0}\)) by showing that fixing the outer variables and minimizing with respect to the inner variables would yield an invalid lower bound. Let \(f(x,y) = x^2 y + \sin y\) for \(x \in [0,1]\) and \(y \in [1,6]\). The optimal point is \((x^*,y^*)=(0,4.7124)\) with (inner) objective value \(f^* = -1\). As Fig. 2a illustrates, if we fix \(x\), e.g., \(\bar{x}=1\), and compute the minimum of the function \(f(\bar{x},y)\), the resulting optimal objective value is \(f'= 1.8415\) at \(y=1\) which is not a valid lower bound for all \(x \in [0,1]\).
Inner upper bounding problem In the same vein as in (\(\mathrm{ILB}_{0}\)), the auxiliary restricted inner problem is:

which has an objective value always greater than or equal to the optimal value \(f^*\) of the inner problem:
Hence, \(f^\mathrm{U} \ge w(x)\) for all \(x \in X\). As a result, \(f^\mathrm{U} \ge w(\bar{x})\) for an \(\bar{x}\in X\). Consequently,
One can observe that the problem above is a nonconvex max-min problem, and thus it is almost as hard as the original bilevel problem [35]. However, as our method only requires a valid inner upper bound, creating and solving a tractable relaxation is enough to overcome the difficulty of the max-min problem. To derive a tractable relaxation of problem (\(\mathrm{IUB}_{0}\)), we employ the KKT-approach as described in [70]. In particular, we first reformulate the problem into its equivalent generalized semi-infinite program:
where \(Y(x)\) is defined as in (6). Problem (20) is also equivalent to the following bilevel problem [67]:
where
Based on Assumption 4 being true, if we replace the lower level optimization problem (22) by its (necessary) KKT conditions, we obtain a relaxation of (21). It is clear by (22) and (InKKT\(_{0}\)) that the first-order conditions of (22) coincide with the KKT conditions of the original inner problem (2).Footnote 8 A finite problem approximating problem (21), and equivalently (20) and (\(\mathrm{IUB}_{0}\)), is:

Problem (\(\mathrm{RIUB}_{0}\)) gives an upper bound on the objective value of (\(\mathrm{IUB}_{0}\)) [68]:
and, by (19), a valid upper bound on \(f^*\). Alternatively, one can explore the use of parametric concave overestimators [61] to derive tractable relaxations for problem (\(\mathrm{IUB}_{0}\)), but such an exposition is beyond the scope of the present article.
Remark 8
Notice that solving problem (\(\mathrm{RIUB}_{0}\)) to local optimality is not enough to guarantee a valid upper bound on the value of (\(\mathrm{IUB}_{0}\)). Let \((x_\mathrm{u},y_\mathrm{u})\) be an optimal solution to problem (\(\mathrm{IUB}_{0}\)). Then, let \((\bar{x_0},\bar{x},\bar{y})\) be a locally optimal point in (\(\mathrm{RIUB}_{0}\)) and \(\bar{f}_{loc}\) be the corresponding objective value. Such a point may be infeasible in (20) (and in (21)). Namely, it could happen that
and thus may yield an upper bound on \(f^\mathrm{U}\), i.e., \(f^\mathrm{U}\le \bar{f}_{loc}\). If \((\bar{x}_0,\bar{x},\bar{y})\) is feasible in (20) (and in (21)), then \((\bar{x},\bar{y})\) is feasible in (\(\mathrm{IUB}_{0}\)) so that \(\bar{f}_{loc}=w(\bar{x})\). Nevertheless, this value of \(\bar{f}_{loc}\) is only a valid upper bound if \(\bar{x}=x_\mathrm{u}\); otherwise,
as is clear by (19). On the other hand, if \((\bar{x_0},\bar{x},\bar{y})\) is a globally optimal point in (\(\mathrm{RIUB}_{0}\)) and \(\bar{f}_{glob}\) is the corresponding objective value, then by similar arguments, infeasibility of the point in (20) (and in (21)) implies \(f^\mathrm{U}\le \bar{f}_{glob}\), whilst its feasibility in (20) (and in (21)) implies \(f^\mathrm{U} = \bar{f}_{glob}\). As a result, solving problem (\(\mathrm{RIUB}_{0}\)) to global optimality or further convexifying it and solving it with a local algorithm is essential to guarantee a valid inner upper bound.
Remark 9
The choice of maximizing with respect to the \(x\) variables in (\(\mathrm{IUB}_{0}\)) is supported by showing that using a feasible point \((\bar{x},\bar{y}) \in {\varOmega }\), such that \(\bar{y} \in O(\bar{x})\), would not yield a valid inner upper bound. Let \(F(x,y)=x^2+y\) and \(f(x,y) =\frac{y^2}{x}\), where \(x \in [1,4]\) and \(y \in [2,4]\). The optimal point is \((x^*,y^*)=(1,2)\) with (inner) objective value \(f^* = 4\). As Fig. 2b demonstrates, if we fix \(x\), e.g., \(\bar{x} = 2\), implying \(\bar{y}=2\), the resulting objective value is \(f'= 2\), which is not a valid inner upper bound.
3.2 Overall problem bounding scheme
Lower bounding problem The proposed lower bounding problem is:

where \({\varOmega }_\mathrm{KKT}\) is defined in (InKKT\(_{0}\)). To show that (LB\(_0\)) is a relaxation of (1), consider a feasible point \((\bar{x},\bar{y})\) in (1). Then, \(G(\bar{x},\bar{y})\le 0,g(\bar{x},\bar{y})\le 0\) and \(f(\bar{x},\bar{y})\le \bar{f}\) by (19) and (23). Based on Assumption 4 being satisfied, \(\bar{y} \in O(\bar{x})\) implies that \((\bar{x},\bar{y}) \in {\varOmega }_\mathrm{KKT}\) and we can conclude that \((\bar{x},\bar{y})\) is feasible in (LB\(_0\)), implying that the feasible region of (LB\(_0\)) contains that of problem (1). In the same vein as in Remark 8, problem (LB\(_0\)) must be solved to global optimality.
Upper bounding problem For the overall upper bounding problem, we first require to solve the following problem:

where \(\bar{x}\) comes from the solution of the lower bounding problem (LB\(_0\)) and \(\breve{f}_y(x,y)\) and \(\breve{g}_y(x,y)\) denote convex underestimators over \(Y\) of, respectively, \(f(x,y)\) and \(g(x,y)\). The value \({{\underline{w}}}(\bar{x})\) then augments the proposed upper bounding problem:

where \(\varepsilon _f\) is the inner objective optimality tolerance. Problem (\(\mathrm{UB}_{0}\)) is based on the upper bounding problem introduced in [60]. However, in the present article, \({{\underline{w}}}(\bar{x})\) has replaced \(w(\bar{x})\) in the original formulation. The use of the former value is not possible in the original formulation in [60] because the (nonconvex) inner problem should always be solved over the whole \(Y\) domain. On the other hand, the partitioning of \(Y\) in our work allows solving convex relaxations of the inner problem over refined \(Y\) subdomains. This implies that after finitely many steps in the branch-and-bound tree we have \({{\underline{w}}}(\bar{x})=w(\bar{x})\) within a given accuracy, for a given \(\bar{x}\), provided that a convergent scheme of underestimators is used as in any branch-and-bound method [45]. For instance, the \(\alpha \)BB convex lower bounding functions [1, 2], that we employ in this work, are quadratically convergent to the corresponding nonconvex functions [17, 52].
A feasible point \(\bar{y}\) in (\(\mathrm{UB}_{0}\)), if it exists, is \(\varepsilon \)-feasible in (1). This is true because \(\bar{y}\) then satisfies the following: \(G(\bar{x},\bar{y})\le 0\) (outer feasibility), \(g(\bar{x},\bar{y})\le 0\) (inner feasibility) and
On the other hand, inner feasibility implies that
By construction, we also have
Eq. (27) with inner and outer feasibility implies that conditions (13)–(15) are true; hence, based on Def. 2, \((\bar{x},\bar{y})\) is \(\varepsilon \)-feasible in (1). Consequently, if a feasible solution of (\(\mathrm{UB}_{0}\)) indeed exists, it provides a valid upper bound on the optimal objective value of the bilevel problem (1). This value is used to set the incumbent value \(F^\mathrm{UB}\), corresponding to the best feasible solution found so far, i.e., the incumbent solution, determined in terms of outer objective function value. If (\(\mathrm{UB}_{0}\)) is infeasible, the incumbent value is initialized to infinity:
Connection to the semi-infinite programming (SIP) literature: For highly nonconvex functions, strict inequality may hold in Eq. (26), resulting in an infeasible restricted approximate problem (\(\mathrm{UB}_{0}\)). To obtain better relaxations for the inner problem for fixed \(x\), one has to partition the inner space as required to achieve equality in Eq. (26) for some \(\bar{x}\) value (cf. Sect. 4.7 and Remark 18).
The issue of a potential infeasible restricted approximate problem has also been encountered when applying convexification/approximation techniques to the nonconvex lower level problem of a semi-infinite programming (SIP) problem [14, 15, 38, 56, 61]. In these works, the existence of SIP-Slater points (cf. [56, Def. A.1]) is assumed in order for the approximate problem to be guaranteed to provide a feasible point in the original SIP problem after a suitably refined subdivision of the inner space.
Although subdivision is required in the existing approaches for the approximate lower level problem to converge to the actual problem, no branching with respect to \(y\), as the lower level variable, is permitted. Hence, the whole inner space is always considered and no (inner) subregion can be fathomed. As a result, a growth in problem complexity with the number of subdivisions is unavoidable.
In our approach, it is possible to consider only some subregions of \(Y\) and eliminate others via fathoming. This is discussed in the next section.
4 Branching scheme and bounding on subdomains
Employing the bounding scheme discussed in Sect. 3, we develop a branch-and-bound algorithm that yields valid bounds for both the inner problem (2) and the overall problem (3) over successively refined partitions of the \(X\times Y\) space. Necessarily, the branching framework for bilevel problems must differ from that for single level problems due to their hierarchical structure. In particular, it has been argued that branching on the inner variable may yield an invalid solution [57, 60, 72]. This is due to the sequential decision making underlying bilevel optimization, that implies the leader committing first and then the whole space \(Y\) being considered to ensure global optimality in the inner problem [57, 72]. However, Mitsos et al. [60] support branching on \(y\) by introducing dummy variables \(z\) in place of \(y\) in the inner problem. Thus, branching is permitted on \(y\), the outer variable, but not permitted on \(z\), the inner variable.
In this work, we pursue a different strategy, in order to permit branching on \(y\), without the need to introduce artificial inner variables. This is achieved by branching on the inner variable as normal, namely making no distinction between the inner and outer variables during branching, but at the same time considering the “whole” \(Y\) via appropriate management of nodes (cf. Sect. 4.1 on list management). This is achieved by introducing a novel branching scheme that allows exhaustive partitioning of the domain \(X\times Y\) for general bilevel problems. The main idea is to maintain several (sub)lists of nodes with special properties in addition to the classical universal list of unfathomed nodes \(\mathcal{L}\). These lists will allow us to examine the “whole” \(Y\) for different subsets of \(X\) despite \(Y\) also being partitioned.
In addition to how the lists of nodes are managed, most properties of a classical branch-and-bound method are affected by allowing partitioning of the inner space. In the forthcoming subsections we develop key steps of the B&S algorithm and show how these ensure that (i) the subdivision process is exhaustive, (ii) the proposed overall lower bounding problem is monotonically improving, (iii) the node fathoming rules discard redundant regions safely, and (iv) the incumbent solution corresponds to a feasible point of (1).
4.1 List management
The crux of the proposed branching scheme is the use of additional lists of nodes over and above the classical list of open nodes \({\fancyscript{L}}\). By “open” nodes we refer to nodes that can be explored further. In the context of our solution method, open nodes in \({\fancyscript{L}}\) correspond to the outer (overall) problem. Nodes that are removed from this list because they are known not to contain the global solution of the bilevel problem are either fully fathomed or outer fathomed within the B&S algorithmic framework. In the former case, it is implied that these nodes need not be explored further in any space, outer or inner; hence, they are deleted from \({\fancyscript{L}}\). In the latter case, it is implied that the nodes are no longer needed for the outer problem but cannot yet be discarded fully from the branch-and-bound tree, because they may contain a globally optimal solution for the inner problem for a subdomain of \(X\) which has not yet been fathomed. For those nodes that are discarded from the overall problem but remain open with respect to the inner problem, we maintain another list of nodes, the so-called list of inner open nodes \({\fancyscript{L}}_\mathrm{In}\), which contains nodes that may be explored further with respect to the inner space only. We also refer to list \({\fancyscript{L}}_\mathrm{In}\) as the list of outer-fathomed nodes, implying that these nodes have been deleted from \({\fancyscript{L}}\). The rules used to determine which nodes are either fully or outer fathomed from \({\fancyscript{L}}\) are stated in Sect. 4.6.
Remark 10
A node that has not yet been fully fathomed belongs either to list \({\fancyscript{L}}\) or to list \({\fancyscript{L}}_\mathrm{In}\). Lists \({\fancyscript{L}}\) and \({\fancyscript{L}}_\mathrm{In}\) never have common nodes, i.e., \({{\fancyscript{L}}} \cap {\fancyscript{L}}_\mathrm{In}=\emptyset \).
Definition 3
(Node) A node \(k \in {{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In}\) represents (sub)domain
The root node is the node with \(k=1\) and corresponds to the whole domain \(X\times Y\).
We now introduce \({{\fancyscript{X}}}_p\), which denotes a subdomain of \(X\) throughout the rest of the paper. Let \(P\) be a finite index set and \(\{{{\fancyscript{X}}}_p\subseteq X:p \in P\}\) be a partition of \(X\):
where \(\partial {{\fancyscript{X}}}_{p}\) denotes the (relative) boundary of \({{\fancyscript{X}}}_{p}\) [45, Def. IV.1.]. In the B&S framework, in addition to lists \({\fancyscript{L}}\) and \({\fancyscript{L}}_\mathrm{In}\), we assign one auxiliary list \({{\fancyscript{L}}}^{p}\) to each member set \({{\fancyscript{X}}}_p\) of the \(X\) partition.Footnote 9 Moreover, each list \({{\fancyscript{L}}}^{p}\), \(p \in P\), consists of a collection of sublists:
The lists \({{\fancyscript{L}}}^{p}\), \(p \in P\), are pairwise disjoint and, for this reason, are referred to as independent:
For instance, consider the four partitioning examples of a two-dimensional space \(X\times Y\) in Fig. 3. The corresponding independent lists and their sublists are identified in Tables 1 and 2, respectively.
Example of partitions for \(X=[-1,1]\) and \(Y = [-1,1]\). All (sub)lists are shown in Tables 1 and 2. Briefly, a \(X = {{\fancyscript{X}}}_1\): one independent list with two sublists; b \(X = {{\fancyscript{X}}}_1 \cup {{\fancyscript{X}}}_2\): two independent lists with one sublist each; c \(X = {{\fancyscript{X}}}_1 \cup {{\fancyscript{X}}}_2\): one independent list with two sublists and one independent list with one sublist; d \(X = {{\fancyscript{X}}}_1 \cup {{\fancyscript{X}}}_2 \cup {{\fancyscript{X}}}_3\): three independent lists with one sublist each. On each diagram, the use of the same pattern for several rectangles denotes nodes that belong to the same independent list
To generate list \({{\fancyscript{L}}}^{p}\), corresponding to set \({{\fancyscript{X}}}_{p}, p \in P\),we first generate sublist(s)
such that
where \(\mathrm {ri}(\cdot )\) denotes the (relative) interior of a set [18]. The meaning of Eqs. (33)–(34) is that every sublist contains nodes with overlapping \(X\) subdomains but non-overlapping \(Y\) subdomains. In particular, every sublist \({{\fancyscript{L}}}^{p}_s\), \(s \in 1,\ldots ,s_p\), must represent a \(Y\) partition. Namely, the collection of subdomains \(\{Y^{(k)}\}\), \({k \in {{\fancyscript{L}}}^{p}_s}\), is a partition of \(Y\) for each \(s \in 1,\ldots ,s_p\). Also, every node in \({{\fancyscript{L}}}^{p}\) has to be in at least one \(Y\) partition.
This requirement can be visualized in Fig. 3, where for a member set \({{\fancyscript{X}}}_p, p \in P\), more than one sublist may satisfy (32)–(34), i.e., \(s_p\ge 1\), and a given node can appear in more than one sublist. In particular, in Fig. 3a, \({{\fancyscript{X}}}_1\) has two sublists, \({{\fancyscript{L}}}^1_{1}\) and \({{\fancyscript{L}}}^1_{2}\), and node \(2\) belongs to both sublists. This is necessary to ensure that each sublist represents a \(Y\) partition.
Remark 11
To recapitulate, each independent list \({{\fancyscript{L}}}^{p}\), \(p \in P\), covers all \(x\) values in the member set \({{\fancyscript{X}}}_p\) of the \(X\) partition, and the “whole” \(Y\) as a collection of \(s_p\) \(Y\) partitions:Footnote 10
In other words, in the B&S framework, the set \(\{{{\fancyscript{X}}}_p:p \in P\}\) cannot be any \(X\) partition, but has to satisfy the requirement that for all \(x \in {{\fancyscript{X}}}_p\) the “whole” \(Y\) is maintained. This requirement is met via the management of the independent lists (30) and their sublists (32).
Finally, let us consider list \({{\fancyscript{L}}}^{p}\), \(p \in P\), and branch on some of its nodes. If, after the partitioning of nodes, there exist index sets \(I\) and \(J\) such that:
this means that list \({{\fancyscript{L}}}^{p}\) can be replaced by two (new) independent lists \({{\fancyscript{L}}}^{p_1}\) and \({{\fancyscript{L}}}^{p_2}\) corresponding to refined subdomains \({{{\fancyscript{X}}}_{p_1}}\) and \({{{\fancyscript{X}}}_{p_2}}\), respectively, that form a partition of \({{{\fancyscript{X}}}_{p}}\). The new independent lists are:
where \(p_1:=p\) and \(p_2:=|P| + 1\). We refer to condition (IC) as the independence condition because it implies that sets \(\{{{\fancyscript{L}}}^p_i : i \in I \}\) and \(\{{{\fancyscript{L}}}_j^p : j \in J\}\) cover no overlapping \(X\) subdomains, i.e., they have become independent. The dimension of \(P\) is increased:
For example, list \({{\fancyscript{L}}}^1\) in Fig. 3a is replaced by lists \({{\fancyscript{L}}}^1\) and \({{\fancyscript{L}}}^2\) in Fig. 3b after branching on the \(X\) space.
Remark 12
A node \(k\) not yet fully fathomed must belong to an independent list \({{\fancyscript{L}}}^{p}\) for some \(p \in P\), i.e., there must exist at least one sublist \({{\fancyscript{L}}}^{p}_s \in {{\fancyscript{L}}}^{p}\) such that \(k \in {{\fancyscript{L}}}^{p}_s\). For simplicity, we use the shorthand notation \(k \in {{\fancyscript{L}}}^{p}\). Combining this with Remark 10, we have
for any node \(k\) in the branch-and-bound tree that has not yet been fully fathomed.
Remark 13
Note that in our approach, lists \({{\fancyscript{L}}}\) and \({{\fancyscript{L}}}_\mathrm{In}\) are core lists as opposed to lists \({{{\fancyscript{L}}}_p}\), \(p \in P\), which are auxiliary. The purpose of the first two lists is to indicate which nodes may require further exploration (branching). The union of these two lists corresponds to the overall list of open nodes in a classical branch-and-bound method. On the other hand, the purpose of the auxiliary lists \({{{\fancyscript{L}}}_p}\), \(p \in P\), is to classify all nodes in the union of \({{\fancyscript{L}}}\) and \({{\fancyscript{L}}}_\mathrm{In}\) according to \(X\) and \(Y\) partitioning.
Having introduced the key partitioning concepts, we now present the bounding problems at some node \(k \ne 1\) in the branch-and-bound tree. These are derived from the bounding problems for the root node presented in Sect. 3.
4.2 Subdivision process
In this paper, at each node \(k\) we consider an \((n+m)\)-rectangle:
and use (exactFootnote 11) bisection for its subdivision.
Definition 4
(Bisection subdivision process [45, 76]) The bisection subdivision process is the partitioning of \(k\) by branching on the midpoint of one of the longest edges, e.g., \([t_{j}^{(k,\mathrm L)}, t_{j}^{(k,\mathrm U)}]\), of \(k\):
Then, this edge is subdivided into two \((n+m)\)-rectangles having equal volume and such that \(b_{j}\) is a vertex of both:
Bisection has been shown to be an exhaustive subdivision process [45, Prop. IV. 2.]. However, it is essential to show that its exhaustiveness property with respect to the subdivision of \(X\) is not compromised in the context of the B&S algorithm. This is because the \(X\) partition is managed by the independent lists (30) and the fewer the independent lists the less refined the \(X\) partition. To guarantee that independent lists are replaced by new independent lists covering refined \(X\) subdomains, we maintain a symmetry in branches across nodes of the same level in the branch-and-bound tree by using the lowest index rule.
Definition 5
(Lowest index coordinate selection rule [24]) Consider a node \(k\). Select a direction \(j^{(k)}\) as follows:
where \(D(i) = \vert t_{i}^\mathrm{U} - t_{i}^\mathrm{L} \vert \).
Namely, if more than one coordinate \(i\), \(i=1,\ldots ,n+m\), satisfy the longest edge requirement, then the one with the smallest index is selected to be subdivided using bisection.
Definition 6
(Subdivision process of the Branch-and-Sandwich algorithm) Consider a node \(k \in {({{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In})} \cap {{\fancyscript{L}}}^{p}\) (recall Remark 12). Then, the B&S subdivision process comprises the following actions.
-
(1)
Apply lowest index selection rule of Def. 5 to select a branching variable.
-
(2)
Partition \(k\) and create two new nodes, \(k_1,k_2\), based on Def. 4.
-
(2.1)
If branching on \(y\)-variable, every sublist \({{\fancyscript{L}}}^{p}_s\) containing \(k\) is modified:
$$\begin{aligned} {{\fancyscript{L}}}^{p}_s = ({{\fancyscript{L}}}^{p}_s \setminus k) \cup \{k_1,k_2\}. \end{aligned}$$(42) -
(2.2)
If branching on \(x\)-variable, every sublist \({{\fancyscript{L}}}^{p}_s\) containing \(k\) is replaced by one or two new sublists:
-
for \(i=1,2\), if \(\mathrm {ri}(X^{(k_i)}) \cap \mathrm {ri}(X^{(j)}) \ne \emptyset \ \forall j \in {{\fancyscript{L}}}^{p}_s\setminus \{k\}\), create:
$$\begin{aligned} {{\fancyscript{L}}}_{s_i}^{p}= ({{\fancyscript{L}}}^{p}_s\setminus \{k\})\cup \{k_i\}. \end{aligned}$$(43)
-
-
(2.1)
-
(3)
If (IC) is true, replace \({{\fancyscript{L}}}^{p}\) with two new independent lists \({{\fancyscript{L}}}^{p_1}\) and \({{\fancyscript{L}}}^{p_2}\) as in (36)–(37) and increase \(|P|\) as in (38).
Theorem 1
The subdivision process of the Branch-and-Sandwich algorithm is exhaustive.
Proof
The proof is provided in Part II of this work [47]. \(\square \)
Remark 14
Bisection is a typical branching strategy, but it has been shown to be non optimal compared to hybrid approaches that combine different subdivision strategies [43]. Nevertheless, exploring branching strategies is beyond the scope of this article.
4.3 Inner lower bound
At a node \(k \in {({{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In})} \cap {{\fancyscript{L}}}^{p}\), the auxiliary relaxed inner problem is:
which is tackled by the following convex relaxation:
where \(\breve{f}^{(k)}_{X,Y}(x,y)\) and \(\breve{g}^{(k)}_{X,Y}(x,y)\) are the convex underestimators of functions \(f(x,y)\) and \(g(x,y)\) over \(X^{(k)} \times Y^{(k)}\), respectively.
4.4 Best inner upper bound
At a node \(k \in {({{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In})} \cap {{\fancyscript{L}}}^{p}\), the auxiliary restricted inner problem is:
which is tackled by the following relaxation, as explained in Sect. 3:
where \(Y^{(k)}=[y^{(k,\mathrm L)},y^{(k,\mathrm U)}]\) and
Remark 15
The set defined above differs from the set \({\varOmega }_\mathrm{KKT}\) in (\(\mathrm{InKKT}_{0}\)) due to the different bound constraints. However, the linearity of these constraints, resulting in nonzero gradients for all \(y\) values,Footnote 12 ensures that the constraint set over each subregion \(Y^{(k)}\subset Y\) still satisfies appropriate constraint qualifications provided that Assumption 4 is satisfied. For instance, if the concave constraint qualification [13] is satisfied for problem (2) over \(Y\), then it also holds for the same problem over any subregion \(Y^{(k)}\).
In what follows, based on the inner upper bounds computed, let \(f^{\mathrm{UB},p}\) denote the best inner upper bound value assigned to each independent list \({{\fancyscript{L}}}^{p}\), \(p\in P\).
Definition 7
(Best inner upper bound) The best inner upper bound is identified in a manner consistent with (IUB), i.e., it is the lowest value over the \(y\) variables but the largest value over the \(x\) variables. In particular, recalling (30), each list \({{\fancyscript{L}}}^{p}\), \(p \in P\), has:
Because within sublists non-overlapping \(Y\) subdomains are kept, the minimum value within a sublist expresses the lowest value with respect to \(y\). On the other hand, different sublists represent overlapping \(X\) subdomains; hence, the largest value over all sublists is the largest value over the \(x\) variables. For instance, consider Example 2 and a potential branch-and-bound tree for its solution in Fig. 4.
Example 2
(Example 3.21 [58])
Figure 5 and Table 3 illustrate how independent lists and their corresponding inner upper bounds evolve for Example 2. Assume that we are interested in the left hand side of the tree, e.g., in node 2. Node 2 is linked to node 3 as they form a \(Y\) partition (cf. Fig. 5a). This is expressed with sublist \({{\fancyscript{L}}}^{1}_1=\{2,3\}\), which is the single member of the independent list \({{\fancyscript{L}}}^{1}\) corresponding to \({{\fancyscript{X}}}_1=[-1,1]\). Using (44), the best inner upper bound of list \({{\fancyscript{L}}}^{1}\) is:
Next, we branch on \(x\) at node 2. The child nodes 4 and 5 remain linked to node 3 due to each node forming a \(Y\) partition with node 3. This is captured by replacing sublist \({{\fancyscript{L}}}^{1}_1\) with sublists \({{\fancyscript{L}}}^{1}_1= \{3,4\}\) and \({{\fancyscript{L}}}^{1}_2= \{3,5\}\) (cf. Fig. 5b). Thus, the independent list \({{\fancyscript{L}}}^{1}\) is updated to \({{\fancyscript{L}}}^{1}=\{{{\fancyscript{L}}}^{1}_1,{{\fancyscript{L}}}^{1}_2\}\) and its best inner upper bound is:
Observe that at node 4, a tighter inner upper bound than the best inner upper bound has been computed. However, the latter cannot be updated to this tighter value since we must use a valid upper bound on the inner problem for the current \(X\) subdomain (recall Remark 9) designated by list \({{\fancyscript{L}}}^{1}\), which captures the whole of \(Y\). Similarly, further branching on node 5 does not lead to an update of \(f^{\mathrm{UB},1}\). The independent list at this stage becomes \({{\fancyscript{L}}}^{1}=\{\{3,4\},\{3,6,7\}\}\) (cf. Fig. 5c) and the best inner upper bound is:
Successive partitioning of \(X\) and \(Y\) based on the tree in Fig. 4
On the other hand, when we replace node 3 by nodes 8 and 9, list \({{\fancyscript{L}}}^{1}\) initially becomes \({{\fancyscript{L}}}^{1}=\{\{4,8\},\{6,7,9\}\}\), but the independence condition (IC) is now satisfied. As a result, list \({{\fancyscript{L}}}^{1}\) is replaced by two new independent lists:
corresponding to refined \(X\) subdomains \({{\fancyscript{X}}}_1=[-1,0]\) and \({{\fancyscript{X}}}_2=[0,1]\), respectively. The bound of node 4 can now safely be used to update the best inner upper bound of \({{\fancyscript{L}}}^{1}\):
The independent list \({{\fancyscript{L}}}^{2}\) inherits the best inner upper bound from its parent list and no improvement is possible since it does not contain any node with a tighter inner upper bound:
Finally, observe in Fig. 5d that each independent list \({{\fancyscript{L}}}^{p}\), \(p=1,2\), covers the whole \(Y\), i.e., \({{\fancyscript{Y}}}_1={{\fancyscript{Y}}}_2=Y\); however, the underlying \(Y\) partitions differ within each list. Also, note that after fathoming is introduced in Sect. 4.6, \({{\fancyscript{Y}}}_p\) may be such that \({{\fancyscript{Y}}}_p \subset Y\) for some \(p \in P\).
4.5 Monotonically improving outer lower bound
Consider a node \(k \in {{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p}\).Footnote 13 The outer lower bounding problem is formulated as follows:
where \(f^{\mathrm{UB},p}\) is computed/updated using (44) (cf. Def. 7). Next, we show that the outer lower bound calculated at each node is at least as tight as the outer lower bound of the parent node based on \(f^{\mathrm{UB},p}\) being improving (non-increasing).
Lemma 1
Consider a node \(k \in {{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p}\). For all successor nodes
for which there exists a corresponding \({{\fancyscript{L}}}^{p'}\) such that \(k_i \in {{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p'}\), where \({{{\fancyscript{X}}}_{p'}} \subseteq {{\fancyscript{X}}}_{p}\), the following holds:
Proof
First recall that independent list \({{\fancyscript{L}}}^{p}\) covers subdomain \({{\fancyscript{X}}}_p \times {{\fancyscript{Y}}}_p\) (cf. Remark 11) and that expression \(k \in {{\fancyscript{L}}}^{p}\) implies that there exists at least one sublist \({{\fancyscript{L}}}^{p}_s \in {{\fancyscript{L}}}^{p}\) such that \(k \in {{\fancyscript{L}}}^{p}_s\), \(s \in 1,\ldots ,s_p\), (cf. Remark 12). In what follows, let us treat “branching on \(y\)” and “branching on \(x\)” cases separately according to Def. 6. In both cases, assume that the branching is such that two successor nodes, \(k_1\) and \(k_2\), are obtained (cf. Sect. 4.2).
-
Branching on \(y\): within list \({{\fancyscript{L}}}^{p}\), every sublist \({{\fancyscript{L}}}^{p}_s\) that contains \(k\) is modified as in (42). This modification results in no change to the overall \({{\fancyscript{X}}}_p\) subdomain covered; hence,
$$\begin{aligned} p' := p. \end{aligned}$$This also means that in each sublist \({{\fancyscript{L}}}^{p'}_s\), containing \(k_1\) and \(k_2\), the underlying subdivision of \(Y\) is now refined since at each successor node, we have \(Y^{(k_i)} \subset Y^{(k)}\), \(i=1,2\). Based on the properties of (RIUB), this implies:
$$\begin{aligned} \min \{\bar{f}^{(k_1)}, \bar{f}^{(k_2)}\} \le \bar{f}^{(k)}. \end{aligned}$$(46)As a result, from (44) (cf. Def. 7) and (46), it is clear that \(f^{\mathrm{UB},p'} \le f^{\mathrm{UB},p}\).
-
Branching on \(x\): within list \({{\fancyscript{L}}}^{p}\), every sublist \({{\fancyscript{L}}}^{p}_s\) that contains \(k\) is replaced by one or two new sublists as in (43). At each successor node, we have \(X^{(k_i)} \subset X^{(k)}\), \(i=1,2\), and by formulation (RIUB):
$$\begin{aligned} \bar{f}^{(k_i)} \le \bar{f}^{(k)},\ i=1,2. \end{aligned}$$(47)Then, if (IC) is not satisfied, list \({{\fancyscript{L}}}^{p}\) is preserved, i.e.,:
$$\begin{aligned} p' := p, \end{aligned}$$(A)and \(k_1,k_2 \in {{\fancyscript{L}}}^{p'}\). Otherwise, if (IC) is satisfied, list \({{\fancyscript{L}}}^{p}\) is replaced by two new independent lists \({{\fancyscript{L}}}^{p_1}\) and \({{\fancyscript{L}}}^{p_2}\) based on (36)–(37) such that:
$$\begin{aligned} k_i \in {{\fancyscript{L}}}^{p_i},\ i=1,2, \end{aligned}$$where \({{{\fancyscript{X}}}_{p_i}} \subset {{{\fancyscript{X}}}_{p}}\). Without loss of generality, let
$$\begin{aligned} p' := p_1. \end{aligned}$$(B)Then, in both cases, (A) and (B), by (44) and (47) we have \(f^{\mathrm{UB},p'} \le f^{\mathrm{UB},p}\).
\(\square \)
Remark 16
Observe that \(f^{\mathrm{UB},p'}\) is at least as tight in case (B) as in case (A), because \({{\fancyscript{X}}}_{p'} \subset {{\fancyscript{X}}}_{p}\) in the former as opposed to \({{\fancyscript{X}}}_{p'} = {{\fancyscript{X}}}_{p}\) in the latter.
Theorem 2
Consider a node \(k \in {{\fancyscript{L}}}^{p}\). For all successor nodes
such that \(k_i \in {{\fancyscript{L}}}^{p'}\), where \({{{\fancyscript{X}}}_{p'}} \subseteq {{\fancyscript{X}}}_{p}\), if the lower bounding problem is feasible at \(k_i\), then
Proof
At each successor node \(k_i\), the outer lower bound \({{\underline{F}}}^{(k_i)}\) differs from that at the parent node in that (i) its domain is reduced, i.e., \(X^{(k_i)} \times Y^{(k_i)} \subset X^{(k)} \times Y^{(k)}\) and (ii) the right hand side of the constraint
is at least as tight as that at the parent node by Lemma 1. This trivially results in an optimal objective value at least as tight as that at the parent node. \(\square \)
4.6 Node fathoming rules
The success of branch-and-bound methods depends on the ability to discard subregions of the original domain due to guarantees ensuring that the global optimal solution cannot be found there. This process is known as fathoming. In the tree of Fig. 4, no fathoming rule was employed and no \(X\) or \(Y\) subregion was deleted. Thus, in this case each independent list held the whole \(Y\), i.e., \({{\fancyscript{Y}}}_p = Y\), \(p=1,\ldots ,|P|\), via a number of \(Y\) partitions.
In what follows, we describe how classical fathoming rules, such as the “fathom-by-infeasibility” and “fathom-by-value-dominance” rules, are incorporated in our algorithm such that subregions of both \(X\) and \(Y\) spaces are discarded safely. As a result, each independent list may not hold the whole \(Y\) any more and \({{\fancyscript{Y}}}_p \subseteq Y\), \(p =1,\ldots ,|P|\).
To start with, we highlight the implicit use of two trees during the course of our algorithm, one for the inner problem and one for the outer problem. In the algorithm, we apply the classical fathoming rules to both trees independently. For brevity, we refer to those as inner- and outer-fathoming rules.
Definition 8
(Inner-fathoming rules) Consider a node \(k \in ({{\fancyscript{L}}} \cup {{\fancyscript{L}}_\mathrm{In}})\cap {{\fancyscript{L}}}^{p}\) and compute \({{\underline{f}}}^{(k)}\) using (RILB). If
-
(1)
\({{\underline{f}}}^{(k)}=\infty \),Footnote 14
-
(2)
\({{\underline{f}}}^{(k)}> f^{\mathrm{UB},p}\),
then (fully) fathom node \(k\), i.e., delete it from \({{\fancyscript{L}}}\) or \({{\fancyscript{L}}_\mathrm{In}}\) and from \({{\fancyscript{L}}}^{p}\).
Definition 9
(Outer-fathoming rules) Given outer objective tolerance \(\varepsilon _F\), consider a node \(k \in {{\fancyscript{L}}}\cap {{\fancyscript{L}}}^{p}\) and compute \({{\underline{F}}}^{(k)}\) using (\(\mathrm{LB}\)). If
-
(1)
\({{\underline{F}}}^{(k)}=\infty \),
-
(2)
\({{\underline{F}}}^{(k)} \ge F^\mathrm{UB}-\varepsilon _F\),
then outer fathom node \(k\), i.e., move it from \({{\fancyscript{L}}}\) to \({\fancyscript{L}}_\mathrm{In}\). Hence, \(k \in {{\fancyscript{L}}}_\mathrm{In} \cap {{\fancyscript{L}}}^{p}\) after outer fathoming.
Moreover, if a sublist contains outer-fathomed nodes only, i.e., it no longer contains any nodes in \({\fancyscript{L}}\) which are open from the perspective of the overall problem, then it can be deleted. This may lead to full fathoming of the corresponding nodes as long as they do not appear in other sublists of the same independent list. The rules are summarized below.
Definition 10
(List-deletion fathoming rules) Consider a sublist \({{\fancyscript{L}}}^{p}_i \in {{\fancyscript{L}}}^{p}\), \(i \in 1,\ldots ,s_p\).
-
1.
If \({{\fancyscript{L}}}^{p}_i \cap {{\fancyscript{L}}} = \emptyset \) and \({{\fancyscript{L}}}^{p}_i \cap {{\fancyscript{L}}}^{p}_j = \emptyset \) for all \(j\ne i \in 1,\ldots ,s_p\), then fully fathom all nodes \(k \in {{\fancyscript{L}}}^{p}_i\), i.e., delete them from \({{\fancyscript{L}}_\mathrm{In}}\) and \({{\fancyscript{L}}}^{p}\). Delete also sublist \({{\fancyscript{L}}}^{p}_i\) and decrease \(s_p\).
-
2.
If \({{\fancyscript{L}}}^{p}_i \cap {{\fancyscript{L}}} = \emptyset \) and \({{\fancyscript{L}}}^{p}_i \cap {{\fancyscript{L}}}^{p}_j \ne \emptyset \) for some \(j\ne i \in 1,\ldots ,s_p\), then delete sublist \({{\fancyscript{L}}}^{p}_i\) and decrease \(s_p\).
-
3.
If \(s_p=0\), delete list \({{\fancyscript{L}}}^{p}\) and decrease \(|P|\).
As a result of our node fathoming and list deletion actions, the branch-and-bound tree may include three kind of nodes:
-
1.
Open nodes: those in \({{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p}\) for some \(p \in P\). We continue exploration of these nodes with respect to both the outer and inner problems.
-
2.
Outer-fathomed nodes: those in \({{\fancyscript{L}}_\mathrm{In}}\cap {{\fancyscript{L}}}^{p}\) for some \(p \in P\). We continue exploration of these nodes with respect to the inner problem only.
-
3.
Fathomed nodes: deleted from all the lists. No further exploration of these nodes is required.
We end this section by proving a useful preliminary result, which guarantees that after fathoming, every independent list \({{\fancyscript{L}}}^{p}\), \(p\in P\), still contains all promising subregions of \(Y\) where global optimal solutions may lie for any \(x \in {{\fancyscript{X}}}_p\).
Lemma 2
Use \({{\fancyscript{Y}}}_p \subseteq Y\) given in (35) to represent the \(Y\) (sub)domain maintained inside the independent list \({{\fancyscript{L}}}^{p}\), \(p\in P\). For any \(x \in {{\fancyscript{X}}}_p\), replace \(Y\) with \({{\fancyscript{Y}}}_p\) in the definition of \(O(x)\) (Eq. (7)):
Then,
Proof
\({{\fancyscript{Y}}}_p\) is the union of the \(Y\) subregions of all the nodes in \({{\fancyscript{L}}}^{p}\), i.e., across all sublists. A subregion \(Y^{(d)} \subset Y\) is permanently deleted from \({{\fancyscript{L}}}^{p}\) only if it is deleted for all \(x \in {{\fancyscript{X}}}_p\) (e.g., cf. Fig. 6). In view of this, define the set of fathomed \(Y\) domains for \({{\fancyscript{X}}}_p\) as follows:
Then,
If \({{\fancyscript{F}}}^p=\emptyset \), then \({{\fancyscript{Y}}}_p = Y\) and (48) holds. Otherwise, if \({{\fancyscript{F}}}^p\ne \emptyset \), then \({{\fancyscript{Y}}}_p \subset Y\). In this case, to prove (48), it suffices to show that
We prove (50) by contradiction. Assume that there exists a point \(y \in O(x)\), for some \(x \in {{\fancyscript{X}}}_p\), such that \(y \in {{\fancyscript{F}}}^p\). The former implies that there exists \(x \in {{\fancyscript{X}}}_p\) such that:
On the other hand, \(y \in {{\fancyscript{F}}}^p\) implies that for all \(x \in {{\fancyscript{X}}}_p\), either the inner problem is infeasible:
contradicting (51), or that the inner objective value is greater than the best inner upper bound:
Since \(w(x)\le f^{\mathrm{UB},p} \ \text {for all} \ x \in {{\fancyscript{X}}}_p\), this contradicts (52). Hence, no inner optimal solution can lie in \({{\fancyscript{F}}}^p\) for any \(x \in {{\fancyscript{X}}}_p\) and this contradicts our assumption that \(y \in O(x)\). \(\square \)
Remark 17
Notice that the sets \({{\fancyscript{F}}}^p\), \(p=1,\ldots ,|P|\), are infeasible in the bilevel problem (1) due to (50), i.e., infeasible in the sense of [45, Def. IV.2.]; hence, these are safely deleted.
4.7 Valid outer upper bound and incumbent solution
Consider a node \(k \in {{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p}\). Then, given \(\bar{x} \in X\) and fixed inner objective tolerance \(\varepsilon _f\), the outer upper bounding problem is:
where
Theorem 3
Consider a node \(k \in {{\fancyscript{L}}}^{p}\). Set \(\bar{x}=x^{(k)}\), where \((x^{(k)},y^{(k)})\) is the solution of the lower bounding problem (LB) at node \(k\). Solve problem (RISP) over all nodes \(j \in {{\fancyscript{L}}}^{p}\) such that \(\bar{x} \in X^{(j)}\). Find \(k' \in {{\fancyscript{L}}}^{p}\) based on (MinRISP). Then, (UB), if feasible, computes a valid upper bound on the optimal objective value of (1).
Proof
To prove that (UB) always yields a valid upper bound on the optimal value of (1), it suffices to show that any feasible point in the former, if there exists one, is \(\varepsilon \)-feasible in the latter. To show that a point \((\bar{x},\bar{y})\) is \(\varepsilon \)-feasible in (1), we must show that it satisfies the conditions (13)–(15) of Def. 2, namely outer and inner feasibility, as well as \(\varepsilon _f\)-global optimality in the inner problem (2):
For some \(\bar{x} \in X\), any feasible point \(\bar{y}\) in (UB) satisfies conditions (13) and (14). Moreover, due to inner feasibility, the following holds:
By feasibility of \(\bar{y}\) in (UB), we also have:
where the equality is by (MinRISP). Then,
where the inequality is due to the properties of the underestimators and the equality is by Lemma 2. Hence,
As a result, (57) follows from (58) and (61). \(\square \)
A point \((\bar{x},\bar{y})\) computed with the proposed upper bounding problem is therefore always \(\varepsilon \)-feasible in (1), thanks to the proposed selection procedure for the appropriate subdomains of \(Y\) based on (MinRISP). If \(\bar{F}^{(k')}\) is lower than the current incumbent value \(F^\mathrm{UB}\), i.e., the best (lowest) outer upper bound known so far, then we update \(F^\mathrm{UB}\):
Remark 18
Recall that in this work, we employ the \(\alpha \)BB convexification techniques [1, 2] whenever we want to construct convex relaxations. As a result, over refined subsets of \(Y\), the convex relaxed problems (RISP) approximate the inner subproblems (\(\mathrm{ISP}\)) with a quadratic convergence rate [17, 52], which helps to achieve near-equality in (60) and to identify a valid upper bound (cf. also [38, Prop. 4.1(ii)]).
4.8 Selection operation
The selection operation of the B&S algorithm includes three steps: (i) a classical selection rule, e.g., lowest (outer) lower bound, is first applied to the open nodes in list \({\fancyscript{L}}\); (ii) then, the list \({{\fancyscript{L}}}^{p}\) corresponding to this node is identified; (iii) finally, a node in that list, i.e., \(k \in {{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p}\), with the lowest level is chosen; if several nodes are at the same level in the tree, the node corresponding to the lowest inner lower bound is chosen:
Furthermore, we branch on outer-fathomed nodes too, i.e., nodes that belong to list \({\fancyscript{L}}_\mathrm{In}\). In particular, for the list \({{\fancyscript{L}}}^{p}\) already identified, we check whether \({{\fancyscript{L}}_\mathrm{In}} \cap {{\fancyscript{L}}}^{p} \ne \emptyset \), in which case a node in \(k_\mathrm{In} \in {{\fancyscript{L}}_\mathrm{In}} \cap {{\fancyscript{L}}}^{p}\) is selected using (ISR). This node is explored further with respect to the inner space only, since nodes in \({\fancyscript{L}}_\mathrm{In}\) are kept to provide information about the inner global optimal solutions. To recapitulate, the selection operation of the proposed algorithm is stated below.
Definition 11
(Selection operation of the Branch-and-Sandwich algorithm) The selection rule of the B&S algorithm is:
-
(i)
find a node in \({\fancyscript{L}}\) with lowest overall lower bound: \(k^\mathrm{LB} = \mathop {\mathrm {arg\, min}}\limits _{j \in {{\fancyscript{L}}}} \{{{\underline{F}}}^{(j)}\}\);
-
(ii)
find the corresponding \({{\fancyscript{X}}}_p\) subdomain, \(p\in P\), such that \(k^\mathrm{LB} \in {{\fancyscript{L}}}^{p}\);
-
(iii)
select a node \(k \in {{\fancyscript{L}}} \cap {{\fancyscript{L}}}^{p}\) and a node \(k_\mathrm{In} \in {{\fancyscript{L}}_\mathrm{In}} \cap {{\fancyscript{L}}}^{p}\), if non empty, using (ISR).
5 Branch-and-Sandwich algorithm
Given outer and inner objective tolerances \(\varepsilon _F\), \(\varepsilon _f\), respectively, the proposed global optimization algorithm for nonconvex bilevel problems is as follows.
Algorithm 1
Branch-and-Sandwich
- Step 0: :
-
Initialization Initialize lists: \({{\fancyscript{L}}}:={{\fancyscript{L}}}_\mathrm{In}:=\emptyset \). Set the incumbent:
$$\begin{aligned} (x^\mathrm{UB},y^\mathrm{UB}):=\emptyset \ \text {and}\ F^\mathrm{UB} := \infty , \end{aligned}$$the iteration counter: \(\mathrm{Iter}:=0\), and the node counter: \(n_\mathrm{node}:=1\) corresponding to the whole domain \(X\times Y\).
- Step 1: :
-
Inner and outer bounds
- Step 1.1: :
-
Solve the auxiliary relaxed inner problem (\(\mathrm{RILB}_{0}\)) to compute \({{\underline{f}}}^{(1)}\). If infeasible goto Step 2.
- Step 1.2: :
-
Solve the auxiliary restricted inner problem (\(\mathrm{RIUB}_{0}\)). Set \(f_X^\mathrm{UB} := \bar{f}^{(1)}\).
- Step 1.3: :
-
Solve the lower bounding problem (LB\(_0\)) globally to obtain \({{\underline{F}}}^{(1)}\). If infeasible, goto Step 2. Otherwise, if a feasible solution \((x^{(1)},y^{(1)})\) is computed, add node to the universal list:
$$\begin{aligned} {{\fancyscript{L}}}:=\{1\} \end{aligned}$$with properties \(({{\underline{f}}}^{(1)},\bar{f}^{(1)},{{\underline{F}}}^{(1)}, x^{(1)}, l^{(1)})\), where \(l^{(1)}:=0\). Initialize the partition of \(X\), i.e., \(p:=1\) and \({{\fancyscript{X}}}_1:= X\), and generate the first independent list:
$$\begin{aligned} {{\fancyscript{L}}}^{1}:=\{1\}. \end{aligned}$$Set the best inner upper bound for \({{\fancyscript{X}}}_1\):
$$\begin{aligned} f^{\mathrm{UB},1}:=f_X^\mathrm{UB}. \end{aligned}$$ - Step 1.4: :
-
Set \(\bar{x}:=x^{(1)}\) and compute \({{\underline{w}}}(\bar{x})\) using (RISP\(_0\)). Then, solve (\(\mathrm{UB}_{0}\)) locally to obtain \(\bar{F}^{(1)}\). If a feasible solution \((x_{f},y_{f})\) is obtained, update the incumbent:
$$\begin{aligned} (x^\mathrm{UB},y^\mathrm{UB})=(x_{f},y_{f}) \ \text {and}\ F^\mathrm{UB} = \bar{F}^{(1)}. \end{aligned}$$
- Step 2: :
-
Node(s) Selection If \({\fancyscript{L}}=\emptyset \), terminate and report the incumbent solution and value. Otherwise, increase the iteration counter, \(\mathrm{Iter}=\mathrm{Iter}+1\), and select a list \({{\fancyscript{L}}}^{p}\), a node \(k \in {{\fancyscript{L}}}^{p} \cap {{\fancyscript{L}}}\) and a node \(k_\mathrm{In} \in {{\fancyscript{L}}}^{p} \cap {\fancyscript{L}}_\mathrm{In}\), if \({{\fancyscript{L}}}^{p} \cap {\fancyscript{L}}_\mathrm{In} \ne \emptyset \), based on Def. 11. Remove \(k\) from \({\fancyscript{L}}\) and \(k_\mathrm{In}\) from \({\fancyscript{L}}_\mathrm{In}\).
- Step 3: :
-
Branching
- Step 3.1: :
-
Apply steps (1)-(4) of Def. 6 on node \(k\) to create two new nodes, i.e., \(n_\mathrm{node} + 1\) and \(n_\mathrm{node} + 2\). Set \(n_\mathrm{new}:=2\) and
$$\begin{aligned} \begin{array}{lllll} {{\underline{f}}}^{(n_\mathrm{node} + 1)} &{}:=&{} {{\underline{f}}}^{(n_\mathrm{node} + 2)} &{}:=&{} {{\underline{f}}}^{(k)};\\ \bar{f}^{(n_\mathrm{node} + 1)} &{}:=&{} \bar{f}^{(n_\mathrm{node} + 2)} &{}:=&{} \bar{f}^{(k)};\\ {{\underline{F}}}^{(n_\mathrm{node} + 1)} &{}:=&{} {{\underline{F}}}^{(n_\mathrm{node} + 2)} &{}:=&{} {{\underline{F}}}^{(k)}; \\ x^{(n_\mathrm{node} + 1)} &{}:=&{} x^{(n_\mathrm{node} + 2)} &{}:=&{} x^{(k)}; \\ l^{(n_\mathrm{node} + 1)} &{}:=&{} l^{(n_\mathrm{node} + 2)} &{}:=&{} l^{(k)} + 1. \end{array} \end{aligned}$$ - Step 3.2: :
-
If a node \(k_\mathrm{In}\) is selected, apply steps (1)-(4) of Def. 6 on \(k_\mathrm{In}\) to create two new (outer-fathomed) nodes, i.e., \(n_\mathrm{node} + 3\) and \(n_\mathrm{node} + 4\). Set \(n_\mathrm{new}:=4\) and
$$\begin{aligned} \begin{array}{lllll} {{\underline{f}}}^{(n_\mathrm{node} + 3)} &{}:=&{} {{\underline{f}}}^{(n_\mathrm{node} + 4)} &{}:=&{} {{\underline{f}}}^{(k_\mathrm{In})};\\ \bar{f}^{(n_\mathrm{node} + 3)} &{}:=&{} \bar{f}^{(n_\mathrm{node} + 4)} &{}:=&{} \bar{f}^{(k_\mathrm{In})};\\ l^{(n_\mathrm{node} + 3)} &{}:=&{} l^{(n_\mathrm{node} + 4)} &{}:=&{} l^{(k_\mathrm{In})} + 1. \\ \end{array} \end{aligned}$$ - Step 3.3: :
-
List management: For \(i = n_\mathrm{node} + 1,\ldots ,n_\mathrm{node} + n_\mathrm{new}\), find the corresponding subdomain \({{\fancyscript{X}}}_{p_i}\) such that \(i \in {{\fancyscript{L}}}^{p_i}\) and set/update \(f^{\mathrm{UB},p_i}\). Apply the inner-value-dominance node fathoming rule (cf. Def. 8).
- Step 4: :
-
Inner lower bound If there is no \(i \in \{n_\mathrm{node} + 1,\ldots ,n_\mathrm{node} + n_\mathrm{new}\}\), such that \(i \in {{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In}\), apply the list-deletion fathoming rules (cf. Def. 10) and goto Step 2. Otherwise, for \(i \in \{n_\mathrm{node} + 1,\ldots ,n_\mathrm{node} + n_\mathrm{new}\}\), such that \(i \in {{\fancyscript{L}}}^{p_i}\), solve the auxiliary relaxed inner problem (RILB) to compute \({{\underline{f}}}^{(i)}\). If feasible and \({{\underline{f}}}^{(i)} \le f^{\mathrm{UB},p_i}\), then:
-
if \(i \in \{n_\mathrm{node} + 1, n_\mathrm{node}+2\}\), add node \(i\) to the list \({\fancyscript{L}}\) with properties
$$\begin{aligned}({{\underline{f}}}^{(i)},\bar{f}^{(i)},{{\underline{F}}}^{(i)}, x^{(i)}, l^{(i)});\end{aligned}$$ -
else if \(n_\mathrm{new}=4\) and \(i \in \{ n_\mathrm{node} + 3, n_\mathrm{node}+4\}\), add node \(i\) to the list \({\fancyscript{L}}_\mathrm{In}\) with properties
$$\begin{aligned}({{\underline{f}}}^{(i)},\bar{f}^{(i)}, l^{(i)}).\end{aligned}$$
Otherwise, remove \(i\) from \({{\fancyscript{L}}}^{p_i}\). Apply the list deletion rule (cf. Def. 10).
- Step 5: :
-
Inner Upper Bound If there is no \(i \in \{n_\mathrm{node} + 1,\ldots ,n_\mathrm{node} + n_\mathrm{new}\}\), such that \(i \in {{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In}\), goto Step 2. Otherwise, for \(i \in \{n_\mathrm{node} + 1,\ldots ,n_\mathrm{node} + n_\mathrm{new}\}\), such that \(i \in {{\fancyscript{L}}} \cup {\fancyscript{L}}_\mathrm{In}\), solve the auxiliary restricted inner problem (RIUB) to compute \(\bar{f}^{(i)}\). Update \(\bar{f}^{(i)}\) in \({\fancyscript{L}}\) or in \({\fancyscript{L}}_\mathrm{In}\) and then update \(f^{\mathrm{UB},p_i}\) using Eq. (44) (cf. Def. 7). Apply the inner-value-dominance node fathoming rule (cf. Def. 8) and, if necessary, the list deletion procedure (cf. Def. 10).
- Step 6: :
-
Outer lower bound If there is no \(i \in \{n_\mathrm{node} + 1,n_\mathrm{node} + 2\}\), such that \(i \in {{\fancyscript{L}}}\), goto Step 2. Otherwise, for \(i \in \{n_\mathrm{node} + 1,n_\mathrm{node} + 2\}\), such that \(i \in {{\fancyscript{L}}}\), solve the lower bounding problem (\(\mathrm{LB}\)) globally to obtain \({{\underline{F}}}^{(i)}\). If a feasible solution \((x^{(i)},y^{(i)})\) is obtained with \({{\underline{F}}}^{(i)} \le F^\mathrm{UB} + \varepsilon _F\), update \({{\underline{F}}}^{(i)}\) and \(x^{(i)}\) in \({\fancyscript{L}}\). If \({{\underline{F}}}^{(i)} \ge F^\mathrm{UB} - \varepsilon _F\), move \(i\) from \({\fancyscript{L}}\) to the list \({\fancyscript{L}}_\mathrm{In}\) with properties \(({{\underline{f}}}^{(i)},\bar{f}^{(i)}, l^{(i)})\) and apply the list deletion procedure (cf. Def. 10).
- Step 7: :
-
Outer upper bound If there is no \(i \in \{n_\mathrm{node} + 1,n_\mathrm{node} + 2\}\), such that \(i \in {{\fancyscript{L}}}\), goto Step 2. Otherwise, for \(i = n_\mathrm{node} + 1,n_\mathrm{node} + 2\), such that \(i \in {{\fancyscript{L}}}\), do:
- Step 7.1: :
-
Set \(\bar{x}:=x^{(i)}\) and, using (RISP), compute \({{\underline{w}}}^{(j)}(\bar{x})\) for all \(j \in {{\fancyscript{L}}}^{p_i}\), such that \(\bar{x} \in X^{(j)}\). Set \(i'\) based on (MinRISP).
- Step 7.2: :
-
Solve (UB) (locally) to obtain \(\bar{F}^{(i')}\). If a feasible solution \((x^{(i')}_{f},y^{(i')}_{f})\) is obtained with \(\bar{F}^{(i')} < F^\mathrm{UB}\) update the incumbent:
$$\begin{aligned} (x^\mathrm{UB},y^\mathrm{UB})=(x^{(i')}_{f},y^{(i')}_{f}) \ \text {and}\ F^\mathrm{UB} = \bar{F}^{(i')}. \end{aligned}$$Move from the list \({\fancyscript{L}}\) to the list \({\fancyscript{L}}_\mathrm{In}\) all nodes \(j\) such that \({{\underline{F}}}^{(j)} \ge F^\mathrm{UB} - \varepsilon _F\) and apply the list deletion procedure (cf. Def. 10). Increase the node counter, i.e., \(n_\mathrm{node} = n_\mathrm{node} + n_\mathrm{new}\), and goto Step 2.
Note that in Steps 4–5, we start by testing whether the new nodes for inner and outer exploration, created in Step 3, still exist following the application of node fathoming in Step 3.3 and in Step 4. As more node fathoming may take place in Step 5 (resp. Step 6), we start Step 6 (resp. Step 7) by testing whether there still exist any new nodes for outer exploration. A detailed step-by-step application of the algorithm on two suitable test problems is presented in Part II of this work [47], which focuses on the application of the algorithm to problems from the literature as well as on its convergence properties.
6 Conclusions
We presented a branch-and-bound scheme, the B&S algorithm, for the solution of optimistic bilevel programming problems that satisfy an appropriate regularity condition in the inner problem. The novelty of our scheme is threefold as it: (i) encompasses implicitly two branch-and-bound trees, (ii) introduces a simple outer lower bounding problem with the useful feature that it is always obtained from the lower bounding problem of the parent node, and (iii) allows branch-and-bound with respect to the inner and the outer variables without distinction, but at the same time it keeps track of the partitioning of \(Y\) for successively refined subdomains of \(X\). The convergence properties of the algorithm are explored in Part II of this work and finite convergence to an \(\varepsilon \)-optimal global solution is proved [47]. The success of the proposed method depends on having good inner upper bounds for value dominance fathoming and for (outer) fathoming by outer infeasibility. The application of the algorithm to numerical examples is also considered in Part II.
Notes
A hybrid approach combining global and local optimization techniques, when appropriate [64], can also be investigated.
Notice that in a maximization framework, the relation between the objective function of a relaxation/restriction and the original objective function is reversed, e.g., a relaxation of a maximization problem has an objective function always greater than or equal to the original objective function.
If there are no \((x,y)\in {\varOmega }\), then the bilevel program (1) is infeasible.
The satisfaction of a constraint qualification ensures that the KKT are necessary conditions for a given point to be a minimizer.
Assuming regularity refers to assuming the satisfaction of an appropriate constraint qualification [40].
The non-branching version has also been extended in [55] to solve the mixed-integer nonlinear bilevel programming problem.
The Lagrange function of (22) is:
$$\begin{aligned} L(x_0,x,y,\mu ,\lambda ,\nu ) = -x_0 + f(x,y) + {\mu }^{\mathrm {T}}g(x,y) + {\lambda }^{\mathrm {T}}(y^\mathrm{L}-y) + {\nu }^{\mathrm {T}}(y-y^\mathrm{U}). \end{aligned}$$If we differentiate it with respect to \(y\), \(x_0\) vanishes, i.e.,:
$$\begin{aligned} \nabla _y L(x_0,x,y,\mu ,\lambda ,\nu ) = \nabla _y f(x,y) + \nabla _y{g}^{\mathrm {T}}(x,y)\mu - \lambda + \nu . \end{aligned}$$Fig. 2 a A valid inner lower bound cannot be found simply by fixing \(x\), e.g., to \(\bar{x}=1\), and minimizing \(f(x,y)\) for a given \(x\) with respect to \(y\) (cf. Remark 7). b Similarly, a point may be bilevel feasible, such as the pair \((\bar{x},\bar{y})=(2,2)\), but it does not necessarily provide a valid upper bound on the inner optimal objective value (cf. Remark 9)
Overall, we have lists \({\fancyscript{L}}\), \({\fancyscript{L}}_\mathrm{In}\) and \(\{{{\fancyscript{L}}}^{1},\ldots ,{{\fancyscript{L}}}^{|P|}\}\).
Recall that we use quotes to refer to the “whole” inner space because some \(Y\) subdomains are eliminated at some point due to fathoming (cf. Sect. 4.6). As a result, we may have \({{\fancyscript{Y}}}_p \subset Y\) for some \(p \in P\).
For subdividing a given node \(k\), one can use the so-called bisection of ratio r. Node \(k\) is divided into subrectangles such that the ratio of the volume of the smaller subrectangle to that of \(k\) equals \(r\), where \(0<r\le 1/2\). When \(r=1/2\), the bisection is called exact [76].
The gradients of the bound constraints are as follows:
$$\begin{aligned} \begin{array}{llcll} \nabla _y\left[ y^{(k,\mathrm L)}-y\right] &{}=&{} -1_m &{}\ne 0 &{}\forall y,\\ \nabla _y\left[ y-y^{(k,\mathrm U)}\right] &{}=&{} 1_m &{}\ne 0 &{}\forall y, \end{array} \end{aligned}$$where \(1_m\) denotes a vector of ones in \(\mathrm{I\!R}^m\).
The outer lower bounding problem is not solved for nodes in list \({\fancyscript{L}}_\mathrm{In}\).
The rule \(\bar{f}^{(k)}=-\infty \) could also be added to inner-fathoming rules only in the cases where the set \({\varOmega }_\mathrm{KKT}\) is independent of the bounds on \(y\).
References
Adjiman, C.S., Dallwig, S., Floudas, C.A., Neumaier, A.: A global optimization method, \(\alpha \)BB, for general twice-differentiable constrained NLPs—I. Theoretical advances. Comput. Chem. Eng. 22(9), 1137–1158 (1998)
Adjiman, C.S., Androulakis, I.P., Floudas, C.A.: A global optimization method, \(\alpha \)BB, for general twice-differentiable constrained NLPs-II. Implementation and computational results. Comput. Chem. Eng. 22(9), 1159–1179 (1998)
Androulakis, I.P., Maranas, C.D., Floudas, C.A.: \(\alpha {\rm BB}\): a global optimization method for general constrained nonconvex problems. J. Global Optim. 7(4), 337–363 (1995). State of the art in global optimization: computational methods and applications (Princeton, NJ, 1995)
Audet, C., Hansen, P., Jaumard, B., Savard, G.: On the linear maxmin and related programming problems. In: Migdalas, A., Pardalos, P.M., Värbrand, P. (eds.) Multilevel Optimization: Algorithms and Applications, pp. 181–208. Kluwer, Dordrecht (1998)
Bard, J.F.: An algorithm for solving the general bilevel programming problem. Math. Oper. Res. 8(2), 260–272 (1983)
Bard, J.F.: Coordination of a multidivisional organization through two levels of management. Omega 11(5), 457–468 (1983)
Bard, J.F.: Convex two-level optimization. Math. Program. 40(1, (Ser. A)), 15–27 (1988)
Bard, J.F.: Production planning with variable demand. Omega 18(1), 35–42 (1990)
Bard, J.F.: Practical Bilevel Optimization, Nonconvex Optimization and its Applications, vol. 30. Kluwer, Dordrecht (1998)
Bard, J.F., Plummer, J., Sourie, J.C.: A bilevel programming approach to determining tax credits for biofuel production. Eur. J. Oper. Res. 120(1), 30–46 (2000)
Bazaraa, M.S., Goode, J.J., Shetty, C.M.: Constraint qualifications revisited. Manag. Sci. 18, 567–573 (1972)
Bazaraa, M.S., Shetty, C.M.: Nonlinear Programming. Wiley, New York (1979)
Bertsekas, D.P.: Nonlinear Programming. Athena Scientific, Belmont (1995)
Bhattacharjee, B., Green Jr, W.H., Barton, P.I.: Interval methods for semi-infinite programs. Comput. Optim. Appl. 30(1), 63–93 (2005)
Bhattacharjee, B., Lemonidis, P., Green Jr, W.H., Barton, P.I.: Global solution of semi-infinite programs. Math. Program. 103(2, Ser. B), 283–307 (2005)
Blankenship, J.W., Falk, J.E.: Infinitely constrained optimization problems. J. Optim. Theory Appl. 19(2), 261–281 (1976)
Bompadre, A., Mitsos, A.: Convergence rate of McCormick relaxations. J. Global Optim. 52(1), 1–28 (2012)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Bracken, J., McGill, J.T.: Defense applications of mathematical programs with optimization problems in the constraints. Oper. Res. 22(5), 1086–1096 (1974)
Cassidy, R.G., Kirby, M.J.L., Raike, W.M.: Efficient distribution of resources through three levels of government. Manag. Sci. 17(8), B462–B473 (1971)
Clark, P.A.: Bilevel programming for steady-state chemical process design—I. Fundamentals and algorithms. Comput. Chem. Eng. 14(1), 87–97 (1990)
Clark, P.A.: Bilevel programming for steady-state chemical process design—II. Performance study for nondegenerate problems. Comput. Chem. Eng. 14(1), 99–109 (1990)
Colson, B., Marcotte, P., Savard, G.: An overview of bilevel optimization. Ann. Oper. Res. 153, 235–256 (2007)
Csendes, T., Ratz, D.: Subdivision direction selection in interval methods for global optimization. SIAM J. Numer. Anal. 34(3), 922–938 (1997)
Demiguel, V., Friedlander, M.P., Nogales, F.J., Scholtes, S.: A two-sided relaxation scheme for mathematical programs with equilibrium constraints. SIAM J. Optim. 16(2), 587–609 (2005)
Dempe, S.: First-order necessary optimality conditions for general bilevel programming problems. J. Optim. Theory Appl. 95(3), 735–739 (1997)
Dempe, S.: A bundle algorithm applied to bilevel programming problems with non-unique lower level solutions. Comput. Optim. Appl. 15(2), 145–166 (2000)
Dempe, S.: Foundations of Bilevel Programming, Nonconvex Optimization and its Applications, vol. 61. Kluwer, Dordrecht (2002)
Dempe, S.: Annotated bibliography on bilevel programming and mathematical programs with equilibrium constraints. Optimization 52(3), 333–359 (2003)
Dempe, S., Dutta, J.: Is bilevel programming a special case of a mathematical program with complementarity constraints? Math. Program. 131(1–2), 37–48 (2012)
Dempe, S., Zemkoho, A.B.: The generalized Mangasarian-Fromowitz constraint qualification and optimality conditions for bilevel programs. J. Optim. Theory Appl. 148(1), 46–68 (2011)
Deng, X.: Complexity issues in bilevel linear programming. In: Multilevel Optimization: Algorithms and Applications, Nonconvex Optim. Appl., vol. 20, pp. 149–164. Kluwer, Dordrecht (1998)
Faísca, N.P., Dua, V., Rustem, B., Saraiva, P.M., Pistikopoulos, E.N.: Parametric global optimisation for bilevel programming. J. Global Optim. 38(4), 609–623 (2007)
Falk, J.E.: A linear max-min problem. Math. Program. 5, 169–188 (1973)
Falk, J.E., Hoffman, K.: A nonconvex max-min problem. Naval Res. Logist. Quart. 24(3), 441–450 (1977)
Floudas, C.A.: Deterministic Global Optimization, Nonconvex Optimization and its Applications, vol. 37. Kluwer, Dordrecht (2000)
Floudas, C.A., Akrotirianakis, I.G., Caratzoulas, S., Meyer, C.A., Kallrath, J.: Global optimization in the 21st century: advances and challenges. Comput. Chem. Eng. 29(6), 1185–1202 (2005)
Floudas, C.A., Stein, O.: The adaptive convexification algorithm: a feasible point method for semi-infinite programming. SIAM J. Optim. 18(4), 1187–1208 (2007)
Fortuny-Amat, J., McCarl, B.: A representation and economic interpretation of a two-level programming problem. J. Oper. Res. Soc. 32(9), 783–792 (1981)
Gauvin, J.: A necessary and sufficient regularity condition to have bounded multipliers in nonconvex programming. Math. Program. 12(1), 136–138 (1977)
Guerra Vázquez, F., Rückmann, J.J., Stein, O., Still, G.: Generalized semi-infinite programming: a tutorial. J. Comput. Appl. Math. 217(2), 394–419 (2008)
Gümüş, Z.H., Floudas, C.A.: Global optimization of nonlinear bilevel programming problems. J. Global Optim. 20(1), 1–31 (2001)
Horst, R.: Bisection by global optimization revisited. J. Optim. Theory Appl. 144(3), 501–510 (2010)
Horst, R., Pardalos, P.M., Thoai, N.V.: Introduction to Global Optimization, Nonconvex Optimization and its Applications, vol. 48, 2nd edn. Kluwer, Dordrecht (2000)
Horst, R., Tuy, H.: Global Optimization, 3rd edn. Springer, Berlin (1996). (Deterministic approaches)
Jongen, H.Th., Shikhman, V.: Bilevel optimization: on the structure of the feasible set. Math. Program. 136(1, Ser. B), 65–89 (2012)
Kleniati, P.-M., Adjiman, C.S.: Branch-and-Sandwich: a deterministic global optimization algorithm for optimistic bilevel programming problems. Part II: convergence analysis & numerical results. J. Global Optim. (2014). doi:10.1007/s10898-013-0120-8
LeBlanc, L.J., Boyce, D.E.: A bilevel programming algorithm for exact solution of the network design problem with user-optimal flows. Transp. Res. B 20(3), 259–265 (1986)
Loridan, P., Morgan, J.: Approximate solutions for two-level optimization problems. In: Trends in Mathematical Optimization (Irsee, 1986), Internat. Schriftenreihe Numer. Math., vol. 84, pp. 181–196. Birkhäuser, Basel (1988)
Loridan, P., Morgan, J.: Weak via strong Stackelberg problem: new results. J. Global Optim. 8(3), 263–287 (1996). Hierarchical and bilevel programming
Lucchetti, R., Mignanego, F., Pieri, G.: Existence theorems of equilibrium points in Stackelberg games with constraints. Optimization 18(6), 857–866 (1987)
Maranas, C.D., Floudas, C.A.: Global minimum potential energy conformations of small molecules. J. Global Optim. 4(2), 135–170 (1994)
Migdalas, A.: Bilevel programming in traffic planning: models, methods and challenge. J. Global Optim. 7(4), 381–405 (1995)
Mirrlees, J.A.: The theory of moral hazard and unobservable behaviour: Part I. Rev. Econ. Stud. 66(1), 3–21 (1999)
Mitsos, A.: Global solution of nonlinear mixed-integer bilevel programs. J. Global Optim. 47(4), 557–582 (2010)
Mitsos, A.: Global optimization of semi-infinite programs via restriction of the right-hand side. Optimization 60(10–11), 1291–1308 (2011)
Mitsos, A., Barton, P.I.: Issues in the development of global optimization algorithms for bilevel programs with a nonconvex inner program. Tech. rep., Massachusetts Institute of Technology (2006)
Mitsos, A., Barton, P.I.: A Test Set for Bilevel Programs. Tech. rep., Massachusetts Institute of Technology (2010). http://yoric.mit.edu/sites/default/files/bileveltestset.pdf
Mitsos, A., Bollas, G.M., Barton, P.I.: Bilevel optimization formulation for parameter estimation in liquid–liquid phase equilibrium problems. Chem. Eng. Sci. 64(3), 548–559 (2009)
Mitsos, A., Lemonidis, P., Barton, P.I.: Global solution of bilevel programs with a nonconvex inner program. J. Global Optim. 42(4), 475–513 (2008)
Mitsos, A., Lemonidis, P., Lee, C.K., Barton, P.I.: Relaxation-based bounds for semi-infinite programs. SIAM J. Optim. 19(1), 77–113 (2008)
Outrata, J., Kočvara, M., Zowe, J.: Nonsmooth approach to optimization problems with equilibrium constraints, Nonconvex Optimization and its Applications, vol. 28. Kluwer, Dordrecht (1998). Theory, applications and numerical results
Pardalos, P.M., Romeijn, H.E., Tuy, H.: Recent developments and trends in global optimization. J. Comput. Appl. Math. 124(1–2), 209–228 (2000)
Pereira, F.E., Jackson, G., Galindo, A., Adjiman, C.S.: The HELD algorithm for multicomponent, multiphase equilibrium calculations with generic equations of state. Comput. Chem. Eng. 36, 99–118 (2012)
Ryu, J.H., Dua, V., Pistikopoulos, E.N.: A bilevel programming framework for enterprise-wide process networks under uncertainty. Comput. Chem. Eng. 28(6–7), 1121–1129 (2004)
Sahin, K.H., Ciric, A.R.: A dual temperature simulated annealing approach for solving bilevel programming problems. Comput. Chem. Eng. 23(1), 11–25 (1998)
Stein, O., Still, G.: On generalized semi-infinite optimization and bilevel optimization. Eur. J. Oper. Res. 142(3), 444–462 (2002)
Stein, O., Still, G.: Solving semi-infinite optimization problems with interior point techniques. SIAM J. Control Optim. 42(3), 769–788 (2003)
Still, G.: Generalized semi-infinite programming: numerical aspects. Optimization 49(3), 223–242 (2001)
Still, G.: Solving generalized semi-infinite programs by reduction to simpler problems. Optimization 53(1), 19–38 (2004)
Tawarmalani, M., Sahinidis, N.V.: Convexification and Global Optimization in Continuous and Mixed-Integer Nonlinear Programming, Nonconvex Optimization and its Applications, vol. 65. Kluwer, Dordrecht (2002)
Tsoukalas, A.: Global Optimization Algorithms for Multi-level and Generalized Semi-infinite Problems. Ph.D. thesis, Imperial College London (2009)
Tsoukalas, A., Parpas, P., Rustem, B.: A smoothing algorithm for finite min-max-min problems. Optim. Lett. 3(1), 49–62 (2009)
Tsoukalas, A., Rustem, B., Pistikopoulos, E.N.: A global optimization algorithm for generalized semi-infinite, continuous minimax with coupled constraints and bi-level problems. J. Global Optim. 44(2), 235–250 (2009)
Tsoukalas, A., Wiesemann, W., Rustem, B.: Global optimisation of pessimistic bi-level problems. In: Lectures on Global Optimization, Fields Inst. Commun., vol. 55, pp. 215–243 (2009)
Tuy, H.: Convex Analysis and Global Optimization, Nonconvex Optimization and its Applications, vol. 22. Kluwer, Dordrecht (1998)
Vicente, L.N., Calamai, P.H.: Bilevel and multilevel programming: a bibliography review. J. Global Optim. 5(3), 291–306 (1994)
Vicente, L.N., Calamai, P.H.: Geometry and local optimality conditions for bilevel programs with quadratic strictly convex lower levels. In: Du, D., Pardalos, P.M. (eds.) Minimax and Applications. Kluwer, Dordrecht (1995)
Visweswaran, V., Floudas, C.A., Ierapetritou, M.G., Pistikopoulos, E.N.: A decomposition-based global optimization approach for solving bilevel linear and quadratic programs. In: State of the Art in Global Optimization (Princeton, NJ, 1995), Nonconvex Optim. Appl., vol. 7, pp. 139–162. Kluwer, Dordrecht (1996)
Ye, J.J.: Constraint qualifications and KKT conditions for bilevel programming problems. Math. Oper. Res. 31(4), 811–824 (2006)
Yezza, A.: First-order necessary optimality conditions for general bilevel programming problems. J. Optim. Theory Appl. 89(1), 189–219 (1996)
Acknowledgments
We gratefully acknowledge funding by the Leverhulme Trust through the Philip Leverhulme Prize and by the EPSRC through a Leadership Fellowship [EP/J003840/1]. We also thank two anonymous referees for their thorough and insightful comments that helped us to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Kleniati, PM., Adjiman, C.S. Branch-and-Sandwich: a deterministic global optimization algorithm for optimistic bilevel programming problems. Part I: Theoretical development. J Glob Optim 60, 425–458 (2014). https://doi.org/10.1007/s10898-013-0121-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-013-0121-7