Abstract
LPPFusion is developing a source of fusion energy using the dense plasma focus device and p-B11 fuel, a combination we call Focus Fusion. So far, this project has led to the achievement of the highest confined ion energies of any fusion experiment (> 200 keV) as well as, recently, the lowest impurities of any fusion plasma. Among privately-funded fusion efforts, our experiments have achieved the highest ratio of fusion energy generation to device energy input (wall-plug efficiency) and the highest nτT product of 3.4 × 1020 keV-s/m3. Our calculations and simulations indicate that the quantum magnetic field effect will allow a great reduction in bremsstrahlung radiation with p-B11 fuel. For commercial fusion, this approach has several major advantages. The small size and simplicity of design of the DPF can lead to 5 MW generators that are much cheaper than any existing energy source, that can be manufactured by mass production and that can be located close to loads. It shares with other p-B11 approaches a lack of neutron damage and radioactive waste. Direct energy conversion of the ion beam and x-rays produced by the device avoids the high costs associated with thermal cycles. With adequate, but still modest, financial resources we anticipate working prototype generators could be ready for production by 2026–2030.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction—the Promise of p-B11 Fusion Fuel
Controlled nuclear fusion using hydrogen-boron-11 (p-B11) fuel would constitute a transformative source of electricity with major advantages over any other known source of energy. No neutrons are produced in this reaction, p + B11 → 3He4, and the released energy is carried only by charged particles. This makes possible the direct conversion of the kinetic energy of these charged particles into electricity without going through the inherently expensive process of using heat to produce steam to run a turbine and generator. It thus opens up the possibly of drastically reducing the cost of electricity generation.
While a secondary reaction, He4 + B11 → N14 + n, does produce neutrons, they carry only 0.2% of the fusion energy and are low-energy neutrons, which are easily shielded. Thus, this fuel makes conceivable the design of a generator that produces insignificant amounts of induced radioactivity, and no radioactive waste. These characteristics give p-B11 very significant operational advantages over deuterium–tritium (DT) fuel.
However, p-B11 presents two major technical challenges that have discouraged funding and research. First, the reaction requires average ion energies above 100 keV, considerably higher than the 40 keV envisioned for DT fuel, and the requirement for plasma density-confinement time product (nτ) is also a factor of 15 times higher for net energy production. Second, the higher atomic charge of boron ions leads to the production of far greater amounts of X-ray energy than with DT, and the emission of such X-ray energy cools the plasma, making plasma heating more difficult. We have taken steps to show how both of these technical challenges can be overcome using the dense plasma focus (DPF) device. We call the combination of p-B11 fuel with the DPF device the “Focus Fusion” approach.
Dense Plasma Focus (DPF)
The DPF is a compact and simple device first developed in the 1960s by N. V. Filippov in the USSR and by J. W. Mather in the USA and has been studied by dozens of groups over the last 60 years, resulting a large and rich literature. It consists of two concentric electrodes enclosed in a vacuum chamber. The chamber is evacuated to low pressure and then backfilled to several torr with the fuel gas. A pulse of electricity with a rise time of 0.2–10 μs from a capacitor bank is discharged across the electrodes during operation. In operation, the capacitors discharge in a pulse, the gas is ionized and a current sheath, consisting of pinched current filaments, forms and runs down the electrodes [1].
When the sheath reaches the end of the inner electrode (the anode), the filaments pinch together, forming dense, magnetically-confined, hot spots or plasmoids [2, 3]. The plasmoids emit x-rays with energy from several keV to over 100 keV. X-ray pinhole images have demonstrated that the plasmoids are tiny, with radii of tens of microns or less [4,5,6,7,8]. The plasmoids have electron densities in the range of 1019—1022/cm3 [9]. These densities have been measured by a number of independent methods including laser interferometry [10], heavy ion and secondary product fusion [11], CO2 laser scattering [12], and x-ray line intensities [13]. These plasmoids emit intense beams of accelerated ions and electrons [14,15,16]. Fusion neutrons are emitted from the device in large quantities (up to 1013) per shot.
The DPF routinely produces hard x-rays and gamma rays indicating the presence of bremsstrahlung radiation from high-energy electrons colliding with nuclei [17]. Together with independent evidence, this indicated that the hot spots contained ions and electrons at very high energies in the range of interest for advanced-fuel fusion [3, 12, 18].
The role of the plasmoids in producing the fusion neutrons and the physical processes involved in their formation and maintenance was hotly debated among DPF researchers for decades. In recent years, however, DPF researchers have developed a consensus on the role of the plasmoids. In 2019 the International Scientific Committee on Dense Magnetized Plasmas, an organization of DPF researchers, unanimously agreed that “In DPF devices with large peak currents and with deuterium fill gas, most of the neutron emission is due to deuterons with mean energy of the order of 100 keV which are confined in limited volumes for times that are long compared with the crossing time of these volumes.” [19]
The model that best fits all the existing data makes the role of the plasmoids central to neutron production. This model, was initially developed by Bostick and Nardi [1], and confirmed by observations of several groups over three decades.
The Bostick-Nardi model describes the DPF as operating by exploiting a series of natural instabilities in the plasma, with each instability further concentrating the plasma and the magnetic field produced by the currents running through the plasma. In the past few decades, substantial advances have occurred in understanding the basic physics of such instabilities through experiments and observations of space plasma.
In the first instability, the current sheath moving through the plasma between electrodes breaks up into an array of filaments, (Fig. 1A) increasing the density of the plasma and magnetic field strength by a factor of 10–20. The filamentary current sheath, driven by the interaction of its own currents and magnetic field, travels down to the end of the inner hollow electrode, where the filaments converge into a single central pinch region, further concentrating both plasma and magnetic fields (B). A third instability then kinks the single central filament (C, D) like an over-twisted phone cord, forming a plasmoid, (E) an extremely dense, magnetically self-confined ball of plasma only tens of microns across. By this time, the density and magnetic fields of the plasma in this small region are tens of thousands of times larger than those present at the start of the process, and a substantial fraction of the energy fed into the device is contained in the plasmoid. A fourth instability causes the magnetic fields at the center of plasmoid to decrease, and these changing magnetic fields induce an electric field, which generates a beam of electrons in one direction and a beam of ions in the other (F). The ions during this process have become highly energetic, initiating fusion reactions. The energy is released in the ion and electron beams and in a burst of x-ray energy from the heated electrons in the plasmoid.
Stages in the plasma focus process. See text for detailed description. Video available here: https://www.youtube.com/watch?v=6ajqD0hoOMw&t=228s credit: Torulf Greek for LPPFusion
The DPF has several large advantages over other fusion devices. It is extremely compact, with electrode on the order of cm in diameter and with an entire device that can fit in a small room. It is also very simple in construction, without either the need for external magnets nor lasers. Both of these features make it extremely economical, with powerful experimental devices, like LPPFusion’s FF-1 and FF-2B, being constructed for less than $500,000. The DPF also has the advantage that the plasmoid is extremely dense. Such a dense plasmoid requires that the ions be confined for only a few thousand orbits, in contrast to the millions of orbits required in tokamaks or most other fusion devices. Thus, the high stability of such devices is not required in the DPF, only meta-stability.
Finally, and perhaps most important, the DPF is unique in attempting to use the natural filamentation instabilities of the plasma to concentrate its energy, rather than trying to fight these instabilities to produce a stable plasma, as in all other fusion devices. This potentially makes the task much easier, allowing the possibility of reaching important scientific and commercial goals without large resources.
However, the DPF faces significant challenges as well. The biggest is that the fusion yield from the device, as a fraction of energy input, the critical “wall-plug efficiency”, has not advanced in 20 years. For DPF with lower current, I, fusion yield increases rapidly with increasing current, by more than I4. Since the input energy of the device increases by about I2, the ratio of fusion energy to input energy, the wall-plug efficiency, also increases with I2, as seen in Fig. 2. However, above about 1MA peak current, this increase flattens into a plateau. As a result, the highest wall-plug efficiency was achieved in 2001 with the Speed-2 device, which produced 1 J of fusion yield with pure D fill gas for an input to the device of 80 kJ, for a wall-plug efficiency of 1.25 × 10−5. While this was actually the highest efficiency achieved by any fusion experiment anywhere using D fuel, it has not yet been exceeded.
Up to peak currents of 1 MA, DPF fusion yield rises sharply with increasing current, but plateaus above 1 MA. At lower currents, FF-1’s performance exceeds those of other DPFs, but was comparable to other best results at 1 MA. Data is from M. Milanese and J. Pouzo [20], except for U of Illinois and FF-1
For the DPF to succeed as a fusion device, the causes of this plateau must be understood and the sharp increase of yield with current resumed. In the past several years, LPPFusion has taken large steps both in theoretical work and experimental results to overcome this problem and pave the way to the achievement of commercial fusion energy with the Focus Fusion approach.
Theoretical Advances by LPPFusion Researchers
Quantitative Model of DPF Functioning
Basing his work on the general Bostick-Nardi model, Lerner elaborated a model of plasmoid formation, first in an astrophysical context [21], and then as a quantitative description of the DPF [22]. In this model, the DPF process can be described using only a few basic assumptions. These are that during the compression into the pinch the ratio B/n, magnetic field/particle density, is a constant as the ions are constrained to move along magnetic field lines; and that the plasmoid compresses until the synchrotron frequency (the frequency that the electrons radiate at) exceeds twice the plasma frequency, the natural oscillation frequency of the plasma. At this point the energy can be radiated, the current begins to drop, and the change in the magnetic field sets up large accelerating potentials that sustain the current. This in turn generates the ion and electron beams that release the energy trapped in the plasmoid and initiate its decay.
From these basic physical relations, it is simple algebra to derive the plasma parameters in the plasmoid, not only for hydrogen, but for any gas or mixture of gases [22]. The results are summarized here:
where B is peak field at cathode (G), Bc is the field in the core of the plasmoid, r is cathode radius (cm), rc is the plasmoid core radius, nc is plasmoid ion density, I is peak current (A), μ is average ionic mass, z is ionic charge, Y is fusion reaction number and f(Ti) is the reaction rate as a function of ion temperature Ti.
The key conclusions, evident in Eq. 4, are that the I4 yield scaling is correctly predicted by the model and that the yield should increase with increasing atomic mass of the fill gas, thus indicating that, independently of the greater reactivity of p-B11, the expected yields for this fuel would be more than 10 times greater than for D, an encouraging result.
Equally important, Eq. 2 indicated that with higher-z fuels such as p-B11, extremely high magnetic fields could be reached within the DPF plasmoid. For example, with B = 100kG, a reachable value, Bc = 10GG, a field ten times higher than had ever been observed in laboratory experiments of any type. The potential for achieving such field led to a second major theoretical advance, the recognition of the importance of the quantum magnetic field effect.
Quantum Magnetic Field (QMF) Effect
In 2003, Lerner theoretically showed [17] that the problem of high X-ray emission with p-B11 could be mitigated through the use of the QMF effect. This effect, first pointed out in the 1970’s, [23] and studied in the case of neutron stars [24], involves the reduction of energy transfer from ions to electrons in the presence of a strong magnetic field. In a DPF plasmoid, as in most fusion plasmas, the plasma is strongly magnetized, meaning that the ions and electrons circle around the magnetic field lines many times before they undergo a collision. For the ions, this results in their velocity vector being closely aligned with the local direction of the magnetic field [17].
In collisions between charged particles, momentum transfer can only occur in the direction perpendicular to the direction of motion. (Somewhat the same way pedestrians move sideways to avoid each other on a busy sidewalk). So for an ion moving along a magnetic field line (in the direction of the magnetic field) to transfer energy to an electron, the electron must move away from the magnetic field direction, acquiring more angular momentum as it moves in a wider circle around the field direction.
In a strong magnetic field, since angular momentum is quantized in units of ħ, electrons can have only discrete energy levels, termed Landau levels (ignoring motion parallel to the magnetic field):
Since maximum momentum transfer is mv, where v is relative velocity, for mv2/2 < Eb almost no excitation of electrons to the next Landau level can occur, so very little energy can be transferred to the electrons in such collisions. Again, ignoring the electron's own motion along the field lines, such a condition will occur when ion energy
For Ei = 300 keV, this implies B > 14GG for p, B > 3.5GG for α, and B > 1.3GG for 11B. As shown in the previous section, such field strengths should be attainable with the DPF. In fact, detailed analysis shows that the effect starts to become important at considerably weaker fields.
As calculated [17], for T = Ti/Eb(M/m) < 1, the energy transfer rate can be reduced by a factor as large as 25 for the heating of electrons by ions, which can only heat electrons that are moving slower than the ions. For the heating of the ions by the much faster thermal electrons, with Te/Eb > > 1, quantum effects can be ignored and the coulomb logarithm in the collision rate formula is simply ln (2 Te/Eb) with no reduction from the classical result. As a result, the ratio of these two heating rates can be as high as 25, which results in a similar value for Ti/Te. This results in a reduction of x-ray emission by as much as a factor of five.
We have performed many simulations of the plasmoid which include this QMF effect, starting in 2005 [17] which show that in this case fusion power can potentially exceed bremsstrahlung emission by as much as a factor of 2, allowing ignition of the fuel and an 80% burn-up of the fuel in the plasmoid (Fig. 3). These 0-D simulations assume the plasmoid is a uniform sphere, so are not fully realistic, but they are adequate to show the impact of the magnetic effect and the possibility for high fusion yields in which the energy emitted in the form of x-rays and ion beams exceeds the total energy input to the plasmoid by at least a factor of two. LPPFusion Simulation Researcher Dr. Warwick Dumas is currently working on a 2-D version of the plasmoid simulation.
Simulations of plasmoid with p-B11 fuel, showing evolution of ion temperature (upper left), electron temperature (upper right) and unburnt fraction of fuel in plasmoid (bottom) Note different scales for ions and electrons. In this run, plasmoid minimum radius is 14 microns and maximum ion density is 4 × 1023/cm 3
Other researchers have reached similar conclusions about the impact of QMFE on p-B11 fuel in the DPF. Abolhasani et al. [25] in 2012 found even more encouraging results, with fusion yield approximately 6 times the input energy.
The QMFE thus allows the existence of conditions in which ignition can occur with p-B11 fuel. At the same time, the necessity of high magnetic fields requires small electrode radii, as shown in Eq. 2—for a given peak current, the B field is maximized with the smallest electrode radius. This consideration led directly to LPPFusion’s patenting of DPF designs with small radii and large magnetic fields [26]. The large magnetic fields required for this effect are achievable only with the DPF or with lasers, so constitute another strong advantage for these two approaches to p-B11 fusion over all others that have much lower B fields.
Control of Angular Momentum and Efficiency of Energy Transfer to the Plasmoid
The appropriate choice of cathode radius, peak current and fill pressure is not enough to ensure the efficient formation of a plasmoid that contains the full magnetic energy input to the device. In fact, in few of the existing DPF devices is the efficiency of energy transfer into the plasmoid very high, limiting yield to well below that predicted by the model described in the Sect. "Quantitative Model of DPF Functioning". For high efficiency, control of angular momentum is required, as first pointed out by Lerner and Blake [26] and elaborated by Lerner, Murali and Haboub [22].
The process of plasmoid formation involves the development of a kink instability in the current flow at the pinch and as such requires a certain amount of angular momentum. We here refer to total angular momentum, both of the magnetic field and of the particles. Another way of looking at this is that the axial field/ azimuthal field ratio has to be sufficient for the kinking to occur. During the compression phase, angular momentum per unit mass is conserved, so this angular momentum can be derived from angular momentum present in the filament array at the time the compression begins. An approximate measure of the angular momentum per unit mass required can be obtained by the formula 0.5 vAr, where vA is the Alfven’s velocity in the plasmoid and r is the plasmoid radius.
Angular momentum can be imparted to the plasma sheath during the rundown by the interaction of the inward flowing electron flows and any small initial axial magnetic field (e.g., the small axial component of the earth’s magnetic field). The J × B force accelerates the electrons slightly in the azimuthal direction, creating an azimuthal component to the current. This in turn increases the axial magnetic field and thus the azimuthal acceleration of the electrons. In this way, a very small initial magnetic field (or small, random initial azimuthal component in the current created by irregularities in the electrodes) can be rapidly magnified.
For example, given a ratio of axial to total magnetic field Bθ/BT = sin θ then any initial axial field will be amplified so that at the end of the run down θ = θieVτ/R, where τ is the run down time and R is the anode radius. Thus final angular momentum per unit mass is vR θievτ/R where v is the Alfven velocity at the anode radius at peak current. This is a simplified analysis, as in the real case BT is rising rapidly during the early stages of the pulse. However, a numerical analysis using a realistic function for BT shows a very similar result, as at later times, the magnitude of the initial axial field is very small compared with BT, so the amplified field dominates, as in the simplified formula.
Since vτ/r is proportional to L/R, the angular momentum is sensitively dependent on this ratio. If there is insufficient angular momentum, the plasmoid radius will be reduced in proportion to angular momentum and the total plasmoid energy and mass will be reduced as the cube of angular momentum. This sensitivity to initial very small angular momentum can in part explain the well-known shot-to-shot variability of plasma focus devices. Calculations show that if this natural amplification mechanism is relied on to provide angular momentum and the initial magnetic field is the earth’s ambient field, L/R must be more than about 7 for high efficiency of energy transfer into the plasmoid. Indeed, in the best-performing DPF devices, this ratio exceeds 7 and can be as high as 17, implying that high vA and longer τ are desirable.
The disadvantage of such long electrodes is their high inductance, around 20 nH. Since external inductance must exceed load inductance, total inductance in the system must be around about 45 nH. As Lee [27] has shown, these considerations lead to limitations on the total amount of current that can be fed into the DPF from a capacitor bank, as the pulse length must increase as capacitance does, unless the charging voltage becomes very high. The high inductance, by forcing up total bank energy, reduces the proportion of that energy that can be converted into the DPF magnetic field. So even if the efficiency of energy transfer from the magnetic field to the plasmoid increases, the total efficiency from capacitor bank to plasmoid does not necessarily increase.
The alternative to relying on amplification of the ambient magnetic field, is to inject angular momentum with a small artificial axial magnetic field, produced by a helical coil. While there have been previous efforts to stabilize DPF pinches with axial fields, these fields have been much greater than those contemplated here, generally thousands of G. If the model described here is valid, too much angular momentum will prevent the plasmoid from being formed and thus drastically reduce fusion yield. Only the optimal amount of field, of the order of a few G, will provide enough angular momentum to just balance the compressional pinch forces and form the largest possible plasmoid. The axial field coil concept is also an integral part of LPPFusion’s main patent [26].
Viscous, Induced Current and Lower Hybrid Heating Mechanisms
Until the last decade, it was not entirely clear how the high ion and electron energies observed in the plasmoids were produced. But here, too, we have made considerable progress, together with others studying the DPF. In 2012, Abolhasani, Habibi and Amrollahi, [25] basing themselves on earlier work by Haines on the z-pinch [28], proposed that the ions in the plasmoid were heated by viscous heating. In this process, as the plasmoid contracts, ions moving inward at different velocities start to mix together, so that their ordered velocity of motion is converted into the random velocity of heat. By analogy this is a bit like trying to rapidly stir a viscous liquid like honey. A more dramatic analogy would be the motion of autos on a highway, which have high ordered motion, but little random motion relative to each other. If, in some catastrophe, the Eastbound and Westbound lanes on a highway were merged, the ordered kinetic energy would be converted to random energy in many collisions. This would be massively undesirable traffic engineering, but is favorable, by analogy, for fusion.
Lerner and Talaei [29] elaborated on this work deriving a formula for expected ion temperature from viscous heating:
where zeff = (\(\sum {{\text{fz}}^{2} }\)) ½, f is the number fraction of a given ion, z is the ionic charge and the summation is over all ions. zeff is thus a dimensionless number, the effective number of charges per ion. Lmax is the distance around the plasmoid, which in our model is 9.7(μz) 1/3 Lp, where Lp is the observed length of the plasmoid core along its axis. Ti is the ion temperature in eV. This formula produced good agreement with observation, as will be detailed in Sect. "Experimental Results". It again indicated that higher Ti could be expected with higher-z fill gas. In addition, the dependency on B and n led to an expectation that Ti ~ r0.4, cathode radius, again indicating that fusion yield would increase with smaller electrodes, and decrease with larger ones, even well short of conditions where QMFE would be relevant. This relation with r provided a partial explanation of the plateauing of fusion yield in larger DPFs, since many of them also had larger-radius electrodes, although it was not the full story.
At the same time, Lerner and Talaei [29] showed that another process could explain the high temperature of the electrons. The electron beam will induce currents in the plasmoid electrons, just as any rapidly changing current induces other currents in a surrounding conductor. But since the plasmoid has a much greater density of electrons that the beam, the same current will be distributed over more electrons, and they will be moving much slower than the beam electrons. These slower electrons will have the time to undergo collisions and convert their kinetic energy to heat. They derive the following formula for Te:
where rb is the beam radius and γ is the relativistic factor for the beam electrons. Again, we will find in Sect. "Experimental Results" that this produces results close to observations.
For the densest plasmoids, a preliminary examination has indicated that the lower hybrid instability will lead to wave heating of the ions by the electron beam, so that for current more than:
the majority of the electron beam energy will go to ion heating, rather than electron heating.
Role of Impurities in Disrupting Filaments and Source of Impurities
As our experimental program advanced, we saw that high-z impurities in the plasma were limiting fusion yield. Because such impurities increase radiation, they have been a problem for nearly all fusion devices. In DPF devices, such impurities decrease the conductivity of the plasma in the current-carrying sheath, leading to disruption of current filaments through over-heating. The elimination of the filaments, combined with enhanced radiation from the impurities, limits the density in the current sheath. This in turn leads to lower plasma density and thus lower fusion yield in the plasmoid. In addition, the disruption of the highly magnetized filaments allows the formation of additional current sheaths, draining energy from the plasmoid and further reducing fusion yield. Third, the unequal distribution of impurities leads to asymmetric compression, also reducing density and yield.
In 2017, Lerner et al. [30] showed that the purity requirements for preserving the filaments until the pinch could be quantified simply by specifying that the hydrodynamic dissipation of energy, which decreased with filamentation, exceed the electrical resistive dissipation, which increased with filamentation. This led to the requirement that
where re is the classical radius of the electron, ra is the radius of the anode, Mp and me are the masses of the proton and electron respectively, N the number of filaments in the sheath and β is vA/c. For impurities that are evenly spread in the plasma, this is not a very demanding criterion, since it requires fzi2 < 11 for deuterium and < 17 for p-B11. However, we determined that the impurities were entering the plasma at the start of the pulse. For them to be diluted early enough for the filaments to form, the impurities at the end of the rundown had to be held to fzi2 < 1.4 or zeff < 1.2, a much more rigorous requirement.
Observations showed that two sources of impurities were arcing between the metal components of our electrodes and vaporization of insulating oxide layers on the electrodes’ surface. We describe our mitigations of these source in Sect. "Experimental Results". But we also theoretically determined that there was an additional source of impurities, caused by runaway electrons generated during the first ns of the breakdown process at the start of the pulse. [30, 31] These high-energy electrons released energy and vaporized the anode near the insulator. We found that they could be eliminated by a small pre-ionization current. This current created sufficient number of free electrons prior to the pulse so that the initial breakdown current was carried by a greater number of electrons, reducing the energy released at the anode below the threshold needed for vaporization.
The increasing presence of impurities generated at higher and higher currents is what we hypothesize to be the main, although not the only, reason for the plateauing of fusion yield in DPF devices with peak I > 1MA.
Experimental Results
Experimental Device
LPPFusion constructed the FF-1 DPF experimental fusion device during 2009 for a cost of close to $500,000 and the device started operation in November of that year. The current was supplied by a bank of 12 capacitors with a total capacitance of 113 microfarads, a maximum charge of 45 kV and a maximum stored energy of 115 kJ. We also routinely ran the device in an 8-capacitor configuration. In our experiments, we increased the charging voltage from 24 to 40 kV and the peak current to slightly over 1MA, (with 8 capacitors) with a rise time of 1.8 microsecond. Our device is one of a less than half a dozen MA DPFs in operation in the world.
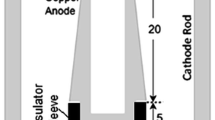
The anode is 2.8 cm in radius, with a length beyond the insulator that varied, depending on our set-up, from 6.6 to 10.6 cm, with a total length of 10-14 cm. The cathode was a ring of conductors 5 cm in radius and the electrodes were housed in a 10-cm radius vacuum chamber with a drift tube attached to the bottom for measurements of the ion beam. The entire device fits within a small room 4 m on a side.
We equipped the device with an extensive array of diagnostic instruments including a Stanford Optics ICCD camera with 0.2 ns minimum exposure time, a silver activation neutron detector, five scintillator-photomultiplier tubes to measure both x-rays and neutrons with 1 ns time resolution, multiple neutron bubble detectors, a main Rogowski coil to measure the current in the device and two beam Rogowski coils to measure ion beam current and energy, a high voltage probe, a time-integrated optical spectrometer, and light detectors to measure the firing time of each switch.
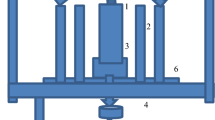
In 2019, we changed the main electrodes to beryllium, and made changes in the external circuits to prepare for remote functioning with p-B11 fuel. These changes were sufficiently important that we then renamed the device FF-2B (Figs. 4 and 5).
High Efficiency Energy Transfer to the Plasmoid
One of the initial goals of our experimental effort was to demonstrate that our compact DPF could achieve a high efficiency of energy transfer into the plasmoid. We could measure the energy emitted from the plasmoid in the form of the ion beam. We demonstrated that this beam did originate from the plasmoid as the beam timing was closely matched to the time of formation of the plasmoid as recorded by the ICCD images. [32, 33]. In relatively early shots we already were measuring ion beams with total energy of 1 kJ.
By 2013, we had improved efficiency so our highest-powered beam, observed Feb 28, 2013 had a peak current of 120kA, a mean ion energy (measured by time-of flight) of 3 MeV, a duration of 5 ns and a total energy of 2 kJ. (Fig. 6). Since the electron beam in the opposite direction was accelerated by the same field, the energy in the two beams was 4 kJ.
This was over 6% of total bank energy, and 12% of the electric energy released by the capacitors prior to the pinch. Most relevantly it was 80% of the magnetic field energy in the current sheath at the time of the pinch, showing highly efficient concentration of energy into the plasmoid.
The actual energy in the beam is probably somewhat higher than this estimate, since, as can be seen in Fig. 6, the initial section of the ion beam (positive current) is followed by a current-neutralizing electron beam (negative current), which may well cancel out the magnetic field for a tailing part of the ion beam. However, this will not be a large effect, as we know that the duration of the electron beam emitted in the opposite direction from the plasmoid is always close to the duration of the ion beam as measured by the positive pulse in the Rogowski coil.
Subsequent analysis of later shots showed that the inductance of the device increased by close to 10nH during the best pinches, also corresponding to an energy transfer into the pinch of 4–5 kJ.
This high efficiency of energy transfer makes it easier for the DPF to achieve net energy than, for example, with laser devices where less than 1% of input energy reaches the plasma.
World-Record Confined Ion Energy
In 2012, LPPFusion published experimental evidence of confined ion energy in our FF-1 plasmoids exceeding 150 keV, a record for any DPF device [33]. In 2017 we broke our own record, publishing evidence of confined ion energies in excess of 200 keV, with the best shot having a mean ion energy of 240 keV ± 20 keV which we reported as a record for any type of fusion device [30]. In both these papers, we demonstrated that an isotropic distribution of the neutrons as measured by bubble detectors located in both the axial and horizontal directions ruled out an anisotropic origin of the neutrons in an unconfined beam. We also demonstrated in both these papers that the ion energies measured by time-of-flight neutron detector in the horizontal plane perpendicular to the axis could only be produced by ions confined to orbits.
We addressed in the 2017 paper the possibility that the ions producing the neutrons were only the high-energy component of a two-component plasma, with an additional denser, low-ion-energy component. We found no evidence of such a low-ion-energy plasma component. The distribution of neutron arrival times was sufficiently close to the Gaussian distribution expected for a Maxwellian velocity distribution that we could exclude, for a wide range of hypothesized parameters, any relatively low-energy, dense background plasma colliding with a 500 keV fast ion population to produce collisions with 250 keV average energy. The low-energy ions would produce a central, sharply peaked distribution of neutron arrival times while the high-energy ions colliding with each other would produce greater-than-Gaussian wings to the arrival time distribution. We observed neither. (see Fig. 7).
PMT signals at 11.5 m (NTF, red) and 17.5 m (FTF, blue) plotted against neutron energy, determined by time of flight. The vertical scale of the NTF signal is expanded to match that of the FTF. The spread in neutron arrival times reflects the spread in velocities, which is in turn a measure of ion energies. There is good agreement with a mean ion energy of 240 keV
The observed high ion energies agreed with predictions from the viscous heating hypothesis. In 2017, we used a number of techniques to estimate zeff at about 3. Using the estimated densities and B field and measured length of the plasmoid, we can use Eq. (7) to derive a predicted Ti from viscous heating. This is 113 keV, a factor 2 short of the highest mean ion energy, but in good agreement with the mean for a ten-shot series, 124 keV. The higher value of Ti could have resulted from random 50% increase in the impurity level from shot to shot.
A viscous heating process would in fact lead to a Maxwellian distribution of velocities even though the collision time for individual ions was much longer than the lifetime of the plasmoid. This is due to the stochastic or random nature of the viscous process.
Since the question of the existence of a cold component of the plasma is important for projecting the scaling of the DPF results, we revisited this question in 2019, when improvements in plasma purity (described in Sect. "World Record Fusion Plasma Purity") allowed us to use calibrated x-ray measurements to determine the total plasma density. The x-ray pulse is a result of hot electron collisions with all ions, not just with hot ions, so the total ion density is measured by the quantity of x-rays emitted. However, since the emitted x-ray energy also is proportional to zeff 2, an unambiguous measurement can only be obtained if it is known that zeff ~ 1, as we determined it to be in our more recent experiments.
Using calibrated medical x-rays detectors to absolutely calibrate our PMTs, we found that the total ion density as measured by x-ray emission was 0.8–2.5 times the density of hot ions, as measured by neutron emission. This leaves very little room for a cold component in the plasma. We can improve on these limits in future experiments.
The importance of these confined ion energies is that they achieve the values that are needed to ignite burning of p-B11 fuel if sufficient density (and magnetic fields) can be obtained. If there is no low-energy component in the plasma, and we have seen no evidence of such, the viscous heating hypothesis indicates that even higher ion temperatures will be achieved at the higher densities and magnetic fields, providing a clear path to net energy with p-B11.
Highest Wall-Plug Efficiency Among Private Fusion Efforts
The same series of experiments that produced the world-record confined ion energies also produced a significant increase in FF-1’s fusion yield, leading to a new record among private fusion companies in wall-plug efficiency, \({\upeta }\). Wall-plug efficiency is a key measure of how close a device is to producing net energy. It is defined as the total energy out of a device divided by the total energy into the device and must exceed 1 for net energy production.
A record yield of 2.5 ± 0.25 × 1011 neutrons was recorded in the best shot of this 2016 series, (May 23, shot 1) with an energy release of 0.2 ± 0.02 J. The energy input to the device capacitors, the total energy fed to the device, was 60 kJ, so with the pure D fill gas \({\upeta }\) = 3.3 × 10−6. While this is not a large number, it is close to the largest obtained in any experiments. The record for \({\upeta }\) with D fuel is actually still held by the DPF experiments with Speed-2 in 2001, with \({\upeta }\) = 1.2 × 10−5. The largest reported \({\upeta }\) by a tokamak with pure D fuel, achieved by JET, was 60 kJ output for 10GJ into the device, \({\upeta }\)= 6 × 10−6 [34].
We can find no published peer-reviewed reports of other private fusion efforts obtaining fusion yield with D fuel. However, a HB11 Energy has published results with p-B11 fuel using the LFEX facility in Osaka, Japan. They published [35] a fusion yield of 1.4 × 1011 alpha particles, for an energy release of 66 mJ with a device energy input of 6.5 MJ, yielding \({\upeta }\) = 1.0 × 10−8, a factor of about 300 less than LPPFusion’s result with D, a less reactive fuel.
Of course, LPPFusion’s results remain far from net energy and the current results do not at all necessarily reflect which approach will be able to reach net energy first or at all. However, by this key measure, LPPFusion’s efforts are far ahead of other private efforts and close to the best achieved by any fusion device.
Highest nτT Product Among Private Fusion Efforts
A second widely used measure of fusion device performance is the nτT product, the product of n—ion density, τ—confinement time and T — temperature. As pointed out in Sect. "World-Record Confined Ion Energy", there is no observational reason to believe that the ion velocity distribution is far from Maxwellian in the plasmoid with high mean ion energy and therefore this ion energy can be used as a measure of ion T. All real plasmas deviate somewhat from a true Maxwellian distribution, yet in practice measures of mean ion energy are used as measure of Ti. We can’t state definitively that the velocity distribution is close to Maxwellian either. But we emphasize that there is nothing optimal for fusion applications about a Maxwellian distribution. Recent results from NIF [36], for example, show that a supra-thermal velocity distribution leads to higher fusion yields than one closer to Maxwellian. This again demonstrates that mean ion energy is a good basis for comparisons, especially the order-of-magnitude comparisons made in this section.
In our experiments, the time-resolved outputs of the PMTs give accurate measures of the confinement time of the ions that produce the fusion neutrons, which are close to 40 ns for the best shots.
The ion density is not directly measured in these shots but was accurately estimated on the basis of two independent observations. First, ICCD images show the volume of the plasmoid at the time of neutron emission to be 1.2 × 10−3cm3 as measured with visible light. This light must be emitted from the cooler outer layers of the plasmoid, so the actual fusion-producing volume must be smaller. Combined with the neutron yield and mean ion energy this allows a calculated minimum ion density of 3 × 1019/cm3. At the same time, measurements of the total charge emitted in the ion beams set a lower limit on the density-volume product and thus an upper limit on n (density) from the fusion yield. This upper limit is 4 × 1019/cm3 [33]. We are therefore confident of our density estimate. It represents a relatively modest 20-fold compression over the filling density in these shots of 1.6 × 1018/cm3.
Combining these numbers, we obtain nτT = 3.4 ± 0.8 × 1014 keV-s/cm3 or, in more commonly-used units, 3.4 ± 0.8 × 1020 keV-s/m3.
This value is far above the nτT value published by any other private fusion effort. The highest values we could find in the literature (although not peer-reviewed) were for TAE Technology’s C-2W device with a nτT product of 2.3 × 1017 keV-s/m3, [37] a factor of more than 1,000 less than for FF-1. By comparison, the highest nτT product achieved in any fusion experiment is 5.1 × 1021 keV-s/m3, produced by the NIF laser facility, a factor of 15 higher than that for FF-1.
World Record Fusion Plasma Purity
LPPFusion had achieved the progress in the lab described in Sects. "World-Record Confined Ion Energy"-"Highest nτT Product Among Private Fusion Efforts" by 2017. But much more recently, we have achieved a new world record for purity in a fusion-producing plasma. Reducing impurity levels has long been extremely important in fusion research. First of all, impurity elements can greatly increase radiation that cools the plasma, preventing the achievement of the high temperatures needed for fusion. The impact on the plasma increases as the square of the atomic charge (z), so heavy (high-z) ions like copper, iron, nickel and tungsten are especially damaging to plasma purity.
Second, the erosion processes that produce the impurities by vaporizing device components reduce their lifetime. Finally, the same erosion processes, if fast enough, can cause experimental results to deteriorate during a few months of experiments. LPPFusion’s reduction of plasma impurity levels are better than any achieved elsewhere, and this is a major step forward for fusion energy research.
The results achieved in 2022 were a product of a years’ long experimental and theoretical struggle with impurities in FF-1 and FF-2B. We initially identified four sources of impurities due to the vaporization of the electrodes: arcing between metal parts; vaporization of oxides from the electrode surface; runaway electrons, and; vaporization by the electron beam and blast waves following the pinch, which gave rise to dust and impurities in the subsequent shot.
In 2015–2016 we took a number of steps to mitigate the problems of impurities and arcing:
-
We doubled the length of the vacuum chamber to reduce the blast wave erosion and blowback of material from the chamber bottom.
-
We replaced the copper electrodes which had multiple screwed-together parts with monolithic tungsten electrodes, which had no joints within the vacuum chamber, eliminating all sources of arcing.
-
We used a low temperature bake-out technique to successfully greatly reduce the amount of oxygen in the chamber (which originated in water molecules adsorbed onto metal surfaces.)
-
We coated the stainless-steel vacuum chamber (which emitted oxygen) with TiN.
-
We used preionization currents to eliminate runaway electrons.
These steps succeeded in reducing the zeff only from 4 to 3, [30] but did enable us to produce the record performance in 2016. Our progress in further reducing impurities was hampered first of all by our inability to remove all the oxides from the tungsten electrodes. We found that some oxides had penetrated deeply into the tungsten which had a high degree of porosity (5%) from the manufacturing process. In addition, the higher z of tungsten than copper meant that we had to reduce impurities as measured by number of ions considerably further to obtain lower zeff. The zeff = 3 was obtained with an impurity by number of only 0.16%.
To improve our plasma impurity, we had to eliminate high-z material entirely. We replaced the tungsten electrodes with beryllium electrodes in 2019. This involved taking a number of steps to ensure our staff’s complete safety from toxic beryllium dust. In addition, we redesigned the anode to allow the electron beam to escape to a dump chamber without eroding the anode. These new steps did indeed lead to a dramatic reduction in impurity and in zeff. We were able to reduce the mass of impurities and the contribution of impurities to zeff, (defined as zeff2 -1), by a factor of 30.
However, even then, we had not fully eliminated the erosion problems with oxides. While beryllium is self-passivating, in that the oxide layer does not allow oxygen to penetrate deep into the metal, the 100 nm layer of oxides that forms on Be in air was vaporized in the first shot in 2019, re-depositing as an extensive coating of fine beryllium dust. While this coating was gradually removed with further firing, it clearly gave rise to irregularities in the anode surface and in the current sheath.
In 2022, we inserted a new beryllium anode, which had been hand-polished to remove the thin oxide layer. This polishing dramatically eliminated the initial oxide coating (Fig. 8) and led to a further three-fold reduction in impurities.
Our 2021 polished beryllium anode (left) still shined mirror-bright after three shots in August, 2021. It is viewed through a window on our vacuum chamber. The anode is a bit more than 5 cm in diameter. The colors on the anode seen here are the result of lighting and camera response. The true color of the anode is still silver. In contrast, our first beryllium anode after one shot in 2019 (right) was covered with a dark beryllium oxide dust, which was vaporized and redeposited by FF-2B’s powerful electric currents. This dust coating is what we avoided by our new polishing procedure
The new advance in plasma impurity levels was measured by two independent methods, both relying on our optical spectrometer:
In the first method, we used the spectrometer to measure the thickness of material deposited on our quartz viewing windows. A layer of material that is thin enough to allow light through absorbs short wavelength light (such as blue light) more than long wavelength light (such as red light), introducing a slope in the whole spectrum. The bigger the slope, the thicker the layer of material. By comparing the slopes with a clean window and after dozens of shots, the total rate of deposition can be measured and thus the total amount of impurities from solid material determined.
Our new FF-2B measurements, taken 140 shots after our new anode was installed in 2021, show a decrease in total deposition by a factor of more than 5 compared with our results in 2019. We measured the light absorption through the quartz window at 32 grid points, after removing the window from the vacuum chamber. The deposition pattern had been focused onto the window by the action of the cylindrical sleeve that the window was mounted on, with the window fortuitously located near the focal plane of the cylinder for the distance to the anode axis. The pattern was the result of the imposition of two separate sources, one a vertical strip pattern, clearly produced by plasma streams escaping from the run down sheath through the gaps between the cathode vanes. The second was a centrally-peaked pattern clearly coming from the tip of the anode after the pinch. Analysis of the measurements allowed a calculation that the deposition from plasma moving into the pinch from the current sheath was 6 ± 1 µg per shot and the deposition from plasma moving out of the pinch region was 14 ± 2 µg per shot. We know the amount of gas in the current sheath is 3.3 mg, so the Be impurity level moving into the pinch region is now no more than 0.2% by mass or 0.05% by number of ions. The zeff has thus been reduced to 1.004. Even if all deposition is assumed to come from plasma entering the pinch, zeff = 1.012.
A second method confirmed the reduction in impurity. We took spectra of the plasma near the top of the anode, where the current discharge begins. In Fig. 9, we have plotted a portion of a typical spectrum from 2019 (red line, from Shot 8, June 21, 2019) with a new spectrum (blue line, from shot 1, April 6, 2022). The big peaks, labeled D, come from the deuterium fuel gas, while the small peaks, labeled Be come from beryllium vaporized into the plasma. The lines are broadened into peaks because of the relatively high pressure of the fill gas (deuterium).
The spectra (blue lines) from April 6, 2022 show the more than threefold decrease in the already small beryllium peaks (labeled Be) from our 2019 experiments (red line), as measured relative to the big deuterium peaks (labeled D). Combined with measurements of deposition on vacuum chamber windows, these spectra demonstrate the achievement of record low impurity levels for fusion plasma
The spectra are scaled in this figure so that the intensities of the deuterium peaks at 436 nm are the same. As is clear, measurement of the areas of the small beryllium peaks show that they are nearly 4 times smaller in the new spectra as in the old ones, confirming the decrease in impurities in the plasma that is compressed into the pinch (plasmoid region). We are currently preparing a paper for publication with a more detailed description of these new results.
These results are by a wide margin the best for any fusion plasma. The best result previously claimed by JET is a zeff of 1.2, with zeff -1 a factor of 17 higher than our new result.
Clearly, the achievement of this high purity is only possible because of the inherent advantages of the DPF, in particular its compact size and its high fill gas density, some 104 times higher than for tokamaks. The DPF’s high fill gas density heavily dilutes impurities, making high purity levels easier to achieve.
Current Experimental Challenges and Path to Net energy
In LPPFusion’s experiments with FF-1, we initially obtained yields that, for the peak current we were using, were considerably larger than those that had been obtained previously. However, despite considerable progress as described in the previous section, we are still encountering the yield plateau that occurs at I > 1 MA and we have not yet succeeded in improving our yield beyond the level achieved in 2016, or in exceeding the record yield achieved by Speed-2 in 2001.
We have firm observational evidence that the filaments are now forming at the beginning of the pulse but are being disrupted and disorganized during the run down. In Fig. 10, the process is clear, with a bright region, which we interpret as a shock wave, propagating backwards from the leading edge of the sheath and disrupting the even structure of the filaments as it passes them. Since the pinch process can only achieve high densities if the filaments are organized and symmetrical during the compression phase, this disruption leads to low densities and lower-than predicted yields. The behavior we have observed contrasts with many images from lower-current DPFs (as in [1], for example) which show parallel and symmetrical filament arrays all the way to the pinch region.
ICCD image of filaments in) a current sheath, viewed from the side, between the cathode vanes. The insulator, where the pulse starts from is at lower left. The current sheath moves towards the upper right, towards the end of the anode, off-image. (See video created from separate shots here: https://www.lppfusion.com/iccd-video-reveals-shocks/) The top image, shows well-formed filaments early in run down while the bottom image shows the progressive disruption of the filaments on right by the passage of the shock wave (bright arc separating ordered filament on left from disordered ones on right). The shockwave is traveling leftward from near the forward edge of the current sheath
We attribute the main reason for this filament disruption to problems we have encountered with the external circuits supplying current to the DPF. First, we have not yet been able to obtain completely reliable and repeatable firing of the switches that allow current to flow from the capacitors. Second, we have had significant problems with high-frequency oscillations observed in the current at frequencies from 14–40 MHz which we have reason to believe are disrupting the filaments before they reach the pinch stage. While we can’t yet prove that the oscillations lead to the current disruptions, they are the only phenomena that we know of that happen early enough in the pulse, as the disruptions begin to emerge clearly as early as 300 ns from the start of the current pulse. We also note that the current oscillations in both our device and in published data from other MA DPFs are considerably larger as a fraction of peak current than for smaller DPFs with regular filament arrays.
After considerable redesign, we believe that we are approaching solutions on these problems. We have set up a rapid test facility to test switches without firing the entire bank, which has greatly sped up progress. We achieved reliable firing of a switch pair with this test facility and will soon test the re-designed switches on FF-2B.
Once we resolve these problems, we anticipate a reduction in the radius of the plasmoid to approximately the radius of the typical filaments that we have observed, around 50 microns, assuming our hypothesis is correct that current oscillations disrupt the filament pattern. The correlation between plasmoid size and filament radius has been observed in smaller-current DPFs, and recently in MA-class DPFs [38]. This will be a fivefold reduction in plasmoid radius from our previously observed radius of 250 microns, leading to an approximately 100-fold increase in density and a similar increase in fusion yield to about 25 J.
We calculate that the decreased inductance of the new switches, combined with a transition to a 12-capacitor configuration and an increase in voltage for 40 to 45 kV will together yield a doubling of peak current to 2.4 MA. With I4 scaling this will yield another 16-fold increase in yield.
At that point we are prepared to rapidly transition to running experiments with decaborane (B10H14), a hydrogen-boron compound that we can use to obtain p-B11 reactions. We already have a limited, but adequate, quantity of isotopically-pure decaborane. Isotopic purity is important, as reactions with B10 will produce radioactive Be7, while p-B11 reactions overwhelmingly produce stable He4 and some C11 with a half-life of only 20 min.
Once we have demonstrated fusion reactions with p-B11, we will upgrade the energy supply system by going up from 8 to 12 capacitors (already in place) and full power operation. Given the much higher reactivity of p-B11 than D and the better compression we expect, these steps should allow us to achieve for the first-time net energy production.
Once we have optimized it, we expect to get a doubling of yield because this fuel burns twice as fast as deuterium; an additional threefold boost in yield because each reaction produces three times more energy than does deuterium. In addition, we’ll get 40% better linear compression, yielding twice the density and giving another fourfold boost in yield. Finally, our confinement time will increase fourfold because much of the fusion energy we produce will be initially recycled back into the magnetic field that holds the plasmoid together. That gives us another fourfold boost in yield. So, switching from deuterium to p-B11 will altogether give us 2 × 3 × 4 × 4 or nearly 100 times the yield. This will therefore bring us all the way up to the 60 kJ we need for net energy production.
Steps from Net Energy to Commercialization
Energy Capture, Conversion to Electricity and Other Engineering Challenges
As described in our basic patent [26], we expect to be able to capture the energy produced by the fusion reactions in two ways (Fig. 11). First, the ion beam energy can be captured by having the beam induce a current in a coil, or in a more complex geometry of conductors. The current in the coil can then be transferred to capacitors. Since the energy will tend to flow back into the beam as it passes out of the coil, fast switches will be required to prevent the backflow, or powerful diodes will be required to allow current to flow in only one direction. While there are design challenges, especially for the switches because of the large amount of power in the pulse, the general technology for converting beam energy back into stored electric energy is mature, as it has been used for decades on accelerator beams. Efficiencies as high as 85% have been demonstrated [39].
Artist’s conception of Focus Fusion 5 MW generator (https://youtu.be/MGEGiyGlomk) Upper capacitor bank feeds energy to electrodes at center, while output energy is collected from ion beam by lower coil and x-rays are converted to electricity by the layered photelectric convertor around the central vacuum chamber. Outside the x-ray convertor is shielding to absorb the small number of neutrons produced by side reactions. Credit: Torulf Greek for LPPFusion
One likely possibility for the fast high-voltage switches needed are diamond-film switches. These use UV light from a laser to briefly convert diamond, a strong insulator, into a good conductor. The ideas for such switches have existed for decades, but LPPFusion would probably have to bring them to full development as the resources needed have not been invested to date.
The second energy capture technique is for the x-rays. About one third of the total energy will be released as x-rays. As described in our patent, these would be captured by a highly multilayered photoelectric device, in which thin metal foils would convert a portion of the x-ray energy into energy of electrons, which would be captured on a set of charged grids. Such a device has never been made, although the principles of photoelectric vacuum tubes are well known. We have calculated that these devices too can have 80% or more energy conversion efficiency. Despite their multilayered structure, they are practical and economical because of the small size of the generators—the x-ray conversion device will only be about 40–50 cm in inner radius and perhaps 50 cm in length.
In addition to energy capture and conversion, we see the main engineering challenge being in cooling the device and, in particular, the tip of the anode which is exposed to the most intense radiation. One key reason for choosing beryllium as the electrode material is that it is nearly transparent to x-rays of the energy (10’s of keV) that will be mainly produced by the plasmoid. However, a fraction of the energy will be produced at relatively lower energy of 1-2 keV. Since absorbance is strongly negatively correlated with x-ray energy, this energy will be absorbed in the outer layers of the anode near the tip.
We have approximately calculated that cooling the tip as well as cooling the rest of the electrodes, which will be heated by contact with the hot background plasma, will be possible with highly compressed helium. This coolant has been proposed for other fusion devices as well. The maximum cooling rates near the tips may have to be as much as 10 kW/cm2, which is high, but still feasible for the short distance that will be required in the Focus Fusion generator.
The maximum possible cooling rate limits the pulse repetition rate to far below the 180 kHz cycle time of the electrical circuit. We calculate that the maximum repetition rate will be close to 200 Hz. Since net energy production in the form of electricity will be about 25 kJ per pulse, this will be a 5 MW electric generator. Such a small generator has significant advantages, as it can be placed close to the load and can be used for mobile applications. With an approximate mass of 3 tons, and a volume of about 30 m3 the generator will be too large and powerful for automobiles but could be used to power charging stations as well as larger transportation devices, such as ships.
A related major engineering challenge is to minimize erosion of the electrode so that they need to be changed out no more than once a month. This again depends mainly on keeping the electrodes cool. But we may also be able to engineer the internal dynamics of the vacuum chamber so that a protective layer of boron is continually deposited and eroded from the electrode, protecting the underlying beryllium.
While we are still in the research phase, we estimate that with adequate funding, of order of $100 million, the engineering phase can be completed in three years. Producing a working prototype will of course have to also involve engineering control systems, and addressing manufacturability and maintenance issues.
Cost and Transition to a Fusion Economy
Given its small size and relatively simple construction, we anticipate that Focus Fusion generators will be able to be mass produced in factories like automobiles. With large scale mass production, we have calculated that the capital cost of a unit will be in the area of $500,000 or $0.10 per W. This is far cheaper than any existing energy source. Unlike solar and wind, Focus Fusion generators would be available 24/7 and could be easily turned on or off to respond to load changes.
Fuel cost, as with any fusion device, will be negligible. A 5 MW device will need only 5 kg of fuel a year.
We anticipate the main costs initially will be in maintenance labor, although eventually much of this could be automated. If the device needs some maintenance every month, we have estimated that the overall cost of electricity, including capital costs will be in the range of 0.3 cent/kWh. By comparison no electric energy source today produces electricity at less than 2 cent/kWh. We know of no other fusion generator that will be this economical.
Since this economical, safe, clean energy source will lead to the replacement of all other sources of energy by fusion, a rapid scale-up of production is needed. To facilitate that, we intend to license this technology to the largest organizations, such as national power authorities or major international engineering firms, which have the capital to rapidly expand mass production. With adequate investment levels, we believe that the phase out fossil fuel burning could be completed by around 2040.
The resource demands of this technology are exceedingly modest. Boron is an abundant element and switching fully to a Focus Fusion economy would require only about a 10% increase in boron production. Beryllium production is very limited at the moment at about 400 tons per year and would have to be scaled up by about ten-fold. At present, only very rich ores are used, but with scale-up, somewhat less-concentrated ores will have to be exploited. However, beryllium is not rare, being about as common as lead in the Earths’ crust.
Since Focus Fusion would be safer than any existing energy source, it could be regulated under existing power safety regulations, perhaps supplemented by requirements for dealing with the very short-lived C11 that the generators produce.
Focus Fusion generators are compact, so they would be ideal for space propulsion. Studies we produced for JPL indicate that Focus Fusion space craft could travel to Mars in as little as two weeks. However, significant engineering challenges are involved in disposing of the waste heat in space, where it has to be radiated.
Private Public Partnership for Fusion
LPPFusion, which was previously called Lawrenceville Plasma Physics, received its earliest funding from Jet Propulsion Laboratory. However, since the end of that funding in 2001, we have been funded almost entirely by $9 million in private investment, most of it from small investors. This is far from an ideal model for the development of a critically-needed energy source.
While we of course believe our Focus Fusion approach is the fastest route to fusion, no one can actually say with certainty which path is best until one demonstrates first net energy and then a working prototype generator. Given the importance of fusion energy and its urgency, we strongly feel that abundant government funding is required. In the absence of certain knowledge of which route to fusion is best, we advocate a crash program that funds all physically-possible routes. Thus, the government should fund all projects that can’t be proven at this time to be physically impossible.
The recently enacted Public–Private Partnerships for Fusion Energy provides an efficient way to allocate resources by requiring private companies to match government funds on a dollar-for-dollar basis. This means that, in general, government funds will be allocated approximately in accord with each company’s immediate needs. For all companies a 100% increase in the resources available will certainly greatly accelerate progress.
However, it is important that such funds be allocated without the limitations of preconceived notions of which paths are best, something which can’t be ascertained at this time. There is a tendency for some administrators to impose arbitrary and unscientific criterion on which fusion paths are most important. For example, in a review of progress towards net fusion energy Wurzle and Hsu [40] specifically limit their coverage to systems where Ti = Te and they continue:
“Non-equilibrium fusion approaches, where Ti > Te, must account for the energy loss channel and timescale of energy transfer from ions to electrons. Analysis of such systems is not included in this paper. Furthermore, this paper does not consider non-thermal ion or electron populations such as those with beam-like distributions.”
As pointed out in this and other peer reviewed papers, fusion plasmas with Ti > > Te, are obtainable with sufficiently high B fields for the QMFE to be relevant, and such plasmas are highly desirable for aneutronic fusion. The authors give no scientific justification for excluding such approaches, nor for excluding those with non-thermal ion or electron populations. Such unscientific and arbitrary exclusions are of great concern.
Conclusion
Despite limited resources, LPPFusion’s Focus Fusion approach has led to record-breaking results in confined ion temperature and plasma purity and to the highest wall plug efficiency and nτT products of any private fusion effort. If successful, this effort will lead to the production of safe and extremely economical 5 MW generators. Matching funding from government agencies will greatly accelerate this effort.
Change history
31 March 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10894-023-00348-w
References
W.H. Bostick et al., Ann. NY Acad. Sci. 251, 2 (1975)
C. R. Haas, et al., Dynamics of Microstructures. Proceeding 3rd International Workshop on Plasma Focus, (1984) pp.87
G. Herziger, et al., Radiation and particle emission from a 1.6 kJ plasma focus. Proceeding International Conference on Plasma Physics, Lausanne, July 2–3, (1984), pp. 31
H. Schmidt, et al., Ion and neutron emission of the Poseidon plasma focus. Proceeding 3rd International Workshop on Plasma Focus, (1984) pp. 63–66
K.N. Koshelev et al., J. Phys. D Appl. Phys. 21, 1827 (1988)
W.H. Bostick, V. Nardi, W. Prior, J. Plasma Phys. 8, 7 (1973)
M. Sadowski et al., Phys. Lett. A 105, 117 (1984)
L. Bertalot et al., Experiments on plasma focus dynamics, neutron production and ion emission. IAEA Plasma Physics and Controlled Nuclear Fusion, International Conference, Brussels, July 1–10, (IAEA, Vienna, 1980), pp. 177
A. Sakurai, K. Shimoda, K. Hirano, Jpn. J. Appl. Phys. 17, 1687 (1978)
J.S. Brzosko et al., Phys. Plasmas 2, 1259 (1995)
G.R. Neil, R.S. Post, Plasma Phys. 14, 425 (1988)
I. Volobuev et al., Sov. J. Plasma Phys. 14, 401 (1988)
K. Hirano, et al. Plasma dynamics and charged particle emission in the plasma focus. Proceeding 11th Europe Conference Controlled Fusion and Plasma Physics Aachen, (European Physics Society, Geneva, 1983), pp. 551
L. Jakubowski, M. Sadowski, J. Zebrowksi, Nucl. Fusion 41, 755 (2001)
L. Bertalot et al., Phys. Lett. A 79, 389 (1980)
V. Nardi et al., Phys. Rev. A 22, 2211 (1984)
E. J. Lerner et al., in Current Trends in International Fusion Research—Proceedings of the Fifth Symposium (2003), Edited by E. Panarella, NRC Research Press, National Research Council of Canada, Ottawa, ON K1A 0R6 Canada, (2007)
E. J. Lerner, R. E. Terry,Current Trends in International Fusion Research—Proceedings of the Sixth Symposium (2005), National Research Council of Canada, (2009), pp. 11-22
Report on the Debate on Mechanism of Neutron Production in the Dense Plasma Focus. https://www.icdmp.pl/images/2019/Debate_Report/Report_on_the_Debate.pdf
M. Milanese, J. Pouzo, Small Plasma Physics Experiments, vol. 66 (World Scientific Publishing, London, 1988)
E.J. Lerner, Laser Part. Beams 4(Pt. 2), 193 (1986)
E.J. Lerner, S.K. Murali, A. Haboub, J. Fusion Energ 30, 367 (2011)
J.R. McNally, Nucl. Fusion 15, 344 (1975)
G.S. Miller, E.E. Salpeter, I. Wasserman, Astrophys. J. 314, 215 (1987)
S. Abolhasani, M. Habibi, R. Amrollahi, J. Fusion Energ 32, 189 (2013)
Method and apparatus for producing x-rays, ion beams and nuclear fusion energy US Patent # 7,482,607
S. Lee, Appl. Phys. Lett. 92, 021503 (2008)
M.G. Haines et al., Phys. Rev. Lett. 96, 075003 (2006)
E. J. Lerner and A. Talaei, 54th Annual Meeting of the Division of Plasma Physics, vol. 57, no. 12, 335 (2012)
E.J. Lerner, S.M. Hassan, I. Karamitsos, F. Von Roessel, Phys. Plasmas 24, 102708 (2017)
E.J. Lerner, H.R. Yousefi, Phys. Plasmas 21(10), 102706 (2014)
E.J. Lerner et al., Nucleonika 57, 205 (2012)
E.J. Lerner et al., Phys. Plasmas 19, 032704 (2012)
M. J. Mantsinen et al., in 42nd EPS Conference on Plasmas Physics, Lisbon, Portugal, Europhysics Conference Abstracts (2015). http://ocs.ciemat.es/EPS2015PAP/pdf/P2.171.pdf
D. Margarone et al., Appl. Sci. 12(3), 1444 (2022)
E.P. Hartouni et al., Nat. Phys. (2022). https://doi.org/10.1038/s41567-022-01809-3
T. Roche, Open Magnetic Systems Conference (2021). https://tae.com/overview-of-c-2w-advanced-beam-driven-frc-experiments/
P. Kube et al., Eur. Phys. J. Plus 136, 810 (2021)
Y. Yamamoto, K. Yoshikawa, H. Toku, T. Haga, Fusion Technol. 17(4), 540–554 (1990)
S.E. Wurzel, S.C. Hsu, Phys. Plasmas 29, 062103 (2022)
Acknowledgements
This research was funded by LPPFusion, Inc. from funds contributed by donors and investors. We wish to thank in particular LPPFusion’s largest donors: Focus Fusion Society, Walter Rowntree, Robert Biegler, Peter Crabb, Andrew Kursar and Edward Peschko. We thank Jose Varela for his contributions to the IT needed for this research and Alexandra Calabro for her help as a student intern in literature searches.
Author information
Authors and Affiliations
Contributions
E.L and S.H directed the experimental work. E.L, S.H and I.K performed the experimental work and collected the data. R.F, E.L and S.H designed components for the devices. E.L and I.K performed data analysis. E.L performed theoretical calculations, with co-authors cited in references. E.L drafted the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised due to error in the unit of Abstract.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lerner, E.J., Hassan, S.M., Karamitsos-Zivkovic, I. et al. Focus Fusion: Overview of Progress Towards p-B11 Fusion with the Dense Plasma Focus. J Fusion Energ 42, 7 (2023). https://doi.org/10.1007/s10894-023-00345-z
Accepted:
Published:
DOI: https://doi.org/10.1007/s10894-023-00345-z