Neutron Diagnostics for Tokamak Plasma: From a Plasma Diagnostician Perspective

Abstract

Neutron measurement is considered to be one of the major diagnostic methods in tokamak plasma. The neutron diagnostics provide key information on plasma physics, machine protection and control issues. In this article, the commonly used techniques of neutron emission diagnostics for tokamak plasma are presented. The requirements and limitations imposed on the diagnostic systems are discussed. Several basic techniques of total neutron yield and neutron spectrum measurements such as neutron counters, neutron activation technique, time-of-flight spectroscopy or magnetic proton recoil spectroscopy are described in a practical way, from a plasma diagnostician point of view. Primary physical quantities that can be derived from those measurements are pointed out and discussed.

The Importance of Neutron Diagnostics

In order to obtain a comprehensive insight into the processes taking place in the tokamak fusion plasma it is necessary to simultaneously determine several plasma parameters. Preferably it should be done with temporal and spatial resolutions smaller than the typical time and length scales of the investigated phenomena. Due to the extreme heat, no physical measurement devices can be placed directly inside the plasma. However, since the thermonuclear plasma is a source of electromagnetic and particle radiation, the plasma diagnostics rely on measurements of the emission, transmission or scattering of particles or electromagnetic radiation. Fusion plasma diagnostics is an extensive subject itself, and constitutes a large and important part of fusion experiments. In this article, we focus on neutron diagnostics which play a major role in plasma research on tokamak machines. The subject is presented in a pragmatic way from a plasma diagnostician point of view.

The role of a plasma neutron diagnostician is to characterize the plasma under study as a source of neutrons [1]. To do that, tokamak devices are equipped with several neutron diagnostics that vary in terms of purpose of application and technical parameters. In fact, measurements of the neutron emission have been carried out since the beginning of thermonuclear fusion research.

In the most promising of the hydrogen fusion reactions, when a mixture of deuterium and tritium is used, about 80% of fusion energy yield is carried by the neutron. Thus, the number of produced neutrons is a direct measure of the progress toward the achievement of controlled thermonuclear reactor. Nevertheless, this is not the only reason why the neutron measurements are of special interest for tokamak plasma. Neutron diagnostics play also a crucial role in study of physical phenomena occurring in tokamak plasmas and will play a prominent role in the control of the next-step thermonuclear power plants. Indeed, since neutrons originate in the fusion reaction, they carry information on the properties of the ions taking part in the reaction. As neutrons do not have the electric charge, they can easily escape from the tokamak magnetic field and be registered by a diagnostic system. The important information on ion species partaking in or affecting the fusion process can be extracted from the neutron source strength or the neutron energy spectrum. Study of the neutron spectrum can provide information on ion temperature and ion density. Neutron emission can be also useful to monitor plasma position, its extend and shape. This requires measurements of spatial emission profiles, so that neutron emissivity distribution can be reconstructed using special tomographic methods.

A lot of effort has been devoted to develop reliable methods of neutron measurement and to improve the accuracy of existing experimental techniques of neutron measurements. A part of neutron measurement techniques that are commonly used in nuclear fusion devices are based on concepts originally developed for fission reactors and experimental neutron physics. However, significant differences between the techniques that are directly applicable for fusion research and those used in conventional fission reactors are defined by the requirements and limitations on the neutron measurements in the thermonuclear plasma environment. This subject will be discussed in “Requirements and Limitations of Neutron Diagnostics” section.

In the currently operational tokamaks the reactions of the primary interest are: D(d,n)³He, D(d,p)T, and D(t,n)⁴He. The first two reactions are almost equally probable branches of fusion reaction involving deuterium fuel. The neutrons produced in deuterium fusion reactions have energy of $E_{n0} =$ 2.45 MeV while the neutrons from deuterium–tritium reaction have energy of $E_{n0} =$ ~14.1 MeV. This allows us to focus mostly on this energy ranges. However, the observation of the neutron emission in tokamak experiments is not uniquely related to the production in thermonuclear reactions. The accelerated ions (³He,p,d,t) of energy greater than 1 MeV are present in the plasma. They can interact with plasma impurities e.g. with Be intrinsically present in the plasma due to plasma interaction with Be walls of modern tokamaks. This leads to emission of energetic neutrons from reactions: ⁹Be(³He,n)¹¹C, ⁹Be(α,n)¹²C, ⁹Be(p,n)⁹B, ⁹Be(d,n)¹⁰B, ⁹Be(t,n)¹¹B [2]. Moreover, photoneutrons can be produced when high energy runaway electrons strike the vacuum vessel structures depositing a considerable amount of energy in a few tens of milliseconds [3]. These high-energy electrons are generated by radio-frequency heating e.g. electron cyclotron resonance heating (ECRH). Non-fusion neutrons are also produced in disintegration of deuterons by these energetic electrons in the reaction D(e′,en)H or by bremsstrahlung photons in the reaction D(γ,n)H. These photoneutrons can be also detected by tokamak neutron diagnostics. Finally, the neutron diagnostics should be able to register scattered fusion neutrons of lower energy. In order to accomplish all the required measurements, modern tokamaks are equipped with numerous complementary neutron diagnostics.

Requirements and Limitations of Neutron Diagnostics

The conditions in which neutron diagnostics have to operate are very severe. This is mostly due to a wide range of plasma temperature (from several eV up to tens of keV) and harsh radiation environment (high fluxes of neutrons, gamma and X-ray radiation). Thus, neutron diagnostics suffer from radiation damage and can be exposed to thermal and mechanical stress. Since the observed neutron flux can vary by a few orders of magnitude, the neutron detectors should have high dynamic range. Another aspect that should be taken into consideration is the magnetic field. If a neutron diagnostic uses magnetic field, an appropriate shielding has to be designed and constructed. The diagnostic magnetic field must not disrupt the tokamak magnetic field and vice versa, the tokamak field should not interfere with the diagnostic. For example, magnetic proton recoil (MPR) neutron spectrometer at Joint European Torus (JET) needs a heavy shielding against the tokamak powerful magnetic fields to avoid interference [4]. An additional challenge in design of plasma neutron diagnostics is a limited access to the plasma. Usually, the space for diagnostics is severely limited and only a small number of ports is available. The complications in precise spectroscopic measurements are also related to the electromagnetic noise from the tokamak high-power auxiliary systems (e.g. Neutral Beam Injection—NBI, Ion Cyclotron Resonance Heating—ICRH or lasers of the Light Detection and Ranging—LIDAR system). This electromagnetic noise can interfere with a neutron diagnostic detection chain and significantly decrease signal-to-noise ratio.

The requirement on spatial, temporal and energy resolution are mostly defined by the physical phenomena to be studied. For the regular neutron yield monitoring, the temporal resolution of 10 ms is usually sufficient. However, investigations of transport properties or magnetohydrodynamics (MHD) instabilities require increased temporal and spatial resolution. In general, a trade-off between high temporal and spatial resolution and the accuracy of the measurements in terms of statistics and signal-to-noise ratio is necessary.

Another important requirement for a neutron diagnostic is its proper characterization and calibration. Due to the nature of the neutron transport, the problems in absolute calibration of neutron diagnostics are not trivial and this task is very often supported by Monte Carlo calculations of neutron transport. Low-activity radioactive sources are used for quick checks, intershot and overnight calibrations of neutron diagnostics. These sources are usually embedded into a tokamak diagnostic near the detector. More precise, but also more laborious, procedures involve in-vessel calibrations where a strong standardized radioisotope neutron source (e.g. ²⁵²Cf) [5] or a neutron generator [6] is inserted and moved around the vacuum vessel to map out the volume occupied by the plasma.

Physical Quantities Determined from Neutron Diagnostics Measurements

Fusion Reaction Rate

Fusion reaction rate (i.e. number of fusion reactions per unit volume per unit time) is given as:

$$r = \frac{{n_{i} n_{j} }}{{1 + \delta_{ij} }}\left\langle {\sigma v} \right\rangle ,$$

(1)

where n_i is the density of ith species, $\delta_{ij}$ is the Kronecker delta. Assuming that the reactants have a distribution of velocities (e.g. a thermal distribution), $\left\langle {\sigma v} \right\rangle$ is the average of the fusion cross section $\sigma$ over the relative velocities $v$, called the reactivity.

The fusion reaction rate is usually determined indirectly from the neutron flux measured by neutron counters or the activation technique. This indirect approach means that other plasma parameters such as density, temperature, impurities concentration along with the discharge parameters have to be known. Then, a transport code that includes a physical model of the interactions (e.g. beam-plasma interactions, or radio frequency wave interactions with a plasma), is used to calculate the fusion reaction rate in an iterative manner. One of the most commonly used transport codes is TRANSP [7].

Plasma Ion Temperature

The ion temperature can be determined from the Doppler broadening measured by a neutron spectrometer. Fusion reactions are two-body exothermic reactions with $Q$ values 3.3 MeV and 17.6 MeV for DD and DT, respectively. Since the reactants are not at rest, energy of the products is shifted by a quantity that depends on the reactant energy and on the emission direction of the neutrons.

Assuming that the reactants have thermal distribution i.e. ion populations are in equilibrium with a Maxwellian velocity distribution of ion temperature $T_{i}$, the resulting neutron energy spectrum is nearly of the Gaussian shape [8]:

$$f\left( {E_{n} } \right) = \frac{1}{W\sqrt \pi }exp\left( { - \frac{{\left( {E_{n} - E_{n0} -\Delta E_{th} -\Delta E_{r} } \right)^{2} }}{{W^{2} }}} \right),\quad W = \left( {\frac{{4m_{n} \left\langle {E_{n} } \right\rangle T_{i} }}{{m_{n} + m_{\alpha } }}} \right),$$

(2)

where $m_{n}$ and $m_{\alpha }$ denote the mass of the neutron and the mass of the alpha particle, respectively. In Eq. 2, $E_{n}$ is the measured neutron energy and $E_{n0}$ is the characteristic neutron emission energy which applies in the limit $T_{i} \to 0$. If $T_{i} > 0$, the distribution is shifted as expressed by $\Delta E_{th}$ parameter. Moreover, finite plasma rotation velocity introduces an additional shift expressed by $\Delta E_{r}$ (see “Toroidal Rotation Velocity” section).

The thermal Doppler width (FWHM) is proportional to $\sqrt {T_{i} }$:

$$FWHM = 2W\sqrt {ln2} .$$

(3)

Equation 3 may be stated in practical units as: $FWHM = 82.2\sqrt {T_{i} }$ and $FWHM = 177.2 \sqrt {T_{i} }$, for DD and DT reaction, respectively, where both neutron energies and ion temperatures are measured in keV.

Toroidal Rotation Velocity

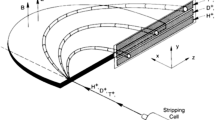
It is foreseen that the neutron spectroscopy can be potentially used for determination of the plasma toroidal rotation velocity $V_{t}$ in the core of burning plasma (e.g. in the ITER tokamak). The plasma rotation velocity $V_{t}$ can be, in principle, calculated from the difference spectrum obtained from simultaneous measurements of neutrons emitted in two opposite tangential directions using spectrometers with collimated lines of sight (LoS), as shown in Fig. 1. Such a technique is an alternative to determination of $V_{t}$ from the Doppler shift of characteristic photon emission lines in the X-ray region.

Fig. 1

A schematic layout of two neutron spectrometers for plasma rotation velocity determination. The information on plasma rotation velocity can be derived by subtracting spectra measured in two tangential LoS

Assuming the conditions of thermonuclear fusion plasma with the Maxwellian ion distribution, the energy distribution of the neutron emission from D(t,n)⁴He reaction is described by Eq. 2. The energy shift due to plasma rotation is given as $\Delta E_{R} = 0.54 V_{t}$, where $\Delta E_{R}$ is expressed in keV and $V_{t}$ in km/s. In ITER, predicted plasma rotation velocity will be in the range of $1 \,{\text{km/s}} < V_{t} < 50\,{\text{km/s}}$.

Determination of $V_{t}$ using a single spectrometer is very challenging due to required accuracy of fusion neutron spectrum measurement. Therefore, it has been proposed [9] to use a pair of spectrometers that view the same plasma volume from opposing directions, i.e. co- and counter-tangential LoS as shown in Fig. 1. A difference spectrum constructed based on the data obtained from both spectrometers can be used to derive $V_{t}$. There are two advantages of such an approach. Firstly, the energy difference, for a given $V_{t}$ is doubled. Secondly, the precision depends now to a lesser degree on the absolute values of the system but is transferred to the relative one relating the two spectrometers to each other. Thus, the accuracy of $V_{t}$ determination is shifted from the absolute calibration of the spectrometers to the relative calibration of the two spectrometers to each other.

The main limitation of the technique, that relies on collimated neutron measurements, is the fact that the measured spectra are integrated over the LoS. Thus, the measured spectrum consists of contributions from plasma volumes with different neutron emissivity, temperature and rotation velocity. It is however a sensible assumption that most of neutrons come from the hot core of the plasma. Therefore, in the first approximation, the observed shift $\Delta E_{R}$ is mostly related to plasma rotation velocity in the hot plasma core.

Neutron Diagnostics

Neutron Counters

During the fusion experiments with auxiliary heating, the neutron yield can change by 2–3 orders of magnitude. Thus, it is necessary to use neutron detectors with a wide dynamic range. Moreover, such a detector should have a fast response time, since fast ions slowing down time is ~ 100 ms. The detector should be also immune to hard X-rays and gamma-rays. Most commonly used neutron detectors in fusion plasma studies are: BF₃ proportional counters, ³He proportional counters and ²³⁵U and ²³⁸U fission chambers.

The BF₃ and ³He counters use ¹⁰B(n,α)⁷Li and ³He(n,p)T reactions, respectively. The ²⁵³U and ²³⁸U fission chambers utilize the ²³⁵U(n, fission) or ²³⁸U(n, fission) reactions releasing up to 200 MeV of energy. Since these detectors are more sensitive to low-energy neutrons, they are often embedded into a moderator to slow down fast neutrons.

A fission chamber is basically an ionization chamber with the electrodes coated with fissile material: ²³⁵U or ²³⁸U. The ionization of the filling gas is caused by fission fragments. Since ²³⁸U(n, fission) reaction has a threshold of ~ 1 MeV, a chamber based on this isotope is sensitive only to fast neutrons. As a common practice, ²³⁵U and ²³⁸U fission chambers are installed in pairs around the fusion devices to monitor the neutron flux. Figure 2 shows a schematic view of a fission chambers pair.

Fig. 2

A schematic view of a pair of ²³⁵U and ²³⁸U fission chambers routinely used as neutron flux monitors

Neutron Activation Systems

Time-integrated measurements of the total neutron yield are routinely preformed using the neutron activation system. In this case, samples of materials (usually in the form of foils) with the well-known neutron reaction cross-sections are used. These samples are transferred to irradiation points located near the plasma. The important quantities for selection of the activation foils include: reaction cross-section, reaction threshold energy, daughter nuclides half-life time and characteristic energies. Table 1 summarizes the most widely used reactions for neutron activation measurements at modern tokamaks. In order to deduce the total neutron emission rate in the whole plasma, based on the neutron flux at the irradiation point, it is necessary to rely on the precise Monte Carlo modelling of neutron transport in the fusion machine.

Table 1 Commonly used reactions for neutron activation measurements

The primary goal of the activation measurements is to provide a reliable measure of fusion energy production over a wide dynamic range. Neutron fluxes from DD and DT reactions are relatively easily measured using several foils with different threshold energy reactions. A full neutron energy spectrum can be retrieved by using a multi-foil activation technique. In this case, several samples with different reaction energy thresholds are used and the spectrum unfolding must be performed using a dedicated computer code. The activation measurements enable also determination of the triton burn-up ratio (for DD plasma) and D/T fuel ratio n_d/n_t in DT plasmas.

Time of Flight Spectrometry

In the inertial confinement experiments, the neutron emission occurs only for a very short time interval (typically hundreds of picoseconds for laser fusion, nanoseconds in plasma focus (PF) devices). The most convenient way to obtain the neutron energy spectrum is thus to use time-resolved neutron detector located far from the plasma. The arrival time of neutrons depends on their velocity and thus on their energy. This is the principle of the time-of flight (ToF) technique that allows for obtaining the neutron energy spectrum from the time-dependant neutron intensity.

Let us focus at first on the emission from a plasma focus device. The device emits a short pulse of hard X-rays and neutrons. In Fig. 3, a time trace of detected radiation emitted from a plasma-focus device operated with deuterium plasma is shown. As a detector, a fast scintillation probe (UFNSP-1, ACS laboratory, Poland) was used and the distance between the plasma and the detector was 5 m. The first peak is associated with the detection of X-rays, while the second peak, separated by ~ 210 ns is due to neutron detection. If the distance between the plasma source and the scintillation probe is known, the energy of neutrons can be simply calculated from the ToF difference between X-rays and neutrons. This is schematically illustrated in Fig. 4 where the ToF for photons and neutrons of 2 MeV, 2.5 MeV and 3 MeV energy is plotted as a function of distance d.

Fig. 3

Separation of the X-ray and neutron signals in ToF method used in pulsed sources registered by ultra-fast scintillation probe

Fig. 4

Time of flight for X-rays and 2 MeV, 2.5 MeV and 3 MeV neutrons as a function of distance d

For plasma discharges longer than nanoseconds, ToF method becomes a bit more complicated. Measured ToF of neutrons has to be associated with proton recoil technique on thin foils or thin scintillators. In Fig. 5, measured neutron n incoming on a thin plastic scintillator S1 gives start pulse of recoiled proton according to the scattering process:

$$n \, + \, p \, \to \, p_{R} + \, n^{{\prime }}$$

(4)

Second stop pulse signal is given by S2 scintillator. ToF of the recoiled neutron n′ is measured on a known distance L between detectors S1 and S2. Energy of measured neutron n, determined by nonrelativistic kinematics is independent on the scattering angle $\theta$ and given by the following formula [10]:

$$E_{n} = 2m_{n} r^{2} /t_{TOF}^{2} ,$$

(5)

where r is radius of the time-of-flight sphere (typically ~ 1 m) shown if Fig. 5 and t_TOF is the flight time of the scattered neutron.

Fig. 5

Principle of ToF method for neutron measurement with long time plasma discharges

Spatially Resolved Neutron Measurements: Neutron Camera

By using several detectors with different LoS located in a common poloidal plasma cross-section, it is possible to measure line-integrated neutron emissivity. The detectors are often arranged in several cameras viewing plasma from different directions. Each LoS is equipped with one or more neutron detectors, typically based on liquid or plastic scintillators (e.g. at JET [11]) or diamond detector (foreseen for ITER). Each detection channel must be properly shielded in order to avoid registration of the back-scattered neutrons. Collimation of neutrons is much more challenging then collimation of light. This is because of the long penetration distance of neutrons in essentially all materials. This imposes that neutron collimators are usually large structures. Ideally, each detector should function as a neutron spectrometer allowing determination of the neutron energy spectrum. In practice however, often the spectrometric capabilities are not available and detectors work simply as counters.

The line-integrated measurements along a number of chords enable to reconstruct the spatial distribution of the neutron emissivity in the poloidal cross-section of the plasma. This is possible by using so-called tomographic inversion methods. This task is however not trivial, since the reconstruction is an ill-posed problem. Several approaches to the tomographic inversion for fusion devices have been developed. The most common ones are based on Tikhonov regularization [12], minimization of the Fisher information [13] or maximum entropy method [14]. The other methods include neural networks [15] or genetic algorithms [16].

The reconstructed distribution of 14.1 MeV neutron emissivity provides information on fusion reactivity and alpha particle birth profile. Moreover, the information on the spatial distribution of neutron emission can be used to determine and control plasma shape and position.

Magnetic Proton Recoil Spectrometry

Magnetic proton recoil (MPR) system is based on n–p elastic scattering and magnetic dispersion. A simple schematic diagram of MPR spectrometer is showed in Fig. 6. A collimated beam of neutrons is converted to protons through n–p elastic scattering in the thin polyethylene (CH₂) foil. The relationship between the recoil proton energy E_p and the neutron energy E_n is given by [17]:

$$E_{p} = E_{n} { \cos }^{2} \theta_{np} ,$$

(6)

where θ_np is the scattering angle between neutron and the recoiled proton. The recoil protons emitted in the forward direction are pre-selected by the proton collimator and the entrance gap of the dipole magnet. The forward recoil protons have a maximum n–p cross-section and a minimum uncertainty in the kinematic energy spread, accordingly enhancing the neutron detection efficiency and energy resolution. The protons are passively spatially separated in the magnetic field according to their momentum as described by [17]:

$$\rho = \frac{p}{qB} = \frac{{\sqrt {2mE_{p} } }}{qB},$$

(7)

where ρ is the bending radius, p is the proton momentum, q is the charge, B is the magnetic field, and m is the mass. Thus, the distribution of recoil proton energies can be converted into a spatial distribution of protons on the scintillators array. Since the bending radius is inversely proportional to the magnitude of magnetic field, to minimize the dimension of MPR spectrometer it is necessary to improve the dipole magnetic field. On the other hand, however, the stronger magnetic field of the diagnostic, the more shielding is required to avoid the interference with the tokamak magnetic field.

Fig. 6

Figure based on [17]

Schematic layout of a MPR spectrometer.

Energy resolution of the MPR spectrometer at FWHM of the recoil proton energy distribution results mainly from energy loss ΔE_f in the CH₂ foil, the kinematic energy broadening ΔE_k and the ion-optical aberrations of the magnet ΔE_m. Thus, the total energy resolution ΔE_t can be estimated as [17]:

$$\Delta E_{t} = \sqrt {\Delta E_{f}^{2} +\Delta E_{k}^{2} +\Delta E_{m}^{2} } .$$

(8)

The neutron detection efficiency of the MPR spectrometer can be expressed by [17]:

$$\varepsilon \left( {E_{n} } \right) = \frac{{d\sigma_{np} }}{d\varOmega } \times N_{H} \times \varOmega_{S} \times T_{P} ,$$

(9)

where dσ_np/dΩ is the differential cross section in the laboratory system for elastic scattering. The cross section depends on the incident neutron energy and the scattering angle. N_H is the number of protons per unit area in the CH₂ foil, Ω_s is the solid angle defined by the proton collimator and entrance gap of the dipole and T_p is the magnet transmission.

Summary

Neutron diagnostics play a crucial role in tokamak plasma physics. They provide key information on the machine performance but also allow studying physical phenomena such as particle transport or MHD activities. Time-integrated measurements e.g. using neutron activation spectroscopy provide reliable assessment of the neutron yield and thus the fusion power. Time-resolved neutron measurements enable to study the neutron flux evolution and investigations of plasma MHD activities. Spatially-resolved measurements provided by neutron cameras enable to determine the spatial distribution of neutron emissivity and alpha particle birth profile. Finally, neutron spectroscopy performed with ToF, MPR or liquid scintillator spectrometers provides an insight into physical properties of plasma such as ion temperature or plasma rotation velocity.

In the era of bigger tokamaks such as ITER the approach to neutron diagnostics must be revised. The high fluxes of neutrons will impose the requirements on a new design of detection systems and necessity to use radiation-hardened electronics. Among many plasma parameters to be measured in ITER, the neutron diagnostics will allow evaluation of the fusion power which plays a key role for machine protection as well as for plasma optimization and achieving the fusion gain factor ${\mathbb{Q}}$, related to the reactor performance. The requirements on ITER neutron diagnostics define the neutron emissivity measurements within 10% accuracy, with a temporal resolution of 1 ms and spatial resolution of a tenth of the minor plasma radius, i.e. 200 mm. The approach to the in-vessel calibration of the neutron diagnostics should be also revised. Indeed, 10% of accuracy in the assessment of the foreseen ITER fusion power is equivalent to more that 3 times fusion power achieved at JET tokamak. This indicates that alternative approaches to the calibration should be considered.