Introduction

Divertor design is an important issue for large fusion experiments. In particular, recent calculations have revealed divertor heat flux to be a serious obstacle for ITER [1, 2] and for tokamak fusion reactors in general. Several proposals have been made to address this problem, such as the snowflake divertor [3] and the super-X divertor [4]. Both of these methods mitigate the problem of heat flux by increasing divertor surface area.

A complementary approach to this problem is to reduce the total amount of heat reaching the divertor plate. This can be done by converting a portion of it into useful work. Since work is not a form of thermal energy, any heat that can be harnessed in this manner does not count towards divertor heat flux, and therefore does not contribute towards material limitations on the resulting fusion reactor. As it turns out, a class of devices for extracting useful work from a plasma were developed in the 1970s. These devices are known as plasma direct converters (PDC’s) [5–8]. The difficulty in using such devices to extract energy from a tokamak divertor channel is that they require a bundle divertor. While designs have been proposed to place bundle divertors on a tokamak [9], such designs have not gained widespread acceptance.

In order to make plasma direct conversion relevant to tokamak plasmas, we propose a new class of PDC’s that are designed to operate in confined spaces subject to intense magnetic fields. Such a design would be able to be placed within the divertor channel of a conventional tokamak; for this reason, we refer to such a device as an energy recovering divertor (ERD).

The goal of this paper is to present one specific mechanism by which an ERD could extract useful energy from a plasma. That mechanism is to first accelerate the plasma to supersonic speeds by using radial variations in toroidal field as a magnetic expander. Once the plasma has achieved a sufficient velocity, its interaction with a series of wiggler magnets would serve to amplify Alfven waves. A confined Alfven eigenmode would then accumulate energy which could then be extracted using an RF antenna. While this mechanism would most likely achieve efficiencies far below the thermodynamic potential of an ERD as well as far below the efficiencies achieved by preexisting PDC’s, it still illustrates the possibility of direct power conversion in a tokamak divertor and thus provides a foundation for future work.

Background

Prior Art in Plasma Direct Conversion

The techniques used for plasma direct conversion when PDC’s were first introduced are very different than the method presented in this paper. For this reason it should be understood that the concepts presented in this section are of primarily historical interest. Because the early concepts for PDC’s are both the oldest and the most widely explored, we will refer to these as conventional PDC’s.

A conventional PDC operates through mirror force and charge separation. First, the plasma goes through a magnetic expander, converting nearly all of its perpendicular thermal energy into parallel kinetic energy. After leaving the magnetic expander, the plasma enters a chamber in which ions are separated from electrons. The electrons are steered into a negatively charged electrode, while the ions are steered into one or more positively charged electrodes. The electrodes are arranged in such a way that the forward momentum of the plasma forces ions into the positive electrodes despite being electrostatically repelled by them. This converts kinetic energy into electrostatic potential energy as ions move up a potential gradient. The net effect of this is that positive charge accumulates at positively biased electrodes and negative charge accumulates at negatively biased electrodes; this constitutes a source of EMF. The efficiency of such a device varies greatly depending on how many electrodes are used and how ions and electrons are separated. The most efficient devices use multiple electrodes to sort ions by energy, thus recovering as much energy as possible from each ion without reflecting it. For instance, a converter of this type using 22 stages was able to achieve 86 % efficiency [10].

The difficulty in applying a conventional PDC to a tokamak has to do with the strength of a tokamak’s toroidal field, as well as the density of the divertor plasma. Because a PDC relies on charge separation to extract energy from the plasma, it can only operate if the plasma’s Debye length is larger than the separation between electrodes. This can only occur at very low densities. Moreover, particle trajectories must deviate from field lines by a distance comparable to the separation between electrodes; otherwise, the first electrode along a field line would receive all particles from the plasma and the remaining electrodes would receive none. This means that the plasma’s ion Larmor radius must be larger than the separation between electrodes. This condition in turn can only occur at very low magnetic field strengths. In a conventional PDC, both conditions are met by using a very large magnetic expander; as the plasma moves to regions of weak magnetic field, it also spreads out, thus achieving low density.

In a tokamak, however, regions of very weak magnetic field cannot easily exist inside the toroidal field coils. Thus, one of two conditions must be met. One is that divertor flux must somehow leave the toroidal field coils. There are proposals to do this on a spherical tokamak by using non-axisymmetric poloidal coils [9]. The difficulty in this is that the coils must be located far from the plasma to avoid losses due to field errors. Moreover, the proposal in question was for a spherical tokamak, where toroidal field is relatively weak far from the center stack; such a technique may have problems with excessive magnetic stress on the bundle coils if used on a conventional tokamak.

The other option is to use an entirely different means of energy extraction that does not depend on charge separation. In such a device, power is coupled out of the plasma by induction rather than conduction. Thus, quasineutrality is maintained, and currents perpendicular to the magnetic field arise only where an appropriate particle drift (mainly polarization drift) arises. This is the aim of the wiggler-Alfven concept.

Motivation for Plasma Direct Conversion in Tokamaks

Traditionally, plasma direct conversion is commonly associated with the use of advanced fuels [11]. The reason for this is that, since advanced fuel reactions release a large fraction of fusion power as charged particles, the effect of PDC efficiency on overall reactor efficiency is correspondingly large. For instance, if burning an aneutronic fuel such as D-3He and given a choice between a 40 % efficient thermal cycle and an 80 % efficient PDC, this represents a doubling of useful power output for a given reactor thermal output. For a D-T plasma at ignition conditions, the effect of PDC efficiency on overall reactor efficiency is much smaller, since roughly 80 % of fusion power escapes as neutrons. Thus, for the same example efficiencies, the effect of this choice on relative reactor efficiency is only 1.2×, not 2×.

The value of PDC use on a D-T reactor becomes apparent if one instead considers the case of a reactor operating well below ignition, i.e. in a regime where significant amounts of recycled power are required to maintain fusion conditions. In this case, a PDC will not only recover energy from alpha burn, it will also recover any power injected into the plasma. Thus, the effects of plasma direct conversion increase rapidly as recycled power fraction increases. Moreover, at high recycled power fraction, the efficiency with which energy can be recovered does not merely affect the overall efficiency of a power plant, it also determines whether the reactor will break even at all.

To illustrate this, let us consider the minimum value of gain Q required to achieve breakeven, economical power production, and effective ignition. For economical power production assume that no more than 20 % of power derived from neutron heating is recycled, and let us define effective ignition as a regime in which no power derived from neutron heating is recycled. In this case, minimum Q for sustained operation can be calculated as follows:

$$ Q=\frac{1/\eta_{h}-r_{pdc}\eta_{pdc}}{r_{th}\eta_{th} (1-f_{ch})+r_{pdc}\eta_{pdc}f_{ch}} $$
(1)

where η h is the efficiency of the plasma heating system, η th is the efficiency of the conventional thermal conversion cycle, η pdc is the efficiency of the PDC including reprocessing of waste heat from the PDC through a conventional thermal conversion cycle, r th is the fraction of thermal power recycled, r pdc is the fraction of PDC power recycled, and f ch is the fraction of fusion power released as charged particles.

Assuming values of η h  = .7, η th  = .4, f ch  = .2, r pdc  = 1, then going from an η pdc of zero (energy from the divertor plates is wasted) to an η pdc of 80 % lowers breakeven Q from 2.56 to a value of 1.31. This is roughly a factor of 2 in fusion gain, which is sufficient to have serious implications for both the minimum scale of a fusion reactor as well as the timetable to achieve a demonstration fusion reactor. Additional values of Q for various values of η pdc and r th are listed in Table 1.

Table 1 Effects on breakeven of power recycling with an ERD
Full size table

In practice, the design presented in this article is not expected to achieve nearly the efficiencies cited in the above example. However, its effect can still be appreciable, even if efficiency is relatively low. This is mainly due to the fact that most of the waste heat from this conversion process eventually reaches the divertor plate as thermal energy and can be harnessed by a conventional thermal cycle. Because an ERD can be stacked on top of a conventional thermal cycle, any efficiency it achieves, no matter how low, is intrinsically superior to that of a conventional thermal cycle alone. In addition to this, there is the previously mentioned fact that the power available for the ERD to harness includes both alpha burn and recycled power, so any increase in recycling efficiency compounds itself as it permits higher recycled power fraction operation and thus increases the relative importance of recycling efficiency.

To illustrate this, consider for instance an ERD with 40 % efficiency. If waste heat from the ERD is further processed by a conventional thermal cycle with 40 % efficiency, then overall η pdc is 64 %. Substituting this into Eq. 1 yields a Q of 1.76. This is a significant improvement over the case without conversion of waste heat from the divertor channel (specifically a 31 % decrease in breakeven Q) achieved with an ERD conversion efficiency that is not beyond the theoretical capabilities of the wiggler-Alfven ERD.

Mechanism and Design

The basic design of a wiggler-Alfven ERD begins with the basic x-point geometry of a super-X divertor. In this arrangement, one leg of the separatrix is made very long, so as to extend to a large radius. Because the magnetic field in a tokamak is dominated by the toroidal field, and because toroidal field varies like 1/R, it follows that the magnetic field at the divertor plate of a super-X divertor will be much weaker than at the x-point. This in turn means that a flux tube will have more area at the divertor plate than at the x-point. The resulting dispersal of heat flux is the primary motivation of the super-X divertor concept. The remaining leg of the separatrix then extends to a small radius, so that heat flux in that direction is reduced by the magnetic mirror effect.

The wiggler-Alfven ERD takes this concept one step further. In the ERD, magnetic expansion along the divertor channel serves not only to disperse heat flux, but to convert thermal energy into kinetic energy as plasma is accelerated by the mirror force. In a super-X divertor, the distinction between thermal and kinetic energy is moot since residual kinetic energy is converted into heat upon impact with the divertor plate. In an ERD, this kinetic energy is instead harnessed to generate radiofrequency electric fields.

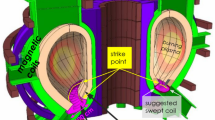
There are three features that allow the wiggler-Alfven ERD to harness this kinetic energy. These are shown in Fig. 1.

Fig. 1
figure 1

Layout of the separatrix and other key components in a wiggler-Alfven ERD

Full size image

The first is a series of wiggler magnets that are placed alongside the divertor channel. There are several different ways to generate this wiggler field: the wigglers may consist of electromagnets, or they may consist of unusually stable permanent magnets, but the most elegant way to generate the wiggler field is simply to use strips of ferromagnetic material that attract magnetic flux from the toroidal field. Regardless of the mechanism by which this field is created, it is structured to have a relatively short period of undulation. This serves both to aid in achieving resonance between the wiggler-Alfven beat wave and to prevent field errors from the wiggler from reaching the bulk plasma. In addition, the wiggler is tapered so that the component of its wavenumber parallel to the magnetic field increases along each field line. This means that the ponderomotive potential wells resulting from the wiggler-Alfven beat wave decelerate along each field line, causing the plasma to decelerate with them.

The second is a loop in the separatrix, in which the divertor channel reverses direction. The purpose of this feature is to maintain a well-confined Alfven eigenmode within the divertor. The significance of this feature is discussed in more detail in “Wave Refraction for a Confined Toroidal Eigenmode” section. The goal of this is to allow an Alfven wave to propagate in the toroidal direction, so that it cycles endlessly while gaining energy from the plasma. As a result, even if gain is weak the mode will still grow in amplitude. Because the wave is kept away from both the divertor plate and the bulk plasma, there are no mechanisms by which the wave can rapidly lose energy. Some energy loss due to viscosity or wall eddy currents can be expected, but the former is small compared to the ideal MHD effects that energize the wave, and the latter can be made small through careful design.

The third is the antenna. This is designed along very different lines than one would use for RF heating. This is because it must operate as a receiving antenna at low frequencies. While operating at low frequencies introduces some design challenges (due to low induced voltage) it also solves some fundamental physics problems associated with extracting energy from a plasma. Specifically, because the wavelength of the Alfven eigenmode is long compared to both the thickness of the divertor plasma and the thickness of the surrounding vacuum region, waves are able to propagate easily to the surface of the plasma and across the vacuum region where they are evanescent.

The following section contains calculations of several important aspects of this design: how thermal energy is converted into kinetic energy, how the wiggler-Alfven beat wave exerts force on the plasma, and how Alfven waves propagate in the divertor channel.

Calculations

Thermodynamic Limitations on ERD Efficiency

The most basic constraint on the efficiency of any heat engine is given by the second law of thermodynamics. This states that no heat engine can exceed Carnot efficiency, \(\epsilon=1-T_{C}/T_{H}\). By itself this is largely irrelevant to ERD’s and PDC’s due to their high operating temperature. For instance, if one assumes an edge plasma temperature of 30 eV and a cold reservoir at room temperature, the Carnot efficiency of an ERD is around 99.9 %. Such a high efficiency is unlikely to be attainable from an engineering point of view, as there will almost inevitably be some loss mechanism other than entropy ejection that amounts to more than a tenth of a percent loss.

In practice, the real constraint on the thermodynamic efficiency of an ERD arises from factors arising from constraints on the divertor cross sectional area. Specifically, a free-streaming plasma is subject to conservation of phase space density. Thus, in order for its temperature to decrease, it must gain volume. However, as its density decreases, the cross-sectional area required to remove plasma from the device increases. Compensating for this by increasing plasma velocity only works up to a point, as any residual kinetic energy is converted into heat on impact with the divertor plate. Thus, if plasma velocity is optimized, the maximum attainable conversion efficiency can be calculated as a function of cross-sectional area by first calculating waste energy per mass:

$$ E_{w}=\frac{1}{2}v^{2}+c T $$
(2)
$$ T\propto \rho^{2/3} $$
(3)
$$ A \rho v=\Upphi $$
(4)

where \(\Upphi\) is the mass flux through the converter and is assumed to be a constant. Minimizing the specific waste heat E w yields the following:

$$ E_{w}=\frac{1}{2}v^{2}+k A^{-2/3}v^{-2/3} $$
(5)
$$ v=A^{-1/4}(2/3 k)^{3/8} $$
(6)
$$ E_{w}=2 A^{-1/2} (2/3 k)^{3/4} $$
(7)

where k is an arbitrary constant of proportionality. Since E w  ∝ A −1/2, it follows that:

$$ \epsilon=1-\left(\frac{A_{H}}{A_{C}}\right)^{1/2} $$
(8)

Since extraction of kinetic energy in the wiggler-Alfven design occurs away from both the x-point and the divertor plate, the cross-section of the plasma stream is simply the cross-section of the associated flux bundle, which is inversely proportional to magnetic field strength. In a tokamak, where the toroidal field is much stronger than the poloidal field, area is simply proportional to radius. Thus, the maximum efficiency for this type of device can be calculated by simply substituting the x-point radius and divertor radius into Eq. 8 in place of A H and A C , respectively.

Expansion Kinetics and Optimal Plasma Deceleration

Expansion and plasma deceleration in an ERD can be divided into three regimes: high collisionality, low collisionality, and transitional. In the high collisionality regime, plasma behaves as a fluid. Since particles are able to exchange energy between their parallel and perpendicular velocities as well as between particles, the mirror force simply accelerates the plasma without altering the shape of its thermal velocity distribution. Under such circumstances, plasma acceleration is equivalent to a gas in a de Laval nozzle with equivalent areal expansion ratio. The accelerated plasma then recompresses slightly as it is decelerated by the wiggler-Alfven structure. The net expansion and consequent energy extraction can be shown to be equivalent to the formula in Eq. 8. Assuming an expansion ratio of 2–3 yields a theoretical efficiency of 29–40 %.

In the low collisionality regime, both ions and electrons escape before undergoing significant numbers of collisions. As a result, a fluid approximation can no longer be used, and a full kinetic treatment of both electrons and ions is required. Such a calculation is beyond the scope of this article.

In the transitional regime, the ion mean free path is much larger than device size, but electrons undergo numerous collisions before escaping. In this case, electrons can be treated as a fluid, but with one caveat: since electron thermal conductivity is high in this regime, expansion is isothermal rather than adiabatic. The work done by electrons can therefore be calculated based on the spatial variation in plasma potential due to density variation from plasma expansion. This can be calculated based on quasineutrality [12] and mirror force:

$$ \Updelta\phi=\frac{k T_{e}}{e}\ln\left(\frac{A_{o}}{A_{i}}\right) $$
(9)

This is mitigated by electron cooling due to parallel thermal conduction; in short, electron temperature in the SOL is much lower than in the edge. In the low collisionality regime, the amount of such cooling can be estimated based on conservation of energy and plasma potential; each electron entering the SOL must, on average, carry as much energy as each electron leaving the sheath carries. The energy lost by electrons leaving the plasma is given by:

$$ E_{s}\equiv \frac{3}{2}k T_{e}+e\phi=k T_{e}\left( \frac{3}{2}+\frac{1}{2}\ln(T_{e}/T_{i})+\frac{1}{2}\ln(m_{i}/m_{e}) +\ln(A_{o}/A_{i})\right) $$
(10)

Taking a ratio of these gives an estimate of energy extraction efficiency:

$$ \epsilon=\frac{\ln(A_{o}/A_{i})}{\frac{3}{2}+\frac{1}{2} \ln(T_{e}/T_{i})+\frac{1}{2}\ln(m_{i}/m_{e})+\ln(A_{o}/A_{i})} $$
(11)

In order to calculate the T e /T i term, it is necessary to make assumptions about energy input to electrons. If electrons enter the SOL at the same temperature as ions, then E s  = 3/2 kT i . For a deuterium plasma (m i /m e  = 3,672), this gives a temperature ratio and efficiency of T e /T i  = .25 and \(\epsilon=.27\) for the case of a factor of 3 area expansion.

For ions, equilibration between parallel and perpendicular velocity does not occur to a significant extent in the low collisionality regime. Therefore, as ions are accelerated due to mirror force there will be a net conversion of perpendicular thermal energy not only into parallel kinetic energy but also into parallel thermal energy. This means that simply decelerating the ion distribution is not a particularly efficient way to extract energy from it, particularly since this would result in low-energy ions potentially being reflected by the ponderomotive potential of the Alfven eigenmode itself (as opposed to the potential wells created by the beat wave). A solution to this can be achieved by synchronizing the taper of the wiggler wavelength with taper in the wiggler amplitude. This results in a series of potential wells that can be loaded while sweeping across the distribution function in one direction, while unloaded while sweeping in velocity in the other direction. The net effect of this is to reverse a portion of the distribution function in velocity space; such a process conserves phase space density, and therefore does not violate any thermodynamic constraints.

In the asymptotic limit of arbitrarily large expansion ratio, an ion distribution that begins as a Maxwellian will end up with a distribution function of the form:

$$ f(v)=v^{2}e^{v^{2}/v_{th}^{2}}\equiv v^{2}g(v) $$
(12)

This distribution is peaked well away from zero. If the portion of this distribution less than some v r is reversed, then the fraction of energy recovered is given by:

$$ \epsilon=1-\frac{\int_{0}^{v_{r}}{v^{2}(v_{r}-v)^{2}g(v)} +\int_{v_{r}}^{\infty}{v^{4}g(v)} } {\int_{0}^{\infty}{v^{4}g(v)}} $$
(13)

For the distribution function shown, the optimal value of v r is roughly 1.6 × v th . This yields an efficiency value of 32 %. For lower expansion ratios, the efficiency with which ion energy can be collected in the low collisionality regime can be expected to be proportionately smaller.

Both of these values are significantly lower than the efficiency estimates for the fluid regime, and the ion estimate is for an asymptotic regime that cannot be achieved in any real reactor; the actual efficiency of ion energy extraction must be estimated by interpolation. However, as both of these values are positive, it follows that energy extraction can still proceed in the low collisionality regime. For a proof-of-concept device, such performance is sufficient. Moreover, as has been previously pointed out, a conventional thermal cycle can be used to process heat from the divertor plate, thus even in the worst case scenario, overall efficiency is significantly higher than with a conventional thermal cycle alone.

Ponderomotive Force from a Wiggler-Alfven Beat Wave

Ponderomotive force due to Alfven waves can be calculated by adding the ponderomotive forces on ions and electrons. These can be added because any imbalance between the two is compensated by quasineutrality; ponderomotive force on electrons results in parallel gradients in plasma potential, which in turn can accelerate or decelerate ions. Thus, as long as electrons are adiabatic, the effective potential felt by ions is the sum of both electron and ion ponderomotive potentials.

The ponderomotive force on a charged particle in a magnetic field due to perpendicular electric fields is given by [13, 14]:

$$ \Upphi=\frac{q^{2}E^{2}}{4 m \omega (\omega+\Upomega_{c})} $$
(14)

This gives a total ponderomotive potential for low frequency waves:

$$ \Upphi_{T}=\frac{q^{2}E^{2}}{4 m_{i}\omega(\omega+\Upomega_{ci})}+\frac{q^{2}E^{2}}{4 m_{e}\omega(\omega-\Upomega_{ce})} \approx -\frac{q^{2}E^{2}}{4 m_{i}\Upomega_{ci}^{2}} $$
(15)

This formula can be re-written in terms of the E × B velocity of the Alfven wave:

$$ \Upphi= -\frac{m_{i}\tilde{v}^{2}}{4} $$
(16)

To calculate the ponderomotive potential associated with the beat wave between the wiggler and the Alfven wave, it is first necessary to convert the wiggler field into a form that can be compared to the oscillating field. This can be done by calculating the apparent electric field experienced by particles moving through the wiggler field:

$$ E_{w}=v_{\parallel}\tilde{B} $$
(17)
$$ \Upphi_{w}= -\frac{m_{i}v_{\parallel}^{2}\tilde{B}^{2}}{4 B^{2}} $$
(18)

The interaction between these potentials can be calculated by first assuming that \(k_{wave}\||k_{wiggler}\). This gives a total ponderomotive potential:

$$ \Upphi=\frac{m_{i}\langle B\tilde{v}\sin(-\omega t) +\tilde{B}v_{parallel}\sin(k x)\rangle^{2}}{2 B^{2}} $$
(19)

The beat wave term from this is:

$$ \Upphi_{B}=-m \tilde{v} \sin(-\omega t) v_{\parallel} \frac{\tilde{B}}{B_{T}} \sin(k x) $$
(20)

This in turn can be represented as two potential waves moving in opposite directions, each with an amplitude of \(1/2 m \tilde{v}\tilde{B}/B_{T}\). Of these, only the forward wave is important for decelerating particles; the reverse wave may contribute to energy losses, but is not otherwise useful at this point.

Wave Amplitude for Optimal Trapping of Thermal Ions

The goal then is to determine how strong an Alfven wave is required to generate a potential well capable of trapping thermal particles, that is to say, \(2 \Upphi_{BF}\approx \Upphi_{B}\approx k T_{\parallel}\). Unfortunately, this calculation is complicated by a number of other factors. Fortunately, these factors ultimately lower the minimum amplitude needed to satisfy this criterion.

The first such factor is that the wave itself (as opposed to the wave-wiggler interaction) generates a ponderomotive force that accelerates particles prior to reaching the wiggler region. This means that, by the time particles reach the wiggler, they are not moving at an inlet speed v i ≈ v th , but instead at a speed \(\sqrt{v_{i}^{2}+\langle\tilde{v}^2\rangle}\approx \tilde{v}/\sqrt{2}\). This extra speed increases the effectiveness of the wiggler due to the v ∥ term in Eq. 20.

The second such factor is that, as the plasma accelerates, it also expands and therefore cools off. Assuming the wave region is small compared to mean free path, compression and expansion exclusively affect parallel thermal speed. This gives a correction to thermal velocity:

$$ v_{thw}=v_{thi}v_{i}/v_{\parallel} $$
(21)

Hence:

$$ T_{\parallel w}=T_{\parallel i} \left(\frac{v_{i}}{v_{\parallel}}\right)^{2} $$
(22)

The third such factor is the fact that, on entering the wiggler region, the plasma is bunched together, and therefore has a higher peak density than if it were uniformly distributed along the field line. This can be represented by introducing an additional coefficient into Eq. 21 to represent this bunching. Thus, if v thw  = α v thi v i /v ∥, where α≈ 2, then:

$$ T_{\parallel w}=T_{\parallel i} \alpha^{2} \left(\frac{v_{i}}{v_{\parallel}}\right)^{2} $$
(23)

Combining these gives a condition:

$$ m \tilde{v}^{2} \frac{\tilde{B}}{B_{T}}\approx \frac{2 k T_{\parallel i} \alpha^{2} v_{i}^{2}}{\tilde{v}} $$
(24)

So if \(v_{i}\approx v_{th}=\sqrt{2 k T/m}\), then we get:

$$ \tilde{v}\approx v_{th} \alpha^{1/2} \left(\frac{\tilde{B}}{B_{T}}\right)^{1/4} $$
(25)

If \(\tilde{B}/ B_{T} \approx .2\) then this yields \(\tilde{v}/v_{th}\approx 2.1\), which is very reasonable.

Wave Refraction for a Confined Toroidal Eigenmode

In order for the wave-wiggler interaction described in “Ponderomotive Force from a Wiggler-Alfven Beat Wave” to be useful as a means of energy extraction, it is necessary that the Alfven wave remain in the wiggler region long enough for energy content greater than its own to be extracted. Moreover, if this extraction is to be efficient, it must be confined in such a way as to avoid parasitic losses. To do this, the wave must avoid both the x-point (where the wave can be absorbed by the bulk plasma) and the divertor plate (where the wave can be absorbed by sheath effects).

The most efficient way to accomplish this is through refraction. If the wave has a lower azimuthal phase velocity at some point in-between the x-point and divertor plate than it does at either end, then the wave will become evanescent as one moves away from that point. This requires an understanding of Alfven wave propagation through the divertor plasma.

To lowest order, the group velocity of a shear Alfven wave is parallel to the magnetic field. This would appear to preclude the use of shear waves, as such a wave will inevitably propagate along field lines until it reaches either the x-point or the divertor plate. However, in a thin plasma sheet, the wave dispersion relation is altered considerably. To demonstrate this effect, let us begin with a generalized set of wave equations:

$$ k_{0}^{2}\xi_{x}=\left(k_{x}^{2}+k_{z}^{2}\right)\xi_{x}-i k_{x} \xi_{y}^{\prime} $$
(26)
$$ k_{0}^{2}\xi_{y}=k_{z}^{2}\xi_{y}-i k_{x}\xi_{x}^{\prime}-\xi_{y}^{\prime\prime} $$
(27)

where k 0 = ω/v A and \(Q^{\prime}=\partial Q/\partial y\). This formula can be used in both the plasma and the vacuum region by setting k 0 = 0 in the vacuum region.

This set of equations yields three solutions. In the vacuum region, there is a single solution, \(\xi=e^{\lambda_{v}y}\), where \(\lambda_{v}=\sqrt{k_{z}^{2}+k_{x}^{2}}\). Polarization in this region is given by the relation ξ x  =  − i k x / λ v ξ y . In the plasma, there are two solutions, either \(\xi_{x}=a \cosh \lambda_{p} y\) and \(\xi_{y}=b \sinh \lambda_{p} y\) (compressional Alfven mode), or \(\xi_{x}=b \sinh \lambda_{p} y\) (shear Alfven mode). In both cases, \(\lambda_{p}=\sqrt{k_{0}^{2}-k_{z}^{2}-k_{x}^{2}}\) and \(a=\frac{-i k_{x} b}{\lambda_{p}}\).

The solutions in the vacuum and in the plasma are subject to two matching conditions. The first is that ξ y be continuous. The other is that magnetic pressure be continuous. Combining these conditions with the solutions above yields a dispersion equation:

$$ k_{0}^{2}-k_{z}^{2}=\frac{\lambda_{p}}{\lambda_{v}}k_{z}^{2}\tanh \lambda_{p}h $$
(28)

where h is half the thickness of the plasma sheet. The solution listed here is for the compressional Alfven wave; the solution for the shear Alfven wave can be found by replacing tanh with coth.

The compressional solution is of interest in designing a wiggler-Alfven converter because plasma does not move towards or away from the wiggler. Since the wiggler field decays exponentially as one moves away from it, the plasma must be close to the wiggler for it to work. As a result waves in the shear direction of sufficient amplitude to produce useful amounts of ponderomotive bunching will cause the plasma to collide with the wiggler. Because of this, all further calculations will be of the compressional solution.

If h is sufficiently small, the solution in Eq. 28 can be approximated by taking \(\tanh x\approx x\). This yields the equation:

$$ k_{0}^{2}\left(1+\frac{k_{z}^{2} h}{\lambda_{v}}\right)-k_{z}^{2}\left(1+h\lambda_{v}\right)=0 $$
(29)

Comparing the derivatives in the x and z directions gives the orientation of group velocity. Retaining only lowest order terms in h yields:

$$ \frac{v_{gx}}{v_{gz}}\approx \frac{k_{z}k_{x}h\left(\frac{k_{0}^{2}} {\lambda_{v}^{2}}+1\right)}{2\lambda_{v}} $$
(30)

In the limit where k x ≫ k z , then this reduces to hk z /2.

Now that it has been established that it is possible for a shear Alfven wave to propagate in a purely toroidal direction, the question remains of how to actually make it do so. Noting in Eq. 29 that k z depends primarily on k 0, it follows that variations in Alfven speed will refract the wave. Variations in radius will also have this effect, since k 0 depends on ω, which is constant across a given eigenmode.

Since magnetic field strength varies with 1/R and so does density (since the plasma spreads out with the magnetic flux), that means that Alfven speed varies as \(1/\sqrt{R}\). For a specific mode number, wavenumber also varies with 1/R so natural mode frequency varies with R −3/2. As a result, the wave will tend to become trapped wherever the divertor channel is at its maximum radius. If the divertor were oriented as a super-X divertor, then this would result in the wave hitting the divertor plate and possibly being absorbed. Instead, if the divertor channel extends to a greater radius than the divertor plate and then loops back in, a confined wave results. The resulting layout of the device is shown in Fig. 1.

The focusing effects of radius must overcome a natural tendency for the wave to defocus. This is because, as plasma enters the wave region, it accelerates and therefore spreads out in the parallel direction. This results in a lower density and therefore a higher Alfven speed. Regions of high Alfven speed will refract the wave towards regions of lower Alfven speed, thus causing a defocusing effect. This results in an amplitude limit for any refractive wave confinement scheme.

Fortunately, that limit is not so severe as to cause problems for the wiggler-Alfven approach. A factor of 2 in radius is sufficient to overcome a factor of 8 in density. To achieve useful amounts of ponderomotive bunching, one only needs sufficient amplitude to cause a factor of 2 reduction in density. This can be accommodated by making the divertor channel extend to 1.26 times the radius of the divertor plate. While this does result in a bulky device, it is not unreasonably bulky and does not introduce any fundamental problem with the concept.

Conclusions

The wiggler-Alfven concept for an energy recovering divertor offers a possible way to extract useful work from a tokamak plasma without relying on traditional heat engines and without the large non-axisymmetric fields needed to create bundle divertors. This is accomplished in a way that is conceptually straightforward. Moreover, it does not necessitate any qualitative changes in the divertor plates themselves, merely in their placement. These changes in placement have the additional effect of spreading out divertor heat flux in addition to reducing total thermal load on the divertor plates. This makes it an attractive design for energy recovery and heat flux mitigation in a tokamak divertor.

The concept does have two significant drawbacks. For one thing, it is bulky, requiring the divertor channel to extend radially to the full radius of the toroidal field coils, then reverse direction. The space requirements of such an extensive divertor channel preclude it from being installed on many existing plasma experiments. The other drawback is that the wiggler-Alfven concept is inefficient compared to the full thermodynamic potential of the ERD concept as a whole. While high efficiencies are still possible by combining the ERD with a conventional thermal cycle, this still represents a missed opportunity to take advantage of the high temperatures present even in the tokamak scrape-off layer.

Despite these drawbacks, the wiggler-Alfven concept is useful from a conceptual standpoint for a number of reasons. First, it demonstrates the relevance of plasma direct conversion to tokamaks, or to any other toroidal plasma configuration. Second, it provides a means of extracting energy from a plasma that does not rely on charge separation. This combination of factors is significant because it opens a line of inquiry that could eventually lead to more compact, efficient devices. Such devices could, in turn, lead to an alternative path forward in fusion research based on improvements in power recycling efficiency rather than improvements in confinement, thus weaning magnetic fusion research off its dependence on reactor scaling to achieve breakeven. Even in the absence of such breakthroughs, the wiggler-Alfven concept in itself represents a novel method for generating RF energy with the potential for wide-ranging commercial spin-offs. As such, it represents a line of research that is worthy of further inquiry.