Skip to main content
SpringerLink
Log in

The Second Moment of the Distribution Function of Nanoparticles in a Limited Region and Their Brownian Diffusion

  • NANOSTRUCTURES
  • Published:
Journal of Engineering Physics and Thermophysics Aims and scope

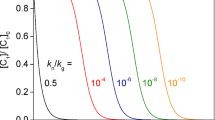
The change of the second moment of the distribution function of nanoparticles in a square under the influence of Brownian diffusion has been studied numerically and analytically. It is shown that the second moment of the distribution function of nanoparticles in an equilibrium system is independent of time, which is an important factor to be taken into account in processing experimental data. It has been established that the second moment of the function of nanoparticles distribution in a nonequilibrium spatially limited system depends on time, with this dependence being nonlinear.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. N. Zubarev, V. Morozov, and G. Röpke, Statistical Mechanics of Nonequilibrium Processes: Basic Concepts, Kinetic Theory, John Wiley & Sons, New York (1996).

    MATH  Google Scholar 

  2. S. P. Fisenko, Yu. A. Khodyko, and D. A. Takopulo, Some engineering applications of the Brownian diffusion of nanoparticles, in: Proc. Int. Conf. ″Nanomeeting–2015,″ World Scientifi c, Singapore (2015), pp. 155–157.

  3. R. Balesku, Equilibrium and Nonequilibrium Statistical Mechanics, John Wiley & Sons, New York (1975).

    Google Scholar 

  4. F. S. Gentile, I. De Santo, G. D’Avino, L. Rossi, G. Romeo, F. Greco, P. A. Netti, and P. L. Maffettone, Hindered Brownian diffusion in a square-shaped geometry, J. Colloid Interface Sci., 447, 25–32 (2015).

    Article  Google Scholar 

  5. C. A. Fletcher, Computational Galerkin Method, Springer, New York (1984).

    Book  Google Scholar 

  6. V. M. Verzhbitskii, Numerical Methods [in Russian], Vysshaya Shkola, Moscow (2002).

    Google Scholar 

  7. S. P. Fisenko and Yu. A. Khodyko, Brownian diffusion of nanoparticles inside of a spherical droplet of variable radius, Dokl. Nats. Akad. Nauk Belarusi, 60, No. 6, 123–128 (2016).

    Google Scholar 

  8. S. P. Fisenko and Yu. A. Khodyko, Brownian diffusion inside a micron-sized droplet and the morphology of ensembles of nanoparticles, J. Eng. Phys. Thermophys., 86, No. 2, 349–355 (2013).

    Article  Google Scholar 

  9. S. E. Dromashko and S. P. Fisenko, Long-time computer videomicroscopy of alive cells: simulation of "metastatic spreading," in: Mathematical Methods in Engineering and Technology [in Russian], Izd. Politekh. Univ., St. Petersburg (2018), Vol. 2, pp. 93–96.

  10. S. A. Rukolaine, A model of alternating ballistic Brownian transfer of particles and asymptotic approximation to it, Zh. Tekh. Fiz., 88, No. 9, 1304–1311 (2018).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. A. V. Luikov Heat and Mass Transfer Institute, National Academy of Sciences of Belarus, 15 P. Brovka Str, 220072, Minsk, Belarus

    S. P. Fisenko

Authors
  1. S. P. Fisenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. P. Fisenko.

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 92, No. 6, pp. 2486–2488, November–December, 2019.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fisenko, S.P. The Second Moment of the Distribution Function of Nanoparticles in a Limited Region and Their Brownian Diffusion . J Eng Phys Thermophy 92, 1443–1445 (2019). https://doi.org/10.1007/s10891-019-02062-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10891-019-02062-x

Keywords

Search

Navigation