Meritocracy and the inheritance of advantage

Abstract

We present a model where more accurate information on the background of individuals facilitates statistical discrimination, increasing inequality and intergenerational persistence in income. Surprisingly, more accurate information on the actual capabilities of workers leads to the same result—firms give increased weight to the more accurate information, increasing inequality, which itself fosters discrimination. The rich take advantage of this through educational investments in their children, and mobility decreases as a consequence of an increase in the ability to reward talent. Using our model to interpret the data suggests that a country like the US might indeed be a land of opportunity for the sufficiently able, as conditional on ability background may have relatively little effect. Nevertheless the US has a relatively low degree of intergenerational mobility precisely because meritocracy facilitates a high correlation of ability with background.

1 Introduction

Meritocracy, as a term, was first coined in the 1950s by British Sociologist Michael Young and was intended to describe the process of selectivity in education and labor markets whereby those perceived to have the most talent received the greatest rewards (Young 1958). Young intended it as a warning—talent can be bought and increasingly unequal rewards breed discontent—but the concept has since garnered significant positive attention. In this paper, we adopt Young’s definition of meritocracy—allowing firms to better judge the abilities of their workers, independently of their backgrounds—and investigate the extent to which it feeds into levels of income inequality and social mobility.

We begin by modeling, in a standard manner, the decisions of parents regarding investment in their children’s education given incomplete capital markets and an income process which they take as exogenous. We then endogenize this process by determining how the market rewards agents based on certain observable characteristics. This is the central feature of our model: firms observe signals on both the human capital and parental income of workers, and decide how much to pay based on these signals.

The decisions made by parents and firms are interconnected. Parents’ investment decisions depend on the extent to which the resulting signals will be rewarded by firms; and the value which firms assign to the signals depends on their accuracy relative to the firm’s priors, itself a function of the amount of inequality in society which results from parental investment decisions. It is very hard in general to find analytical solutions to models of this sort, as the whole distribution of heterogeneous agents both determines the equilibrium and is determined by the equilibrium. Nevertheless we set up the environment in such a way that we can solve analytically not only for the steady state, but for the whole dynamic path of the equilibrium.

We calculate the equilibrium weight given to the signals on human capital and parental income, and how these weights change when we exogenously vary the accuracy of the signals. This is how we provide more accurate information on human capital (meritocracy) and on parental income (inherited advantage). We then look at the implications of these changing weights for steady state income inequality and social mobility.

Our model explains a new mechanism behind the well-known negative relationship between income inequality and social mobility.¹ This comes about because more inequality implies firms have weaker priors about workers’ human capital and come to rely more heavily on information which is correlated with parental income, reducing mobility. Moreover, this increased discrimination feeds back into income inequality. This creates a multiplier whereby small changes in fundamentals can have large steady state effects.

The model shows how this increased discrimination by firms can come about as a result of more precise information on human capital. Thus better information on human capital increases inequality and lowers social mobility. This fall in mobility can happen directly, through greater weight being given to both the parental income and human capital signals, or indirectly, where the parental income signal plays less of a role in firms’ decisions, but the human capital signal is used more, and is sufficiently highly correlated with parental income through human capital investment, that mobility falls nonetheless. Thus, we show that if a society is better able to judge (and reward) individuals according to their human capital, then the unconditional intergenerational income correlation will necessarily increase, albeit the partial correlation (controlling for human capital) could decrease.

This is one of our key results: societies that reward human capital handsomely—and where as a consequence the children of the rich do not enjoy advantages once human capital is accounted for—are nonetheless bound to show larger inequalities and lower social mobility because richer parents use the rewards to human capital to create advantages for their children through educational investment. We use a numerical illustration to show that this process describes the situation in the US, a very meritocratic society but one in which intergenerational mobility is very low.

Moreover, there is a similar process whereby more information on parental income leads to lower mobility and greater inequality by allowing for greater statistical discrimination in favor of the children of the rich. This describes the situation in Italy. It makes clear that very different underlying processes can have very similar outcomes and how the degree of meritocracy has qualitatively the same effects on inequality and mobility as giving more information on an individual’s background.

The paper proceeds in the following way: Section 2 discusses some related literature. Section 3 outlines the model and solves for the equilibrium levels of discrimination and income inequality given optimal behavior by parents and firms. Section 4 characterizes the effects of changes in the accuracy of information that firms receive. Section 5 is a bit more philosophical and considers different possible meanings of the word "meritocracy". It shows that our results are robust to these alternative possibilities. Section 6 describes a numerical illustration which allows us to estimate the degree of accuracy of the signals in different countries, and the weights which they are given. Section 7 puts forward some ideas for extensions and Sect. 8 concludes. All proofs can be found in the appendix.

2 Related literature

This paper relates to several strands of the existing literature. Firstly, it is a model of statistical discrimination. The discrimination present in the model is a rational response by firms faced with limited information about workers’ human capital, and the relative weights given to different priors, and especially agents’ backgrounds, is an efficient way to plug this informational gap. This is the same process as in seminal models of statistical discrimination, such as Arrow (1973), Coate and Loury (1993), Norman (2003) and Moro and Norman (2004). The presence of this informational gap is also central to papers such as Simon and Warner (1992), who show that “old boys” networks improve information signaling for firms, explaining why referrals from employees account for a large percentage of hiring. Corak and Piraino (2011) show that children are much more likely to work in the same firms as their parents than chance would suggest, again implying uncertainty over labor market hires. Flabbi et al. (2019) show that increasing prevalence of female CEOs widens the wage distribution of female workers while improving firm performance, suggesting that this is consistent with statistical discrimination in that female CEOs are better at discerning the productivity of female workers.

Another component of the model outlined below is parental investment in human capital when faced with inefficient capital markets. The study of this in the economics literature goes back to Galor and Zeira (1993), which was followed by a large literature linking unequal access to education to inequality. While this is true in our model (the rich invest more heavily in their children than the poor), the extent to which it is mitigated by better information, and the role of background conditional on human capital, allow us to look at this in the context of meritocracy.

In addition to inequality, we consider intergenerational income mobility as examined by Becker and Tomes (1979). A number of theoretical papers have considered the negative relationship between inequality and mobility. These include Hassler et al. (2007), who show that such a negative correlation would arise if the main differences between economies lie in the education system rather than the labor market. Likewise, Solon (2004) shows that differences in the degree of progressivity of the education system generate this negative correlation. More recently, Krueger (2012) has illustrated this relationship in the data, naming it the ‘Great Gatsby curve’, and it has been shown to hold across countries (Corak 2013), across US commuting zones (Chetty et al. 2014), and across Italian provinces (Güell et al. 2015).

One final related strand of the literature, though one which we do not address directly in the model, considers the role of learning in the labor market and whether initial sorting really matters for lifetime income. We implicitly assume that it does. One way of reading the firm’s side of our story is as a short-cut to modeling individuals’ initial occupation allocations from a menu of careers with persistent wage differences. Oreopoulos et al. (2012), Kahn (2010), and Oyer (2006) provide direct evidence that initial wages have persistent effects. Guvenen et al. (2017) show that the first years of labor experience account for an extraordinarily large share of the total variance of lifetime income of individuals (and that it is changes in what has happened over these early years which explain the trend in lifetime income dispersion). Moreover, Baker et al. (1994a) and Baker et al. (1994b) show that initial sorting into employment tracks matters. If you start in a low wage track, you tend to be promoted within that track and not towards higher wage ones. Pavan (2011) shows that wage growth is critically affected by career and firm tenure, Kambourov and Manovskii (2009) and Sullivan (2010) show that occupation-specific considerations are an important component of human capital, while Gathmann and Schonberg (2010) and Poletaev and Robinson (2008) stress the importance of task-specific considerations. Cortes and Gallipoli (2016) show (and rationalize) that there are large costs to switching occupations. This issue will be discussed further in section 7.

3 The model

We have two types of agents: parents (who choose how to divide their income between their own consumption and investment in their children’s human capital), and firms (which determine how much are they willing to pay to workers based on their observable characteristics).

3.1 The parent’s problem

The parent’s problem is as follows:

$$\begin{aligned} W\left( Y_{t}^{i}\right)&=\max _{X_{t}^{i}}\left\{ \ln C_{t}^{i} +\frac{1}{1+\delta }EW\left( Y_{t+1}^{i}|Y_{t}^{i},X_{t}^{i}\right) \right\} \end{aligned}$$

(1)

$$\begin{aligned} s.t.\quad \quad&C_{t}^{i} = Y_{t}^{i}-X_{t}^{i};\quad X_{t}^{i}\ge 0 \end{aligned}$$

(2)

$$\begin{aligned}&H_{t+1}^{i} = Z \left( X_{t}^{i}\right) ^{\alpha } e^{{\tilde{\omega }}_{t+1}^{i}} \quad \text {with} \quad {\tilde{\omega }}_{t+1}^{i}\sim N\left( -\frac{V_{\omega }}{2},V_{\omega }\right) \end{aligned}$$

(3)

Equation (1) is the parent’s value function, where $Y_t^i$ is the (lifetime) income of parent i in generation t, $C_t^i$ is their consumption, and $X_t^i$ is their investment in the human capital of their offspring. Notice that parents care about their children’s utility, and not about their income or about the inheritance they receive as it is often assumed in the literature. Thus, in our model the share of expenditure in education is endogenous and depends on the perception that parents have on the impact of education on the children’s welfare.

We assume there are no capital markets, and so Eq. (2) is the budget constraint that parents face.

Equation (3) is the human capital production function, where $H_{t+1}^i$ is the human capital that the offspring achieves, Z is a constant akin to total factor productivity, and ${\tilde{\omega }}_{t+1}^{i}$ is a normally distributed i.i.d. shock with a mean such that $E\left( e^{{\tilde{\omega }}_{t+1}^{i}}\right) =1$. We assume that the elasticity of human capital with respect to parental investment, $\alpha \in \left( 0,1\right)$.

Equation (3) states that human capital is a stochastic function of the parent’s investment, without a role for other forms of inheritance (genetic or otherwise). This assumption is made for analytical tractability, but is interesting in its own right. It would be relatively easy to imagine a model where human capital was inherited and more precise information on genetic endowments adds to intergenerational persistence in incomes. Life would be “unfair” in the sense that, barring some good luck, a child’s income would be determined by the genes their parent happened to give them. This genetic inheritance would be correlated with parental income and so would compound the impact of the educational investment. So to this extent our model is conservative in how it transmits inequality over the generations, and our results would be starker in the presence of such a genetic mechanism.

Notice that we are assuming that the human capital of agents will be heterogeneous even if parental investment were identical. This is, parents choose the investment, and this affects the human capital of their children, but there is scope of differences in talent, or luck among the children that generate this heterogeneity.²

$Y_{t+1}^i$ is the wage offered to the child by the firm. This will be determined optimally when we solve the firm’s problem in Section 3.2. But in order to solve the parent’s problem, we need parents to take a view on firm behaviour. Parents know that when firms (the market) determines the wage of the child, it will use two sources of information: a noisy signal on the human capital of the child and a noisy signal on their own (the parents’) income. Parents can not alter the signals that the market will receive on their own income, but they can affect (albeit with noise) the human capital signal of the child by determining the investment. The exact way in which the market values the signals, and thus human capital investment and parental income, is of course endogenous to the model.

Competition forces firms to pay workers as close to their human capital as possible. Firms do not observe the exact value of $H^i_{t+1}$, and know that the educational investment that parents optimally make will be constrained by their income. Therefore, information on parental income and child’s human capital will affect the wage receive by the children. Parents know this, and incorporate this into their own optimisation. To determine the exact stochastic relationship in which human capital and parental income determine the income of the child we use a guess-and-verify strategy. We start by guessing that:

$$\begin{aligned} Y_{t+1}^{i}&= a^0_t (H^i_{t+1})^{a^1_t} (Y^i_t)^{a^2_t} \end{aligned}$$

for $a^0_t, a^1_t,a^2_t$, that the parents take as exogenous to their investment decisions. We will later show that this is indeed the equilibrium relationship.

Note that $a^1_t$ and $a^2_t$ are the elasticities of the child’s wage with respect to the realised value of human capital, and actual value of parental income respectively, while $a^0_t$ is stochastic and incorporates any noise in this mapping. Substituting human capital from (3), we can rewrite the parental problem as:

$$\begin{aligned} W\left( Y_{t}^{i}\right)&=\max _{X_{t}^{i}}\left\{ \ln C_{t}^{i} +\frac{1}{1+\delta }EW\left( Y_{t+1}^{i}|Y_{t}^{i},X_{t}^{i}\right) \right\} \end{aligned}$$

(4)

$$\begin{aligned} s.t.\quad \quad&C_{t}^{i} = Y_{t}^{i}-X_{t}^{i};\quad X_{t}^{i}\ge 0 \end{aligned}$$

(5)

$$\begin{aligned}&Y^i_{t+1} = e^{\gamma _{0_{t+1}}} \left( Y_{t}^{i}\right) ^{\gamma _{1_{t+1}}} \left( X_{t}^{i}\right) ^{\gamma _{2_{t+1}}} e^{\varepsilon _{t+1}^{i}} \end{aligned}$$

(6)

where Eq. (6) is the reduced form relationship between children’s income (on one hand) and both parental income and educational investment (on the other). The values of the parameters $\gamma _{0_{t+1}}$, $\gamma _{1_{t+1}}$ and $\gamma _{2_{t+1}}$, and the stochastic structure of the random variable $\varepsilon _{t+1}^{i}$ (which reflects noise in the human capital accumulation process, ${\tilde{\omega }}_{t+1}^i$, and noise in how firms conditionally respond given $Y_t^i$ and $H_{t+1}^i$), are endogenous to the model (while exogenous to the parent when choosing how much to invest). They will be determined below, once we have considered how the firms sets income.³ At this stage we just take the relationship (both the parameters and the functional form) as given. This leads to our first result:⁴

Result 2

If $\gamma _{2_{t+1}}\ge 0$, $\gamma _{1_{t+1}}>1+\delta$ and $\gamma _{1_{t+1}}+\gamma _{2_{t+1}}<1+\delta$, then the solution to the maximization problem in Eq. (4) requires that investment is a fixed proportion of the parent’s income:

$$\begin{aligned} X_{t}^{i}&=\lambda _t Y_{t}^{i} \end{aligned}$$

(7)

$$\begin{aligned} \text{ with, }&\lambda _t=\frac{\gamma _{2_{t+1}}}{1+\delta -\gamma _{1_{t+1}}} \end{aligned}$$

(8)

We will show that in equilibrium the restrictions $\gamma _{2_{t+1}}\ge 0$, $\gamma _{1_{t+1}}>1+\delta$ and $\gamma _{1_{t+1}}+\gamma _{2_{t+1}}<1+\delta$ do indeed hold.

Since parents invest a fixed fraction of their income, $\lambda _t$, it follows that, in absolute terms, the rich invest more heavily in their children than the poor. Since this is a known feature of the economy, the children of the rich will be perceived to have more human capital than the children of the poor when human capital is unobservable. This leads to statistical discrimination in favour of the children of the rich. Note also that how much the parent invests (at time t) depends on the value of that investment in the labor market faced by the child (at time $t+1$).

As a consequence of investment being a fixed proportion of income, Eq. (3) can be written as (once we take logs and denoting $h_{t+1}$ as the log of $H_{t+1}$):

$$\begin{aligned} h_{t+1}^{i}=\ln Z+\alpha \ln \lambda _t-\frac{V_{\omega }}{2}+\alpha y_{t}^{i}+\omega _{t+1}^{i} \end{aligned}$$

(9)

where $\omega _{t+1}^{i}\sim N\left( 0,V_{\omega }\right)$ is i.i.d. noise and $h_{t+1}^{i}$ and $y_{t}^i$ represent the log of the child’s human capital and the log of the parent’s income respectively. This is the equation for the accumulation of human capital. Human capital depends positively on parental income and the fraction of income which parents invest in their children.

3.2 The firm’s problem

We now consider how the firm sets incomes, specifically the income of the next generation. We assume that output equals the human capital of the child one-for-one. Hence, firms pay the child an income equal to their expectation of her human capital, given the information available, $\Omega _{t+1}^i$:

$$\begin{aligned} Y_{t+1}^{i}&= E\left( \exp \left\{ h_{t+1}^{i}\right\} |\Omega _{t+1}^{i} \right) \end{aligned}$$

(10)

When determining how much are they willing to pay to a certain worker, firms are aware of how parental characteristics map into the child human capital (Eq. (9)) and the distribution of income among parents (a log normal distribution⁵ with mean and variance taking endogenous values $\mu _t$ and $V_{y_t}$). What firms do not know is the exact level of human capital of a particular worker and their exact parental income. We assume that the firm receives imperfect signals on both.

To be precise, we assume that the information set of the firm is given by, $\Omega _{t+1}^{i}$, where:

$$\begin{aligned} \Omega _{t+1}^{i}&= \left\{ a_{t+1}^{i}, m_{t+1}^i; \mu _t,V_{y_t}\right\} \end{aligned}$$

(11)

and,

$$\begin{aligned} a_{t+1}^i&= y_{t}^{i} + \varepsilon _{t+1}^{ia} \quad \quad \text {with} \quad \varepsilon _{t+1}^{ia}\sim N(0,V_{a}) \end{aligned}$$

(12)

$$\begin{aligned} m_{t+1}^i&= h_{t+1}^{i} + \varepsilon _{t+1}^{im} \quad \quad \text {with} \quad \varepsilon _{t+1}^{im}\sim N(0,V_{m}) \end{aligned}$$

(13)

$a_{t+1}^i$ and $m_{t+1}^i$ are signals on parental income and human capital respectively. The precision of each of these signals is determined by the variances $V_a$ and $V_m$ which can take any finite non negative value.

A larger value of $V_a$, implies that firms observe parental income less accurately. If it approaches infinity, they would not be observing parental income at all. If it approaches zero, parental income would be perfectly observable.

Likewise, $V_m$ determines how much the firm knows about the human capital of a worker independently of her background. It is the available amount of “hard” information on the human capital of the worker, unaffected by prejudice of any sort. If $V_m$ were approaching infinity, firms would not have any direct information on the productive capacity of the worker, and would have to rely on inference from whatever they know on her background. If $V_m$ were zero, firms would have perfect knowledge on the productivity of the worker, and any information on her background would be irrelevant to determine her wage. Thus, we define a society with a lower $V_m$ to be more meritocratic in the sense that more direct information on human capital is being revealed (and rewarded). This is, by the way, the original definition of meritocracy as intended by Young when he coined the word.⁶

We will solve for the dynamic equilibrium, and show that it converges to a unique steady state. We proceed in two steps to find how the firm determines the income of the child: first, we use Bayes rules to form a posterior belief on the log of the human capital of the child, conditional on the information available to the firm; second, we see how this translates into income for the child. The end result of this gives the following relationship between the two signals and income:⁷

Result 3

Given a distribution of log parental income $N(\mu _t,V_{y{}_t})$, and if $\lambda _t$ is the share of investment in education performed by the parents, then the income of an individual in the following generation whose idiosyncratic observable characteristics are $a_{t+1}^{i}$ and $m_{t+1}^{i}$ equals:

$$\begin{aligned} y_{t+1}^{i}&= \left( 1-\beta _{m_{t+1}}\right) \bigg [ \ln Z + \alpha \ln \lambda _t - \frac{V_{\omega }}{2} + \alpha \left[ \left( 1-\beta _{a_{t+1}}\right) \mu _t + \beta _{a_{t+1}} a_{t+1}^{i} \right] \bigg ]\nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \beta _{m_{t+1}} \left( m_{t+1}^{i} + \frac{1}{2} V_{m}\right) \end{aligned}$$

(14)

$$\begin{aligned}&= \Phi _t + {{\hat{\beta }}}_{a_{t+1}} a_{t+1}^{i} + \beta _{m_{t+1}}m_{t+1}^{i} \end{aligned}$$

(15)

$$\begin{aligned} \text{ where: }&\quad \nonumber \\ \Phi _t&= \left( 1-\beta _{m_{t+1}}\right) \left[ \ln Z + \alpha \ln \lambda _t - \frac{V_{\omega }}{2} + \alpha \left( 1-\beta _{a_{t+1}}\right) \mu _t\right] +\beta _{m_{t+1}}\frac{V_{m}}{2} \end{aligned}$$

(16)

$$\begin{aligned} \beta _{a_{t+1}}&=\frac{V_{y_t}}{V_{y_t}+V_{a}} \end{aligned}$$

(17)

$$\begin{aligned} \beta _{m_{t+1}}&=\frac{\alpha ^{2}\beta _{a_{t+1}}V_{a} + V_{\omega }}{\alpha ^{2}\beta _{a_{t+1}}V_{a}+V_{\omega } + V_{m}} \end{aligned}$$

(18)

$$\begin{aligned} {{\hat{\beta }}}_{a_{t+1}}&= \alpha \beta _{a_{t+1}}\left[ 1-\beta _{m_{t+1}}\right] \end{aligned}$$

(19)

Thus, log income is a linear function of both signals. The constant depends on, amongst other things, the human capital production technology, the share of income invested, and the mean of log income in the parent’s generation and the variance of the signals (as this affects the variance of the posterior beliefs on human capital). The values of each of the signals to income depends on the precision of the information contained in the signals and on the dispersion of income in the parent’s generation (and hence the firm’s prior).

To understand Result 2 it is useful to start by looking at hypothetical scenarios:

Example 1

Imagine first that firms had perfect knowledge on the individual’s human capital ($V_m=0$ and $m_{t+1}^{i}=h_{t+1}^{i}$, $\forall i$). Not surprisingly, in this case the wage would be the exact human capital of the worker (since $\beta _{m_{t+1}}=1$ and $\Phi _t=0$) and firms would never overpay or underpay a worker (relative to her productivity).

Example 2

Next, imagine that parents invest a fix percentage of their income⁸$\lambda >0$ in education, and firms have no individual information whatsoever, that is: they know the distribution of income among the parents; and know the investment process from Result 1; but observe nothing about the specific worker whose wage they are about to decide (both $V_m$ and $V_a$ approach infinity). In this hypothetical case they would pay all workers the same wage (so the income distribution next period would collapse to a singleton) equal to their expected human capital. This follows a log normal distribution with mean $\ln Z+\alpha \ln \lambda + \alpha \mu _{y{}_t}$ and variance $\alpha ^2 V_{y{}_t}$. Thus the log of the income of any worker equals $\ln Z+\alpha \ln \lambda + \alpha \mu _{y{}_t}+\frac{1}{2} \alpha ^2 V_{y{}_t}$. Insofar as $\lambda$ is positive, firms always face heterogeneity and make “mistakes" (ex-post overpaying or underpaying workers relative to their productivity), but would pay all of them equally.

Example 3

Again, imagine that parents invest a fix percentage of their income $\lambda >0$ in education, and now imagine firms had no direct information on the human capital ($V_m\rightarrow \infty$) but some information on parental income. Firms would try to infer individual human capital from the information that they have on parental income and the fact that parental income is related to investment via Result 1. In this case we immediately see that $\beta _{m_{t+1}}=0$, and after some algebra that individual income would equal

$$\begin{aligned} y_{t+1}^{i} = \ln Z + \alpha \ln \lambda + \alpha \big [ (1-\beta _{a_{t+1}}) \mu _{y{}_t} + \beta _{a_{t+1}} a_{t+1}^{i}\big ] + \frac{1}{2} \alpha ^2 \frac{V_{y_t} V_a}{V_{y_t}+V_a} \end{aligned}$$

(20)

where $\beta _{a_{t+1}}$ is the weight on the signal on the posterior of parental income, and $\alpha ^2 \frac{V_{y_t} V_a}{V_{y_t}+V_a}$ is the variance of the posterior on parental income. Insofar as $\lambda$ is positive there would be statistical discrimination and the observable differences in parental income would result in heterogeneous treatment of the agents.

In our general case both $V_a$ and $V_m$ are positive and finite. This is, firms know about human capital and about parental income, but with noise. Before observing any signals, firms’ prior belief on the distribution of log of human capital of a worker i is:

$$\begin{aligned} h_{t+1}^i \sim N\big ( \ln Z + \alpha \ln \lambda _t - \frac{1}{2} V_\omega + \alpha \mu _t \, , \, \alpha ^2 V_{y{}_t} + V_{\omega } \big ) \end{aligned}$$

(21)

For the sake of argument let’s imagine that firms first observe $a_{t+1}^i$ and then $m_{t+1}^i$. After observing the parental income signal, the belief of the firm on the log human capital of the worker follows:⁹

$$\begin{aligned} h_{t+1}^i|a_{t+1}^i&\sim N\big ( \ln Z + \alpha \ln \lambda _t - \frac{1}{2} V_\omega + \alpha E(y_t|a_{t+1}^i) \, , \, \alpha ^2 V_{y{}_t|a^i_{t+1}} + V_{\omega } \big ) \nonumber \\&\sim N\big ( \ln Z + \alpha \ln \lambda _t - \frac{1}{2} V_\omega + \alpha (\beta _{a_{t+1}} a_{t+1}^i \nonumber \\&\quad + (1-\beta _{a_{t+1}}) \mu _t) \, , \, \alpha ^2 \beta _{a_{t+1}} V_a+ V_{\omega } \big ) \end{aligned}$$

(22)

Now introducing $m_{t+1}^i$, the independent signal on $h_{t+1}^i$, it is easy to look at result 2. Firms update Eq. 22 resulting in a posterior distribution from which it derives the Result. Its mean is expressed in Eqs. 14 and 15, and its posterior variance is $\beta _{m_{t+1}}m_{t+1}^{i}$. The weight on the signal, $\beta _{m_{t+1}}$ in Eq. 18, depends just on the relative variances of the signal and its “prior" (Eq. 22). Notice in Eq. 14 that income equals the weighted sum of the signal m and the "prior" derived from Eq. 22 plus a term that depends on the variance of the posterior. This last term is a consequence from the fact that the expectation of the log normal distribution increases with the variance.

If the signal m is perfectly informative (as in the example above) the payment is exactly equal to the human capital of the agent, and the “prior" (Eq. 22) would not be used; the signal on parental income would thus be irrelevant. The less informative this direct signal is, the more firms would rely on their “prior" (Eq. 22), and thus on their information on parental income via the signal $a^i_{t+1}$.

The signal on parental income, $a^i_{t+1}$, is valuable insofar as $V_m>0$, as any information on the parental income helps improve the accuracy of the “prior" in Eq. 22, and this is still valuable. The prevalence of statistical discrimination (measured by ${{\hat{\beta }}}_a$ in Eq. 19) is bigger (i) the larger is the elasticity of human capital to educational investment, (ii) the bigger is the weight of the signal a in determining the posterior of parental income, and (iii) the smaller the weight of the direct signal m in updating Eq. 22.

3.3 Equilibrium

Result 2 allows to write the income process in its Becker-Tomes representation. Noticing that $a^i_{t+1}$ and $m^i_{t+1}$ are both stochastic functions of $y^i_t$, we can write the law of motion of income as:

$$\begin{aligned} y_{t+1}^{i}&= \ln Z + \alpha \ln \lambda _t - \frac{V_{\omega }}{2} + \alpha (1-\beta _{a_{t+1}})(1-\beta _{m_{t+1}})\mu _t + \frac{\beta _{m_{t+1}} V_m}{2} \nonumber \\&\quad + \alpha \left[ \beta _{a_{t+1}}(1-\beta _{m_{t+1}})+\beta _{m_{t+1}}\right] y_t^i \nonumber \\&\quad + \alpha \beta _{a_{t+1}} (1-\beta _{m_{t+1}}) \epsilon _{t+1}^{ia} + \beta _{m_{t+1}} (\epsilon _{t+1}^{im} + \omega _{t+1}^i) \nonumber \\&= \Psi _{t+1} + \rho _{t+1} y_t^i + u_t^i \end{aligned}$$

(23)

where the intergenerational income elasticity is

$$\begin{aligned} \rho _{t+1} = \alpha \left[ \beta _{a_{t+1}}(1-\beta _{m_{t+1}})+\beta _{m_{t+1}}\right] \end{aligned}$$

(24)

From 23 we can determine the dynamics of the economy by noticing that the laws of motion for the mean and variance of log income are:

$$\begin{aligned} \mu _{t+1}&= \ln Z+ \alpha \ln \lambda _t - \frac{1}{2} \bigg (V_\omega -\beta _{m_{t+1}} V_m\bigg ) + \alpha \mu _t \end{aligned}$$

(25)

$$\begin{aligned} V_{y_{t+1}}&= \rho _{t+1}^2 V_{y_t} + \alpha ^2 \beta _{a_{t+1}}^2 (1-\beta _{m_{t+1}})^2 V_a + \beta _{m_{t+1}}^2 (V_m + V_\omega ) \nonumber \\&= ... = \alpha \rho _{t+1} V_{y_{t}} + \beta _{m_{t+1}} V_\omega \end{aligned}$$

(26)

Finally, in order to close the model, all that remains is to verify that the guess made in Eq. (6) is correct. By substituting for $a_{t+1}^i$, $m_{t+1}^i$, and $h_{t+1}^i$ in Eq. (15), it is straightforward to write the incomes awarded by the firm as a function of parental income and investment, with:

$$\begin{aligned} \gamma _{0_{t+1}}&= \Phi _t + \beta _{m_{t+1}} \left[ \ln Z - \frac{V_{\omega }}{2}\right] ;\quad \gamma _{1_{t+1}} =\alpha \beta _{a_{t+1}}\left[ 1-\beta _{m_{t+1}}\right] \\ \gamma _{2_{t+1}}&=\alpha \beta _{m_{t+1}} ;\quad \varepsilon ^i_{t+1} =\alpha \beta _{a_{t+1}}\left[ 1-\beta _{m_{t+1}}\right] \varepsilon ^{ai}_{t+1}+\beta _{m_{t+1}}\left[ \omega ^i_{t+1}+\varepsilon ^{mi}_{t+1}\right] \end{aligned}$$

and, consequently, the share of income invested in the child’s human capital as:¹⁰.

$$\begin{aligned} \lambda _t=\frac{\alpha \beta _{m_{t+1}}}{1+\delta -\alpha \beta _{a_{t+1}}\left[ 1-\beta _{m_{t+1}}\right] } \end{aligned}$$

(27)

Equation 27 can be understood intuitively as, if firms were not putting weight on the merit signal, i.e. if $\beta _m=0$, then there would be no point in parents investing in their children. Parents invest in your children only to the extent that it makes them look more productive and to the extent that it is taken into account by firms. The larger the elasticity of children’s income to the direct signal on their ability, the more parents invest in their children.

Likewise, the larger the elasticity of your children’s income to the parental signal (${{\hat{\beta }}}_a$, or just $\beta _a$ for given values of $\beta _m$ and $\alpha$), the more parents want to invest in their children. This is an interestingly subtle effect. One could have expected the opposite, that if statistical discrimination is more powerful, parents could have less interest in investing, as it is something that they can not affect. The reason why they invest more is that more investment makes children richer, and if there is more statistical discrimination this makes grandchildren richer, who are also present in the original parents’ valuations.

Finally, the share of income that you devote to investment also grows with the elasticity of human capital accumulation to educational investment ($\alpha$), and decreases with the discount rate ($\delta$).

It is immediate to determine the equilibrium of the economy:

Result 4

For any non-negative finite values of $V_m$, $V_a$ and $V_\omega$ the dynamic equilibrium of the economy is fully described by Eqs. 26, 17and 18. Using 27, 24and 25this generates a complete dynamic description of the economy.

Let us remark that we are thus able to solve analytically a complex heterogeneous agent economy. This will allow us in the following section to report analytical solutions to comparative static exercises without the need to find numerical solutions or calibrate the model. Moreover, we are able to solve not just for the steady state, but for the whole sequence of dynamic equilibria.

The limits of the equilibrium when the variances of shocks and noise become degenerate are non-obvious, but well behaved. It is interesting to explore some of them, as they provide with intuition that will help understand the comparative static exercises that we will perform.

Example 4

Take the case that $V_m$ approaches infinity i.e. firms have no direct information whatsoever about the human capital of workers. In this case, if parents were investing a positive share of their income in education, firms would use their information on parental income (as we saw in Example 3 above). Nevertheless in equilibrium parents know that their offspring’s abilities would be judged exclusively by their (the parent’s) income. Investment in education would have zero return, and obviously then $\lambda$ would approach zero. Consequently, if $V_m\rightarrow \infty$, firms know that the human capital of all agents is zero, and so income and output are all zero. Notice that this is perfectly consistent with Result 3 and the limit of the equations which describe it.

Example 5

Another interesting limiting case is when $V_a$ equals zero. In that case firms know perfectly the income of the parents, and thus their investment (via $\lambda _t$). If $V_w>0$ things are rather obvious: firms value the the direct information on human capital (m) because even if they know the investment made in the child, they do not know the final outcome of the human capital accumulation process, which it is what they care about. Thus $\beta _m$ would be positive and parents would invest a positive share of their income in education. However the alternative case, that in addition to $V_a=0$ there is no idiosyncratic noise in human capital acquisition ($V_\omega =0$), is not realistic in any way but makes things more complicated and interesting, so is worth exploring because in this case firms do not only know parental income and investment, they also know the exact human capital of the child without the need for any direct signal on it (though crucially there is a direct signal on human capital, with $V_m>0$).¹¹

Of course, in this case firms would not pay anything for the direct signal ($\beta _m=0$), and anticipating this, parents would not invest at all in their children ($\lambda =0$). Notice that this does not contradict Result 3 at all, as from Eq. 14 it is clear that the income paid to all agents is zero (the log income $y^i_{t+1}$ is negative infinity) irrespective of parental income. In this case, the constant in the determination of log income dwarfs the value of the parental income because firms know that there is no investment. Remember that what firms care about is not parental income, but the human capital of the child. In this case their prior on it has zero variance (and zero mean), so parental income is actually irrelevant in spite of being perfectly observable.

Thus, in the model a certain amount of noise is good for the economy, and increases long run output because it increases the return to educational investment.

3.4 Steady state

Before describing the properties of the steady state of the system we find it useful to make two observations.

• 1. In our model there is no role for self-fulfilling expectations. Expectations never drive the dynamics.

  This sets our model apart form the bulk of the literature on equilibrium-based statistical discrimination. In that literature the observed characteristic has no intrinsic value as there is nothing inherently good or bad in belonging to a given race or gender. Nevertheless, the fact that a characteristic is observable may make it acquire informative value: if everybody expects people of a certain race or gender to act in a certain way (investing little in education, for instance), it might be optimal to privately act in accordance with such an expectation (you will invest little in education if people expect you to have little education and it is your race, not your education, that is observed).

  Multiple equilibria are natural in such an environment, as the informative content of an observable characteristic depends on how people are expected to act and those expectations feed back into actions. Other expectations would lead to other actions, and those actions could feed those different expectations. Most obviously: the race or gender that is expected to have lower education could be changed and nothing of substance would be altered.

  Our model is very different in this respect because it is objectively good to be the child of rich parents, and it is objectively good to have high productive ability. There is no way of sustaining an equilibrium where low income parents invest in their children as much as rich parents do, as the marginal utility of consumption of poor parents is larger. It is easy then to see that the market will always discriminate against the children from deprived backgrounds. If it did not, the rich would still invest more in their children than the poor, so it would be irrational not to discriminate. Likewise, an individual with a large value of $m_t$ is always going to be paid more than another that differs only in having a lower value of $m_t$. More productivity is more productivity, and there is no other conceivable way of interpreting it.

• 2. There is a positive feedback mechanism by which inequality fosters further inequality.

  On the one hand, the more inequality there is (large $V_{y_t}$), the more heterogeneous agents are in their productive ability, and the more uncertainty firms face. Consequently, the market more heavily rewards indications of productive ability, both the direct ones ($m_t^i$), and the suggestive ones via parental investment ($a_t^i$). $\beta _{a_{t+1}}$ and $\beta _{m_{t+1}}$ are increasing in $V_{y_t}$. On the other hand, the larger the value given to the signals ($\beta _{m_{t+1}}$ and $\beta _{a_{t+1}}$), the larger the amount of inequality the next generation will endure, as the differences among agents are more salient.

  Thus, the more that society values the observable differences between agents, the more inequality it creates, and because of that, the more that it values the observable differences between agents. Or, looking at it from the other side, inequality fosters further inequality via increasing the extent to which society differentiates among its members. This positive feedback mechanism is ingrained in the process of statistical discrimination. It implies a multiplier effect: the effect of any exogenous change in parameters which leads to an increase in inequality will be amplified.¹²

Thus, our model does not allow for the existence of different sets of strategies and beliefs which could be mutually compatible for a single set of state variables: equilibrium is unique. Nevertheless, the existence of the positive feedback mechanism generates the possibility of multiple path dependent steady states. This happens if different values of the state variables lead you to different steady states in the long run, but there is no possibility of moving from one of those steady states once the economy has settled in it.

In our model multiple steady states arise if the elasticity of human capital to investment is large enough. If $\alpha \ge 1$ there are three steady states, of which two are stable, one with infinite variance. The other stable equilibrium is qualitatively identical to the unique equilibrium that we exists when $\alpha <1$. We prefer to restrict the parameter space to ensure that multiplicity does not arise. Therefore, from now on we assume that $\alpha < 1$.

In Appendix C we prove the following result:

Result 5

If $\alpha <1$, then for any set of finite values of $V_a$, $V_m$ and $V_w$ there exists a unique steady state of the economy which is globally stable and given by:

$$\begin{aligned} \mu&= \frac{1}{1-\alpha } \bigg [\ln Z + \alpha \ln \lambda + \frac{1}{2} \bigg (V_\omega - \beta _m V_m \bigg )\bigg ] \end{aligned}$$

(28)

$$\begin{aligned} V_y&= \frac{\beta _m V_\omega }{1-\alpha \rho } \end{aligned}$$

(29)

$$\begin{aligned} \beta _a&=\frac{V_y}{V_y+V_a} \end{aligned}$$

(30)

$$\begin{aligned} \beta _m&=\frac{\alpha ^2 \beta _a V_a + V_\omega }{\alpha ^2 \beta _a V_a+V_\omega + V_m} \end{aligned}$$

(31)

$$\begin{aligned} \rho&= \alpha (\beta _a(1-\beta _m)+\beta _m) \end{aligned}$$

(32)

$$\begin{aligned} \lambda&= \frac{\alpha \beta _m}{1+\delta -\alpha \beta _a(1-\beta _m)} \end{aligned}$$

(33)

Where the distribution of income follows a non-degenerate log normal distribution with mean and variance $\mu$ and $V_y$

4 Comparative statics

The following section lays out the main theoretical results of our paper.

4.1 An exogenous increase in the amount of information on background

A decrease of $V_a$ means that the market will have more accurate information on the background of agents. This is not good news for equality. Being better able to differentiate who received more education, the market will be more inclined to discriminate in their favor, providing greater advantages to those from affluent backgrounds. But how much the market chooses to discriminate is a function of the degree of inequality in the economy, and this is a state variable whose path is determined endogenously. This increase in the prevalence of inheritance may result in a decrease in human capital investment, as it is deemed unnecessary given that more weight is given to the parental signal.

In Appendixes E and G we prove the following result, which characterizes the effects of $V_a$

Result 6

An increase in the accuracy of the signal on background (a decrease of $V_{a}$) results, in steady state, in more inequality, greater persistence of income across generations, more discrimination based on perceptions of the background of an agent, and a smaller elasticity of income to the signal on ability:

$$\begin{aligned} \frac{dV_{y}}{dV_{a}}<0; \;\; \frac{d\rho }{dV_{a}}<0; \;\; \frac{d\beta _{a}}{dV_{a}}<0; \;\; \frac{d{\hat{\beta }}_{a}}{dV_{a}}<0; \;\; \frac{d\beta _{m}}{dV_{a}}>0 \end{aligned}$$

(34)

This decrease in $V_a$ may increase or decrease educational investment, $\lambda$. However, for $V_m$ sufficiently low, we have $\frac{d\lambda }{dV_{a}}<0$.

More accurate information on the background of an individual increases the attention that firms give to this signal, increasing the persistence of income across generations and its variance across individuals. This result is far from obvious: decreasing the amount of noise in the economy (i.e., increasing the information that agents have) increases the dispersion of incomes. You reduce noise, but as result you increase dispersion.

The reason lies in the increase in the persistency of the income process. Better information on the background of the individuals allows firms to discriminate more accurately between agents, directly favoring those from better backgrounds. A more persistent income process is bound to have a larger unconditional variance. Thus, inequality increases, which itself increases even further the value of the information on background via the positive feedback mechanism discussed above.

Notice also that the effect on the human capital signal ($\beta _m$) is the opposite. Better information on background results in a lower elasticity of income to the ability of individuals. This might look surprising, given that inequality is larger. More inequality implies that firms are less aware on the abilities of any specific worker, and thus, one could have expected that firms would give more attention to the meritocratic signal of human capital ($m_t^i$). They do not, and the reason is that, albeit the unconditional variance of income increases, the variance of log income conditional on the signal $a_{t}^{i}$ decreases. Thus, the dispersion of human capital conditional on $a_{t}^{i}$ decreases, and there is less demand for the meritocratic signal. There is a crowding-out effect, background replacing merit in the determination of one’s income and, consequently, a decrease in inter-generational mobility.

There are two offsetting effects which make the effects of a decrease in $V_a$ on human capital investment, $\lambda$, non obvious. On the one hand, the increased salience of background decreases the incentive to invest, because with respect to your own children you cannot change your background and direct signals on human capital are rewarded less. On the other hand, it increases the incentive to invest due to the rewards that will be given to your grandchildren (and subsequent generations) because you are changing the background of your children: insofar as parental investment still raises an agent’s income, it can be used to generate advantages for more distant generations of the family through the perception that richer parents provide. Still, we can determine an area of the parameter space where the first of these effects dominates, and the increase in the quality of the background signal results unambiguously in a decrease in the share of income devoted to human capital investment.

4.2 An exogenous increase in the degree of meritocracy

Next we want to consider the effect of exogenously reducing $V_m$, improving the quality of the human capital signal. What we deem (with all the caveats discussed above) as an increase of the degree of “meritocracy".

It is instructive to start by assuming that there is no signal on background ($V_a\rightarrow \infty$). In such a case the law of motion along the equilibrium is determined by:¹³

$$\begin{aligned} V_{y_{t+1}}&= \alpha ^{2}\beta _{m_{t+1}} V_{y_{t}}+\beta _{m_{t+1}}V_{\omega } ;\quad \quad \beta _{m_{t+1}} =\frac{\alpha ^{2}V_{y_{t}} + V_{\omega }}{\alpha ^{2}V_{y_{t}}+V_{\omega } + V_{m}} \end{aligned}$$

(35)

More information on merit (lower $V_m$) induces the market to rely more heavily on such information, increasing $\beta _{m_{t+1}}$. This necessarily increases the spread of incomes, as the differences between agents become more salient. The increase in inequality makes firms less sure of the human capital of their workers in the following generation, increasing the value that they assign to any information on merit, increasing $\beta _m$ further, which itself increases inequality, and so on.

It is easy to see that the unique steady state of (35) is the unique solution to:

$$\begin{aligned} V_{y} =\frac{\beta _{m}V_{\omega }}{1-\alpha ^{2}\beta _{m} } ;\quad \quad \beta _{m} =\frac{{\alpha ^{2}V_y}+V_{\omega }}{\alpha ^{2}V_y + V_{\omega }+V_{m}} \end{aligned}$$

(36)

and that the steady state values of $V_{h}$, $V_{y}$ and $\beta _{m}$ are all decreasing in $V_{m}$. The intergenerational income elasticity (now equal to $\alpha \beta _m$) increases as $V_m$ is reduced.

Contrary to what could be thought, more information on people’s ability is bound to decrease intergenerational mobility because ability and background are correlated and, by increasing income dispersion, meritocracy increases the value of any existing information on people’s ability. The children of the rich, being on average more productive than the children of the poor, benefit from the increase in the accuracy of information on merit, leading to more persistent income shocks and further inequality. Meritocracy has very much the same effects on income inequality and intergenerational mobility as an increase in the information available on background.

The effect on human capital accumulation, though, are very different: by increasing the return to the signal of human capital, an increase of the precision of the merit signal fosters the accumulation of human capital unambiguously. The more meritocratic society will be less equal, and less mobile, but richer.

It is now easier to consider the effect of an exogenous improvement in the quality of the human capital signal when both signals are available and useful to the firm (i.e. $V_a$ is finite).¹⁴

Result 7

An increase in the accuracy of the signal on ability (a decrease of $V_{m}$) results, in steady state, in more inequality, greater persistence of income across generations, a larger share of investment in education, a larger elasticity of income to the signal on ability and more weight given to the signal on background when evaluating an agent’s parental income (which is what $\beta _a$ measures):

$$\begin{aligned} \frac{dV_{y}}{dV_{m}}<0;\;\; \frac{d\rho }{dV_{m}}<0;\;\; \frac{d\lambda }{dV_{m}}<0;\;\; \frac{d\beta _{m} }{dV_{m}}<0;\;\;\frac{d\beta _{a}}{dV_{m}}<0 \end{aligned}$$

(37)

If society is better endowed to judge its members’ merit, it is doomed to increase the dispersion of their incomes (paying more to those judged to be better). This increased dispersion has effects on both the value assigned to merit, $\beta _{m}$, and the value assigned to “advantages”, ${\hat{\beta }}_{a}$.

First, it increases the dispersion of the abilities of the children, thus feeding back into increased underlying uncertainty and the value of the signal on human capital in the following period. Thus, not surprisingly, better information on human capital increases the market value of that signal.

The effects on the weight given to background when determining income (${\hat{\beta }}_{a}$) are more complicated. First of all, there is a “crowding-out effect” in the opposite direction to that in result 5. Better information on human capital makes you place less weight on background as merit replaces inherited advantages in the determination of human capital. This is clear from the fact that $\beta _{m}$ enters negatively in ${\hat{\beta }}_{a}=\alpha \beta _{a}\left( 1-\beta _{m}\right)$. However, there is an effect on the other direction too: as income variance increases, the signal on background becomes more valuable in judging parental income. This increase in $\beta _a$ acts in the opposite direction to the increase in $\beta _m$. The net effect on ${\hat{\beta }}_{a}$ depends on the relative size of the effects on $\beta _{a}$ and $\beta _{m}$.¹⁵

We can understand the net effect by doing the following mental exercise. Imagine that $V_{m}$ were very low (and thus, firms have good information on ability). In that case $\beta _{m}$ would be very large (close to one), and the effect of the increase of $\beta _{a}$ would be very small $\left( \frac{\partial \hat{\beta }_{a}}{\partial \beta _{a}}=\alpha \left( 1-\beta _{m}\right) \right)$. The net effect of a decrease in $V_{m}$ would be an increase in the market value of the human capital signal, but a decrease in the value of the parental income one. There would be a trade-off between meritocracy and advantages as the crowding-out effect dominates.

Now imagine the polar opposite case where $V_{m}$ is very large. In such a case $\beta _{m}$ would be close to 0 and background information would play the dominant role in the determination of human capital. Any increase in the quality of information on ability would increase the market value of both signals because, in this case, the effect of an increase in $\beta _a$ on ${\hat{\beta }}_a$ is relatively large.

In any case, notice that the degree of intergenerational mobility always decreases whenever the society becomes more meritocratic as a consequence of a decrease of $V_{m}.$ This occurs both when there is a trade-off (and advantages become less important) or when there is not. This is a consequence of inheritance. The talented become richer, and thus incomes are bound to become more dispersed. This increased dispersion of incomes is going to be translated into a further dispersion of abilities as the rich invest more in their children. Abilities then, being better evaluated, translate into more income for the children of the rich even if it is perfectly possible that firms care less about the background of agents.

This is one of the main insights of our paper. Meritocracy in and of itself is not going to increase intergenerational mobility or decrease the prevalence of inheritance. And this is bound to happen even if an increase in meritocracy does produce a decrease in the advantages associated with being from a good background, which is by no means a foregone conclusion.

This is not to say that meritocracy is a bad thing, as it increases the share of income invested in human capital, since a better signal on talent increases the return to investing in human capital.

The significance of our result is to notice that there are several roads that lead to countries having low intergenerational mobility and high inequality: one is the “aristocratic” route, where the children of the rich benefit from positive statistical discrimination as the rich are known to invest more heavily in their children’s education than the poor; but a very different road, leading to the same mobility and inequality outcomes, is the meritocratic one. If one focuses only on the degree of mobility and inequality, then meritocracy and the weight of background are almost equivalent. Both of them produce a negative correlation between inequality and mobility, reproducing the observed data.

Nevertheless, the meritocratic society has the redeeming quality of unambiguously fostering educational investment and, thus, increasing income. The meritocratic society is unequal and shows little intergenerational mobility; but it is rich.

4.3 The role of uncertainty generating a Great Gatsby Curve

The discussion on the pre-eminence of inheritance and the possible end of the American dream has focused a substantial amount of attention in the so-called “Great Gatsby Curve”. This is an empirical relationship¹⁶ between the degree of inequality and a measure of the intergenerational persistence of income across countries. Corak (2013), across US commuting zones (Chetty et al. 2014) and across Italian provinces (Güell et al. 2015), among others.

The standard Becker-Tomes model suggests a possible explanation for this relationship due to, perhaps, institutional differences in the educational system across countries or locations.¹⁷ We recover the standard Becker-Tomes model income process from Eq. 23 if information is perfect ($V_m=0$):

$$\begin{aligned} y^i_{t+1} = \ln Z + \alpha \ln \frac{\alpha }{1+\delta }+\frac{1}{2} V_w + \alpha y^i_t + w^i_{t+1} \end{aligned}$$

Thus, the intergenerational income elasticity equals the elasticity of human capital to educational investment ($\rho =\alpha$), and inequality equals $V_y=\frac{\alpha }{1+\delta }$. If locations are defined by this Becker-Tomes income process, each with its own $\alpha$ (which could be interpreted as institutional differences in their educational systems), then we will observe a positive correlation between inequality and intergenerational persistence: a Great Gatsby Curve.

Our model suggests an alternative (and not incompatible) explanation for the Great Gatsby Curve, due to uncertainty. From the previous results it follows that changes in the quality of information of the signal on talent and changes in the quality of the information of the signal on parental income, both generate a positive correlation between inequality and intergenerational persistence. Even if we posit a uniform $\alpha$ across locations, any decrease in the accuracy of the observation of human capital (any increase in $V_m$) or in the accuracy of the observation of parental income (any increase in $V_a$) would decrease both intergenerational persistence, $\rho$, and inequality, $V_y$.

5 On semantics: the definition of meritocracy

We recognize that other people may have different conceptions on what “meritocracy” means, and some people have strong opinions on this semantic issue. Clearly, many people associate the word with a reduction of the privileges that some members of society may enjoy. These privileges (which we might call “cronyism”) mean that some people may be rewarded far in excess to their contribution to society. Examples would be the corruption in the allocation of public positions via friendship or connections, or the impossibility of accessing higher education and positions of power and substance without the benefit of parental wealth and connections. Notice that the reduction of those privileges is not what we mean by “meritocracy”. It could be another perfectly reasonable definition, but is not the one that we use, and it is not what Young meant when he invented the word.

Since Becker (1957) we have known that irrational discrimination has negative effects not only on those discriminated against, but also on the discriminator. Competition and market forces should work against the extent of those privileges: a firm that hires a person because he has an aristocratic name rather than talent, is a firm that will lose money and be driven out of a competitive market. Thus, our approach is to model the advantages that the rich enjoy as a result of rational statistical discrimination of firms with limited information.

In Appendix H we include “cronyism” (privileges not backed by reason) as an extension of our analysis. We remove the signal on parental income and instead assume that firms irrationally reward the children of the rich to some extent while rationally rewarding the signal on merit. We show that (in exactly the same manner as for the quality of signals on parental background in Result 5) the reduction in the extent irrational reward to background (“cronyism") does indeed decrease the intergenerational persistence of income and (in most cases) the degree of inequality. Still, even in the presence of such cronyism, the effects of improving the technology to determine one’s ability (“meritocracy” in our sense) are qualitatively the same as in our main analysis. An equivalent result to 6 still holds.

The difference between “cronyism" and “meritocracy" does not lie in their effects on inequality or mobility, but on their efficiency and their incentives for human capital accumulation.

6 A numerical illustration

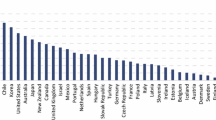
In this section we map cross-country data on inequality, mobility, and educational investment into the model’s parameters, allowing us to examine cross-country differences in the rewards to the two signals. The value of the exercise is that it allows us to transform the observed data on inequality and mobility (as shown in Fig. 1) into our measures of “meritocracy" and “advantages" for each of the countries.

The exercise that we will perform is the following: we assume that the only margins in which countries differ are the precision of the signals on merit and background. Parents in all countries are assumed to have the same preferences, and the technology for human capital accumulation is assumed to be identical everywhere. We want to be upfront about the limitations of this exercise. We abstract from many relevant issues such as the redistributive aspects of the tax system, and the fact that the level of public education is not a parental choice, but a societal one. Given the very stylized nature of the theoretical model, this mapping is intended as an illustration, rather than a rigorous empirical test of the model, but nonetheless provides interesting examples of the underlying differences behind international performances on measures of inequality and intergenerational mobility. These are discussed in Sect. 6.3.

This exercise exploits the results of Sects. 4.1 and 4.2, in that changes in $V_m$ and $V_a$ have different effects on the share of income invested in education. Specifically, precise signals on merit will be associated with higher shares of income invested in education.¹⁸

6.1 Data

For each country we use three pieces of data: (i) the variance of log income, (ii) the intergenerational elasticity of income and (iii) the share of GDP in education.

We obtain data on inequality from OECD (2015b),¹⁹ the intergenerational elasticity of income comes from Corak (2013), and the share of GDP of education from OECD (2015a).

Summary data on the 15 countries included in our dataset is given in table 1.²⁰

Table 1 International Data

6.2 Procedure

The set of parameters that we calibrate are: $V_\omega> 0, \delta > 0$, which are common across countries; and values $V^j_a>0$ and $V_m^j>0$, specific to each country j (we actually choose $\beta _a^j \in (0,1)$ and $\beta _m^j \in (0,1)$, but this is equivalent).²¹²² We assume that the elasticity of human capital to investment, $\alpha$, takes a value of $\frac{1}{2}$. We do so as it seems plausible and facilitates the calibration procedure.²³ This leaves us with 45 data moments and 32 parameters.

With these parameters we create simulated economies and calculate in each of them three moments: the intergenerational elasticity of income, ${\tilde{\rho }}^j$, the variance of log income, ${\tilde{V}}_y^j$, and the share of educational investment in GDP, ${\tilde{\lambda }}^j$. We choose the parameters of the model to minimize the weighted sum of squared percentage errors between the values ${\tilde{\rho }}^j$, ${\tilde{V}}_y^j$, and ${\tilde{\lambda }}^j$ that the model generates, and the values ${\hat{\rho }}^j$, ${\hat{V}}_y^j$, and ${\hat{\lambda }}^j$ that these moments take in the data set described above:

$$\begin{aligned} \left[ V_\omega ,\delta ,\left\{ \beta _m^j,\beta _a^j\right\} _{\forall j} \right] = \arg \min \sum _{j=1}^{15} \left[ W_\rho \left( 1-\frac{{\tilde{\rho }}^j}{{\hat{\rho }}^j}\right) ^2 + W_{V_y} \left( 1-\frac{{\tilde{V}}_y^j}{{\hat{V}}_y^j}\right) ^2 + W_\lambda \left( 1-\frac{{\tilde{\lambda }}^j}{{\hat{\lambda }}^j}\right) ^2\right] \end{aligned}$$

where:

$$\begin{aligned} {\tilde{\rho }}^j= & {} \alpha (\beta _a^j(1-\beta _m^j)+\beta _m^j)\\ {\tilde{V}}_y^j= & {} \frac{\beta _m^j V_\omega }{1-\alpha ^2(\beta _a^j(1-\beta _m^j)+\beta _m^j)}\\ {\tilde{\lambda }}^j= & {} \frac{\alpha \beta _m^j}{1+\delta -\alpha \beta _a^j(1-\beta _m^j)} \end{aligned}$$

and the weights, $W_\rho$, $W_{V_y}$, and $W_\lambda$, are chosen so that the sum of relative percentage errors is approximately equal in the three margins:

$$\begin{aligned} \sum _{j=1}^{15} \left( 1-\frac{{\tilde{\rho }}^j}{{\hat{\rho }}^j}\right) ^2 \approx \sum _{j=1}^{15} \left( 1-\frac{{\tilde{V}}_y^j}{{\hat{V}}_y^j}\right) ^2 \approx \sum _{j=1}^{15} \left( 1-\frac{{\tilde{\lambda }}^j}{{\hat{\lambda }}^j}\right) ^2 \end{aligned}$$

6.3 Results

Our calibration results consist of a set of values for $\beta _m^j$ and $\beta _a^j$ for each of the countries (these results are in Fig. 2), as well as values for our global parameters: $V_\omega = 1.64$ and $\delta = 2.41$. Note that this value for $\delta$ has not been targeted, yet if we deem time periods in the model to be of the order of 40 years, then this corresponds to an annual discount rate of around $3\%$, which seems very reasonable.

Fig. 1

The Great Gatsby Curve

Fig. 2

Rewards to merit and background $\beta _m^j$, ${{\hat{\beta }}}_a^j \equiv \alpha \beta _a^j \left( 1-\beta _m^j \right)$

Notice that in the Great Gatsby (Fig. 1), the US suffers from a high degree of inequality and intergenerational income persistence. This has been seen as indicative of the demise of the American Dream (see for instance Krueger (2012)).

In the light of our model though, the interpretation is different. In Fig. 2 we plot the implied values for $\beta ^j_m$ and ${{\hat{\beta }}}^j_a$ for each of the countries. The value of $\beta ^{US}_m$ for the US is the highest, suggesting that the US has low intergenerational mobility because wages are strongly related to direct measures of the productivity of workers, relying relatively less on statistical discrimination that would favor the children of the better off. Part of the reason why the US is calibrated to have such an accurate signal on human capital is because the share of income invested in education is so high there, and the strongest incentive to invest comes when information on human capital is revealed accurately to firms. You could have high persistence by having very accurate signals on either margin; but only highly accurate merit signal produce both high persistence and high educational investment.

It is informative to compare the behavior of the US and Italy at the light of the model. In the Great Gatsby Curve both countries have similarly high levels of income inequality and intergenerational persistence of income relative. Yet when we filter the data through the model, they look very different: the model implies a relatively high degree of meritocracy for the US, and relatively high rewards to parental incomes in Italy. This makes clear, first and foremost, that it is naive to imply that a country with a high correlation of incomes across generations is not meritocratic. The US effectively measures and rewards human capital, but in doing so creates a situation where an agent’s income is strongly correlated with that of their parents. Moreover, this strong unconditional effect of background occurs whilst the parental income signal is relatively less rewarded.

The one liner lesson: low intergenerational mobility by no means implies a low level of “meritocracy”.

7 Further research

We believe that there are several extensions of this paper that are worth consideration.

As noted in Sect. 2, we have not directly addressed learning by firms about an individual’s human capital, either in the theoretical model or in the numerical exercise. Instead we have a single period of adult employment. We argue there that the impact of signals on the lifetime income paid by firms could be thought of as a shorthand for an income process where initial job allocation has long-run effects. For the purposes of creating a more rigorous numerical calibration, we should explicitly model this process. This could be through task specific learning (which leads initial perceptions to have permanent effects), or through path dependence in the human capital accumulation process (for example, where the specific high school attended, or grades achieved, determines the quality of university attended, itself having permanent labor market effects).

Likewise, we did not include any consideration of public education or redistribution in our analysis. Including them in our model would reduce inequalities in the acquisition of human capital and, by disconnecting human capital from parental income, would also reduce the persistence of these inequalities across generations. Their introduction would affect the quantitative aspects of the model, which is why we think of our numerical exercise more as an informal example of the workings of the model rather than a measurement exercise. Any rigorous empirical calibration should include these. Notice, however, that including public education or redistribution will not affect any of the qualitative points that we made. Insofar as they do not eliminate inequality or private investments in children, the mechanisms described above will still be present.

8 Conclusions

Our main result is to show that more accurate information on the productivity of individuals leads to lower intergenerational mobility and more inequality, while increasing the effort in educational investment that agents do. The reason is that more accurate information on productivity leads to more dispersion of wages for a given distribution of productivities. This increase in inequality translates one generation later in larger differences in parental income, human capital accumulation, and productivity. This itself would have a direct effect reducing mobility, but this effect is magnified by the fact that in this more unequal world, the weight that firms give to any specific information on the agent becomes more valuable, further increasing inequality, and further decreasing mobility... and so on. There is though another effect of the increased accuracy of observing the human capital of agents: it translates into increasing incentives to invest in education, as the increase in rewards of observed productivity increases the incentives to invest in human capital acquisition.

In our model, two individuals with exactly the same observable human capital signals will receive different wages because firms rationally discriminate favoring the children of the rich. Better information on background facilitates this discrimination, having similar effects on inequality and intergenerational mobility as better objective and direct information on human capital, albeit it does not increase the return on human capital accumulation in the same manner as an increase in “meritocracy".

We believe that a non-trivial contribution of our paper is to be able to analytically solve a very complex heterogeneous agent model where the return to education, optimal levels of investment, and the reward schedule offered by firms (to both signals) are tractable, and solutions can be presented for the whole dynamics of the economy.

Summarising, better information on the quality of workers (allowing wages to be more “objectively" related to performance) turns out to have similar effects on inequality and intergenerational mobility to better information on their background (which generates more statistical discrimination favouring agents with good backgrounds). Better information on either human capital and parental background have similar effects on inequality and mobility, and different effects on human capital accumulation; but to believe that the one is somehow more equitable than the other (either in a cross sectional or in an intergenerational sense) could perhaps be argued to be purely an illusion. This lesson has implications when looking at the state of the world and for policy. It suggests that it would be futile to hope that increasing the degree of “meritocracy" a society will increase intergenerational mobility.

Appendices

Appendix

Appendix A: Proof of Result 1

Proof

We solve the program:

$$\begin{aligned}&W\left( Y_{t}^{i}\right) \\&\quad = \max _{X_{t}^{i}}\left\{ \ln \left[ Y_{t} ^{i}-X_{t}^{i}\right] +\frac{1}{1+\delta }EW\left( e^{\gamma _{0_{t+1}}}\left( Y_{t}^{i}\right) ^{^{\gamma _{1_{t+1}}}}\left( X_{t}^{i}\right) ^{\gamma _{2_{t+1}} }e^{\varepsilon _{t}^{i}}\right) \right\} \end{aligned}$$

First we prove that parents invest a fixed percentage of their income in their children:

$$\begin{aligned} X_{t}^{i}=\lambda _t Y_{t}^{i} \end{aligned}$$

To do so we guess

$$\begin{aligned} W\left( Y_{t}^{i}\right) =A+B\ln Y_{t}^{i} \end{aligned}$$

which we will later verify. The Euler equation is:

$$\begin{aligned} \frac{1}{Y_{t}^{i}-X_{t}^{i}}=\frac{1}{1+\delta }\frac{\partial EW\left( e^{\gamma _{0_{t+1}}}\left( Y_{t}^{i}\right) ^{^{\gamma _{1_{t+1}}}}\left( X_{t} ^{i}\right) ^{\gamma _{2_{t+1}}}e^{\varepsilon _{t}^{i}}\right) }{\partial X_{t} ^{i}} \end{aligned}$$

Since,

$$\begin{aligned} EW&\left( e^{\gamma _{0_{t+1}}}\left( Y_{t}^{i}\right) ^{^{\gamma _{1_{t+1}}}}\left( X_{t}^{i}\right) ^{\gamma _{2_{t+1}}}e^{\varepsilon _{t}^{i}}\right) \\&=A+B\left[ {\bar{\varepsilon }}+\gamma _{0_{t+1}}+\gamma _{1_{t+1}}\ln Y_{t}^{i}+\gamma _{2_{t+1}}\ln X_{t} ^{i}\right] \end{aligned}$$

the Euler equation becomes:

$$\begin{aligned} \frac{1}{Y_{t}^{i}-X_{t}^{i}}=\frac{1}{1+\delta }B\gamma _{2_{t+1}}\frac{1}{X_{t}^{i}} \end{aligned}$$

implying,

$$\begin{aligned} X_{t}^{i}=\frac{B\gamma _{2_{t+1}}}{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}Y_{t}^{i} \end{aligned}$$

and

$$\begin{aligned} C_{t}^{i}=\frac{\left( 1+\delta \right) }{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}Y_{t}^{i} \end{aligned}$$

Now, substituting $X_{t}^{i}$ into the expectation we get:

$$\begin{aligned}&EW\left( Y_{t+1}^{i}|Y_{t}^{i},X_{t}^{i}\right) =EW\left( e^{\gamma _{0_{t+1}}}\left( Y_{t}^{i}\right) ^{^{\gamma _{1_{t+1}}}}\left( X_{t}^{i}\right) ^{\gamma _{2_{t+1}}}e^{\varepsilon _{t}^{i}}\right) \\&\quad =A+B\left[ {\bar{\varepsilon }}+\gamma _{0_{t+1}}+\left[ \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right] \ln Y_{t}^{i}+\gamma _{2_{t+1}}\ln \frac{B\gamma _{2_{t+1}}}{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}\right] \end{aligned}$$

and the value function will be:

$$\begin{aligned} W\left( Y_{t}^{i}\right)&=\ln \frac{\left( 1+\delta \right) }{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}+\ln Y_{t}^{i}+\frac{A}{\left( 1+\delta \right) }\\&\quad +\frac{B}{\left( 1+\delta \right) }\left[ {\bar{\varepsilon }}+\gamma _{0_{t+1}}+\left[ \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right] \ln Y_{t}^{i}+\gamma _{2_{t+1}}\ln \frac{B\gamma _{2_{t+1}}}{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}\right] \end{aligned}$$

So, if the guess is right:

$$\begin{aligned} A=&\ln \frac{\left( 1+\delta \right) }{\left( 1+\delta \right) +B\gamma _{2_{t+1}} }+\frac{A}{\left( 1+\delta \right) }\\&+\frac{B}{\left( 1+\delta \right) }\left[ {\bar{\varepsilon }}+\gamma _{0_{t+1}}+\gamma _{2_{t+1}}\ln \frac{B\gamma _{2_{t+1}}}{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}\right] \end{aligned}$$

and

$$\begin{aligned} B= 1 + \frac{B}{\left( 1+\delta \right) }\left[ \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right] \end{aligned}$$

Solving for B

$$\begin{aligned} B=\frac{\left( 1+\delta \right) }{\left( 1+\delta \right) -\left[ \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right] } \end{aligned}$$

which should be positive. We will show that the equilibrium values of $\gamma _{1_{t+1}}$ and $\gamma _{2_{t+1}}$ are always such that this happens. It is useful to notice that

$$\begin{aligned} 1-\lambda&= \frac{\left( 1+\delta \right) }{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}\\&=\frac{\left( 1+\delta \right) -\left[ \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right] }{\left( 1+\delta \right) -\gamma _{1_{t+1}}}=1-\frac{\gamma _{2_{t+1}}}{ \left( 1+\delta \right) -\gamma _{1_{t+1}} } \end{aligned}$$

so:

$$\begin{aligned} \lambda _t&= \frac{\gamma _{2_{t+1}}}{ \left( 1+\delta \right) -\gamma _{1_{t+1}} } \end{aligned}$$

This is what is given in Eq. (7)

Finally, solving for A

$$\begin{aligned} \delta A=&\left( 1+\delta \right) \ln \frac{\left( 1+\delta \right) }{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}\\&+\frac{\left( 1+\delta \right) }{\left( 1+\delta \right) -\left[ \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right] }\left[ {\bar{\varepsilon }}+\gamma _{0_{t+1}}+\gamma _{2_{t+1}}\ln \frac{B\gamma _{2_{t+1}}}{\left( 1+\delta \right) +B\gamma _{2_{t+1}}}\right] \end{aligned}$$

so:

$$\begin{aligned} A =&\frac{{\bar{\varepsilon }}+\gamma _{0_{t+1}}}{\left[ \left( 1+\delta \right) -\left( \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right) \right] \frac{\delta }{1+\delta }}\\&+\frac{\ln \left[ \left( 1+\delta \right) -(\gamma _{1_{t+1}}+\gamma _{2_{t+1}})\right] ^{\left[ \left( 1+\delta \right) -\left( \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right) \right] } + \ln \frac{\gamma _{2_{t+1}}^{\gamma _{2_{t+1}}} }{\left[ \left( 1+\delta \right) -\gamma _{1_{t+1}}\right] ^{\left[ \left( 1+\delta \right) -\gamma _{1_{t+1}}\right] }}}{\left[ \left( 1+\delta \right) -\left( \gamma _{1_{t+1}}+\gamma _{2_{t+1}}\right) \right] \frac{\delta }{1+\delta }} \end{aligned}$$

$\square$

Appendix B: Proof of Result 2

Proof

Since $(h_{t+1}^{i},a_{t+1}^{i},m_{t+1}^{i})$ has a multivariate normal distribution, we can appeal to the conditional normal p.d.f. to find the distribution of $h_{t+1}^{i}|\Omega _{t+1}^{i}$.

Let ${\mathbf {X}}$ be a partitioned multivariate normal random vector with ${\mathbf {X}}^{T}=\left[ \begin{array}{cc} {\mathbf {X}}_{1}&{\mathbf {X}}_{2}^T \end{array} \right]$, where ${\mathbf {X}} _{1}=\left[ h_{t+1}^{i}\right]$ and ${\mathbf {X}}_{2}^{T}=\left[ a^i_{t+1} \;\; m^i_{t+1} \right]$. The mean of ${\mathbf {X}}$ is given by:

$$\begin{aligned} {\mu }= \genfrac[]{0.0pt}{}{{\mu }_{1}}{{\mu }_{2}} \end{aligned}$$

where ${\mu }_{1}=\left[ \mu _{h_{t+1}}\right]$ and ${\mu }_{2} ^{T}=\left[ \mu _{y_t} \;\; \mu _{h_{t+1}} \right]$.

The variance-covariance matrix of ${\mathbf {X}}$ is given by:

$$\begin{aligned} {\varvec{\Sigma }}=\left[ \begin{array}{cc} {\varvec{\Sigma }}_{11} &{} {\varvec{\Sigma }}_{12}\\ {\varvec{\Sigma }}_{21} &{} {\varvec{\Sigma }}_{22} \end{array} \right] \end{aligned}$$

where:

$$\begin{aligned} {\varvec{\Sigma }}_{11}&=\left[ \begin{array}{c} V_h \end{array} \right] \\ {\varvec{\Sigma }}_{12}&=\left[ \begin{array}{cc} \alpha V_{y_t}&V_h \end{array} \right] ={\varvec{\Sigma }}_{21}^{T}\\ {\varvec{\Sigma }}_{22}&=\left[ \begin{array}{cc} V_{y_t}+V_{a} &{} \alpha V_{y_t}\\ \alpha V_{y_y} &{} V_{h}+V_{m} \end{array} \right] \end{aligned}$$

Then the distribution of $h_{t+1}^{i}$ conditional on $\Omega _{t+1}^{i}$ is univariate normal with the following mean and variance:

$$\begin{aligned}&E\left( h_{t+1}^{i}|\Omega _{t+1}^{i}\right) \\&\quad ={\mu }_{1}+{\varvec{\Sigma }}_{12}{\varvec{\Sigma }}_{22}^{-1}\left( {\mathbf {x}}_{2}-{\mu }_{2}\right) \\&\quad =\mu _{h_{t+1}}+\alpha \beta _{a_{t+1}}\left( 1-\beta _{m_{t+1}}\right) \left[ a_{t+1} ^{i}-\mu _{y_t}\right] +\beta _{m_{t+1}}\left[ m_{t+1}^{i}-\mu _{h_{t+1}}\right] \\&\quad = \beta _{m_{t+1}}m_{t+1}^{i}\\&\quad \quad + \left( 1-\beta _{m_{t+1}}\right) \left[ \ln Z + \alpha \ln \lambda _t - \frac{V_{\omega }}{2} + \alpha \beta _{a_{t+1}}a_{t+1}^{i} + \alpha \left( 1-\beta _{a_{t+1}}\right) \mu _{y_t}\right] \end{aligned}$$

and,

$$\begin{aligned}&Var\left( h_{t+1}^{i}|\Omega _{t+1}^{i}\right) \\&\quad ={\varvec{\Sigma }}_{11}-{\varvec{\Sigma }}_{12}{\varvec{\Sigma }}_{22} ^{-1}{\varvec{\Sigma }}_{21}\\&\quad =V_{h}-\alpha ^{2}V_{y_t}\beta _{a_{t+1}}\left( 1-\beta _{m_{t+1}}\right) -\beta _{m_{t+1}}V_{h}\\&\quad =\alpha ^{2}V_{y_t}\left( 1-\beta _{m_{t+1}}\right) \left( 1-\beta _{a_{t+1}}\right) +\left( 1-\beta _{m_{t+1}}\right) V_{\omega }\\&\quad =\beta _{m_{t+1}} V_{m} \end{aligned}$$

Given the conditional distribution of the log of human capital is normal, the conditional distribution of human capital is log normal with mean:

$$\begin{aligned} Y_{t+1}^{i}= E\left( exp\left\{ h^i_{t+1}\right\} |\Omega ^i_{t+1} \right) = \exp \left\{ \mu _{h^i_{t+1}|\Omega ^i_{t+1}}\right\} \exp \left\{ \frac{V_{h^i_{t+1}|\Omega ^i_{t+1}}}{2} \right\} \end{aligned}$$

Substituting and taken logarithms produces expression (15). $\square$

Appendix C: Proof of Result 4

Proof

We just show next the uniqueness of the solution of the dynamic equations defined by Eqs. 26, 17 and 18, as they are independent of $\lambda$. It is straight forward to extend the result for $\rho$, $\lambda$ and $\mu$ by using their definitions.

$\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )$ is defined as in appendix D. It follows that:

$$\begin{aligned}&\frac{d\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{dV_{y}} \end{aligned}$$

(38)

$$\begin{aligned}&\quad =\frac{\partial \Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{\partial V_{y}}+\frac{\partial \Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{\partial \beta _{a}}\frac{d\beta _{a}}{dV_{y}}\nonumber \\&\qquad +\frac{\partial \Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{\partial \beta _{m}} \frac{d\beta _{m}}{dV_{y}} \end{aligned}$$

(39)

$$\begin{aligned}&\quad =\alpha ^{2}\left[ \beta _{a}(1-\beta _{m})+\beta _{m}\right] +\alpha ^{2}(1-\beta _{m})V_{y}\frac{d\beta _{a}}{dV_{y}}+\left[ \alpha ^{2}\beta _{a}V_{a}+V_{\omega }\right] \frac{d\beta _{m}}{dV_{y}} \end{aligned}$$

(40)

Since,

$$\begin{aligned} \frac{d\beta _{a}}{dV_{y}}=\frac{1-\beta _{a}}{V_{y}+V_{a}}>0 \end{aligned}$$

(41)

and,

$$\begin{aligned} \frac{d\beta _{m}}{dV_{y}}=\alpha ^{2}\frac{(1-\beta _{m})\left( 1-\beta _{a}\right) ^{2}}{\alpha ^{2}\beta _{a}V_{a}+V_{\omega }+V_{m}}>0 \end{aligned}$$

(42)

it follows that,

$$\begin{aligned} \frac{d\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{dV_{y}}&=\alpha ^{2}\left[ \beta _{a}(1-\beta _{m})+\beta _{m}\right] \left\{ 1+(1-\beta _{m})\left( 1-\beta _{a}\right) \right\} \end{aligned}$$

(43)

$$\begin{aligned}&=\alpha \rho ~\left[ 1+(1-\beta _{m})\left( 1-\beta _{a}\right) \right] >0 \end{aligned}$$

(44)

while the second derivative is:

$$\begin{aligned} \frac{d^{2}\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{dV_{y}^{2}}&=\frac{\partial \left[ \frac{d\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{dV_{y}}\right] }{\partial \beta _{a}}\frac{d\beta _{a}}{dV_{y}} \nonumber \\&\quad +\frac{\partial \left[ \frac{d\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{dV_{y}}\right] }{\partial \beta _{m}}\frac{d\beta _{m}}{dV_{y}} \end{aligned}$$

(45)

$$\begin{aligned}&=2\alpha ^{2}\left( 1-\beta _{a}\right) (1-\beta _{m})\left[ (1-\beta _{m})\frac{d\beta _{a}}{dV_{y}}+\left( 1-\beta _{a}\right) \frac{d\beta _{m} }{dV_{y}}\right] >0 \end{aligned}$$

(46)

We also know that:

$$\begin{aligned} \Psi (0,\beta _{a},\beta _{m},V_{\omega },\alpha )&=\frac{V_{\omega }^{2} }{V_{\omega }+V_{m}} \end{aligned}$$

(47)

$$\begin{aligned} \Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )&\rightarrow \infty \text { as }V_{y}\rightarrow \infty \end{aligned}$$

(48)

$$\begin{aligned} \frac{d\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )}{dV_{y}}&\rightarrow \alpha ^{2}\text { \ as \ }V_{y}\rightarrow \infty \end{aligned}$$

(49)

Since $\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )$ starts above the 45 degree line, is upward sloping and convex in $V_{y}$, and has a maximum slope of $\alpha ^{2}<1$, it must cut the 45 degree line once from above. This gives the unique, stable, steady state value of $V_{y}$. The determination of the steady state is illustrated in Fig. 3.

Fig. 3

Law of motion of $V_y$

Note that the shape of the curve implies there will be a multiplier effect from changes in the parameters. Any parameter change which causes a shift in $\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )$ will lead to a larger change in $V_y$. This multiplier effect was described in appendix D and will be discussed further when we consider the comparative statics of the model. $\square$

Appendix D: Proof of the existence of a multiplier of inequality

This appendix proves the existence of the multiplier effect described in Sect. 3.4 and calculates its magnitude.

Proof

Imposing the steady state condition, $V_{y_{t}}=V_{y_{t-1} }=V_{y}$ on the law of motion of the variance of log income gives:

$$\begin{aligned} V_{y}=\alpha ^{2}\left[ \beta _{a}(1-\beta _{m})+\beta _{m}\right] V_{y} +\beta _{m}V_{\omega } \end{aligned}$$

(50)

Solving this gives the equation for steady state variance of log income given in result 4. We will call the right-hand side of Eq. 50: $\Psi (V_{y},\beta _{a},\beta _{m},V_{\omega },\alpha )$.

We can then examine two things: the shift in $\Psi$ from a change in one of the exogenous parameters, keeping $V_{y}$ fixed; and the total derivative of $V_{y}$ with respect to the same parameter. The ratio of the latter to the former is the multiplier.

Take $V_a$ as an example. For a given $V_y$, the effect of a change in $V_a$ on the $\Psi$ function is given by:

$$\begin{aligned} \frac{\partial \Psi }{\partial V_{a}}= & {} \frac{\partial \Psi }{\partial \beta _{a}}\frac{\partial \beta _{a}}{\partial V_{a}}+\frac{\partial \Psi }{ \partial \beta _{m}}\left[ \frac{\partial \beta _{m}}{\partial V_{a}}+\frac{ \partial \beta _{m}}{\partial \beta _{a}}\frac{\partial \beta _{a}}{\partial V_{a}}\right] \end{aligned}$$

(51)

This is the partial effect for a fixed $V_y$. Allowing $V_y$ to fully adjust however, we find the effect of a change in $V_a$ to be:

$$\begin{aligned} \frac{dV_{y}}{dV_{a}}= & {} \frac{\partial \Psi }{\partial V_{y}}\frac{dV_{y}}{ dV_{a}}+\frac{\partial \Psi }{\partial \beta _{a}}\frac{d\beta _{a}}{dV_{a}}+ \frac{\partial \Psi }{\partial \beta _{m}}\frac{d\beta _{m}}{dV_{a}} \nonumber \\= & {} \left[ \frac{\partial \Psi }{\partial V_{y}}+\left[ \frac{\partial \Psi }{ \partial \beta _{a}}+\frac{\partial \Psi }{\partial \beta _{m}}\frac{ \partial \beta _{m}}{\partial \beta _{a}}\right] \frac{\partial \beta _{a}}{ \partial V_{y}}\right] \frac{dV_{y}}{dV_{a}}+\frac{\partial \Psi }{\partial \beta _{a}}\frac{\partial \beta _{a}}{\partial V_{a}}\nonumber \\&+\frac{\partial \Psi }{ \partial \beta _{m}}\left[ \frac{\partial \beta _{m}}{\partial V_{a}}+\frac{ \partial \beta _{m}}{\partial \beta _{a}}\frac{\partial \beta _{a}}{\partial V_{a}}\right] \nonumber \\= & {} \frac{1}{1-\left[ \frac{\partial \Psi }{\partial V_{y}} +\left[ \frac{\partial \Psi }{\partial \beta _{a}}+\frac{\partial \Psi }{ \partial \beta _{m}}\frac{\partial \beta _{m}}{\partial \beta _{a}}\right] \frac{\partial \beta _{a}}{\partial V_{y}}\right] }\left\{ \left[ \frac{ \partial \Psi }{\partial \beta _{a}}+\frac{\partial \Psi }{\partial \beta _{m}}\frac{\partial \beta _{m}}{\partial \beta _{a}}\right] \frac{\partial \beta _{a}}{\partial V_{a}}+\frac{\partial \Psi }{\partial \beta _{m}}\frac{ \partial \beta _{m}}{\partial V_{a}}\right\} \end{aligned}$$

(52)

The first term on the right-hand side (i.e the fraction) is the multiplier term. The second term is the shift in the $\Psi$ curve calculated in 51. If the multiplier is greater than 1, it tells us that the total (or long-run) effect on $V_{y}$ of a change in $V_{a}$ is larger than the partial effect when $V_{y}$ is fixed (or the short-run effect, since $V_{y,t-1}$ is fixed).

By substitution, the multiplier term is:

$$\begin{aligned} \frac{1}{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{a}\right) ^{2}\left( 1-\beta _{m}\right) ^{2}\right] }>1 \end{aligned}$$

(53)

Thus any change in $V_a$ is amplified since the additional discrimination which it creates feeds into next period’s income variance and the levels of discrimination which individuals in that generation are subjected to.

We can carry out exactly the same exercise for $V_m$, $V_{\omega }$ and $\alpha$. Although the partial effect of a change in each of the parameters differs, the multiplier is the same in each case. In all cases it is given by Eq. 53. $\square$

Appendix E: Proof of Result 5

Proof

Notice:

$$\begin{aligned} \frac{d\beta _{a}}{dV_{a}}=\frac{\partial \beta _{a}}{\partial V_{y}}\frac{dV_{y}}{dV_{a}}+\frac{\partial \beta _{a}}{\partial V_{a}}=\frac{1}{V_{y} +V_{a}}\left[ \left( 1-\beta _{a}\right) \frac{dV_{y}}{dV_{a}}-\beta _{a}\right] \end{aligned}$$

(54)

and

$$\begin{aligned} \frac{d\beta _{m}}{dV_{a}}=\frac{\partial \beta _{m}}{\partial \beta _{a}} \frac{d\beta _{a}}{dV_{a}}+\frac{\partial \beta _{m}}{\partial V_{a}} =\frac{\alpha ^{2}(1-\beta _{m})}{\alpha ^{2}\beta _{a}V_{a}+V_{\omega }+V_{m} }\left[ \left( 1-\beta _{a}\right) ^{2}\frac{dV_{y}}{dV_{a}}+\beta _{a} ^{2}\right] \end{aligned}$$

(55)

So, after some algebra

$$\begin{aligned} \frac{dV_{y}}{dV_{a}}=\frac{-\alpha ^{2}\beta _{a}^{2}(1-\beta _{m})^{2} }{1-\alpha \rho ~\left[ 1+(1-\beta _{m})\left( 1-\beta _{a}\right) \right] } \end{aligned}$$

(56)

Note also that:

$$\begin{aligned} 1-\alpha \rho \left[ 1+(1-\beta _{m})\left( 1-\beta _{a}\right) \right] =1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] >0 \end{aligned}$$

(57)

Therefore, the effect of a change in $V_{a}$ on $V_{y}$ is:

$$\begin{aligned} \frac{dV_{y}}{dV_{a}}=\frac{-\alpha ^{2}\beta _{a}^{2}(1-\beta _{m})^{2} }{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }<0 \end{aligned}$$

(58)

The effects of a change in $V_{a}$ on $\beta _{a}$ and $\beta _{m}$ are:

$$\begin{aligned} \frac{d\beta _{a}}{dV_{a}}&=-\frac{\beta _{a}(1-\beta _{a})}{V_{a}}\left[ 1+\frac{\alpha ^{2}\beta _{a}(1-\beta _{a})(1-\beta _{m})^{2}}{\left( 1-\alpha ^{2}\right) +\alpha ^{2}(1-\beta _{a})^{2}\left( 1-\beta _{m}\right) ^{2}}\right] <0 \end{aligned}$$

(59)

$$\begin{aligned}&=-\frac{\beta _{a}(1-\beta _{a})}{V_{a}}\left[ \frac{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{a}\right) \left( 1-\beta _{m}\right) ^{2}\right] }{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }\right] \end{aligned}$$

(60)

$$\begin{aligned} \frac{d\beta _{m}}{dV_{a}}&=\frac{\alpha ^{2}\beta _{a}^{2}(1-\beta _{m})^{2} }{V_{m}}\left[ \frac{1-\alpha ^{2}}{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }\right] >0 \end{aligned}$$

(61)

The extent to which firms value and use the signal on background is not measured by $\beta _{a}$ but by ${\hat{\beta }}_{a}=\alpha \beta _{a}\left( 1-\beta _{m}\right)$. A change in the precision of the advantage signal has the following effect on ${\hat{\beta }}_{a}$:

$$\begin{aligned} \frac{d{\hat{\beta }}_{a}}{dV_{a}}&=\alpha \left( 1-\beta _{m}\right) \frac{d\beta _{a}}{dV_{a}}-\alpha \beta _{a}\frac{d\beta _{m}}{dV_{a}}<0 \end{aligned}$$

(62)

The effect of a change in $V_{a}$ on $\rho$ is:

$$\begin{aligned} \frac{d\rho }{dV_{a}}&=\alpha \left( 1-\beta _{m}\right) \frac{d\beta _{a} }{dV_{a}}+\alpha \left( 1-\beta _{a}\right) \frac{d\beta _{m}}{dV_{a}} \end{aligned}$$

(63)

$$\begin{aligned}&=-\frac{\alpha \beta _{a}\left( 1-\beta _{a}\right) \left( 1-\beta _{m}\right) ^{2}}{V_{a}V_{m}\left[ 1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] \right] } \end{aligned}$$

(64)

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad .\left\{ \left( 1-\alpha ^{2}\right) \left( V_{\omega }+V_{m}\right) +\alpha ^{2}(1-\beta _{a})\left( 1-\beta _{m}\right) V_{m}\right\} <0 \end{aligned}$$

(65)

$\square$

Appendix F: Proof of Result 6

Proof

Notice that:

$$\begin{aligned} \frac{d\beta _{a}}{dV_{m}}=\frac{\partial \beta _{a}}{\partial V_{y}}\frac{dV_{y}}{dV_{m}}=\frac{(1-\beta _{a})}{V_{y}+V_{a}}\frac{dV_{y}}{dV_{m}} \end{aligned}$$

(66)

and

$$\begin{aligned} \frac{d\beta _{m}}{dV_{m}}&=\frac{\partial \beta _{m}}{\partial \beta _{a} }\frac{d\beta _{a}}{dV_{m}}+\frac{\partial \beta _{m}}{\partial V_{m}} \end{aligned}$$

(67)

$$\begin{aligned}&=\frac{\alpha ^{2}(1-\beta _{a})^{2}(1-\beta _{m})}{\alpha ^{2}\beta _{a} V_{a}+V_{\omega }+V_{m}}\frac{dV_{y}}{dV_{m}}-\frac{\beta _{m}}{\alpha ^{2} \beta _{a}V_{a}+V_{\omega }+V_{m}} \end{aligned}$$

(68)

Then,

$$\begin{aligned} \frac{dV_{y}}{dV_{m}}=\frac{-\beta _{m}^{2}}{1-\alpha \rho ~\left[ 1+(1-\beta _{m})\left( 1-\beta _{a}\right) \right] } \end{aligned}$$

(69)

As above:

$$\begin{aligned} 1-\alpha \rho ~\left[ 1+(1-\beta _{m})\left( 1-\beta _{a}\right) \right] =1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] \end{aligned}$$

(70)

Therefore, the effect of a change in $V_{m}$ on $V_{y}$ is:

$$\begin{aligned} \frac{dV_{y}}{dV_{m}}=-\frac{\beta _{m}^{2}}{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }<0 \end{aligned}$$

(71)

The effects of a change in $V_{m}$ on $\beta _{a}$ and $\beta _{m}$ are:

$$\begin{aligned} \frac{d\beta _{a}}{dV_{m}}= & {} -\frac{(1-\beta _{a})^{2}}{V_{a}}\left[ \frac{\beta _{m}^{2}}{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }\right] <0 \end{aligned}$$

(72)

$$\begin{aligned} \frac{d\beta _{m}}{dV_{m}}= & {} -\frac{\beta _{m}\left( 1-\beta _{m}\right) }{V_{m}}\left[ 1+\frac{\alpha ^{2}\beta _{m}(1-\beta _{m})\left( 1-\beta _{a}\right) ^{2}}{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }\right] <0 \end{aligned}$$

(73)

The effect of a change in $V_{m}$ on $\rho$ is:

$$\begin{aligned} \frac{d\rho }{dV_{m}}&=\alpha \left( 1-\beta _{m}\right) \frac{d\beta _{a} }{dV_{m}}+\alpha \left( 1-\beta _{a}\right) \frac{d\beta _{m}}{dV_{m}} \end{aligned}$$

(74)

$$\begin{aligned}&=-\frac{\alpha \beta _{m}\left( 1-\beta _{a}\right) \left( 1-\beta _{m}\right) }{V_{a}V_{m} }\left\{ V_{a} + \frac{(1-\beta _{a})\beta _{m}V_{m}}{ \left[ 1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] \right] }\right\} <0 \end{aligned}$$

(75)

Now turning to the effect on ${\hat{\beta }}_{a}.$ A change in the precision of the ability signal has the following effect on ${\hat{\beta }}_{a}$:

$$\begin{aligned} \frac{d{\hat{\beta }}_{a}}{dV_{m}}&=\alpha \left( 1-\beta _{m}\right) \frac{d\beta _{a}}{dV_{m}}-\alpha \beta _{a}\frac{d\beta _{m}}{dV_{m}} \end{aligned}$$

(76)

$$\begin{aligned}&=\frac{\alpha \beta _{m}\left( 1-\beta _{m}\right) }{V_{a}V_{m}\left[ 1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] \right] }\nonumber \\&\quad \quad \left\{ \beta _{a}V_{a}\left( 1-\alpha ^{2}\right) -V_{\omega }\left( 1-\beta _{m}\right) (1-\beta _{a} )^{2}\right\} \end{aligned}$$

(77)

This is $\lesseqgtr$ zero if:

$$\begin{aligned} \beta _{a}V_{a}\left( 1-\alpha ^{2}\right) \lesseqgtr V_{\omega }\left( 1-\beta _{m}\right) \left( 1-\beta _{a}\right) ^{2} \end{aligned}$$

(78)

There is a turning point at ${\hat{V}}_{m}$ where ${\hat{V}}_{m}$ gives values of $\beta _{a}$ and $\beta _{m}$ which solve the following equation:

$$\begin{aligned} \beta _{a}V_{a}\left( 1-\alpha ^{2}\right) =V_{\omega }\left( 1-\beta _{m}\right) (1-\beta _{a})^{2} \end{aligned}$$

(79)

The left-hand side of the above equation is decreasing in $V_{m}$ while the right-hand side is increasing. Therefore ${\hat{V}}_{m}$ is a unique turning point and a maximum:

$$\begin{aligned} \frac{d\left[ \beta _{a}V_{a}\left( 1-\alpha ^{2}\right) \right] }{dV_{m}}&=V_{a}\left( 1-\alpha ^{2}\right) \frac{d\beta _{a}}{dV_{m}}<0 \end{aligned}$$

(80)

$$\begin{aligned} \frac{d\left[ V_{\omega }\left( 1-\beta _{m}\right) (1-\beta _{a})^{2}\right] }{dV_{m}}&=-V_{\omega }(1-\beta _{a})\left\{ 2\left( 1-\beta _{m}\right) \frac{d\beta _{a}}{dV_{m}}+(1-\beta _{a})\frac{d\beta _{m}}{dV_{m}}\right\} >0 \end{aligned}$$

(81)

For values of $V_{m}<{\hat{V}}_{m}$, $\beta _{a}V_{a}\left( 1-\alpha ^{2}\right) >V_{\omega }\left( 1-\beta _{m}\right) (1-\beta _{a})^{2}$ and $\frac{d{\hat{\beta }}_{a}}{dV_{m}}>0$.For values of $V_{m}>{\hat{V}}_{m}$, $\beta _{a}V_{a}\left( 1-\alpha ^{2}\right) <V_{\omega }\left( 1-\beta _{m}\right) (1-\beta _{a})^{2}$ and $\frac{d{\hat{\beta }}_{a}}{dV_{m}}<0$. $\square$

Appendix G: Comparative statics on the steady state share of income invested

The partial derivatives of $\lambda$ with respect to $\beta _{m}$ and $\beta _{a}$ are:

$$\begin{aligned} \frac{\partial \lambda }{\partial \beta _{m}}&=\frac{\alpha \left[ \left( 1+\delta \right) -\alpha \beta _{a}\right] }{\left[ 1+\delta -\left( 1-\beta _{m}\right) \alpha \beta _{a}\right] ^{2}}>0 \\ \frac{\partial \lambda }{\partial \beta _{a}}&=\frac{\alpha ^{2}\beta _{m}\left( 1-\beta _{m}\right) }{\left[ 1+\delta -\left( 1-\beta _{m}\right) \alpha \beta _{a}\right] ^{2}}>0 \end{aligned}$$

So:

$$\begin{aligned} \frac{d\lambda }{dV_{m}}=\frac{\alpha \left[ \left( 1+\delta \right) -\alpha \beta _{a}\right] }{\left[ 1+\delta -\left( 1-\beta _{m}\right) \alpha \beta _{a}\right] ^{2}}\frac{d\beta _{m}}{dV_{m}}+\frac{\alpha ^{2} \beta _{m}\left( 1-\beta _{m}\right) }{\left[ 1+\delta -\left( 1-\beta _{m}\right) \alpha \beta _{a}\right] ^{2}}\frac{d\beta _{a}}{dV_{m}}<0 \end{aligned}$$

With respect to $V_{a}$:

$$\begin{aligned} \frac{d\lambda }{dV_{a}} =\frac{\alpha \left[ \left( 1+\delta \right) -\alpha \beta _{a}\right] }{\left[ 1+\delta -\left( 1-\beta _{m}\right) \alpha \beta _{a}\right] ^{2}}\frac{d\beta _{m}}{dV_{a}}-\frac{\alpha ^{2} \beta _{m}\left( 1-\beta _{m}\right) }{\left[ 1+\delta -\left( 1-\beta _{m}\right) \alpha \beta _{a}\right] ^{2}}\frac{d\beta _{a}}{dV_{a}} \end{aligned}$$

This is positive if:

$$\begin{aligned} \alpha \left[ \frac{ 1-\alpha ^{2} }{1-\alpha ^{2}\left[ 1-\left( 1-\beta _{m}\right) ^{2}\left( 1-\beta _{a}\right) ^{2}\right] }\right] (1-\beta _{m}) >\frac{V_{m}}{V_{\omega }}\left[ \frac{1-\alpha ^{2}\left[ \beta _{a}\left( 1-\beta _{m}\right) +\beta _{m}\right] }{\left[ \left( 1+\delta \right) -\alpha \beta _{a}\right] }\right] \end{aligned}$$

(82)

Note that in the limit, as $V_m \rightarrow 0$: $\beta _m =1$, $\frac{1-\beta _m}{V_m} \rightarrow \infty$, and $0<\beta _a<1$. The above inequality then holds.

Appendix H: Privilege and meritocracy

In this section we present an extension to the model where the children of the rich get an advantage independently of how productive they are thought to be.

As in the main text, human capital is a function of parental investment in education, and parents invest a fixed percentage of their income in education. Consequently, we can write the process of human capital acquisition as:

$$\begin{aligned} H^i_{t+1} = A \times \left( Y^i_{t}\right) ^\alpha \times e^{\epsilon ^i_{h,t+1}} \quad \rightarrow \quad h^i_{t+1} = \ln A + \alpha y^i_{t} + \epsilon ^{ih}_{t+1} \quad ;\quad \epsilon ^{ih}_{t+1} \sim N\left( 0,V_h\right) \end{aligned}$$

(83)

Also as in the main text, firms receive a signal on the human capital of agents. But, like in Sect. 4.2 we assume that firms have no signal on the agent’s background (i.e., $V_a\rightarrow \infty$). Therefore, the information available to the firm when forming an expectation about the agent’s human capital is $\Omega ^{ip}_{t+1} = \left\{ m^i_{t+1} , \mu _{y_t}, V_{y_t} \right\}$, where

$$\begin{aligned} m^i_{t+1}=h^i_{t+1} + \epsilon ^{im}_{t+1} \end{aligned}$$

(84)

The difference to the main text is that we assume that the pricing mechanism discriminates against the poor. Not statistical discrimination, but raw preference-based discrimination. Firms somehow prefer to hire the children of the rich even when conditioning on what one would rationally think about their human capital. Formally, an agent with certain observable traits $m^i_{t+1}$ and parental income $Y^i_{t}$ gets as income:

$$\begin{aligned} Y^i_{t+1} = \left( E\left( H^i_{t+1}|\Omega ^{ip}_{t+1}\right) \right) ^{1-\pi } \times \left( Y^i_{t}\right) ^\pi \times e^{\epsilon ^{iu}_{t+1}} \quad ;\quad \epsilon ^{iu}_{t+1}\sim N\left( 0,V_u\right) \end{aligned}$$

(85)

where $\pi$ is a parameter measuring how much privilege the children of the rich enjoy. If the elasticity of income to parental income when conditioning on expected human capital equals one, the income process is exogenously determined to be a random walk, with maximal correlation between parental and children’s income (and unconditional income variance approaching infinity). The polar opposite case is the one that we study in the main text, where $\pi =0$ and parental income is irrelevant given the expectations on human capital.

Of course parental income could be used to form those expectations (as we do in the main text). The difference now is that there is an advantage above and beyond the news that parental income may provide on human capital. Firms, thus, are inefficient in the sense of not maximizing profits because they overpay employees who have rich parents. In Becker’s parlance they “prefer” to employ the children of the rich, and are willing to pay them more for the same expected output. We do not explain how it turns out that these firms exist, and why they are not driven to extinction by competitive firms that do not prefer the children of the rich (like the ones in the main text). Notice that if there was any information on parental income, the firms in the main text would also pay more to the children of the rich, but not beyond their expected human capital.

Given this set up, it is straightforward to notice that if the distribution of log income among the parents generation is $y^i_{t}\sim N(\mu _{y_t},V_{y_t})$, the prior (before observing $m^i_{t+1}$) of the log of human capital of a certain individual i is:

$$\begin{aligned} h^i_{t+1} \sim N(\ln A+\alpha \mu _{y_t}, \alpha ^2 V_{y_t}+V_h) \end{aligned}$$

(86)

and the posterior (after observing a certain realization of $m^i_{t+1}$) is:

$$\begin{aligned} h^i_{t+1} | \Omega ^{ip}_{t+1} \sim N\left( \beta _{t+1} m^i_{t+1} +(1-\beta _{t+1}) (\ln A+\alpha \mu _{y_t}), \quad\quad \frac{\left( \alpha ^2 V_{y_t}+V_h\right) V_m}{\alpha ^2 V_{y_t}+V_h+V_m} \right) \end{aligned}$$

(87)

with

$$\begin{aligned} \beta _{t+1} = \frac{\alpha ^2 V_{y_t}+V_h}{\alpha ^2 V_{y_t}+V_h+V_m} \end{aligned}$$

(88)

Thus,

$$\begin{aligned} log E\left( H^i_{t+1}|\Omega ^{ip}_{t+1} \right) = \beta _{t+1} m^i_{t+1} + \left( 1-\beta _{t+1}\right) \left( \ln A+\alpha \mu _{y_t}\right) + \frac{\beta _{t+1} V_m}{2} \end{aligned}$$

(89)

and

$$\begin{aligned} y^i_{t+1} = \pi y^i_{t} + \left( 1-\pi \right) \left[ \beta _{t+1} m^i_{t+1} + \left( 1-\beta _{t+1}\right) \left( \ln A+\alpha \mu _{y_t}\right) + \frac{\beta _{t+1} V_m}{2}\right] +\epsilon ^{iu}_{t+1} \end{aligned}$$

(90)

which can be written in a Becker-Tomes form by substituting $m^i_{t+1}$ for its value $h^i_{t+1} +\epsilon ^{im}_{t+1}$ (and then $h^i_{t+1}$ by $\ln A + \alpha y^i_{t} + \epsilon ^{ih}_{t+1}$):

$$\begin{aligned} y^i_{t+1}&= (1-\pi ) \left[ lnA+\alpha (1-\beta _{t+1})\mu _{y_t} +\frac{\beta _{t+1} V_m}{2}\right] \nonumber \\&\quad +\left[ \pi +(1-\pi )\alpha \beta _{t+1}\right] y^i_{t} +(1-\pi )\beta _{t+1}(\epsilon ^{ih}_{t+1}+\epsilon ^{im}_{t+1}) +\epsilon ^{iu}_{t+1} \end{aligned}$$

(91)

Equation 91 determines a law of motion for the variance of log income, the persistence of the income process and $\beta$:

$$\begin{aligned} V_{y_{t+1}}= & {} (\rho _{t+1})^2 V_{y_t} +(1-\pi )^2(\beta _{t+1})^2(V_h+V_m)+V_u \end{aligned}$$

(92)

$$\begin{aligned} \rho _{t+1}= & {} \pi +(1-\pi )\alpha \beta _{t+1} \end{aligned}$$

(93)

$$\begin{aligned} \beta _{t+1}= & {} \frac{\alpha ^2 V_{y_t}+V_h}{\alpha ^2 V_{y_t}+V_h+V_m} \end{aligned}$$

(94)

In this extension we solve numerically, not analytically, for the properties of the solution of this system.

It is easy to check numerically that

Result 7 As in our main model, in steady state, an exogenous increase in the degree of meritocracy (a decrease of $V_m$) leads to a new steady state with a higher degree of intergenerational correlation ($\rho$), greater weight given to the observable signal ($\beta$), and a higher degree of inequality ($V_y$).

The reasons are the same as in our main model: more meritocracy increases the differences between agents, as they are paid more accurately according to their productive ability, and given that the children of the rich are indeed on average more capable, this effect only increases the inequalities inherited via the privilege channel. The increase in inequality increases the value that the market assigns to objective information in the determination of the wage, $\beta$, increasing further the degree of inequality, etc...

This is the main result of this section: nothing of interest changes by introducing “irrational” privilege, at least with respect to the effects of meritocracy. It still increases inequality and still decreases mobility.