Abstract
We find a relationship between geographic factors and numeracy in more than 300 regions of Europe around the year 1900. We argue that the distribution of land ownership is a plausible mechanism, given that it is related to the geographic factors under study. Consistent with theoretical studies in the Unified Growth Theory framework, we find that inequality in land distribution has a negative correlation with human capital formation as landowners did not have incentives to promote educational institutions or were not willing to pay the necessary taxes. This study explains a substantial share of the differences in development gradients between rural European regions in a historical perspective.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Geography has often been considered as a potential factor implying that biogeographical characteristics that were conducive for the onset of the Neolithic Revolution (Diamond 1997) and the disease environment (Sachs and Warner 1999) have had a persistent effect on comparative economic development across regions. More recently, geography has gained even greater attention for development in a long-term perspective. Migratory distance from the cradle of human kind in Africa and the effect of genetic diversity have been shown to have a hump shaped effect of comparative economic development (Ashraf and Galor 2013) and regional variations in the return to agricultural investment contributed to the distribution of long-term orientation across societies (Galor and Ozak 2016).
Our study contributes to this recent strand of literature, but with a new approach: we study human capital in a cross-section of more than 300 European regions around 1900. Our first set of regressions uses geographic factors (soil quality, altitude, ruggedness) and other geographic variables as explanatory variables. We focus on the following questions: does crop yield matter, and which other agricultural specializations might be important? In a second step, we study the question why geographic factors and human capital might be correlated. One plausible causal channel for explaining the relationship between soil qualities and numeracy is land inequality. In a seminal paper, Galor et al. (2009, GMV from here) argue that inequality in land distribution has a negative effect on the development of institutions that promote human capital. During the transition from an agricultural economy to an industrial economy, a major conflict arose between agricultural landholders on the one hand, and capitalists, on the other. Landholders did not benefit as much from an increase in the human capital of their workers as did capitalists: human capital raises the productivity of workers much more in industry than in agriculture, because land and human capital are less complementary. Consequently, the return on land declines as the wages of workers rise; due to the higher level of education that individuals obtain. Moreover, educated workers have more incentives to migrate to urban, industrial areas than their less educated counterparts. This departure of workers from their fields is clearly contrary to the interests of landholders. Consequently, they attempt to hinder the formation of this “rural exodus”.
For this reason, as GMV describe the process, landowners inhibit educational policies and reforms that aim at augmenting the general education of the people. Consequently, inequality in land distribution may be viewed as an obstacle to human capital formation and thus as a factor in slowing down the process of industrialisation and the generation of economic growth. We would argue that this effect may have been even more pronounced in the case of countries such as Russia, Hungary, Italy and Spain, where landed elites were still very powerful around 1900. In this respect, land inequality is a driving force in the emergence of the great divergence in income per capita, which has long-run implications that we can still observe throughout the world today.
GMV assess and confirm their theoretical model through empirical, state-level evidence from the US for the first decades of the twentieth century; even if, in this case, the industrial elites may have already partly dominated national politics. Other historical studies observe insignificant and sometimes contradictory results (Gray and Clark 2014, Goñi 2016, see also the literature review below).
The value-added of our study consists of the analysis of whether GMV theory can be confirmed when a very large regional sample is used. It turns out that the European experience provides such a sample. The advantage of using a historical European multi-country sample from the nineteenth century is that many decisions and concrete designs of educational investments were realised at the regional level during this period. Even if there were national laws, regional committees hired teachers and decided how school buildings were built and equipped. Many educational issues decreed in Madrid or Saint Petersburg became considerably modified in the provinces in which local elites held power.
We employ the age heaping method, which measures the share of individuals in the population who could report their own age exactly rather than reporting a rounded age in censuses. By using a new and large dataset on numeracy, adding relevant data on land distribution and including several control variables, we trace the relationship between land inequality and human capital throughout Europe at the regional level. It is important to use an outcome variable such as numeracy because school inequality was very high in nineteenth century Europe: some local committees hired incapable but inexpensive teachers simply to fill the schools, but the human capital effect of underpaid and undereducated teachers was negligible (on the difference between school inputs and their effects on mathematical ability, see Hanushek and Woessmann 2012). Other local committees decided to provide mostly religious education (Lindert 2004a).
We also take care to differentiate between the situations in the less industrialised east and south and the more industrial western parts of Europe; an issue which has not been studied in earlier research. Based on GMV theory, we would expect that the land inequality effect depends on the balance of bargaining power between large land owners and industrialists. It is very likely that in the less industrialised east and south, the political power of landowners was still considerably stronger than in the western European countries where industrialists had attained a large share of the decision-making power.
Although the relationship between land inequality and education that we are testing below is based on a well-founded microeconomic theory, we avoid causal language in the interpretation of our regression tables. We only discuss correlations and relationships instead. Only in the conclusion, where we bring together theory and empirics once again, we find that the correlations are in line with our theoretical expectations. We gain insights into identification issues by applying Altonji–Elder–Taber ratios and Oster’s strategies, and find that omitted variables would probably not eliminate the land inequality effect. Additional hints on causality issues are gained from an IV-estimation applied to Spain, one of the countries studied here. Exogenous variation comes from the military event of the late medieval Reconquista, and from family farm structure versus latifundial differences in earlier centuries.
The paper is structured as follows. Firstly, we revisit the literature on human capital, land distribution and land reform. Secondly, we present the underlying theoretical framework and the existing qualitative evidence. Thirdly, we describe the data used in this study and present the state of regional land distribution in Europe in the past. We highlight the modelling strategy and empirical results in the following section. The last section concludes.
2 Literature review
A recent strand of literature emphasizes geographic factors as explanations for the development levels of human societies and economies. Ashraf and Galor (2013) argue that the distance to the cradle of mankind—east Africa—matters for human genetic diversity. Following a number of genetic studies on 53 different populations throughout the world, the closer a population is to Africa, the stronger the variety of genetic characteristics. Ashraf and Galor argue that there is a medium level of genetic diversity in regions such as Europe and east Asia and that the amount of variety has both advantages and disadvantages, leading to a trade-off. If there are many differences—as Ashraf and Galor argue—the amount of ideas and the degree of potential innovation is very high, but this amount comes at a cost. Namely, if the genetic variety is very large, then there are also more conflicts, less trust, and less social capital between social groups; which potentially lead to further civil war and violent conflict. On the other extreme, populations that are relatively homogenous normally have high social capital.
Another influential paper on the relationship between geographic factors and economic development is the recent study by Galor and Ozak (2016), who argue that there are geographic origins of time preferences and long-term orientation. They use a recent long-term orientation index to identify the countries and regions that are more interested in investing in the present period and reaping the returns at some point in the future, whereas other societies may be more interested in obtaining smaller returns closer to the present. Galor and Ozak also use the natural experiment of the Columbian exchange in order to properly identify this relationship. These two studies suggest that geographic factors are important for long-term development. Some relationships did not receive as much attention before these influential studies, because institutional factors were preferred in the discussions of the last decades (North 1981). We argue here that geography and agriculture also matter for European regional development, partly because they influence land inequality.
As we study land inequality and economic development, we also review some of the main titles in this field. Initially, the inequality literature focused on redistributive policies. In particular, proponents of the political economy approach initially argued that the majority of voters would vote for policies that favour redistribution in contrast to growth. For this reason, higher tax rates may be expected in more equal societies (Alesina and Rodrik 1994; Persson and Tabellini 1994). However, Perotti (1996) does not find evidence for this mechanism.
In addition, Engerman and Sokoloff (2000) argue that the initial factor endowments in the New World had a major influence on the development of institutions and thus, on economic growth. For example, the quality of soil and climate determined which commodities could be grown in these colonies. Moreover, some commodities, like sugar, are much more suitable for large-scale production because considerable economies of scale can be achieved. The advantage of their large-scale production led to larger farms and favoured the import of cheap slaves to work on these large plantations. Under these circumstances, inequality arose in terms of landownership, wealth and human capital. Although Williamson (2009) and Dobado and García (2014) challenge the view of Engerman and Sokoloff with regard to the long-run persistence of inequality in Latin America since the sixteenth century conquista, the basic mechanism for the period since the nineteenth century remains plausible.
Easterly (2007) also addresses the inequality-growth relationship for developing countries in recent decades, finding that a high level of structural inequality hinders the development of schooling. He further argues that this structural inequality was brought about by agrarian conditions.
Did earlier studies find an effect of land inequality on human capital in particular? Erickson and Vollrath (2004) study both cross-sectional and panel samples of developing and developed countries (the US, Australia, etc.) for 5-year periods from 1960 to 1984. They do not find a significant effect of land inequality when the Gini coefficient of land inequality is applied (in contrast to older studies such as that by Deininger and Squire 1998).Footnote 1 By contrast, Cinnirella and Hornung (2016) find that, in the north German kingdom of Prussia during the nineteenth century, the share of large landowners in the population had an influence on regional differences in educational investment.
Recently, Wegenast (2009) studied plantation-type cash crops (the share of exports of coffee, bananas, sugar, etc.) and their impact on schooling, while studying a sample of Latin American and Asian countries for the period 1960–2000. He finds that plantation-type countries invested less in secondary schooling and—interestingly—more in tertiary education (i.e., elite education). Although plantation-type cash crops may be correlated with land inequality, as he notes, his measures may also reflect the historical legacy of slave economies.Footnote 2 Other scholars argue that tropical countries with large plantations and a large share of previous slaves entered a path-dependent process and invested less in education (Bruhn and Gallego 2012).
Gray and Clark (2014) rejected the influence of land inequality on human capital formation for England. They use the share of farmers as an indicator for low land inequality in the west and north west of England, and show that geographical factors determine this land inequality variable. However, they find that this variable does not have a consistent influence on human capital formation. This is also confirmed by Goñi (2016). In contrast, Oto-Peralías and Romero-Ávila (2016) find for Spain that the speed of the medieval conquest of the previously Islamic principalities had an impact via land and power inequality on subsequent development (see also Beltrán Tapia and Martínez-Galarraga 2015). The emphasis of all these authors on the subnational level is also based on the finding by several scholars that the regional differences were surprisingly persistent across history (see, for example, on Latin America: Maloney and Valencia Caicedo 2015). Ashraf et al. (2017) expanded the human capital determinants to include capital-skill complementarities, also controlling for land inequality. In summary, some studies provide support for the impact of land inequality on human capital whereas others find the opposite. Among more recent studies rejecting the impact of land inequality on human capital, many are situated in industrializing countries, such as England, or describe post-WWII situations. Hence, we will differentiate by industrial development level, below. None of these previous studies have used a regional multi-country data set that reflects the political economy of land owner influence at the regional level.
3 Theoretical underpinnings and qualitative evidence of the land inequality impact
After this review of related literature, we can now introduce the GMV approach in more detail. We briefly present some basic features of the GMV model to summarize some of the deeper insights arising from their argument.Footnote 3
As the authors put forward, they assume an overlapping generations model in which the production of the economy is limited to one homogeneous good per period. This good can later be consumed and invested. The economy is constituted by two sectors, agriculture and manufacturing. Both sectors use standard constant returns to scale production technology. The factors of production are land, physical capital, human capital and raw labour. Land supply is constant over time but physical and human capital are variable. In fact, the physical capital stock in a given period is determined by the output of the previous period (without investment in human capital and consumption). In contrast, the human capital stock in a given period depends on the investment in public education in the previous period.
Thus, in the GMV model the final output can be formally written as follows:
where \(y_{t}\) is output in period t, A is the agricultural and M is the manufacturing sector. The production of output in A is given by
where X is land and L are the workers that work in the sector. The manufacturing sector uses Cobb–Douglas production technology which does not use land but human capital instead. This shows that the productivity of workers in the manufacturing sector is increased by human capital, whereas human capital is not relevant in the agricultural sector. Thus, output in the manufacturing sector is produced by
where K is the quantity of physical capital, H is the quantity of human capital and k is the physical-human capital ratio (\(K_{t}/H_{t})\). Note that \(\alpha \) is between 0 and 1.
Initially, individuals are part of one of three different groups: landowners, capitalists (who do not own land) and workers (who own neither land nor capital). Every period is characterised by the birth of one new generation.
The provision of public education is affected by the political structure which characterises this economy, i.e. the existence of the three different groups. If the land owners had most of the political power, any educational investment would have needed their consent. In this way, they may inhibit educational progress.
GMV show in their following modelling steps that inequality in landownership leads to slower human capital accumulation.Footnote 4 In contrast, capitalists gained from the arrival of new workers as, over time, they needed more skilled workers. For this reason, Galor and Moav (2006) stress that landowners and capitalists did not share the same interests. This presents a major contradiction to the consensus of the existing literature which emphasises the conflict between the elites and the masses.
Any theoretical model needs some level of abstraction in order to provide a clear message. In the specific situation of Europe around 1900, a fourth relevant group might be family farmers who share some interests with workers and industrialists, as they were interested in a certain level of education for their children and had more local political influence than landless labourers. In agricultural societies, such as in southern and eastern Europe, they were politically influential in the regions not dominated by large land owners. For the theoretical model, it does not matter whether the group that had similar educational policy aims, only consisted of industrialists or was a mixture of these and family farmers. The important point is that there was a large group of landowners opposed to educational investment.
In general, anecdotal historical evidence shows that landowners have used their local power to influence policy, particularly with regards to education. In Spain, the land reform was initiated at the beginning of the 1930s under the Second Spanish Republic because leftist politicians thought that large land owners would influence local voters in order to obtain seats in the Spanish parliament (Carmona Pidal and Rosés 2011) and pursue their own interests.
In Italy, the government was not eager to promote land redistribution measures that would have improved productivity in the agricultural sector. It did not want to decrease land- owners’ incomes because they had an important share of the votes until 1911 (Federico 2009). Thus, the policies of the state were marked by an absence of action in the south and an activist aid for commercial land owners in the north (Elazar 1996).
Lobbying was also an important factor in preserving the large estates held by the landed aristocracy in countries like Hungary. The aristocracy controlled the state and could therefore protect their farms from competition with smaller and more efficient farms (Kopsidis 2009).
In England and Wales, large land owners had a 60% share of parliamentary seats before the Voting Reform Act in 1885, which gave farm workers the right to vote (Swinnen 2002). As a consequence, the landowner share dropped considerably, to 30% in 1885 and to 10% in 1919. Up until this time, landowners dominated the political scene and could influence the government actions that suited their needs. The opposition of landowners in England to providing better education to labourers is well illustrated by a comment made by Davies Giddy (later president of the Royal Society) in the House of Commons in 1807: “giving education to the labouring classes of the poor... would... be prejudicial to their morals and happiness; it would teach them to despise their lot in life, instead of making them good servants in agriculture [...]; it would render them insolent to their superiors...” (quoted in Lindert 2004a, p. 100).
Finally, in a historical comparison, Lindert (2004a, b) analyses the factors accounting for the differences in primary school enrolment for a range of countries in the period 1881–1937. He confirms that landowners were an important obstacle to educational reforms. Landowners feared paying higher taxes for financing the education of the masses. Lindert emphasises that these taxes were typically raised at the local level in Europe, even in a centralised country such as France during most of the nineteenth century. Similarly, landowners could effectively block local initiatives for more education.Footnote 5 Therefore, the local power of landowners translated into local differences in education. In addition to using the indirect effect of education, landowners tried to directly reduce the mobility of workers by legal means, as highlighted by Huber and Safford (1995).
4 Data
We first test whether differences of geography matter for human capital in 300 European regions. As geographic variables, we employ cereal, pasture, potato and sugar suitability; as well as temperature, precipitation, land size, altitude, and ruggedness (the standard deviation of altitude).Footnote 6 The suitability evidence is based on raster data, with a resolution of 5 arc-minutes, provided by the Food and Agriculture Organization (FAO) and related organisations, which generated this evidence in their project on Suitability of global land area. Data on altitude (median) and ruggedness (standard deviation of altitude) are ESRI grid raster data, with a resolution of 30 arc-seconds, provided by Hijmans et al. (2005). Altitude is defined as the elevation above sea level (in meters).
After studying the influence of geography on numeracy, we test the GMV model and assess the relationship between land inequality and numeracy. To that end, we primarily use data from population and agricultural censuses from European countries in the nineteenth and twentieth centuries. We define a large agricultural land holding as extending more than 50 ha, although the 100 ha threshold yields similar results. Below, we test all size categories. The obvious assumption would be that the largest land owners are the driving force here. However, looking closer at the political economy of the regions, this is less clear because the largest land owners were mostly active in national politics, whereas the aristocracy of more modest standing and wealth (including those who had only 50 hectares) were active in regional and communal politics. “Kartoffeladel” (‘potato nobility’) was the term in Central Eastern Europe for nobility that had to rely on modestly sized estates, and often demonstrated their identification with the nobility group by emphasizing conservative, anti-educational social values even more than the better-endowed parts of the nobility. Moreover, the nobility that had declined to estate sizes of 50–100 ha had the greatest difficulty in affording additional taxes and was, hence, extremely opposed to primary schooling (see Wagner 2005 on these issues). Empirically, we are the first who have really assessed different size categories of large land owners. We find that there is still a contribution of those landowners between 50 and 100 ha. The slightly less large land owners established their GMV influence on educational policy.
This definition is also well compatible with contemporary classification. Data on the area of agricultural holdings are normally available by bin size (e.g., 0–20, 20–50, 50–100 ha, and over 100 ha), which allows us to directly calculate the share of large holdings by dividing the total area of holdings larger than 50 ha by the total area of all holdings.Footnote 7 Summary statistics on this variable are provided in Table 1.
One potential caveat is that detailed agricultural censuses that include information on the size of farms were only taken in most European countries during the second half of the nineteenth and in the first decades of the twentieth centuries. Our numeracy evidence refers to the same period, but we would have preferred inequality data from an earlier period to avoid potential contemporaneous correlation problems. For example, the first agricultural census was taken in the western part of the Habsburg Empire in 1902 (i.e. Austria/Czech Lands and south Poland et al. below). The earliest evidence (see Table 2) comes from the United Kingdom (1875) and the latest from Italy and Spain (1930). Clearly, the unavailability of earlier data may appear to be a methodological challenge. However, the regional differences in land inequality can generally be viewed as very stable over time. Although the average land inequality changed in some cases, the regional differences survived. Agrarian reforms were enacted in France in response to the French Revolution at the beginning of the nineteenth century. However, after the early nineteenth century, no radical changes amongst those who owned land or rented it occurred. To avoid a potential misunderstanding, landless agricultural labourers do not affect our measure of land inequality. Although landless labour may have been absorbed by the industrial sector in the early twentieth century, this absorption did not affect the rural political economy of landholding (for the process in Spain, see Carmona Pidal and Rosés 2011). Please note that the standard definition of land inequality that we adopt here is the ratio between land owned (or rented) by large estates, and land owned (or rented) by medium and small farmers, not relative to landless labour. Although poor labourers may have benefitted from better schooling, medium farmers were the group in rural regions that was able to articulate their political interests, and that sometimes challenged the large land owners on educational issues (Dovring 1965).
This agrarian situation is confirmed by taking a closer look at the evidence from some of the countries. For example, Eddie (1967) shows that the share of large land holdings remained almost constant in Habsburg–East (Transleithania, the Hungarian-dominated part of the Habsburg Empire) in the period between 1867 and 1914. Regional changes in other countries were also minor. For example, at the regional level, the share (in area) of large land holdings in England, Wales and Scotland changed, on average, by less than 2 percent between 1875 and 1895 (see details in Table A.2 in the Appendix). This result once again highlights the stability of the share of large land holdings over time.
The First World War altered the political and economic positions of many countries. In addition, the creation of new countries as a consequence of the war encouraged major agricultural reforms in some European countries. Nevertheless, our data stem from all countries from before this period of major transition, except in the case of Spain and Italy where earlier data are not available. These agricultural censuses were the first to be taken in Spain and Italy. How, then, was land distribution affected in the nineteenth century and in the first decades of the twentieth century in Italy and Spain?
The south of Spain has had an important share of large estates since the Reconquista. A liberal reform was enacted at the turn of the nineteenth century but did not have a very strong effect on land distribution—the large estates of Andalusia remained intact. The next important change was a reform that was only approved in 1936. However, it was not entirely implemented due to the Civil War (Carmona Pidal and Rosés 2011). For this reason, we argue that the share of large land holdings in the 1930 data is a reasonable indicator of late nineteenth century land inequality.Footnote 8
In Italy, discussions on the redistribution of land began after the unification of the country. Nevertheless, few policy initiatives were introduced and fewer still had any strong effect (Dovring 1965). Although minor transfers between large land owners and smaller peasant owners occurred until later in the century, no major redistribution of farm sizes occurred. Therefore, our argument for Italy is similar to that for Spain.
What about land reforms in other countries in the nineteenth century? For example, in France, the government did not make great efforts to change the farm structure that had been in existence since the French Revolution. Dovring (1965) notes that, until 1940, France was one of the most inactive nations when considering political land redistribution.
In Austria–Hungary, no active land reform was undertaken in the time period considered (Dovring 1965). In Russia, the incompetence of many landowners with regards to agrarian organisation and production, and the competition arising from peasant labour, led to a modest decrease in large estates after the liberation of the serfs in 1861 (Dovring 1965). However, the dominance of large estates was still overwhelming at the end of the nineteenth century, and the regional differences in large farms remained stable until the Communist Revolution of 1917. In summary, differences in regional land inequality remained stable over time. In the appendix, we also run robustness tests by using subsequent human capital measurements to ensure that the regional cross-section is not distorted by intertemporal changes.
In addition to the regional distribution of land, the measurement and development of regional numeracy in Europe in the nineteenth century is a focal point of this study. In contrast to literacy data, evidence on numeracy has the advantage of being available earlier and more broadly at the regional level. Therefore, we are able to use a new and large dataset (on the descriptives, see Hippe and Baten 2012). The fact that many countries were characterised by considerable regional differences in numeracy underlines the importance of taking a more disaggregated view. Although regional differences are important, they also remain extremely persistent over time. Overall, numeracy and education in general improve, but the lagging regions of 1850 are the same as those in 1900, and also lag in literacy and schooling in 1930. Our Appendix discusses this issue for the most important countries of our study.
Given that we do not have data on land inequality in some northern European countries, we include the countries and empires of Habsburg (and its subdivisions), the UK, France, Italy, RussiaFootnote 9 and Spain.
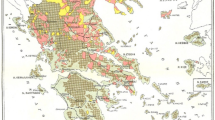
Our indicator of numeracy is the ABCC index. The ABCC has been used in a multitude of recent publications (e.g., Hippe and Baten 2012; Hippe 2012a, b; Crayen and Baten 2010; A’Hearn et al. 2009).Footnote 10 The ABCC indicator is a proxy for basic numerical skills. Basic numerical cognitive skills are preconditions for more advanced skills. The relevance of these cognitive skills is also highlighted by contemporary studies on international test scores in mathematics and science (see also Baten and Juif 2014). For example, Hanushek and Woessmann (2012) show that cognitive skills explain a large part of the variance in international growth rates. As an indicator of human capital, cognitive skills are also more significant than alternative academic measures, which turn insignificant in the presence of test scores. An additional advantage of numeracy in the form of the ABCC is that it is largely insensitive to different cultural contexts. In other words, global studies have shown that the heaping phenomenon is characteristic for most countries in the world, most importantly for European countries (Crayen and Baten 2010; see also Hippe 2012a). Therefore, it is comparable across different countries. In this respect, numeracy is also less dependent on the predominance of a certain language in a region, as is the case for literacy measures (Fig. 1).

Source: Hippe and Baten (2011). Albania, Benelux, Bosnia-Herzegovina, Cyprus, Denmark, Finland, France, FYROM, Greece, Kosovo, Montenegro, Portugal, Sweden and parts of Bulgaria and Romania are missing values
Regional ABCC differences in the nineteenth century. Note The map is based on Census data recorded between 1861 and 1900. Numeracy (ABCC) values are always calculated for a certain age range which represents a birth decade. The youngest birth decade is 23–32 years and the oldest is 63–72 years. For the map, values referring to the birth decade of 1830 were used in order to make the regions comparable between countries (which took their censuses in different years).
The ABCC index is calculated as follows:
where i stands for the years of age and n stands for the number of observations.Footnote 11 As in the literature, we only take ages between 23 and 72.Footnote 12 Because we are only interested in the mean level of numeracy in this study, we take all ages (23–72 years) together.
We use current regional boundaries as defined by the NUTS classification of the European Union. This classification begins at the national level (NUTS 0) and goes down to the county level (NUTS 3).Footnote 13 Clearly, there were considerable border changes in Europe in the twentieth century, particularly in Eastern Europe. However, in some countries, such as France and Spain, internal and external borders barely changed. Nevertheless, border changes are considered as well as possible by attributing the historical regions to the current NUTS regions.Footnote 14 Because our data are very detailed for many countries, such as for Austria–Hungary, and are sometimes even more detailed than NUTS 3, we avoid border problems in many cases because smaller regions are factored into larger NUTS regions. In general, the data are mostly available for NUTS 2 and NUTS 3.Footnote 15
5 Results
5.1 Was there a correlation between geographic factors and numeracy?
We start with the question concerning the degree to which geographic factors were related to numeracy. In the following section, we focus on soil suitability for cereals, pasture, potatoes, sugar beets, as well as temperature, precipitation, land size, altitude, and ruggedness. In Table 3, we regress numeracy on the whole set of potential geographic determinants. In each model (except model 1), we omit one of the countries (or parts of the Empire) in order to obtain an impression of robustness.
Pasture suitability actually results in a positive correlation with numeracy (Table 3). By contrast, the impact of cereal and potato suitability is not statistically significant in most cases. Sugar suitability is clearly negative in its impact, although we should note that, in reality, sugar beets were planted in a modest geographic extension during the period under study.Footnote 16 Additionally, ruggedness displays negative correlations with numeracy, whereas temperature is mostly insignificant. Population density mostly provides small negative coefficients.
What might have caused this correlation between geographic factors and numeracy? One possibility could be that dairy farming and other cattle-oriented agriculture that is encouraged by the suitability of pasture requires greater levels of numeracy than the main alternative in Europe, grain-oriented agriculture. However, grain production also requires a substantial degree of numeracy-intensive work, perhaps even more—given that the success of grain harvests depends very much on appropriate timing, the use of calendars and processing of weather information. The model of GMV might offer an explanation here, as land inequality might be the intervening variable: European large land owners were usually active and more productive in expansive landscapes in which crops with substantial economies of scale could be planted; sugar beet in the Russian empire was famous, as were grain fields that stretched over wide areas in eastern Europe, and southern Italy and Spain.
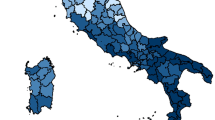
In Fig. 2, we show the share of large land holdings within European regions. The south of Spain, Andalusia in particular, and the south of Italy are generally viewed as strongholds of latifundia. This perception is mostly confirmed by our data. In Italy, the southern regions of Basilicata, Calabria and Puglia, the island Sardegna and the region around Rome (today’s Lazio), in particular, are also characterised by a high share of large farms. Within the Habsburg Empire, the Czech lands have a lower land share of large farms, whereas Galicia is much more unequal (south Poland and western Ukraine today). Hungary is characterised by higher land inequality that, however, differs regionally. Interestingly, the Transylvanian region appears to be the least unequal. With regard to the European part of the Russian Empire, a high share of large farms can be found in the west-central parts (and particularly in the Belorussian regions) and a central corridor stretching eastward.
In contrast, family farms (defined as small to medium farm sizes; segments of 20–50 ha and run by families) were typical for soils that were suitable for mixed agriculture, including both dairy farming and some grain production on a smaller scale. The rugged terrain of the Dinaric Mountains in the west Balkans and the Central Spanish highlands were dominated by family farmers. Hence, if there is a relationship between family farms and climate, geography, as well as certain soil characteristics, we would expect rugged terrain and soil suitable for pasture to be more likely associated with family farms. Consequently, this would imply greater numeracy, as family farms benefited more from this mixed dairy-and-grain mode of production. In contrast, large territories and those suitable for sugar beet might be associated with large farms and lower numeracy.Footnote 17 Hence, for grain, we would expect a mixed effect as grains were planted both by family farms and large land owners.Footnote 18
Was there a relationship between these geographic factors and land inequality? We test this relationship by taking land inequality as a dependent variable (Table 4). Pasture suitability is negatively correlated with land inequality. This finding corresponds to the observation that there are more farms of medium size in the European regions where dairy farming was efficient. By contrast, cereal suitability is significantly positively correlated with land inequality, whereas sugar suitability is only sometimes significant and positive (and potato suitability has mixed effects). Temperature has a negative effect, but it is not always significant. Altitude has a negative sign while that of ruggedness is positive.Footnote 19
For our study, perhaps the most relevant finding of these correlations is that pasture suitability correlates negatively with land inequality, but positively with numeracy. Hence, the theoretical argument of GMV could possibly be the mechanism behind the effect of pasture on numeracy. In the next section, we regress numeracy on land inequality and other covariates. We will include the geographic variables to assess whether they affect the land inequality-numeracy relationship to the degree that the correlation disappears.
5.2 Was there a relationship between land inequality and numeracy?
Did the share of area owned by large land owners have a systematic correlation with the numeracy of the regional population? To better understand this relationship, we use the following OLS regression model:
where i denotes the specific region, c denotes the country, ABCC denotes the level of numeracy, share_50 ha is the share of the land owned by estates larger than 50 ha (\(=\) share of large farmers), popdens is the population density,Footnote 20 metropolis is a dummy variable for capital city regions,Footnote 21 share prot is the percentage share of protestants,Footnote 22 \(\upbeta {'}X\) denotes a vector of geographic variables which we include in some models, \({\upmu }_{\mathrm{c}}\) represents country fixed effects, and \(\varepsilon \) comprises the non-observed influences on the ABCC.
In addition to the variable in which we are most interested, land inequality, we consider a number of controls. First, we include population density because a more dense population allows schooling with much lower commuting costs (Boucekkine et al. 2007). Second, we add a dummy variable for capital cities because more public goods in education were created by the government. Finally, we construct a Protestant share variable. Protestantism has a reputation for more substantial educational inputs for large parts of the population (Becker and Woessmann 2009). Jewish minorities account for only small shares of the population.
We group our data into two different categories according to the level of industrialisation. The criterion is the share of the industrial and service sector working population, as opposed to the agricultural labour force: in Spain, Hungary et al. (the east of the Habsburg Empire), Russia, and Italy, only 33, 40, 41 and 44% of the population worked outside of agriculture, respectively. Similarly, in the northern and southern periphery of the Habsburg Empire (South Poland, western Ukraine and the western Balkans) even less of the population worked outside agriculture.Footnote 23 In the UK and France, it was 90 and 59%, respectively.Footnote 24 Similarly, Austria and the Czech lands (the west of the Habsburg Empire) reached a 65% share outside of agriculture. Hence, the latter three countries and parts of the Habsburg Empire would be classified as industrialised.
We first separately consider each country and empire (or part thereof). This strategy allows us to account for potential measurement heterogeneity. For example, the possibility that the obtained findings may not be entirely comparable across countries remains because the definition of a land holding may vary slightly between historical countries, even if the problem of comparability of the definition is addressed by the inclusion of country fixed effects in the joint regressions below.Footnote 25
In Table 5, we include the most rural countries, i.e. contemporary Spain, Italy, Hungary et al., Russia and south Poland et al. Their focus on agricultural production may have provided more power to regional landowners.
We find that land inequality has a highly significant negative relationship with numeracy at the 1 or 5% level in all countries and empires. The coefficients for all countries are substantial in size, suggesting that we are finding a very consistent pattern here. For the Spanish regions included in column 1, for example, the effect of a one standard deviation shock to the share \(>50\) ha is -3.33. In other words, the difference between a district of average land inequality and one with an additional standard deviation of land inequality results in 3.33% less numeracy. In the bottom row we quantify which share of a standard deviation of the dependent variable this accounts for: for all countries and empires, the effect of one standard deviation amounts to between one-quarter and one-half of the standard deviation of numeracy; hence, it is an effect that, economically, is substantial. In addition, the metropoles of the countries have positively significant coefficients in Spain and Russia, showing the possible impact of more schooling investment for government officials and their environment. The population density variable is sometimes insignificant and in three countries even negative. Only in Hungary et al. is it significantly positive, while the share of protestants is significantly positive in Russia.
Next, in Table 6, we only take into account the most industrialised European countries in our sample, i.e., France, the United Kingdom and Austrian/Czech Lands. Following GMV, we would expect a different relationship here, given that industrialists had more political power, even at the regional level. In contrast to our results for rural Europe, the coefficient of land inequality is indeed now positive and significant for France and the United Kingdom, whereas it is not significant for Austria and the Czech Lands. Overall, the more advanced development status of these countries has altered the relationship between land inequality and numeracy.
Finally, in Table 7, we include all countries in our regression. Land inequality is negatively significant in rural areas throughout Europe (insofar as it is included here), and it is positive in industrial Europe. Metropoles are more numerate in rural and less numerate in industrial Europe, and the Protestant religion variable is positive in the former.
We also study whether including geographic suitability variables would have such a strong impact on numeracy that they invalidate the land inequality variable. One could imagine that, for example, pasture suitability encourages a protein-rich diet (Baten et al. 2014). Pasture suitability has in fact a positive coefficient, but only in industrial European countries (and cereal suitability has a positive one in agricultural Europe).Footnote 26 However, in spite of the inclusion of the suitability variables, the coefficient of land inequality is only modestly reduced in size when these geographic suitability variables are included (columns 1, 3 and 5 in Table 7). Even more important, they do not render the land inequality coefficient insignificant. Moreover, and this point is crucial, the adjusted \(\hbox {R}^{2}\) increases only marginally by adding the suitability variables—the main effect of geography runs via GMV forces of land inequality, which is included both in columns 2, 4 and 6, and in columns 1, 3 and 5 of Table 7, between which the \(\hbox {R}^{2}\) do not differ much.
We also want to know whether the results are potentially driven by a small number of outliers. For this reason, we construct a residual plot for which we regress the numeracy value on all of the other variables, such as Protestantism, the country dummies and the other variables (except for land inequality). In the second step, we regress the land inequality variable on all of the other variables but not on numeracy. Such a residual plot is shown in Fig. 3. We observe that the residual numeracy strongly corresponds with the residual land inequality. For example, districts such as Palencia in northern Spain and Astrachan in the eastern part of Russia clearly have high residual numeracy and low residual land inequality. On the other hand, there are cases such as Cádiz, Sardinia and the district of Szabolcs–Szatmár–Bereg in Hungary that feature high land inequality and low residual numeracy. Another interesting aspect of this Figure pertains to the cases that are located northeast and southwest of the regression line, e.g., Friuli-Venezia Giulia. Interestingly, most of the cases that deviate to the northeast are actually the northern Italian districts in which the Habsburg government invested heavily in basic education. This is clearly a case in which land inequality cannot play the most important role because the Habsburg Empire invested in numeracy to gain legitimacy for its government in northern Italy. This region is actually one of the few regions in which such an imperial government was installed, although it was not necessarily legitimised by a strong developmental difference. Other cases could have been regions in Hungary, but most Hungarian parts were less developed than the Hungarian heartland. Thus, in general, we observe a very close relationship between residual land inequality and residual numeracy.
6 Identification issues: Altonji/Elder Taber ratios, Oster methodology, and instrumental variable estimates
Clearly, other variables that are unobserved might matter as well. Altonji et al. (2005) have suggested a method to estimate the selection on unobservables relative to the selection on observables. Recently, this method has been applied in a variety of empirical frameworks; including Nunn and Wantchekon (2011) on the long-run effects of slavery. The basic question is ‘How large does the effect of unobservables have to be in order to destroy the effect of the main explanatory variable’, in our case land inequality? In most multiple regressions, the coefficient of the main explanatory variable declines as more (observable) control variables are added. Hence, the Altonji–Elder–Taber (AET) ratio compares the size of the coefficient of interest (land inequality) in a restricted regression including only a constant (and, in our case, country fixed effects), \({\ss }_{\mathrm{restr}}\), to the coefficient of a regression with many controls \(({\ss }_{\mathrm{full}})\). \(({\ss }_{\mathrm{restr}}-{\ss }_{\mathrm{full}})\) is the denominator of the AET ratio and \({\ss }_{\mathrm{full}}\) is the numerator, because the larger it is, the stronger is the effect of the variable of interest (land inequality). If control variables only remove a small part of the land inequality coefficient, then unobservables would probably need to have a very strong effect to eliminate the land inequality impact completely. In our case (Table 8) they need to be at least three times larger.Footnote 27 We also assessed the robustness by differentiating (a) between all countries and (b) the case in in which the geographically largest country is removed (Russia, column 2). Finally, we studied the robustness by excluding soil suitabilities, economic and demographic variables as well as temperature and precipitation (line 2–4). The result remains robust (Table 8). Omitted variables would need to have a much larger effect than observables to remove the GMV variable effect of land inequality. We can conclude that the AET ratio indicates a low probability of omitted variable bias.
The AET ratios discussed above are exclusively based on coefficient movements after the inclusion of observable covariates. Oster suggested that the authors rely implicitly on the assumption that the variation in the outcome variable would have been totally explained if unobservables were observed. However, “coefficient movements alone are not a sufficient statistic to calculate bias” (Oster 2017, p. 1). In particular, it is not only the stability of coefficients which matters for the detection of omitted variable biases but also their importance. Hence, if the \(\hbox {R}^{2}\) is not close to one in the baseline specification, coefficient movements and variations in \(\hbox {R}^{2}\) have to be evaluated concurrently. While scaling coefficient movements to shifts in \(\hbox {R}^{2}\), an omitted variable bias is proportional to adapted changes in coefficients. Similar to the AET, Table 9 reports the relative degree of selection on unobservables such that the effect of land inequality is totally eliminated, while taking into account \(\hbox {R}^{2}\) movements as well, following Oster (2017). In particular, the degree of relative selection on unobservables ranges between 1.40 and 4.15 depending on the model specification and is consistently above 1. Hence, the unobservables have to be more important by factors ranging between 1.40 and 4.15 compared to observables in order to eliminate the main effect of land inequality. In all specifications country fixed effects are included as controls.
Another major issue of identification is, of course, endogeneity. Hence we perform an instrumental variable regression for one of the countries in order to understand potential endogeneity effects. Ideally we would perform this for all countries under study, but suitable instruments are only available for one country, namely Spain. We are instrumenting with two different variables, one is the share of family farms in 1750. The other one is whether a region was under Muslim rule in the twelfth century, as the land conquered during the following Reconquista was given to large land owners (Kamen 2004). Its impact on the distribution of income has already been studied by other researchers. For instance, Oto-Peralías and Romero-Ávila (2016) find evidence that the Reconquista has left land and economic power in only a few hands, thus excluding many from the benefits of economic progress and slowing down economic development in the long run. Similarly, Beltrán Tapia and Martínez-Galarraga (2015) used the timing of the reconquista (and its implications on the farm size structure) to instrument the share of farm laborers (relative to farmers). They can explain a high share of literacy differences between Spanish districts.
We include family farms as a second instrument, because Gray and Clark (2014) argued convincingly that a high farmer share is a reasonable correlate of low land inequality: in regions in which family farms could produce efficiently (due to soil characteristics etc.), large landholdings could not develop. The Spanish government performed a census (“Catastro de Ensenada”) during the mid-eighteenth century which has survived for a large number of Spanish provinces. We could calculate the ratio between farmers and the total agricultural population as suggested by Gray and Clark (2014). Autocorrelation might be an issue for this instrument, but given the temporal distance of 150 years—which implies a large number of generations, especially in countries with low life expectancy such as early-modern Spain—this might be less likely.
Potential criticism of the family farm instrument could be that it measures simply the inverse of land inequality. However, there is more to family farms than just one segment of the size distribution. For example, the family farm component is also strongly influenced by the demographic structure. Only a certain type of family structure led to the establishment of this type of family farm (Gray and Clark 2014), although some geographic and climatic variables are certainly also beneficial for establishing these types of farms. In addition, one attractive component of our family farm instrument is that it was already collected in the mid-eighteenth century. This reduces the risk of reverse causality—it is less likely that numeracy around 1900 had an impact on family farm shares 150 years earlier.
The second instrument that we employ in the second IV regression is a dummy variable indicating whether a territory was under Muslim rule in the twelfth century. In the Reconquista during the twelfth to fifteenth century, a substantial part of the land was redistributed towards the nobility who bore the burden of the Reconquista (Kamen 2004). This was one of the founding moments of the large land holdings in southern Spain. Hence, we would expect a negative correlation of farm share with land inequality and a positive correlation between Muslim government in the twelfth century and large land holdings.
If we look at the regression Table 10 we see that in the first stage these two variables are significantly correlated with land inequality, the F-statistic is as large as 13.3 in the first case and even reaches 15.3 in the second. As a main result, instrumenting land inequality using these two variables we obtain a significantly negative effect of farm share on numeracy, even though admittedly the number of cases is quite small.
One important issue is whether the exclusion restriction holds. There are very few—if any—examples of IV regressions in which no doubts about the exclusion restriction arise. It is always possible to imagine a causal channel in which the IV has a separate influence on the dependent variable (not via the potentially endogenous variable), or there might be omitted variables correlated with the IV. Clearly, family and other farms are embedded in a complex set of demographic factors.Footnote 28 Hence, a strong word of caveat about the exclusion restriction should be added to the discussion of the family farm variable as an instrument. In order to assess this potential direct influence of other demographic factors, we will also consider one IV regression model in which the family farm instrument is not included. Certainly, we will be cautious with causal language in this article. Nevertheless, for the family farm variable a substantial violation might not seem as likely, as this variable is quite closely associated with the size structure of farms. The cultural connotation of family farms that might increase education incentives is basically what we expect of normal families who are not hindered by the education-adverse environment of large landowner regions. In the case of the Muslim reign IV, one could hypothesize that the south of Spain might always have been backward relative to the north, or that the conflict during the Reconquista had long-lasting direct consequences for southern economic development. However, after considering trends in urbanization, neither of the alternative hypotheses seem plausible. The south was much more urbanized and developed than the north of Spain before the Reconquista; all the large cities were situated in the south: Seville (80,000 inhabitants), Granada and Cordoba (both 60,000). Moreover, this size structure remained intact for centuries after the Reconquista. In 1500, all three large cities were still in the territory which we define under Muslim reign in the twelfth century: Granada (70,000), Seville (45,000), Valencia and Malaga (both 43,000), all data from Bosker et al. (2013). In addition, Oto-Peralías and Romero-Ávila (2016) have demonstrated convincingly that the reconquista variable is not correlated to pre-Reconquista backwardness.
If we compare the IV regression with our earlier OLS regression (Table 5, model 1), we observe that the land inequality coefficients are substantially larger in the IV estimates. The larger coefficient in the IV models might be a result of the reduced measurement error compared to previous models without instrumental variables. Nunn (2008, pp. 159–163) emphasized that the second function of instrumental variable techniques—to estimate with less measurement error—results sometimes in larger coefficients of the second stage, compared to OLS estimates. If the instrumented variable is measured with a certain amount of error, while the instruments are not, it is not astonishing if the coefficients are larger. This is certainly the case for our land inequality variable, because all inequality evidence is known to suffer from some degree of measurement error.
In conclusion, while the IV estimation might not be a smoking gun, we can still provide additional evidence for a certain exogeneity of land inequality. Moreover, the Altonji–Elder–Tabor and Oster ratios calculated above suggest that the identification strategy applied here is unlikely to be affected by omitted variables bias.
7 Discussion: potential caveats
In this section, we discuss a number of potential caveats, such as the possible impact of lower initial development on numeracy, the selective migration of high and low-skilled workers to the different regions, the timing of land inequality and human capital data, the ratio of land inequality to rural labour, the potential impact of the franchise, and individual farm sizes and their relative impacts on education.
7.1 Initial development?
Could it be that it was not land inequality but simply lower initial development that had a negative influence on numeracy? Simultaneously, less initial development could lead to less redistributive policies. However, in a number of cases, initial development was higher in the areas of higher land inequality and subsequently lower numeracy. For example, considering the urbanisation indicator for Italy as a measure of initial development, we find the south to be the most urbanised. Naples belonged to the top 4 European cities (jointly with Istanbul, London and Paris—the latter two only grew to become very large cities in the eighteenth century; see Malanima and Volckart 2010) as late as 1800. Malanima and Volckart report that, when considering cities with over 5000 inhabitants, Sicily would account for an urbanisation rate of 66% in 1800, arguably the highest in the world. Similarly, southern Spain was heavily urbanised (Malanima and Volckart 2010). If we were to expect greater numeracy induced by urbanisation, then we would need to look to the south of Spain. Amongst the northern districts we actually find the highest numeracy value, and also the highest literacy value, in the agricultural districts of northern Castilia.
7.2 Selective migration?
Can we imagine that migrants within Europe sorted themselves such that the more skilled moved to the regions with low land inequality whereas the unskilled stayed or moved to the agricultural regions with high inequality? This potential issue does not seem realistic for most countries because the typical migration pattern was either from rural to urban places or the migrants went to destinations in the New World. In addition, migration between agricultural regions within Old Europe was very limited, except for temporary harvest migrations from Poland to Germany and back. The migration process may have played a role in the settlement of the eastern and southern regions of the Russian Empire, but we do not have specific information on the skill selectivity of these migrants. From qualitative accounts, however, it emerges that these settlers were somewhat limited in their skills (except perhaps for some ethnic and religious minorities such as German protestant groups that moved to New Russia and Siberia, but we cover these with the Protestantism variable).
7.3 Timing?
Other data available at the regional and national levels allow us to compare and validate our results for the relationship between numeracy and land inequality in Europe during the nineteenth and twentieth centuries. Human capital can alternatively be measured by literacy, i.e., the share of individuals who are able to read and write. We are able to employ regional literacy data for 1930 in the case of Italy and Spain. Figure 4 shows that there is a clear negative relationship between literacy and land inequality in these countries, once again underlining the appropriateness of our findings.

Source: literacy data from Kirk (1946)
Literacy and landshare \(>100\) ha in Spain and Italy, 1930. a Spain 1930, b Italy 1930. Note For correspondence with the ABCC data the Italian region ‘Venezia Tridentina’ (today’s Alto Adige and Trento) has been dropped (the region was part of the Austrian Empire until the end of Wold War I).
Unfortunately, comparable regional literacy evidence on nineteenth century Europe is not available for all the countries; especially the regions of Eastern Europe lagged in statistical sophistication. Hence, the numeracy evidence presented above has clearly added value, even if we confirm the results here with smaller literacy samples.
In “Appendix A”, we also add later human capital evidence on Russia. In summary, in Italy, Spain and Russia, we also find significant negative influence when we use human capital measurements that are dated after the land inequality measurement. We also discuss the effects of the political franchise in “Appendix A”.
7.4 Different farm size categories
We used a cut-off of more than 50 ha because we explicitly tested all bin sizes of farm categories that we could calculate. How important were the different size categories? For the countries in rural southern and eastern Europe that were most relevant for the land inequality effect, the land shares of small farms and very large farms were substantial: 36% of land was held by farms of less than 20 ha, and 52% was held by very large farms of 100 ha and more (Appendix Table A.5). Another category represented 8% of land farmed by the 20–50 ha category. This category is typically associated with “middle-class” farms. The small number of 8% suggests that middle-class farms were weak in the southern and eastern European countries for which we find the main effect. The already very large farms of the 50–100 ha category represent only 4.5% of farm land.
Table 11 demonstrates the effect of the four different bin sizes on numeracy. Given that we have some relatively strong multicollinearity effects in two of the models, we include only the three larger bin sizes and exclude the share of farms of less than 20 ha. Despite their small share, the effect of large farms of the 50–100 ha category is very remarkable: a one standard deviation effect of its coefficient in column (1) is \(0.03 \times (-74.90) = -2.24\). The effect of the 100 ha and more category is also substantial: \(0.15\times (-14.00) = -2.10\). These are both economically substantive effects. In summary, we find negative effects for both large farm size categories and, therefore, include both together in the main regressions shown above. The only farm size category with positive, albeit insignificant, coefficients is the 20–50 ha category.
In “Appendix B” we also discuss the question whether deflation by agricultural labour makes a difference and find that this was not the case. In sum, the caveats discussed here do not invalidate the land inequality-numeracy relationship.
8 Comparison of our results with other data
As a further alternative to our main database, we take data on literacy and the share of family farms from Vanhanen (2003) as a rough proxy for small and medium-sized farms, in contrast to large farms. Clearly, “family farms” have different extensions. Vanhanen (2003), whose data cover the years 1850–2000, accepts various definitions from the sources on which he relies. One frequently covered size category is 20–50 ha. This analysis allows us to obtain a cross-country impression of the education-inequality relationship in European countries over time.
Figures A.1–A.3 show this relationship in 1858, 1888 and 1918 for a range of European countries. A clear, positive relationship is discernible in the second part of the nineteenth century. This result can either be interpreted to confirm the prediction that a somewhat strong representation of farm sizes in the 20–50 ha range (“family farms”) favours human capital formation, or it indicates that the residual share of large firms (and perhaps very small ones) has a negative effect. Given the other results in our study, the latter relationship appears more plausible. Consistent with GMV’s theory, this relationship becomes less significant over time. As countries became more industrialised, the power of large land owners above the family farm range decreased because newly rich capitalists exercised an increasingly higher degree of influence in politics and in the economy, promoting education. Nevertheless, the proposed negative relationship between land inequality and human capital is confirmed by the data.
9 Conclusion
We find a relationship between geographic factors (soil qualities, temperature, altitude, etc.) and numeracy in more than 300 regions of Europe around the year 1900. What could explain this relationship? We argue that land inequality is a plausible mechanism, given that it is influenced by these geographic factors—specific soil qualities resulted in different agricultural specialisations of both “inequality crops” (exclusive grain and in some regions sugar beet, for example) and “equality crops” (mixed dairy farming and grain). Hence, in the next step, this paper analyses the relationship between inequality in land distribution and numeracy, as proposed by Unified Growth Theory (Galor et al. 2009; see also Galor 2011).
We employ a large new dataset on numeracy (in the form of age-heaping-based ABCC indices) and land inequality throughout Europe around 1900, in order to test these relationships. It is important to study an outcome variable related to education because, in some regions, inexpensive and uneducated teachers were hired. Hence, school enrolment rates were not as informative as numeracy is, here. In addition, some local committees decided to prioritise religious education over mathematical skills. We also control for several other explanatory factors. Moreover, we use country-specific regressions to check the robustness of our results. We carefully assess whether our results are sensitive to changes in the regional differences in land inequality over time in each country (note that the average changes in the level of land inequality would not invalidate the results), and we find that the cross-section of land inequality and numeracy differences is remarkably stable over time. We also included a large set of geographic variables (soil suitabilities, temperature, altitude etc.) and found that it does not change the effect of land inequality. We assess our identification strategy by, firstly, studying potential omitted variable bias using Altonji–Elder–Taber and Oster ratios, and find that this bias is not likely to eliminate the land inequality effect. We also use an IV estimation to circumvent potential endogeneity.
Our results suggest that, in earlier phases of industrialisation, the unequal distribution of land did indeed have a substantial negative correlation with the development of numeracy. In Fig. 5, which gives a summary of our study, the five countries and territories on the top have large negative effects of land inequality. Interestingly, the relationship holds for every single country and empire in rural southern and eastern Europe. The finding is also consistent with the theory of GMV, because they argue that the effect depends on bargaining between large land owners and industrialists; hence, even if we are not claiming causality (in spite of certain hints towards exogenous variation based on one country), the observed correlation corresponds to a solid microeconomic underpinning. It is highly likely that, in the less industrialised east and south, the political power of landowners was still considerably stronger than in western European countries where industrialists had taken over a large share of decision-making power (the three countries on the bottom of Fig. 5). This impact implies that a more equal distribution of land, for example, through the implementation of land reform, may help to foster educational attainment and economic growth at this stage of development.
Notes
Instead, they advocate a measure of agricultural population (head count) per number of agricultural holdings, which has a significant effect in some of the periods. Erickson and Vollrath (2004) argue that this indicator may also be a measure of land inequality, especially for the late twentieth century, because it accounts for the landless labourers often not considered in traditional land inequality measures, which refer to landholders only. Hence, their measure may partially reflect income inequality in the agricultural sector, which could also be an important factor. This argument is very important in the debate. However, one may wonder whether this indicator reflects a number of other factors apart from agricultural inequality. Types of agriculture and the family size of agricultural families could play a role, in addition to the opportunity costs to farmers. To conclude, although land inequality by itself did not have a significant effect in this multi-country study, additional components also played a role.
However, Wegenast lists a number of exceptions where these crops are grown mostly on family farms; see Wegenast (2009), p. 96.
Note that we limit ourselves to some basic foundations; a complete elaboration of the original model is beyond the objectives and the scope of this paper.
More specifically, they wanted to reduce the mobility of the workers on their fields who could potentially gain higher salaries in the industrial centres. Their departure was a major threat for landowners and even if they stayed, landowners would need to payer higher wages. In other words, more education would increase the landowner’s cost of labour by more than the rise in productivity of more skilled workers. Moreover, they did not want to pay higher taxes for higher public investments in education.
More specifically, he notes that “the initiative [to create local tax-based schools] had to come from a local group according to a weighted-voting scheme. Even at the local level, voting rights on bills to be submitted to Parliament were in proportion to property held, with a high minimum property ownership for having any local vote at all” (Lindert 2004a, b, p. 114).
Nunn and Puga suggest a variety of ruggedness measures. We include here the standard deviation of altitude—Nunn and Puga’s measure 2.2, as is it called in their nomenclature. It is one of the accepted measures for ruggedness. It is also highly correlated with other indicators, such as Nunn and Puga’s alternative measure “ruggedness index”, as shown in Figure A.8. In Appendix Table A.9, we test also this alternative “ruggedness index”. The results for land inequality are identical.
This calculation is used for all countries except for the west of the Habsburg Empire (Austria/Czech Lands and south Poland et al.), where only data on the number of agricultural land holdings by size categories are available at the county level. Here, we assume that the area of all farms within a given size category is equal to the value of the average size of that particular category, as proposed by GMV. Moreover, in Russia, the shares are calculated by using two separate publications. More detailed information on the calculation and sources of land inequality is provided in the appendix.
The regions in the north of Spain are not included in this census. The first time that they were included was in the 1960s. Because this agricultural census is very late, we have not included these data. In addition, note that Carmona Pidal and Rosés (2011) show that “from 1890 to 1930, [...] the quantity of people with access to land remained stable, while the amount of landless peasants practically halved” (Carmona Pidal and Rosés 2011, p. 2). Some previously landless peasants may have obtained land, whereas others may have migrated to industry or to countries in the New World. Our land inequality variable actually has the advantage of considering large landowners who own large areas. It is unlikely that landless peasants became large landowners during these years; hence, the stability of our variable over time is warranted.
Not all regions of the European part of the Russian Empire (excluding Poland and the Caucasus regions) are included because data on small land holdings are not available for these regions.
See the appendix for further details on this index.
This formula is derived from transforming the original Whipple Index into the ABCC index and simplifying the formula.
We also adjust for the first birth decade (23–32 years), as proposed by Crayen and Baten (2010).
We use the NUTS 2006 classification. Moreover, the LAU (Local Area Units) are the next smaller level, including districts.
That is, historical regions were matched as closely as possible to current NUTS regions.
More precisely, data are available on NUTS 3 for the former regions of Austria–Hungary (i.e., Austria, Croatia, the Czech Republic, Hungary, Slovakia, Slovenia and parts of Italy, Poland, Romania, Ukraine and Serbia), France and Spain, in addition to on NUTS 2 for Italy and the UK. Exceptions include the greater regions of London (on NUTS 1) and Paris (on NUTS 2). For countries where the NUTS classification is not applicable (e.g. Russia), we use data for the current administrative provinces.
Some additional geographic controls were included, please see Appendix Table A.6 for the full results. Altitude displays positive correlations with numeracy, whereas precipitation is mostly insignificant. Area of the district (in logs) mostly provides negative coefficients.
With their large-scale sugar beet-producing estates, the ideal type of this category would be the Belarussian and Ukrainian territories of the Russian Empire.
However, some additional influences can be imagined. The Galor and Ozak (2016) results of cereal suitability implying more patience could lead to more numeracy as well. However, Galor and Ozak did not contrast cereal suitability with dairy farming or pasture, but rather contrasted intensive agriculture with the less intensive agriculture that was practiced on poorer soils.
Some additional geographic controls were included, please see Appendix Table A.7 for the full results. Precipitation is positively related to land inequality, especially as precipitation was a precondition for large scale agriculture. Area of the district (in logs) mostly provides negative coefficients.
That is, the number of individuals in a region per square kilometre. The data refer to the same census year as the numeracy data. See the appendix for more details.
This variable includes the major cities in the countries under study. These are always the capital cities except for Russia, where historically both Moscow and St. Petersburg have been capital cities and have obtained similar levels of importance with regard to population size and political influence. These are: in Russia, St. Petersburg and Moscow; in Austria, Vienna; in France, Paris; in Italy, Rome; in Hungary, Budapest; in Spain, Madrid; and in the UK, London.
More concretely, it is the number of Protestants in a region divided by the total population in a region. The data refer to the same census year as the numeracy data. See the appendix for more details.
Friendly Communication by Max Schulze.
Based on Buyst and Franasek (2010), p. 210. The values for the Habsburg monarchy mentioned in the following refer to 1913 for Austria and 1920 for Hungary.
We include only countries for which sufficient numbers of regional observations were available. However, given the modest number of regions in some countries, an outlying region can readily make a coefficient insignificant, which is the case in Hungary. The Fejer region is an outlier.
After controlling for economic factors, temperature is negatively correlated with numeracy, and ruggedness insignificant. Also sugar and potato suitabilities are mostly insignificant.
AET ratios require the assumption that the variation of the dependent variable to the observables has a similar relationship with the main explanatory variable as the part of the variation reflecting unobservables.
For example, Tur-Prats (2015) argued that the Spanish Reconquista and the antagonism between kings and nobility during this process led to indivisible inheritance of stem family farms in the north and northeast of Spain, and equal inheritance rules of landless day labourers in the south. This had implications on intimate partnership violence until today, according to Tur-Prats, because gender equality was higher in stem family farm regions.
References
A’Hearn, B., Crayen, D., & Baten, J. (2009). Quantifying quantitative literacy: Age heaping and the history of human capital. The Journal of Economic History, 68, 783–808.
Alesina, A., & Rodrik, D. (1994). Distributive politics and economic growth. The Quarterly Journal of Economics, 109, 465–490.
Altonji, J. G., Elder, T. E., & Taber, C. R. (2005). Selection observed and unobserved variable: Assessing the effectiveness of catholic schools. Journal of Political Economy, 113(1), 151–148.
Ashraf, Q., & Galor, O. (2013). The “Out of Africa” hypothesis, human genetic diversity, and comparative economic development. The American Economic Review, 103(1), 1–46.
Ashraf, Q., Cinnirella, F., Galor, O., Gershman, B., & Hornung, E. (May 2017). Capital-skill complementarity and the emergence of labor emancipation. In CESifo working paper seriesno. 6423.
Baten, J., Crayen, D., & Voth, J. (2014). Numeracy and the impact of high food prices in industrializing Britain, 1780–1850. Review of Economics and Statistics, 96(3), 418–430.
Baten, J., & Juif, D. (2014). A story of large landowners and math skills: Inequality and human capital formation in long-run development, 1820–2000. Journal of Comparative Economics, 42, 375–401.
Becker, S. O., & Woessmann, L. (2009). Was Weber wrong? A human capital history of protestant economic history. The Quarterly Journal of Economics, 124, 531–596.
Beltrán Tapia, F. J., & Martínez-Galarraga, J. (2015). Land access inequality and education in pre-industrial Spain. University of Oxford discussion papers in Economic and Social History, 137.
Bosker, M., Buringh, E., & van Zanden, J. L. (2013). From Baghdad to London: Unraveling Urban Development in Europe, the Middle East, and North Africa, 800–1800. Review of Economics and Statistics, 95(4), 1418–1437.
Boucekkine, R., de la Croix, D., & Peeters, D. (2007). Early literacy achievements, population density, and the transition to modern growth. Journal of the European Economic Association, 5, 183–226.
Bruhn, M., & Gallego, F. (2012). Good, bad, and ugly colonial activities: Do they matter for economic development? Review of Economics and Statistics, 94, 433–461.
Buyst, E., & Franasek, P. (2010). Sectoral developments. In S. Broadberry & K. H. O’Rourke (Eds.), Cambridge economic history of modern Europe. Cambridge: Cambridge University Press.
Carmona P. J., & Rosés, J. R. (2011). Was land reform necessary? Access to land in Spain, 1860 to 1931. In Universidad Carlos III de Madrid working papers 11-01.
Cinnirella, F., & Hornung, E. (2016). Landownership concentration and the expansion of education. Journal of Development Economics, 121, 135–152.
Crayen, D., & Baten, J. (2010). Global trends in numeracy 1820–1949 and its implications for long-run growth. Explorations in Economic History, 47, 82–99.
Deininger, K., & Squire, D. (1998). New ways of looking at old issues: Inequality and growth. Journal of Development Economics, 57, 259–287.
Diamond, J. (1997). Guns, germs and steel: The fates of human societies. New York: Verlag Norton.
Dobado, R., & García, H. (2014). Neither so low nor so short! Wages and heights in eighteenth and early nineteenth centuries colonial Hispanic America. Journal of Latin American Studies, 46(2), 291–321.
Dovring, F. (1965). Land and labour in Europe in the twentieth century. The Hague: Martinus Nijhoff.
Easterly, W. (2007). Inequality does cause underdevelopment: Insights from a new instrument. Journal of Development Economics, 84, 755–776.
Eddie, S. M. (1967). The changing pattern of landownership in Hungary, 1867–1914. The Economic History Review, 20, 293–310.
Elazar, D. S. (1996). Agrarian relations and class hegemony: A comparative analysis of landlord, social and political power-Italy 1861–1920. The British Journal of Sociology, 47, 232–254.
Engerman, S., & Sokoloff, K. L. (2000). Institutions, factor endowments, and paths of development in the new world. Journal of Economic Perspectives, 14, 217–232.
Erickson, L. & Vollrath, D. (2004). Dimensions of land inequality and economic development. In IMF working paper WP/04/158. Washington, D.C.
Federico, G. (2009). Agriculture and economic growth in Italy, 1870–1939. In P. Lains & V. Pinilla (Eds.), Agriculture and economic development in Europe since 1870. London and New York: Routledge.
Galor, O. (2011). From stagnation to growth: Unified growth theory. In P. Aghion & S. N. Durlauf (Eds.), Handbook of economic growth (Vol. 1A). Amsterdam: Elsevier.
Galor, O., & Ozak, O. (2016). The agricultural origins of time preference. The American Economic Review, 106(10), 3064–3103.
Galor, O., & Moav, O. (2006). Das human-kapital: A theory of the demise of the class structure. The Review of Economic Studies, 73, 85–117.
Galor, O., Moav, O., & Vollrath, D. (2009). Inequality in landownership, the emergence of human-capital promoting institutions, and the great divergence. The Review of Economic Studies, 76, 143–179.
Goñi, M. (2016). Landed Elites and Education Provision in England and Wales. Evidence from School Boards, 1870-99. Working Paper University of Vienna.
Gray, R., & Clark, G. (2014). Geography is not destiny: geography, institutions and literacy in England, 1837–1863. Oxford Economic Papers, 66(4), 1042–1069.
Hanushek, E. A., & Woessmann, L. (2012). Do better schools lead to more growth? Cognitive skills, economic outcomes, and causation. Journal of Economic Growth, 17, 267–321.
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G., & Jarvis, A. (2005). Very high resolution interpolated climate surfaces for global land areas. International Journal of Climatology, 25, 1965–1978.
Hippe, R. (2012a). How to measure human capital? The relationship between numeracy and literacy. Economies et Sociétés, 45, 1527–1554.
Hippe, R. (2012b). Spatial clustering of human capital the European regions. Economies et Sociétés, 46, 1077–1104.
Hippe, R., & Baten, J. (2011). Regional inequality in human capital formation in Europe, 1790–1880. In University of Tübingen working paper.
Hippe, R., & Baten, J. (2012). Regional inequality in human capital formation in Europe, 1790–1880. Scandinavian Economic History Review, 60, 254–289.
Huber, E., & Safford, F. (Eds.). (1995). Agrarian structure and political power: Landlord and Peasant in the making of Latin America. Pittsburgh: University of Pittsburgh Press.
Kamen, H. A. F. (2004). The duke of alba. New Haven/London: Yale University Press.
Kirk, D. (1946). Europe’s population in the interwar years. Princeton: Princeton University Press.
Kopsidis, M. (2009). Agricultural development and impeded growth: the case of Hungary, 1870–1973. In P. Lains & V. Pinilla (Eds.), Agricultural and economic development in Europe since 1870. Abingdon: Routledge.
Lindert, P. (2004a). Growing public: Social spending and economic growth since the eighteenth century (Vol. I). Cambridge: Cambridge University Press.
Lindert, P. (2004b). Growing public: Social spending and economic growth since the eighteenth century (Vol. II). Cambridge: Cambridge University Press.
Malanima, P., & Volckart, O. (2010). Urbanisation, 1700–1870. In S. Broadberry & K. H. O’Rourke (Eds.), The Cambridge Economic History of Modern Europe (Vol. I). Cambridge: Cambridge University Press.
Maloney, W. F., & Valencia Caicedo, F. (2015). The persistence of (subnational) fortune. The Economic Journal, 126, 2363–2401.
North, D. C. (1981). Structure and change in economic history. New York: Norton.
Nunn, N. (2008). The long-term effects of Africa’s slave trades. The Quarterly Journal of Economics, 123(1), 139–176.
Nunn, N., & Wantchekon, L. (2011). The slave trade and the origins of mistrust in Africa. American Economic Review, 101(7), 3221–3252.
Oster, E. (2017). Unobservable selection and coefficient stability: Theory and evidence. Journal of Business and Economic Statistics. https://doi.org/10.1080/07350015.2016.1227711.
Oto-Peralías, D., & Romero-Ávila, D. (2016). The economic consequences of the Spanish reconquest: The long-term effects of medieval and colonization. Journal of Economic Growth, 21(4), 409–464.
Perotti, R. (1996). Growth, income distribution, and democracy: What the data say. Journal of Economic Growth, 1, 149–187.
Persson, T., & Tabellini, G. (1994). Is inequality harmful for growth? The American Economic Review, 84, 600–621.
Sachs, J. D., & Warner, A. M. (1999). The big push, natural resource booms and growth. Journal of Development Economics, 59, 43–76.
Swinnen, J. F. M. (2002). Political reforms, rural crises, and land tenure in western Europe. Food Policy, 27, 371–394.
Tur-Prats, A. (2015). Family types and intimate-partner violence: A historical perspective. In Universitat Pompeu Fabra Economics Working Papers.
Vanhanen, T. (2003). Democratization and power resources 1850–2000 [computer file]. FSD1216, version 1.0 (2003-03-10). Tampere: Finnish Social Science Data Archive [distributor].
Wagner, P. (2005). Bauern, Junker und Beamte. Lokale Herrschaft und Partizipation im Ostelbien des 19. Jahrhunderts. Goettingen: Wallstein Publisher.
Wegenast, T. (2009). The legacy of landlords: educational distribution and development in a comparative perspective. Zeitschrift für vergleichende Politikwissenschaft, 3, 81–107.
Williamson, J. G. (2009). History without evidence: Latin American inequality since 1491. In NBER Working Paper 14766.
Author information
Authors and Affiliations
Corresponding author
Additional information
Disclaimer: The views expressed are purely those of the writers and may not in any circumstances be regarded as stating an official position of the European Commission.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Baten, J., Hippe, R. Geography, land inequality and regional numeracy in Europe in historical perspective. J Econ Growth 23, 79–109 (2018). https://doi.org/10.1007/s10887-017-9151-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10887-017-9151-1