Abstract
This paper concerns the behavior of time-periodic solutions to 1D dissipative autonomous semilinear hyperbolic PDEs under the influence of small time-periodic forcing. We show that the phenomenon of forced frequency locking happens similarly to the analogous phenomena known for ODEs or parabolic PDEs. However, the proofs are essentially more difficult than for ODEs or parabolic PDEs. In particular, non-resonance conditions are needed, which do not have counterparts in the cases of ODEs or parabolic PDEs. We derive a scalar equation which answers the main question of forced frequency locking: Which time shifts \(u(t+\varphi )\) of the solution u(t) to the unforced equation do survive under which forcing?
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The following phenomenon is usually called forced frequency locking (but also injection locking or frequency entrainment): If \(u^0\) is a \(T^0\)-periodic solution to a nonlinear autonomous evolution equation, if this solution is locally unique up to phase shifts (for example if \(\{u^0(t): t \in \mathbb {R}\}\) is a limit cycle), and if the autonomous equation is forced by a periodic forcing with intensity \(\varepsilon \approx 0\) and period \(T \approx T^0\), then generically there exist \(\tau \in \mathbb {R}\) (the so-called scaled period deviation) and \(\varphi \in \mathbb {R}\) (the so-called asymptotic phase) such that for all \(\varepsilon \) and T with
there exist T-periodic solutions \(u=u_{\varepsilon ,T}\) of the type
to the forced equation. These so-called locked periodic solutions to the forced equation are locally unique and depend continuously on \(\varepsilon \) and T. Moreover, if \(u^0\) is an exponentially orbitally stable periodic solution to the unforced equation, then at least one of the locked periodic solutions to the forced equation is exponentially stable.
Forced frequency locking appears in many areas of nature, and it is used in diverse applications in technology, starting with the poineering work of van der Pol [42], Andronov and Witt [2] and Adler [1]. Moreover, since a long time it is mathematically rigorously described for ODEs with smooth forcing (see, e.g. [13, 22, 24, 39, 41] and [5, Chapter 5.3.5]) or with Dirac-function like forcing (cf. [31]), for functional-differential equations (cf., e.g. [27]) as well as for parabolic PDEs (cf., e.g. [38]).
It turns out that forced frequency locking appears also in dissipative hyperbolic PDEs, but up to now there does not exist a rigorous mathematical description. Reasons for that seem to be the following.
First, the question, if a nondegenerate time-periodic solution to a dissipative nonlinear hyperbolic PDE is locally unique (up to time shifts in the autonomous case) and depends continuously or even smoothly on the system parameters, is much more delicate than for ODEs or parabolic PDEs (cf., e.g. [11, 12, 16]). In particular, for smoothness of the data-to-solution map of hyperbolic PDEs it is necessary, in general, that the equation depends smoothly not only on the unknown function u, but also on the space variable x (and the time variable t in the non-autonomous case). This is completely different to what is known for parabolic PDEs (cf. [9]). Similarly, the description of Hopf bifurcation for dissipative hyperbolic PDEs is much more complicated than for ODEs or parabolic PDEs (cf. [15, 18,19,20]).
Second, linear autonomous hyperbolic partial differential operators with one space dimension essentially differ from those with more than one space dimension: They satisfy the spectral mapping property (see [26] in \(L^p\)-spaces and, more important for applications to nonlinear problems, [23] in C-spaces) and they generate Riesz bases (see, e.g. [10, 25]), what is not the case, in general, if the space dimension is larger than one (see the celebrated counter-example of Renardy in [35]). Therefore, the question of Fredholmness of those operators in appropriate spaces of time-periodic functions is highly difficult.
The main consequence (from the point of view of applied mathematical techniques) of the fact, that the space dimension of the hyperbolic PDEs, which we consider, is one, consists in the following: We can use integration along characteristics in order to replace the nonlinear PDEs by nonlinear partial integral equations (see, e.g. [3] for the notion “partial integral equation”). After that, we can apply known Fredholmness criteria to the linearized partial integral equations (see [16, Corollary 4.11] and [17, Theorem 1.2]). Here we need the strict hyperbolicity condition (for first-order systems it is (1.7), and for second-order equations it is automatically fulfilled), which does not have a counterpart in the case of ODEs or parabolic PDEs.
And third, we have to assume conditions (for first-order systems it is (1.11) or (1.12), and for second-order equations it is (1.27) or (1.28)) implying that small divisors, related to the linear parts of the unforced equation (linearization in the periodic solution of the unforced equation), cannot come too close to zero. There are no counterparts to that condition in the case of ODEs or parabolic PDEs.
In the present paper we will describe forced frequency locking for boundary value problems for 1D semilinear first-order hyperbolic systems of the type
as well as for 1D semilinear second-order hyperbolic equations of the type
We suppose that the unforced problems, i.e. (1.3) and (1.4) with \(\varepsilon =0\), have time-periodic solutions \(u^0\) with period one, that the functions \(f_j(\cdot ,x)\) and \(g_j\) in (1.3) and the functions \(f(\cdot ,x)\) and \(g_j\) in (1.4) are 1-periodic, i.e. that the functions \(f_j(\cdot /T,x)\) and \(g_j(\cdot /T)\) in (1.3) and the functions \(f(\cdot /T,x)\) and \(g_j(\cdot /T)\) in (1.4) are T-periodic, and we show how to find \(\tau \) and \(\varphi \) such that, for all parameters \(\varepsilon \) and T with (1.1) and with \(T^0=1\), there exist T-periodic in time solutions of the type (1.2) to problems (1.3) and (1.4), that those solutions are locally unique and depend continuously on \(\varepsilon \) and T, and we describe their asymptotic behavior for \(\varepsilon \rightarrow 0\).
Remark 1.1
Using a more abstract point of view, one can say that forced frequency locking is a symmetry breaking problem. Indeed, if one formulates the evolution equation as an abstract equation in a space of functions with fixed time period, then the unforced equation is equivariant with respect to time shifts, i.e. equivariant with respect to an action of the rotation group SO(2) on the function space, and the small forcing breaks this equivariance. The solution \(u^0\) to the unforced problem generates a whole family of solutions, the family of all its time shifts, i.e. its orbit under the group action. The phenomenon of forced frequency locking is the phenomenon, that some of the members of the group orbit may survive under appropriate small symmetry breaking perturbations. Hence, in order to answer the main questions (Which members do survive under which forcing?) one can use the machinery of equivariant bifurcation theory (new coordinates in a tubular neighbourhood of the group orbit, scaling, implicit function theorem), and this is, what we are going to do. But there is one necessary condition for this machinery to work: The linearization in \(u^0\) of the equation should be Fredholm of index zero in the function space. The verification of this condition in the case of hyperbolic PDEs is much more complicated than for ODEs or parabolic PDEs.
Remark 1.2
We do not believe that our main results (Theorems 1.5–1.8 below) are true for multidimensional hyperbolic problems of the type (1.3) and (1.4), in general. It turns out that in the multidimensional case one cannot expect to have locally unique time-periodic solutions without imposing additional conditions (like prescribed spacial frequency vectors, cf. [20, 21]). In other words: We do not believe that the linearized multidimensional problems are Fredholm of index zero in appropriate spaces of time-periodic functions, in general.
Remark 1.3
We do not know if dynamic stability properties of the 1-periodic solutions to the unforced problems become inherited on some of the locked T-periodic solutions to the forced problems (1.3) and (1.4). For ODEs and parabolic PDEs this is known to be true, and we expect that this is true also for (1.3) and (1.4). But for showing this, we should consider the initial-boundary value problems corresponding to (1.3) and (1.4), what we do not do in the present paper.
Remark 1.4
In many technical applications the forcing is discontinuous, for example step-like, in time (and, in the case of PDEs, in space also). In cases of ODEs or parabolic PDEs this does not essentially change the phenomenon of forced frequency locking, only the classical solution setting has to be replaced by an appropriate weak one. But, unfortunately, we don’t know what happens in problems (1.3) and (1.4) if the forcing is discontinuous. It would be important and interesting for applications to know, which discontinuous forcing in (1.3) and (1.4) destroys the phenomenon of forced frequency locking and which do not destroy.
1.1 Results for First-Order Systems
In order to formulate our results for problem (1.3) we introduce a new scaled time and new scaled unknown functions \(u=(u_1,u_2):\mathbb {R}\times [0,1]\rightarrow \mathbb {R}^2\) as follows:
Then the problem of T-periodic solutions to (1.3) is transformed into the following one (with \((t,x) \in \mathbb {R}\times [0,1])\)):
Concerning the data of problem (1.5) we suppose (for \(j=1,2\))
and
Speaking about solutions to (1.5) (or its linearizations) we mean classical solutions, i.e. \(C^1\)-functions \(u:\mathbb {R}\times [0,1]\rightarrow \mathbb {R}^2\).
Concerning the unforced problem, i.e. (1.5) with \(\varepsilon =0\) and \(T=1\), we suppose that
Further, for \(j,k=1,2\) and \(t\in \mathbb {R}\) and \(x,y \in [0,1]\) we set
and we consider the conditions
and
Below (cf. Sect. 2.5) we will show that, if the assumptions (1.6), (1.7) and (1.9) are satisfied and if one of the conditions (1.11) and (1.12) is satisfied, then not only the first partial derivatives \(\partial _tu^0\) and \(\partial _xu^0\) exist and are continuous, but also the second partial derivatives \(\partial _t^2u^0\) and \(\partial _t\partial _xu^0\) exist and are continuous. Therefore, the function \(u=\partial _tu^0\) solves the linear homogeneous problem
Hence, the following assumption makes sense:
Remark that, if assumptions (1.6), (1.7) and (1.9) are satisfied, but neither (1.11) nor (1.12), then it may happen that \(\partial _t^2u^0\) does not exist (cf. Remark 2.8). Further, we consider the linear homogeneous problem adjoint to (1.13), namely
and we suppose that
It follows from assumption (1.16) that \(\partial _tu^0\) is not the zero function, i.e. that \(u^0\) is not constant with respect to time. Therefore, assumption (1.14) yields that the space of all solutions to (1.13) has dimension one, and, hence, the space of all solutions to (1.15) has dimension one also. Moreover, assumption (1.16) means that these two one-dimensional spaces are not \(L^2\)-orthogonal. In other words: Zero is a geometrically and algebraically simple eigenvalue to the eigenvalue problem corresponding to (1.13).
In order to formulate our results concerning problem (1.5), we introduce some further notation. We will work with the 1-periodic function \(\Phi :\mathbb {R}\rightarrow \mathbb {R}\), which is defined by
Further, we will work with the maximum norm
for continuous functions \(u:\mathbb {R}\times [0,1] \rightarrow \mathbb {R}^2\), which are periodic with respect to t, and with shift operators \(S_\varphi \) (for \(\varphi \in \mathbb {R}\)), which work on those functions as
And finally, for \(\varepsilon _0>0\) and \(\tau _0 \in \mathbb {R}\) we consider triangles \(K(\varepsilon _0,\tau _0) \subset \mathbb {R}^2\), which are defined by
Theorem 1.5 below concerns existence, local uniqueness and continuous dependence of families of solutions \(u=u_{\varepsilon ,T}\) to (1.5) (with \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0)\) and with certain \(\varepsilon _0>0\) and \(\tau _0 \in \mathbb {R}\)), and it describes the asymptotic behavior of \(u_{\varepsilon ,T}\) for \(\varepsilon \rightarrow 0\):
Theorem 1.5
Suppose (1.6)–(1.9), (1.14) and (1.16), and assume that one of the conditions (1.11) and (1.12) is satisfied. Let \(\varphi _0,\tau _0 \in \mathbb {R}\) be given such that
Then the following is true:
-
(i)
existence and local uniqueness: There exist \(\varepsilon _0 >0\) and \(\delta >0\) such that for all \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0)\) there exists a unique solution \(u=u_{\varepsilon ,T}\) to (1.5) with \(\Vert u-S_{\varphi _0}u^0\Vert _\infty <\delta \).
-
(ii)
continuous dependence: The map \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0) \mapsto u_{\varepsilon ,T}\) is continuous with respect to \(\Vert \cdot \Vert _\infty \).
-
(iii)
asymptotic behavior: We have
$$\begin{aligned} \sup _{(\varepsilon ,T) \in K(\varepsilon _0,\tau _0)}\frac{1}{\varepsilon }\;\inf _{\varphi \in \mathbb {R}}\Vert u_{\varepsilon ,T}-S_\varphi u^0\Vert _\infty <\infty . \end{aligned}$$ -
(iv)
asymptotic phases: There exists a continuous function \(\tau \in (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0) \mapsto \varphi _\tau \in \mathbb {R}\) with \(\varphi _{\tau _0}=\varphi _0\) and
$$\begin{aligned}&\Phi (\varphi _\tau )= {} \tau \quad \text{ and }\nonumber \\&\ \ \lim _{\varepsilon \rightarrow 0}\left\| [u_{\varepsilon ,T}-S_\varphi u^0]_{T=1+\varepsilon \tau ,\varphi =\varphi _\tau }\right\| _\infty = {} 0\quad \text{ for } \text{ all }\quad \tau \in (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0). \end{aligned}$$(1.20)
The next theorem claims, roughly speaking, that almost any solution u to (1.5) with \(\varepsilon \approx 0\), \(T\approx 1\) and with \(\inf _{\varphi \in \mathbb {R}}\Vert u-S_\varphi u^0\Vert _\infty \approx 0\) is described by one of the solution families from Theorem 1.5:
Theorem 1.6
Suppose (1.6)–(1.9), (1.14) and (1.16), and assume that one of the conditions (1.11) and (1.12) is satisfied. Let \((\varepsilon _k,T_k,u_k)\), \(k \in \mathbb {N}\), be a sequence of solutions to (1.5) such that
and let \(\varphi _k \in [0,1]\), \(k \in \mathbb {N}\), be a sequence such that \(\inf _{\varphi \in \mathbb {R}}\Vert u_k-S_\varphi u^0\Vert _\infty = \Vert u_k-S_{\varphi _k} u^0\Vert _\infty \). Then
In particular, if there exist \(\varphi _0 \in \mathbb {R}\) such that \(\varphi _k \rightarrow \varphi _0\) for \(k \rightarrow \infty \) and \(\Phi '(\varphi _0)\not =0\), then for large k we have \(u_k=u_{\varepsilon _k,T_k}\), where \(u_{\varepsilon ,T}\) is the family of solutions to (1.5), described by Theorem 1.5, corresponding to \(\varphi _0\) and \(\tau _0=\Phi (\varphi _0)\).
1.2 Results for Second-Order Equations
If we introduce a new scaled time and new scaled unknown functions \(u:\mathbb {R}\times [0,1]\rightarrow \mathbb {R}\) as in Sect. 1.1, then the problem of time-periodic solutions with period T to (1.4) is transformed into the following one (with \((t,x) \in \mathbb {R}\times [0,1])\)):
Concerning the data of problem (1.22) we suppose that
Speaking about solutions to (1.22) (or its linearizations), we mean classical solutions again, i.e. \(C^2\)-functions \(u:\mathbb {R}\times [0,1]\rightarrow \mathbb {R}\). We suppose that
Further, for \(t\in \mathbb {R}\) and \(x,y \in [0,1]\), we write
where \(\partial _jb\) is the partial derivative of the function b with respect to its jth variable, i.e. \(\partial _2b\) is the derivative of the function b with respect to the place of u, \(\partial _3b\) is the derivative of the function b with respect to the place of \( \partial _tu/T\), and \(\partial _4b\) is the derivative of the function b with respect to the place of \(\partial _x u\). We also write
and we consider the conditions
and
In Sect. 3.2 we will show that, if one of the conditions (1.27) and (1.28) is satisfied, then \(u^0\) is not only \(C^2\)-smooth, but even the third partial derivatives \(\partial _t^3u^0\) and \(\partial _t\partial _x^2u^0\) exist and are continuous. Therefore, the function \(u=\partial _tu^0\) solves the linear homogeneous problem
We assume that
Further, we consider the linear homogeneous problem adjoint to (1.29), namely
We suppose that there exists a solution \(u=u^*\) to (1.31) such that
Remark that, if neither (1.27) nor (1.28) are satisfied, then it may happen that \(\partial _t^3u^0\) does not exist (cf. Remark 3.4).
In order to formulate our results concerning problem (1.22), we introduce further notation. We will work with the 1-periodic function \(\Phi :\mathbb {R}\rightarrow \mathbb {R}\), which is defined by
And again, we will work with the maximum norm \(\Vert u\Vert _\infty :=\max \{|u(t,x)|: (t,x) \in \mathbb {R}\times [0,1]\}\) for continuous functions \(u:\mathbb {R}\times [0,1] \rightarrow \mathbb {R}\), which are periodic with respect to t, and with shift operators \(S_\varphi \), which work on those functions as \([S_\varphi u](t,x):=u(t+\varphi ,x).\)
The following two theorems are similar to Theorems 1.5 and 1.6.
Theorem 1.7
Suppose (1.23), (1.24), (1.30) and (1.32), and assume that one of the conditions (1.27) and (1.28) is satisfied. Let \(\varphi _0,\tau _0 \in \mathbb {R}\) be given such that
Then the following is true:
-
(i)
existence and local uniqueness: There exist \(\varepsilon _0 >0\) and \(\delta >0\) such that for all \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0)\) there exists a unique solution \(u=u_{\varepsilon ,T}\) to (1.22) with \(\Vert u-S_{\varphi _0}u^0\Vert _\infty <\delta \).
-
(ii)
continuous dependence: The map \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0) \mapsto u_{\varepsilon ,T}\) is continuous with respect to \(\Vert \cdot \Vert _\infty \)
-
(iii)
asymptotic behavior: We have
$$\begin{aligned} \sup _{(\varepsilon ,T) \in K(\varepsilon _0,\tau _0)}\frac{1}{\varepsilon }\;\inf _{\varphi \in \mathbb {R}}\Vert u_{\varepsilon ,T}-S_\varphi u^0\Vert _\infty <\infty . \end{aligned}$$ -
(iv)
asymptotic phases: There exists a continuous function \(\tau \in (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0) \mapsto \varphi _\tau \in \mathbb {R}\) such that \(\varphi _{\tau _0}=\varphi _0\) and
$$\begin{aligned} \Phi (\varphi _\tau )= & {} \tau \quad \hbox {and}\quad \lim _{\varepsilon \rightarrow 0}\left\| [u_{\varepsilon ,T}-S_\varphi u^0]_{T=1+\varepsilon \tau ,\varphi =\varphi _\tau }\right\| _\infty \\= & {} 0\quad \hbox {for all}\quad \tau \in (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0). \end{aligned}$$
Theorem 1.8
Suppose (1.23)–(1.24), (1.30) and (1.32), and assume that one of the conditions (1.27) and (1.28) is satisfied. Let \((\varepsilon _k,T_k,u_k)\), \(k \in \mathbb {N}\), be a sequence of solutions to (1.22) such that
and let \(\varphi _k \in [0,1]\), \(k \in \mathbb {N}\), be a sequence such that \(\inf _{\varphi \in \mathbb {R}}\Vert u_k-S_\varphi u^0\Vert _\infty = \Vert u_k-S_{\varphi _k} u^0\Vert _\infty \). Then
In particular, if there exist \(\varphi _0 \in \mathbb {R}\) such that \(\varphi _k \rightarrow \varphi _0\) for \(k \rightarrow \infty \), and if \(\Phi '(\varphi _0)\not =0\), then for large k we have \(u_k=u_{\varepsilon _k,T_k}\), where \(u_{\varepsilon ,T}\) is the family of solutions to (1.22), described by Theorem 1.7, corresponding to \(\varphi _0\) and \(\tau _0=\Phi (\varphi _0)\).
Remark 1.9
For all \(u,v \in C_{per}^2(\mathbb {R}\times [0,1];\mathbb {R})\) with u satisfying the boundary conditions in (1.29), we have
Hence, if \(\int _0^1\int _0^1\left( \partial _t^2u-a^2\partial _x^2u+b_2u+b_3\partial _tu+b_4\partial _xu\right) v\,dtdx=0\) for certain v and all u, then v satisfies (1.31). This way one gets the structure of the adjoint boundary value problem (1.31).
1.3 Further Remarks
First we formulate some remarks concerning problem (1.5), but could be stated similarly for problem (1.22).
Remark 1.10
If \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0)\), then \(T=1+\varepsilon \tau \) with \(\varepsilon \in (0,\varepsilon _0)\) and \(\tau \in (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0)\), i.e.
is a scaled period deviation parameter. Hence, the so-called phase equation \(\Phi (\varphi )=\tau \) describes the relationship between the scaled period deviation \(\tau \) and the corresponding asymptotic phase \(\varphi =\varphi _\tau \) (cf. (1.20)) of the solution family \(u_{\varepsilon ,T}\). More precisely: The phase equation answers, asymptotically for \(\varepsilon \rightarrow 0\), the main question of forced frequency locking, i.e. which phase shifts of \(u^0\) (described by \(\varphi \)) survive under which forcing (described by \(\tau \)). Remark that the phase equation, i.e. the function \(\Phi \), depends surprisingly explicitly on the shapes of the forcing, i.e. on the functions \(f_j\) and \(g_j\). The only data, which are needed for the computation of \(\Phi \), but which are not explicitly given, is the solution \(u^*\) to the adjoint linearized problem (1.15). There exists a huge literature about the question, how to compute (numerically or, sometimes, analytically) the solution to the adjoint linearized problem (in the ODE case \(u^*\) is a time-periodic vector function, often called perturbation projection vector).
Remark 1.11
We expect that the phase equation \(\Phi (\varphi )=\tau \) describes not only the relationship between the scaled period deviation \(\tau =(T-1)/\varepsilon \) and the corresponding asymptotic phase \(\varphi \), but also the stability of the locked periodic solutions \(u_{\varepsilon ,T}\). More precisely, we expect the following to be true: Let the assumptions of Theorem 1.5 be satisfied, and let \(u^0\) be exponentially orbitally stable as a periodic solution to
Then for all \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0)\) with sufficiently small \(\varepsilon _0\) the periodic solution \(u_{\varepsilon ,T}\) to
is exponentially stable if \(\Phi '(\varphi _0)>0\) and unstable if \(\Phi '(\varphi _0)<0\). For ODEs those results are well-known, cf., e.g., [24, Theorem 3] or [32, Theorem 5.1].
Remark 1.12
If there exist \(\varphi _0,\tau _0 \in \mathbb {R}\) with (1.19), i.e. \(\Phi (\varphi _0)=\tau _0\) and \(\Phi '(\varphi _0)\not =0\), then there exist intervals \([\varphi _-,\varphi _+]\) and \([\tau _-,\tau _+]\) such that
and Theorem 1.5 works in any \(\varphi _0 \in [\varphi _-,\varphi _+]\) with corresponding \(\tau _0=\Phi (\varphi _0)\). Moreover, the proof of Theorem 1.5 shows that the constants \(\varepsilon _0\) and \(\delta \) from assertion (i) of Theorem 1.5 may be chosen uniformly with respect to \(\varphi _0 \in [\varphi _-,\varphi _+]\). Hence, Theorem 1.5 can be generalized as follows:
Suppose (1.6)–(1.9), (1.14) and (1.16), and assume that one of the conditions (1.11) and (1.12) is satisfied. Let intervals \([\varphi _-,\varphi _+]\) and \([\tau _-,\tau _+]\) be given with (1.34). Then the following is true:
-
(i)
There exist \(\varepsilon _0,\delta >0\) such that for all \(\varepsilon \in (0,\varepsilon _0)\) and all \(T>0\) with \(\varepsilon \tau _- \le T-1 \le \varepsilon \tau _+\) there exists a unique solution \(u=u_{\varepsilon ,T}\) to (1.5) with \(\inf \{\Vert u-S_{\varphi }u^0\Vert _\infty : \varphi \in [\varphi _-,\varphi _+]\}<\delta \).
-
(ii)
The map \((\varepsilon ,T) \mapsto u_{\varepsilon ,T}\) is continuous with respect to \(\Vert \cdot \Vert _\infty \)
-
(iii)
We have
$$\begin{aligned} \sup \left\{ \frac{1}{\varepsilon }\;\inf _{\varphi \in \mathbb {R}}\Vert u_{\varepsilon ,T}-S_\varphi u^0\Vert _\infty : \varepsilon \in (0,\varepsilon _0), \;\tau _- \le \frac{T-1}{\varepsilon } \le \tau _+ \right\} <\infty . \end{aligned}$$ -
(iv)
Let \(\varphi =\varphi _\tau \in [\varphi _-,\varphi _+]\) be the unique solution to the phase equation \(\Phi (\varphi )=\tau \) with \(\tau \in [\tau _-,\tau _+]\). Then
$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\left\| [u_{\varepsilon ,T}-S_\varphi u^0]_{T=1+\varepsilon \tau ,\varphi =\varphi _\tau }\right\| _\infty =0\quad \hbox {for all}\quad \tau \in [\tau _-,\tau _+]. \end{aligned}$$(1.35)
Remark 1.13
Assertion (1.35) claims that \(u_{\varepsilon ,1+\varepsilon \tau }\) tends uniformly to \(S_{\varphi _\tau }u^0\) for \(\varepsilon \rightarrow 0\), and the limit \(S_{\varphi _\tau }u^0\) depends on \(\tau \), in general. In other words: If the point \((\varepsilon ,T)\) tends to the point (0, 1) along a straight line, then \(u_{\varepsilon ,T}\) converges uniformly. But, in general, \(u_{\varepsilon ,T}\) does not converge if \((\varepsilon ,T)\) tends to (0, 1) not along a straight line.
Remark 1.14
It is easy to show that Theorems 1.5 and 1.6 can be generalized to problems of the type
In the definition of the function \(\Phi \) one has to replace \(g_1(t)\), \(g_2(t)\) and \(f_j(t,x)\) by \(g_1(t,u^0(t,0))\), \(g_2(t,u^0(t,1))\) and \(f_j(t,x,u^0(t,x))\), respectively.
Remark 1.15
We believe that Theorems 1.5 and 1.6 can be generalized to quasilinear systems of the type
but probably the proofs will essentially be more difficult than in the semilinear case.
Remark 1.16
Theorems 1.5 and 1.6 can be generalized to problems for \(n \times n\) first-order hyperbolic systems of the type (with natural numbers \(m<n\))
where for all \(x \in [0,1]\) it is supposed \(a_j(x)\not =0\) and \(a_j(x)\not =a_k(x)\) for \(j\not =k\). Here conditions (1.11) and (1.12) are replaced by the conditions
and
If one of these two conditions is satisfied, then the linearization of the system of partial integral equations, corresponding to (1.36), is Fredholm of index zero (cf. [16]).
Finally we formulate two remarks which concern generalizations of the phenomenon of forced frequency locking.
Remark 1.17
If the unforced autonomous evolution equation is equivariant under an action of a compact Lie group and if the solution to the unforced equation is a rotating wave (relative equilibrium) or even a modulated wave (relative periodic orbit) and if the forcing is also of rotating wave type or of modulated wave type, then again phenomena of forced frequency locking type may appear. For ODEs this is described, e.g. in [6, 30, 32,33,34, 36]. For applications of those phenomena to the behavior of optical devices (self-pulsating semiconductor lasers) see [4, 28, 29].
Remark 1.18
In many applications of forced frequency locking the \(T^0\)-periodic solution to the unforced autonomous equation is born in a Hopf bifurcation from a stationary solution, and it is natural to ask how this Hopf bifurcation interacts with small T-periodic forcing for \(T\approx T^0\). In ODE cases this is done, e.g. in [8, 37, 43].
The remaining part of this paper is organized as follows:
Section 2 concerns the first-order system (1.5), and Sect. 3 the second-order Eq. (1.22).
In Sect. 2.1 we show by means of integration along characteristics that first-oder PDE system (1.5) is equivalent to system (2.4) of partial integral equations, we discuss the advantages and disadvantages of (1.5) and (2.4), and we write (2.4) as abstract nonlinear operator Eq. (2.10) in the function space \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
In Sects. 2.2 and 2.3 we show that the linearization in \(\varepsilon =0\), \(T=1\) and \(u=u^0\) of the abstract nonlinear operator Eq. (2.10) is Fredholm of index zero in \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). In Sect. 2.4 we describe the kernel and the image of this Fredholm operator. This is needed for the Liapunov–Schmidt-like procedure used later.
In Sect. 2.5 we use the abstract solution regularity result Theorem 4.1 of E. N. Dancer in order to show that the solution \(u^0\) to the unforced problem has some additional regularity in time (and, hence, in space also).
In Sect. 2.6 we introduce new coordinates in a tubular neighborhood of the set \(O(u^0)\) of all phase shifts of \(u^0\) according to the A. Vanderbauwhede’s Theorem 4.2.
In Sect. 2.7 we show that all solutions to the abstract nonlinear operator Eq. (2.10) with \(\varepsilon \approx 0\), \(T\approx 1\) and \(u \approx O(u^0)\) can be scaled as \(|T-1|\sim \varepsilon \) and dist \((u;O(u^0))\sim \varepsilon \). This is used in Sect. 2.8 in order to derive the scaled abstract nonlinear operator equation (2.50). By means of this equation Theorem 1.5 can be proved (using the Implicit Function Theorem 5.1) as well as Theorem 1.6. In particular, formula (1.17) for the phase equation will be derived.
In Sect. 3 the rigorous way from problem (1.22) to formula (1.33) of the phase equation is even one step longer: From the second-oder Eq. (1.22) to first-order system (3.2) (this is done in Sect. 3.2), then to nonlinear operator Eq. (3.12) and finally to scaled nonlinear operator Eq. (3.23). Therefore, in Sect. 3.1 we show how formula (1.33) of the phase equation can be derived directly from second-oder Eq. (1.22) by formal calculations.
Finally, in Appendices 1 and 2 we present Theorems 4.1, 4.2 and 5.1 from abstract nonlinear analysis.
2 Proofs for First-Order Systems
In this section we will prove Theorems 1.5 and 1.6. Hence, we will suppose that all assumptions of these theorems are satisfied. For the sake of clearness, in all lemmas we will list the assumptions which are used in the lemma.
We will work with the function space
which is equipped and complete with the maximum norm \(\Vert \cdot \Vert _\infty \).
2.1 Integration Along Characteristics
In this subsection we will show that problem (1.5) is equivalent to a system of two partial integral equations. By tactical reasons, which will be useful later, we add artificial linear terms \(\beta _j(t,x) u_j(t,x)\) to the left-hand and the right-hand sides of the PDEs in (1.5), i.e.
We show that the differential operator on the left-hand side of (2.1) has a right inverse, which is a partial integral operator. This procedure is well-known as “integration along characteristics”.
In order to simplify notation we introduce the nonlinear superposition operator B from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)^2\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), defined by
Because of assumption \(b_j \in C^3([0,1]\times \mathbb {R}^3)\) (cf. (1.6)), the superposition operator B is \(C^3\)-smooth. The right-hand side of (2.1) is the value of the function \(B_j(\beta ,u)+\varepsilon f_j\) in the point (t, x).
Further, for \(j=1,2\), \(t \in \mathbb {R}\), \(x,y \in [0,1]\), \(T>0\) and \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), we write
where \(\alpha _j(x,z)\) is defined in (1.10). Then the system of partial integral equations, for \((t,x) \in \mathbb {R}\times [0,1]\)), reads
Lemma 2.1
Suppose (1.6) and (1.8). Then for all \(\varepsilon >0\), \(T>0\) and \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) the following is true:
- (i)
-
(ii)
If \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) is a solution to (2.4) and if the partial derivatives \(\partial _tu\) and \(\partial _t\beta \) exist and are continuous, then u is \(C^1\)-smooth and is a solution to (1.5).
Proof
Let \(\varepsilon >0\), \(T>0\) and \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) be fixed.
-
(i)
Let a \(C^1\)-function \(u:\mathbb {R}\times [0,1]\rightarrow \mathbb {R}^2\) be given. Because of \(\alpha _j(x,x)=0\) and \(c_j(t,x,x,T,\beta )=1\), we have
$$\begin{aligned}&u_1(t,x)-c_1(t,x,0,T,\beta )u_1(t+\alpha _1(x,0)/T,0)\\&\quad =\int _0^x\partial _y[c_1(t,x,y,T,\beta )u_1(t+\alpha _1(x,y)/T,y)]\,dy\\&\quad =\int _0^x\partial _yc_1(t,x,y,T,\beta )u_1(t+\alpha _1(x,y)/T,y)\,dy\\&\qquad +\int _0^xc_1(t,x,y,T,\beta )[\partial _tu_1(s,y),y)\partial _y\alpha _1(x,y)/T+\partial _xu_1(s,y)]_{s=t+\alpha _1(x,y)/T}\,dy. \end{aligned}$$From \(\partial _yc_1(t,x,y,T,\beta )=\beta _1(t+\alpha _1(x,y)/T,y)c_1(t,x,y,T,\beta )/a_1(y)\) and \(\partial _y\alpha _1(x,y)=1/a_1(y)\) it follows that
$$\begin{aligned}&u_1(t,x)-c_1(t,x,0,T,\beta )u_1(t+\alpha _1(x,0)/T,0)\\&\quad =\int _0^x\frac{c_1(t,x,y,T,\beta )}{a_1(y)}\left[ \frac{1}{T}\partial _tu_1(s,y)+a_1(y)\partial _xu_1(s,y)+\beta _1(s,y)u_1(s,y)\right] _{s=t+\alpha _1(x,y)/T}\,dy. \end{aligned}$$Hence, if u is a solution to (1.5), i.e. to (2.1), then it solves the first equation in (2.4). Similarly one shows that it solves the second equation in (2.4).
-
(ii)
Let \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) be a solution to (2.4). Then the first equation in (2.4) with \(x=0\) yields
$$\begin{aligned} u_1(t,0)=c_1(t,0,0,T,\beta )[r_1u_2(s,0)+\varepsilon g_1(s)]_{s=t+\alpha _1(0,0)/T}=r_1u_2(t,0)+\varepsilon g_1(t), \end{aligned}$$i.e. the first boundary condition in (1.5) is satisfied. Similarly one shows that second boundary condition in (1.5) is satisfied also.
Moreover, if \(\partial _tu\) and \(\partial _t\beta \) exist and are continuous, then it follows directly from (2.4) that also \(\partial _xu\) exists and and is continuous, i.e. u is \(C^1\)-smooth.
Now let us show that the first differential equation in (1.5) is satisfied. For that we use that
$$\begin{aligned} \left( \frac{1}{T}\partial _t+a_1(x)\partial _x\right) \phi (t+\alpha _1(x,y)/T,y)=0\quad \hbox {for all}\quad \phi \in C^1(\mathbb {R}). \end{aligned}$$(2.5)Therefore, (2.3) yields
$$\begin{aligned} \left( \frac{1}{T}\partial _t+a_1(x)\partial _x\right) c_1(t,x,y,T,\beta )=-\beta _1(t,x)c_1(t,x,y,T,\beta ). \end{aligned}$$(2.6)Applying the differential operator \(\frac{1}{T}\partial _t+a_1(x)\partial _x\) to the first equation in (2.4) and using (2.5) and (2.6), we get
$$\begin{aligned}&\frac{1}{T}\partial _tu_1(t,x)+a_1(x)\partial _xu_1(t,x)\\&\qquad +\beta _1(t,x)c_1(t,x,0,T,\beta )[r_1u_2(s,0)+\varepsilon g_1(s)]_{s=t+\alpha _1(x,0)/T}\\&\quad =[\varepsilon f_1+B_1(\beta ,u)](t,x)\\&\qquad -\beta _1(t,x)\int _0^x\frac{c_1(t,x,y,T,\beta )}{a_1(y)}[\varepsilon f_1+ B_1(\beta ,u)](t+\alpha _1(x,y)/T,y)\,dy. \end{aligned}$$Using the first equation in (2.4) again, we get the first equation in (2.1), i.e. the first equation in (1.5). Similarly one shows that also the second equation in (1.5) is satisfied.\(\square \)
Remark 2.2
Roughly speaking, the advantages and disadvantages of systems (1.5) and (2.4) are the following: System (1.5) depends smoothly on the control parameter T uniformly with respect to the state parameter u. This is not the case for system (2.4) because, if one differentiates equations in (2.4) with respect to T, then u loses one degree of differentiability with respect to t. On the other hand, the linearizations of (2.4) with respect to u are Fredholm of index zero on a T-independent function space (see Sect. 2.3), what is not the case for (1.5).
Let us write system (2.4) in an abstract form. In order to do so, we introduce the function space
which is equipped and complete with the maximum norm, which will be denoted by \(\Vert \cdot \Vert _\infty \) again, i.e. \(\Vert w\Vert _\infty :=\max \{|w_j(t)|: j=1,2,\; t\in \mathbb {R}\}\) for \(w \in C_{per}(\mathbb {R};\mathbb {R}^2)\). Further, we introduce the linear bounded operator \(R:C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\rightarrow C_{per}(\mathbb {R};\mathbb {R}^2)\), defined by
Finally, for \(T>0\) and \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), we introduce linear bounded operators \(C(T,\beta ):C_{per}(\mathbb {R};\mathbb {R}^2)\rightarrow C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) and \(D(T,\beta ):C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\rightarrow C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), defined by
and
Then problem (2.4) can be written as
Note that the variable \(\beta \) in (2.10) is still artificial, i.e. if u satisfies (2.10), then u satisfies (2.10) with \(\beta \) replaced by any other \({\widetilde{\beta }}\in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) also. Therefore, we have the following:
From the definitions (2.3), (2.8) and (2.9) it follows that the maps \(\beta \mapsto C(T,\beta )R\) and \(\beta \mapsto D(T,\beta )\) are \(C^\infty \)-smooth from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into \({{\mathcal {L}}}(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2))\) (with respect to the uniform operator norm). Similarly, from (2.2) and from the smoothness assumption \(b_j \in C^3([0,1]\times \mathbb {R})\) [cf. (1.6)] it follows that the map \((\beta ,u)\mapsto B(\beta ,u)\) is \(C^2\)-smooth from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)^2\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
Unfortunately, the maps \(T \mapsto C(T,\beta )R\) and \(T \mapsto D(T,\beta )\) are not continuous from \((0,\infty )\) into \(\mathcal{L}(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2))\) (with respect to the uniform operator norm). This causes some technical difficulties in the analysis of Eq. (2.10). But we have
for any \(c>0\) and, moreover, we have
from \((0,\infty )\times C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)^2\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)^2\).
2.2 Invertibility of \(I-C(T,\beta ^0)R\)
In what follows, we introduce a function \(\beta ^0 \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) by (cf. (1.10))
Lemma 2.3
Suppose (1.6), (1.7) and (1.9), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then there exists \(\varepsilon _0 \in (0,1)\) such that for all T with \(|T-1|<\varepsilon _0\) and all \(f \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) there exists a unique solution \(u=u_{T,f} \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to the equation \(u=C(T,\beta ^0)Ru+f\), and, moreover,
Proof
Because of \(\beta =\beta ^0\) is fixed, we will skip the dependence on \(\beta \) in the notation
Remark that the map \(T \mapsto C(T)\) is not uniformly continuous, but only strongly continuous. Hence, for proving the invertibility of the operator \(I-C(T)R\) for \(T\approx 1\) it is not sufficient to prove the invertibility of the operator \(I-C(1)R\).
Take \(f \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). We have to show that for \(T \approx 1\) there exists a unique solution \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to the equation
and that \(\Vert u\Vert _\infty \le \hbox {const}\Vert f\Vert _\infty \), where the constant does not depend on T and f. Equation (2.15) is satisfied if and only if for all \(t \in \mathbb {R}\) and \(x \in [0,1]\) we have
System (2.16)–(2.17) is satisfied if and only if (2.16) is true and if
Put \(x=0\) in (2.18) and get
Similarly, system (2.16)–(2.17) is satisfied if and only if (2.17) is true and
i.e. if and only if (2.17) and (2.20) are true and
Let us consider Eq. (2.19). It is a functional equation for the unknown function \(u_2(\cdot ,0)\). In order to solve it, let us denote by \(C_{per}(\mathbb {R})\) the Banach space of all 1-periodic continuous functions \(\tilde{u}:\mathbb {R}\rightarrow \mathbb {R}\) with the norm \(\Vert \tilde{u}\Vert _\infty :=\max \{|\tilde{u}(t)|: t \in \mathbb {R}\}\). Equation (2.19) is an equation in \(C_{per}(\mathbb {R})\) of the type
with \(\tilde{u},\tilde{f}(T)\in C_{per}(\mathbb {R})\) defined by \(\tilde{u}(t):=u_2(t,0)\) and
and with \(\widetilde{C}(T)\in \mathcal{L}(C_{per}(\mathbb {R}))\) defined by
From the definitions of the functions \(c_1\) and \(c_2\) (cf. (2.3)) it follows that
and, hence,
Consequently, if assumption (1.11) is satisfied, then \(|r_1r_2c_1(t+\alpha _2(0,1),1,0,1) c_2(t,0,1,1)|\not =1\) for all \(t \in \mathbb {R}\).
First, let us consider the case that
Then there exists \(\varepsilon _0 \in (0,1)\) such that for \(|T-1|<\varepsilon _0\) we have
Therefore,
Hence, for \(|T-1|<\varepsilon _0\) the operator \(I-\widetilde{C}(T)\) is an isomorphism on \(C_{per}(\mathbb {R})\), and, moreover,
Therefore, for \(|T-1|<\varepsilon _0\) there exists a unique solution \(u_2(\cdot ,0)\in C_{per}(\mathbb {R})\) to (2.19), and \( \Vert u_2(\cdot ,0)\Vert _\infty \le \hbox {const}\Vert \tilde{f}(T)\Vert _\infty \le \hbox {const}\Vert f\Vert _\infty , \) where the constants do not depend on T and f. Inserting this solution into the right-hand sides of (2.18) and (2.16), we get the unique solution \(u=(u_1,u_2) \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to (2.16)–(2.17). Moreover, this solution satisfies the a priori estimate \(\Vert u\Vert _\infty \le \hbox {const}\Vert f\Vert _\infty \), where the constant does not depend on T and f.
Now, let us consider the case that
Then there exists \(\varepsilon _0>0\) such that for all \(|T-1|<\varepsilon _0\) we have
Equation (2.19) is equivalent to
This equation is of the type (2.22) again, but now with
Hence, we can proceed as above.
Similarly one deals with the case if condition (1.12) is satisfied. Then Eq. (2.21) is uniquely solvable with corresponding estimate, and so is Eq. (2.20) and, hence, system (2.16)–(2.17). \(\square \)
2.3 Fredholmness of \(I-C(T,\beta ^0)R-D(T,\beta ^0)\partial _uB(\beta ^0,u^0)\)
In this subsection we prove the following Fredholmness result.
Lemma 2.4
Suppose (1.6), (1.7) and (1.9), and assume that one of the conditions (1.11) and (1.12) is satisfied. Take \(\varepsilon _0>0\) from Lemma 2.3. Then, for all T with \(|T-1|<\varepsilon _0\), the operator \(I-C(T,\beta ^0)R-D(T,\beta ^0)\partial _uB(\beta ^0,u^0)\) is Fredholm of index zero from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself.
Proof
Because of T and \(\beta =\beta ^0\) are fixed, in the notations below we will not mention the dependence on T and \(\beta \), i.e.
and [cf. the definitions of the functions \(c_1\),\(c_2\) and \(\beta ^0\) in (2.3) and (2.14)]
On account of Lemma 2.3, the operator \(I-CR-DB^0\) is Fredholm of index zero if and only if the operator \(I-(I-CR)^{-1}DB^0\) is Fredholm of index zero. Hence, it suffices to show that the operator \(((I-CR)^{-1}DB^0)^2\) is compact. This is a consequence of the following Fredholmness criterion of S. M. Nikolskii (cf. e.g. [14, Theorem XIII.5.2]): If a Banach space U and a linear bounded operator \(K:U\rightarrow U\) are given such that \(K^2\) is compact, then the operator \(I-K\) is Fredholm of index zero.
A straightforward calculation shows that
Using this and Lemma 2.3 again, we get that it suffices to show that the operators \(DB^0D\) and \(DB^0CR\) are compact.
Let us show that \(DB^0D\) is compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself. Here the key point is, that the partial integral operator D is not compact, but the “full” integral operator \(DB^0D\) is compact.
Take \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). From (2.2) and (2.23) it follows that
Hence, the definitions (2.9) and (2.23) imply that the first component of \([DB^0u](t,x)\) is
Using (2.9) and (2.23), we get
where
Now we change the order of integration in (2.27) according to
Let us consider the first summand in the right-hand side of (2.28), it is
In the inner integral in (2.29) we replace the integration variable y by \(\eta \) according to
Here we used the definitions (1.10) of \(\alpha _j\). Because of assumption \(a_1(x)\not =a_2(x)\) for all \(x \in [0,1]\) (cf. (1.6)) we have
i.e. the function \(y \mapsto \widehat{\eta }(t,x,y,z)\) is strictly monotone. Let us denote its inverse function by \(\eta \mapsto \widehat{y}(t,x,\eta ,z)\). Then
and
The smoothness assumptions in (1.6) and (1.14) on the data \(a_j\), \(b_j\) and \(u^0\) yield that the functions d, \(\widehat{\eta }\), \(\widehat{y}\) and \(\partial _\eta \widehat{y}\) are \(C^1\)-smooth with bounded partial derivatives. Therefore,
where the constant does not depend on t, x and u.
Similarly one shows that also the second summand in the right-hand side of (2.28), which is
is \(C^1\)-smooth with respect to t and x and that its partial derivatives can be estimated by \(\hbox {const}\,\Vert u\Vert _\infty \), where the constant does not depend on t, x and u. Similarly one shows that also \(D_2B^0Du\) is \(C^1\)-smooth with respect to t and x and that its partial derivatives can be estimated by \(\hbox {const}\,\Vert u\Vert _\infty \), where the constant does not depend on t, x and u. This way we get \( \Vert \partial _t DB^0Du\Vert _\infty +\Vert \partial _x DB^0Du\Vert _\infty \le \hbox {const}\,\Vert u\Vert _\infty , \) where the constant does not depend on u. Hence, the Arzela–Ascoli Theorem yields that the operator \(DB^0D\) is compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself.
Finally, let us show that the operator \(DB^0CR\) is compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself. From (2.7), (2.8) and (2.26) it follows that
where
Now we change the integration variable y to \(\eta =t+(\alpha _2(x,y)+\alpha _1(y,1))/T\) and proceed as above. This way we get the desired bound \(\Vert \partial _t DB^0CRu\Vert _\infty +\Vert \partial _x DBCRu\Vert _\infty \le \hbox {const}\,\Vert u\Vert _\infty \), where the constant does not depend on u. \(\square \)
Remark 2.5
In the proof above one can see the reason for inserting the artificial term \(\beta _j(t,x)u_j(t,x)\) into (2.1) and for the choice \(\beta =\beta ^0\) (cf. (2.14)): It leads to the linear operator \(B^0\), which has the property that the first component \([B^0_1u](t,x)\) does not depend on \(u_1\) and the second component \([B^0_2u](t,x)\) does not depend on \(u_2\). This leads to (2.27) and, hence, to the change of integration variables \(y \mapsto \eta \). If one would not introduce the artificial term, i.e. if one would choose \(\beta =0\), then the operator \(DB^0D\) would not be compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself, in general.
2.4 Kernel and Image of \(I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _uB(\beta ^0,u^0)\)
In this subsection we describe the kernel and the image of the Fredholm operator \(I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _uB(\beta ^0,u^0)\). For that we need some more notation.
We denote by \(C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) the space of all \(C^1\)-smooth \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). Further, for \(T>0\) we consider linear operators \(\mathcal{A}(T)\) from \(C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) with components
We also consider the linear bounded functional \(\phi :C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2) \rightarrow \mathbb {R}\), which is defined for \(u \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) by
Because of \(u^*\) is \(C^1\)-smooth, we have \(\sup \{|\phi (u)|: u \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2), \; \Vert u\Vert _\infty \le 1\}<\infty \). Hence, although (2.31) defines the values of \(\phi \) on a dense subspace only, it really determines a linear bounded functional on \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
Lemma 2.6
Suppose (1.6), (1.7), (1.9), (1.14) and (1.16), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then the following is true:
-
(i)
\(\ker \left[ I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _uB(\beta ^0,u^0)\right] =\hbox {span}\{\partial _tu^0\}\)
-
(ii)
\(\mathop {\textrm{im}}\left[ I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _uB(\beta ^0,u^0)\right] =\ker \phi \)
-
(iii)
\(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2) =\ker \phi \oplus \hbox {span}\{D(1,\beta ^0)\partial _tu^0\}.\)
Proof
-
(i)
In the proof of Lemma 2.4 we showed that, if (1.6), (1.7) and (1.9) and one of the conditions (1.11) and (1.12) are satisfied, then for any \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) the element \( \left[ (I-C(1,\beta ^0)R)^{-1}D(1,\beta ^0)\partial _uB(\beta ^0,u^0)\right] ^2u \) is \(C^1\)-smooth. Especially, any solution \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to
$$\begin{aligned} u-C(1,\beta (u^0))Ru =D(1,\beta ^0)\partial _u B(\beta ^0,u^0)u, \end{aligned}$$(2.32)is \(C^1\)-smooth. Therefore, Lemma 2.1 (with \(\varepsilon =0\), \(T=1\), \(\beta =\beta ^0\) and \(B(\beta ,u)\) replaced by \(\partial _uB(\beta (u^0),u^0)u\)) yields that any solution to (2.32) is a solution to (1.13), and vice versa. Hence, assumption (1.14) yields assertion (i) of the lemma.
-
(ii)
In Lemma 2.1 (with \(\varepsilon =0\) and with \(\beta \) and \(B(\beta ,u)\) replaced by \(\beta ^0\) and \(\partial _u(\beta ^0,u^0)\), respectively) we have shown that
$$\begin{aligned} \mathcal{A}(T)C(T,\beta ^0)Ru= \mathcal{A}(T)D(T,\beta ^0)u-u=0 \end{aligned}$$(2.33)for all \(T>0\) and \(u \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). Therefore,

for all \(u \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). Here, along with the integration by parts, we used the definition (1.10) of the coefficients \(b_{j}\), the definitions (2.2) and (2.30) of the operators \(B_j\) and \(\mathcal{A}_j(T)\), the properties (2.25) of the operators \(B^0_j=\partial _uB_j(\beta ^0,u^0)\) and (2.33) of \(\mathcal{A}_j(T)\) and the fact that \(u^*\) is a solution to (1.15). If we write \(v:=(I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _u(\beta ^0,u^0))u\), then \(v_1(t,0)= u_1(t,0)-r_1u_2(t,0)\) and \(v_2(t,1)=u_2(t,1)-r_2u_1(t,1)\), and we get

Therefore, \(\phi ((I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _u(\beta ^0,u^0))u)=0\) for all \(u \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) and, hence, for all \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). In other words,
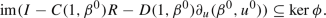
On the other side, it follows from Lemma 2.4 and from assertion (i) that

Hence, for proving assertion (ii), it remains to show that \(\mathop {\textrm{codim}}\ker \phi =1\), i.e. that \(\phi \not =0\). In order to show this, we do the following calculations: Let \(v^0:=D(1,\beta ^0)\partial _tu^0\). Then \(v^0_1(t,0)=v^0_2(t,1)=0\) [cf. (2.33)] and \(\mathcal{A}v^0=\partial _tu^0\). Hence,
$$\begin{aligned} \phi (D(1,\beta ^0)\partial _tu^0) =\int _0^1\int _0^1 (\partial _tu^0_1u_1^*+\partial _tu_2^0u_2^*)\,dtdx=1. \end{aligned}$$(2.34)Here we used assumption (1.16). Finally, assertion (iii) follows from (2.34). \(\square \)
Remark 2.7
It follows from (2.34) that the projection, corresponding to the algebraic sum in assertion (iii) of Lemma 2.6, is \(Pu:=\phi (u)D(1,\beta ^0)\partial _tu^0\), i.e.
2.5 Additional Regularity of \(u^0\)
In this subsection we will show that, if conditions (1.6), (1.7) and (1.9) and one of the conditions (1.11) and (1.12) are satisfied, then not only the first partial derivatives \(\partial _tu^0\) and \(\partial _xu^0\) exist and are continuous (this is by assumption (1.9)), but also the second partial derivative \(\partial _t^2u^0\) exists and is continuous. For that we use Theorem 4.1.
Let us introduce the setting of Theorem 4.1 as follows: The Banach space U is the function space \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) with its norm \(\Vert \cdot \Vert _\infty \). The map \(\mathcal{F}:U \rightarrow U\) is defined by
where
The element \(u^0 \in U\) in Theorem 4.1 is our function \(u^0 \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) from assumption (1.9). Because of (1.9) and of Lemma 2.1 we have \(\mathcal{F}(u^0)=0\).
The Lie group \(\Gamma \) is the rotation group \(\textrm{SO}(2)=S^1=\{e^{2\pi i \varphi }: \varphi \in \mathbb {R}\}\), and the representation is \(S_\varphi \) defined by (1.18). It is easy to verify that
Therefore, we have \(S_\varphi \mathcal{F}(u)=\mathcal{F}(S_\varphi u)\) for all \(u \in U\).
In order to state a formula for \(\mathcal{F}'(u)\), one has to use the definition of the map \(\mathcal{F}\) and the chain rule. But, if u is a solution to the equation \(\mathcal{F}(u)=0\), then the formula for \(\mathcal{F}'(u)\) is surprisingly simple. Indeed, from (2.11) it follows that,
In particular, \(\mathcal{F}'(u^0)= I-C(1,\beta ^0)R -D(1,\beta ^0)\partial _u B(\beta ^0,u^0)\). Here we used that \(\beta (u^0)=\beta ^0\) (cf. (2.14)). Hence, Lemma 2.4 claims that \(\mathcal{F}'(u^0)\) is Fredholm of index zero from U into U. Because the map \(\mathcal{F}\) is \(C^2\)-smooth, Theorem 4.1 yields also that the map \(\varphi \in \mathbb {R}\mapsto S_\varphi u^0\in U\) is \(C^2\)-smooth, i.e. \(\partial _t^2u^0\) exists and belongs to \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
Remark 2.8
The following example shows that, if (1.6), (1.7) and (1.9) are satisfied but neither (1.11) nor (1.12), then it may happen that \(\partial _t^2u^0\) does not exist. We take \(a_1(x)\equiv 1\), \(a_2(x)\equiv -1\), \(b_j(x,u)\equiv 0\), \(r_1=r_2=1\) and
where \(\Psi \in C^1(\mathbb {R}){\setminus } C^2(\mathbb {R})\) is 1-periodic.
2.6 Ansatz for the Unknown Function u
Using Theorem 4.2, in this section we introduce new coordinates close to the orbit
of \(u^0\). We introduce the setting of Theorem 4.2 as follows: The Banach space U is again \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) with its norm \(\Vert \cdot \Vert _\infty \). The Lie group \(\Gamma \) is the rotation group \(SO(2)=S^1=\{e^{2\pi i \varphi }: \varphi \in \mathbb {R}\}\), with the representation \(S_\varphi \) defined in (1.18). Hence, the tangential space to \(\mathcal{O}(u^0)\) at the point \(u^0\) is (cf. Lemma 2.6(i))
We define
Then V is a closed subspace in \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), and assumption (1.16) yields that
Hence, Theorem 4.2 implies that there exists an open neighborhood \(\mathcal{V}_0 \subset V\) of zero such that \(\{S_\gamma (u^0+v)\in U: \gamma \in \Gamma , \; v \in \mathcal{V}_0\}\) is an open neighborhood of \(\mathcal{O}(u^0)\).
Since Theorems 1.5 and 1.6 are about solutions to (1.5) such that \(u\approx \mathcal{O}(u^0)\) in the sense of \(\Vert \cdot \Vert _\infty \), we are allowed to make the following ansatz in (2.10):
Moreover, in what follows we choose the artificial \(\beta \) in (2.10) depending on the new state parameter \(\varphi \) as [cf. notion (2.14)]
We insert (2.41) and (2.42) into (2.10), apply \(S_{\varphi }^{-1}\) on the resulting equation, use (2.36) and get
Because of \(u^0=C(1,\beta ^0)Ru^0 +D(1,\beta ^0)(B(\beta ^0,u^0)\) and the Taylor formulas
this is equivalent to
Here we use the notion \(S_\varphi \) also for the shift operators on the space \(C_{per}(\mathbb {R};\mathbb {R}^2)\), i.e. \([S_\varphi ^{-1}g](t):=g(t-\varphi )\) for \(\varphi \in \mathbb {R}\) and \(g \in C_{per}(\mathbb {R};\mathbb {R}^2)\).
The notions \(\partial _TC(1+s(T-1),\beta ^0)Ru^0\) and \(\partial _TD(1+s(T-1),\beta ^0)B(\beta ^0,u^0)\) in (2.43) have to be used with some care: The map \(T\mapsto C(T,\beta )\) is not continuous from \((0,\infty )\) into \(\mathcal{L}\left( C_{per}(\mathbb {R};\mathbb {R}^2);C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\right) \) (in the sense of the uniform operator norm). But the map \(T\mapsto C(T,\beta )w\) is \(C^1\)-smooth from \((0,\infty )\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) if \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) and \(w \in C_{per}(\mathbb {R};\mathbb {R}^2)\) are both \(C^1\)-smooth. This follows from the definitions (2.3) and (2.8), which lead, for example, for the first component, to
In particular, \(\beta ^0\) and \(u^0\) are \(C^1\)-smooth, hence the limit
exists in \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), and this is what we denote by \(\partial _TC(T,\beta ^0)Ru^0\), for the sake of shortness (and similarly for \(\partial _TD(T,\beta ^0)B(\beta ^0,u^0)\)).
We end up with the following: Solutions u to (1.5) with \(u\approx \mathcal{O}(u^0)\) in the sense of \(\Vert \cdot \Vert _\infty \) and with (2.41) are solutions to (2.43) and vice versa.
Remark 2.9
If the minimal time-period of \(u^0\) is 1/n with \(n \in N\), then any solution \((\varphi ,v)\) to (2.43) also \((\varphi +1/n,v)\), \((\varphi +2/n,v)\) etc. are solutions to (2.43), but as solutions to (1.5) via (2.41) they are not different.
If the minimal time-period of the forcings f and g is 1/m with \(m \in N\), \(m>1\), then again along with any solution \((\varphi ,v)\) to (2.43) also \((\varphi +1/m,v)\), \((\varphi +2/m,v)\) etc. are solutions to (2.43), and as solutions to (1.5) via (2.41) these solutions now are various, in general.
2.7 A Priori Estimate
In this subsection we prove the following statement.
Lemma 2.10
Suppose (1.6), (1.7), (1.9), (1.14), (1.16), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then there exist \(\varepsilon _0>0\) and \(c>0\) such that for all solutions \((\varphi ,v) \in \mathbb {R}\times V\) to (2.43) with \(\varepsilon +|T-1|+\Vert v\Vert _\infty \le \varepsilon _0\) we have
Proof
Suppose the contrary. Then there exists a sequence \((\varepsilon _k,T_k,\varphi _k,v_k) \in (0,\infty ) \times \mathbb {R}^2\times V\), \(k \in \mathbb {N}\), of solutions to (2.43) such that
Without loss of generality, we may assume that \(\varphi _k \in [0,1]\) for all k. Hence, we may assume (by choosing an appropriate subsequence) that there exists \(\varphi _0\) such that
Similarly, without loss of generality we may assume that there exists \(\tau _0\) such that
If we divide equation (2.43) by \(|T_k-1|+\Vert v_k\Vert _\infty \) and set \(w_k:=v_k/(|T_k-1|+\Vert v_k\Vert _\infty )\), then we get
Hence, for \(k \rightarrow \infty \) we get the convergence
in \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). From Lemma 2.3 it follows that
Multiplying by \(I+(I-C(T_k,\beta ^0))^{-1}D(T_k,\beta ^0)\partial _uB(\beta ^0,u^0)\), we get that also
Here we used that \(\Vert (I-C(T_k,\beta ^0))^{-1}u\Vert _\infty \le \hbox {const}\Vert u\Vert _\infty \) (cf. Lemma 2.3) and (2.12).
But for any k the operators \(((I-C(T_k,\beta ^0))^{-1}D(T_k,\beta ^0)\partial _uB(\beta ^0,u^0))^2\) are compact in \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) (cf. the proof of Lemma 2.4). Therefore, there exists a subsequence \(w^1_1,w^1_2,\ldots \) of the sequence \(w_1,w_2,\ldots \) such that
Similarly, there exists a subsequence \(w^2_1,w^2_2,\ldots \) of the sequence \(w^1_1,w^1_2,\ldots \) such that
Proceeding this way and taking the “diagonal” subsequence \(w^1_1,w^2_2,\ldots \), which is also a subsequence of \(w_1,w_2,\ldots \), we get that
Hence, (2.44) yields that without loss of generality we may assume that there exists \(w_0 \in V\) such that \(\Vert w_k-w_0\Vert _\infty \rightarrow 0\), and, hence, \(\Vert C(T_k,\beta ^0)Rw_k-C(1,\beta ^0)Rw_0\Vert _\infty \rightarrow 0\) and \(\Vert D(T_k,\beta ^0)\partial _uB(\beta ^0,u^0)w_k-D_k(1,\beta ^0)\partial _uB(\beta ^0,u^0)w_0\Vert _\infty \rightarrow 0\) for \(k \rightarrow \infty \) [cf. (2.13)]. It follows that
but
If we apply the functional \(\phi \) to both sides of (2.45), then Lemma 2.6 (ii) implies that
In order to calculate \(\phi \left[ \partial _TC(1,\beta ^0)Ru^0 +\partial _TD(1,\beta ^0)B(\beta ^0,u^0)\right] \), we proceed as follows: The definitions (2.2) and (2.7)–(2.9) yield that \( [C_1(T,\beta ^0)Ru^0 +D_1(T,\beta ^0)B(\beta ^0,u^0)](t,0)=r_2u^0_2(t,0). \) Hence, we have \([\partial _TC_1(1,\beta ^0)Ru^0 +\partial _TD_1(1,\beta ^0)B(\beta ^0,u^0)](t,0)=0\). Similarly one shows that \([\partial _TC_2(1,\beta ^0)Ru^0 +\partial _TD_2(1,\beta ^0)B(\beta ^0,u^0)](t,1)=0\). Therefore,
On the other hand, the identity (2.33) implies
for all \(u \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) such that \(\partial _t^2u\) exist and is continuous. Therefore,
But (2.11) implies that
hence
Here we used assumption (1.16).
From (2.47) and (2.48) it follows that \(\tau _0=0\), and, therefore, (2.45) implies that \([I-C(1,\beta ^0)R-D(1,\beta ^0)\partial _uB(\beta ^0,u^0)]w_0=0\). Hence, (2.38) yields \(w_0 \in T_{u^0}\mathcal{O}(u^0)\). But \(v \in V\), hence (2.40) yields \(v=0\), which contradicts to (2.46). \(\square \)
2.8 Proof of Theorem 1.5
Theorems 1.5 and 1.6 concern solutions \((\varepsilon ,T,u) \in (0,\infty )^2\times C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to (1.5) with \(\varepsilon \approx 0\) and \(T\approx 1\) and \(u \approx \mathcal{O}(u^0)\), i.e. solutions \((\varepsilon ,T,\varphi ,v) \in (0,\infty )^2\times [0,1]\times V\) to (2.43) with \(\varepsilon \approx 0\), \(T\approx 1\) and \(v \approx 0\). Hence, in order to prove Theorems 1.5 and 1.6, Lemma 2.10 allows to make the following ansatz in (2.43):
Inserting (2.49) into (2.43) and dividing by \(\varepsilon \), we get the following equation:
In particular, for \(\varepsilon =0\) we have
Because of Lemma 2.6(ii), this equation is equivalent to the two equations \(PF(0,\tau ,\varphi ,w)=0\) and \((I-P)F(0,\tau ,\varphi ,w)=0\), and because of (2.48), the first equation is equivalent to the scalar equation
In order to determine \(\phi (C(1,\beta ^0)S_\varphi ^{-1}g+D(1,\beta ^0)S_\varphi ^{-1}f)\), we calculate as above. We have
Therefore,
i.e. (cf. (1.17))
Hence, Eq. (2.52) is just the phase equation \(\Phi (\varphi )=\tau \).
In order to prove Theorem 1.5, we fix \((\tau ,\varphi )=(\tau _0,\varphi _0)\) to be a solution to the phase Eq. (2.52), and insert it into \((I-P)F(0,\tau ,\varphi ,w)=0\). This way we get
This equation has a unique solution \(w=w_0 \in V\). Indeed, the linear operator \(I-C(1,\beta ^0)-D(1,\beta ^0)\partial _uB(\beta ^0,u^0)\) is injective on V because of (2.38) and (2.40), and it is surjective from V onto \(\mathop {\textrm{im}}P\), again because of (2.38) and (2.40).
Let us summarize: Eq. (2.50) has a solution \(\varepsilon =0\), \(\tau =\tau _0\), \(\varphi =\varphi _0\), \(w=w_0\), and we are going to solve (2.50) for \(\varepsilon \approx 0\), \(\tau \approx \tau _0\), \(\varphi \approx \varphi _0\) and \(w\approx w_0\) by means of Theorem 5.1. To this end, we put (2.50) into the setting of Theorem 5.1. The Banach spaces \(U_1\) and \(U_2\) are \(U_1=\mathbb {R}\times V\) and \(U_2=C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) with norms \(\Vert (\varphi ,w)\Vert _1=|\varphi |+\Vert w\Vert _\infty \) and \(\Vert \cdot \Vert _2=\Vert \cdot \Vert _\infty \), respectively. The vector space \(\Lambda =\mathbb {R}^2\) is normed by \(\Vert (\varepsilon ,\tau )\Vert _2=|\varepsilon |+|\tau |\). The map \(\mathcal{F}\) from Theorem 5.1 is just the map F , which is defined in (2.50). The control parameter is \((\varepsilon ,\tau )\), and the state parameter is \((\varphi ,w)\). The starting solution \((\lambda _0,u_0)\) is \((0,\tau _0,\varepsilon _0,w_0)\), i.e. we are going to solve the equation \(F(\varepsilon ,\tau ,\varphi ,w)=0\) with \((\varepsilon ,\tau )\approx (0,\tau _0)\) with respect to \((\varphi ,w)\approx (\varphi _0,w_0)\).
It is easy to verify that conditions (5.1) and (5.2) of Theorem 5.1 are satisfied. In order to verify the remaining conditions (5.3)–(5.5), we calculate the partial derivatives
and
Here we used that \(\partial _\varphi [S_\varphi ^{-1}g](t)= \partial _\varphi g(t-\varphi )=-g'(t-\varphi )=-[S_\varphi ^{-1}g'](t)\) and similarly for \(\partial ^2_\varphi [S_\varphi ^{-1}g]\), \(\partial _\varphi [S_\varphi ^{-1}f]\) and \(\partial ^2_\varphi [S_\varphi ^{-1}f]\). Using these formulas, it is easy to verify that the assumption (5.5) of Theorem 5.1 is satisfied.
It remains to verify conditions (5.3) and (5.4) of Theorem 5.1. Both these assumptions concern the operators
with \((\varepsilon ,\tau )\approx (0,\tau _0)\). In order to prove, that these conditions are satisfied for all \((\varepsilon ,\tau )\approx (0,\tau _0)\), unfortunately, it is not sufficient to prove that these assumptions are satisfied for \(\varepsilon =0\) and \(\tau =\tau _0\). The reason for that is that the operator \(\partial _{w}F(\varepsilon ,\tau ,\varphi _0,w_0)\) does not depend continuously (with respect to the uniform operator norm) on \(\varepsilon \) and \(\tau \).
First, let us verify condition (5.4) of Theorem 5.1.
Lemma 2.11
Suppose (1.6), (1.7), (1.9), (1.14), (1.16), (1.19), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then there exist \(\varepsilon _0>0\) and \(c>0\) such that for all \((\varepsilon ,\tau ,\varphi ,w) \in [0,\infty )\times \mathbb {R}^2 \times V\) with \( \varepsilon +|\tau -\tau _0| \le \varepsilon _0 \) we have
Proof
We proceed as in the proof of Lemma 2.10. Suppose the contrary. Then there exists a sequence \((\varepsilon _k,\tau _k,\varphi _k,w_k) \in (0,\infty ) \times \mathbb {R}^2\times V\), \(k \in \mathbb {N}\), with \(|\varphi _k|+\Vert w_k\Vert _\infty =1\) for all k, but
Without loss of generality we may assume that there exists \(\varphi _*\) such that \(\varphi _k \rightarrow \varphi _*\) and, hence,
Then (2.56) yields that \(\partial _wF(\varepsilon _k,\tau _k,\varphi _0,w_0)w_k\) converges in \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), and (2.12) and (2.54) imply that
As in the proof of Lemma 2.10, by using a “diagonal” subsequence, without loss of generality we may assume that there exists \(w_* \in V\) such that \(\Vert w_k-w_*\Vert _\infty \rightarrow 0\) for \(k \rightarrow \infty \). Hence, (2.54), (2.55) and (2.56) imply that
but
We apply the functional \(\phi \) (cf. (2.31)) to (2.57) and use (2.53) in order to get \(\varphi _* \Phi '(\varphi _0)=0\), i.e. \(\varphi _*=0\), i.e. \( (I-C(1,\beta ^0)-D(1,\beta ^0) \partial _u B(\beta ^0,u^0))w_*=0. \) But the operator \(I-C(1,\beta ^0)-D(1,\beta ^0) \partial _u B(\beta ^0,u^0)\) is injective on V, hence \(w_*=0\). This way we get a contradiction to condition (2.58). \(\square \)
Finally, let us verify condition (5.3) of Theorem 5.1, i.e. the condition that for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\) the operator \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _0,w_0)\) is Fredholm of index zero from \(\mathbb {R}\times V\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). Because of Lemma 2.11, this is equivalent to the condition that for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\) the operator \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _0,w_0)\) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
Lemma 2.12
Suppose (1.6)–(1.9), (1.14), (1.16), (1.19), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then there exists \(\varepsilon _0>0\) such that, for all \((\varepsilon ,\tau ) \in [0,\infty )\times \mathbb {R}\) with \( \varepsilon +|\tau -\tau _0| \le \varepsilon _0, \) the operator \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _0,w_0)\) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
Proof
We have \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _0,w_0)(\varphi ,w)= I_{\varepsilon ,\tau }(\varphi ,w)+\varepsilon J_{\varepsilon ,\tau }w \) with linear operators \(I_{\varepsilon ,\tau }\) and \(J_{\varepsilon ,\tau }\) defined by
and
Further, for all \(\varepsilon \in [0,1]\), \(\tau \in (-1,1)\) and \(w \in V\) we have \(\Vert J_{\varepsilon ,\tau }w\Vert _\infty \le \,\)const \(\Vert w\Vert _\infty \), where the constant does not depend on \(\varepsilon \), \(\tau \) and w. Hence, Lemma 2.11 yields that
for \(\varepsilon \approx 0\), \(\tau \approx \tau _0\), \(\varphi \in \mathbb {R}\) and \(w \in V\), where the constant is positive and does not depend on \(\varepsilon \), \(\tau \), \(\varphi \) and w. Below we will show that
Then (2.59) yields that for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\) the operator \(I_{\varepsilon ,\tau }\) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), and \(\Vert I_{\varepsilon ,\tau }^{-1}u\Vert _\infty \le \hbox {const}\,\Vert u\Vert _\infty \), where the constant does not depend on \(\varepsilon \), \(\tau \) and u. Hence, the operator \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _0,w_0) =I_{\varepsilon ,\tau }+\varepsilon J_{\varepsilon ,\tau }\) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) if the operator \(I+\varepsilon I_{\varepsilon ,\tau }^{-1}J_{\varepsilon ,\tau }\) is an isomorphism from \(\mathbb {R}\times V\) onto itself, and this is the case for small \(\varepsilon \).
It remains to prove (2.60). We proceed as in the proof of Lemma 2.4. Because of \(\varepsilon \) and \(\tau \) are fixed, in the notations below we will not mention the dependence on \(\varepsilon \) and \(\tau \), i.e. \( C:=C(1+\varepsilon \tau ;\beta ^0),\; D:=D(1+\varepsilon \tau ,\beta ^0),\; B^0:=\partial _u B(\beta ^0,u^0). \) Then
The projection corresponding to the algebraic sum (2.40) is \( Q\in \mathcal{L}(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2))\) with
The map \(u \mapsto \left( \sum _{j=1}^2\int _0^1\int _0^1u_ju_j^*\,dtdx, (I-Q)u\right) \) is an isomorphism from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) onto \(\mathbb {R}\times V\). Hence, to prove (2.60), it suffices to show that the linear map
is Fredholm of index zero from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself. Because of Lemma 2.3, it suffices to prove that the linear map
is Fredholm of index zero from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself. But the operators Q and \(u \mapsto \sum _{j=1}^2\int _0^1\int _0^1u_ju_j^*\,dtdx\; (I-CR)^{-1}(CS_{\varphi _0}^{-1}g'+ DS_{\varphi _0}^{-1}\partial _tf)\) have finite dimensional images. Finally, due to Lemma 2.3, the linear map \( u \mapsto (I-(I-CR)^{-1}DB^0)u \) is Fredholm of index zero from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself, what finishes the proof. \(\square \)
Now we can solve (2.50) for \(\varepsilon \approx 0\), \(\tau \approx \tau _0\), \(\varphi \approx \varphi _0\), \(w\approx w_0\) by means of Theorem 5.1. We get the following result:
Suppose (1.6)–(1.9), (1.14), (1.16), (1.19), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then the following is true:
There exist \(\varepsilon _0 >0\) and \(\delta >0\) such that for all \((\varepsilon ,\tau ) \in (0,\varepsilon _0) \times (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0)\) equation (2.50) has a unique solution \((\varphi ,w)=(\varphi _{\varepsilon ,\tau },w_{\varepsilon ,\tau })\) with \(|\varphi -\varphi _0|+\Vert w-w_0\Vert _\infty <\delta \). Moreover, the map \((\varepsilon ,\tau ) \mapsto (\varphi _{\varepsilon ,\tau }, w_{\varepsilon ,\tau })\) is continuous from \((0,\varepsilon _0) \times (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0)\) into \(\mathbb {R}\times V\).
Let us translate this result into the language of Theorem 1.5 via \(T=1+\varepsilon \tau \) and \(u_{\varepsilon ,T}= S_{\varphi _{\varepsilon ,\tau }}(u^0+\varepsilon w_{\varepsilon ,\tau })\). Then we have \((\varepsilon ,\tau ) \in (0,\varepsilon _0) \times (\tau _0-\varepsilon _0,\tau _0+\varepsilon _0)\) if and only if \((\varepsilon ,T) \in K(\varepsilon _0,\tau _0)\). Hence, assertions (i) and (ii) of Theorem 1.5 are satisfied if assertion (ii) of Lemma 2.1 works, i.e. if \(\partial _tu_{\varepsilon ,T}\) exists and is continuous, i.e. if \(\partial _tw_{\varepsilon ,\tau }\) exists and is continuous.
Lemma 2.13
Suppose (1.6)–(1.9), (1.14), (1.16), and assume that one of the conditions (1.11) and (1.12) is satisfied. Then, if \(\varepsilon _0\) is sufficiently small, \(\partial _tw_{\varepsilon ,\tau }\) exists and is continuous for all \(\varepsilon >0\) and \(\tau \in \mathbb {R}\) with \(\varepsilon +|\tau -\tau _0|<\varepsilon _0\).
Proof
We know that \(\varphi =\varphi _{\varepsilon ,\tau }-\psi \), \(w=S_\psi w_{\varepsilon ,\tau }\) is a solution to equation \(S_\psi F(\varepsilon ,\tau ,\varphi -\psi ,S_\psi ^{-1}w)=0\) (cf. (2.50)). But (2.36) and the definition (2.50) of F yields that
Now, the maps \(\psi \mapsto S_\psi \beta ^0\), \(\psi \mapsto S_\psi u^0\) and \(\psi \mapsto S_\psi f\) are \(C^1\)-smooth from \(\mathbb {R}\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), and similarly for \(\psi \mapsto S_\psi g\). Hence, the map \((\psi ,\varphi ,w) \mapsto \mathcal{F}(\varepsilon ,\tau ,\psi ,\varphi ,w)\) is \(C^1\)-smooth from \(\mathbb {R}^2 \times V\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
Let us consider the equation \(\mathcal{F}(\varepsilon ,\tau ,\psi ,\varphi ,w)=0\). We use the implicit function theorem not to solve it with respect to \((\varphi ,w)\approx (\varphi _{\varepsilon ,\tau },w_{\varepsilon ,\tau })\) in terms of \(\psi \approx 0\) (because the solution is known, it is \(\varphi =\varphi _{\varepsilon ,\tau }-\psi \), \(w=S_\psi w_{\varepsilon ,\tau }\)), but to get the \(C^1\)-smoothness of the data-to-solution map \(\psi \mapsto (\varphi _{\varepsilon ,\tau }-\psi ,S_\psi w_{\varepsilon ,\tau })\). This \(C^1\)-smoothness of the data-to-solution map yields that \(\partial _tw_{\varepsilon ,\tau }\) exists and is an element of the space \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\).
It remains to show that the implicit function theorem is applicable, i.e. that the linear operator \(\partial _{(\varphi ,w)}\mathcal{F}(\varepsilon ,\tau ,0,\varphi _{\varepsilon ,\tau },w_{\varepsilon ,\tau }) =\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _{\varepsilon ,\tau },w_{\varepsilon ,\tau }) \) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1]:\mathbb {R}^2)\) for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\). But the Lemmas 2.11 and 2.12 yield that for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\) the linear operator \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _{0},w_{0})\) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1]:\mathbb {R}^2)\), and the operator norm of \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _{0},w_{0})^{-1}\) is bounded uniformly with respect to \(\varepsilon \) and \(\tau \).
Let us summarize: We know that \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi _{\varepsilon ,\tau },w_{\varepsilon ,\tau })\) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1]:\mathbb {R}^2)\) if
is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1]:\mathbb {R}^2)\). But for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\) we know that \(|\varphi _{\varepsilon ,\tau }-\varepsilon _0|\approx 0\) and \(\Vert w_{\varepsilon ,\tau }-w_0\Vert _\infty \approx 0\). Moreover, the operators \(\partial _{(\varphi ,w)}F(\varepsilon ,\tau ,\varphi ,w)\) depend continuously (with respect to the operator norm) on \(\varphi \) and w, uniformly with respect to \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\). Hence,
is smaller than one for \(\varepsilon \approx 0\) and \(\tau \approx \tau _0\), i.e. for those \(\varepsilon \) and \(\tau \) the operator (2.61) is an isomorphism from \(\mathbb {R}\times V\) onto \(C_{per}(\mathbb {R}\times [0,1]:\mathbb {R}^2)\). \(\square \)
Assertion (iii) of Theorem 1.5 follows from
Assertion (iv) of Theorem 1.5 (with \(\varphi _\tau \) from there defined by \(\varphi _{0,\tau }\) from here) follows from (2.51) and (2.53) and from \(u_{\varepsilon ,1+\varepsilon \tau }-S_{\varphi _{0,\tau }}u^0= (S_{\varepsilon _{\varepsilon ,\tau }}-S_{\varepsilon _{0,\tau }})u^0+ \varepsilon w_{\varepsilon ,\tau }\rightarrow 0\) for \(\varepsilon \rightarrow 0\).
2.9 Proof of Theorem 1.6
Suppose (1.6)–(1.9), (1.14) and (1.16), and assume that at least one of the conditions (1.11) and (1.12) is satisfied. Let \((\varepsilon _k,T_k,u_k)\), \(k\in \mathbb {N}\), be a sequence of solutions to (1.5) with (1.21). Because of Lemma 2.1 this sequence is also a sequence of solutions to (2.10). Further, Lemma 2.10 yields that \(T_k=1+\varepsilon _k\tau _k\) and \(u_k=S_{\varphi _k}(u^0+\varepsilon _k w_k)\) where \(\tau _k \in \mathbb {R}\) and \(w_k \in V\) are bounded sequences. We, therefore, have (2.50), i.e. \( F(\varepsilon _k,\tau _k,\varphi _k,w_k)=0. \) In particular, (2.34), (2.53) and the definition (2.50) of the map F yield
Hence, (2.12) and (2.13) imply that \(\Phi (\varphi _k)-\tau _k \rightarrow 0\) for \(k \rightarrow \infty \).
3 Proofs for Second-Order Equations
In this section we will prove Theorems 1.7 and 1.8. We suppose that all assumptions of these theorems are satisfied.
3.1 Formal Calculations
In this subsection we show how one can find, by simple formal calculations, the formula (1.33) for the phase equation. Similar calculations could also be done in Sect. 2 in order to get the formula (1.17) in advance, without the long rigorous calculations.
We insert \(T=1+\varepsilon \tau \) and \(u=S_\varphi (u^0+ \varepsilon v)\) into (1.22), then apply \(S_{\varphi }^{-1}\) to the differential equation and the boundary conditions, and afterwards divide by \(\varepsilon \) and tend \(\varepsilon \) to zero. Using Taylor expansions like \(1/(1+\varepsilon \tau )=-\varepsilon \tau +O(\varepsilon )\) and \(1/(1+\varepsilon \tau )^2=-2\varepsilon \tau +O(\varepsilon )\) and also the differential equation and the boundary conditions satisfied by \(u^0\), i.e.
one gets
After multiplying the differential equation by \(u^*\), integrating over t and x, and using the boundary conditions for \(u^*\) and v, one ends up with
Because of (1.32) and (1.33), this is just the phase equation \(\Phi (\varphi )=\tau \).
3.2 Transformation of the Second-Order Equation Into a First-Order System
In this subsection we show that any solution u to problem (1.22) for a second-order equation creates a solution
to the following problem for a first-order system of integro-differential equations:
And vice versa. Here the nonlinear operator \(\mathcal{B}\) is defined by
with a partial integral operator J defined by
and with “pointwise” operators K and L defined by
As in Sect. 2, we denote by \(C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) the space of all \(C^1\)-smooth functions \(v:\mathbb {R}\times [0,1] \rightarrow \mathbb {R}^2\) such that \(v(t+1,x)=v(t,x)\) for all \(t \in \mathbb {R}\) and \(x \in [0,1]\). Similarly, by \(C^2_{per}(\mathbb {R}\times [0,1];\mathbb {R})\) we denote the space of all \(C^2\)-smooth functions \(u:\mathbb {R}\times [0,1] \rightarrow \mathbb {R}^2\) such that \(u(t+1,x)=u(t,x)\) for all \(t \in \mathbb {R}\) and \(x \in [0,1]\).
Lemma 3.1
For all \(\varepsilon >0\) and \(T>0\) the following is true:
-
(i)
If \(u \in C_{per}^2(\mathbb {R}\times [0,1];\mathbb {R})\) is a solution to (1.22), then the function \(v \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), which is defined by (3.1), is a solution to (3.2).
-
(ii)
Let \(v \in C_{per}^{1}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) be a solution to (3.2). Then the function u, which is defined by
$$\begin{aligned} u(t,x)=\varepsilon g_1(t)+\frac{1}{2}\int _0^x\frac{v_1(t,y)-v_2(t,y)}{a(y)}\,dy, \end{aligned}$$(3.4)is \(C^2\)-smooth and is a solution to (1.22). Moreover, if \(\partial ^2_tv\) exists and is continuous, then \(\partial _t^3u\) exists and is continuous also.
Proof
-
(i)
Let \(u \in C_{per}^2(\mathbb {R}\times [0,1];\mathbb {R}^2)\) be given, and let \(v \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) be defined by (3.1). Then
$$\begin{aligned} \partial _tu=T\frac{v_1+v_2}{2}=Kv,\; \partial _xu=\frac{v_1-v_2}{2a}=L v \end{aligned}$$(3.5)and \(\partial _tv_1=\partial ^2_tu/T+a\partial _t\partial _xu\), \(\partial _xv_1=\partial _t\partial _xu/T+a' \partial _xu + a\partial _x^2u\), \(\partial _tv_2=\partial ^2_tu/T-a\partial _t\partial _xu\) and \(\partial _xv_2=\partial _t\partial _xu/T-a' \partial _xu - a\partial _x^2u\). Hence
$$\begin{aligned} \frac{1}{T^2}\partial _t^2u-a^2\partial _x^2u-aa'\partial _xu= \frac{1}{T} \partial _tv_1-a\partial _xv_1= \frac{1}{T} \partial _tv_2+a\partial _xv_2. \end{aligned}$$(3.6)Further, let u be a solution to problem (1.22). Then (3.5) and the boundary conditions \(u(t,0)=\varepsilon g_1(t)\) and \(\partial _xu(t,1)+\gamma u(t,1)=\varepsilon g_2(t)\) imply that \(v_1(t,0)+v_2(t,0)=2\varepsilon g'_1(t)/T\) and \(v_1(t,1)-v_2(t,1)+\gamma a(1) [Lv](t,1)=2\varepsilon a(1)g_2(t)\), i.e. the boundary conditions of (3.2). Moreover, from \(u(t,0)=\varepsilon g_1(t)\) and (3.5) it follows that \(u(t,x)=\varepsilon g_1(t)+[Jv](t,x)\). Hence, (3.5), (3.6) and the differential equation in (1.22) yield the differential equations in (3.2).
-
(ii)
Let \(v \in C_{per}^{1}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) be a solution to (3.2), and let \(u \in C_{per}^{1}(\mathbb {R}\times [0,1];\mathbb {R})\) be defined by (3.4). Then
$$\begin{aligned} \partial _tu(t,x)= & {} \varepsilon g_1'(t)+\frac{1}{2}\int _0^x\frac{\partial _tv_1(t,y)-\partial _tv_2(t,y)}{a(y)}\,dy\\= & {} \varepsilon g_1'(t)+\frac{T}{2} \int _0^x(\partial _xv_1(t,y)+\partial _xv_2(t,y)\,dy= \frac{T}{2} (v_1(t,x)+v_2(t,x)). \end{aligned}$$Here we used the first boundary condition and the differential equations in (3.2). It follows that \(\partial _tu\) is \(C^{1}\)-smooth, and
$$\begin{aligned} \partial ^2_tu=\frac{T}{2}(\partial _tv_1+\partial _tv_2). \end{aligned}$$(3.7)Further, (3.4) yields that \(\partial _xu=\partial _x Jv=L v\), i.e. \(\partial _xu\) is \(C^{1}\)-smooth also, i.e. u is \(C^{2}\)-smooth, and \(2(a'\partial _xu+a\partial _x^2u)=\partial _xv_1-\partial _xv_2\), i.e.
$$\begin{aligned} a^2\partial ^2_xu=\frac{a}{2}(\partial _xv_1-\partial _xv_2)-\frac{a'}{2}(v_1-v_2). \end{aligned}$$(3.8)But (3.2), (3.7) and (3.8) imply the differential equation in (1.22).
The first boundary condition in (1.22) follows from (3.4), and the second boundary conditions in (3.2) follows from \(\partial _xu=Kv\) and from the second boundary condition in (3.2).
Finally, suppose that \(\partial ^2_tv\) exists and is continuous. Then (3.7) yields that also \(\partial _t^3u\) exists and is continuous. \(\square \)
Unfortunately, we cannot apply Theorems 1.5 and 1.6 directly to system (3.2) because of the two small differences between (3.2) and (1.5): First, there is an \(\varepsilon \)-dependence in the nonlinearity \(B(\varepsilon ,v)\) which leads to an additional (in comparison with (1.17)) term in the formula for the function \(\Phi \). Second, the equations and one boundary condition in (3.2) are nonlocal. Therefore, we have to check again whether the linearization of (3.2) creates a Fredholm operator of index zero.
Hence, we adapt the content of Sect. 2 to the situation of system (3.2).
3.3 Fredholmness
As in Sect. 2, we introduce artificial terms \(\beta _j(t,x)v_j(t,x)\) with some \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) and rewrite (3.2) as
where
Similar to Sect. 2.1, system (3.2) of integro-differential equations is equivalent to a system of partial integral equations. In order to state this more precisely, for \(j=1,2\), \(t \in \mathbb {R}\), \(x,y \in [0,1]\), \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) and \(T>0\), we write
where the function \(\alpha \) is defined in (1.25). The system of partial integral equations is (for \((t,x) \in \mathbb {R}\times [0,1]\))
and, as in Sect. 2.1, one can prove the following statement.
Lemma 3.2
For all \(\varepsilon >0\), \(\beta \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) and \(T>0\) the following is true:
- (i)
-
(ii)
If \(v \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) is a solution to (3.11) and if the partial derivatives \(\partial _tv\) and \(\partial _t\beta \) exist and are continuous, then v is \(C^1\)-smooth and v is a solution to (3.9).
Further, as in Sect. 2.1, we write system (3.11) in an abstract form. For that we introduce linear operators
and functions \(\tilde{f}:\mathbb {R}\times [0,1]\rightarrow \mathbb {R}^2\) and \(\tilde{g}:\mathbb {R}\rightarrow \mathbb {R}^2\) and by
Then problem (2.4) can be written analogously to (2.10) as
In what follows we will work with the solution \(v^0 \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to (3.2) with \(\varepsilon =0\) and \(T=1\), which corresponds to the solution \(u^0\) to (1.22) with \(\varepsilon =0\) and \(T=1\) via (3.1), i.e.
In order to calculate the linearization with respect to v in \(\varepsilon =0\) and \(v=v^0\) of the operator \(\mathcal{B}\) (cf. (3.3)), we use the notation (1.25). We have
with coefficients \(\beta ^0_j\) defined in (1.26). From (3.10) it follows that
Hence, the linearization with respect to v in \(\varepsilon =0\), \(\beta =\beta ^0\) and \(v=v^0\) of the nonlinearity B has a special structure: It is the sum of a partial integral operator and of a “pointwise” operator, which has vanishing diagonal part.
Lemma 3.3
For all \(T\approx 1\) the operator \(I-C(\beta ^0,T)R-D(\beta ^0,T)\partial _vB(0,\beta ^0,v^0) +E(\beta ^0,T)\) is Fredholm of index zero from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself.
Proof
The conditions (1.11) and (1.12) with \(a_1=-a\), \(a_2=a\), \(r_1=-1\) and \(r_2=1\) are just the conditions (1.27) and (1.28). Hence, Lemma 2.3 yields that for \(T \approx 1\) the operator \(I-C(\beta ^0,T)R\) is an isomorphism from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) onto itself, and \((I-C(\beta ^0,T)R)^{-1}\) is bounded uniformly with respect to \(T \approx 1\). Therefore, we can proceed as in the proof of Lemma 2.4.
Because of the Fredholmness criterion of Nikolskii, it suffices to show that the operator \( \left( (I-C(\beta ^0,T)R)^{-1}( D(\beta ^0,T)\partial _vB(0,\beta ^0,v^0) +E(\beta ^0,T))\right) ^2 \) is compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself. Further, because of (3.14), we have
In what follows, we will not mention the dependence of the operators and the coefficient functions on \(\beta ^0\) and T. As in the proof of Lemma 2.4 (cf. (2.24)), it suffices to show that the operators
and
are compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself. Since in the proof of Lemma 2.4 we already showed that the operators \(DB^0D\) and \(DB^0CR\) are compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) to itself, it suffices to show that the operators
are compact from \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into itself.
Let us start with \(D\mathcal{J}\). The first component of this operator works as follows:
In the inner integral we change the integration variable y by \(\eta =\widehat{\eta }(t,y,z):=t-\alpha (y,z)/T\), hence \(d\eta =\frac{dy}{Ta(y)}\). If \(y=\widehat{y}(t,\eta ,z)\) is the inverse transformation, then we get
Now one can see that, for all \(v \in C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\), the function \(D_1\mathcal{J}v\) is \(C^1\)-smooth, and similarly for the second component \(D_2\mathcal{J}v\). Moreover, we have
Hence the Arzela–Ascoli Theorem yields the needed result.
Now, let us consider \(DB^0E\). Because of \(E_1=0\), we have \(B_2^0E=0\) and, hence, \(D_2(T)B_2^0E=0\). The first component \(D_1B^0E\) works as
where
In the inner integral we change the integration variable y to \(\eta =t-(\alpha (x,y)-\alpha (y,1))/T\), and further proceed as above.
Next we consider ED. Since \(E_1=0\), we are reduced to deal with the second component \(E_2D\), which works as
where \(d_1\) and \(d_2\) are certain smooth functions, which do not depend on v. In the first inner integral we change the integration variable y to \(\eta =t-(\alpha (x,1)-\alpha (y,z))/T\), and in the second inner integral to \(\eta =t-(\alpha (x,1)+\alpha (y,z))/T\). Afterwards, we can proceed as above.
Now, let us consider \(E^2\). Because of \(E_1=0\) we have to consider the second component \(E_2E\), which works as
with a smooth function d, which does not depend on v. In the inner integral we change the integration variable y to \(\eta =t+(\alpha (x,1)+\alpha (y,1))/T\), and we again can proceed as above.
Finally, let us consider the last operator in (3.15), which is ECR. The second component works as
with smooth functions \(d_1\) and \(d_2\), which do not depend on v. In both integrals we change the integration variable y by \(\eta =t+(\alpha (x,1)-\alpha (y,0))/T\), and we can proceed as above. \(\square \)
Now, as in Sect. 2.5, one can show that the solution \(v^0\) to the autonomous nonlinear problem (3.2) with \(\varepsilon =0\) and \(T=1\) has additional regularity, i.e. additionally to the \(C^1\)-smoothness of \(v^0\) the second derivative \(\partial ^2_tv^0\) exists and is continuous. Hence, Lemma 3.1(ii) yields, that also the solution \(u^0\) to the autonomous nonlinear problem (1.22) with \(\varepsilon =0\) and \(T=1\) has additional regularity, namely that \(\partial _t^3u^0\) exists and is continuous.
Remark 3.4
The following example shows that, if (1.24) is satisfied but neither (1.27) nor (1.28) is satisfied, then it may happen that \(\partial _t^3u^0\) does not exist. We take \(a(x)\equiv 4\), \(b(x,u,v,w)\equiv 0\), \(\gamma =0\) and
where \(\Psi \in C^1(\mathbb {R}){\setminus } C^2(\mathbb {R})\) satisfies \(\Psi (t+2)=-\Psi (t)\) for all \(t \in \mathbb {R}\). Then
Hence, \(\partial ^2_tu^0(t,x)=2(\Psi '(4t+x)-\Psi '(4t-x))\) is not differentiable with respect to t. On the other hand,
i.e. \(\partial ^2_tu^0(t,x)=16\partial _x^2u^0(t,x)\) and \(u^0(t,0)=\partial _xu^0(t,1)=0\).
3.4 Proofs of Theorems 1.7 and 1.8
Analogously to Lemma 2.6 one can prove that
where the functional \(\phi \) is defined analogously to (2.31) by
for \(v \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\). The operator \(\mathcal{A}\) from \(C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) into \(C_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) is defined analogously to (2.30) by
Moreover, \(v^* \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) is the solution to the linear homogeneous problem
with normalization
The following calculation shows that (3.17) is the adjoint problem to the linearization of (3.2) with respect to v in \(\varepsilon =0\), \(T=1\) and \(v=v^0\): For all \(v,w \in C^1_{per}(\mathbb {R}\times [0,1];\mathbb {R}^2)\) with \(v_1(t,0)+v_2(t,0)=0\) and \(v_1(t,1)-v_2(t,1) +\gamma a(1)\int _0^1(v_1(t,y)-v_2(t,y))/a(y)\,dy=0\) we have
Lemma 3.5
We have \(v_1^*=(u^*-\tilde{u})/2\) and \(v_2^*=(u^*+\tilde{u})/2\) with
Proof
Let us show that the functions \(v_1:=(u^*-\tilde{u})/2\) and \(v_2:=(u^*+\tilde{u})/2\) satisfy (3.17) and (3.18).
We have \(v_1(t,0)+v_2(t,0)=u^*(t,0)=0\) because of the boundary condition of \(u^*\) at \(x=0\) (cf. (1.31)). Moreover, we have \(v_1(t,1)-v_2(t,1)=\tilde{u}(t,1)=0\) because of (3.19).
Now, to verify that the integro-differential equations in (3.17) are satisfied, we have to show that
This is satisfied if and only if the sum and the difference of these two equations are satisfied, i.e.
Equation (3.20) is satisfied because of \(\beta _1+\beta _2=b_3\) (cf. (1.26)) and (3.19).
In order to verify equation (3.21), we use the definition (3.19) of \(\tilde{u}\) and the fact that \(u^*\) satisfies (1.31). It follows that
Since \(\beta _1-\beta _2=a'+b_4/a\) (cf. (1.26)) this is just Eq. (3.21).
Finally, let us verify the normalization condition (3.18). Using normalization condition (1.32), definition (3.13) of \(v^0\), Eq. (3.20) and the boundary conditions \(u^0(t,0)=\tilde{u}(t,1)=0\), we get
\(\square \)
Now we proceed as in Sect. 2.6. We make the following ansatz in (3.12):
Inserting this into (3.12), applying \(S_\varphi ^{-1}\), dividing by \(\varepsilon \) and tending \(\varepsilon \) to zero, we get
This is an analogue of (2.51), with one additional term \(D(\beta ^0,1)\partial _\varepsilon B(0,\beta ^0,v^0))\). As in Sect. 2, we have
and \(\phi (\partial _TC(\beta _0,1)Rv^0 +\partial _TD(\beta _0,1) B(0,\beta _0,v^0))=1\) [cf. (2.48)]. Hence,
In order to prove Theorem 1.7, it remains to show that this is the phase equation, i.e. that
To prove (3.24), let \(h_j:=C_j(\beta _0,1)S_\varphi ^{-1}\tilde{g}+ D_j(\beta _0,1)(\partial _\varepsilon B(0,\beta _0,v^0) +S_\varphi ^{-1}\tilde{f})\) for \(j=1,2\). Then (3.16) yields

Since \(\tilde{f}_j=f\) for \(j=1,2\), then, due to (3.3) and (3.10), \(\partial _\varepsilon B_j(0,\beta _0,v^0)](t,x)=-b_2(t,x)g_1(t-\varphi )\). Hence, (3.19) implies the equality
Moreover, \(h_1(t,0)=\tilde{g}_1(t-\varphi )=2g_1'(t-\varphi )\), \(h_2(t,1)=\tilde{g}_2(t-\varphi )=2a(1)g_2(t-\varphi )\), \(v_1^*(t,0)=\tilde{u}(t,0)/2\) and \(v_2^*(t,1)=u^*(t,1)/2\). Therefore,
On the other hand, (3.22) yields
References
Adler, R.: A study of locking phenomena in oscillators. Proc. IRE 34, 351–357 (1946)
Andronov, A.A., Witt, A.A.: Zur Theorie des Mitnehmens von van der Pol. Archiv für Elektronik 24, 99–110 (1930)
Appell, J., Kalitvin, A.S., Zabrejko, P.P.: Partial Integral Operators and Integro-Differential Equations. Pure and Appl. Math., vol. 230. Marcel Dekker (2000)
Bandelow, U., Recke, L., Sandstede, B.: Frequency regions for forced locking of self-pulsating multi-section DFB lasers. Opt. Commun. 147, 212–218 (1998)
Chicone, C.: Ordinary Differential Equations with Applications. Texts in Applied Math., Springer, Berlin (1999)
Chillingworth, D.: Generic multiparameter bifurcation from a manifold. Dyn. Stab. Syst. 15, 101–137 (2000)
Dancer, E.N.: The \(G\)-invariant implicit function theorem in infinite dimensions. Proc. R. Soc. Edinb. 92A, 13–30 (1982)
Gambaudo, J.-M.: Perturbation of a Hopf bifurcation by an external time-periodic forcing. J. Differ. Equ. 57, 172–195 (1985)
Griepentrog, J.A., Recke, L.: Local Existence, uniqueness and smooth dependence for nonsmooth quasilinear parabolic problems. J. Evol. Equ. 10, 341–375 (2010)
Guo, B.-Z., Wang, J.-M.: Control of Wave and Beam PDEs. The Riesz Basis Approach, Communications in Control Engineering, Springer, Berlin (2019)
Hale, J.K., Raugel, G.: A modified Poincare method for the persistence of periodic orbits and applications. J. Dyn. Differ. Equ. 22, 3–68 (2010)
Hale, J.K., Raugel, G.: Persistence of periodic orbits for perturbed dissipative dynamical systems. In: Mallet-Paret, J., et al. (eds.) Infinite Dimensional Dynamical Systems, Fields Institute Communications, vol. 64, pp. 1–55. Springer, Berlin (2012)
Hale, J.K., Táboas, P.: Interaction of damping and forcing in a second order equation. Nonlinear Anal. TMA 2, 77–84 (1978)
Kantorovich, L.V., Akilov, G.P.: Functional Analysis, 2nd edn. Pergamon Press, 1982, Appl. Math. Sciences 156, Springer, 2004
Kmit, I., Recke, L.: Hopf bifurcation for semilinear dissipative hyperbolic systems. J. Differ. Equ. 257, 246–309 (2014)
Kmit, I., Recke, L.: Solution regularity and smooth dependence for abstract equations and applications to hyperbolic PDEs. J. Differ. Equ. 259, 6287–6337 (2015)
Kmit, I., Recke, L.: Time-periodic second-order hyperbolic equations: Fredholm solvability, regularity, and smooth dependence. In: Pseudodifferential Operators and Generalized Funktions, Operator Theory: Advances and Applications, vol. 245, pp. 147–181. Birkhäuser (2015)
Kmit, I., Recke, L.: Hopf bifurcation for general 1D semilinear wave equations. J. Dyn. Differ. Equ. 34, 1393–1431 (2022)
Kosovalić, N., Pigott, B.: Self-excited vibrations for damped and delayed 1-dimensional wave equations. J. Dyn. Differ. Equ. 31, 129–152 (2019)
Kosovalić, N., Pigott, B.: Self-excited vibrations for damped and delayed higher dimensional wave equations. Discret. Contin. Dyn. Syst. 39, 2413–2435 (2019)
Kosovalić, N., Pigott, B.: Symmetric vibrations of higher dimensional wave equations. Sel. Math. New Ser. 28, No. 3, Paper No. 48 (2022)
Levinson, N.: Small periodic perturbations of an autonomous system with a stable orbit. Ann. Math. 52, 727–738 (1950)
Lichtner, M.: A spectral mapping theorem for linear hyperbolic systems. Proc. Am. Math. Soc. 136(6), 2091–2101 (2008)
Loud, W.S.: Periodic solutions of a perturbed autonomous system. Ann. Math. 70, 490–529 (1959)
Luo, Z.-H., Guo, B.-Z., Mogul, O.: Stability and Stabilization of Infinite Dimensional Systems with Applications. Springer, Berlin (1999)
Neves, A.F., de Souza Ribeiro, H., Lopes, O.: On the spectrum of evolution operators generated by hyperbolic systems. J. Funct. Anal. 670, 320–344 (1986)
Novicenko, V., Pyragas, K.: Phase reduction of weakly perturbed limit cycle oscillations in time-delay systems. Physica D 241, 1090–1098 (2012)
Peterhof, D., Sandstede, B.: All-optical clock recovery using multisection distributed-feedback lasers. J. Nonlinear Sci. 9, 575–613 (1999)
Radziunas, M.: Numerical bifurcation analysis of traveling wave model of multisection semiconductor lasers. Physica D 213, 575–613 (2006)
Recke, L.: Forced frequency locking of rotating waves. Ukrainian Math. J. 50, 94–101 (1998)
Recke, L.: Forced frequency locking for differential equations with distributional forcings. Ukrainian Math. J. 70, 124–141 (2018)
Recke, L., Peterhof, D.: Abstract forced symmetry breaking and forced frequency locking of modulated waves. J. Differ. Equ. 144, 233–262 (1998)
Recke, L., Samoilenko, A.M., Teplinsky, A., Tkachenko, V., Yanchuk, S.: Frequency locking by external forcing in systems with rotational symmetry. Discret. Contin. Dyn. Syst. 31, 847–875 (2011)
Recke, L., Samoilenko, A.M., Tkachenko, V., Yanchuk, S.: Frequency locking of modulated waves. SIAM J. Appl. Dyn. Syst. 11, 771–800 (2012)
Renardy, M.: On the linear stability of hyperbolic PDEs and viscoelastic flows. Z. Angew. Math. Phys. (ZAMP) 45, 854–865 (1994)
Samoilenko, A.M., Recke, L.: Conditions for synchronization of an oscillatory system. Ukrainian Math. J. 57, 1089–1119 (2005)
Scheurle, J. (1987) Asymptotic properties of Arnold tongues. In: Oscillation, Bifurcation and Chaos. Proc. Annu. Semin. Toronto, CMS Proc., vol. 8, pp. 655–663
Táboas, P.: Periodic solutions for a forced Lotka–Volterra equation. J. Math. Anal. Appl. 124, 82–97 (1987)
Vanderbauwhede, A.: Symmetry and bifurcation near families of solutions. J. Differ. Equ. 36, 173–187 (1980)
Vanderbauwhede, A.: Local Bifurcation and Symmetry, Res. Notes in Math., vol. 75. Pitman, Boston (1982)
Vanderbauwhede, A.: Note on symmetry and bifurcation near families of solutions. J. Differ. Equ. 47, 99–106 (1983)
van der Pol, B.: Forced oscillations in a circuit with nonlinear resistance. Philos. Mag. Ser. 7 3(13), 65–80 (1927)
Zhang, Y., Golubitsky, M.: Periodically forced Hopf bifurcations. SIAM J. Appl. Dyn. Syst. 10, 1272–1306 (2011)
Acknowledgements
Irina Kmit was supported by the VolkswagenStiftung Project “From Modeling and Analysis to Approximation”.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Data availability statements
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Let U be a Banach space and \(\Gamma \) a compact Lie group. Moreover, let \(\gamma \in \Gamma \mapsto S_\gamma \in \mathcal{L}(U)\) be a strongly continuous representation of \(\Gamma \) in U, i.e.
The following theorem is due to E. N. Dancer (see [7, Theorem 1 and Remark 4]). Roughly speaking, it claims the following: The map \(\gamma \in \Gamma \mapsto S_\gamma u \in U\) is not \(C^1\)-smooth, in general, but it is if u solves an equivariant equation \(\mathcal{F}(u)=0\) with a \(C^1\)-Fredholm map \(\mathcal{F}:U \rightarrow U\).
Theorem 4.1
Suppose (4.1) and let a \(C^1\)-map \(\mathcal{F}:U \rightarrow U\) be given such that
Moreover, let \(u^0 \in U\) be given such that
Then the following is true:
-
(i)
The map \(\gamma \in \Gamma \mapsto S_\gamma u^0 \in U\) is \(C^1\)-smooth.
-
(ii)
If \(\mathcal{F}\) is \(C^2\)-smooth, then the map \(\gamma \in \Gamma \mapsto S_\gamma u^0 \in U\) is \(C^2\)-smooth also.
The following theorem is due to E. N. Dancer and A. Vanderbauwhede (see [39,40,41]). It describes a parametrization of a tubular neighborhood of the orbit of a “good” element \(u^0 \in U\):
Theorem 4.2
Suppose (4.1), and let \(u^0 \in U\) be given such that the map \(\gamma \in \Gamma \mapsto S_\gamma u^0 \in U\) is \(C^1\)-smooth. Then the \(\Gamma \)-orbit \(\mathcal{O}(u^0):=\{S_\gamma u^0 \in U: \gamma \in \Gamma \}\) of \(u^0\) is a \(C^1\)-submanifold in U, and for any closed subspace V in U with
there exists an open neighborhood \(\mathcal{V}_0 \subset V\) of zero such that \(\{S_\gamma (u^0+v)\in U: \gamma \in \Gamma , \; v \in \mathcal{V}_0\}\) is an open neighborhood of \(\mathcal{O}(u^0)\).
Appendix 2
Let \((U_1,\Vert \cdot \Vert _1)\) and \((U_2,\Vert \cdot \Vert _2)\) be Banach spaces, \((\Lambda ,\Vert \cdot \Vert _\Lambda )\) be a normed vector space and \(\mathcal{F}:\Lambda \times U_1 \rightarrow U_2\) be a map. The following theorem is folklore, and we prove it for the convenience of the reader. It is a version of the implicit function theorem for cases, such that \(\partial _u\mathcal{F}\) exists, but \(\partial _u\mathcal{F}(\cdot ,u)\) may be discontinuous, and \(\mathcal{F}(\cdot ,u)\) may be non-differentiable.
Theorem 5.1
Let \(\lambda _0 \in \Lambda \) and \(u_0 \in U_1\) with \(\mathcal{F}(\lambda _0,u_0)=0\) be given elements. Suppose that
Moreover, suppose that there exist \(\varepsilon _0>0\) and \(c>0\) such that for all \(\lambda \in \Lambda \) and all \(u,v,w \in U_1\) with \(\Vert \lambda -\lambda _0\Vert _\Lambda +\Vert u-u_0\Vert _1<\varepsilon _0\) it holds that
Then the following is true:
-
(i)
There exist \(\varepsilon \in (0,\varepsilon _0)\) and \(\delta >0\) such that for all \(\lambda \in \Lambda \) with \(\Vert \lambda -\lambda _0\Vert _\Lambda <\varepsilon \) there exists a unique \(u=\hat{u}(\lambda ) \in U_1\) with \(\Vert u-u_0\Vert _1<\delta \) and \(\mathcal{F}(\lambda ,u)=0\).
-
(ii)
The data-to-solution map \(\hat{u}\) is continuous.
Proof
(i) Take \(\lambda \in \Lambda \) with \(\Vert \lambda -\lambda _0\Vert _\lambda <\varepsilon _0\). Due to (5.3) and (5.4), the operator \(\partial _u\mathcal{F}(\lambda ,u_0)\) is an isomorphism from \(U_1\) onto \(U_2\). Hence, the equation \(F(\lambda ,u)=0\) is equivalent to the fixed point problem
For \(\delta >0\), write \(B_\delta :=\{u \in U_1: \Vert u-u_0\Vert _1 \le \delta \}\). Take \(u \in B_\delta \) and \(v \in U\). Then
Hence, if \(\delta <\varepsilon _0\), then (5.4) and (5.5) yield that \(\Vert \left( I-\partial _u\mathcal{F}(\lambda ,u_0)^{-1}\partial _u\mathcal{F}(\lambda ,u)\right) v\Vert _1 \le c^2\delta \Vert v\Vert _1\). Therefore, for \(u_1,u_2 \in B_\delta \) we get
Moreover, for \(u\in B_\delta \) we have
Hence, (5.1) yields that for the map \(\mathcal{G}(\lambda ,\cdot )\) is strictly contractive from \(B_\delta \) into itself. Therefore, the Banach fixed point theorem yields claim (i).
(ii) Take \(\lambda _1,\lambda _2 \approx \lambda _0\). Then
Hence, (5.1) yields \( \Vert \hat{u}(\lambda _1)-\hat{u}(\lambda _2)\Vert _1 \le 2c \Vert \mathcal{F}(\lambda _1,\hat{u}(\lambda _2))\Vert _2 \rightarrow 0 \hbox { for } \lambda _1 \rightarrow \lambda _2. \) \(\square \)
Remark 5.2
Since \(\partial _u\mathcal{F}(\cdot ,u_0)\) is not supposed to be continuous (with respect to the uniform operator norm in \(\mathcal{L}(U_1;U_2)\)), conditions (5.3) and (5.4) are not satisfied for all \(\lambda \approx \lambda _0\), in general, if these conditions are satisfied for \(\lambda =\lambda _0\) only.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Kmit, I., Recke, L. Forced Frequency Locking for Semilinear Dissipative Hyperbolic PDEs. J Dyn Diff Equat (2022). https://doi.org/10.1007/s10884-022-10236-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10884-022-10236-0