Shilnikov Saddle-Focus Homoclinic Orbits from Numerics: Higher Dimensions

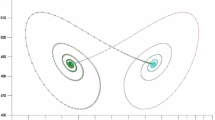
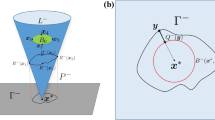
Abstract

In a previous paper we studied parametrized autonomous systems and gave a computable criterion that an approximate orbit connecting hyperbolic equilibria is shadowed by a true connecting orbit. This criterion was used to give rigorously verified examples of Shilnikov saddle-focus homoclinic orbits in three dimensions. This involved verifying a condition on the eigenvalues of the linearization at the equilibrium. In dimensions greater than three, there are three more conditions which must be established: general position, asymptotic tangency and a transversality condition. In this paper we give computable criteria for verifying these three conditions. An example in four dimensions, in which detailed rigorous computations are carried out, is given.

Appendices

Appendix 1: Constants and Inequalities for Existence Theorem

A complete proof of the Existence Theorem for Homoclinic orbits stated in Sect. 2 is available in Coomes et al. [8]. For the convenience of the reader, in this Appendix we collect certain quantitative information about the constant C in the Existence Theorem and the conditions which $\delta$ and $\delta _1$ need to satisfy.

For each $k\in \mathrm{Z}\mathrm{Z}$, $R_k$ is a positive number such that if $0\le t\le h_k$, then $|\phi ^t(y_k,a_0)-y_k|\le R_k$. Then the rigorous containment region is

$$\begin{aligned} U=\bigcup _k \{x\in \mathrm{I}\mathrm{R}^n: |x-y_k|\le 2R_k\}. \end{aligned}$$

$\Delta _0$ is a positive number such that if $|x-z|\le \Delta _0$, then $x\in U$, and the constants $M_1$, $M_2$, $M_3$, $M_4$, $M_5$ are bounds on the norms of the derivatives $f_x$, $f_{xx}$, $f_a$, $f_{xa}$, $f_{aa}$ in $x\in U$, $|a-a_0|\le \Delta _0$. Next we have the quantities

$$\begin{aligned} h_{\mathrm{max}}= & {} \sup \,h_k,\quad M_6=M_2e^{M_1h_{\mathrm{max}}},\quad M_7={1\over 2}M_2M_3h_{\mathrm{max}}e^{M_1h_{\mathrm{max}}}+M_4, \nonumber \\ M_{8}= & {} {1\over 3}M_2M^2_3h^2_{\mathrm{max}}\cosh (M_1h_{\mathrm{max}})+M_3M_4h_{\mathrm{max}}+M_5, \nonumber \\ M= & {} (M_6+2M_7+M_{8})e^{M_1h_{\mathrm{max}}}. \end{aligned}$$

(35)

In view of the eigenvalue assumptions in Hypothesis 1, there exist positive constants K, $\alpha$ and $\beta$ such that for $t\ge 0$

$$\begin{aligned} |e^{tA}P|\le Ke^{-\alpha t},\quad |e^{-tA}(I-P)|\le Ke^{-\beta t}. \end{aligned}$$

(36)

Next, we have the quantities

$$\begin{aligned} \mu= & {} \min \{\Delta _0,[4K(\alpha ^{-1}+\beta ^{-1})M_2]^{-1}\},\nonumber \\ \Delta _1= & {} \min \{\Delta _0,[2K(\alpha ^{-1}+\beta ^{-1})M_3]^{-1}\mu , [4K(\alpha ^{-1}+\beta ^{-1})M_4]^{-1} \}, \end{aligned}$$

(37)

and $\Delta _2$ as the largest positive number $\le \Delta _0$ such that for all k

$$\begin{aligned}{}[1+M_3h_k]e^{M_1h_k}\Delta _2\le R_k. \end{aligned}$$

(38)

Recall that H is the matrix of the eigenvectors of A, and let

$$\begin{aligned} N= \max \{1, K|H^{-1}|(\beta ^{-1}+\alpha ^{-1}e^{\alpha h_{\mathrm{max}}})\},\quad f_a=f_a(z,a_0). \end{aligned}$$

(39)

Then the constant C is given by

$$\begin{aligned} C =2\max \left\{ N\Vert L^{-1}\Vert , K\left[ N\Vert L^{-1}\Vert ((\alpha ^{-1}+\beta ^{-1})|f_a| \!+\!|H|)\!+\!\alpha ^{-1}e^{\alpha h_{\mathrm{max}}}\!+\!\beta ^{-1}\right] \right\} . \end{aligned}$$

(40)

Finally, we list the inequalities that $\delta$ and $\delta _1$ must satisfy:

$$\begin{aligned}&2MC^2\delta<1, \quad 2C\delta \le \Delta _1, \quad \quad 2C\delta <\Delta _2 \end{aligned}$$

(41)

$$\begin{aligned}&2Ce^{M_1h_{\mathrm{max}}}(1+M_3h_{\mathrm{max}})\delta \le \mu ,\quad \delta _1\le \Delta _2,\quad C(M_6+M_7)e^{M_1h_{\mathrm{max}}}\delta _1\le 1. \end{aligned}$$

(42)

Appendix 2: Proofs of Inequalities (7), (15) – (17) in Section 3.

In these proofs we refer to Appendix 1 for the definitions of the quantities which appear.

First we prove (7). Since $y_k=z$ for large k, $x_k\rightarrow z(a^*)$ as $k\rightarrow \pm \infty$ and $|x_k-y_k|\le 2C\delta$ for all k, it follows that

$$\begin{aligned} |z(a^*)-z|\le 2C\delta \end{aligned}$$

(43)

also. Next since by Eqs. (38) and  (41), $2C\delta <R_k$ for all k and $y_k=z$ for large |k|, it follows that $z(a^*)$ is in the ball of radius $R_k$, center $y_k=z$, for large |k| and so we can use the bounds $M_i$ defined before Eq. (35). Then it follows that

$$\begin{aligned} |f_x(z(a^*),a^*)-f_x(z,a_0)| \le M_2|z(a^*)-z|+M_4|a^*-a_0|\le 2(M_2+M_4)C\delta . \end{aligned}$$

(44)

So inequality (7) is proved.

Inequalities (15) require us to show that for $t\ge T_1=t_{N_1}$ and $t\le -T_2=t_{-N_2}$

$$\begin{aligned} \begin{aligned} |\phi ^t(x_0,a^*)-z(a^*)|\le & {} \mu _1=(4C\delta +\delta _1)e^{M_1h_{\mathrm{max}}},\\ |f_x(\phi ^t(x_0,a^*),a^*)-f_x(z,a_0)|\le & {} \rho =M_2\mu _1+2(M_2+M_4)C\delta . \end{aligned} \end{aligned}$$

(45)

The main problem here is controlling what happens to $|\phi ^t(x_0,a^*)-z(a^*)|$ when t is between $t_k$ and $t_{k+1}=t_k+h_k$. Note since by Eqs. (5) and (41),

$$\begin{aligned} |x_k-y_k|\le 2C\delta<\Delta _2,\quad |a^*-a_0|\le 2C\delta <\Delta _2, \end{aligned}$$

it follows from Lemma  1 in Coomes et al. [8] that for all k

$$\begin{aligned} |\phi ^t(x_k,a^*)-y_k|\le 2R_k\quad \mathrm{for}\quad 0\le t\le h_k. \end{aligned}$$

Next, using Eqs. (43), (3), (38), (41) and (42), we get

$$\begin{aligned} |z(a^*)-y_k|\le |z(a^*)-z|+|y_k-z|\le 2C\delta +\delta _1\le 2\Delta _2\le 2R_k \end{aligned}$$

(46)

if $k\ge N_1$ or $k<-N_2$. It follows that for $t_k\le t\le t_{k+1}$ with $k\ge N_1$ and $k<-N_2$, the points $\phi ^t(x_k,a^*)$ and $z(a^*)$ belong to a ball of radius $2R_k$ centered at some $y_k$ and therefore we may use the $M_i$ defined before Eq. (35) to obtain for these k and t that

$$\begin{aligned}&|f(\phi ^t(x_k,a^*),a^*)-f(z(a^*),a^*)|\le M_1|\phi ^t(x_k,a^*)-z(a^*)|,\nonumber \\&|f_x(\phi ^t(x_k,a^*),a^*)-f_x(z(a^*),a^*)|\le M_2|\phi ^t(x_k,a^*)-z(a^*)|. \end{aligned}$$

(47)

Then if $k\ge N_1$ and $0\le t\le h_k$, it follows that

$$\begin{aligned} |\phi ^t(x_k,a^*)-z(a^*)|&=\left| x_k-z(a^*)+\int ^t_0[f(\phi ^s(x_k,a^*),a^*)-f(z(a^*),a^*)]ds\right| \\&\le |x_k-z(a^*)|+M_1\int ^t_0|\phi ^s(x_k,a^*)-z(a^*)|ds \end{aligned}$$

and hence, by Gronwall’s lemma and using Eqs. (5) and (46), we obtain for $0\le t\le h_k$

$$\begin{aligned} |\phi ^t(x_k,a^*)-z(a^*)|\le |x_k-z(a^*)|e^{M_1t}\le (4C\delta +\delta _1)e^{M_1h_{\mathrm{max}}}. \end{aligned}$$

It follows that for $t\ge t_{N_1}$, and similarly for $t\le t_{-N_2}$ that

$$\begin{aligned} |\phi ^t(x_0,a^*)-z(a^*)|\le \mu _1=(4C\delta +\delta _1)e^{M_1h_{\mathrm{max}}}. \end{aligned}$$

Hence we have derived the first inequality in Eq. (45). Also we conclude that for the same t, using Eq. (47), that

$$\begin{aligned} |f_x(\phi ^t(x_0,a^*),a^*)-f_x(z(a^*),a^*)|\le M_2\mu _1 \end{aligned}$$

and hence, using Eq. (7), that for $t\ge T_1=t_{N_1}$ and $t\le -T_2=t_{-N_2}$

$$\begin{aligned} |f_x(\phi ^t(x_0,a^*),a^*)-f_x(z,a_0)|\le \rho =M_2\mu _1+2(M_2+M_4)C\delta . \end{aligned}$$

Thus we have derived the second inequality in Eq. (45).

Next we prove inequality (16). First since $|y_0-x_0|\le 2C\delta<\Delta _2<R_k$, $y_0$ and $x_0$ are both in the ball of radius $2R_0$, center $y_0$. Also $|a^*-a_0|\le 2C\delta \le \Delta _1\le \Delta _0$. So we may use $M_1$ and $M_3$ as Lipschitz constants to get

$$\begin{aligned} |f(y_0,a_0)-f(x_0,a^*)| \le M_1|y_0-x_0|+M_3|a_0-a^*| \le 2C(M_1+M_3)\delta , \end{aligned}$$

thus proving inequality (16).

Finally we prove inequality (17). In fact, using Lemma  2 in Coomes et al. [8], we obtain for $k=-N_2+1,\ldots ,N_1-1$

$$\begin{aligned} |\phi ^{h_k}_x(x_k,a^*)-\phi ^{h_k}_x(y_k,a_0)| \le M_6h_ke^{M_1h_k}|x_k-y_k|+M_7h_ke^{M_1h_k}|a^*-a_0| \le \delta _2, \end{aligned}$$

where

$$\begin{aligned} \delta _2=2C(M_6+M_7)h_{\mathrm{max}}e^{M_1h_{\mathrm{max}}}\delta , \end{aligned}$$

thus establishing Eq. (17).

Appendix 3: Proofs of Lemmata

Here we give the proofs of Lemmas  1–5 in Sect. 3.

Proof of Lemma 1

Let E be the Banach space of continuous $\mathrm{I}\mathrm{R}^n-$valued functions x(t) on $[T_1,\infty )$ equipped with the supremum norm $\Vert \cdot \Vert _{\infty }$, that is, $\Vert x\Vert _{\infty }=\sup _{t\ge T_1}|x(t)|$. We define $T:E\rightarrow E$ according to

$$\begin{aligned} (Tx)(t)=e^{(t-T_1)A}\xi +\int ^t_{T_1}e^{(t-s)A}PB(s)x(s)ds -\int ^{\infty }_{t}e^{(t-s)A}(I-P)B(s)x(s)ds, \end{aligned}$$

(48)

where $B(t)=f_x(q(t),a^*)-A$. We see that Tx is continuous and, using the inequalities (11), we find that

$$\begin{aligned} \Vert Tx\Vert _{\infty }\le K|\xi | +K(\alpha ^{-1}+\beta ^{-1})\rho \Vert x\Vert _{\infty }<\infty \end{aligned}$$

(49)

so that Tx is in E. Moreover, if x and y are in E, then

$$\begin{aligned} \Vert Tx-Ty\Vert _{\infty }\le K(\alpha ^{-1}+\beta ^{-1})\rho \Vert x-y\Vert _{\infty }. \end{aligned}$$

Thus T is a contraction and its unique fixed point is the desired solution. The inequality for $\sup _{t\ge T_1}|x(t)|$ follows from Eq. (49) taking $Tx=x$. We denote this solution by $x(t,\xi )$.

From Eq. (48) with $Tx=x$ and $t=T_1$, we see that

$$ x(T_1,\xi )=R_+\xi =\xi -\int ^{\infty }_{T_1}e^{(T_1-s)A}(I-P)B(s)x(s,\xi )ds.$$

$R_+$ is linear since, by uniqueness, $x(t,\xi )$ is linear in $\xi$. Then for all $\xi \in \mathcal{R}(P)$,

$$\begin{aligned} |R_+\xi -\xi |\le K^2\alpha \rho (\alpha \beta -K(\alpha +\beta )\rho )^{-1}|\xi |=\rho _1|\xi |. \end{aligned}$$

Define

$$\begin{aligned} S=R_+P+I-P. \end{aligned}$$

Then for all vectors x,

$$\begin{aligned} |Sx-x|=|R_+Px-Px|\le \rho _1|Px|\le K\rho _1|x|. \end{aligned}$$

Since $K\rho _1<1$, S is invertible and

$$\begin{aligned} |S-I|\le K\rho _1,\quad |S^{-1}| \le (1-K\rho _1)^{-1},\quad |S^{-1}-I| \le (1-K\rho _1)^{-1}K\rho _1. \end{aligned}$$

The projection

$$\begin{aligned} P_+=SPS^{-1} \end{aligned}$$

has the same nullspace as P and its range is the range of $R_+$. This means that the solutions x(t) of Eq. (18) bounded on $[T_1,\infty )$ are exactly those with $x(T_1)$ in the range of $P_+$. Note that

$$\begin{aligned} |P_+-P|\le |S-I|\,|P|\,|S^{-1}|+|P|\,|S^{-1}-I| \le 2(1-K\rho _1)^{-1}K^2\rho _1. \end{aligned}$$

This completes the proof of the lemma. $\square$

Proof of Lemma 2

This follows from Lemma  1 by reversing time, that is, by applying Lemma  1 to the equation $\dot{y}=-f_x(q(-t),a^*)y$, replacing A, $\alpha$, $\beta$ by $-A$, $\beta$, $\alpha$.

Proof of Lemma 3

Using Eq. (14), this follows from Lemma 2 with $f_x(q(t),a^*)$, A, P, $\alpha$, $\beta$ replaced by $f_x(q(t),a^*)-\nu I$, $A-\nu I$, Q, $\nu -\beta$, $\sigma -\nu$, respectively.

Proof of Lemma 4

This is proved as Lemma  1, replacing $f_x(q(t),a^*)$, A, P, $\alpha$, $\beta$ by $-(f_x(q(t),a^*)^T-\nu )$, $-(A^T-\nu I)$, $I-Q^T$, $\sigma -\nu$, $\nu -\beta$ respectively, and using the fact that with $A_1=A-\nu I$, taking transposes in Eq. (14) and using $AQ=QA$, we have for $t\ge 0$,

$$\begin{aligned} |e^{t(-A_1^T)}(I-Q^T)|\le Ke^{-(\sigma -\nu )t},\quad |e^{-t(-A_1^T)}Q^T|\le Ke^{-(\nu -\beta )t}. \end{aligned}$$

$\square$

Proof of Lemma 5

This is proved as Lemma  2, replacing $f_x(q(t),a^*)$, A, P, $\alpha$, $\beta$ by $-f_x(q(t),a^*)^T$, $-A^T$, $I-P^T$, $\beta$, $\alpha$ respectively and using the fact that taking transposes in Eq. (11) and using $AP=PA$, we have for $t\ge 0$,

$$\begin{aligned} |e^{t(-A^T)}(I-P^T)|\le Ke^{-\beta t},\quad |e^{-t(-A^T)}P^T|\le Ke^{-\alpha t}. \end{aligned}$$

$\square$

Appendix 4: Computational Details for the Example

Here we supply more details concerning the computations in the example in Sect. 4. First in (i) we describe how the approximate homoclinic orbit is found, and how the rigorous containment region and the quantities $\delta$ and $\delta _1$ are determined. Next in (ii) we show how the eigenvalues and dichotomy constants are determined, and how (D1) is verified. Finally in (iii) we describe how to verify that $\mathcal{C}$ from Proposition 2 (hence also $\mathcal{B}$ from Proposition 3) has a left inverse and calculate an upper bound on its norm.

(i) Determination of the approximate homoclinic orbit and parameter value, the rigorous containment region, and $\delta _1$ and $\delta$: To obtain the approximate homoclinic orbit and parameter value in Eq. (33), we set $\kappa$ to a small positive value and use Beyn’s method (see Eqs. (4.1a), (4.1b), (4.1c), (3.6) in Beyn [4]) with $(0,\,0,\,\zeta _0(t),\,{{\dot{\zeta }}}_0(t))$ as our initial orbit and parameter value $\gamma =0$ as an initial guess for the BVP solver, padding the initial orbit with copies of the equilibrium $z=0$ at each end as needed so that the output of Beyn’s method is suitably close to the equilibrium at each end. The BVP solver we use is the 2012 version of the Fortran 90/95 software developed by Boisvert et al. [5]. Then Beyn’s method yields the corresponding value of $\gamma$ and the new approximate homoclinic orbit. Then we use these as initial guesses for a slightly higher value of $\kappa$. And so on until we reach $\kappa =1.0$. The raw output of the BVP solver is in general a variable step size orbit. We then use the solver’s interpolating routines to produce two constant step size orbits, one for forward time and one for backward time since the time scaling for the BVP is different in these two directions. Because the solver produces times instead of steps and because of round off errors, the step size $h_k$ ends up being not quite uniform.

Thus we obtain finite sequences $y_k$, $-N_2=-1221\le k\le N_1=340$ and $h_k$, $-N_2\le k<N_1$ and a parameter value

$$\begin{aligned} \gamma =-0.53237259116071756\end{aligned}$$

such that

$$\begin{aligned} h_{\mathrm{min}}=0.074999999999988631\le h_k\le 0.075000000000002842=h_{\mathrm{max}}. \end{aligned}$$

Then if we define $y_k=0$ for $k>N_1$, $h_k=h_{\mathrm{max}}$ for $k\ge N_1$ and $y_k=0$, $h_k=h_{\mathrm{max}}$ for $k<-N_2$, we obtain infinite sequences $y_k$, $h_k$ as required in the definition of approximate homoclinic orbit. Moreover we have

$$\begin{aligned} |y_{N_1}|\le \delta _1=2.4647560945643079\times 10^{-15}\end{aligned}$$

so that Eq. (3) holds.

We follow the procedure described in Sect. 6.3 in Coomes et al. [8] with $m=3$ to compute the sequence of positive numbers $\{R_k\}_{k=-N_2}^{N_1}$ and hence the rigorous containment region $U=\bigcup _k \{x\in \mathrm{I}\mathrm{R}^n: |x-y_k|\le 2R_k\}$.

We determine $\delta$ in Hypothesis 2 following the procedure given in the last paragraph in Sect. 6.2 in Coomes et al. [8]. The only difference here is that we work in each ball center $y_k$, radius $R_k$, rather than in the trapping region which is not available here.

(ii) Eigenvalues, dichotomy constants and verification of (D1): For the matrix

$$\begin{aligned} A=A(\gamma _0)=f_x(0,\gamma _0)=\left[ \begin{array}{llll}0&{}1&{}0&{}0\\ -1&{}1&{}1&{}0\\ 0&{}0&{}0&{}1\\ 1&{}0&{}1&{}\gamma _0 \end{array}\right] , \end{aligned}$$

we use a standard linear algebra routine to compute approximations for the eigenvalues $-{{\tilde{\alpha }}}=1.4059364946668556$, ${{\tilde{\sigma }}}=1.1282487657053040$, ${{\tilde{\beta }}}\pm i{{\tilde{\omega }}}$ with ${{\tilde{\beta }}}=0.37265756890041568$, ${{\tilde{\omega }}}=1.0592283643884413$. The eigenvectors corresponding to $-{{\tilde{\alpha }}}$, ${{\tilde{\sigma }}}$ and ${{\tilde{\beta }}}+i{{\tilde{\omega }}}$ are approximately ${{\tilde{u}}}_1$, $\tilde{u}_2$, ${{\tilde{v}}}+i{{\tilde{w}}}$, where ${{\tilde{H}}}=[{{\tilde{u}}}_{1}\;\tilde{v}\; {{\tilde{w}}}\; {{\tilde{u}}}_{2}]$, is given by

$$\begin{aligned} {{\tilde{H}}}=\left[ \begin{array}{llll} 0.128939 &{} -0.201547 &{} 0.572869 &{} 0.436384\\ -0.18128 &{} -0.681907 &{} 0 &{} 0.492349\\ 0.565086 &{} 0.226242 &{} -0.149426 &{} 0.499527\\ -0.794475 &{} 0.242587 &{} 0.183958 &{} 0.563591\\ \end{array} \right] . \end{aligned}$$

Now, using the approximate eigenvalues and eigenvectors just found, we want to rigorously estimate the eigenvalues and eigenvectors of A but we also want to estimate the eigenvalues of the matrix $A(\gamma )$, noting that $|A(\gamma )-A|_{\infty }\le 2C\delta$. To this end, we use a similar method to that used in Symm and Wilkinson [19] and Yamamoto [22, 23] and apply the Newton method Lemma 4.1 of Coomes et al. [7] to, in the case of a real eigenvalue $\lambda$, the function G from $\mathrm{I}\mathrm{R}\times \mathrm{I}\mathrm{R}^4$ to $\mathrm{I}\mathrm{R}^4$, given by

$$\begin{aligned} G(\lambda ,v) = A(\gamma )v - \lambda v, \end{aligned}$$

and in the case of a complex eigenvalue $a+ib$ to the function G from $\mathrm{I}\mathrm{R}\times \mathrm{I}\mathrm{R}\times \mathrm{I}\mathrm{R}^4\times \mathrm{I}\mathrm{R}^4$ to $\mathrm{I}\mathrm{R}^4\times \mathrm{I}\mathrm{R}^4$ given by

$$\begin{aligned} G(a,b,w,v) =\left[ \begin{array}{ll}A(\gamma )v - av + bw&A(\gamma )w- bv - aw \end{array}\right] . \end{aligned}$$

We conclude that $A(\gamma )$ has eigenvalues $-\alpha _1$, $\sigma _1$, $\beta _1\pm i\omega _1$, where $\alpha _1\ge 1.4059364945327910$, $\sigma _1\ge 1.1282487656074565$, $0.37265756884438972\le \beta _1\le 0.37265756895644164$, $\omega _1\ge 1.0592283643324152$. So these eigenvalues satisfy (D1).

In particular, we conclude that A has eigenvalues $-\alpha _2$, $\sigma _2$, $\beta _2\pm i\omega _2$, where $\alpha _2\ge \alpha = 1.4059364946668425$, $\sigma _2\ge \sigma =1.1282487657052955$, $\beta _2\ge \beta =0.37265756890039831$, $\omega _2\ge 1.0592283643884237$. The corresponding eigenvectors are $u_1$, $u_2$, $v\pm iw$ where if $H=[u_1\;v\;w\;u_2]$, using a standard a posteriori technique applied to an approximate inverse of ${{\tilde{H}}}$, we verify that H is invertible and obtain the rigorous upper bounds

$$\begin{aligned} |H| \le 1.1608562757978054,\quad |H^{-1}| \le 1.9476125853957360. \end{aligned}$$

Next, with a view to obtaining the dichotomy constants, note that

$$\begin{aligned} AH=HD,\quad \mathrm{where}\quad D=\left[ \begin{array}{llll}-\alpha _2 &{}0&{}0&{}0\\ 0&{}\beta _2&{}-\omega _2&{}0\\ 0&{}\omega _2&{}\beta _2&{}0\\ 0&{}0&{}0&{}\sigma _2\end{array}\right] , \end{aligned}$$

so that $e^{tA}H=He^{tD}$ and hence for $t\ge 0$,

$$\begin{aligned} |e^{tA}P|=|He^{tD}P_1H^{-1}|\le Ke^{-\alpha t},\quad |e^{-tA}(I-P)|=|He^{tD}(I-P_1)H^{-1}|\le Ke^{-\beta t}, \end{aligned}$$

where $P=HP_1H^{-1}$ (recall that $P_r=\left[ \begin{array}{ll}I_r&{}0\\ 0&{}0\end{array}\right]$) and

$$\begin{aligned} |H^{-1}||H|\le K=2.2608982925794296, \end{aligned}$$

and

$$\begin{aligned} |e^{t(A-\nu I)}Q|\le Ke^{-(\nu -\beta )t},\quad |e^{-t(A-\nu I)}(I-Q)|\le Ke^{-(\sigma -\nu )t}, \end{aligned}$$

where $Q=HP_3H^{-1}$. So our dichotomy constants are

$$\begin{aligned} \begin{array}{ll}\alpha =1.4059364946668425,&{} \beta =0.37265756890039831,\\ \sigma = 1.1282487657052955, &{} K=2.2608982925794296. \end{array} \end{aligned}$$

(iii) Verification that $\mathcal{C}$ has a left inverse and calculation of an upper bound on its norm: Here we show how we verify that $\mathcal{C}$ has a left inverse and we find an upper bound for the norm of this left inverse. Denote by ${{\hat{C}}}$ the computed $\mathcal{C}$ (not to be confused with the matrix ${{\hat{C}}}$ in Section 3.4). We have a rigorous upper bound for $|{{\hat{C}}}-\mathcal{C}|\le E$, where here if A is a matrix $[a_{ij}]$, then $|A|=[|a_{ij}|]$ is the matrix of absolute values, E is a matrix and $\le$ is to be interpreted entrywise. We perform a QR factorization ${{\hat{C}}}=QR$, where R is square upper triangular, and set $T=R^{-1}Q^T$ as computed. We obtain a rigorous upper bound $|T|\le F$ and hence also a rigorous bound for $\Vert T\Vert _{\infty }$. Proceeding as we do with L in Sect. 6.7 in Coomes et al. [8], we find a rigorous $\varepsilon _1$ such that $\Vert T{{\hat{C}}}-I\Vert _{\infty }\le \varepsilon _1$. Then we estimate

$$\begin{aligned} |T\mathcal{C}-T{{\hat{C}}}|=|T({{\hat{C}}}-\mathcal{C})|\le |T|\,|{{\hat{C}}}-\mathcal{C}|\le EF \end{aligned}$$

and hence, by obtaining an upper bound for $\Vert EF\Vert _{\infty }$, get a rigorous $\varepsilon _2$ such that

$$\begin{aligned} \Vert T\mathcal{C}-T{{\hat{C}}}\Vert _{\infty }\le \varepsilon _2. \end{aligned}$$

Then

$$\begin{aligned} \Vert T\mathcal{C}-I\Vert _{\infty }\le \varepsilon =\varepsilon _1+\varepsilon _2. \end{aligned}$$

If $\varepsilon <1$, then we conclude that $T\mathcal{C}$ is invertible and $|(T\mathcal{C})^{-1}|\le (1-\varepsilon )^{-1}$. Then

$$\begin{aligned} (T\mathcal{C})^{-1}T\mathcal{C}=I \end{aligned}$$

so that $\mathcal{C}^{-1}=(T\mathcal{C})^{-1}T$ is a left inverse for $\mathcal{C}$ and we observe that

$$\begin{aligned} \Vert \mathcal{C}^{-1}\Vert _{\infty }\le (1-\varepsilon )^{-1}\Vert T\Vert _{\infty }. \end{aligned}$$

It is similarly verified that $\mathcal{B}$ has a left inverse and an upper bound for the norm of the left inverse is calculated similarly.