Skip to main content
SpringerLink
Log in

Dirac Physical Measures on Saddle-Type Fixed Points

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

Abstract

In this article we study some statistical aspects of surface diffeomorphisms. We first show that for a \(C^1\) generic diffeomorphism, a Dirac invariant measure whose statistical basin of attraction is dense in some open set and has positive Lebesgue measure, must be supported in the orbit of a sink. We then construct an example of a \(C^1\)-diffeomorphism having a Dirac invariant measure, supported on a saddle-type hyperbolic fixed point, whose statistical basin of attraction is a nowhere dense set with positive Lebesgue measure. Our technique can be applied also to construct a \(C^1\) diffeomorphism whose set of points with historic behaviour has positive measure and is nowhere dense.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

Notes

  1. This is a non-trivial consequence of the specification property, see [36, Theorem 4]. The fact that specification holds for transitive Anosov diffeomorphisms was proved by Bowen [6].

  2. The same statement holds for periodic points, with a similar proof.

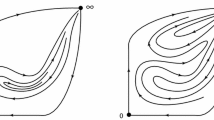
  3. The adjective exterior refers to the fact the boxes \(S_n^e\) will be contained in the exterior connected components of the complement of the figure-eight attractor we shall produce in this section.

  4. The dependence of \({\mathcal {S}}\) and \({\tilde{{\mathcal {S}}}}\) on \(n_0\) is not explicit in our notation because we shall fix once and for all the integer \(n_0\).

  5. See [30] for instance.

  6. Recall that this means that, inside V, the map f is topologically conjugate to its linear part Df at O.

  7. We have used here the well known fact that every periodic orbit of a planar vector field bounds a disk containing a zero of the vector field inside. This can be proved combining Poincaré-Bendixon’s theorem with Zorn’s lemma.

  8. Just as an example, fix some \(R>1\) and let \(p=(0,0) \in U=B(0,1) \subset W_0=B(0,R)\). Consider first the real function \(g:W_0{\setminus }{\overline{U}}\rightarrow (0,1)\) given by

    $$\begin{aligned} g(x,y)=\frac{1}{R-1}\,\frac{1}{\sqrt{x^2+y^2}}\,\big (R-\sqrt{x^2+y^2}\big )\,, \end{aligned}$$

    and then let \(\psi _{U}:W_0{\setminus }{\overline{U}} \rightarrow U{\setminus }\{p\}\) be given by  \(\psi _{U}(x,y)=g(x,y)\,\big (x,y\big )\).

  9. A point \(x\in M\) is said to have historic behaviour if the sequence \(\frac{1}{n}\sum \limits _{j=0}^{n-1}\delta _{f^{j}(x)}\) does not converge in the weak-* topology.

  10. It may be that the diffeomorphism \(h_1\) is useless to get the desired result; however it simplifies significantly the proofs.

  11. This phenomenon has already been shown in Lemma 4.5.

  12. For boxes \(s_v(S_n)\) of the exterior \({\mathcal {L}}^e\) of the attractor, one has to change the powers of 16 by powers of 4, as the return map of \(f_1\) to the union of such boxes is, after renormalization, a rotation of angle \(\pi \).

References

  1. Avila, A., Lyubich, M., de Melo, W.: Regular or stochastic dynamics in real analytic families of unimodal maps. Inventiones mathematicae 154(3), 451–550 (2003)

    Article  MathSciNet  Google Scholar 

  2. Benedicks, M., Carleson, L.: On iterations of \(1-ax^2\) on \((-1, 1)\). Ann. Math. 122, 1–25 (1985)

    Article  MathSciNet  Google Scholar 

  3. Bochi, J., Bonatti, C.: Perturbation of the Lyapunov spectra of periodic orbits. Proc. Lond. Math. Soc. 105(1), 1–48 (2012)

    Article  MathSciNet  Google Scholar 

  4. Bonatti, C., Díaz, L.J., Pujals, E.R.: A \(C^1\)-generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources. Ann. Math. (2) 158(2), 355–418 (2003)

    Article  MathSciNet  Google Scholar 

  5. Bonatti, C., Crovisier, S.: Récurrence et généricité. Inventiones mathematicae 158(1), 33–104 (2004)

    Article  MathSciNet  Google Scholar 

  6. Bowen, R.: Periodic points and measures for axiom a diffeomorphisms. Trans. Am. Math. Soc. 154, 377–397 (1971)

    MathSciNet  MATH  Google Scholar 

  7. Bowen, R.: Invariant measures for Markov maps of the interval. Commun. Math. Phys. 69(1), 1–17 (1979)

    Article  MathSciNet  Google Scholar 

  8. Bruin, H., Rivera-Letelier, J., Shen, W., van Strien, S.: Large derivatives, backward contraction and invariant densities for interval maps. Inventiones mathematicae 172(3), 509–533 (2008)

    Article  MathSciNet  Google Scholar 

  9. Catsigeras, E., Cerminara, M., Enrich, H.: The Pesin entropy formula for \(C^1\) diffeomorphisms with dominated splitting. Ergod. Theory Dyn. Syst. 35(3), 737–761 (2015)

    Article  Google Scholar 

  10. Collet, P., Eckmann, J.-P.: Positive Lyapunov exponents and absolute continuity for maps of the interval. Ergod. Theory Dyn. Syst. 3(1), 13–46 (1983)

    Article  Google Scholar 

  11. Colli, E., Vargas, E.: Non-trivial wandering domains and homoclinic bifurcations. Ergod. Theory Dyn. Syst. 21(6), 1657–1681 (2001)

    Article  MathSciNet  Google Scholar 

  12. Conley, C.C.: Isolated Invariant Sets and the Morse Index, vol. 38. American Mathematical Society, Providence (1978)

    Book  Google Scholar 

  13. Crovisier, S., Guarino, P., Palmisano, L.: Ergodic properties of bimodal circle maps. Ergod. Theory Dyn. Syst. 39(6), 1462–1500 (2019)

    Article  MathSciNet  Google Scholar 

  14. Fayad, B., Katok, A., Windsor, A.: Mixed spectrum reparameterizations of linear flows on \({\mathbb{T}}^2\). Mosc. Math. J. 1(4), 521–537 (2001)

    Article  MathSciNet  Google Scholar 

  15. Gaunersdorfer, A.: Time averages for heteroclinic attractors. SIAM J. Appl. Math. 52(5), 1476–1489 (1992)

    Article  MathSciNet  Google Scholar 

  16. Golenishcheva-Kutuzova, T., Kleptsyn, V.: Investigation of the convergence of the Krylov–Bogolyubov procedure in Bowen’s example. Mat. Zametki 82(5), 678–689 (2007)

    Article  MathSciNet  Google Scholar 

  17. Gourmelon, N.: A Franks’ lemma that preserves invariant manifolds. Ergod. Theory Dyn. Syst. 36(4), 1167–1203 (2016)

    Article  MathSciNet  Google Scholar 

  18. Hirsch, M.W.: Differential topology. Graduate Texts in Mathematics, vol. 33. Springer-Verlag, New York-Heidelberg (1976)

  19. Hofbauer, F., Keller, G.: Quadratic maps without asymptotic measure. Commun. Math. Phys. 127(2), 319–337 (1990)

    Article  MathSciNet  Google Scholar 

  20. Hu, H.Y., Young, L.-S.: Nonexistence of SBR measures for some diffeomorphisms that are “almost Anosov”. Ergod. Theory Dyn. Syst. 15(1), 67–76 (1995)

    Article  MathSciNet  Google Scholar 

  21. Jakobson, M.: Absolutely continuous invariant measures for one-parameter families of one-dimensional maps. Commun. Math. Phys. 81(1), 39–88 (1981)

    Article  MathSciNet  Google Scholar 

  22. Kiriki, S., Soma, T.: Takens’ last problem and existence of non-trivial wandering domains. Adv. Math. 306, 524–588 (2017)

    Article  MathSciNet  Google Scholar 

  23. Kleptsyn, V.: An example of non-coincidence of minimal and statistical attractors. Ergod. Theory Dyn. Syst. 26(3), 759–768 (2006)

    Article  MathSciNet  Google Scholar 

  24. Kwapisz, J., Mathison, M.: Diophantine and minimal but not uniquely ergodic (almost). Nonlinearity 25(7), 2027–2037 (2012)

    Article  MathSciNet  Google Scholar 

  25. Ledrappier, F.: Some properties of absolutely continuous invariant measures on an interval. Ergod. Theory Dyn. Syst. 1(1), 77–93 (1981)

    Article  MathSciNet  Google Scholar 

  26. Lyubich, M.: Almost every real quadratic map is either regular or stochastic. Ann. Math. 156, 1–78 (2002)

    Article  MathSciNet  Google Scholar 

  27. Mañé, R.: Ergodic Theory and Differentiable Dynamics, vol. 8. Springer, Berlin (2012)

    Google Scholar 

  28. Morales, C.A., Pacifico, M.J.: Lyapunov stability of \(\omega \)-limit sets. Discrete Contin. Dyn. Syst. A 8(3), 671–674 (2002)

    Article  MathSciNet  Google Scholar 

  29. Newhouse, S.E.: Lectures on dynamical systems. In: Dynamical systems (C.I.M.E. Summer School, Bressanone, 1978), pp. 1–114, Progr. Math., 8, Birkhäuser, Boston, Mass (1980)

  30. Palis, J., de Melo, W.: Geometric theory of dynamical systems. Springer, New York. An Introduction. Translated from the Portuguese by A.K. Manning (1982)

  31. Palis, J.: A global view of dynamics and a conjecture on the denseness of finitude of attractors. Astérisque 261(xiiixiv), 335–347 (2000)

    MathSciNet  MATH  Google Scholar 

  32. Potrie, R.: Generic bi-Lyapunov stable homoclinic classes. Nonlinearity 23(7), 1631 (2010)

    Article  MathSciNet  Google Scholar 

  33. Saghin, R., Sun, W., Vargas, E.: On Dirac physical measures for transitive flows. Commun. Math. Phys. 298(3), 741–756 (2010)

    Article  MathSciNet  Google Scholar 

  34. Saghin, R., Vargas, E.: Invariant measures for Cherry flows. Commun. Math. Phys. 317(1), 55–67 (2013)

    Article  MathSciNet  Google Scholar 

  35. Santiago, B.: Dirac physical measures for generic diffeomorphisms. Dyn. Syst. 33(2), 185–194 (2018)

    Article  MathSciNet  Google Scholar 

  36. Sigmund, K.: On dynamical systems with the specification property. Trans. Am. Math. Soc. 190, 285–299 (1974)

    Article  MathSciNet  Google Scholar 

  37. Takens, F.: Heteroclinic attractors: time averages and moduli of topological conjugacy. Bol. Soc. Bra. Mat. (N.S.) 25(1), 107–120 (1994)

    Article  MathSciNet  Google Scholar 

  38. Wang, Q., Young, L.-S.: Nonuniformly expanding 1d maps. Commun. Math. Phys. 264, 255–282 (2006)

    Article  MathSciNet  Google Scholar 

  39. Whitney, H.: Analytic extensions of differentiable functions defined in closed sets. Trans. Am. Math. Soc. 36(1), 63–89 (1934)

    Article  MathSciNet  Google Scholar 

  40. Young, L.-S.: Recurrence times and rates of mixing. Israel J. Math. 110, 153–188 (1999)

    Article  MathSciNet  Google Scholar 

  41. Young, L.-S.: What are SRB measures, and which dynamical systems have them? J. Stat. Phys. 108(5), 733–754 (2002)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Instituto de Matemática e Estatística, Universidade Federal Fluminense, Rua Professor Marcos Waldemar de Freitas Reis, s/n, Bloco H - Campus do Gragoatá, Niterói, RJ, CEP 24.210-201, Brazil

    Pablo Guarino & Bruno Santiago

  2. Sorbonne Université, Université de Paris, CNRS, Institut de Mathématiques de Jussieu-Paris Rive Gauche, 75005, Paris, France

    Pierre-Antoine Guihéneuf

Authors
  1. Pablo Guarino
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pierre-Antoine Guihéneuf
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bruno Santiago
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pablo Guarino.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

We warmly thank Sylvain Crovisier for his ideas concerning Theorem A, Christian Bonatti for the attention he paid to this work and Davi Obata for his reading of a first draft. We express our very great appreciation to the referee for very keen remarks leading to a considerable improvement of our exposition. P.G. and P.A.G were partially supported by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES) Grant 23038.009189/2013-05. P.A.G. was partially funded by the France-Brazil network (RFBM). P.A.G and B.S. were partially supported by a PEPS (CNRS) Grant. B.S. was partially financed by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001 and also acknowledges the support of Fondation Louis D—Institut de France (Project coordinated by M. Viana).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guarino, P., Guihéneuf, PA. & Santiago, B. Dirac Physical Measures on Saddle-Type Fixed Points. J Dyn Diff Equat 34, 983–1048 (2022). https://doi.org/10.1007/s10884-020-09911-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-020-09911-x

Keywords

Mathematics Subject Classification

Search

Navigation