Topics in Mathematical Pharmacology

Abstract

Mathematical analysis of pharmacological models is becoming increasingly relevant for drug development. Emphasis on mechanistic models has grown and qualitative understanding of complex biological systems has improved a great deal. In this paper we present two examples of basic modular processes which are involved in a wide range of physiological systems. The first model concerns the interaction of a drug with its target, the way the compounds bind and then elicit an effect. The second model is central in signal transduction across the cell wall. Both models demonstrate the complex and interesting dynamics which is directly relevant for the impact of the drug.

1 Introduction

In recent years, mathematical ideas and methods gain increasing traction in the pharmacological community, as it becomes evident that they can contribute to an understanding of complex physiological and biochemical processes as well as the analysis of complex data sets. With expanding knowledge about biological and physiological processes, thanks to results obtained in System Biology, systems-based studies are being carried out in which mathematical ideas about dynamical systems are used. We mention the modelling of complex regulatory networks such as studied by Fujioka et al. [11] and Sasagawa et al. [26].

Simultaneously, mathematical analysis is also contributing in translating insights about complex systems studied in Systems Biology into tools which the practical pharmacologist can use for making reliable predictions on the basis of limited data (cf. Benson et al. [5]). These tools often involve smaller systems of typical modules that are found in complex systems, or they may be models which focus on particular aspects of drug dynamics (cf. Hartwell et al. [14] and Shankaran et al. [27]). Their study is often referred to as Systems Pharmacology. For more detailed reviews we refer to Benson et al. [4] and [7].

In light of the increasing relevance of mathematical ideas and methods in the realm of pharmacology the time seems ripe to coin the term Mathematical Pharmacology for the field of study that is aimed at using mathematical approaches to achieve a better understanding of pharmacological processes. In this paper we present two examples of complex systems designed to address fundamental questions in pharmacology. Both examples involve mathematical models describing rich and complex dynamics. Gaining an understanding of these models: understanding the shape of their signature profiles, dissect the different processes which make up the full system and quantitively determine the impact of the different rate constants and concentrations of the compounds, not only serves increased pharmacological understanding, but also makes for fascinating mathematical challenges.

Target-mediated drug disposition. In 1994 Levy [17] introduced the concept of target-mediated drug disposition (TMDD) for the phenomenon of drug distribution through binding to the pharmacological target in the context of pharmacokinetic–pharmacodynamic (PKPD) behaviour. TMDD has featured prominently in the literature as a saturable clearance mechanism for biologics, in particular peptides, proteins and monoclonal antibodies (mAbs). Over the last few years a large body of literature has developed addressing the theoretical aspects of TMDD, typically based on mathematical analysis and simulations.

Signal transduction across the cell wall. Receptor tyrosine kinases (RTK’s) are high-affinity cell surface receptors for many polypeptide growth factors, cytokines, and hormones which straddle the cell wall and possess a binding domain, which faces extra-cellular space and a kinase domain, which faces the intra-cellular space. (cf. Haugh and Lauffenburger [16], Robinson et al. [25]). It is important to know how one can influence (inhibit or stimulate) cellular processes from outside the cell, i.e. from interstitial space, by binding a suitable compound to the binding domain of RTK’s, and to determine quantitatively the impact of such binding. This requires intimate knowledge of the dynamics of these proteins.

2 Target Mediated Drug Disposition (TMDD)

Target mediated drug disposition is the phenomenon in which a drug binds with high affinity to its pharmacological target, such as a receptor, to such an extent that this affects its pharmacokinetic characteristics (cf. Levy [17]).

The basic TMDD model introduced by Levy [17] (see also Sugiyama [28] and Mager and Jusko [19]) is shown schematically in Fig. 1: drug or ligand (L) binds the target (R) to form complex (RL). Drug and target are supplied and eliminated and complex is internalised. In many practical situations, the drug is also present in a peripheral compartment from which it may or may not be eliminated.

Fig. 1

Schematic description of the basic TMDD model

Mathematically, the TMDD model shown in Fig. 1 can be formulated as a system of three nonlinear ordinary differential equations, one for each compound:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}}{{ dt}} &{}=&{} -k_{\mathrm{on}} L \cdot R + k_{\mathrm{off}} RL - k_{\mathrm{el}}L \\ \dfrac{{ dR}}{{ dt}} &{}=&{} k_{\mathrm{syn}} - k_{\mathrm{deg}} R -k_{\mathrm{on}} L \cdot R + k_{\mathrm{off}} RL \\ \dfrac{{ dRL}}{{ dt}} &{}=&{} k_{\mathrm{on}} L \cdot R - (k_{\mathrm{off}}+ k_{\mathrm{int}})RL \end{array}\right. \end{aligned}$$

(2.1)

The symbols L, R and RL stand for the concentrations of ligand, target and ligand-target complex, $k_{\mathrm{on}}$ and $k_\mathrm{off}$ denote the second-order on- and first-order off-rate of the ligand. Ligand is eliminated according to a first order process involving the rate constant $k_{\mathrm{el}}= Cl/V_c$, where Cl denotes the clearance of ligand from the central compartment, and $V_c$ the volume of this compartment. Ligand-target complex is internalised according to a first order process with a rate constant $k_{\mathrm{int}}$. Finally, receptor synthesis and degeneration are, respectively, a zeroth order process ($k_{\mathrm{syn}}$) and a first order process ($k_{\mathrm{deg}}$).

Plainly, the steady state of this system is given by

$$\begin{aligned} L=0, \qquad R=R_0 \mathop {=}\limits ^{\mathrm{def}} \frac{k_\mathrm{syn}}{k_{\mathrm{deg}}}, \qquad RL=0 \end{aligned}$$

(2.2)

In this paper we focus on the dynamics of the TMDD-system (2.1) after an initial drug dose has been administered intravenously to the system in equilibrium, i.e., with $R(0)=R_0$ and $RL(0)=0$. The resulting initial drug concentration is denoted by $L_0$.

Remark 1

The TMDD model (2.1) is closely related to the classical Michaelis–Menten (MM) model [22] in enzyme kinetics:

$$\begin{aligned} S + E \begin{array}{c} {k_{\mathrm{on}}}\\ {\rightleftarrows }\\ {k_{\mathrm{off}}}\end{array} ~SE \mathop {\mathop {\longrightarrow }\limits ^{k_{\mathrm{int}}}} E + P \end{aligned}$$

(2.3)

Here S denotes the substrate, E the enzyme, SE the substrate-enzyme complex and P a product. Formally, the TMDD model reduces to the MM model when we put $k_{\mathrm{syn}}=k_{\mathrm{int}}R$ and $k_{\mathrm{deg}}=0$.

It has long been established that when the amount of substrate is much larger than the total amount of enzyme ($E_{\mathrm{tot}}=E+SE$)—which is a conserved quantity—then to good approximation

$$\begin{aligned} SE = E_{\mathrm{tot}} \cdot \frac{S}{K_m+ S} \qquad (\textit{The Langmuir equation}\, [15]) \end{aligned}$$

(2.4)

and that the substrate dynamics may be captured by the simpler model

$$\begin{aligned} \frac{dS}{dt}= - V_{\mathrm{max}}\frac{S}{K_m+ S} \qquad \text {where} \qquad V_{\mathrm{max}}=k_{\mathrm{int}}E_{\mathrm{tot}}, \qquad K_m= \frac{k_{\mathrm{off}}+k_{\mathrm{int}}}{k_{\mathrm{on}}} \end{aligned}$$

(2.5)

We shall see that comparable reductions can be established for the full TMDD model.

In contrast to linear first order elimination, TMDD leads to complex elimination dynamics. In Fig. 2 we show typical drug-versus-time data obtained after four iv bolus bolus administrations resulting in initial drug concentrations amounting to $L_0=30,\, 100, \, 300$ and 900 mg/L.

Fig. 2

Drug-time courses after four iv bolus dose administrations of $D=1.5,\, 5,\, 15$ and 45 mg/kg and a compartment volume of $V=0.05$ L/kg

Characteristic phases of the time course are easily identified in Fig. 2. Initially the data show a binding phase (A) followed by a linear phase (B), a nonlinear phase (C) and a second linear phase (D). For convenience we indicate the times of the transitions between by these phases by $T_1$ (A/B), $T_2$ (B/C) and $T_3$ (C/D). We observe in Fig. 2 that the times $T_2$ and $T_3$ shift to the right as the drug dose increases by a equal amounts $\Delta T$ which appear to be more or less proportional to the logarithm of the drug dose, $\log (D)$. The phases A, B, C and D are shown schematically in Fig. 3.

Fig. 3

The TMDD signature profile exhibiting four phases, which characterise different processes in the drug disposition

The TMDD model poses interesting challenges to pharmacologists and mathematicians alike.

$\bullet$ From the perspective of data analysis one would like to (i) Identify characteristic features in data sets of drug-versus-time series which call for a TMDD model. (ii) Exploit the complexity of the data set to draw conclusions about the underlying physiology, and (iii) Determine how physiological assumptions can be used to simplify the TMDD model and so make it possible to estimate the values of the parameters in the model when data is limited.

$\bullet$ From an analytical perspective, the TMDD model is very rich: it involves a series of different processes, each with its own time scale: (i) ligand-target binding, (ii) target internalisation, (iii) target synthesis and degradation, and (iv) ligand elimination. Combined with often very disparate ligand and target concentrations, this results in a variety of different types of dynamics.

Specifically, one would like to know how different parameters involved in the model affect the dynamics, and derive estimates for their impact, and determine for what parameter ranges the dynamics can be described by simpler models. This last question is important, because in many practical situations data are only available for the free drug concentration (L).

We conclude with a slightly different formulation of ligand and receptor dynamics which will prove very useful.

Conservation laws: In light of the rapid binding of ligand and receptor, the total amounts of free and bound drug and receptor,

$$\begin{aligned} L_{\mathrm{tot}}=L+RL\qquad \text {and}\qquad R_{\mathrm{tot}}=R+RL \end{aligned}$$

(2.6)

are very useful quantities in the analysis of the TMDD model. They satisfy the following balance equations:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}_{\mathrm{tot}}}{{ dt}} &{}=&{} - k_{\mathrm{el}}L - k_{\mathrm{int}}RL\\ \dfrac{{ dR}_{\mathrm{tot}}}{{ dt}} &{}=&{} k_{\mathrm{syn}} - k_{\mathrm{deg}} R - k_{\mathrm{int}}RL \end{array} \right. \end{aligned}$$

(2.7)

2.1 Simulations

In order to gain an impression of the dynamics of the three compounds we show simulations for the parameter values associated with the data set shown in Fig. 2. They are listed in Table 1.

Table 1 Parameter values

The dissociation constant $K_d$, and a related constant $K_m$ are here given by

$$\begin{aligned} K_d = \frac{k_{\mathrm{off}}}{k_{\mathrm{on}}} = 0.011~\text {mg/L}\qquad \text {and} \qquad K_m = \frac{k_{\mathrm{off}} + k_{e(RL)}}{k_{\mathrm{on}}} = 0.044~ \text {mg/L}. \end{aligned}$$

(2.8)

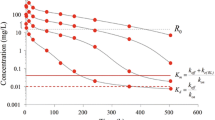
In Fig. 4 we show graphs of the concentrations of the three compounds versus time: free drug (L) on a semi-logarithmic scale, and free receptor (R), and receptor-drug complex (RL) on a linear scale.

Fig. 4

Graphs of L on a semi-logarithmic scale (left), and R (middle) and RL (right) on a linear scale, versus time. The parameters are listed in Table 1 and the initial receptor and receptor-drug complex value are the baseline concentrations, given by (2.2). The initial drug concentrations are $L_0$ = 30, 100, 300, 900 mg/L. The dashed line indicates the target baseline level $R_0$ and the dotted line the reference value $K_m$ defined in (2.8)

We make the following observations:

Drug dynamics:

(a) The drug concentration curves shown in Fig. 4 exhibit the signature profile shown in Fig. 3, except that the initial phase A appears to be absent.

(b) In Phase B, where $\log (L)$ is linear, the slope is independent of the dose, and shifts upwards as the drug dose increases. In addition, $R\approx 0$.

(c) Phase C is a transitional phase in which the ligand concentration suddenly drops more quickly. The timing of Phase C shifts— horizontally—to the right as the drug dose increases over a distance which appears to by approximately proportional to $\log (L_0)$.

(d) Phase D, in which $\log (L)$ is linear, is the terminal phase with slope $- \lambda _z$ which appears to be independent of the drug dose. For the parameter values of Table 1 one finds that $\lambda _z \approx k_{\mathrm{int}}=0.003 \hbox { h}^{-1}$ [24].

Receptor dynamics:

(a) Evidently, very quickly the drug binds the receptor, exhausting the initial receptor supply and raising the complex concentration to $R_0$.

(b) On a longer time scale, receptor is synthesised and binds to the drug to form additional drug-receptor complex. In fact, RL(t) climbs along a curve $\Gamma$ which starts at $RL(0)\approx R_0$ and ultimately levels off at some ceiling value $R_*$, as long as $R(t) \approx 0$. Over this period of time, the equation for $R_{\mathrm{tot}}$ in (2.7) becomes to good approximation

$$\begin{aligned} \frac{dR_{\mathrm{tot}}}{dt} = k_{\mathrm{syn}} - k_{\mathrm{int}}R_{\mathrm{tot}} \end{aligned}$$

(2.9)

since $R(t) \approx 0$ so that $R_{\mathrm{tot}} \approx RL$. Thus, as long as $R(t) \approx 0$ we have

$$\begin{aligned} RL(t) \approx R_{\mathrm{tot}} = R_* + (R_0-R_*)e^{-k_{\mathrm{int}}t}, \qquad R_* = \frac{k_{\mathrm{syn}}}{k_{\mathrm{int}}} \end{aligned}$$

(2.10)

In fact, one can prove the universal upper bound [24],

$$\begin{aligned} R_{\mathrm{tot}}(t) \le \max \{R_*,R_0\} \qquad \text {for} \qquad t \ge 0 \end{aligned}$$

(2.11)

(c) Beyond Phase C, R returns to $R_0$ and RL to 0. This phase also involves interesting dynamics as Fig. 5 clearly demonstrates.

Fig. 5

Graphs of $R_0-R$ (Left) and RL (Right) on a semi-logarithmic scale versus time (Note that $0<t<5000$ h in the left picture and $0<t<8000$ h in the right picture). The parameters are listed in Table 1, the initial receptor and receptor-drug complex value are the baseline values given by (2.2) and the initial drug concentrations are $L_0 = 30$, 100, 300, 900 mg/L

The drug-receptor complex RL decays mono-exponentially, whilst the graph of the receptor concentration R exhibits a kink and hence $R_0-R$ decays bi-exponentially. Eventually RL and $R_0-R$ decay with the same terminal slope $\lambda _z$, which is approximately equal to $k_{\mathrm{int}}$ for the parameter values of Table 1 [24].

2.2 Reduced Models

From the early studies of TMDD on, beginning with the paper of Mager and Jusko in [19], simplifications of the TMDD model have been proposed, based on assumptions about the underlying physiology. Below we describe a few.

1. The Constant Target Pool hypothesis. When no information about the target is available it is sometimes assumed that the target pool is constant, i.e.,

$$\begin{aligned} R_{\mathrm{tot}}(t) =R(t)+RL(t) = R_0 \qquad \text {for} \qquad t \ge 0 \end{aligned}$$

(2.12)

This is equivalent to assuming that $k_{\mathrm{deg}} = k_{\mathrm{int}}$. To see this we eliminate R from the second equation in the system (2.7) to obtain

$$\begin{aligned} \frac{dR_{\mathrm{tot}}}{dt} = k_{\mathrm{syn}} - k_{\mathrm{deg}} R_{\mathrm{tot}} +(k_{\mathrm{deg}}- k_{\mathrm{int}})RL \end{aligned}$$

(2.13)

It is now readily seen that in light of the initial data (2.2) we may conclude that $R_{\mathrm{tot}}(t) = R_0=k_\mathrm{syn}/k_{\mathrm{deg}}$ for all $t \ge 0$ if and only if $k_{\mathrm{deg}} = k_{\mathrm{int}}$.

Mager and Jusko [19] first studied this case (see also [23] and [18]). It is particularly interesting from an instructional point of view because the identity $R+RL=R_0$ makes it possible the eliminate one variable and so reduce (2.1) to a two dimensional system, which can be analysed in the Phase Plane. Thus, if R is eliminated, solutions can be studied geometrically as Orbits in the (L, RL)-plane, starting at the point $(L,RL)=(L_0,0)$ and converging to the origin (0,0).

2. The Quasi-Equilibrium (QE) hypothesis (cf. Mager and Krzyzanski [20]) assumes that within a brief initial period drug, target and drug-target complex reach (quasi-)equilibrium, i.e.,

$$\begin{aligned} L \cdot R = K_d \,RL \qquad \text {where} \qquad K_d = \frac{k_\mathrm{off}}{k_{\mathrm{on}}} \end{aligned}$$

(2.14)

and from then on remain in quasi-equilibrium.

3. The Quasi-Steady State (QSS) hypothesis (cf. Gibiansky et al. [12]) assumes that drug, target and internalisation quickly reach (quasi-)equilibrium so that

$$\begin{aligned} L \cdot R = K_m \,RL \qquad \text {where} \qquad K_m= \frac{k_\mathrm{off}+k_{\mathrm{int}}}{k_{\mathrm{on}}} \end{aligned}$$

(2.15)

and remain in quasi-steady state throughout later times.

Once in (quasi-)equilibrium or quasi-steady state, we have to good approximation:

$$\begin{aligned} RL = R_{\mathrm{tot}} \frac{L}{L + K} \qquad \text {where}\quad K=K_d ~~\text {or}~~ K=K_m \end{aligned}$$

(2.16)

Because rapid binding of drug to target is assumed, the QE and QSS approximations focus on the total drug concentration $L_{\mathrm{tot}}=L+RL$ and the total receptor concentration $R_{\mathrm{tot}}=R+RL$ as principal variables. They satisfy the system (2.7). When we eliminate $R=R_{\mathrm{tot}}-RL$ and RL through (2.16) we obtain the system

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}_{\mathrm{tot}}}{{ dt}} &{}=&{} - k_{\mathrm{el}}L - k_{\mathrm{int}}R_{\mathrm{tot}} \dfrac{L}{L + K}\\ \dfrac{{ dR}_{\mathrm{tot}}}{{ dt}} &{}=&{} k_{\mathrm{syn}} - k_{\mathrm{deg}} R_{\mathrm{tot}} +(k_{\mathrm{deg}}- k_{\mathrm{int}})R_{\mathrm{tot}} \dfrac{L}{L + K} \end{array} \right. \end{aligned}$$

(2.17)

where $K=K_d$ in the QE-approximation and $K=K_m$ in the QSS-approximation.

Finally, L is related to $L_{\mathrm{tot}}$ and $R_{\mathrm{tot}}$ through the implicit relation

$$\begin{aligned} L_{\mathrm{tot}} = L+RL= L + R_{\mathrm{tot}} \frac{L}{L + K} \end{aligned}$$

(2.18)

Because for each value of $R_{\mathrm{tot}}$ the right-hand side of (2.18) is a strictly increasing function of L, we may solve for L in terms of $L_{\mathrm{tot}}$ and $R_{\mathrm{tot}}$ to obtain the expression

$$\begin{aligned} L = F(L_{\mathrm{tot}},R_{\mathrm{tot}}) {\mathop {=}\limits ^{\mathrm{def}}} \frac{1}{2}\left\{ L_{\mathrm{tot}} - R_{\mathrm{tot}} -K + \sqrt{(L_{\mathrm{tot}} - R_{\mathrm{tot}} - K)^2+4 K L_{\mathrm{tot}}}\right\} \end{aligned}$$

(2.19)

When we substitute $L=F(L_{\mathrm{tot}},R_{\mathrm{tot}})$ into the system (2.17) we obtain two equations which only involve the total concentrations of drug $L_{\mathrm{tot}}$ and receptor $R_{\mathrm{tot}}$:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}_{\mathrm{tot}}}{{ dt}} &{}=&{} (k_{\mathrm{int}}- k_{\mathrm{el}}) F - k_{\mathrm{int}}R_{\mathrm{tot}}\\ \dfrac{{ dR}_{\mathrm{tot}}}{{ dt}} &{}=&{} k_{\mathrm{syn}} + (k_{\mathrm{int}}- k_\mathrm{deg})F -k_{\mathrm{int}} R_{\mathrm{tot}} \end{array} \right. \end{aligned}$$

(2.20)

What has been gained through this reduction is that the on- and off-rates of drug and target no longer feature individually in the model, but only in combination, through$K_d$ or $K_m$, in the expression for the function F.

4. QE or QSS hypothesis and constant target pool combined: Since $R_{\mathrm{tot}}$ is now constant and equal to $R_0$ it follows that (2.16) yields an expression for RL in terms of L. Using this expression in the ligand equation in the system (2.17) we obtain an equation in L only:

$$\begin{aligned} \frac{d}{dt}\left( L + R_{0} \frac{L}{L + K}\right) = - k_{\mathrm{el}}L - k_{\mathrm{int}} R_{0} \frac{L}{L + K} \end{aligned}$$

(2.21)

or

$$\begin{aligned} \frac{dL}{dt} = - \frac{\displaystyle {k_{\mathrm{el}}L + k_{\mathrm{int}} R_{0} \frac{L}{L + K}}}{\displaystyle {1 + \frac{R_0K}{(L + K)^2}}} \end{aligned}$$

(2.22)

This equation was first derived by Wagner in [29].

The question as to when the QE-approximation, and when the QSS-approximation is correct has been the subject of numerous investigations. This is a delicate issue and the answer may depend, not only on the parameter values, but also on the phase of the process. Thus, in some of the phases (A–D), one approximation is valid, whilst in different phases the other approximation holds. An example of this situation is shown in Fig. 6.

Fig. 6

Graph of $\Delta = L \times R - K_d\, RL$ for $L_0 = 300$ and 900 mg/L and the parameter values of Table 1 (In the figure $k_\mathrm{in}$ is $k_\mathrm{syn}$.)

Evidently, for the parameter values given in Table 1, the QE approximation is valid in the terminal phase (Phase D). This is consistent with the fact that for these parameter values, the terminal slope is approximately equal to $k_{\mathrm{int}}$ (cf. [24]). In the earlier Phase B, when the drug dose is large enough, we have $R(t) \approx 0$, and $dR/dt \approx 0$ (cf. Aston et al. [1] and [24]), so that we deduce from the equation for R in the system (2.1) that in this phase

$$\begin{aligned} \Delta {\mathop {=}\limits ^{\mathrm{def}}} L \times R-K_d \, RL = \frac{k_\mathrm{syn}}{k_{\mathrm{on}}}. \end{aligned}$$

(2.23)

We see this confirmed numerically in Fig. 6. Thus, in Phase B, the QE approximation does not hold. However, in that part of Phase B in which RL assumes its global maximum, i.e., $RL(t) \approx R_* = k_{\mathrm{syn}}/k_{\mathrm{int}}$ (cf. Eq. (2.10) and Fig. 4) we have

$$\begin{aligned} L \times R-K_d \, RL = \frac{k_{\mathrm{int}}}{k_{\mathrm{on}}} \cdot \frac{k_{\mathrm{syn}}}{k_{\mathrm{int}}} \approx \frac{k_{\mathrm{int}}}{k_{\mathrm{on}}} RL \qquad \Longrightarrow \qquad L \times R \approx K_m \, RL. \end{aligned}$$

(2.24)

Thus, in this period of time, the QSS approximation is valid.

The results above are confined to a single set of parameter values. It is an interesting question to delineate the conditions under which the two approximations are valid for a wider set of values. In this connection we mention the work of Gibiansky et al. [12] who show that the QE approximation fails when $k_{\mathrm{int}} \gg k_{\mathrm{off}}$.

We conclude with a model that is often used as a simpler alternative to the TMDD model.

5. The Michaelis–Menten model

In what is commonly referred to as the the Michaelis–Menten (MM) model, drug elimination is assumed to be partly first order linear ($k_{\mathrm{el}}$) and partly nonlinear and saturable, i.e.,

$$\begin{aligned} \frac{dL}{dt} = - k_{\mathrm{el}} L - V_{\mathrm{max}}\frac{L}{K+L} \end{aligned}$$

(2.25)

where the saturable term is modelled by a typical MM-function. Note the similarity of the Eqs. (2.22) and (2.25). Evidently,

$$\begin{aligned} \frac{d}{dt}\log (L) = - k_{\mathrm{el}} - \frac{V_{\mathrm{max}}}{K+L} \end{aligned}$$

(2.26)

The right hand side of this equation is an increasing function of L. Therefore, since L is decreasing with time, the graph of $\log (L)$ versus time is concave. This means that the MM model can only be used to fit data which exhibit only Phases B and C (cf. Bauer et al. [3]).

2.3 Discussion

Over the years a rich literature has built up about the TMDD model and its applications in data analysis. Below we briefly dwell upon a few topics.

$\bullet$ Mathematical analysis: The basic TMDD model (2.1) has been studied from a mathematical perspective in order to understand intrinsic properties of the system, such as the characteristic form of the signature profiles of drug-, receptor- and drug-receptor complex versus time and the subdivision phases A–D. In Peletier and Gabrielsson [23] and Ma [18] the system was analyzed subject to the restriction of a constant target pool, using phase plane methods to inspect the validity of the QE and the QSS approximation. Aston et al. [1] studied the initial binding Phase A estimating $R_{\mathrm{min}}$ and obtained conditions for initial overshoot after an iv bolus dose. In Peletier and Gabrielsson [24] the full system was studied, subject to a-priori assumptions on the parameter values: (i) a large affinity of drug to receptor, (ii) the elimination rate of ligand and receptor, and the internalization rate of complex are all comparable in size to $k_{\mathrm{off}}$ and (iii) $L_0>R_0$. This results in a sequence of well defined time scales, analytic estimates of the transition times of the different phases, and the corresponding values of the concentration of drug-, receptor- and drug-receptor concentration. It would be interesting to explore how robust these estimates are when some of the assumptions are relaxed.

$\bullet$ Peripheral compartment: In many practical situations the central compartment is connected to a peripheral compartment. Transfer between the central and peripheral compartment adds another time scale to the process and thus affects the concentration versus time graphs in the central compartment and the estimates obtained in [24] for the basic system (2.1). In particular, the initial behaviour will reveal the impact of distribution over the two compartments and in the long-term behaviour the effect on the terminal slope will show up, especially when the transfer between the two compartments is slow.

$\bullet$ Target in peripheral compartment: In a recent study Cao and Jusko [9] investigated the situation when the target is located in the interstitial fluid (ISF), i.e., in a peripheral compartment. It is found that the parameters which are related to the receptor and its binding to the drug, such as $R_{\mathrm{tot}}$, $K_{d}$, $K_{m}$ and $k_{\mathrm{int}}$ are affected. Thus, this calls for a generalisation of the analysis performed in Peletier and Gabrielsson [24], in which characteristic properties of the drug-versus-time graphs were interpreted in terms of properties and parameters in the model.

For recent reviews of the TMDD model and its literature we refer to Zheng et al. [31] and Dua et al. [10].

3 Dynamics of Receptor Tyrosine Kinases (RTK’s)

RTK’s are composed of small networks of reactions situated across the cell wall. In this section we dissect the dynamics of these networks and compare ways they can be exploited in order to influence cellular processes.

In Fig. 7 we give a schematic picture of a Receptor Tyrosine Kinase as it is situated on the cell wall between the Interstitial fluid compartment (IF) and the cellular compartment with its Binding domain facing the IF compartment and the Kinase domain facing the cell.

Fig. 7

Schematic picture of a Receptor Tyrosine Kinase situated on the cell wall with its Binding domain facing the interstitial fluid compartment and the Kinase domain facing the cellular compartment

On the left, the receptor in its free state, with its binding domain $R_1$ ¹ and its kinase domain $K_2$, the latter in equilibrium with the constant receptor pool $PK_2$. The receptor binds to an endogenous ligand $L_1$ in the IF compartment; the receptor-ligand complex is shown in the middle, with its binding domain $RL_1$ and its kinase domain $KL_2$, the latter shaded to highlight a conformational change. On the right $KL_2$ is shown in its phosphorylated state, denoted by $P_2$, which induces a cellular response.

Thus, the RTK ligand–receptor system involves the following system of reaction equations:

$$\begin{aligned} \left\{ \begin{array}{cc} \mathop {\mathop {\longrightarrow }\limits ^{k_{\mathrm{syn}}}} L_1 + R_1\begin{array}{c} {k_{\mathrm{Lf}}}\\ {\rightleftarrows }\\ {k_{\mathrm{Lb}}}\end{array} RL_1, &{}L_1 \mathop {\mathop {\longrightarrow }\limits ^{k_{\mathrm{deg}}}}, \\ R_1 \begin{array}{c} {Cl_{\mathrm{R12}}}\\ {\rightleftarrows }\\ {Cl_{\mathrm{R21}}}\end{array} K_2, &{}RL_1 {\begin{array}{c} {Cl_{\mathrm{K12}}}\\ {\rightleftarrows }\\ {Cl_{\mathrm{K21}}}\end{array}} KL_2 , \\ K_2 {\begin{array}{c} {k_{\mathrm{PKb}}}\\ {\rightleftarrows }\\ {k_{\mathrm{PKf}}}\end{array}} PK_2,&KL_2 \mathop {\mathop {\longrightarrow }\limits ^{k_{\mathrm{cat}}}} P_2 . \end{array}\right. \end{aligned}$$

(3.1)

We compare three ways of inhibiting a cellular process, i.e., the production of $P_2$. We do this by analysing the following scenarios.

(1) In Scenario 1 the inhibitor D binds the ligand and so prevents it from binding the receptor and forming the complex $RL_1$, which produces the product $P_2$. It is a large molecule drug, such as a mAb which is confined to the interstitial fluid.

(2) In Scenario 2 the inhibitor D binds the receptor as well as its ligand-complex. It is a small molecule drug which can move easily across the cell wall. It binds the receptor, and its ligand-complex, both on their binding domains and their kinase domains.

(3) In Scenario 3 the inhibitor is confined to the cell where it binds the receptor and its complex.

In the first two scenario’s drug action involves two compartments, the interstitial fluid and the cell, whilst in the third scenario drug action involves only one compartment, the cell. Thus, we compare (i) the impact of large and small molecule drugs, each with their own mode of action, and (ii) a two- and a one-compartment model for the small molecule.

The outline of this section is the following. We first give a brief description of the structure of the RTK-system in the absence of inhibitor: we derive the model, do some simulations, and sketch the underlying mathematical analysis. Then we model the three scenario’s and compare the impact of the inhibitor.

Mathematically the system of reaction equations (3.1) can be written by the following two systems of differential equations, one for the IF compartment:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}_1}{{ dt}} &{}=&{} k_{\mathrm{syn}} - k_{\mathrm{deg}} L_1 - k_{\mathrm{Lf}}L_1\cdot R_1 + k_{\mathrm{Lb}}RL_1, \\ \dfrac{{ dR}_1}{{ dt}} &{}=&{} - k_{\mathrm{Lf}}L_1\cdot R_1 + k_{\mathrm{Lb}}RL_1, \\ \dfrac{{ dRL}_1}{{ dt}} &{}=&{} k_{\mathrm{Lf}}L_1\cdot R_1 - k_{\mathrm{Lb}}RL_1, \end{array} \right. \end{aligned}$$

(3.2)

and one for the cellular compartment:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dK}_2}{{ dt}} &{}=&{} - k_{\mathrm{PKb}}K_2 + k_{\mathrm{PKf}}PK_2, \\ \dfrac{{ dKL}_2}{{ dt}} &{}=&{} -k_{\mathrm{cat}}KL_2, \\ \dfrac{{ dP}_2}{{ dt}} &{}=&{} k_{\mathrm{cat}}KL_2. \end{array} \right. \end{aligned}$$

(3.3)

The signal transduction across the membrane carried out by the receptors situated in the cell membrane, i.e., between $R_1$ and $K_2$ and between $RL_1$ and $KL_2$, is modelled by the following equations

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dR}^*_1}{{ dt}} &{}=&{} Cl_{\mathrm{R21}}K^*_2 - Cl_{\mathrm{R12}}R^*_1, \\ \dfrac{{ dRL}^*_1}{{ dt}} &{}=&{} Cl_{\mathrm{K21}}KL^*_2 - Cl_{\mathrm{K12}}RL^*_1, \end{array} \right. \end{aligned}$$

(3.4)

where $R_1^*$, $RL_1^*$, $K_2^*$ and $KL_2^*$ denote the number of molecules of these compounds, and $Cl_{\mathrm{R21}}$, $Cl_{\mathrm{R12}}$, $Cl_{\mathrm{K21}}$ and $Cl_{\mathrm{K12}}$ equilibrium constants (1/min).

To be consistent with Eqs. (3.2) and (3.3) in which the dependent variables are concentrations measured in micro-molars, we transform the quantities $R_1^*$ etc. into quantities measured in micro-molars. This involves dividing these quantities in the system (3.4) by the number of Avogadro $N_a$ and the respective volumes $V_1=V_{\mathrm{if}}$ or $V_2=V_c$:

$$\begin{aligned} R_1=\frac{R^*_1}{N_a V_1}, \qquad RL_1 = \frac{RL_1^*}{N_a V_1}, \qquad K_2=\frac{K^*_2}{N_a V_2}, \qquad KL_2 = \frac{KL_2^*}{N_a V_2}. \end{aligned}$$

(3.5)

With these new variables, the system (3.4) becomes

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dR}_1}{{ dt}} &{}=&{} \mu \,Cl_{\mathrm{R21}}K_2 - Cl_{\mathrm{R12}}R_1, \\ \dfrac{{ dRL_1}}{{ dt}} &{}=&{} \mu \,Cl_{\mathrm{K21}}KL_2 - Cl_{\mathrm{K12}}RL_1. \end{array}\right. \qquad \text {where} \quad \mu =\frac{V_2}{V_1}, \end{aligned}$$

(3.6)

Comparable equations can be derived for $K_2$ and $KL_2$.

Combining equations (3.2), (3.3) and (3.6) we obtain the following basic sets of differential equations:

For the compounds in the IF compartment:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}_1}{{ dt}} &{} =&{} k_{\mathrm{syn}} - k_{\mathrm{deg}} L_1 - k_{\mathrm{Lf}}L_1\cdot R_1 + k_{\mathrm{Lb}}RL_1, \\ \dfrac{{ dR}_1}{{ dt}} &{}=&{} \mu Cl_{\mathrm{R21}} K_2 - Cl_{\mathrm{R12}}R_1 -k_{\mathrm{Lf}}L_1\cdot R_1 + k_{\mathrm{Lb}}RL_1, \\ \dfrac{{ dRL}_1}{{ dt}} &{} =&{} \mu Cl_{\mathrm{K21}} KL_2 - Cl_{\mathrm{K12}}RL_1 + k_{\mathrm{Lf}}L_1\cdot R_1 - k_{\mathrm{Lb}}RL_1, \end{array}\right. \end{aligned}$$

(3.7)

and for the compounds in the cellular compartment:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dK}_2}{{ dt}} &{}=&{} \dfrac{ 1}{\mu }Cl_{\mathrm{R12}}R_1 - Cl_{\mathrm{R21}}K_2 - k_{\mathrm{PKb}}K_2 + k_{\mathrm{PKf}}PK_2, \\ \dfrac{{ dKL}_2}{{ dt}} &{} =&{} \dfrac{ 1}{\mu }Cl_{\mathrm{K12}}RL_1 - Cl_\mathrm{K21}KL_2 -k_{\mathrm{cat}}KL_2. \end{array}\right. \end{aligned}$$

(3.8)

This amounts to a system of five equations for the concentrations of five compounds. Once the dynamics of this system is known, the generation of the product $P_2$ follows from the equation

$$\begin{aligned} \frac{dP_2}{dt} = k_{\mathrm{cat}}KL_2. \end{aligned}$$

(3.9)

For simplicity we assume throughout that $Cl_{\mathrm{R12}}=Cl_\mathrm{R21}=Cl_{\mathrm{K12}}=Cl_{\mathrm{K21}}{\mathop {=}\limits ^{\mathrm{def}}}Cl$.

Remark 2

An elementary computation shows that when $k_{\mathrm{cat}}=0$ the steady state concentrations are given by:

$$\begin{aligned} L_1= L_0 {\mathop {=}\limits ^{\mathrm{def}}} \frac{k_{\mathrm{syn}}}{k_{\mathrm{deg}}} \qquad \text {and} \qquad K_2 = K_0 {\mathop {=}\limits ^{\mathrm{def}}}\frac{k_{\mathrm{PKf}}}{k_{\mathrm{PKb}}}PK_2 \end{aligned}$$

(3.10)

and

$$\begin{aligned} R_1 =R_0 {\mathop {=}\limits ^{\mathrm{def}} }\mu K_0 \qquad \text {and} \qquad RL_1=RL_0 { \mathop {=}\limits ^{\mathrm{def}} }\frac{k_{\mathrm{Lf}}}{k_{\mathrm{Lb}}} L_0 \cdot R_0. \end{aligned}$$

(3.11)

When $k_{\mathrm{cat}}>0$, ligand and receptor are eliminated as complex $KL_2$. On the other hand, ligand is supplied at a constant rate in the IF compartment and receptor is supplied from a constant receptor pool $PK_2$ in the cellular compartment. Therefore, concentrations drop and converge to lower, but still positive, limiting values. Since $KL_2$ is converted into product, ultimately $P_2$ will increase at a constant rate.

3.1 Simulations

In Fig. 8 we demonstrate the dynamics of the RTK system through a simulation of the system (3.7)–(3.9), which shows how the concentrations of the compounds $L_1$, $R_1$ and $RL_1$ in the IF compartment, and $K_2$, $KL_2$ and $P_2$ in the cellular compartment, evolve with time.

Fig. 8

Graphs of the six compounds versus time based on simulations of the full model defined by the systems (3.7)–(3.9) for parameter values from Table 2 and initial data from Table 3. The graphs of the compounds in the interstitial fluid compartment are solid and those in the cellular compartment are dashed. On the left the long time behaviour and on the right the short time behaviour. We see that the graphs of $R_1$ and $RL_1$ nearly coincide with those of, respectively, $\mu K_2$ and $\mu KL_2$

We take the parameter values for the ligand–receptor-membrane system from Sasagawa et al. [26]; they are listed in Table 2.

Table 2 Parameter values of the ligand–receptor system

Note that

$$\begin{aligned} K_L = \frac{k_{\mathrm{Lb}}}{k_{\mathrm{Lf}}} = 1 \times 10^{-5}~\mu \mathrm{M}, \qquad K_{P} = \frac{k_{\mathrm{PKb}}}{k_{\mathrm{PKf}}}= 0.34, \qquad K_\mathrm{el} = \frac{k_{\mathrm{cat}}}{k_{\mathrm{Lf}}}=0.16~\mu \mathrm{M}.\nonumber \\ \end{aligned}$$

(3.12)

For the volume of the interstitial fluid compartment $V_1$ and the cellular compartment $V_2$ we take $V_1=12$ L and $V_2=10^{-3}$ L. The former is a well known estimate and the latter is based on a neuron volume of 1 nL (cf. Groves and Rebec [13]) and a target population of neurons (e.g. containing pain sensors) of 1 million. This results in the estimate given for $V_2$. We denote the ratio of the two volumes by $\mu = V_2/V_1$; for the volumes quoted above, $\mu = 0.833 \times 10^{-4}$.

For the initial concentrations of the compounds we choose the steady state values of the concentrations of the compounds in the absence of inhibitor when there is no elimination of $KL_2$, i.e., when $k_{\mathrm{cat}}=0$. They are given in (3.10) and (3.11). For the parameter values shown in Table 2 they result in the values shown in Table 3. We assume that initially $P_2=0$.

Table 3 Initial concentrations in $\mu \hbox {M}$

The constant concentration of the receptor pool is taken to be $PK_2 = 0.020631\, \mu \hbox {M}$ (cf. Sasagawa et al. [26]).

We make the following observations:

$\bullet$ Over time, the compounds $L_1$, $R_1$ and $K_2$ converge towards steady states with a half-life $t_{1/2} \approx 400$ min, whilst $RL_1$ and $KL_2$ drop to very small values over a very short time ($t_{1/2} \approx 0.04$ min).

$\bullet$ Initially, $P_2$ rises very rapidly ($t_{1/2} \approx 0.04$ min) to a quasi-steady state or plateau value and then proceeds to rise slowly at an eventually constant rate.

$\bullet$ The graphs of $R_1$ and $\mu K_2$ and those of $RL_1$ and $\mu KL_2$ appear to coincide.

3.2 The Reduced Ligand–Receptor System

Thanks to the very large value of the permeability Cl of the membrane between the two compartments (cf. Table 2), the concentrations of the receptors at each side of the membrane converge very quickly ($t_{1/2} \approx 10^{-4}$ min) (cf. Benson et al. [6]) so that throughout we may assume that

$$\begin{aligned} \mu K_2 = R_1 \qquad \text {and} \qquad \mu KL_2 = RL_1. \end{aligned}$$

(3.13)

This makes it possible to reduce the model (3.7), (3.8) for the ligand–receptor system to one which involves only three differential equations:

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dL}_1}{{ dt}} &{} =&{} k_{\mathrm{syn}} - k_{\mathrm{deg}} L_1 - k_{\mathrm{Lf}}L_1\cdot R_1 + k_{\mathrm{Lb}}RL_1, \\ \dfrac{{ dR}_1}{{ dt}} &{}=&{} -\frac{1}{2}k_{\mathrm{Lf}}L_1\cdot R_1 + \frac{1}{2}k_{\mathrm{Lb}}RL_1 -\frac{1}{2}k_{\mathrm{PKb}}R_1 + \frac{1}{2} k_{\mathrm{PKf}} (\mu PK_2), \\ \dfrac{{ dRL}_1}{{ dt}} &{} = &{}\frac{1}{2}k_{\mathrm{Lf}}L_1\cdot R_1 - \frac{1}{2}k_{\mathrm{Lb}}RL_1 - \frac{1}{2}k_{\mathrm{cat}}RL_1. \end{array}\right. \end{aligned}$$

(3.14)

In addition, because of (3.13), the production of $P_2$, as given by equation (3.9), can be computed by means of the equation

$$\begin{aligned} \frac{d(\mu P_2)}{dt} = k_{\mathrm{cat}}RL_1. \end{aligned}$$

(3.15)

It is interesting to note that the system (3.14) is very similar to the basic model for TMDD (cf. equation (2.1) and Mager and Jusko [19]). In fact, were it not for the factor 1/2, the systems would be identical.

3.3 Mathematical Analysis of Reduced Ligand–Receptor System

We briefly summarise the main points of the analysis of the ligand–receptor system (3.14) given in Benson et al. [6], and present quantitative estimates of the short and long time scale displayed in Fig. 2.

In order to compare the different terms in (3.14) we introduce dimensionless variables using the initial concentrations of ligand ($L_0$), receptor ($R_0$) and complex ($RL_0$) as reference values for $L_1$, $R_1$ and $RL_1$, and $(k_\mathrm{Lf}R_0)^{-1}$ for the time t. Thus we put

$$\begin{aligned} x= \frac{L_1}{L_{0}}, \qquad y = \frac{R_1}{R_0}, \qquad z=\frac{RL_1}{RL_0}, \qquad \tau = k_{\mathrm{Lf}}R_0\, t. \end{aligned}$$

(3.16)

Translating the system (3.14) into these new dimensionless variables we obtain

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dx}}{d\tau } &{}=&{} a(1-x) - \left( x \cdot y - z\right) , \\ \dfrac{{ dy}}{d\tau } &{}=&{} - \frac{1}{2} b \left( x \cdot y - z\right) - \frac{1}{2} c \left( y - 1 \right) , \\ \dfrac{{ dz}}{d\tau } &{}=&{} \frac{1}{2}d \left( x \cdot y - z\right) - \frac{1}{2}e \,z, \end{array} \right. \end{aligned}$$

(3.17)

where we have defined the following dimensionless constants:

$$\begin{aligned} a = \frac{k_{\mathrm{deg}}}{k_{\mathrm{Lf}}R_0}, \qquad b = \frac{L_0}{R_0}, \qquad c = \frac{k_{\mathrm{PKb}}}{k_{\mathrm{Lf}}R_0}, \qquad d=\frac{K_L}{R_0}, \qquad e = \frac{k_{\mathrm{cat}}}{k_{\mathrm{Lf}}R_0}. \end{aligned}$$

(3.18)

For the parameter values quoted in Table 2 the constants $a, \dots , e$ become

$$\begin{aligned} a = 0.68, \qquad b = 5.9, \qquad c = 9.05, \qquad d= 2.04, \qquad e = 3.2 \times 10^4. \end{aligned}$$

(3.19)

Short-time behaviour. We observe that the constants a, b, c and d are all of moderate size, but that due to the large value of $k_{\mathrm{cat}}$, the constant e is very large. It can be shown (cf. [6]) that this implies that $z(\tau )$ is approximately given by the mono-exponential function

$$\begin{aligned} z(\tau _0) = \overline{z}+ (1-\overline{z})e^{-e \tau /2},\qquad \overline{z}= \frac{d}{e} = 0.64 \times 10^{-4}. \end{aligned}$$

(3.20)

In terms of the original variables this yields

$$\begin{aligned} RL_1(t) = {\overline{RL}}_1 + (RL_{0}-{\overline{RL}}_1)e^{-\frac{1}{2}k_{\mathrm{cat}}t}, \qquad {\overline{RL}}_1 = RL_{0}\, \overline{z}. \end{aligned}$$

(3.21)

Therefore, $RL_1(t)$ quickly drops off exponentially to a small plateau value ${\overline{RL}}_1$ with a half-life that amounts to

$$\begin{aligned} t_{1/2} = \frac{2}{k_{\mathrm{cat}}}\, \ln (2) \approx 0.023 ~~\text {min}. \end{aligned}$$

(3.22)

Over the same period of time, $P_2(t)$ climbs to its plateau value $\overline{P}_2$:

$$\begin{aligned} \mu \overline{P}_2 \approx k_{\mathrm{caat}} \int _0^\infty RL_1(s)\,ds \approx 2 RL_0. \end{aligned}$$

(3.23)

Large-time behaviour. After the initial rapid depletion of receptor–ligand complex, $z=RL_1/RL_0$ is very small, and remains so, so that $x(\tau )$ and $y(\tau )$ are well approximated by the solution of the reduced system obtained by putting $z=0$ in (3.17):

$$\begin{aligned} \left\{ \begin{array}{rcl} \dfrac{{ dx}}{d\tau } &{}=&{} a(1-x) - x \cdot y, \\ \dfrac{{ dy}}{d\tau } &{}=&{} - \frac{1}{2} b \, x \cdot y - \frac{1}{2} c \left( y - 1 \right) , \end{array}\right. \end{aligned}$$

(3.24)

whilst $z(\tau )$ is shown to be in quasi-steady state with $x(\tau )$ and $y(\tau )$, so that by (3.17),

$$\begin{aligned} d \left\{ x(\tau ) \cdot y(\tau ) - z(\tau )\right\} - e \,z(\tau ) = 0 \qquad \Longrightarrow \qquad z(\tau ) = \frac{d}{d+e} \, x(\tau ) \cdot y(\tau ). \end{aligned}$$

(3.25)

It is readily seen that

$$\begin{aligned} x(\tau ) \rightarrow x_{\mathrm{ss}}, \qquad y(\tau ) \rightarrow y_{\mathrm{ss}}\qquad \text {and} \qquad z(\tau ) \rightarrow z_{\mathrm{ss}} \qquad \text {as}\qquad \tau \rightarrow \infty , \end{aligned}$$

(3.26)

where $(x_{\mathrm{ss}},y_{\mathrm{ss}})$ is the unique equilibrium point of the system (3.24) and

$$\begin{aligned} z_{\mathrm{ss}} = \frac{d}{e + d}a(1-x_{\mathrm{ss}}). \end{aligned}$$

(3.27)

For the data of Table 2, the half-life of this convergence is estimated at $\tau _{1/2} = 0.55$. In terms of the original time variable this gives a half-life of $t_{1/2}$ = 295 min. We see this behaviour, and the estimate of the half-life, confirmed in the simulations shown in Fig. 8.

3.4 Inhibition

We consider two kinds of drugs:

Large molecule drugs, such as monoclonal antibodies (mAb). These drugs are confined to the IF compartment, where they may bind to the ligand:

$$\begin{aligned} D_1 + L_1 \begin{array}{c} {k_{\mathrm{Df}}}\\ {\rightleftarrows }\\ {k_{\mathrm{Db}}}\end{array} DL_1, \end{aligned}$$

(3.28)

and so, down the road, inhibit the formation of the product $P_2$.

Small molecule drugs. These drugs may pass through the cell wall, and inside the cell bind to the receptor and its complex in their respective kinase domains, $K_2$ and $KL_2$:

$$\begin{aligned} D_2 + K_2 \begin{array}{c} {k_{\mathrm{Df}}}\\ {\rightleftarrows }\\ {k_{\mathrm{Db}}}\end{array} DK_2 \qquad \text {and} \qquad D_2 + KL_2 \begin{array}{c} {k_{\mathrm{Df}}}\\ {\rightleftarrows }\\ {k_{\mathrm{Db}}}\end{array} DKL_2. \end{aligned}$$

(3.29)

We compare the impact of a large- and a small molecule drug through three scenario’s. In the first two scenario’s the drug is supplied to the IF compartment and in the third scenario, a small molecule drug is supplied to the cellular compartment from where it cannot escape into the IF compartment.

For the sake of transparency, the on- and off-rates of the drug are taken the same, whether it binds to the ligand, the receptor or the ligand–receptor complex. The rates are given in Table 4.

Table 4 Drug-related rates

In all three scenario’s we assume that drug, free and bound, does not degenerate.

The drug doses in the three scenario’s are the same: $D_1(0)=0.0,~0.1,~0.2,~0.3\, \mu \hbox {M}$ and $D_2(0)=0\, \mu \hbox {M}$.

In Fig. 9 we show how the concentration of the product $P_2$ (scaled by $\mu =V_2/V_1$) in the cellular compartment increases with time in each of the three scenario’s, and how the growth is inhibited by the drug, given in three doses.

Fig. 9

Growth of $\mu P_2$ over 6000 min ($=100\hbox { h} \approx 4$ days) in scenarios 1, 2 and 3 with parameters given by Table 2, initial data given by Table 3 and drug-related rates given by Table 4. The doses are $D_1(0)=0.0$, 0.1, 0.2, 0.3 and $D_2(0)=0$. The red - dashed - curve is obtained for $D_1(0)=0$ and $D_2(0)=0\,\mu \hbox {M}$ (Color figure online)

It is evident that in the third scenario—drug action in the cell only—the impact of the drug is much smaller than in the other two scenario’s for which the impact is of the same order, though larger for the large molecule drug than for the small molecule drug.

In order to understand these simulations, and obtain quantitative estimates for the impact of the drug, the RTK-model needs to be extended to include the drug reactions in the IF compartment and in the cell.

For the large molecule inhibitor, (Scenario 1) a model extending the RTK model which incorporates the drug action was developed by Benson et al. [6]. It was found that to good approximation

$$\begin{aligned} RL_1(t) = RL_{1;\mathrm{ss}}(1-e^{-t/T_L}), \qquad T_L = A_L \, \frac{D_0}{K_d}, \end{aligned}$$

(3.30)

where $RL_{1;\mathrm{ss}}$ is the steady-state concentration of $RL_1$ and $A_L$ a constant which is drug-independent. For the parameter values of Table 2 we obtain $A_L=607$ min. Therefore, in light of (3.9) and (3.13) we then conclude that

$$\begin{aligned} \mu \,P_2(t) = k_{\mathrm{cat}}\int _0^t RL_1(\tau )\,\tau = k_\mathrm{cat}\,RL_{1;\mathrm{ss}} \left( t- T_L+ O(e^{-t/T_L})\right) \end{aligned}$$

(3.31)

We see that eventually, the inhibitor causes a shift in the quantity $\mu P_2$ over a distance $T_L$ in time, and that this shift increases when the drug dose increases or the dissociation constant $K_d$ decreases.

For the small molecule inhibitor (Scenario 2) the RTK model had to be extended differently because (i) the drug binds the receptors and (ii) the drug is present in both compartments. Publication of this extension is in preparation (cf. Benson et al. [8]). We obtain:

$$\begin{aligned} \mu \,P_2(t) = k_{\mathrm{cat}}RL_{1;\mathrm{ss}} \left( t- T_S+ O(e^{-t/T_S}) \right) ,\qquad T_S = A_S \, \frac{D_0}{K_d}, \end{aligned}$$

(3.32)

where $A_S = 52$ min for the parameter values of Table 2. We see that the inhibitory effect is similar to that of the large molecule drug, except that the shift $T_S$ is smaller by a factor of O(10).

We conclude that under these conditions on drug dose and affinity the impact of the large molecule drug in Scenario 1, is significantly greater than that of the small molecule drug in Scenario 2. This is confirmed by the simulations shown in Fig. 9.

Finally, that Scenario 3 is so much inferior to the other two scenario’s can also understood from a detailed analysis as done in Benson et al. [8]. The main reason turns out to be that because $V_2 \ll V_1$ the amount of drug that is supplied is much smaller and hence, that free receptors are much sooner back up to their original level.

3.5 Discussion

We have seen how the three scenario’s compare when the drug properties such as binding rates to ligand and to receptor and the manner of administration (iv bolus) are the same. Plainly the third scenario, the “one-compartment” scenario, is inferior to the other two scenario’s whilst under these conditions, the large molecule and the small molecule inhibitor show comparable impact. Thus, in the context of an enquiry into understanding dose response relationships, this work emphasises the need for appropriate and accurate account of physiology.

It should be emphasised though that the conditions under which the three scenario’s have been compared are a little artificial: in practice, both drugs are eliminated, small molecule drugs rapidly, at such a rate that doses need to be repeated daily, whilst large molecule drugs much more slowly, so that the dosing period can be much longer. Also, the affinity of the large molecule drug is significantly larger than that of the small molecule drug. In Benson et al. [8] the two two-compartment scenario’s are compared under more realistic conditions.