1 Introduction

It is well known that hereditary indecomposability can be found in the structure of invariant sets of even very regular dynamical systems. Recall that a nondegenerate compact and connected set, continuum, is said to be indecomposable if it cannot be decomposed to the union of two proper subcontinua, and it is hereditarily indecomposable if every subcontinuum is indecomposable. Handel [26] showed that Bing’s pseudo-circle [11], a hereditarily indecomposable cofrontier, can appear as a minimal set for a \(C^\infty \)-smooth volume preserving planar diffeomorphism. A related example was given by Herman [28] in the complex plane. Quite recently Herman’s construction has been extended by Chéritat [21] to show that the pseudo-circle can also emerge as the boundary of a Siegel disk. Other prominent examples include those given by Kennedy and Yorke, who exhibited that there exist \(C^\infty \)-smooth dynamical systems in dimensions greater than 2 with uncountably many minimal pseudo-circles, and any small \(C^1\) perturbation of which manifests the same property (see [33, 34]). Curiously, it is still an open question whether hereditarily indecomposable continua admit dynamical systems with finite, nonzero entropy (see e.g. [41]). Since by a result of Ito ([31], Theorem 1) topological entropy of a diffeomorphism on a compact finite-dimensional Riemannian manifold must be finite, a potential solution could carry important new insights on the interplay between complexity of dynamics and topology of invariant sets. An important facet of this problem appears to be to determine the answer for shift homeomorphisms on inverse limits of graphs. On the one hand side, inverse limits of graphs are often used to construct attractors of dynamical systems on manifolds, where the dynamics on the attractor is conjugate to the shift homeomorphism (see e.g. [4, 6, 7, 19, 38, 43]). On the other hand, famously there are situations where the converse is true: a dynamical system on a manifold can be locally translated to the dynamics of a shift homeomorphism on an inverse system of graphs (see e.g. [9, 14, 48]). Note that, it is well known that many 1-dimensional hereditarily indecomposable continua, such as the pseudo-arc, pseudo-circle or pseudo-solenoids, can be obtained as inverse limits of graphs with a single bonding map (see [32]), and any such bonding map induces a shift homeomorphism on the inverse limit space (see Sect. 3) that, according to [8], extends to a homeomorphism of \({\mathbb {R}}^3\). In the case of the pseudo-arc, techniques to construct appropriate bonding maps on the unit interval were first developed by Henderson [27] (a nontransitive map with zero entropy) and Minc and Transue [37] (a transitive map, hence with positive entropy). It had been known for a while that a bonding map that generates the pseudo-arc as the inverse limit must have entropy at least \(\log (2)/2\), when positive [16], and recently it has been proved by Mouron [42] that such a positive entropy must be in fact infinite. The main ingredient of Mouron’s proof is the notion of stretching and taut cover, especially properties of taut covers (and patterns) of hereditarily indecomposable compacta [44]. In this paper we extend Mouron’s result and show that if the entropy is positive then there exists an entropy set with infinite entropy. Our approach is not restricted to interval and works for all inverse limits of topological graphs. Our result is obtained by a careful analysis of the structure of horseshoes in graph maps. The main ingredient of our proof is an old result of Brown [18] which associates a degree of “crookedness” to higher iterates of maps which define hereditarily indecomposable compacta as their inverse limits. Combined with a result of Ito, it also shows that if the attractor constructed this way in a compact finite-dimensional Riemannian manifold is hereditarily indecomposable, then the dynamical system must either have zero entropy, or be non-differentiable. In Sect. 4 we discuss an application of our results to hereditarily indecomposable circle-like continua. We show that when G is the circle and the degree of f is positive then the entropy is always infinite and the rotation set of f is nondegenerate. This shows that the Anosov-Katok type constructions of the pseudo-circle as a minimal set in volume-preserving smooth dynamical systems, or in complex dynamics, obtained previously by Handel [26], Herman [28] and Chéritat [21] cannot be modeled on inverse limits. This resembles a known fact for Hénon-type attractors: Williams [48] showed that every hyperbolic, one-dimensional, expanding attractor for a discrete dynamical system is topologically conjugate to the induced map on an inverse limit space based on a branched one-dimensional manifold, but Barge [5] proved that certain dynamical systems with Hénon-type attractors cannot me modeled on inverse limits. In addition, authors’ recent example of torus homeomorphism with an attracting pseudo-circle as Birkhoff-type attractor in [17] is non-differentiable and has infinite entropy (see Fig. 1).

Fig. 1
figure 1

Strange attractors, supporting annulus homeomorphisms with non-unique rotation numbers, obtained by a construction on an inverse limit of circles, as described in [17]

Full size image

2 Preliminaries

2.1 Entropy

Topological entropy is one of the most common measures of complexity of dynamical systems. The reader not familiar with this notion is referred to [1, 47] for more details. Below we recall only the main definitions related to this notion.

Given two finite open covers \(\mathcal {U}, \mathcal {V}\) of X we define the cover \(\mathcal {U}\vee \mathcal {V}\) by

$$\begin{aligned} \mathcal {U}\vee \mathcal {V}= \{U\cap V: U\in \mathcal {U}, V\in \mathcal {V}\}. \end{aligned}$$

For each \(n\ge 0\) we denote \(T^{- n} (\mathcal {U})=\left\{ T^{-n}(U)\; : \; U\in \mathcal {U}\right\} \). Similarly, for any \(0\le m\le n\) define

$$\begin{aligned} \mathcal {U}_m^n= T^{- m} (\mathcal {U})\vee T^{- m-1} (\mathcal {U})\vee \cdots \vee T^{- n} (\mathcal {U}). \end{aligned}$$

Denote by \(N (\mathcal {U})\) the minimal cardinality among all subcovers \(\mathcal {V}\subseteq \mathcal {U}\) and then define

$$\begin{aligned} h_{\text {top}}(f,\mathcal {U})= \limsup _{n\rightarrow +\infty } \frac{1}{n} \log N (\mathcal {U}_0^{n- 1}). \end{aligned}$$

Clearly, if \(\mathcal {V}\) is a subcover of \(\mathcal {U}\) then \(h_{\text {top}}(f,\mathcal {U})\le h_{\text {top}}(f, \mathcal {V})\). The topological entropy of (X, f) is defined by \( h_{\text {top}}(f)= \sup _{\mathcal {U}} h_{\text {top}}(f,\mathcal {U})\) where the supremum is taken over all open covers \(\mathcal {U}\) of X.

For any \(n\in \mathbb {N}\), the \(d_n\)-distance between \(x,y\in X\) is defined as

$$\begin{aligned} d_n(x,y):=\max _{0\le i\le n-1}\{d(f^{i}x,f^{i}y)\}. \end{aligned}$$

Fix a set \(A\subset X\) and \(\varepsilon >0\). A set \(S\subset A\) is \((n,\varepsilon )\) -separated for A if \(d_n(x,y)>\varepsilon \) for any distinct \(x,y\in S\). Denote \(s_n(A,\varepsilon ) = \sup ~\{|S|:S ~\text {is}~ (n,\varepsilon )-\text {separated for}~ A\}\) where |S| denotes the cardinality of S.

For any compact set \(A\subset X\) we define its topological entropy by

$$\begin{aligned} h_{\text {top}}(f,A)=\lim _{\varepsilon \rightarrow 0}\lim _{n\rightarrow \infty }\frac{\log s_n(A,\varepsilon )}{n}. \end{aligned}$$

Since X is compact, it is well known that \(h_{\text {top}}(f)=h_{\text {top}}(f,X)\). If the map f is clear from the context we simply write \(h_{\text {top}}(A)\).

Entropy pairs were introduced by Blanchard in [12] and later studied by various authors. The main feature related to entropy pairs is that the dynamical system has positive topological entropy if and only if it has an entropy pair. An important generalization of this concept are entropy sets, introduced in [22]. A set \(K\subset X\) with at least two points is an entropy set if for any finite open cover \(\mathcal {U}\) of X such that K is not contained in the closure of any of its elements we have \(h_{\text {top}}(f, \mathcal {U}) > 0\).

It is much easier to detect if a set is an entropy set, if we use the concept IE-tuples (the terminology comes from [35], but the concept appeared earlier in the literature, e.g. [29, Theorem 8.2]). We call a tuple \(x=(x_1, \ldots , x_k)\in X^k\) an IE-tuple if for every product neighborhood \(U_1\times \ldots \times U_k\) of x, the tuple \((U_1, \ldots ,U_k)\) has an independence set \(T\subset \mathbb {N}\) of positive upper density, that is for every finite subset \(P \subset T\) and function \(\zeta :P \rightarrow \left\{ 1, 2, \ldots , k\right\} \) we have \(\bigcap _{j\in P} f^{-j}(U_{\zeta (j)})\ne \emptyset \). Recall that the upper density of a set \(A\subset \mathbb {N}\) is the number \( \limsup _{n\rightarrow \infty }\frac{1}{n}\# (A\cap [0,n)). \) It is known (see [13, 29, 35]) that a set K, which is not a singleton, is an entropy set iff every finite selection of its points \(x_1,\ldots , x_n\in K\) forms an IE-tuple.

Note that the closure of an entropy set is an entropy set, so in this paper we will consider only closed entropy sets. By the same observation (and Zorn lemma), every entropy set is always contained in a maximal entropy set (in the sense of inclusion).

Positive entropy implies existence of entropy sets. It may happen however that there is no entropy set with entropy close to entropy of the map. The following simple example shows that entropy can be infinite, while every entropy set has finite entropy.

Example 2.1

Call a map g on a nondegenerate interval [a, b] n-fold, \(n \ge 2\) if

$$\begin{aligned} g(a+j(b-a)/n)= a+(b-a)(1+(-1)^{j+1})/2 \end{aligned}$$

for \(j=0,\ldots ,n\).

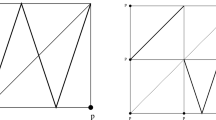
Put \(I_n=[1/2^{n}, 1/2^{n-1}]\) for \(n=1,2,\ldots \) and let \(f:[0,1]\rightarrow [0,1]\) be defined by \(f(0)=0\) and \(f|_{I_n}\) is \((2n+1)\)-fold map (see Fig. 2). Observe that f is continuous and \(h_{\text {top}}(f)=\infty \) since entropy of n-fold map is \(\log n\).

But every entropy set of f must be contained completely in one of the intervals \(I_n\) and hence its entropy is finite.

Fig. 2
figure 2

Sketch of the graph of map g in Example 2.1

Full size image

2.2 Graphs and Horseshoes

A (topological) graph is a continuum G which can be represented as a union of finitely many arcs, any two of them having at most one point in common. Each topological graph is homeomorphic to a simplical complex embedded in the Euclidean space \({\mathbb {R}}^3\) (see [40]), hence we may consider each graph G endowed with the taxicab metric, that is, the distance between any two points of G is equal to the length of the shortest arc in G joining these points. A set \(I\subseteq G\) is a closed interval if there is a homeomorphism \(\varphi :[0,1]\rightarrow I\) such that the set \(\varphi ((0,1))\) is open in G. A path in a graph G is any map \(\omega : [0,1]\rightarrow G\). If \(\omega :[0,1]\rightarrow G\) is a homeomorphism on its image and \(q,r\in [0,1]\) then we say that \(\omega ([q,r])\) is an arc in G and we denote it by \(\left\langle a,b\right\rangle \), where \(a=\omega (q)\) and \(b=\omega (r)\). In such a case, without loss of generality, we shall always assume that \(\omega \) is an isometry and we shall write \(t_1<t_2\) (resp. \(t_1\le t_2\)) for \(t_1,t_2\in \omega ([0,1])\) if \(\omega ^{-1}(t_1)<\omega ^{-1}(t_2)\) (resp. \(\omega ^{-1}(t_1)\le \omega ^{-1}(t_2)\)). We say that the set \((a,b)=\left\langle a,b\right\rangle \setminus \left\{ a,b\right\} \) is an open arc. Note that sometimes (a, b) is not open in G hence it is not interior of \(\left\langle a,b\right\rangle \) in G (however it is an open set in \(\left\langle a,b\right\rangle \)).

Given a map \(f:G\rightarrow G\) and arcs I, J in G we say that I f-covers J if there exists an arc \(K \subseteq I\) such that \(f (K) = J\). Properties of f-covering relation presented below are adapted from [2, p. 590].

Lemma 2.2

Let \(I,J,K,L\subseteq G\) be arcs, and let \(f, g:G\rightarrow G\).

  1. (1)

    If I f-covers I, then there exists \(x\in I\) such that \(f(x)=x\).

  2. (2)

    If \(I\subseteq K\), \(L\subseteq J\) and I f-covers J, then K f-covers L.

  3. (3)

    If I f-covers J and J g-covers K, then I \((g\circ f)\)-covers K.

  4. (4)

    If \(J\subseteq f(I)\), and \(K_1,K_2\subseteq J\) are arcs such that \(K_1\cap K_2\) is at most one point, then I f-covers \(K_1\), or I f-covers \(K_2\).

Fix an integer \(s\ge 2\). An s-horseshoe for f is an arc \(I\subseteq G\) and subarcs \(J_1,\ldots , J_s\) of I with pairwise disjoint interiors, such that \(f( S_j) = I\) for \(j = 1,\ldots , s\). An s-horseshoe is strong if in addition all the arcs \(J_i\) are contained in the interior of I and are pairwise disjoint. It is not hard to show that if f has an s-horseshoe for \(s\ge 4\) then it has an \((s-2)\)-strong horseshoe [36].

Definition 2.3

Let \(f:G\rightarrow G\) be a map of a graph G with metric d and let \(\varepsilon >0\). A path \(\omega :[0,1]\rightarrow G\) is \((f,\varepsilon )\)-crooked, if there exist s and t with \(0<s \le t<1\) such that \(d(f \circ \omega (s),f \circ \omega (1) ) \le \varepsilon \) and \(d(f\circ \omega (t),f \circ \omega (0)) \le \varepsilon \) (see Fig. 3).

Remark 2.4

It is an immediate consequence of the definition, that if for some \(\varepsilon >0\) and \(n>0\) the path \(\omega :[0,1]\rightarrow G\) is \((f^n,\varepsilon )\)-crooked then it is also \((f^{n+1},\varepsilon )\)-crooked.

Fig. 3
figure 3

\(\epsilon \)-crooked arc

Full size image

3 Graphs, Inverse Limits, Crookednes and Entropy Sets

Given a map \(f:X\rightarrow X\) on a metric space X, the inverse limit space \(X_f=\varprojlim (X,f)\) is the space given by

$$\begin{aligned} X_f=\left\{ (x_1,x_2,x_3,\ldots )\in X^\mathbb {N}:f(x_{i+1})=x_i\right\} . \end{aligned}$$

The topology of \(X_f\) is induced from the product topology of \(X^\mathbb {N}\), with the basic open sets in \(X_f\) given by

$$\begin{aligned} U_\leftarrow =\left( f^{i-1}(U),f^{i-2}(U),\ldots ,U,f^{-1}(U),f^{-2}(U),\ldots \right) , \end{aligned}$$

where U is an open subset of the i-th factor space X. The map f is called a bonding map and there is a natural homeomorphism \(\sigma _f:X_f\rightarrow X_f,\) called the shift homeomorphism, given by

$$\begin{aligned} \sigma _f(x_1,x_2,x_3,\ldots )=(f(x_1),f(x_2),f(x_3),\ldots )=(f(x_1),x_1,x_2,\ldots ). \end{aligned}$$

It is well known that \(\sigma _f\) preserves many dynamical properties of f. In particular, topological entropies of f and \(\sigma _f\) are the same (see [20] for details).

The following result of Brown [18, Lemma 3] will be crucial in the proof of our main results.

Lemma 3.1

Let G be a topological graph. If the inverse limit \(\varprojlim (G,f)\) is hereditarily indecomposable then for every \(\delta >0\) there is \(n>0\) such that each path \(\omega :[0,1]\rightarrow G\) is \((f^n,\delta )\)-crooked.

We will also need an important extension of the result of Misiurewicz and Szlenk first proved for interval maps, connecting topological horseshoes with positive topological entropy [36, Theorem B].

Lemma 3.2

If \(f:G\rightarrow G\) has positive topological entropy (i.e. \(h_{\text {top}}(f)>0\)) then there exist sequences \(\left\{ m_i\right\} _{i=1}^\infty \) and \(\left\{ k_i\right\} _{i=1}^\infty \) of positive integers such that for each n the map \(f^{m_n}\) has a \(k_n\)-horseshoe and

$$\begin{aligned} \limsup _{n\rightarrow \infty } \frac{1}{m_n} \log (k_n) = h_{\text {top}}( f ). \end{aligned}$$

If \(\left\langle a',b'\right\rangle \) is an arc, \(a'<a<b<b'\) and \(\varepsilon >0\) is such that \(d(a,a')\ge \varepsilon \) and \(d(b,b')\ge \varepsilon \) then, since distance on G is given by arc length, there are points \(a'\le a_\varepsilon \le a\) and \(b\le b_\varepsilon \le b'\) such that \(d(a,a_\varepsilon )=\varepsilon \) and \(d(b,b_\varepsilon )=\varepsilon \). Therefore we will use the following natural notation \(\left\langle a-\varepsilon ,b+\varepsilon \right\rangle =\left\langle a_\varepsilon ,b_\varepsilon \right\rangle \).

Lemma 3.3

Let G be a topological graph, \(\varepsilon >0\) be a number, and let \(\left\langle a-\varepsilon ,b+\varepsilon \right\rangle \) and \(\left\langle c,d\right\rangle \) be arcs in G. Fix any even integer \(k>0\) and let \(\delta <\varepsilon /6k\). If \(g:G\rightarrow G\) is a map such that \(\left\langle a-\epsilon ,b+\epsilon \right\rangle \subseteq g(\left\langle c,d\right\rangle )\) and each path in G is \((g, \delta )\)-crooked then there are points \(p_i,l_i\in \left\langle c,d\right\rangle \) such that

$$\begin{aligned} c\le l_1<p_1<\ldots < l_k<p_k\le d \end{aligned}$$

and such that one of the following conditions holds:

  1. (i)

    \(g(l_i)\in \left\langle a-\varepsilon ,a\right\rangle \), \(g(p_i)\in \left\langle b,b+\varepsilon \right\rangle \) for all \(1\le i\le k\), or

  2. (ii)

    \(g(p_i)\in \left\langle a-\varepsilon ,a\right\rangle \), \(g(l_i)\in \left\langle b,b+\varepsilon \right\rangle \) for all \(1\le i \le k\).

Proof

There are \(c\le l_1<p_k\le d\) such that \(g(l_1)=a-\varepsilon /2\), \(g(p_k)=b+\varepsilon /2\) or \(g(p_k)=a-\varepsilon /2\), \(g(l_1)=b+\varepsilon /2\).

Let us assume that \(g(l_1)=a-\varepsilon /2\), \(g(p_k)=b+\varepsilon /2\) (for the second case the proof is the same, and corresponds to (ii)). Since any path in G is \((g,\delta )\)-crooked, there are \(l_1<p_1<l_k<p_k\) such that

$$\begin{aligned} d(g(p_1),b+\varepsilon /2)<\delta \hbox { and }d(g(l_k),a-\varepsilon /2)<\delta . \end{aligned}$$

Next, let us assume that for some \(j\ge 1\), \(j<k/2\) there are points

$$\begin{aligned} c\le l_1<p_1<\ldots <l_j<p_j<l_{k-j+1}<p_{k-j+1}<\ldots <l_k<p_k\le d \end{aligned}$$

such that for \(i=1,2,\ldots , j\) we have

$$\begin{aligned} g(p_{k-i}),g(p_i)\in \left\langle b+\varepsilon /2-2(i-1)\delta , b+\varepsilon /2+2(i-1)\delta \right\rangle , \end{aligned}$$

and

$$\begin{aligned} g(l_{k-i}),g(l_i)\in \left\langle a-\varepsilon /2-2(i-1)\delta ,a-\varepsilon /2+2(i-1)\delta \right\rangle . \end{aligned}$$

Using again the fact that g is \(\delta \)-crooked, there are

$$\begin{aligned} p_i<l_{i+1}<p_{k-i}<l_{k-i+1} \end{aligned}$$

such that

$$\begin{aligned} g(l_{i+1})\in & {} \left\langle g(l_{i})-\delta ,g(l_{i})+\delta \right\rangle \\\subseteq & {} \left\langle a-\varepsilon /2-(2i-1)\delta ,a-\varepsilon /2+(2i-1)\delta \right\rangle , \end{aligned}$$

and

$$\begin{aligned} g(p_{k-i})\in & {} \left\langle g(p_{k-i+1})-\delta ,g(l_{k-i+1})+\delta \right\rangle \\\subseteq & {} \left\langle b+\varepsilon /2-(2i-1)\delta ,b+\varepsilon /2+(2i-1)\delta \right\rangle . \end{aligned}$$

Similarly, there are

$$\begin{aligned} l_{i+1}<p_{i+1}<l_{k-i}<p_{k-i} \end{aligned}$$

such that

$$\begin{aligned} g(p_{i+1})\in & {} \left\langle g(p_{k-i})-\delta ,g(l_{k-i})+\delta \right\rangle \\\subseteq & {} \left\langle b+\varepsilon /2-2i\delta ,b+\varepsilon /2+2i\delta \right\rangle .\\ g(l_{k-i})\in & {} \left\langle g(l_{i+1})-\delta ,g(l_{i+1})+\delta \right\rangle \\\subseteq & {} \left\langle a-\varepsilon /2-2i\delta ,a-\varepsilon /2+2i\delta \right\rangle , \end{aligned}$$

By induction on \(j=1,2,\ldots ,k/2\), we eventually obtain that there are \(c\le l_1<p_1<\ldots < l_k<p_k\le d\) such that for \(i=1,\ldots ,k\) we have

$$\begin{aligned} g(l_i)\in \left\langle a-\varepsilon /2-k\delta ,a-\varepsilon /2+k\delta \right\rangle \subseteq \left\langle a-\varepsilon ,a\right\rangle \end{aligned}$$

and

$$\begin{aligned} g(p_i)\in \left\langle b+\varepsilon /2-k\delta ,b+\varepsilon /2+k\delta \right\rangle \subseteq \left\langle b,b+\varepsilon \right\rangle . \end{aligned}$$

The proof is complete.\(\square \)

We have now collected enough tools to prove that the entropy of maps with hereditarily indecomposable inverse limits cannot be bounded, because the size of horseshoes grows very fast when the iteration increases.

Lemma 3.4

Let G be a topological graph, assume that the inverse limit \(\varprojlim (G,f)\) is hereditarily indecomposable. Let J, L be closed intervals such that \(J\subset int L\) and there is \(n>0\) such that J \(f^n\)-covers L. Then for every \(\alpha >0\) there are \(m,k>0\) and pairwise disjoint intervals \(J_0,J_1,\ldots ,J_k\subset J\) such that \(J_i\) \(f^{mn}\)-covers L for each \(i=0,\ldots ,k\) and

$$\begin{aligned} \frac{1}{mn} \log (k)>\alpha . \end{aligned}$$

Proof

Fix any integer \(\tilde{k}>0\) such that \(\frac{1}{n} \log (\tilde{k})>\alpha \). Denote \(g=f^{n}\) and \(r=\tilde{k}^2\). Without loss of generality we may assume that \(g(J)=L\). Therefore, there are \(\varepsilon >0\) and \(a<b\) such that \(J\subseteq (a,b)\subset (a-2\varepsilon ,b+2\varepsilon )\subset L\). Fix any \(\delta <\varepsilon /6r\) and let s be provided by Lemma 3.1, that is each path in G is \((g^s,\delta )\)-crooked. Arc J for g can be “iterated” for \(g^s\), that is we may replace J by its subinterval \(J'\) in such a way that \(g^s(J')=L\).

Let us apply Lemma 3.3 to \(\left\langle c',d'\right\rangle =J'\subset J=\left\langle c,d\right\rangle \) obtaining numbers \(c'\le l_1<p_1<\ldots <l_r<p_r\le d'\) and for simplicity of notation suppose that \(g^s(l_j)\in \left\langle a-\varepsilon ,a\right\rangle \) and \(g^s(p_j)\in \left\langle b,b+\varepsilon \right\rangle \) for all j (the arguments for the symmetric case \(g^s(p_j)\in \left\langle a-\varepsilon ,a\right\rangle \) and \(g^s(l_j)\in \left\langle b,b+\varepsilon \right\rangle \) are the same). Then, since we may view \(g^s :J' \rightarrow L\) as a map between subintervals of the real line, a simple argument shows that each arc \(\langle l_j,p_j\rangle \) \(g^s\)-covers J. Hence, there are arcs \(J_{1},\ldots , J_{r}\) such that \(g^s(J_i)=J\) and since \(g(J)=L\) we obtain that each \(J_{i}\) \(g^{s+1}\)-covers L. But each path in G is also \((g^{s+1},\delta )\)-crooked, so we can continue this procedure recursively. After s steps, we obtain pairwise disjoint arcs \(J_{i_1,i_1,i_2,\ldots , i_s}\subseteq J\), \(i_1,\ldots ,i_s\in \left\{ 1,\ldots , r\right\} \), such that each arc \(J_{i_1,i_2,\ldots , i_s}\) \(g^{2s}\)-cover L. Then there are at least \(r^s\) pairwise disjoint intervals which \(g^{2s}\)-cover \(\left\langle a-\varepsilon ,b+\varepsilon \right\rangle \).

But then easy calculation yields that

$$\begin{aligned} \frac{1}{n}\frac{1}{2s}\log (r^s) \ge \frac{1}{2n}\log (r) \ge \frac{1}{n} \log (\tilde{k}) > \alpha \end{aligned}$$

hence it is enough to put \(k=r^s\) and \(m=2s\) to end the proof.\(\square \)

Theorem 3.5

Let G be a topological graph. If the inverse limit \(\varprojlim (G,f)\) is hereditarily indecomposable and \(h_{top}(f)>0\) then there exists an entropy set A such that \(h_{top}(A)=\infty \).

Proof

Take any \(\alpha >0\) such that \(h_{top}(f)>\alpha \). By Lemma 3.2 there are \(s,k>0\) such that \(\frac{1}{s} \log (k)>\alpha \) and a strong \((k+1)\)-horseshoe \(J_0,\ldots ,J_k\subset int L\) for \(f^s\).

Next we will present a method for enlarging invariant sets induced by horseshoes. For this purpose, suppose that we have constructed pairwise disjoint intervals \(J_0,\ldots ,J_k\subset int L\) and there is \(s>0\) such that each \(J_i\) \(f^s\)-covers L. By Lemma 3.4 for every \(N>0\) there are \(r,m>0\) and pairwise disjoint intervals \(I_0,I_1,\ldots ,I_r\subset J_0\) such that \(I_i\) \(f^{sm}\)-covers L for each \(i=0,\ldots ,r\), and

$$\begin{aligned} \frac{1}{sm} \log (r)>N \alpha . \end{aligned}$$

Furthermore, by the definition of horseshoe, for every \(w\in \left\{ 1,\ldots ,k\right\} ^{m}\) there is an interval J(w) such that \(f^{sj}(J(w))\subset J_{w(j)}\) for all \(0\le j<m\) and \(f^{sm}(J(w))=L\). Simply we put \(J(w)=\bigcap _{j=0}^{m-1}f^{-sj}(J_{w_j})\). In particular intervals J(w), \(w\in \left\{ 1,\ldots ,k\right\} ^{m}\) form a (strong) horseshoe for \(f^{sm}\) in L. Intervals \(I_0,I_1,\ldots ,I_r\subset J_0\), hence we can add them to the collection of intervals J(w) obtaining a larger horseshoe (with \(k^{m}+r+1\) elements).

Now we will present a construction from the proof of Proposition II.15 in [15]. While the construction is standard, we will need to make some essential modifications in two places, so we need to recall this construction briefly. For each \(a\in \left\{ 1,\ldots ,k\right\} \) write \(J(a)=J_a\). Since \(J_1,\ldots , J_k\) is a strong horseshoe for \(f^s\), for every \(a,b\in \left\{ 1,\ldots , k\right\} \) we can find an interval \(J(ab)\subset J(a)\) such that \(f(J(ab))=J(b)\).

Next, fix n and assume that for any sequence \(a_1,\ldots , a_n\in \left\{ 1,\ldots , k\right\} \) we have already constructed intervals

$$\begin{aligned} J(a_1 a_2\ldots a_n)\subset J(a_1 a_2\ldots a_{n-1})\subset \ldots \subset J(a_1 a_2)\subset J(a_1) \end{aligned}$$
(1)

and \(f^s(J(a_1 a_2\ldots a_{k}))=J(a_2\ldots a_{k})\) for every \(2\le k\le n\)

By the above construction, for any sequence \(\xi \in \left\{ 1,\ldots , k\right\} ^\mathbb {N}\) the set \(A_\xi =\bigcap _{i=1}^\infty J(\xi _1\xi _2\ldots \xi _i)\) is a nonempty interval, because it is an intersection of a nested sequence of closed intervals. Let \(\Lambda \) be a set that consists of endpoints of all possible sets \(A_\xi \). That way we obtain an invariant set \(\Lambda \subset L\) for \(f^s\) and a continuous onto map \(\pi :\Lambda \rightarrow \Sigma _k\) such that \(\pi \) is one-to-one for all but countably many points, \(\sigma :\Sigma _k\rightarrow \Sigma _k\) is the full shift on k symbols and \(\pi \circ f^s=\sigma \circ \pi \). Namely, \(\pi \) sends endpoints of \(A_\xi \) to \(\xi \) but it may happen that some (but at most countably many) intervals \(A_\xi \) are nondegenerate.

We have to make one important remark at this point. In the case that \(A_\xi \) is an interval, it could happen that one of its endpoints is isolated in \(\Lambda \). To remedy this situation we can take \(x\in \Lambda \) such that \(\pi (x)\) has dense orbit in \(\Sigma _k\) and \(\pi ^{-1}\pi (x)\) is a singleton. Then x is recurrent, \(\hat{\Lambda }=\overline{\left\{ f^{sn}(x):n\ge 0\right\} }\) is a closed \(f^s\)-invariant set without isolated points, and \(\pi (\hat{\Lambda })=\Sigma _k\). Therefore in what follows, we assume that sets \(\Lambda \) constructed by the use of horseshoe are without isolated point.

Furthermore observe that if we take intervals \(J_w=J(w)\), \(w\in \left\{ 1,\ldots ,k\right\} ^{m}\) then we obtain a strong horseshoe for \(f^{sm}\). If we fix \(w_1, w_2\in \left\{ 1,\ldots ,k\right\} ^{m}\) then by the construction \(J(w_1 w_2)\subset J_{w_1}\) and \(f^{sm}(J(w_1w_2))=J_{w_2}\). Hence, in the construction of invariant set for \(f^{sm}\) and horseshoe \(J_w\), \(w\in \left\{ 1,\ldots ,k\right\} ^{m}\) we can take \(J((w_1)(w_2))=J(w_1w_2)\) and extend it inductively on the longer sequences of symbols \(J((w_1)(w_2)\ldots (w_n))=J(w_1w_2\ldots w_n)\). Condition (1) ensures that

$$\begin{aligned} A_\xi= & {} \bigcap _{i=1}^\infty J(\xi _1\xi _2\ldots \xi _i)=\bigcap _{i=1}^\infty J(\xi _1\xi _2\ldots \xi _{ni})\\= & {} \bigcap _{i=1}^\infty J((\xi _1\ldots \xi _{n})(\xi _{n+1}\ldots \xi _{2n})\ldots (\xi _{n(i-1)+1}\ldots \xi _{ni})) \end{aligned}$$

using horseshoe J(w), \(w\in \left\{ 1,\ldots ,k\right\} ^{m}\) we obtain the same set \(\Lambda \), but now it is invariant for \(f^{sm}\) and connecting factor map is now \(\hat{\pi }:\Lambda \rightarrow \Sigma _{k^m}\). This immediately implies, that using the above extension of horseshoe, if \(\Lambda \) was \(f^{s}\)-invariant set produced using horseshoe \(J_1,\ldots , J_k\) and \(\Gamma \) is \(f^{sm}\)-invariant set constructed using horseshoe consisting of sets J(w), \(w\in \left\{ 1,\ldots ,k\right\} ^{m}\) together with \(I_i\), \(0\le i \le r\) then \(\Lambda \subset \Gamma \) and we can extend \(\hat{\pi }\) to a map \(\hat{\pi }:\Gamma \rightarrow \Sigma _{k^m+r}\). As before, we may assume that \(\Gamma \) does not have isolated points.

By the construction \(h_{top}(\Lambda )\ge \frac{1}{s}\log (k)\) and

$$\begin{aligned} h_{top}(\Gamma )= h_{\text {top}}(f^{sm}|_\Gamma )=\frac{1}{sm}\log (k^m+r)>\frac{1}{sm}\log (r). \end{aligned}$$

Recall that if \(\pi \) is a factor map, and \(x_1,\ldots ,x_n\) is an IE-tuple, then the fiber \(\pi \times \ldots \times \pi (\left\{ (x_1,\ldots ,x_n)\right\} )\) contains at least one IE-n-tuple (see elementary properties of entropy tuples, e.g. in [29]). But \(\pi \) is one-to-one on all but countably many points and sets \(\Lambda , \Gamma \) do not have isolated points, hence it is not hard to see that \(\Lambda \) (the same for \(\Gamma \)) is an entropy set, since \(\Sigma _k\) is an entropy set. Namely, in arbitrarily neighborhood of any tuple of distinct points \(x_1,\ldots , x_n\) in \(\Lambda \) we can find a tuple which is IE n-tuple, and hence \((x_1,\ldots ,x_n)\) is IE n-tuple itself. Then by the above procedure we can construct a sequence of closed entropy sets \(\Lambda _1\subset \Lambda _2\subset \ldots \) such that \(h_{top}(\Lambda _n)\ge n\alpha \). Now, if we denote \(D=\overline{\bigcup _j \Lambda _j}\) then clearly D is also an entropy set, but now \(h_{top}(D)=\infty \).\(\square \)

As a consequence of Lemma 3.4 we easily obtain the following result. It is a direct consequence of Theorem 3.5, but proving it this way would be overcomplicated.

Corollary 3.6

Let G be a topological graph. If the inverse limit \(\varprojlim (G,f)\) is hereditarily indecomposable and \(h_{\text {top}}(f)>0\) then \(h_{\text {top}}(f)=\infty \).

Proof

If \(h_{\text {top}}(f)>0\) then by Lemma 3.2 there is n such that \(f^n\) has a 3-horseshoe. In particular, if we denote by J the middle interval of three intervals defining 3-horseshoe, then J satisfies assumptions of Lemma 3.4 and hence for every \(\alpha >0\) there are m, k such that

$$\begin{aligned} h_{\text {top}}(f)=\frac{1}{mn}h_{\text {top}}(f^{mn})\ge \frac{1}{mn}\log (k)>\alpha . \end{aligned}$$

The proof is finished.\(\square \)

Corollary 3.6 has an important consequence for smooth dynamical systems on compact finite-dimensional Riemannian manifolds, when combined with the following result of Ito.

Theorem 3.7

(Ito [31]) Let (M, g) be a compact n-dimensional Riemannian manifold and \(F:M\rightarrow M\) a \(C^1\)-diffeomorphism. Then \(h_{\text {top}}(F)\), the topological entropy of F, is finite.

Corollary 3.8

Let (M, g) be a compact n-dimensional Riemannian manifold and \(F:M\rightarrow M\) be a homeomorphism with an invariant hereditarily indecomposable continuum X; i.e. \(F(X)=X\). If F|X is conjugate to a shift homeomorphism on a graph inverse limit \(\varprojlim (G,f)\) then either \(h_{\text {top}}(F)=0\) or F is non-differentiable.

4 Circle-Like Hereditarily Indecomposable Continua and Entropy

There is a well known example of Henderson [27], who proved that shift homeomorphism on the pseudo-arc can have zero topological entropy. For the pseudo-circle, there is also an important example of Handel [26] who constructed a homeomorphism on the pseudo-circle (extendable to the whole plane) with zero topological entropy. Related results in complex dynamics were obtained by Herman [28] and Chéritat [21]. The natural question is whether the example of [27] can be somehow generalized to obtain the pseudo-circle as an inverse limit with one bonding map and with zero entropy. So far such an example was not constructed. We will show, that the reason for lack of such an example is very natural. Simply, such an example does not exist. This situation is in some sense similar to the case of Hénon-type attractors. First, Williams showed that every hyperbolic, one-dimensional, expanding attractor for a discrete dynamical system is topologically conjugate to the induced map on an inverse limit space based on a branched one-manifold [48]. Later Barge showed, however, that certain dynamical systems with Hénon-type attractors cannot me modeled on inverse limits [5].

In this section we are going to show that if \(\Lambda _f=\varprojlim ({\mathbb {S}}^1, f)\) is hereditarily indecomposable, but \(\Lambda _f\) is not the pseudo-arc, then \(h_{\text {top}}(f)=\infty \). In particular, one cannot construct a finite entropy homeomorphism on the pseudo-circle, or pseudo-solenoids conjugate to the shift homeomorphism on \(\varprojlim ({\mathbb {S}}^1, f)\). Recall that hereditarily indecomposable circle-like continua were classified by Fearnley [25] and Rogers [45]. The classification depends on the degree of the bonding map. According to the classification any continuum in this class is one of the following:

  • (\(\mathrm{deg}(f)=0\)) Knaster’s pseudo-arc: the unique arc-like hereditarily indecomposable continuum.

  • (\(|\mathrm{deg}(f)|=1\)) R.H. Bing’s pseudo-circle: the unique plane separating hereditarily indecomposable circle-like continuum.

  • (\(|\mathrm{deg}(f)|>1\)) Nonplanar pseudosolenoids: an uncountable family of continua.

Note that every proper subcontinuum of either hereditarily indecomposable circle-like continuum must be arc-like and hereditarily indecomposable so it is homeomorphic to the pseudo-arc.

In what follows we will use some standard fact on rotation numbers and sets for maps on the circle. The reader not familiar with this topic is refereed to Chapter 3 in [1].

We will need the following result of Auslander and Katznelson [3], which extends the classification of periodic-point-free circle homeomorphisms, and implies that every periodic-point-free circle map is semi-conjugate to an irrational rotation.

Theorem 4.1

Suppose \(f:{\mathbb {S}}^1\rightarrow {\mathbb {S}}^1\) is such that \(\mathrm{Per}(f)=\emptyset \). Then

  1. (1)

    for every \(x\in {\mathbb {S}}^1\) there is an interval \(J_x=[a_x,b_x]\) such that \(x\in J_x\),

  2. (2)

    \(f(J_x)\) is an interval with endpoints \(f(a_x)\) and \(f(b_x)\),

  3. (3)

    \(f^m(x)\notin f(J_x)\) for \(m>1\),

  4. (4)

    \(f^m(J_x)\cap J_{f^m(x)}\) for \(m=1,2,3,\ldots \),

  5. (5)

    intervals \(J_{f^m(x)}\) for \(m=0,1,2,\ldots \) are pairwise disjoint,

  6. (6)

    if \(f(x)=f(y)\) then \(J_x=J_{y}\),

  7. (7)

    the sets \(\mathcal {J}=\{J_x:x\in {\mathbb {S}}^1\}\) form a decomposition of \({\mathbb {S}}^1\); i.e. \(J_x=J_y\) or \(J_x\cap J_y=\emptyset \) for all \(x,y\in {\mathbb {S}}^1\),

  8. (8)

    for at most countably many x we have \(J_x\ne \{x\}\),

  9. (9)

    \(J_x=J_y\) if and only if \(J_{f^n(x)}=J_{f^n(y)}\) for some (every) \(m=0,1,2,\ldots \).

Theorem 4.2

Suppose \(f:{\mathbb {S}}^1\rightarrow {\mathbb {S}}^1\) and \(\mathrm{Per}(f)=\emptyset \). Then \(\Lambda _f=\varprojlim ({\mathbb {S}}^1, f)\) is decomposable.

Proof

Let f be as above and let \(\mathcal {J}\) be the collection of intervals guaranteed by (7) in Theorem 4.1. Without loss of generality we may assume that there is an \(x\in {\mathbb {S}}^1\) such that \(J_x\ne \{x\}\), since otherwise by (6) in Theorem 4.1 f would be a homeomorphism and \(\Lambda _f={\mathbb {S}}^1\). Additionally observe that \(f^{-n}(z)\ne \emptyset \) for every \(z\in {\mathbb {S}}^1\) as otherwise it is not hard to see that f has a fixed point.

First we claim that \(f^{-n}(J_x)\) is an interval in \(\mathcal {J}\) for every n. To see this, fix any \(n>0\) and any \(y,z\in f^{-n}(J_x)\). By Theorem 4.1 (4) we have \(f^n(J_y)\cap J_x\ne \emptyset \) and \(f^n(J_z)\cap J_x\ne \emptyset \) which by Theorem 4.1(7) gives \(f^n(J_y)=f^n(J_z)=J_x\). The proof of the claim is completed by Theorem 4.1 (9).

Put \(K_n=f^{-n}(J_x)\). Since \(K_n\) is an element of \(\mathcal {J}\), without loss of generality we can write \(K_n=[a_n,b_n]\) and \(f(a_n)=a_{n-1}\) and \(f(b_n)=b_{n-1}\). Put \(L_n=\left\{ a_n,b_n\right\} \cup ({\mathbb {S}}^1\setminus K_n)\). Then \(L_n\) is an interval,

$$\begin{aligned} f(L_n)=\left\{ f(a_n),f(b_n)\right\} \cup ({\mathbb {S}}^1\setminus f(K_n))=\left\{ a_{n-1},b_{n-1}\right\} \cup ({\mathbb {S}}^1\setminus K_{n-1})=L_{n-1} \end{aligned}$$

and hence the following two maps are onto: \(f|_{K_n}:K_n \rightarrow K_{n-1}\), \(f|_{L_n}:L_n \rightarrow L_{n-1}\) for \(n=1,2, \ldots \). Therefore the following inverse limits

$$\begin{aligned} \Gamma= & {} \varprojlim (K_n,\; f|_{K_n}:n\ge 0),\\ \Lambda= & {} \varprojlim (L_n,\; f|_{L_n}:n\ge 0) \end{aligned}$$

are arc-like continua such that \(\Lambda _f=\Gamma \cup \Lambda \), in particular \(\Lambda _f\) is decomposable.\(\square \)

Although this is not essential for the reasoning in the present paper, note that periodic-point-free circle maps are of degree 1 (see [23]).

Theorem 4.3

If \(\Lambda _f=\varprojlim ({\mathbb {S}}^1, f)\) is hereditarily indecomposable and \(\Lambda _f\) is not the pseudo-arc (i.e. \(\mathrm{deg}(f)\ne 0\)) then \(h_{\text {top}}(f)=\infty \).

Proof

Suppose \(\Lambda _f=\varprojlim ({\mathbb {S}}^1, f)\) is hereditarily indecomposable and \(|\mathrm{deg}(f)|>0\). Then \(\Lambda _f\) is either the pseudo-circle or it is nonplanar. If \(\Lambda _f\) is nonplanar then \(\mathrm{deg}(f)=n\), for some \(|n|>1\) (see [45, Theorem 9]). Consequently \(h_{\text {top}}(f)\ge \log |n|\) by [1] and further, by Theorem 3.6, we obtain that \(h_{\text {top}}(f)=\infty \).

Now suppose \(\mathrm{deg}(f)=\pm 1\). By Theorem 4.2 we have \({{\mathrm{Per}}}(f)\ne \emptyset \). By [30, Theorem 15, p.9] for any integer \(m>0\) we have

$$\begin{aligned} \varprojlim ({\mathbb {S}}^1,\; f)=\varprojlim ({\mathbb {S}}^1, f^m) \end{aligned}$$

and \(h_{\text {top}}(f^m)=m\cdot h_{\text {top}}(f)\), hence without loss of generality we may assume that \(deg(f)=1\) and \(\mathrm{Fix}(f)\ne \emptyset \). Clearly, for any m we have \(h_{\text {top}}(f)=\infty \) if and only if \(h_{\text {top}}(f^m)=\infty \).

Let \({\hat{f}}:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a lift of f to the universal covering \(({\mathbb {R}},\tau )\), where \(\tau (t)=(\cos (t),\sin (t))\) and \({\mathbb {S}}^1\) is the unit circle in the plane, centered at the origin. It is known that \({\hat{f}}\) can be extended to \(\hat{\mathbb {R}}={\mathbb {R}}\cup \{+\infty ,-\infty \}\), with \({\hat{f}}(\pm \infty )=\pm \infty \). Because \({\hat{{\mathbb {R}}}}\) is homeomorphic to [0, 1] and \(\varprojlim ({\mathbb {R}}, {\hat{f}})\) is a universal covering of \(\Lambda _f\) with the covering map given by \({\hat{\tau }}(x_1,x_2,x_3,\ldots )=(\tau (x_1),\tau (x_2),\tau (x_3),\ldots )\) (see [17, Lemma 3.8]), we get that \(\varprojlim ({\hat{{\mathbb {R}}}}, {\hat{f}})\) is the pseudo-arc [10]. Since \(\mathrm{Fix}(f)\ne \emptyset \), \({\hat{f}}\) can be chosen in such a way so that \(\mathrm{Fix}({\hat{f}})\ne \emptyset \). Indeed, any lift of f is uniquely determined by specifying where it sends a single point, and if c is a fixed point of f then there is \({{\hat{c}}}\in [0,2\pi ]\) such that \(\tau ({{\hat{c}}})=c\), hence it is enough to set \({{\hat{c}}}={\hat{f}}({\hat{c}})\).

Set \(K_i={\hat{f}}^{i}([0,2\pi ])\) and note that \({\hat{c}}\in K_i\) for every i. We shall show that the rotation set \(\rho (f)\) is nondegenerate. To demonstrate this, we claim that

$$\begin{aligned} \lim _{i\rightarrow \infty }\sup {{\mathrm{diam}}}(K_i)=\infty . \end{aligned}$$
(2)

In order to prove (2), first we claim that

$$\begin{aligned} \lim _{i\rightarrow \infty }\sup {{\mathrm{diam}}}(K_i)\ne 0. \end{aligned}$$

Recall that f is an onto map, and if B is an interval of length less than \(2\pi \) then \(\tau (B)\) is a proper subset of \({\mathbb {S}}^1\). Then it is enough to observe that

$$\begin{aligned} \tau (K_1)=\tau ({\hat{f}}([0,2\pi ]))=f(\tau ([0,2\pi ])) =f({\mathbb {S}}^1)={\mathbb {S}}^1, \end{aligned}$$

so we must have \({{\mathrm{diam}}}(K_1)\ge 2\pi \). Then working by induction, using the relation \(K_{i+1}={\hat{f}} (K_i)\), we obtain that \({{\mathrm{diam}}}(K_i)\ge 2\pi \) for every \(i>0\).

Next, let us suppose that \(\lim _{i\rightarrow \infty }\sup {{\mathrm{diam}}}(K_i)<\infty \). Set \(K=\bigcup _{i=1}^{\infty }K_i\) and note that K is connected, bounded and \({\hat{c}}\in K_i\) for every i. Now define sets \(L_i\) for \(i=1,2, \ldots \) as follows. Denote by \(L_1\) a component of \({\hat{f}}^{-1}(K)\) such that \({\hat{c}}\in L_1\), and then for \(i>1\) take as the set \(L_{i}\) a component of \({\hat{f}}^{-1}(L_{i-1})\) that contains \({\hat{c}}\). Finally put \(L=cl(\bigcup _{i\ge 0} L_i)\). Note that \(K\subseteq L\). It is easy to see that L is connected, as \({\hat{c}}\in L_i\) for every i. We claim that L is bounded. Indeed, since \({\hat{f}}(x+2k\pi )={\hat{f}}(x)+2k\pi \) we must have \(\sup _{x\in [0,2\pi ]} {{\mathrm{diam}}}(\{{\hat{f}}^n(x):n\ge 0\})=\sup _{x\in {\mathbb {R}}} {{\mathrm{diam}}}(\{{\hat{f}}^n(x){:}n\!\ge \! 0\})\). Since K is bounded we must have \(\sup _{x\in [0,2\pi ]} {{\mathrm{diam}}}(\{{\hat{f}}^n(x):n\ge 0\})<M\) for some real number M. But now, if \(p,q\in L_i\) then

$$\begin{aligned} {{\mathrm{diam}}}(K)\ge d(f^i(p),\; f^i(q))\ge d(p,q)-2M \end{aligned}$$

and hence \({{\mathrm{diam}}}(L_i)\le {{\mathrm{diam}}}(K)+2M\), which gives \({{\mathrm{diam}}}(L)\le 2{{\mathrm{diam}}}(K)+4M\). By the definition \({\hat{f}}(L_i)\subset L_{i-1}\) for \(i>1\) and for every n we have

$$\begin{aligned} \bigcup _{i=n+1}^\infty K_i\subset \hat{f}^n (K) \subset \hat{f}^n(L)\subset \hat{f}^{n-1}(L) \subset \ldots \subset L. \end{aligned}$$

If we denote \(K_i=[p_i,q_i]\) and let \(p=\liminf _{i\rightarrow \infty } p_i\), \(q=\limsup _{i\rightarrow \infty } q_i\). Then

$$\begin{aligned} \hat{c}\in [p,q]\subset \bigcup _{i=n+1}^\infty K_i \end{aligned}$$

for every \(n>0\) and \(q-p\ge 2\pi \).

Then if we denote \(S=\bigcap _{i=0}^\infty {\hat{f}}(L)\) then S is a continuum such that \({\hat{f}}(S)=S\) and \([p,q]\subset S\), so S is a closed nondegenerate interval in \({\mathbb {R}}\). Now let \(\Lambda _S=\varprojlim (S, {\hat{f}}|_S)\). Since \(\Lambda _S\subseteq \varprojlim ({\mathbb {R}}, {\hat{f}})\), the continuum \(\Lambda _S\) is the psuedo-arc. But

$$\begin{aligned} {\mathbb {S}}^1=\tau ([0,2\pi ])\subseteq \tau ([p,q])\subseteq \tau (S) \end{aligned}$$

and so \(\hat{\tau }(x_1,x_2,x_3,\ldots )=(\tau (x_1),\tau (x_2),\tau (x_3),\ldots )\) defines a continuous onto map from the pseudo-arc \(\Lambda _S\) onto the pseudo-circle \(\Lambda _f\). But the pseudo-circle cannot be obtained as the image of the pseudo-arc via a continuous map [46], which is a contradiction. This proves that \(\lim _{i\rightarrow \infty }\sup {{\mathrm{diam}}}(K_i)=\infty \), completing the proof of (2).

Because \({\hat{f}}\) has a fixed point in \([0,2\pi ]\) we get by (2) that the rotation set \(\rho ({\hat{f}})\) is nondegenerate. This implies in turn that \(h_{\text {top}}(f)>0\) (see [39]) and so, again by Theorem 3.6, we obtain that \(h_{\text {top}}(f)=\infty \) which ends the proof.\(\square \)

The following theorem follows from the above proof.

Theorem 4.4

Suppose \(f:{\mathbb {S}}^1\rightarrow {\mathbb {S}}^1\) is a map with \(\mathrm{deg}(f)=1\). If \(\Lambda _f=\varprojlim ({\mathbb {S}}^1, f)\) is hereditarily indecomposable then the rotation set \(\rho (f)\) is nondegenerate.

In [17] the authors showed that there exists a 2-torus homeomorphism h homotopic to the identity with an attracting R.H. Bing’s pseudocircle C such that the rotation set of h|C is not a unique vector. It follows from Theorem 4.3 that the topological entropy of this homeomorphism is infinite.

In [46] Rogers considered a special class of circle-like continua which he called self-entwined. Among the many results, he showed that the pseudo-circle is self-entwined, any continuum in this class is indecomposable and no self-entwined continuum is a continuous image of the pseudo-arc. Adapting the proof of Theorem 4.3 and properties of self-entwined continua sketched above, we get the following.

Theorem 4.5

Suppose \(\Lambda _f=\varprojlim ({\mathbb {S}}^1, f)\) is self-entwined. Then \(h(f)>0\).

Proof

Since \(\Lambda _f\) is indecomposable, by Theorem 4.2, f must have a periodic point. Again, without loss of generality assuming that f has a fixed point we can consider \({\hat{f}}:{\mathbb {R}}\rightarrow {\mathbb {R}}\), a lift of f to the universal covering \(({\mathbb {R}},\tau )\). Then \({\hat{f}}\) can be extended to \(\hat{\mathbb {R}}={\mathbb {R}}\cup \{+\infty ,-\infty \}\), with \({\hat{f}}(\pm \infty )=\pm \infty \). Because \({\hat{{\mathbb {R}}}}\) is homeomorphic to [0, 1] and \(\varprojlim ({\mathbb {R}}, {\hat{f}})\) is a universal covering of \(\Lambda _f\) with the covering map given by \(\hat{\tau }(x_1,x_2,x_3,\ldots )=(\tau (x_1),\tau (x_2),\tau (x_3),\ldots )\) (see [17, Lemma 3.8]), we get that \(A=\varprojlim (\hat{\mathbb {R}}, {\hat{f}})\) is an arc-like continuum. Now if we assume by contradiction that \(h(f)=0\) then f has a one-point rotation set by [39]. Therefore, repeating arguments from the proof of Theorem 4.3, there is a closed \(\hat{f}\)-invariant arc \(S\subset {\mathbb {R}}\) such that arc-like continuum \(\Lambda _S=\varprojlim (S, {\hat{f}}|_S)\subset A\) satisfies \(\hat{\tau }(\Lambda _S)=\Lambda _f\). In this case \(\Lambda _f\) would be a continuous image of an arc-like continuum. But since every arc-like continuum is a continuous image of the pseudo-arc [24] this leads to a contradiction with Roger’s result that no self-entwined continuum is such an image and the proof is complete.\(\square \)