Existence and Homogenisation of Travelling Waves Bifurcating from Resonances of Reaction–Diffusion Equations in Periodic Media

Abstract

The existence of travelling wave type solutions is studied for a scalar reaction diffusion equation in $\mathbb {R}^2$ with a nonlinearity which depends periodically on the spatial variable. We treat the coefficient of the linear term as a parameter and we formulate the problem as an infinite spatial dynamical system. Using a centre manifold reduction we obtain a finite dimensional dynamical system on the centre manifold with fully degenerate linear part. By phase space analysis and Conley index methods we find conditions on the parameter and nonlinearity for the existence of travelling wave type solutions with particular wave speeds. The analysis provides an approach to the homogenisation problem as the period of the periodic dependence in the nonlinearity tends to zero.

Appendices

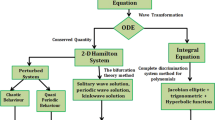
Appendix 1: Calculation of Reduction Map for One Dimensional Centre Manifold

In order to calculate the equation on $X_c$ up to quadratic order in $U^c$ we need to calculate all the linear terms and the quadratic term on the $U_0^-$ component of the reduction map $\psi$. Thus we need to satisfy

$$\begin{aligned} D_{\left( U_c,\delta \right) }\psi \left( U^c,\delta \right) \left( \begin{array}{c}\pi _cF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\ 0 \end{array}\right) = \mathcal {A}\psi \left( U^c,\delta \right) + \pi _h F\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \end{aligned}$$

(55)

for these terms. We do this by expanding the reduction map in terms of the eigenfunctions and solving the equation on each eigenfunction component for the relevant terms, thus we write

$$\begin{aligned} \psi \left( U^c,\delta \right) = \psi _0^-\left( U^c,\delta \right) U_0^- + \sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }\psi _m^\pm \left( U^c,\delta \right) U_m^\pm . \end{aligned}$$

Now if we let $\psi _0^+\left( U^c,\delta \right) : = u^c_1$ and suppress the arguments of the functions $\psi _m^\pm$, then we can obtain equations for the projections of $F$ onto $X_c$ and $X_h$

$$\begin{aligned} \pi _cF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) =&\quad -\delta \left( \frac{\psi _0^++\psi _0^-}{\lambda _0^+-\lambda _0^-}\right) U_0^+\end{aligned}$$

(56)

$$\begin{aligned}&- \left( \sum _{n,k\in \mathbb {Z}^2}q_2p_n\frac{\left( \psi _k^++\psi _k^-\right) \left( \psi _{-n-k}^++\psi _{-n-k}^-\right) }{\lambda _0^+-\lambda _0^-}\right) U_0^+ \end{aligned}$$

(57)

and

$$\begin{aligned} \pi _hF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) =&\quad \delta \left( \frac{\psi _0^++\psi _0^-}{\lambda _0^+-\lambda _0^-}\right) U_0^-\\&\quad + \left( \sum _{n,k\in \mathbb {Z}^2}q_2p_n\frac{\left( \psi _k^++\psi _k^-\right) \left( \psi _{-n-k}^++\psi _{-n-k}^-\right) }{\lambda _0^+-\lambda _0^-}\right) U_0^-\\&\quad +\sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }\mp \Bigg (\delta \left( \frac{\psi _m^++\psi _m^-}{\lambda _m^+-\lambda _m^-}\right) U_m^\pm \\&\quad +\left( \sum _{n,k\in \mathbb {Z}^2}q_2p_n\frac{\left( \psi _k^++\psi _k^-\right) \left( \psi _{m-n-k}^++\psi _{m-n-k}^-\right) }{\lambda _m^+-\lambda _m^-}\right) U_m^\pm \Bigg ); \end{aligned}$$

up to quadratic order in $U^c$ by substituting this expansion into $F$.

We now want to calculate the linear terms of the Taylor expansion of $\psi$. Thus let

$$\begin{aligned} \psi \left( U^c,\delta \right) = \left( L_0^-(\delta )U^c\right) U_0^- + \sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }\left( L_m^\pm (\delta )U^c\right) U^\pm _m + O\left( \left\| U^c\right\| ^2\right) , \end{aligned}$$

where the functions $L_m^\pm (\delta ) :X_c\rightarrow \mathbb {C}$ are linear. Thus, if we substitute the equations for $F$ on $X_c$ and $X_h$ into (55) and use the above expansion for $\psi$, we get that up to linear terms

$$\begin{aligned}&D_{\left( U^c,\delta \right) }\psi \left( U^c,\delta \right) \left( \begin{array}{c}\pi _cF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\ 0 \end{array}\right) \\&\quad = L_0^-(\delta )\left( -\delta \left( \frac{u^c_1+L_0^-(\delta )U^c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) U_0^- \\&\qquad + \sum _{m\in \mathbb {Z}\setminus \left\{ 0\right\} }L_m^\pm (\delta )\left( -\delta \left( \frac{u^c_1+L_0^-(\delta )U^c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) U_m^\pm + O\left( \left\| U^c\right\| ^2\right) \end{aligned}$$

and

$$\begin{aligned}&\mathcal {A}\psi \left( U^c,\delta \right) + \pi _h F\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\&\quad = \left( \lambda _0^-L_0^-(\delta )U^c\right) U_0^- + \sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }\left( \lambda _m^\pm L_m^\pm (\delta )U^c\right) U^\pm _m\\&\qquad + \delta \left( \frac{u_1^c+L_0^-(\delta )U^c}{\lambda _0^+-\lambda _0^-}\right) U_0^- + \delta \sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }\mp \left( \frac{L_m^+(\delta )U^c+L_m^-(\delta )U^c}{\lambda _m^+-\lambda _m^-}\right) U_m^\pm \\&\qquad + O\left( \left\| U^c\right\| ^2\right) . \end{aligned}$$

So on the $U_0^-$ component of (55) we have the equation

$$\begin{aligned} -\delta L_0^-(\delta )\left( \left( \frac{u_1^c+L_0^-(\delta )U^c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) = \lambda _0^-\left( L_0^-(\delta )U^c\right) + \delta \left( \frac{u^c_1+L_0^-(\delta )U^c}{\lambda _0^+-\lambda _0^-}\right) . \end{aligned}$$

(58)

Now, as $X_c = \text {Span}_\mathbb {R}\left\{ U_0^+\right\}$, we can write $U^c = y U_0^+$ for $y \in \mathbb {R}$ and $L_0^-(\delta )\left( yU_0^+\right) := a_0^- y$ for some $a_0^-\in \mathbb {R}$. Then, since $\lambda _0^+ = 0$ and $\lambda _0^- = -c$, the equation on the $U_0^-$ component (58) becomes

$$\begin{aligned} -\delta a_0^-\left( \frac{y+a_0^-y}{c}\right) =-ca_0^-y + \delta \left( \frac{y+a_0^-y}{c}\right) , \end{aligned}$$

which can be rearranged to get

$$\begin{aligned} \delta \left( 1+a_0^-\right) ^2 = c^2 a_0^-. \end{aligned}$$

Thus we get two possible values for $a_0^-$

$$\begin{aligned} a_0^-&= \frac{\left( c^2-2\delta \right) + \sqrt{\left( c^2-2\delta \right) ^2-4\delta ^2}}{2\delta } = \frac{c^2}{\delta } -2 -\frac{2\delta }{c^2} + O(\delta ^2)\text { as }\delta \rightarrow 0\\ \text { or}\\ a_0^-&= \frac{\left( c^2-2\delta \right) - \sqrt{\left( c^2-2\delta \right) ^2-4\delta ^2}}{2\delta } = \frac{2\delta }{c^2} +O(\delta ^2)\text { as }\delta \rightarrow 0; \end{aligned}$$

however if we choose the first of these then the reduction map $\psi$ would not satisfy the condition

$$\begin{aligned} D_{\left( U^c,\delta \right) }\psi (0,0) = 0. \end{aligned}$$

So we take

$$\begin{aligned} a_0^- {:=} \frac{\left( c^2-2\delta \right) - \sqrt{\left( c^2-2\delta \right) ^2-4\delta ^2}}{2\delta }. \end{aligned}$$

Now on the $U_m^\pm$ components of (55) for $m\ne 0$ we have the equation

$$\begin{aligned} -\delta L_m^\pm (\delta )\left( \left( \frac{u_1^c+L_0^-(\delta )U^c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) = \lambda _m^\pm \left( L_m^\pm (\delta )U^c\right) \mp \delta \left( \frac{L_m^+(\delta )U_c+L_m^-(\delta )U^c}{\lambda _m^+-\lambda _m^-}\right) ; \end{aligned}$$

which is satisfied if we take $L_m^\pm =0$. Hence we have determined the linear terms of the reduction map.

Next we want to find the quadratic terms on the $U_0^-$ component. Thus we let

$$\begin{aligned} \psi \left( U^c,\delta \right) = \left( L_0^-(\delta )U^c + Q_0^-\left( U^c,\delta \right) \right) U_0^- + \sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }Q_m^\pm \left( U^c,\delta \right) + O\left( \left\| U^c\right\| ^3\right) ; \end{aligned}$$

where $Q_m^\pm \left( \cdot ,\delta \right) :X_c\rightarrow \mathbb {C}$ are quadratic functions. Then, substituting the equations for $F$ on $X_c$ and $X_h$ into (55) and using the above expansion for $\psi$ in terms of the linear and quadratic terms, we get that the quadratic terms of

$$\begin{aligned}&D_{\left( U^c,\delta \right) }\psi \left( U^c,\delta \right) \left( \begin{array}{c}\pi _cF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\ 0 \end{array}\right) \\&\quad = L_0^-\left( -\delta \left( \frac{Q_0^-\left( U^c,\delta \right) }{\lambda _0^+-\lambda _0^-}\right) U_0^+ - \frac{q_2p_0}{\lambda _0^+-\lambda _0^-}\left( u_1^c + L_0^-(\delta )U_c\right) ^2U_0^+\right) U_0^-\\&\qquad + D_{U^c} Q_0^-\left( U^c,\delta \right) \left( -\delta \left( \frac{u_1^c+L_0^-(\delta )U_c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) U_0^-\\&\qquad +\sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} } D_{U^c}Q_m^\pm \left( U^c,\delta \right) \left( -\delta \left( \frac{u_1^c+L_0^-(\delta )U_c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) U_m^\pm \end{aligned}$$

and the quadratic terms of

$$\begin{aligned}&\mathcal {A}\psi \left( U^c,\delta \right) + \pi _h F\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\&\quad =\lambda _0^- Q_0^-\left( U^c,\delta \right) U_0^- + \sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} } \lambda _m^\pm Q_m^\pm \left( U^c,\delta \right) U^\pm _m\\&\qquad +\delta \left( \frac{Q_0^-\left( U^c,\delta \right) }{\lambda _0^+-\lambda _0^-}\right) U_0^-+ \frac{q_2p_0}{\lambda _0^+-\lambda _0^-}\left( u_1^c+ L_0^-(\delta )U_c\right) ^2U_0^-\\&\qquad +\sum _{m\in \mathbb {Z}^2\setminus \left\{ 0\right\} }\mp \Bigg ( \delta \left( \frac{Q_m^+\left( U^c,\delta \right) +Q_m^-\left( U^c,\delta \right) }{\lambda _m^+-\lambda _m^-}\right) U_m^\pm + \\&\qquad \quad \frac{q_2p_m}{\lambda _m^+-\lambda _m^-}\left( u_1^c+L_0^-(\delta )U^c\right) ^2U_m^\pm \Bigg ). \end{aligned}$$

Thus on the $U_0^-$ component of (55) we have the equation

$$\begin{aligned}&L_0^-\left( -\delta \left( \frac{Q_0^-\left( U^c,\delta \right) }{\lambda _0^+-\lambda _0^-}\right) U_0^+ - \frac{q_2p_0}{\lambda _0^+-\lambda _0^-}\left( u_1^c + L_0^-(\delta )U_c\right) ^2U_0^+\right) \nonumber \\&\quad +D_{U^c} Q_0^-\left( U^c,\delta \right) \left( -\delta \left( \frac{u_1^c+L_0^-(\delta )U_c}{\lambda _0^+-\lambda _0^-}\right) U_0^+\right) \nonumber \\&\qquad = \lambda _0^-Q^-_0\left( U^c,\delta \right) +\delta \left( \frac{Q_0^-\left( U^c,\delta \right) }{\lambda _0^+-\lambda _0^-}\right) + \frac{q_2p_0}{\lambda _0^+-\lambda _0^-}\left( u_1^c+ L_0^-(\delta )U_c\right) ^2 \end{aligned}$$

(59)

and, since $X_c =\text {Span}_\mathbb {R}\left\{ U_0^+\right\}$, we can let $U^c = y U_0^+$, $L_0^-(\delta )\left( yU_0^+\right) = a_0^- y$ and $Q_0^-\left( yU_0^+,\delta \right) = b_0^- y^2$ for some $b_0^-\in \mathbb {R}$. Thus the equation on the $U_0^-$ component (59) becomes

$$\begin{aligned}&-a_0^-\left( \frac{\delta b_0^-y^2 + q_2p_0\left( y+a_0^-y\right) ^2}{c}\right) -2b_0^-y\left( \delta \frac{\left( y+a_0^-y\right) }{c}\right) \\&\quad = -cb_0^-y^2 + \delta \frac{b_0^-y^2}{c} + \frac{q_2p_0}{c}\left( y+a_0^-y\right) ^2; \end{aligned}$$

rearranging we get

$$\begin{aligned} \left( c^2 -3 \delta \left( 1+a_0^-\right) \right) b_0^- = q_2p_0\left( 1+a_0^-\right) ^3. \end{aligned}$$

Hence we have

$$\begin{aligned} b_0^- = \frac{q_2p_0\left( 1+a_0^-\right) ^3}{c^2 -3 \delta \left( 1+a_0^-\right) }. \end{aligned}$$

Thus we have determined the terms of the reduction map necessary to calculate the equation on the $X_c$ up to quadratic order in $U^c$.

Appendix 2: Calculation of Reduction Map for Two Dimensional Centre Manifold

In order to calculate the equation on $X_c$ up to quadratic order in $U^c$ we will need to calculate all the linear terms and the quadratic terms on the $U_\eta ^+$ and $U_{-\eta }^+$ components of the reduction map. Thus we need to satisfy the equation

$$\begin{aligned} D_{\left( U^c,\delta \right) }\psi \left( U^c,\delta \right) \left( \begin{array}{c}\pi _cF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\ 0 \end{array}\right) = \mathcal {A}\psi \left( U^c,\delta \right) + \pi _h F\left( U^c \!+\! \psi \left( U^c,\delta \right) ,\delta \right) ; \end{aligned}$$

(60)

for these terms. We do this by expanding the reduction map in terms of the eigenfunctions and solving the equation on each eigenfunction component. Thus we let

$$\begin{aligned} \psi \left( U^c,\delta \right) = \psi _\eta ^-\left( U^c,\delta \right) U_\eta ^- + \psi _{-\eta }^-\left( U^c,\delta \right) U_{-\eta }^- + \sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} }\psi _m^\pm \left( U^c,\delta \right) U^\pm _m. \end{aligned}$$

Now if we let $U_c = zU_\eta ^++\overline{z}U_{-\eta }^+$ and, for notational convenience, set $\psi _\eta ^+\left( U^c,\delta \right) :=z$ and $\psi _{-\eta }^+\left( U^c,\delta \right) :=\overline{z}$. Then, suppressing the arguments of the functions $\psi _m^\pm$ and substitute the above expansion into $F$, we get equations for the projections of $F$ onto $X_c$ and $X_h$,

$$\begin{aligned} \pi _c F\left( U^c+\psi \left( U^c,\delta \right) ,\delta \right) =&\quad -\delta \left( \frac{\psi _\eta ^++\psi _\eta ^-}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+ -\delta \left( \frac{\psi _{-\eta }^++\psi _{-\eta }^-}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^+\nonumber \\&\quad - \sum _{n,k\in \mathbb {Z}^2}q_2p_{\eta + n} \frac{\left( \psi _k^++\psi _k^-\right) \left( \psi ^+_{-n-k}+\psi _{-n-k}^-\right) }{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^+\nonumber \\&\quad -\sum _{n,k\in \mathbb {Z}^2} q_2p_{-\eta + n} \frac{\left( \psi _k^++\psi _k^-\right) \left( \psi ^+_{-n-k}+\psi _{-n-k}^-\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^+\quad \end{aligned}$$

(61)

and

$$\begin{aligned} \pi _h F\left( U^c +\psi \left( U^c,\delta \right) ,\delta \right) =&\quad \delta \left( \frac{\psi _\eta ^++\psi _\eta ^-}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^-+\delta \left( \frac{\psi _{-\eta }^++\psi _{-\eta }^-}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^-\nonumber \\&\quad + \sum _{n,k\in \mathbb {Z}^2}q_2p_{\eta + n} \frac{\left( \psi _k^++\psi _k^-\right) \left( \psi ^+_{-n-k}+\psi _{-n-k}^-\right) }{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^-\nonumber \\&\quad +\sum _{n,k\in \mathbb {Z}^2} q_2p_{-\eta + n} \frac{\left( \psi _k^++\psi _k^-\right) \left( \psi ^+_{-n-k}+\psi _{-n-k}^-\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^-\nonumber \\&\quad + \sum _{m\in \mathbb {Z}^2 \setminus \left\{ \pm \eta \right\} } \mp \Bigg (\delta \left( \frac{\psi _m^++\psi _m^-}{\lambda _m^+-\lambda _m^-}\right) U_m^\pm +\nonumber \\&\quad \sum _{n,k\in \mathbb {Z}^2}q_2p_{m+n} \frac{\left( \psi _k^++\psi _k^-\right) \left( \psi _{-k-n}^++\psi _{-k-n}^-\right) }{\lambda _m^+-\lambda _m^-}U_m^\pm \Bigg ) \end{aligned}$$

(62)

up to quadratic order in $U^c$.

Now we start finding the terms of the reduction map $\psi$ by working out the its linear terms, so we let

$$\begin{aligned} \psi \left( U^c,\delta \right) = \left( L_\eta ^-(\delta )U^c\right) U_\eta ^- + \left( L_{-\eta }^-(\delta )U^c\right) U_{-\eta }^- +\sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} }\left( L_m^\pm (\delta )U^c\right) U_m^\pm +O\left( \left\| U^c\right\| ^2\right) ; \end{aligned}$$

where the functions $L_m^\pm (\delta ):X_c\rightarrow \mathbb {C}$ are linear. Now if we let $U^c = z U_\eta ^++\overline{z}U_{-\eta }^+$ for $z\in \mathbb {C}$. Then using the equations for the projections of $F$ onto $X_c$ and $X_h$ with the above expansion some calculation shows that up to linear terms in $U^c$

$$\begin{aligned}&D_{\left( U^c,\delta \right) }\psi \left( U^c,\delta \right) \left( \begin{array}{c}\pi _c F\left( U^c +\psi \left( U^c,\delta \right) ,\delta \right) \\ 0\end{array}\right) \\&\quad = L_\eta ^-(\delta )\left( -\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+-\delta \left( \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^+\right) U_\eta ^-\\&\qquad + L_{-\eta }^-(\delta )\left( -\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+-\delta \left( \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^+\right) U_{-\eta }^-\\&\qquad +\sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} } L_m^\pm (\delta )\left( -\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+-\delta \left( \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^+\right) U_m^\pm \end{aligned}$$

and

$$\begin{aligned}&\mathcal {A}\psi \left( U^c,\delta \right) +\pi _hF\left( U^c+\psi \left( U^c,\delta \right) ,\delta \right) \\&\quad = \left( \lambda _\eta ^-L_\eta ^-(\delta )U^c\right) U_\eta ^- + \left( \lambda _{-\eta }^-L_{-\eta }^-(\delta )U^c\right) U_{-\eta }^- +\sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} } \left( \lambda _m^\pm L_m^\pm (\delta ) U^c\right) U_m^\pm \\&\qquad +\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^- + \delta \left( \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^-\\&\qquad + \delta \sum _{m\in \mathbb {Z}^2 \setminus \left\{ \pm \eta \right\} }\mp \left( \frac{L_m^+(\delta )U^c+L_m^-(\delta )U^c}{\lambda _m^+-\lambda _m^-}\right) U_m^\pm . \end{aligned}$$

Thus on the $U_\eta ^-$ and $U_{-\eta }^-$ components of (55) we have the equations

$$\begin{aligned}&L_\eta ^-(\delta )\left( -\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+-\delta \left( \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^+\right) \\&\quad = \lambda _\eta ^-L_\eta ^-(\delta )U^c +\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) \end{aligned}$$

and

$$\begin{aligned}&L_{-\eta }^-(\delta )\left( -\delta \left( \frac{z+L_\eta ^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+-\delta \left( \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) U_{-\eta }^+\right) \\&\quad = \lambda _{-\eta }^-L_{-\eta }^-(\delta )U^c +\delta \left( \frac{z+L_{-\eta }^-(\delta )U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) . \end{aligned}$$

However, since $\psi$ maps into $X_h\subset X$, we have that $L_\eta ^-(\delta ) =\overline{L_{-\eta }^-(\delta )}$ and it follows that the two equation above are complex conjugates of each other.

Now, since $U^c = z U_\eta ^+ +\overline{z}U_{-\eta }^+$, we have that $L_\eta ^-(\delta )\left( z U_\eta ^+ +\overline{z}U_{-\eta }^+\right) = \alpha _\eta ^- z + \beta _\eta ^- \overline{z}$ for some $\alpha _\eta ^-,\beta _\eta ^- \in \mathbb {C}$ and we can express the equation on $U_\eta ^-$ in terms of $z$ to get,

$$\begin{aligned}&-\delta \alpha _\eta ^- \left( \frac{z + \left( \alpha _\eta ^-z + \beta _\eta ^- \overline{z}\right) }{\lambda _\eta ^+-\lambda _\eta ^-}\right) - \delta \beta _\eta ^-\left( \frac{\overline{z}+\left( \overline{\beta _\eta ^-}z + \overline{\alpha _\eta ^-} \overline{z}\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) \\&\quad = \lambda _\eta ^-\left( \alpha _\eta ^-z+\beta _\eta ^-\overline{z}\right) + \delta \left( \frac{z+ \left( \alpha _\eta ^-z +\beta _\eta ^- \overline{z}\right) }{\lambda _\eta ^+-\lambda _\eta ^-}\right) . \end{aligned}$$

From this equation we can work out the coefficients $\alpha _\eta ^-$ and $\beta _\eta ^-$ by equating the coefficients of the $z$ and $\overline{z}$ terms,

$$\begin{aligned} z:&-\delta \left( \frac{\alpha _\eta ^-\left( 1+\alpha _\eta ^-\right) }{\lambda _\eta ^+-\lambda _\eta ^-} + \frac{\left| \beta _\eta ^-\right| ^2}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) = \lambda _\eta ^-\alpha _\eta ^- + \delta \left( \frac{1+\alpha _\eta ^-}{\lambda _\eta ^+-\lambda _\eta ^-}\right) \\ \overline{z}:&-\delta \left( \frac{\alpha _\eta ^-\beta _\eta ^-}{\lambda _\eta ^+-\lambda _\eta ^-}+\frac{\beta _\eta ^-\left( 1+\overline{\alpha _\eta ^-}\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) = \lambda _\eta ^-\beta _\eta ^- + \delta \left( \frac{\beta _\eta ^-}{\lambda _\eta ^+-\lambda _\eta ^-}\right) . \end{aligned}$$

Now the $\overline{z}$ equation implies that $\beta _\eta ^- = 0$, so rearranging the $z$ equation we get the quadratic equation

$$\begin{aligned} \delta \left( \alpha _\eta ^-\right) ^2 +\left( 2\delta +\lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) \right) \alpha _\eta ^-+\delta = 0. \end{aligned}$$

So we have two possible values for $\alpha _\eta ^-$ namely,

$$\begin{aligned} \alpha _\eta ^-&= \frac{-\left( 2\delta +\lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) \right) +\sqrt{\left( 2\delta +\lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) \right) ^2-4\delta ^2}}{2\delta }\\&= O(\delta )\text { as }\delta \rightarrow 0 \end{aligned}$$

or

$$\begin{aligned} \alpha _\eta ^-&=\frac{-\left( 2\delta +\lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) \right) -\sqrt{\left( 2\delta +\lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) \right) ^2-4\delta ^2}}{2\delta }\\&= -\frac{\lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) }{2\delta } - 2 +O(\delta )\text { as }\delta \rightarrow 0. \end{aligned}$$

However if we choose the second of these values then the reduction map would not satisfy the condition,

$$\begin{aligned} D_{\left( U^c,\delta \right) }\psi (0,0) = 0. \end{aligned}$$

Thus we choose the first of the values given above and hence we have determined $L_\eta ^-(\delta )$ and $L_{-\eta }^-(\delta )$, since $L_{-\eta }^-(\delta )$ is the complex conjugate of $L_\eta ^-(\delta )$.

Now on the $U^\pm _m$ component of Eq. (55) for $m \ne \pm \eta$ we have the equation,

$$\begin{aligned}&-\delta L_m^\pm (\delta )\left( \frac{z+L_\eta ^-(\delta )U_c}{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^+ + \frac{\overline{z}+L_{-\eta }^-(\delta )U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^+\right) \\&\quad = \lambda _m^\pm L_m^\pm (\delta ) U^c \mp \delta \left( \frac{L_m^+(\delta )U^c+L_m^-(\delta )U^c}{\lambda _m^+-\lambda _m^-}\right) ; \end{aligned}$$

which is satisfied if we choose $L_m^\pm (\delta ) = 0$ for all $m \ne \pm \eta$. Thus we have determined all the linear terms of the reduction map, we summaries this information below;

$$\begin{aligned} L_\eta ^-(\delta )\left( zU_\eta ^+\overline{z}U_\eta ^+\right)&= \alpha _\eta ^- z\\ L_{-\eta }^-(\delta )\left( zU_\eta ^+\overline{z}U_\eta ^+\right)&= \overline{\alpha _\eta ^-}\overline{z}\\ L_m^\pm (\delta )\left( zU_\eta ^+\overline{z}U_\eta ^+\right)&= 0 \text { for all }m\ne \pm \eta . \end{aligned}$$

Hence it just remains to determine the quadratic terms on the $U_\eta ^-$ and $U_{-\eta }^-$ components. Thus we let

$$\begin{aligned} \psi \left( U^c,\delta \right) \,&=\,\left( L_\eta ^-(\delta )U^c+Q_\eta ^-\left( U^c,\delta \right) \right) U_{-\eta }^-+\left( L_{-\eta }^-(\delta )U^c+Q_{-\eta }^-\left( U^c,\delta \right) \right) U_{-\eta }^- \\&\quad + \sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} }Q_m^\pm \left( U^c,\delta \right) U_m^\pm +O\left( \left\| U^c\right\| ^3\right) ; \end{aligned}$$

where $Q_m^\pm \left( \cdot ,\delta \right) :X_c\rightarrow \delta$ are quadratic functions. Then, if we let $U^c = zU_\eta ^-+\overline{z}U_{-\eta }^+$ and use the equation for the projections of $F$ onto $X_c$ and $X_h$ with the above expansion, we get that the quadratic terms in $U^c$ of

$$\begin{aligned}&D_{(U^c,\delta )}\psi \left( U^c,\delta \right) \left( \begin{array}{c}\pi _cF\left( U^c + \psi \left( U^c,\delta \right) ,\delta \right) \\ 0 \end{array}\right) \\&\quad = \left( L_\eta ^-(\delta )V\right) U_\eta ^-+\left( L_{-\eta }^-(\delta )V\right) U^-_{-\eta } + \left( D_{U^c}Q_\eta ^-\left( U^c,\delta \right) W\right) U_\eta ^- \\&\qquad + \left( D_{U^c}Q_{-\eta }^-\left( U^c,\delta \right) W\right) U_{-\eta }^-+\sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} }\left( D_{U^c}Q_m^\pm \left( U^c,\delta \right) W\right) U_m^\pm ; \end{aligned}$$

where

$$\begin{aligned} V =&\,-\frac{\delta Q_\eta ^-\left( U^c,\delta \right) }{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^+-\frac{\delta Q_{-\eta }^-\left( U^c,\delta \right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^+\\&-\frac{q_2\left( p_{-\eta }\left( z+L_\eta ^-(\delta )U^c\right) ^2+2p_\eta \left| z+L_\eta ^-(\delta )U^c\right| ^2+p_{3\eta }\left( \overline{z}+L_{-\eta }^-(\delta )U^c\right) ^2\right) }{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^+\\&- \frac{q_2\left( p_{-3\eta }\left( z+L_\eta ^-(\delta )U^c\right) ^2+2p_{-\eta }\left| z+L_\eta ^-(\delta )U^c\right| ^2+p_{\eta }\left( \overline{z}+L_{-\eta }^-(\delta )U^c\right) ^2\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^+ \end{aligned}$$

and

$$\begin{aligned} W = -\delta \left( \frac{z+L_\eta ^-U^c}{\lambda _\eta ^+-\lambda _\eta ^-}\right) U_\eta ^+ -\delta \left( \frac{\overline{z}+L_{-\eta }^-U^c}{\lambda _{-\eta }^+-\lambda _{-\eta }}\right) U_{-\eta }^+, \end{aligned}$$

and on the other hand using the same method we get that the quadratic terms in $U^c$ of

$$\begin{aligned}&\mathcal {A}\psi \left( U^c,\delta \right) +\pi _h F\left( U^c+\psi \left( U^c,\delta \right) ,\delta \right) \\&\quad = \left( \lambda _\eta ^-Q_\eta ^-\left( U^c,\delta \right) \right) U_\eta ^-+\left( \lambda _{-\eta }^-Q_{-\eta }^-\left( U^c,\delta \right) \right) U_{-\eta }^-+\sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} }\left( \lambda _m^\pm Q_m^pm\left( U^c,\delta \right) \right) U_m^\pm \\&\qquad + \tilde{V} + \sum _{m\in \mathbb {Z}^2\setminus \left\{ \pm \eta \right\} }\mp \Bigg (\delta \left( \frac{Q_m^+\left( U^c,\delta \right) +Q_m^-\left( U^c,\delta \right) }{\lambda _m^+-\lambda _m^-}\right) U_m^\pm \\&\qquad +q_2\left( \frac{p_{m-2\eta }\left( z+L_\eta ^-(\delta )U^c\right) ^2+p_m\left| z+L_\eta ^-(\delta )U^c\right| ^2 +p_{m+2\eta }\left( \overline{z}+L_{-\eta }^-(\delta )U^c\right) ^2}{\lambda _m^+-\lambda _m^-}\right) U_m^\pm \Bigg ); \end{aligned}$$

where

$$\begin{aligned} \tilde{V}\,&=\,\frac{\delta Q_\eta ^-\left( U^c,\delta \right) }{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^-+\frac{\delta Q_{-\eta }^-\left( U^c,\delta \right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^-\\&\quad +\frac{q_2\left( p_{-\eta }\left( z+L_\eta ^-(\delta )U^c\right) ^2+2p_\eta \left| z+L_\eta ^-(\delta )U^c\right| ^2+p_{3\eta }\left( \overline{z}+L_{-\eta }^-(\delta ) U^c\right) ^2\right) }{\lambda _\eta ^+-\lambda _\eta ^-}U_\eta ^-\\&\quad + \frac{q_2\left( p_{-3\eta }\left( z+L_\eta ^-(\delta )U^c\right) ^2+2p_{-\eta }\left| z+L_\eta ^-(\delta ) U^c\right| ^2+p_{\eta }\left( \overline{z}+L_{-\eta }^-(\delta )U^c\right) ^2\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}U_{-\eta }^-. \end{aligned}$$

Now, as we only want to workout $Q_\eta ^-$ and $Q_{-\eta }^-$ we can just look at the equation on the $U_\eta ^-$ component, as $\overline{Q_\eta ^-} = Q_{-\eta }^-$. The equation on the $U_\eta ^-$ component is

$$\begin{aligned}&L_\eta ^-(\delta )V + D_{U^c}Q_\eta ^-\left( U^c,\delta \right) W \\&\quad = \lambda _\eta ^- Q_\eta ^-\left( U^c,\delta \right) + \frac{\delta Q_\eta ^-\left( U^c,\delta \right) }{\lambda _\eta ^+-\lambda _\eta ^-}\\&\qquad +\frac{q_2\left( p_{-\eta }\left( z+L_\eta ^-(\delta )U^c\right) ^2+2p_\eta \left| z+L_\eta ^-(\delta )U^c\right| ^2+p_{3\eta }\left( \overline{z}+L_{-\eta }^-(\delta ) U^c\right) ^2\right) }{\lambda _\eta ^+-\lambda _\eta ^-}. \end{aligned}$$

Now we know that $L_\eta ^-(\delta )\left( zU_\eta ^++\overline{z}U_{-\eta }^+\right) = \alpha _\eta ^- z$ and we can write $Q_\eta ^-\left( zU_\eta ^++\overline{z}U_{-\eta }^+\right) = \gamma _\eta ^-z^2 + 2\zeta _\eta ^-\left| z\right| ^2 + \sigma _\eta ^- \overline{z}^2$ for some $\gamma _\eta ^-,\zeta _\eta ^-,\sigma _\eta ^- \in \mathbb {C}$. So therefore the above equation can be written in terms of $z$ as

$$\begin{aligned}&-\frac{\alpha _\eta ^-}{\lambda _\eta ^+-\lambda _\eta ^-}\bigg (\delta \left( \gamma _\eta ^-z^2+2\zeta _\eta ^-\left| z\right| ^2+\sigma _\eta ^-\overline{z}^2\right) +q_2\bigg (p_{-\eta }\left( 1+\alpha _\eta ^-\right) ^2z^2+2p_\eta \left| 1+\alpha _\eta ^-\right| ^2\left| z\right| ^2\\&\quad +p_{3\eta }\left( 1+\overline{\alpha _\eta ^-}\right) ^2\overline{z}^2\bigg )\bigg ) \!-\!2\delta \! \left( \frac{\left( \gamma _\eta ^-z+\zeta _\eta ^-\overline{z}\right) \left( 1+\alpha _\eta ^-\right) z}{\lambda _\eta ^+-\lambda _\eta ^-}+\frac{\left( \zeta _\eta ^-z+\sigma _\eta ^-\overline{z}\right) \left( 1+\overline{\alpha _\eta ^-}\right) \overline{z}}{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) \\&\qquad = \lambda _\eta ^-\left( \gamma _\eta ^-z^2+2\zeta _\eta ^-\left| z\right| ^2+\sigma _\eta ^-\overline{z}^2\right) + \frac{1}{\lambda _\eta ^+-\lambda _\eta ^-}\bigg (\delta \left( \gamma _\eta ^-z^2+2\zeta _\eta ^-\left| z\right| ^2 +\sigma _\eta ^-\overline{z}^2\right) \\&\qquad \quad + q_2\left( p_{-\eta }\left( 1+\alpha _\eta ^-\right) ^2z^2+2p_\eta \left| 1+\alpha _\eta ^-\right| ^2\left| z\right| ^2 +p_{3\eta }\left( 1+\overline{\alpha _\eta ^-}\right) ^2\overline{z}^2 \right) \bigg ), \end{aligned}$$

and if we now equate the coefficients of the $z^2$, $\left| z\right| ^2$ and $\overline{z}^2$ terms and rearrange we get the following three equations.

$$\begin{aligned} z^2:&\quad \left( \lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) +3\delta \left( 1+\alpha _\eta ^-\right) \right) \gamma _\eta ^- = -q_2p_{-\eta }\left( 1+\alpha _\eta ^-\right) ^3\\ \left| z\right| ^2:&\quad \left( \lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) +2\delta \left( 1+\alpha _\eta ^-\right) +\delta \frac{\left( 1+\overline{\alpha _\eta ^-}\right) \left( \lambda _\eta ^+-\lambda _\eta ^-\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) \zeta _\eta ^- \\&\quad =-q_2p_\eta \left( 1+\alpha _\eta ^-\right) ^2\left( 1+\overline{\alpha _\eta ^-}\right) \\ \overline{z}^2:&\quad \left( \lambda _\eta ^-\left( \lambda _\eta ^+-\lambda _\eta ^-\right) +\delta \left( 1+\alpha _\eta ^-\right) +2\delta \frac{\left( 1+\overline{\alpha _\eta ^-}\right) \left( \lambda _\eta ^+-\lambda _\eta ^-\right) }{\lambda _{-\eta }^+-\lambda _{-\eta }^-}\right) \sigma _\eta ^- \\&\quad = -q_2 p_{3\eta }\left( 1+\alpha _\eta ^-\right) \left( 1+\overline{\alpha _\eta ^-}\right) ^2 \end{aligned}$$

These three equations determine $\gamma _\eta ^-$, $\zeta _\eta ^-$ and $\sigma _\eta ^-$ and thus we have determined $Q_\eta ^-\left( U^c,\delta \right)$ and $Q_{-\eta }^-\left( U^c,\delta \right)$ to be

$$\begin{aligned} Q_\eta ^-\left( zU_\eta ^++\overline{z}U_{-\eta }^+,\delta \right)&= \gamma _\eta ^-z^2 +2\zeta _\eta ^- \left| z\right| ^2 +\sigma _\eta ^-\overline{z}^2\\ Q_{-\eta }^-\left( zU_\eta ^++\overline{z}U_{-\eta }^+,\delta \right)&= \overline{\sigma _\eta ^-} z^2 +2\overline{\zeta _\eta ^-} \left| z\right| ^2+\overline{\gamma _\eta ^-} \overline{z}^2. \end{aligned}$$

Thus we have determined the terms of the reduction map needed to calculate the ordinary differential equation on $X_c\times \mathbb {R}$ up to quadratic order in $U^c$.