Abstract
In this paper we discuss a topological treatment for the planar system
where \(f:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) and \(g:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) are \(T\)-periodic in time and \(g(t,z)\) is bounded. Namely, we study the effect of \(g(t,z)\) in two different frameworks: isochronous centers and time periodic systems having subharmonics. The main tool employed in the proofs consists of a topological strategy to locate fixed points in the class of orientation preserving embedding under the condition of some recurrence properties. Generally speaking, our topological result can be considered as an extension of the main result in Brown (Pac J Math 143:37–41, 1990) (concerning two cycles) to any recurrent point.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Incorporating a perturbation, not necessarily small, in differential equations naturally arises in many mechanical situations due to effects caused by friction or an external force; and, in general, in most areas of the science by the errors in the modelling process. Because of this range of applicability, perturbation theory has attracted the attention of many researchers during the last decades. In consequence, a variety of mathematical tools, including methods of geometric, topological or variational type have been used in the field, see [10, 14, 15, 23, 29] and the references therein. In spite of this fact, many substantial questions remain to be answered since the introduction of a perturbation into a mathematical model may completely alter its dynamical behavior. For instance, a small perturbation can create chaos, see Melnikov’s method [20] or unbounded solutions.
In this paper we discuss a topological treatment for the planar system
where \(f:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) and \(g:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) are \(T\)-periodic in time, \(g(t,z)\) is bounded, (1.1) has uniqueness of solution for the initial value problem, and the solutions are globally defined in the future for every initial condition. In more detail, we study the effect of \(g(t,z)\) in (1.1) in two different frameworks: isochronous centers and time periodic systems having subharmonics.
One of our aims here is to continue the work initiated by several authors to understand some resonant phenomena arising when we consider a perturbation of an isochronous center. Specifically, assume that \(p\in \mathbb {R}^{2}\) is an equilibrium of
and all solutions of (1.2), different from \(p\), are periodic with the same period \(\tau \). Moreover, in (1.1), we impose that
Note that as \(f\) does not depend on time, system (1.1) can be written as
In this framework, we are able to deduce the following theoretical phenomenon: (P) If the set of \(T\) -periodic solutions of (1.3) is bounded, then for each \(n\in \mathbb {N}\), the set of \(nT\) -periodic solutions of (1.3) is bounded as well.
In a direct way, (P) enables us to achieve a criterion of multiplicity of \(T\)-periodic solutions for system (1.3). Namely, if for some \(n\in \mathbb {N}\), the set of \(nT\)-periodic solutions is unbounded, then there are infinite \(T\)-periodic solutions in (1.3).
Many physical situations are described by an autonomous differential equation subject to a time dependent perturbation and fall into the framework presented above. Indeed, some of the motivating examples that we have in mind are the classical oscillator
or the asymmetric oscillator
where \(\mu \) and \(\nu \) are positive constants, \(x^{+}=\max \{0,x\}\) and \(x^{-}=\max \{0,-x\}\), \(g\) is bounded and \(\frac{2K\pi }{\sqrt{\mu }}\)-periodic in (1.4) or \(K\pi (\frac{1}{\sqrt{\mu }}+\frac{1}{\sqrt{\nu }})\)-periodic in (1.5) with \(K\in \mathbb {N}\). In the related literature, starting with the pioneering work of Dancer [12, 13] and Fucik [18], there has been a large amount of papers to describe the dynamics of (1.5). Despite its simplicity, the dynamical behaviour of (1.5) has surprisingly a very rich structure. Assuming that the function \(g\) share the same period with all solutions of the homogeneous equations, many authors dedicated their efforts to particular aspects of (1.5), e.g. [14] and their references. It is interesting to note that (P) is caused by the resonant condition (A). For instance, if we take \(\mu =\nu =1\) and consider \(g\equiv 0\) in (1.5) as a periodic function of period \(\pi \), the set of \(\pi \)-periodic solutions is clearly bounded since we have only the trivial solution. Nevertheless, the set of \(2\pi \)-periodic solutions in (1.5) is unbounded.
Another purpose of this paper is to develop a new abstract methodology to prove the existence of \(T\)-periodic solutions of (1.1) when \(f\) is a Lipschitz-continuous map in \(z\). Specifically, we first assume that
has a \(nT\)-periodic solution with \(n>1\) (non \(T\)-periodic) and then, we compute a constant \(M>0\) satisfying that (1.1) has a \(T\)-periodic solution provided \(\Vert g(t,z)\Vert \le M\) for all \((t,z)\in \mathbb {R}\times \mathbb {R}^{2}\). Moreover, our methodology provides some insights on the location of the \(T\)-periodic solution. In contrast with our approach, the most popular techniques used to study the existence of \(T\)-periodic solutions in (1.1) are: (1) the obtention of a priori bound for the possible \(T\)-periodic solutions and then, the application of topological degree arguments; (2) upper and lower solutions; (3) different fixed points theorems such as Poincaré-Birkhoff, Schauder or Krasnoselskii theorem, see, for instance, [4, 30] and the references therein.
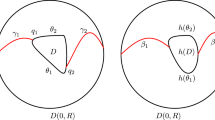
The main tool employed in the proofs of the present paper consists of a topological strategy to locate fixed points in the class of orientation preserving embedding under the condition of some recurrence properties. These results are obtained in the paper in Sect. 2 and could be perceived not only as a tool for finding periodic solutions of differential equations, but have their own interest. Generally speaking, our strategy is inspired by Morton Brown theorem [6], which shows the existence of a fixed point in the presence of a two-cycle. We prove a stronger result (Theorem 2.2) that can be described as follows: assume that \(p\) is a recurrent point so that \(p\) and \(h^{n}(p)\) are near (according to Definition 2.3). In this scenario, take \(\gamma \) any arc joining \(p, h^{n}(p)\), and \(h(p)\) so that the sub-arc joining \(p\) and \(h^{n}(p)\) is in a small neighbourhood of \(p\). Then, one of the following conditions holds:
-
\(h\) has a fixed point in \(\gamma \).
-
\(h\) has a fixed point in a bounded connected component of
$$\begin{aligned} \mathbb {R}^{2}\backslash \gamma \cup ...\cup h^{n}(\gamma ). \end{aligned}$$
By Theorem 2.2, we also get criteria for ensuring the existence of fixed points for orientation preserving embeddings not defined on the whole plane under the presence of a recurrent point. Furthermore, we introduce some metric conditions on \(h\) by considering Kister homeomorphisms and Lipschitz-continuous maps. By our main result we obtain automatic bounds for \(n\)-cycles expressed by a bound of the fixed point set (which is a generalization of [9]) for Kister homeomorphisms and are able to determine the location of fixed points for perturbed Lipschitz-continuous embeddings. Finally, Theorem 2.2 enables us to prove the existence of fixed points for Identity\(+\) Lipschitz-continuous map (Theorem 3.4).
The content of the paper is organized as follows. In Sect. 2 we develop a theoretical framework used along the paper. Among the results in that section, we recall some well-known concepts on the theory of translations arcs. The reader can consult, for instance, [16, 21, 24, 27, 31] for recent applications of this tool. In Sect. 3 we introduce some metric conditions in the results of the previous section. Finally, in Sect. 4, we apply our theoretical results in planar systems of differential equations.
Notation:
Although the notation in the paper is quite standard, we prefer to give the precise definitions for the reader’s convenience. The Euclidean norm is given by \(\Vert (x,y)\Vert =\sqrt{x^{2}+y^{2}}\). Given two different apoints \(p,q\) and a number \(\epsilon \in (0,1)\), \(\mathcal {E}(\textit{p},\textit{q};\epsilon )\) refers to the closed domain limited by the ellipse of foci at \(p\), \(q\) and eccentricity \(\epsilon \), namely
We employ the notation \(B(p,r)\) for the closed Euclidean ball with center at \(p\) and radius \(r\). An arc is the image of an injective and continuous function \(\gamma :[0,1]\longrightarrow \mathbb {R}^{2}\). Throughout the paper, for simplicity, \(\gamma \) sometimes refers to \(\gamma ([0,1])\). The segment with ends at \(p,q\) is represented by \([p,q]\). Given a set \(U\), the \(c\)-neighbourhood of \(U\) is given by
For convenience, \([p,q]_{M}\) denotes the \(M\)-neighbourhood of the segment \([p,q].\) Finally, the classical Brouwer degree of the map \(h\) in the set \(U\) is denoted by \(deg(h,U),\) see [22]. \(Fix(h)\) denotes the fixed point set of the map \(h\). We employ \(int( U)\) and \(\partial U\) to refer the interior and the boundary of \(U\) respectively.
2 Fixed Points for Orientation Preserving Planar Embeddings
In this section we develop the topological part of this paper related to the existence and location of fixed points for orientation preserving planar embeddings. In the first subsection we recall some known results on the theory of translation arcs mainly taken from [28]. The reader can consult [7, 8, 17, 26] for other references in this direction. In the second subsection we provide a strategy for locating fixed points in the presence of recurrent points. As we will see, our results can be considered as an extension of the main result in [6] (concerning two cycles) to any recurrent point.
2.1 Existence of Translation Arcs
Given \(V\subset \mathbb {R}^{2}\) a connected and open set, we say that a map \(h:V\longrightarrow \mathbb {R}^{2}\) is an embedding if it is continuous and injective. In the class of embeddings there are two important subclasses, namely the orientation preserving and orientation reversing embeddings. Rigorously, an embedding \(h\) preserves the orientation if
where \(q_{0}=h(p_0)\) and \(U\) is any bounded and open neighbourhood of \(p_{0}\) contained in \(V\). Here \(\mathcal {E}(V)\) and \(\mathcal {E}_{*}(V)\) denote the classes of embeddings and orientation preserving embeddings defined on \(V\), respectively. Next, we recall the notion of translation arc.
Definition 2.1
A translation arc for an embedding \(h\in \mathcal {E}(V)\) is an arc \(\alpha \) contained in \(V\), with ends at \(q\) (non fixed point) and its image \(h(q)\), and satisfying that
Note that by the definition, a translation arc does not contain fixed points and \(h^{2}(q)\) can belong to \(\alpha \backslash \{h(q)\}\). The notion of translation arc is important in dynamical systems due to the following classical result.
Theorem 2.1
(Brouwer’s Lemma) Assume that \(h\in \mathcal {E}_{*}(V)\) and \(\alpha \) is a translation arc with
for some \(n_{0}\ge 2\) and the topological hull of \(\alpha \cup h(\alpha )\cup ...\cup h^{n_{0}}(\alpha )\) is contained in \(V\). Then there exists a Jordan curve \(\Gamma \subset V\backslash Fix(h)\) such that
with \(R_{i}(\Gamma )\subset V\), where \(R_{i}(\Gamma )\) is the bounded connected component of \(\mathbb {R}^{2}\backslash \Gamma .\)
In the previous theorem, by the topological hull of a set \(A\subset \mathbb {R}^{2}\), we understand the union of \(A\) and all of its bounded complementary domains. It is important to note that from the proof of Theorem 2.1 one can deduce the following result.
Corollary 2.1
In the setting of the previous theorem, \(h\) has a fixed point in the topological hull of \(\alpha \cup h(\alpha )\cup \dots \cup h^{n_{0}}(\alpha )\).
The proofs of Theorem 2.1 and Corollary 2.1 can be found in [28]. Note that the results in that reference are relative to embeddings defined on the whole plane. However, the same proofs work in the statement presented above.
The main purpose of this section is to formulate some criteria concerning the construction of translation arcs.
Definition 2.2
We say that a family of topological disks \(\{D_{t}\}_{t\in [0,1]}\) is admissible if
Note that we are dealing with monotone families in the sense that
Moreover, we observe that an admissible family of disks is stable under homeomorphisms, that is, \(\{\phi (D_{t})\}\) is another admissible family provided \(\phi \) is a homeomorphism. Next, we present two useful results on admissible families of disks. For the proofs of them the reader may consult [28].
Lemma 2.1
Let G be an open and connected subset of \(\mathbb {R}^{2}\) containing two disjoint disks \(D\) and \(\Delta \). Then there exists an admissible family of disks \(\{D_{t}\}\) satisfying that
Lemma 2.2
Assume that \(\{D_{t}\}\) is an admissible family of disks contained in \(V\) and \(f:V\longrightarrow f(V)\subset V\) is a homeomorphism satisfying that
Then, for some \(\tau \in (0,1]\),
Finally, we present the statement that enables us to construct a translation arc which goes through given points.
Proposition 2.1
Assume that \(h:V\longrightarrow h(V)\subset V\) belongs to \(\mathcal {E}_{*}(V)\) and \(D\subset V\) is a topological disk with
Then, given points \(w_{1},\ldots ,w_{n}\in D\), there exists a translation arc \(\alpha \) with ends at \(q, h(q)\) and satisfying that
Proof
First, as \(V\) is connected and open; and \(h:V\longrightarrow V\) is an orientation preserving embedding, the connected components of \(V\backslash Fix(h)\) are positively invariant under \(h\), see Proposition 20 in Chapter 3 in [28]. Now, we consider the disjoint disks \(D_{0}:=D\), \(\Delta :=h(D)\) and \(G\) the connected component of \(V\backslash Fix(h)\) containing \(D\) and \(h(D)\). Next, we construct an admissible family \(\{D_{t}\}\subset G\) by applying Lemma 2.1. As a result we obtain the family \(\{D_{t}\}\) such that \(D_{1}\cap h(D)\not =\emptyset \). As \(\{D_{t}\}\) is admissible with \(D_{1}\cap h(D)\not =\emptyset \) and \(h(D)\subset h(D_1)\), it is clear that \(D_{1}\cap h(D_{1})\ne \emptyset \). Now we use Lemma 2.2 to find a number \(\tau \) satisfying conditions (2.3). Finally, we take any arc \(\alpha \) with ends at \(q\) and \(h(q)\), where \(q \in \partial D_{\tau }\) and \(h(q) \in \partial D_{\tau }\cap \partial h(D_{\tau })\), satisfying that \(\dot{\alpha }\subset int(D_{\tau })\). By the definition of \(G\), we get that \(q\ne h(q)\) and \(h(q) \ne h^2(q)\) and therefore (2.2) is satisfied i.e. \(\alpha \) is a translation arc. \(\square \)
2.2 \(\varepsilon \)-Periodic Points and the Location of Fixed Points
The aim of this subsection is to describe a general strategy inspired by [6] for locating fixed points under the presence of a recurrent point. In more detail, we focus our attention on an extension of the main theorem in [6], concerning two cycles, to any recurrent point. Our method of the proof is essentially different from that of M. Brown, since the latter relies on an elegant computation of a winding number, while our approach is based on the theory of translation arcs. Following this goal, we need to present a crucial concept in this paper.
Definition 2.3
Consider \(h:V\subset \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) a continuous map. Given \(\varepsilon \ge 0\), we say that \(p\in V\) is an \(\varepsilon \)-periodic point of order \(n>1\) if
-
\(h^{n}(p)\in B(p,\varepsilon )\),
-
\(B(p,\varepsilon )\cap h(B(p,\varepsilon ))=\emptyset \).
Remark 2.1
Note that any recurrent point different from a fixed point is an \(\varepsilon \)-periodic point of order \(n\) for a suitable \(n\) and \(\varepsilon \ge 0\). On the other hand, Definition 2.3 is stable under perturbations. In particular, given \(p\) a periodic point of order \(n\) of \(h\) in the classical sense, that is, \(h^{n}(p)=p\), and \(h_{\delta }\) a small perturbation of \(h\), we can guarantee that \(p\) is an \(\varepsilon \)-periodic point of order \(n\) for a suitable \(\varepsilon \ge 0\) associated with \(h_{\delta }\).
Now we are in a position to formulate the main theorem of this section.
Theorem 2.2
Consider \(h:\mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) an orientation preserving embedding with \(p\in \mathbb {R}^{2}\) an \(\varepsilon \)-periodic point of order \(n\). Take a continuous map \(\gamma :[0,1]\longrightarrow \mathbb {R}^{2}\) so that the image \(\gamma :=\gamma ([0,1])\) joins \(p, h^{n}(p), h(p)\) in the following way:
- i) :
-
\(\gamma (0)=p\),
- ii) :
-
there exists \(t_{0}\ge 0\) with \(\gamma (t_{0})=h^{n}(p)\) and \(\gamma ([0,t_{0}])\subset B(p,\varepsilon )\),
- iii) :
-
\(\gamma (1)=h(p)\).
Then \(h\) has a fixed point in the topological hull of \(\gamma \cup h(\gamma )\cup ...\cup h^{n}(\gamma )\).
Proof
Assume that \(h\) has no fixed points in \(\gamma \), otherwise the proof is clear. Given \(\delta >0\), we first find a Jordan curve \(\Gamma \) contained in a \(\delta \)-neigbourhood of \(\gamma \cup h(\gamma )\cup \ldots \cup h^{n}(\gamma )\), say \(U\), and satisfying that \(h\) has a fixed point in the bounded connected component of \(\mathbb {R}^{2}\backslash \Gamma \). To realize this aim observe that by continuity we can take \(\widetilde{\delta }>0\) small enough so that \(\widetilde{U}\), the \(\widetilde{\delta }\)-neighbourhood of \(\gamma \), satisfies that
Next, we take two disjoint topological disks \(D\) and \(\Delta \) contained in \(\widetilde{U}\) with the following conditions: \(p,h^{n}(p)\in D\) and \(h(p)\in \Delta \), see i), ii) and the definition of \(\varepsilon \)-periodic point. Now we apply Lemma 2.1 in the set \(int(\widetilde{U})\) with disks \(\Delta \) and \(D\) in order to find an admissible family of disks \(\{D_{t}\}\) with \(D_{0}=D\). Note that as \(\gamma \) is the image of a continuous map defined on \([0,1]\) then \(int(\widetilde{U})\) is an open and connected set. After that we use Lemma 2.2 with the previous family and we obtain an index \(\tau >0\) so that \(\partial h(D_{\tau })\cap \partial D_{\tau }\not =\emptyset \) with \(int(D_{\tau })\cap h(int(D_{\tau }))=\emptyset \) for all \(t<\tau \). Observe that \(D_{0}\cap h(D_{0})=\emptyset \) and \(D_{1}\cap h(D_{1})\not =\emptyset \). Then, as a consequence of Proposition 2.1 (see also its proof) we get a translation arc \(\alpha \) contained in \(D_{\tau }\) and passing through \(p\) and \(h^{n}(p)\). What is more,
Finally, Theorem 2.1 and Corollary 2.1 apply since \(h^{n}(p)\in \alpha \cap h^{n}(\alpha )\). To complete the proof of the theorem, we tend with \(\delta \) to zero. \(\square \)
Some remarks are in order. First, in the proof of the previous theorem there are some ideas taken from [16, 17, 21, 24]. Nevertheless, we have preferred to provide a self-contained proof for the reader’s convenience. On the other hand, it is well known that every orientation preserving embedding of the plane with a recurrent point necessarily has a fixed point. However, in general, this is not true when our map is not defined on the whole plane. For instance, any non trivial rotation defined on \(\mathbb {R}^{2}\backslash \{0\}\) has infinite recurrent points and none fixed point. In this scenario, it is worth mentioning the following remark.
Remark 2.2
Working with \(h\in \mathcal {E}_{*}(V)\) where \(V\) is an open and connected set with \(h:V\longrightarrow h(V)\subset V\), Theorem 2.2 holds if we assume that the topological hull of \(\gamma \cup ...\cup h^{n}(\gamma )\) is contained in \(V\).
The reader can consult [2] for an interesting result concerning the existence of fixed point for maps which are not defined on the whole plane.
Apart from this remark, note that when \(h^{n}(p)=p\), we can just apply Theorem 2.2 with \(\gamma \) any arc joining \(p\) and \(h(p)\), that is, \(t_{0}=0\) in ii).
In most cases, if we consider \(p\), an \(\varepsilon \)-periodic point of order \(n\), we usually apply Theorem 2.2 with \(\gamma \) given by the juxtaposition of the segments \([p,h^{n}(p)]\) and \([h^{n}(p),h(p)]\).
3 Adding Metric Conditions in Theorem 2.2
The results in the previous section provide us some topological ideas concerning the location of fixed points. Some rather striking conclusions appear when additional metric conditions are added, for instance, when we consider Kister homeomorphisms or Lipschitz-continuous maps. Namely, we ultimately prove the existence of automatic bounds for any cycle from the knowledge of a bound for the fixed points. We also determine the location of a fixed point for perturbations of embeddings having a recurrent point. These conclusions are not only interesting in their own right but have deep applications in periodic systems of differential equations.
The notion of Kister homeomorphism is taken from [5] and means that the distance to the identiy is bounded: \(h:\mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is a Kister homeomorphism if there is a constant \(M>0\) so that
for all \(x\in \mathbb {R}^{2}\). We recall that a Kister homeomorphism preserves the orientation, see [5]. One of our main results in this section (Theorem 3.1) asserts that condition (3.1) produces some restrictions on the \(n\)-cycles of \(h\).
Theorem 3.1
Assume that \(h:\mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is a Kister homeomorphism with constant \(M\). If the fixed point set of \(h\) is bounded by \(\beta (1)\) then, for every \(n\), the \(n\)-cycle set of \(h\) is bounded by \(\beta (n)\) with
Before giving the proof of the previous result we present an elementary lemma taken from [9].
Lemma 3.1
Assume that for some \(R>0\) the disk of radius \(R\) centered at the origin has a non-empty intersection with
Then
Proof of Theorem 3.1
Take a periodic point \(p\) of order \(n\). First, note that
and, inductively,
To prove these claims we have to see that by (3.1) if \(x\in [p,h(p)]\), then \(\Vert h(x)-x\Vert \le M\), and thus
and inductively
On the other hand, it is clear that \([p,h(p)]_{nM}\) is a convex set. Taking this fact into account we apply Theorem 2.2 with \(\gamma =[p,h(p)]\). By inclusions (3.2) and (3.3) we deduce that \(\gamma \) and the bounded connected components of
are contained in \([p,h(p)]_{n M}\). Therefore \(h\) has a fixed point in \([p,h(p)]_{n M}\). As a consequence, using that the fixed point set of \(h\) is bounded by \(\beta (1)\), we obtain that
Finally we apply Lemma 3.1 and get that
\(\square \)
Remark 3.1
Proposition 2 in [9] is a special case of Theorem 3.1. Specifically, the result in that paper corresponds with the case of \(n\)-cycles of order being power of 2. As it was stressed by the authors in [9], their method of proof cannot cover the general case since it is based on the results for two cycles proved in [6].
The previous theorem shows how to deduce automatic bounds for cycles from a bound for the fixed points. Now we locate a fixed point for perturbed embeddings assuming that it is possible to estimate the position of a \(n\)-cycle. Instead of Kister homeomorphisms, from now on we work with Lipschitz-continuous embeddings with respect to the Euclidean norm. For simplicity, we discuss here the case of two cycles. The case of \(n\)-cycles can be treated in the same way but it involves tedious expressions describing the sets in which we are able to find a fixed point.
Theorem 3.2
Assume that \(h:\mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is a Lipschitz-continuous orientation preserving embedding with Lipschitz constant \(L\) and having a \(2\)-cycle \(\{p,h(p)\}\) with \(\Vert p-h(p)\Vert \ge d>0\). Define the constants
and
If \(h_{\delta }:\mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is an orientation preserving embedding with
for all \(x\), then \(h_{\delta }\) has a fixed point in a \(c\)-neighbourhood of \(\mathcal {E}(p,h(p),\frac{1}{L^{2}}).\)
Proof
First, we note that
and
Indeed, take \(x\in [p,h(p)]\). We get that
where in the inequality we have used the fact that \(h\) is Lipschitz-continuous and in the first equality, we have used that \(x\in [p,h(p)]\), see (1.7) to check (3.7). In an analogous way,
We have used (3.7) in the second inequality. On the other hand, note that \(L\ge 1\) since \(h\) has a two cycle. Therefore,
and so
Now, we prove that \(p\) is an \(\varepsilon \)-periodic point of order \(2\) for \(h_{\delta }\) with \(\varepsilon =\frac{d}{2+L}\). In fact, by (3.6) we get by a simple analysis using \(h(h_{\delta }(p))\) that
On the other hand, \(h_{\delta }(B(p,\varepsilon ))\) is contained in a \(\delta \)-neighbourhood of \(B(h(p),L \varepsilon )\). In a direct way we can check that
and therefore,
Finally, we apply Theorem 2.2 with \(\gamma \) the juxtaposition of \([p,h^2_{\delta }(p)]\) and \([h^{2}_{\delta }(p), h_{\delta }(p)]\). Observe that \(\gamma \) is contained in an \(\varepsilon \)-neighbourhood of \([p,h(p)]\). Moreover notice that
for all \(x,y\in \mathbb {R}^{2}\) with \(\Vert x-y\Vert \le \varepsilon \). Indeed,
At this moment it is clear that
and the bounded connected components of
are contained in a \(L^{2}\varepsilon +\delta (1+L)\)-neighbourhood of
Realize that \(L^{2}\varepsilon +\delta (1+L)=c.\) This fact ends the proof of the theorem. \(\square \)
In the related literature one can find several papers treating different techniques for locating fixed points for Lipschitz continuous orientation preserving embeddings, see [1, 3, 9, 19]. Theorem 3.2 was stated in [9] for two cycles and \(h\) (without considering perturbations). As mentioned in Remark 3.1 due to the limitation of method of the proof used in that paper, it was impossible to cover our general setting. On the other hand, different strategies for locating fixed points for maps of type Identity \(+\) Contraction were developed in [1, 19]. Specifically, they obtain the following result. Recall that Identity \(+\) Contraction is always an orientation preserving embedding, see [1].
Theorem 3.3
Let \(h:\mathbb {R}^{2} \rightarrow {\mathbb R^2}\) be a continuous map where \(h(x)=x+K(x)\) with \(K(x)\) a contraction of constant \(k\) and stand \(x_{n}=h^{n-1}(x)\). Assume that there is a finite sequence \(\{x_1, \ldots , x_{n+1}\}\) satisfying that for some \(w \in [x_n, x_{n+1}]\),
Then there exists a point \(y\) in the convex hull of \(\{x_1, \ldots , x_{n+1}\}\) such that \(K(y)=0\).
In [19] Theorem 3.3 was improved, namely it was shown that the thesis remains true if we replace the inequality (3.15) by \(||w-x_1||\le 1/k\;||K(x_1)||\).
It turns out that we can easily obtain a version of Theorem 3.2 for maps of the type Identity \(+\) Lipschtz-continuous map when this map is an orientation preserving embedding. The main advantage of the next theorem with respect to Theorem 3.3 is that we enlarge the range of maps in which it is possible to guarantee the existence of a fixed point since we do not impose the condition of contraction. For convenience, we assume in the following theorem the same notation as before. Specifically, \(h(z)=z+K(z)\) with \(K(z)\) a Lipschitz-continuous map of Lipschitz-constant \(k\).
Theorem 3.4
Assume that
Then there exists a point \(y\) such that \(K(y)=0\).
Proof
Let us take \(\varepsilon =||x_n-x_1||\). By Theorem 2.2, it suffices to prove that \(x_1\) is \(\varepsilon \)-periodic point of order \(n>1\). We verify that
-
\(x_n=h^{n}(x_1)\in B(x_1,\varepsilon )\), by the definition of \(\varepsilon \).
-
\(B(x_1,\varepsilon )\cap h(B(x_1,\varepsilon ))=\emptyset \): Assume, contrary to our claim, that there is \( z\in B(x_1,\varepsilon )\cap h(B(x_1,\varepsilon )) \ne \emptyset \). Then, as \(h(B(x_{1},\varepsilon ))\subset B(h(x_{1}),(1+k) \varepsilon )\), we deduce that \(||x_1-h(x_1)||\le ||x_{1}-z||+||z-h(x_1)||\le \varepsilon +\varepsilon (k+1)=\varepsilon (k+2)\). On the other hand \(||x_1-h(x_1)||=||K(x_1)||\), thus we obtain the contradiction with assumption (3.16). \(\square \)
4 Applications in Differential Equations
The aim of these two subsections is to apply the results of Sect. 3 to (1.1). We assume for the rest of the paper without further mention that (1.1) has uniqueness of solution for the Cauchy problem. In this setting, the key to link our results for planar embeddings (Sect. 3) with the dynamics of (1.1) is the Poincaré map
where \(z(t;\xi )\) is the solution of (1.1) satisfying that \(z(0;\xi )=\xi \). We recall that \(P\) is well defined provided the solutions of (1.1) are globally defined in the future. To ensure this property, we assume that \(f\) is Lipschitz-continuous with respect to \(z\) and \(g\) is bounded. We note that \(P\) is an orientation preserving embedding and many dynamical properties of (1.1) are coded in \(P\). For instance, \(Fix(P^{k})\) corresponds to the initial conditions producing \(kT\)-periodic solutions in (1.1). Moreover, if \(Fix(P^{k})\) is a bounded set then the \(kT\)-periodic solutions in (1.1) are bounded as well.
4.1 Global Perturbations of Isochronous Centers
This subsection shows some phenomena on boundedness of subharmonics for global perturbations of a planar autonomous system having an isochronous center. In more detail, we consider
and \(p\in \mathbb {R}^{2}\), an equilibrium of
so that the whole plane is covered by periodic orbits of (4.2) surrounded \(p\) and satisfying that the map which associates to any periodic orbit \(\gamma \) its period is constant, say \(\tau \). Moreover, we impose the following conditions:
- H1 :
-
\(f:\mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is a Lipschitz-continuous map with constant \(L>0.\)
- H2 :
-
\(g:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is \(T\)-periodic in time with \(T=n \tau \) (where \(n\) is given) and bounded by \(R.\)
Examples of systems (4.2) verifying the previous assumptions are easily found in an infinity of physical situations. For instance, the classical oscillator
or the asymmetric oscillator
have an isochronous center at \(0\) where the period is \(\frac{2 \pi }{\omega }\) and \(\pi (\frac{1}{\sqrt{\mu }}+\frac{1}{\sqrt{\nu }})\) respectively. The reader can consult [11, 32] for criteria concerning isochronous centers.
Note that under H1-H2, if \(z(t;z_{0})\) and \(y(t;z_{0})\) denote the solutions of (4.1) and (4.2) satisfying that \(z(0;z_{0})=z_{0}\) and \(y(0;z_{0})=z_{0}\), then
In the first equality we use the fact that \(y(T;z_{0})=z_{0}\) by the property \(T=n \tau \) and in the second inequality we use H1-H2 in a direct way. Then, by Gronwall’s lemma we deduce that the Poincaré map (at time \(T\)) associated with (4.1) is a Kister homeomorphism with constant \(M= R T e^{TL}\). Finally, Theorem 3.1 is applicable and we directly obtain the following result.
Theorem 4.1
Assume that \(p\) is an isochronous center of (4.2) where the period of the orbits is \(\tau \) (likely not the minimal period) and conditions H1-H2 are satisfied. If the set of \(T\)-periodic solutions of (4.1) is bounded, then, for each \(n\in \mathbb {N}\), the set of \(nT\)-periodic solutions of (4.1) is bounded as well.
The previous theorem can be used contrapositively to deduce the following principle: if for some \(n\in \mathbb {N}\), the set of \(nT\)-periodic solutions of (4.1) is unbounded, then (4.1) has infinite \(T\)-periodic solutions. Note that it is well known that in the setting of Theorem 4.1, under the existence of a recurrent point there is at least a T-periodic solution.
4.2 Perturbation of Systems Having Subharmonics
The aim of this subsection is to design a strategy to prove the existence and location of \(T\)-periodic solutions in perturbed systems of the type
where
- A1 :
-
\(f:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is \(T\)-periodic in time and Lipschitz continuous with Lipschitz-constant \(L\) in the space-variable, that is,
$$\begin{aligned} \Vert f(t,z_{1})-f(t,z_{2})\Vert \le L\Vert z_{1}-z_{2}\Vert \end{aligned}$$for all \((t,z_{1}), (t,z_{2})\),
- A2 :
-
\(g:\mathbb {R}\times \mathbb {R}^{2}\longrightarrow \mathbb {R}^{2}\) is \(T\)-periodic and
$$\begin{aligned} \Vert g(t,z)\Vert \le R \end{aligned}$$for all \((t,z)\in \mathbb {R}\times \mathbb {R}^{2}\).
Here, the system
plays a crucial role. The following result is a version of Theorem 3.2 in the framework of system (4.3). This result enables us to deduce the following theoretical phenomenon:
(T) Assume that (4.4) has a subharmonic. Then we can find a bound \(R>0\) for \(g\) so that (4.3) has a \(T\) -periodic solution provided \(\Vert g(t,z)\Vert \le R\) for all \((t,z)\).
Theorem 4.2
Consider (4.3) satisfying conditions A1-A2 and assume that \(y(t)\) is a \(2T\)-periodic solution of (4.4) satisfying that \(y(0)\in B(z_{1},r_{1})\) and \(y(T)\in B(z_{2},r_{2})\) with \(0<d\le \Vert y(0)-y(T)\Vert \). Define
If \(RT \exp (LT)\le \delta \) then system (4.3) has a \(T\)-periodic solution with initial condition in a \(c\)-neighbourhood of
where \(r=\Vert z_{1}-z_{2}\Vert \).
Proof
Denote by \(P\) and \(P_{\delta }\) the Poincaré maps of (4.4) and (4.3) respectively. As a direct application of the Gronwall’s lemma, we get that \(P\) is a Lipschitz-continuous embedding with Lipschitz-constant \(\exp (LT)\) and
for all \(z\in \mathbb {R}^{2}.\) Then, in a direct application of Theorem 3.2, we obtain the first conclusions of our theorem. To deduce the second part, we apply the next lemma. \(\square \)
Lemma 4.1
Consider two points in the plane \(z_{1},z_{2}\) with
and two positive \(r_{1},r_{2}\). Then
for all \(p_{i}\in B(z_{i},r_{i})\) with \(i=1,2.\)
Proof
Take \(z\in \mathcal {E}(p_{1},p_{2};\frac{1}{\epsilon })\). Then
\(\square \)
Theorem 4.2 gives a criterion for proving the existence of \(T\)-periodic solutions in (4.3) when we can estimate the location of a subharmonic in (4.4). In the related literature, there are several tools to guarantee the existence of subharmonics in (4.4), e.g. Poincaré Birkhoff theorem, see [4, 30] or the theory of topological horseshoes, see [25].
References
Aarao, J., Martelli, M.: Stationary states for discrete dynamical systems in the plane. Topol. Methods Nonlinear Anal. 20, 15–23 (2002)
Bonino, M.: A dynamical property for planar homeomorphisms and an application to the problem of canonical position around an isolated fixed point. Topology 40, 1241–1257 (2001)
Bonnati, C., Kolev, B.: Existence de points fixes enlacés \(\grave{a}\) une orbite périodique d’un homéomorphisme du plan. Ergodic Theory Dynam. Syst. 12, 667–682 (1992)
Boscaggin, A., Zanolin, F.: Pairs of positive periodic solutions of second order nonlinear equations with indefinite weight. J. Differ. Equ. 252, 2900–2921 (2012)
Brown, M.: A note on Kister’s isotopy. Michigan Math J. 14, 95–96 (1967)
Brown, M.: Fixed points for orientation preserving homeomorphisms of the plane which interchange two points. Pac. J. Math. 143, 37–41 (1990)
Brown, M.: A new proof of Brouwer’s lemma on translation arcs. Houst. J. Math. 10, 35–41 (1984)
Brown, M.: Homeomorphisms of two dimensions manifolds. Houst. J. Math. 11, 455–469 (1985)
Campos, J., Ortega, R.: Location of fixed points and periodic solutions in the plane. Discret. Contin. Dyn. Syst. Ser. B 9, 517–523 (2008)
Capietto, A., Dambrosio, W., Ma, T., Wang, Z.: Unbounded solutions and periodic solutions of perturbed isochronous hamiltonian systems in resonance. Discret. Contin. Dyn. Syst. 33, 1835–1856 (2013)
Chavarriga, J., Sabatini, M.: A survey of isochronous centers. Qual. Theory Dyn. Syst. 1, 1–70 (1999)
Dancer, E.N.: On the Dirichlet problem for weakly non-elliptic partial differential equations. Proc. R. Soc. Edinb. A 76, 283–300 (1977)
Dancer, E.N.: Boundary-value problems for weakly nonlinear ordinary differential equations. Bull. Aust. Math. Soc. 15, 321–328 (1976)
Fabry, C., Fonda, A.: Unbounded motions of perturbed isochronous hamiltonian systems in resonance. Adv. Nonlinear Stud. 5, 351–373 (2005)
Fonda, A., Mawhin, J.: Planar differential equations at resonance. Adv. Differ. Equ. 11, 1111–1133 (2006)
Franks, J.: Recurrence and fixed points of surfaces homeomorphisms. Ergod. Theory Dynam. Syst. 8, 99–107 (1988)
Franks, J.: A new proof of the Brouwer plane translation theorem. Ergod. Theory Dynam. Syst. 12, 217–226 (1992)
Fucik, S.: Solvability of Nonlinear Equations and Boundary value problems. Reidel, Dordrecht (1980)
Graff, G., Nowak-Przygodzki, P.: Fixed points of planar homeomorphisms of the form identity + contraction. Rocky Mt. J. Math. 37, 299–314 (2007)
Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcation of Vector Fields. Springer-Verlag, New York (1983)
Handel, M.: A fixed-point theorem for planar homeomorphisms. Topology 38, 235–264 (1999)
Jezierski, J., Marzantowicz, W.: Homotopy Methods in Topological Fixed and Periodic Point Theory. Topological Fixed Point Theory and Its Applications, vol. 3. Springer, Dordrecht (2006)
Lanzer, A., Leach, D.E.: Bounded perturbations of forced harmonics oscillators at resonance. Ann. Mat. Pura Appl. 82, 49–68 (1969)
Le Calvez, P.: Pourquoi les points périodiques des homéomorphisme du plan tournent-ils autour de certains points fixes? Ann. Sci. Ec. Norm. Super. 41, 141–176 (2008)
Margueri, A., Rebelo, C., Zanolin, F.: Chaos in periodically perturbed planar hamiltonian systems using linked twist maps. J. Differ. Equ. 249, 3233–3257 (2010)
Murthy, P.: Periodic solutions of two dimensional forced systems: the Massera theorem and its extension. J. Dynam. Differ. Equ. 10, 275–302 (1998)
Ortega, R., Ruiz-Herrera, A.: Index and persistence of stable Cantor sets. Rend. Inst. Mat. Univ. Trieste 44, 33–44 (2012)
Ortega, R.: Topology of the Plane and Periodic Differential Equations (2013). www.ugr.es/local/ecuadif/fuentenueva.htm
Ortega, R., Verzini, G.: A variational method for the existence of bounded solutions of a sublinear forced oscillator. Proc. Lond. Math. Soc. 88, 775–795 (2004)
Rebelo, C., Zanolin, F.: Multiplicity results for periodic solutions of second order ODE’s with asymmetric nonlinearities. Trans. Amer. Math. Soc. 348, 2349–2389 (1998)
Ruiz-Herrera, A.: Topological criteria of global attraction with applications in population dynamics. Nonlinearity 25, 2823–2841 (2012)
Urabe, M.: The potential force yielding a periodic motion whose period is an arbitrary continuous function of the amplitude of the velocity. Arch. Ration. Mech. Anal. 11, 27–33 (1962)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Graff, G., Ruiz-Herrera, A. A Strategy to Locate Fixed Points and Global Perturbations of ODE’s: Mixing Topology with Metric Conditions. J Dyn Diff Equat 26, 93–107 (2014). https://doi.org/10.1007/s10884-013-9345-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-013-9345-y