Towards the Complete Classification of the Two Lines Inverse Limit

Abstract

For positive numbers $r<1$ and $\rho >1$, let $L_{r,\rho }$ be the union of two line segments in $[0,1] \times {[}0,1{]}$, one from (0, 0) to (1, r) and the other one from (0, 0) to $(\frac{1}{\rho },1)$. In Banič et al. (2022), it was proven for all such r and $\rho$ that, if r and $\rho$ never connect, then the Mahavier product of $L_{r,\rho }$’s is homeomorphic to the Lelek fan. In this paper, we show that for all such r and $\rho$, if r and $\rho$ do connect, the Mahavier product of $L_{r,\rho }$’s is a fan F with top v with some additional properties. More precisely, it is the union of a countable family $\mathcal {C}$ of Cantor fans such that

• 1. for each $C_1,C_2\in \mathcal {C}$, if $C_1\ne C_2$, then $C_1\cap C_2 = \{v\}$ and

• 2. the set of limit points of the set of end-points of F, forms in each arc from v to an end-point, a harmonic sequence.

This solves the open problem from Banič et al. (2022).

1 Introduction

In [2], the authors examine a family of Mahavier products $M_{r,\rho }$ of closed relations $L_{r,\rho }$ on [0, 1]. These relations $L_{r,\rho }$ are the unions of two line segments joint in (0, 0) that have positive slopes r and $\rho$ and extend to the opposite boundary of $[0,1]\times [0,1]$. More precisely, let r,  $\rho >0$. It is shown in [2] that

• 1. if $r=\rho$ and $r\le 1$, then $M_{r,\rho }$ is an arc from $(0,0,0,\ldots )$ to $(1,r,r^2,r^3,\ldots )$.

• 2. if $r=\rho$ and $r>1$, then $M_{r,\rho }=\{(0,0,0,\ldots )\}$.

• 3. if $r\ne \rho$, the following possibilities are considered.

  • 1. If $r>1$ and $\rho >1$, then $M_{r,\rho }=\{(0,0,0,\ldots )\}$.

  • 2. If $r\le 1$ and $\rho \le 1$, then $M_{r,\rho }$ is a Cantor fan.

  • 3. If $r=1$ and $\rho > 1$, then $M_{r,\rho }$ is as pictured in Fig. 1. See [2] for a detailed description of the fan.

  • 4. If $r<1$, $\rho >1$ and r and $\rho$ never connect (see Definition 11), $M_{r,\rho }$ is homeomorphic to the Lelek fan, i.e., the fan with the dense set of end-points, see Fig. 2 and [7] for more information about the Lelek fan.

Fig. 1

The fan $M_{r,\rho }$ for $r=1$ and $\rho > 1$

Fig. 2

The Lelek fan

In this paper, we study the final case where $r<1$, $\rho >1$ and there are integers k and $\ell$ such that

• 1. $k\ne 0$ or $\ell \ne 0$, and

• 2. $r^k = \rho ^{\ell }$.

Explicitly, we prove that the Mahavier product $M_{r,\rho }$ of $L_{r,\rho }$’s in this case is a fan with certain additional properties. More precisely, let $E(M_{r,\rho })$ be the set of end-points of $M_{r,\rho }$ and for each $e\in E(M_{r,\rho })$, let $A_e$ be the straight line segment in $M_{r,\rho }$ from its top v to e. Then $M_{r,\rho }$ is the union of a countable family $\mathcal {C}$ of Cantor fans such that

• 1. for each $C_1,C_2\in \mathcal {C}$, if $C_1\ne C_2$, then $C_1\cap C_2 = \{v\}$ and

• 2. for each $e\in E(M_{r,\rho })$, the set of limit points of the set $E(M_{r,\rho })$ in $M_{r,\rho }$ forms a harmonic sequence in $A_e$.

This gives a solution to the open problem from [2].

The paper is divided into the following parts: In Section 2, we give definitions and notation that we use later in the paper and in Section 3, among other things, our main result is presented and proved.

2 Definitions and Notation

In this section, we introduce definitions and notation that is used later in the paper. These follow [8, 9].

Definition 1

For each positive integer n, let $X_n$ be a compact metric space and let $f_n:X_{n+1}\rightarrow X_n$ be a continuous function. We then define the inverse limit as the subspace of $\prod _{n=1}^{\infty }X_n$:

$$\underleftarrow{\text {lim}}\{X_n,f_n\}_{n=1}^\infty = \{(x_1,x_2,x_3,\ldots )\ \mid \ \forall n\in \mathbb {N}: x_n = f_n(x_{n+1})\}.$$

We will shorten the notation to $X_\infty$ to denote the inverse limit $\underleftarrow{\text {lim}}\{X_n,f_n\}_{n=1}^\infty$.

Definition 2

Let X be a compact metric space. We use $2^X$ to denote the set of all non-empty closed subsets of X. Now, let $G \in 2^{X\times Y}$ and $x\in X$. Then we define

$$G(x) = \{y\in Y\ \mid \ (x,y)\in G\}.$$

Definition 3

Let X, Y be compact metric spaces. A function $F:X\rightarrow 2^Y$ is called a set-valued function from X to Y. We will use $F:X\multimap Y$ to denote F as a set-valued function from X to Y. Now, let $F:X\multimap Y$ be a set-valued function. We say that F is upper semicontinuous at a point $x_0\in X$ if for each open set $U\subseteq Y$ such that $F(x_0)\subseteq U$, there is an open set V in X such that

• 1. $x_0\in V$ and

• 2. for each $x\in V, F(x)\subseteq U$.

A set-valued function is upper semicontinuous, abbreviated to USC, if it is upper semicontinuous at every point in X.

We give a characterization of USC set-valued functions, which makes detecting them much more intuitive. This characterization can be found in [1, Prop. 11, page 128] as well as [5, Theorem 1.2, page 3].

Theorem 1

Let $F:X\multimap Y$ be a set-valued function. Then F is USC if and only if the graph of F, defined as

$$\Gamma _F = \{(x,y)\in X\times Y\ \mid \ y\in F(x)\},$$

is closed in $X\times Y$.

Definition 4

For each positive integer n, let $X_n$ be a compact metric space and let $F_n:X_{n+1}\multimap X_n$ be a USC set-valued function. We define the generalized inverse limit of the double sequence $\{X_n,F_n\}_{n=1}^\infty$ as the subspace of the product space $\prod _{n=1}^{\infty }X_n$:

$$\mathop {\lim }\limits _ {\circ \hspace{-1.8pt}-\!\!-\!\!-}\{X_n,F_n\}_{n=1}^\infty = \{(x_1,x_2,x_3,\ldots )\ \mid \ \forall n\in \mathbb {N}: x_n \in F(x_{n+1})\}.$$

We use $X_\infty$ to denote the generalized inverse limit $\mathop {\lim }\limits _ {\circ \hspace{-1.8pt}-\!\!-\!\!-}\{X_n,F_n\}_{n=1}^\infty$. Notice that this is a generalization of the inverse limit as defined before in Definition 1.

The following is a well-known result for generalized inverse limits. Thus, the proof is omitted. Further information can be found in [6, Theorems 5.1 and 5.2, page 125].

Theorem 2

For each positive integer n (Fig. 3), let:

• 1. $X_n$ and $Y_n$ be compact metric spaces,

• 2. $F_n:X_{n+1}\multimap X_n$, $G_n:Y_{n+1}\multimap Y_n$ be USC set-valued functions and

• 3. $\phi _n:X_n\rightarrow Y_n$ be a continuous function such that for each $x\in X_{n+1}$:

  $$\phi _n(F_n(x)) \subseteq G_n(\phi _{n+1}(x)).$$

Fig. 3

A diagram from Theorem 2

Then the function $\phi : X_\infty \rightarrow Y_\infty$ where for each $(x_1,x_2,x_3,\ldots ) \in X_\infty :$

$$\phi ((x_1,x_2,x_3,\ldots )) = (\phi _1(x_1),\phi _2(x_2),\phi _3(x_3),\ldots ),$$

is continuous. Furthermore, if the function $\phi _n$ is a homeomorphism for each positive integer n and it also holds that for each $x\in X_{n+1}:$

$$\phi _n(F_n(x)) = G_n(\phi _{n+1}(x)),$$

then the function $\phi$ is also a homeomorphism.

Next, we define Mahavier products. First, we introduce the following notation.

Definition 5

Let X, Y be compact metric spaces and $G \in 2^{X\times Y}$. We define the inverse of G, denoted as $G^{-1}$, as

$$G^{-1} = \{(y,x) \in Y\times X\ \mid \ (x,y) \in G\}.$$

Definition 6

Let X be a compact metric space, $G \in 2^{X\times X}$. We use

• 1. $\star _{i=1}^{\infty }G = \{(x_1,x_2,\ldots )\in \prod _{i=1}^{\infty }X\ \mid \ \forall i\in \{1,2,\ldots \}: (x_{i},x_{i+1})\in G\}$ to denote the Mahavier product of G.

• 2. $\star _{i=1}^\infty G^{-1} = \{(x_1,x_2,\ldots )\in \prod _{i=1}^\infty X\ \mid \ \forall i\in \mathbb {N}: (x_{i+1},x_i)\in G\}$ to denote the Mahavier product of $G^{-1}$.

Observation 3

Let X be a compact metric space, let $F: X \multimap X$ be a USC set-valued function. Then

$$ \mathop {\lim }\limits _ {\circ \hspace{-1.8pt}-\!\!-\!\!-}\{X,F\}_{n=1}^\infty = \star _{n=1}^\infty \Gamma _F^{-1}. $$

Definition 7

For each positive integer i, let $X_i$ be a compact metric space. We use

• 1. $p_n$ to denote the nth standard projection, $p_n:\prod _{i=1}^\infty X_i \rightarrow X_n$,

  $$p_n(x_1,x_2,\ldots ) = x_n.$$

• 2. $p_{1,n}(\underline{x})$ to denote the projection $p_{1,n}:\prod _{i=1}^\infty X_i \rightarrow \prod _{i=1}^nX_i$

  $$p_{1,n}(x_1,x_2,\ldots ) = (x_1,x_2,\ldots ,x_n).$$

• 3. $p_{n,\infty }$ to denote the projection $p_{n,\infty }:\prod _{i=1}^\infty X_i \rightarrow \prod _{i=n}^\infty X_i$,

  $$p_{n,\infty }(x_1,x_2,\ldots ) = (x_n,x_{n+1},\ldots ).$$

The following definition is needed in Theorem 14.

Definition 8

Let $(x_1,x_2,\ldots ,x_{n-1},x_n)$ be a finite sequence and $(x_n,x_{n+1},x_{n+2},\ldots )$ be a sequence. We use $(x_1,x_2,\ldots ,x_{n-1},x_n)\star (x_n,x_{n+1},x_{n+2},\ldots )$ to denote

$$(x_1,x_2,\ldots ,x_{n-1},x_n)\star (x_n,x_{n+1},x_{n+2},\ldots ) = (x_1,x_2,\ldots ,x_{n-1},x_n,x_{n+1},\ldots ).$$

Definition 9

A continuum is a non-empty compact connected metric space. A subcontinuum is a subspace of a continuum, which is itself a continuum.

Definition 10

Let X be a continuum.

• 1. The continuum X is unicoherent, if for any subcontinua A and B of X such that $X = A\cup B$, the compactum $A\cap B$ is connected.

• 2. The continuum X is hereditarily unicoherent provided that each of its subcontinua is unicoherent.

• 3. The continuum X is a dendroid, if it is an arcwise connected, hereditarily unicoherent continuum.

• 4. Let X be a continuum. If X is homeomorphic to [0,1], then X is an arc.

• 5. A point x in an arc X is called an end-point of the arc X, if there is a homeomorphism $\phi :[0,1]\rightarrow X$ such that $\phi (0) = x$. The set of all end-points of the arc X is denoted by E(X).

• 6. Let X be a dendroid. A point $x\in X$ is called an end-point of the dendroid X, if for every arc A in X that contains x, x is an end-point of A. The set of all end-points of X will be denoted by E(X).

• 7. A continuum X is a simple triod, if it is homeomorphic to $([-1,1]\times \{0\})\cup (\{0\}\times [0,1])$.

• 8. A point x in a simple triod X is called the top-point or, briefly, the top of the simple triod X, if there is a homeomorphism $\phi : ([-1,1]\times \{0\})\cup (\{0\}\times [0,1])\rightarrow X$ such that $\phi ((0,0)) = x$.

• 9. Let X be a dendroid. A point $x\in X$ is called a ramification point of the dendroid X, if there is a simple triod T in X with top x. The set of all ramification points of X will be denoted by R(X).

• 10. The continuum X is a fan, if it is a dendroid with at most one ramification point v, which is called the top of the fan X (if it exists).

• 11. Let X be a fan. We say that X is a Cantor fan, if X is homeomorphic to the continuum

  $$\bigcup _{c\in C}A_c,$$

  where $C\subseteq [0,1]$ is the standard Cantor set and for each $c\in C$, $A_c$ is the straight line segment in the plane from (0, 0) to (c, 1).

Observation 4

Note that a space is a Cantor set if and only if it is a non-empty, compact, completely disconnected space with no isolated points. See [9, Theorem 7.14, page 109] for details and more information.

3 Connected Numbers and a Family of Fans

In this section, we answer the open problem from [2]. First, we introduce the notation that is needed later.

Definition 11

Let $r\in (0,1)$ and $\rho \in (1,\infty )$. We say that r and $\rho$ never connect if for all integers k and l,

$$r^k = \rho ^l \iff k=l=0.$$

We use $(r,\rho )\in \mathcal{N}\mathcal{C}$ to denote that r and $\rho$ never connect.

Definition 12

Let $r\in (0,1)$ and $\rho \in (1,\infty )$. We say that r and $\rho$ connect if there exist positive integers M, N such that

$$r^M\rho ^N = 1.$$

We use $(r,\rho )\in \mathcal {C}$ to denote that r and $\rho$ connect.

Observation 5

Let $r\in (0,1)$ and $\rho \in (1,\infty )$. Then r and $\rho$ connect if and only if there exist positive integers M, N such that

$$r=\rho ^{-\frac{N}{M}}.$$

Theorem 6

Let $r\in (0,1)$ and $\rho \in (1,\infty )$. Then $(r,\rho )\in \mathcal C$ if and only if they do not never connect.

Proof

First, let $(r,\rho )\in \mathcal C$. By Definition 12, there exist positive integers M, N such that

$$r^M\rho ^N = 1.$$

Let $k = M$ and $l = -N$ be integers, then

$$r^k = \rho ^l.$$

Since k and l are non-zero, it follows that r and $\rho$ do not never connect.

Now, let r and $\rho$ be such that they do not never connect. There must then exist integers k, l such that

$$r^k = \rho ^l$$

and at least one of them is non-zero. It is clear that neither can be zero, otherwise the other would also have to be zero or either r or $\rho$ would have to equal 1, all of which are contradictions. Since r is less than 1 and $\rho$ is greater than 1, it is also clear that one of the integers k, l is negative and the other is positive. Without loss of generality let k be negative. It follows that for positive integers $M = -k$ and $N = l$,

$$r^M\rho ^N = 1.$$

This means that r and $\rho$ connect. $\square$

Definition 13

Let r, $\rho >0$. We define the following sets:

• 1. $L_r = \{(x,y)\in [0,1]^2\ \mid \ y = r\cdot x\}$,

• 2. $L_\rho = \{(x,y)\in [0,1]^2\ \mid \ y = \rho \cdot x\}$,

• 3. $L_{r,\rho } = L_r \cup L_\rho$,

• 4. $M_{r,\rho } = \star _{i=1}^\infty L_{r,\rho }$.

Example 1

In Fig. 4, an example of such an $L_{r,\rho }$ for $r = \frac{1}{2}$ and $\rho = 2$ is given.

Fig. 4

$L_{\frac{1}{2},2}$

Definition 14

Let A be a non-empty set. We use $A^\mathbb {N}$ to denote the set

$$\{{\textbf {a}}\ \mid \ {\textbf {a}}:\mathbb {N}\rightarrow A\}$$

of all sequences in A.

Definition 15

Let $(r,\rho )\in \mathcal {C}$ and let ${\textbf {a}} = (a_i)_{i=1}^\infty \in \{r,\rho \}^\mathbb {N}$.

• 1. We define the set $L_{\textbf {a}}$ as follows:

  $$L_{\textbf {a}} = \star _{i=1}^\infty L_{a_i} = \{(x,a_1x,a_2a_1x,\ldots )\ \mid \ x\in [0,1]\}\cap M_{r,\rho }.$$

• 2. We say that ${\textbf {a}}$ is a useful sequence if $L_{{\textbf {a}}}$ is an arc in $M_{r,\rho }$.

• 3. We define $\mathcal {L}_{r,\rho } = \{L_{\textbf {a}}\ \mid \ {\textbf {a}}\in \{r,\rho \}^\mathbb {N}\}.$

First, we prove the following theorem.

Theorem 7

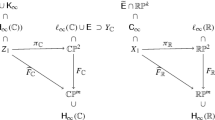
Let $(r_1,\rho _1), (r_2,\rho _2)\in \mathcal {C}$ such that $r_{1}^{M}\rho _{1}^{N} = r_{2}^{M}\rho _{2}^{N} = 1$ for some positive integers M, N. Then $M_{r_1,\rho _1}$ and $M_{r_2,\rho _2}$ are homeomorphic (Fig. 5).

Proof

We prove this using Theorem 2. To do this, we define the following:

For each positive integer n, let

$$f_n:[r_1^{\frac{n}{N}},r_1^{\frac{n-1}{N}}]\rightarrow [r_2^{\frac{n}{N}},r_2^{\frac{n-1}{N}}]$$

be such that it’s graph is the line segment from $(r_1^{\frac{n}{N}},r_2^{\frac{n}{N}})$ to $(r_1^{\frac{n-1}{N}},r_2^{\frac{n-1}{N}})$. Explicitly, for each $x\in [r_1^{\frac{n}{N}},r_1^{\frac{n-1}{N}}]$,

$$f_n(x) = \left( \frac{r_2}{r_1}\right) ^{\frac{n-1}{N}}\cdot \frac{1-r_2^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\cdot x + r_2^{\frac{n-1}{N}}\cdot \frac{r_2^{\frac{1}{N}}-r_1^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}.$$

Next, we define $f:[0,1]\rightarrow [0,1]$ as follows:

$$\forall x\in [0,1]: f(x) = {\left\{ \begin{array}{ll} 0; &{} x = 0\\ f_n(x); &{} x\in [r_1^{\frac{n}{N}},r_1^{\frac{n-1}{N}}]; \end{array}\right. }$$

see Fig. 4.

Fig. 5

The graph of the function f

It is clear that such f is a homeomorphism. Now, for each positive integer n, let

• 1. $X_n = Y_n = [0,1]$,

• 2. $F_n:X_{n+1}\multimap X_n, G_n:Y_{n+1}\multimap Y_n$ be set-valued functions such that their graphs are $L_{r_1,\rho _1}^{-1}$ and $L_{r_2,\rho _2}^{-1}$, respectively, and

• 3. $\phi _n = f$.

To use Theorem 2, we show that for each $x\in [0,1],$

$$\phi _n(F_n(x)) = G_n(\phi _{n+1}(x)).$$

To prove this, we need to prove that

$$ \{f(r_1\cdot x), f(\rho _1\cdot x)\} = \{r_2\cdot f(x), \rho _2\cdot f(x)\}, $$

since $\Phi _n(F_n(x)) = \{f(r_1\cdot x), f(\rho _1\cdot x)\}$ and $G_n(\Phi _{n+1}(x)) = \{r_2\cdot f(x), \rho _2\cdot f(x)\}$. It is enough to prove the two following claims:

• Claim 1. For each $x\in [0,\rho _1^{-1}] = [0,r_1^{\frac{M}{N}}]: f(\rho _1\cdot x) = \rho _2\cdot f(x)$.

• Proof: We treat the following possible subcases.

  • (i) $x = 0:$ This is clearly true.

  • (ii) $x \ne 0:$ Then there exists some positive integer n such that

    $$x\in [r_1^{\frac{n}{N}},r_1^{\frac{n-1}{N}}]$$

    and because of that (noting that $n>M$),

    $$\rho _1x\in [r_1^{\frac{n-M}{N}},r_1^{\frac{n-M-1}{N}}].$$

    It follows then that

    $$f(\rho _1x) = f_{n-M}(\rho _1x) =$$
    $$= \left( \frac{r_2}{r_1}\right) ^{\frac{n-M-1}{N}}\cdot \frac{1-r_2^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\cdot r_1^{-\frac{M}{N}}x + r_2^{\frac{n-M-1}{N}}\cdot \frac{r_2^{\frac{1}{N}}-r_1^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}.$$

    On the other hand,

    $$\rho _2f(x) = \rho _2f_n(x) =$$
    $$= \rho _2\cdot \left[ \left( \frac{r_2}{r_1}\right) ^{\frac{n-1}{N}}\cdot \frac{1-r_2^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\cdot x + r_2^{\frac{n-1}{N}}\cdot \frac{r_2^{\frac{1}{N}}-r_1^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\right] $$

    and we can quickly see that these two values are the same.

• Claim 2. For each $x\in [0,1]: f(r_1\cdot x) = r_2\cdot f(x)$.

• Proof: We treat the following possible subcases.

  • (i) $x = 0:$ This is clearly true.

  • (ii) $x \ne 0:$ Then there exists some positive integer n such that

    $$x\in [r_1^{\frac{n}{N}},r_1^{\frac{n-1}{N}}]$$

    and because of that,

    $$r_1x\in [r_1^{\frac{n+N}{N}},r_1^{\frac{n+N-1}{N}}].$$

    It follows then that

    $$f(r_1x) = f_{n+N}(r_1x) =$$
    $$= \left( \frac{r_2}{r_1}\right) ^{\frac{n+N-1}{N}}\cdot \frac{1-r_2^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\cdot r_1x + r_2^{\frac{n+N-1}{N}}\cdot \frac{r_2^{\frac{1}{N}}-r_1^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}.$$

    On the other hand,

    $$r_2f(x) = r_2f_n(x) =$$
    $$= r_2\cdot \left[ \left( \frac{r_2}{r_1}\right) ^{\frac{n-1}{N}}\cdot \frac{1-r_2^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\cdot x + r_2^{\frac{n-1}{N}}\cdot \frac{r_2^{\frac{1}{N}}-r_1^{\frac{1}{N}}}{1-r_1^{\frac{1}{N}}}\right] $$

    and we can quickly see that these two values are the same.

Having proven this, it follows that

• 1. if $x\in [0,\rho _1^{-1}]$, then for each positive integer n,

  $$\phi _n(F_n(x)) = f(L_{r_1,\rho _1}^{-1}(x)) = f(\{r_1\cdot x, \rho _1\cdot x\}) = \{r_2\cdot f(x), \rho _2\cdot f(x)\} = G_n(\phi _{n+1}(x))$$

  and

• 2. if $x\in (\rho _1^{-1},1]$, then for each positive integer n,

  $$\phi _n(F_n(x)) = f(L_{r_1,\rho _1}^{-1}(x)) = f(r_1\cdot x) = r_2\cdot f(x) = G_n(\phi _{n+1}(x))$$

and, therefore, by Theorem 2 and Observation 3, $M_{r_1,\rho _1}$ and $M_{r_2,\rho _2}$ are homeomorphic. $\square$

Observation 8

Let $(r,\rho )\in \mathcal {C}$. For each point ${\textbf {x}}\in M_{r,\rho }$ there are a point $x\in [0,1]$ and a sequence $(a_1,a_2,a_3,\ldots )\in \{r,\rho \}^\mathbb {N}$ such that

$${\textbf {x}} = (x, a_1x, a_2a_1x,\ldots ).$$

If $x\ne 0$, then there is only one such sequence $(a_1,a_2,a_3,\ldots )$.

The following lemmas are needed in the proof of our main result.

Lemma 9

Let $(r,\rho )\in \mathcal {C}$ and let ${\textbf {a}} = (a_1,a_2,\ldots )\in \{r,\rho \}^\mathbb {N}$ be such that the set

$$A = \left\{ \prod _{i=1}^{n}a_i\ \mid \ n\in \mathbb {N}\right\} $$

has no maximum in $\mathbb R$. Then the set A has no upper bound in $\mathbb R$.

Proof

Suppose the set A has no maximum, but does have a supremum, let

$$M = \sup \left\{ \prod _{i=1}^{n}a_i\ \mid \ n\in \mathbb {N}\right\} .$$

Then, for each $\varepsilon >0$ there exists a positive integer n such that

$$M-\varepsilon< \prod _{i=1}^{n}a_i < M.$$

It follows that there is a strictly increasing sequence $(m_n)_{n=1}^\infty$ of positive integers such that

• 1. for each positive integer n: $a_1a_2\cdot \ldots \cdot a_{m_n} < a_1a_2\cdot \ldots \cdot a_{m_n+1}$ and

• 2. $\displaystyle \lim _{n\rightarrow \infty }a_1a_2\cdot \ldots \cdot a_{m_n} = M$.

Note that for each positive integer n, from

$$\prod _{i=1}^{m_{n+1}}a_i = \left( \prod _{i=1}^{m_n}a_i\right) \cdot a_{m_n+1}\cdot \ldots \cdot a_{m_{n+1}} > \prod _{i=1}^{m_n}a_i,$$

it follows that

$$a_{m_n+1}\cdot \ldots \cdot a_{m_{n+1}} > 1.$$

We see also that

$$\frac{\prod _{i=1}^{m_{n+1}}a_i}{\prod _{i=1}^{m_n}a_i} = a_{m_n+1}\cdot \ldots \cdot a_{m_{n+1}}$$

and applying the limit as n approaches infinity, we get

$$\lim _{n\rightarrow \infty }(a_{m_n+1}\cdot \ldots \cdot a_{m_{n+1}}) = \lim _{n\rightarrow \infty }\frac{\prod _{i=1}^{m_{n+1}}a_i}{\prod _{i=1}^{m_n}a_i} = \frac{M}{M} = 1.$$

It follows that for each $\varepsilon > 0$ there exists a positive integer n such that

$$1< a_{m_n+1}\cdot a_{m_n+2}\cdot \ldots \cdot a_{m_{n+1}} < 1+\varepsilon .$$

Since $(r,\rho )\in \mathcal {C},$ there exist positive integers M, N such that $r^M\rho ^N = 1$ or, equivalently, $r = \rho ^{-\frac{N}{M}}$, so every such product can be written as

$$a_{m_n+1}\cdot a_{m_n+2}\cdot \ldots \cdot a_{m_{n+1}} = \rho ^{A_n-B_n\cdot \frac{N}{M}},$$

where $A_n$, $B_n$ are non-negative integers. For each positive integer n, let $A_n,B_n$ be such integers.

It follows then that

$$\inf \left\{ A_n-B_n\cdot \frac{N}{M}\ \mid \ n\in \mathbb {N}\right\} = 0$$

and 0 is not the minimum of this set. Note that for each positive integer n,

$$A_n-B_n\cdot \frac{N}{M} = \frac{A_nM-B_nN}{M},$$

but since the integer M is fixed and $A_nM-B_nN$ is an integer, for each positive integer n, these numbers cannot get arbitrarily close to 0, which is a contradiction. $\square$

Lemma 10

Let $(r,\rho )\in \mathcal {C}$. Then ${\textbf {a}} = (a_1,a_2,\ldots )\in \{r,\rho \}^\mathbb {N}$ is a useful sequence if and only if there exists

$$\max \left\{ \prod _{i=1}^{n}a_i\ \mid \ n\in \mathbb {N}\right\} .$$

Proof

Let ${\textbf {a}}$ be a useful sequence. By Definition 15, $L_{{\textbf {a}}}$ is an arc. Since

$$L_{{\textbf {a}}} = \{(x,a_1x,a_2a_1x,\ldots )\ \mid \ x\in [0,1]\}\cap M_{r,\rho },$$

it follows that there is $m\in (0,1]$ such that

$$L_{\textbf {a}} = \{(x,a_1x,a_2a_1x,\ldots )\ \mid \ x\in [0,m]\}.$$

Suppose the set $\{\prod _{i=1}^{n}a_i\ \mid \ n\in \mathbb {N}\}$ has no maximum. By Lemma 9, $\{\prod _{i=1}^{n}a_i\ \mid \ n\in \mathbb {N}\}$ then has no upper bound, meaning that for any $x\in (0,m]$ there exists a positive integer n such that,

$$a_{n-1}\cdot \ldots \cdot a_2a_1 > \frac{1}{x}$$

or, equivalently, that

$$a_{n-1}\cdot \ldots \cdot a_2a_1x > 1.$$

The only value of x where such $(x,a_1x,a_2a_1x,\ldots )$ could be in $M_{r,\rho }$ is therefore $x=0$, but then $L_{\textbf {a}} = \{(0,0,0,\ldots )\}$ is not an arc $M_{r,\rho }$. Then ${\textbf {a}}$ is not a useful sequence, which is a contradiction. This proves the first implication.

To prove the second implication, let

$$m = \max \left\{ \prod _{i=1}^{n}a_i\ \mid \ n\in \mathbb {N}\right\} .$$

It is clear then that $L_{{\textbf {a}}} = \{(x,a_1x,a_2a_1x,\ldots )\ \mid \ x\in [0,\min \{1,\frac{1}{m}\}]\},$ showing that it is an arc. Therefore, ${\textbf {a}}$ is a useful sequence. $\square$

Remark 1

Note that for any useful sequence ${\textbf {a}}$,

$$(0,0,0,\ldots ) \in E(L_{{\textbf {a}}}).$$

In the following two theorems, the properties of arcs $L_{{\textbf {a}}}$ are studied.

Theorem 11

Let $(r,\rho )\in \mathcal {C}$, let ${\textbf {a}}$ be a useful sequence and let $x\in (0,1]$. Then

$$ (x,a_1x,a_2a_1x,\ldots ) $$

is an end-point of $L_{{\textbf {a}}}$ if and only if either $x=1$ or there exists a positive integer n such that $a_{n}\cdot \ldots \cdot a_2a_1x = 1$.

Proof

First, suppose that $x=1$ or that there exists a positive integer n such that $a_na_{n-1}\cdot \ldots \cdot a_1x = 1$. We prove that $(x,a_1x,a_2a_1x,\ldots )$ is an end-point of $L_{\textbf {a}}$. If $x=1$, then obviously, $(x,a_1x,a_2a_1x,\ldots )$ is an end-point of ${\textbf {a}}$. Now let $x<1$. Let $(x,a_1x,a_2a_1x,\ldots )$, where $x\ne 0$, be such that there exists a positive integer n so that $a_{n}\cdot \ldots \cdot a_2a_1x = 1$. Since

$$ L_{\textbf {a}} = \left\{ (t,a_1t,a_2a_1t,\ldots )\ \mid \ t\in \left[ 0,\frac{1}{a_1a_2\cdot \ldots \cdot a_n}\right] \right\} $$

is an arc from $(0,0,0,\ldots )$ to $(x,a_1x,a_2a_1x,\ldots )$ where $x=\frac{1}{a_1a_2\cdot \ldots \cdot a_n}$, it is clear then that $(x,a_1x,a_2a_1x,\ldots )$ is the end-point of $L_{{\textbf {a}}}$ which is different from $(0,0,0,\ldots )$.

Next, let $(x,a_1x,a_2a_1x,\ldots )$, where $x \ne 0$, be an end-point of $L_{{\textbf {a}}}$. Since ${\textbf {a}}$ is a useful sequence, and $x>0$, it follows that

$$ m = \max \{a_n\cdot \ldots \cdot a_2a_1\ \mid \ n\in \mathbb {N}\} $$

exists and it follows that

$$ \sup \{a_{n}\cdot \ldots \cdot a_2a_1x\ \mid \ n\in \mathbb {N}\} = x \cdot \sup \{a_n\cdot \ldots \cdot a_2a_1\ \mid \ n\in \mathbb {N}\} = $$

$$ = x \cdot \max \{a_n\cdot \ldots \cdot a_2a_1\ \mid \ n\in \mathbb {N}\} = x\cdot m. $$

It is clear then that

$$x\cdot m = \max \{a_{n}\cdot \ldots \cdot a_2a_1x\ \mid \ n\in \mathbb {N}\}.$$

We consider the following possible cases.

• 1. If $m\le 1$, then

  $$L_{{\textbf {a}}} = \{(t,a_1t,a_2a_1t,\ldots )\ \mid \ t\in [0,1]\}$$

  and since $(x,a_1x,a_2a_1x,\ldots )$ is an end-point of $L_{{\textbf {a}}}$, it follows that $x=1$.

• 2. Now let $m>1$. Then

  $$L_{{\textbf {a}}} = \left\{ (t,a_1t,a_2a_1t,\ldots )\ \mid \ t\in \left[ 0,\frac{1}{m}\right] \right\} $$

  and since $(x,a_1x,a_2a_1x,\ldots )$ is an end-point of $L_{{\textbf {a}}}$, it follows for some n, $xa_1a_2\cdot \ldots \cdot a_n = 1$.

$\square$

Theorem 12

Let $(r,\rho )\in \mathcal {C}$ and ${\textbf {a}}, {\textbf {b}}$ be two different useful sequences, then

$$L_{{\textbf {a}}} \cap L_{{\textbf {b}}} = \{(0,0,0,\ldots )\}.$$

Proof

Suppose that this is not true and there is a non-zero point $(x,a_1x,a_2a_1x,\ldots ) = (x,b_1x,b_2b_1x,\ldots ) \in L_{{\textbf {a}}} \cap L_{{\textbf {b}}}$. It immediately follows that for each positive integer n: $a_n = b_n$ and therefore ${\textbf {a}} = {\textbf {b}}$, a contradiction. $\square$

Remark 2

Let $(r,\rho ) \in \mathcal {C}$. From previous theorems we see that $M_{r,\rho }$ is the union of a collection of arcs, joint only in $(0,0,0,\ldots )$. Also, it is easy to check that the dimension of $M_{r,\rho }$ is 1. To see that, one can use the main result from [3].

Our next goal is to prove that $M_{r,\rho }$ is a fan. To see this, we introduce the following notation about end-points.

Definition 16

Let $(r,\rho )\in \mathcal {C}$. For every positive integer n, we use $E_n(r,\rho )$ to denote the set

$$E_n(r,\rho ) = \{(x_1,x_2,x_3,\ldots )\in M_{r,\rho }\ \mid \ x_n = 1\ and\ \forall i\in \{1,2,\ldots ,n-1\}: x_i \ne 1\}.$$

Definition 17

Let $(r,\rho )\in \mathcal {C}$. For each useful sequence ${\textbf {a}}$, let $e_{{\textbf {a}}}$ be the non-zero end-point of $L_{\textbf {a}}$ and let

$$E(r,\rho ) = \{e_{\textbf {a}}\ \mid \ {\textbf {a}}\ is\ a\ useful\ sequence\}.$$

Observation 13

$$E(r,\rho ) = \bigcup _{n\in \mathbb {N}}E_n(r,\rho )$$

Next, we prove some properties of the above defined sets.

Theorem 14

Let $(r,\rho )\in \mathcal {C}$. For each positive integer n, $E_n(r,\rho )$ is an uncountable set.

Proof

Let $(r,\rho )\in \mathcal {C}$ and let M, N be positive integers such that

$$r^M\rho ^N = 1.$$

The proof is by induction on n.

• 1. $n = 1$. First, we define two finite sequences:

  $${\textbf {x}} = (1,r,r^2,\ldots ,r^M,r^M\rho ,\ldots ,r^M\rho ^{N-1},1)$$
  $${\textbf {y}} = (1,r,r^2,\ldots ,r^{2M},r^{2M}\rho ,\ldots ,r^{2M}\rho ^{N-1},r^M,r^M\rho ,\ldots ,r^M\rho ^{N-1},1)$$

  It follows then that

  $$\{\star _{i=1}^\infty {\textbf {z}}_i\ \mid \ \forall i\in \mathbb {N}: {\textbf {z}}_i\in \{{\textbf {x}},{\textbf {y}}\}\}\subseteq E_1(r,\rho )$$

  and since this subset is uncountable, so is $E_1(r,\rho )$.

• 2. Let $n\in \mathbb {N}\setminus \{1\}$ be some positive integer and $E_{n-1}(r,\rho )$ be uncountable. We prove that $E_n(r,\rho )$ is uncountable as well. Let $(x_1,x_2,\ldots ,x_{n-2},1,x_{n},\ldots )\in E_{n-1}(r,\rho )$. We see then that

  $$(\rho ^{-1}x_1,x_1,x_2,\ldots ,x_{n-2},1,x_{n},\ldots )\in E_n(r,\rho )$$

  because it’s nth coordinate is 1 and $\rho ^{-1}x<1$ since $\rho >1$ and $x<1$. Thus there exists an injection from $E_{n-1}(r,\rho )$ to $E_n(r,\rho )$. Since $E_{n-1}(r,\rho )$ is uncountable, it follows then that $E_n(r,\rho )$ is also uncountable.

$\square$

The following lemma is needed in Theorem 16.

Lemma 15

Let $(r,\rho )\in \mathcal {C}$ and let ${\textbf {x}}=(x_1,x_2,x_3,\ldots )\in M_{r,\rho }$ be any point. Then for each positive integer k, there is a point ${\textbf {y}}_k\in M_{r,\rho }$ such that

• 1. $p_1({\textbf {y}}_k) = x_k$ and

• 2. $p_{k,\infty }({\textbf {x}}) \ne {\textbf {y}}_k$.

Proof

Let k be a positive integer. We treat the following possible cases.

• 1. There exists a positive integer l such that $x_{k+l} = \rho \cdot x_{k+l-1}$. Then let

  $$ {\textbf {y}}_k = (x_k,x_{k+1},\ldots ,x_{k+l-1},r\cdot x_{k+l-1},r^2\cdot x_{k+l-1},\ldots ). $$

  Then $p_1({\textbf {y}}_k) = x_k$ and $p_{k,\infty }({\textbf {x}})\ne {\textbf {y}}_k$.

• 2. For each positive integer l, $x_{k+l} = r\cdot x_{k+l-1}$. Then there is a positive integer $m>k$ such that $\rho \cdot x_m < 1$. Then let

  $$ {\textbf {y}}_k = (x_k,x_{k+1},\ldots ,x_m,\rho \cdot x_m,r\cdot \rho \cdot x_m,r^2\cdot \rho \cdot x_m,\ldots ). $$

  Then $p_1({\textbf {y}}_k) = x_k$ and $p_{k,\infty }({\textbf {x}})\ne {\textbf {y}}_k$.

$\square$

Theorem 16

Let $(r,\rho ) \in \mathcal {C}.$ For each positive integer n, $E_n(r,\rho )$ has no isolated points.

Proof

Let ${\textbf {x}} = (x_1,x_2,\ldots ,x_{n-1},1,x_{n+1},\ldots ) \in E_n(r,\rho )$. Since $(r,\rho )\in \mathcal {C},$ let M, N be positive integers such that

$$r^M\rho ^N = 1.$$

We construct a sequence $({\textbf {x}}^k)_{k=1}^\infty$ in $E_n(r,\rho )$ such that it converges to ${\textbf {x}}$ and for each positive integer k, ${\textbf {x}}^k \ne {\textbf {x}}$.

For each positive integer k, $k>n$, let ${\textbf {y}}_k\in M_{r,\rho }$ be a point such that

• 1. $p_1({\textbf {y}}_k) = x_k$ and

• 2. $p_{k,\infty }({\textbf {x}})\ne {\textbf {y}}_k$.

Such ${\textbf {y}}_k$ does exist by Lemma 15. For each positive integer $k>n$, let

$$ {\textbf {x}}_k = p_{1,k}({\textbf {x}})\star {\textbf {y}}_k. $$

Then $\displaystyle \lim _{k\rightarrow \infty }{} {\textbf {x}}_k = {\textbf {x}}$ and for each such k, ${\textbf {x}}_k\ne {\textbf {x}}$. $\square$

Theorem 17

Let $(r,\rho )\in \mathcal {C}$. For each positive integer n, $E_n(r,\rho )$ is compact.

Proof

Let $(r,\rho )\in \mathcal {C}$ and let M, N be positive integers such that

$$r^M\rho ^N = 1.$$

• 1. $n = 1:$ Let $({\textbf {x}}^k)_{k=1}^\infty$ be a sequence in $E_1(r,\rho )$:

  $${\textbf {x}}^1 = (1,x_2^1,x_3^1,\ldots )$$
  $${\textbf {x}}^2 = (1,x_2^2,x_3^2,\ldots )$$
  $${\textbf {x}}^3 = (1,x_2^3,x_3^3,\ldots )$$
  $$\vdots $$

  and let ${\textbf {x}} = (x_1,x_2,\ldots ) = \displaystyle \lim _{k\rightarrow \infty }{} {\textbf {x}}^k$. Then, obviously, $x_1 = 1$ and ${\textbf {x}}\in E_1(r,\rho )$ follows.

• 2. Let $n\in \mathbb {N}\setminus \{1\}$ be some positive integer and suppose that $E_{n-1}(r,\rho )$ is compact. We prove that $E_n(r,\rho )$ is compact. Let $({\textbf {x}}^k)_{k=1}^\infty$ be a sequence in $E_n(r,\rho )$ and let ${\textbf {x}} = (x_1,x_2,\ldots ) = \displaystyle \lim _{k\rightarrow \infty }{} {\textbf {x}}^k$. Then

  $$(p_{2,\infty }({\textbf {x}}^k))_{k=1}^\infty $$

  is a sequence in $E_{n-1}(r,\rho )$ such that

  $$\lim _{k\rightarrow \infty }p_{2,\infty }({\textbf {x}}^k) = p_{2,\infty }({\textbf {x}}).$$

  It follows that $p_{2,\infty }({\textbf {x}})\in E_{n-1}(r,\rho )$. All that is left to see is that $x_1\ne 1$. For each positive integer k, we denote the elements of ${\textbf {x}}^k$ by

  $${\textbf {x}}^k = (x_1^k,x_2^k,x_3^k,\ldots ).$$

  Note that since all ${\textbf {x}}^k \in E_n(r,\rho )$, it follows that for each positive integer k, $x_1^k < 1$ and $x_n^k = 1$. Suppose now that $x_1 =\displaystyle \lim _{k\rightarrow \infty }x_1^k = 1$. For each positive integer k, there exist $a_{n-1}^k,\ldots ,a_2^k,a_1^k\in \{r,\rho \}$ and positive integers $A_k,B_k$ such that

  $$1 = x_n^k = a_{n-1}^k\cdot \ldots \cdot a_2^ka_1^kx_1^k = x_1^k\cdot r^{A_k - B_k\cdot \frac{N}{M}}.$$

  It follows that for each positive integer k,

  $$x_1^k = \left( \frac{1}{r}\right) ^{A_k - B_k\cdot \frac{N}{M}}.$$

  Because of this,

  $$1 = \lim _{k\rightarrow \infty }x_1^k = \lim _{k\rightarrow \infty }\left( \frac{1}{r}\right) ^{A_k - B_k\cdot \frac{N}{M}} = \left( \frac{1}{r}\right) ^{\displaystyle \ \lim _{k\rightarrow \infty }\left( A_k - B_k\cdot \frac{N}{M}\right) }.$$

  This would imply that there exists a double sequence of positive integers $\{A_k,B_k\}_{k=1}^\infty$ such that

  $$\lim _{k\rightarrow \infty }\left( A_k - B_k\cdot \frac{N}{M}\right) = \lim _{k\rightarrow \infty }\left( \frac{A_kM-B_kN}{M}\right) = 0$$

  and for each positive integer k,

  $$\frac{A_kM-B_kN}{M}\ne 0.$$

  Since M is fixed and $A_kM-B_kN$ are all integers, this is not possible. This leads to a contradiction.

$\square$

Theorem 18

Let $(r,\rho )\in \mathcal {C}$. For each positive integer n, $E_n(r,\rho )$ is a Cantor set.

Proof

Let n be any positive integer. Every element of $E_n(r,\rho )$ can be uniquely represented by a useful sequence

$${\textbf {a}} = (a_1,a_2,a_3,\ldots ).$$

This representation is unique because different elements of $E_n(r,\rho )$ are elements of different arcs in $M_{r,\rho }$. With this in mind, let $f:E_n(r,\rho )\rightarrow \{r,\rho \}^\mathbb {N}$ be a function such that for each $(x,a_1x,a_2a_1x,\ldots )\in E_n(r,\rho )$,

$$ f(x,a_1x,a_2a_1x,\ldots ) = (a_1,a_2,a_3,\ldots ). $$

This function is injective. To prove that it is continuous, let

$$ {\textbf {x}}^1 = (x_1^1,x_2^1,x_3^1,\ldots )\in E_n(r,\rho ) $$

$$ {\textbf {x}}^2 = (x_1^2,x_2^2,x_3^2,\ldots )\in E_n(r,\rho ) $$

$$ {\textbf {x}}^3 = (x_1^3,x_2^3,x_3^3,\ldots )\in E_n(r,\rho ) $$

$$ \vdots $$

$$ {\textbf {x}} = (x_1,x_2,x_3,\ldots )\in E_n(r,\rho ) $$

such that $\displaystyle \lim _{k\rightarrow \infty }{} {\textbf {x}}^k = {\textbf {x}}$. We prove that $\displaystyle \lim _{k\rightarrow \infty }f({\textbf {x}}^k) = f({\textbf {x}})$. For each positive integer k, there is a useful sequence ${\textbf {a}}^k = (a_1^k,a_2^k,a_3^k,\ldots )$ of r’s and $\rho$’s such that for each positive integer k,

$$ {\textbf {x}}^k = (x_1^k, a_1^kx_1^k, a_2^ka_1^kx_1^k,\ldots ) $$

and there is a useful sequence ${\textbf {a}} = (a_1,a_2,\ldots )$ of r’s and $\rho$’s such that

$$ {\textbf {x}} = (x_1,a_1x_1,_2a_1x_1,\ldots ). $$

It follows that $\displaystyle \lim _{k\rightarrow \infty }x_1^k = x_1$. It follows from

$$ \lim _{k\rightarrow \infty }x_2^k = \lim _{k\rightarrow \infty }(a_1^kx_1^k) = a_1x_1 $$

that $\displaystyle \lim _{k\rightarrow \infty }a_1^k = a_1$. Now, let $n>1$ be a positive integer and for each positive integer $l<n$, let

$$ \lim _{k\rightarrow \infty }a_l^k = a_l. $$

It follows from

$$ \lim _{k\rightarrow \infty }x_{n+1}^k = \lim _{k\rightarrow \infty }(a_n^ka_{n-1}^k\cdot \ldots \cdot a_2^ka_1^kx_1^k) = a_na_{n-1}\cdot \ldots \cdot a_2a_1x_1 $$

that $\displaystyle \lim _{k\rightarrow \infty }a_n^k = a_n$. It follows that

$$ \lim _{k\rightarrow \infty }(a_1^k,a_2^k,a_3^k,\ldots ) = (a_1,a_2,a_3,\ldots ). $$

Therefore, $\displaystyle \lim _{k\rightarrow \infty }f({\textbf {x}}^k) = f({\textbf {x}})$. So, f is continuous.

Since $E_n(r,\rho )$ is homeomorphic to a subspace of $\{r,\rho \}^\mathbb {N}$, it is also totally disconnected. Therefore, $E_n(r,\rho )$ is a Cantor set. $\square$

Theorem 19

Let $(r,\rho )\in \mathcal {C},$ then $(0,0,0,\ldots ) \in Cl (E(r,\rho )).$

Proof

For each positive integer n, let

$${\textbf {x}}^n = \left( \left( \frac{1}{\rho }\right) ^n,\left( \frac{1}{\rho }\right) ^{n-1},\ldots ,\left( \frac{1}{\rho }\right) ^2,\frac{1}{\rho },1,\ldots \right) \in E_{n+1}(r,\rho ).$$

It follows that $\displaystyle \lim _{n\rightarrow \infty }{} {\textbf {x}}^n = (0,0,0,\ldots )$. $\square$

Observation 20

Let $(r,\rho )\in \mathcal {C}.$ The set $E(r,\rho ) = \cup _{n\in \mathbb {N}}E_n(r,\rho )$ is not compact. This follows from Theorem 19. To show this using a different approach (proving also that $E(r,\rho )\cup \{(0,0,0,\ldots )\}$ is not compact), let $(r,\rho )\in \mathcal {C}$ and let M, N be positive integers such that

$$r^M\rho ^N = 1.$$

First, we define the following:

$${\textbf {x}} = (r^M,r^{M+1},\ldots ,r^{2M},r^{2M}\rho ,\ldots ,r^{2M}\rho ^{N-1},r^M) $$

$${\textbf {y}} = (r^M,r^M\rho ,\ldots ,r^M\rho ^{N-1},1,r,r^2,r^3,\ldots )$$

It is clear that each coordinate of ${\textbf {x}}$ is less than 1 since $r<1$, $\rho >1$, M is a positive integer and for each positive integer $k<N$,

$$ r^{2M}\cdot \rho ^k< r^{2M}\cdot \rho ^N = r^M < 1. $$

For each positive integer k, let

$${\textbf {x}}^k = (\star _{i=1}^k{\textbf {x}})\star {\textbf {y}} = {\textbf {x}}\star {\textbf {x}}\star \ldots \star {\textbf {x}}\star {\textbf {y}} \in E(r,\rho ),$$

where ${\textbf {x}}$ is repeated k-times. It is clear then that

$$\lim _{k\rightarrow \infty }{} {\textbf {x}}^k = \star _{i=1}^\infty {\textbf {x}} = {\textbf {x}}\star {\textbf {x}}\star {\textbf {x}}\star \ldots \notin E(r,\rho ).$$

In the following definition, special sets $F(M_{r,\rho })$ are defined. They play an important role in the proof of Theorem 21.

Definition 18

Let $(r,\rho )\in \mathcal {C}$ and let M,N be such positive integers that $r^M\rho ^N = 1$. Let also $\mathbb {Z}_0^-$ denote the set of all non-positive integers. We use $F(M_{r,\rho })$ to denote the set

$$F(M_{r,\rho }) = \{(x_1,x_2,\ldots )\in M_{r,\rho }\ \mid \ x_1\ne 0,\ \forall z\in \mathbb {Z}_0^-:\ x_1 \ne \rho ^{\frac{z}{M}}\}.$$

Theorem 21

Let $(r,\rho )\in \mathcal {C}$ and let ${\textbf {x}}\in M_{r,\rho }$ be such a point that

$${\textbf {x}}\ne (0,0,0,\ldots )\ and \ {\textbf {x}}\notin E(r,\rho ).$$

Then ${\textbf {x}}\in M_{r,\rho }\setminus F(M_{r,\rho })$ if and only if there exists a sequence $({\textbf {x}}^k)$ in $E(r,\rho )$ such that

$${\textbf {x}} = \lim _{k\rightarrow \infty }{} {\textbf {x}}^k.$$

Proof

Let $(r,\rho )\in \mathcal {C}$ and let M, N be positive integers such that $r^M\rho ^N = 1$, or, equivalently, that $r = \rho ^{-\frac{N}{M}}$. We may assume that the greatest common divisor of M and N, denoted as $GCD (M,N)$, equals 1.

First, let ${\textbf {x}} = (x_1,x_2,\ldots )\in M_{r,\rho }\setminus F(M_{r,\rho })$. By Definition 18 and since ${\textbf {x}}\ne (0,0,0,\ldots )$ there exists a non-positive integer $z_1$ such that

$$ x_1 = \rho ^{\frac{z_1}{M}}. $$

Since for each positive integer k, $x_{k+1}\in \{r\cdot x_k,\rho \cdot x_k\}$, it follows that ${\textbf {x}}$ is of the form:

$$ {\textbf {x}} = \left( \rho ^{\frac{z_1}{M}},\rho ^{\frac{z_2}{M}},\ldots \right) $$

where for each positive integer k, $z_{k+1} \in \{z_k-N,z_k+M\}$ is a negative integer. Since $GCD (M,N) = 1$, it follows from Euler’s theorem that there exist integers x,y such that

$$Mx+Ny = 1.$$

Since both M and N are positive integers, it is clear that either x or y is positive while the other is negative. Without loss of generality, let $x>0$ and $y<0$. Then for $u = x$ and $v = -y$, it follows that

$$Mu-Nv = 1.$$

Multiplying by $-\frac{z_k}{M}$, we see that

$$-uz_k - vz_k\cdot \left( -\frac{N}{M}\right) = -\frac{z_k}{M}.$$

Note that $-uz_k$ and $-vz_k$ are both positive integers. With this in mind, for each positive integer k, let

$$ {\textbf {y}}^k = \left( \rho ^\frac{z_k}{M}, r\cdot \rho ^\frac{z_k}{M}, \ldots , r^{-vz_k}\cdot \rho ^\frac{z_k}{M},\rho \cdot r^{-vz_k}\cdot \rho ^\frac{z_k}{M},\ldots ,\rho ^{-uz_k-1}\cdot r^{-vz_k}\cdot \rho ^\frac{z_k}{M}, 1\right) $$

and

$$ {\textbf {x}}^k = p_{1,k}({\textbf {x}}) \star {\textbf {y}}^k \star (1,r,r^2,\ldots )\in E(r,\rho ). $$

It is then clear that

$$\lim _{k\rightarrow \infty }{} {\textbf {x}}^k = {\textbf {x}}.$$

This proves the first implication.

To prove the other implication, let ${\textbf {x}} = (x_1,x_2,\ldots )$ be the limit of a sequence $({\textbf {x}}^k)$ in E and for each positive integer k, let ${\textbf {x}}^k = (x_1^k, x_2^k, x_3^k,\ldots )$. For each positive integer k, ${\textbf {x}}^k\in E$, therefore for each positive integer k there exists a useful sequence

$$ {\textbf {a}}^k = (a_1^k,a_2^k,\ldots ) $$

such that

$$ {\textbf {x}}^k = (x_1^k, a_1^kx_1^k, a_2^ka_1^kx_1^k,\ldots ) $$

and either $x_1^k = 1$ or $a_n^k\cdot \ldots \cdot a_1^kx_1^k = 1$ for some positive integer n. Also, for each positive integer k, let

$$ m_k = \max \left\{ \prod _{i=1}^na_i^k\ \mid \ n\in \mathbb {N}\right\} . $$

Since for each positive integer k, ${\textbf {a}}^k \in \{r,\rho \}^\mathbb {N}$ and $r = \rho ^{-\frac{N}{M}}$, there exist positive integers $A_k$,$B_k$ such that

$$ m_k = \rho ^\frac{A_kM-B_kN}{M}. $$

Since ${\textbf {x}}^k$, for each positive integer k, is the end-point of $L_{{\textbf {a}}^k}$, different from $(0,0,0,\ldots )$ it follows that

$$ x_1^k = \frac{1}{m_k} = \rho ^{\frac{B_kN-A_kM}{M}}. $$

It then also follows that

$$ x_1 = \lim _{k\rightarrow \infty }x_1^k = \lim _{k\rightarrow \infty }\rho ^{\frac{B_kN-A_kM}{M}} = \rho ^{\displaystyle \ \lim _{k\rightarrow \infty }\left( \frac{B_kN-A_kM}{M}\right) }. $$

Since ${\textbf {x}}\notin E(r,\rho )$, $x_1$ must be less than 1 and so the limit of integers $B_kN-A_kM$ must be some negative integer. By Definition 18, ${\textbf {x}}\notin F(M_{r,\rho })$. $\square$

Observation 22

Let n be a positive integer. For each ${\textbf {e}}\in E_n(r,\rho )$ let $K_{\textbf {e}}$ be the straight line segment in the Hilbert cube from $(0,0,0,\ldots )$ to ${\textbf {e}}$. Note that

• 1. $\displaystyle \bigcup _{{\textbf {e}}\in E_n(r,\rho )}K_{\textbf {e}} \subseteq M_{r,\rho }$ and $\bigcup _{{\textbf {e}}\in E_n(r,\rho )}K_{\textbf {e}}$ is a Cantor fan. We denote $F_n = \displaystyle \bigcup _{{\textbf {e}}\in E_n(r,\rho )}K_{\textbf {e}}$.

• 2. $M_{r,\rho } = \displaystyle \bigcup _{n\in \mathbb {N}}F_n.$

• 3. $M_{r,\rho }$ is a fan which is a union of a countable family $\mathcal {C}$ of Cantor fans such that

  • 1. for each $C_1,C_2\in \mathcal {C}$, if $C_1\ne C_2$, then $C_1\cap C_2 = \{(0,0,0,\ldots )\}$ and

  • 2. the set of limit points of the set of end-points of F, forms in each arc from $(0,0,0,\ldots )$ to an end-point, a harmonic sequence.

  and $E(M_{r,\rho }) = E(r,\rho ).$

Finally, we are ready to state and prove Theorem 24, which is the main result of the paper. First, we introduce the following definitions and present some examples.

Definition 19

Let F be a fan with top v and let

$$ \mathcal {A}(F) = \{L\subseteq F\ \mid \ L\ is\ an\ arc\ in\ F\ from\ v\ to\ some\ point\ {\textbf {e}}\in E(F)\}. $$

For each $L\in \mathcal {A}(F)$, we use $S\!_{\!F}(L)$ to denote the set

$$ S\!_{\!F}(L) = \{x\in L\ \mid \ \exists (e_n)\ in\ E(F)\ such\ that\ \lim _{n\rightarrow \infty }e_n = x\}. $$

For each $L\in \mathcal {A}(F)$, we call the elements of $S\!_{\!F}(L)$ the end-point-significant points in L.

Example 2

Let F be the Lelek fan, then for each $L\in \mathcal {A}(F),$

$$S\!_{\!F}(L) = L.$$

Note that F is a Lelek fan if and only if for each $L\in \mathcal {A}(F)$, $S\!_{\!F}(L) = L.$

Example 3

Let F be the Cantor fan with top v, then for each $L\in \mathcal {A}(F),$

$$S\!_{\!F}(L) = E(L)\setminus \{v\}.$$

Definition 20

Let $X\subseteq [0,1]$ be closed and non-empty and let F be a fan with top v. We say that F is X-end-point-generated if for each $L\in \mathcal {A}(F)$ there exists a homeomorphism $\phi _L:[0,1]\rightarrow L$ such that

• 1. $\phi _L(0) = v$, $\phi _L(1) \in E(F)$ and

• 2. $\phi _L(X) = S\!_{\!F}(L)$.

Observation 23

Let F be a fan. Then F is a Lelek fan if and only if it is [0, 1]-end-point-generated.

Finally, we prove our main result.

Theorem 24

Let $(r,\rho )\in \mathcal {C}$. Then $M_{r,\rho }$ is a fan having the following two properties.

• 1. $M_{r,\rho }$ is the union of a countable family $\mathcal {F}$ of Cantor fans such that for all $F_1$ and $F_2$ from $\mathcal {F}$,

  $$ F_1\ne F_2 \implies F_1\cap F_2 = \{(0,0,0,\ldots )\}, $$

  and

• 2. $M_{r,\rho }$ is $\left\{ \frac{1}{n}\ \mid \ n\in \mathbb {N}\right\} \cup \left\{ 0\right\}$-end-point-generated.

Proof

Let $(r,\rho )\in \mathcal {C}$ and let M, N be positive integers such that

$$r^M\rho ^N = 1.$$

We have seen from Observation 22 that $M_{r,\rho }$ is a union of countably many Cantor fans satisfying 1. It follows (also using Theorem 21), that for each $L\in \mathcal {A}(M_{r,\rho })$,

$$ S\!_{\!F}(L)\!=\! L\setminus F(M_{r,\rho })\!=\!\left\{ {\textbf {x}}\in L\ \mid \ there\ is\ z\in \mathbb {Z}_0^-\ such\ that\ p_1({\textbf {x}})\! =\! \rho ^{\frac{z}{M}}\right\} \cup \{(0,0,0,\ldots )\}. $$

Note that for each $L\in \mathcal {A}(F)$, $S\!_{\!F}(L)$ is homeomorphic to $\left\{ \frac{1}{n}\ \mid \ n\in \mathbb {N}\right\} \cup \left\{ 0\right\}$. Therefore, $M_{r,\rho }$ is $\left\{ \frac{1}{n}\ \mid \ n\in \mathbb {N}\right\} \cup \left\{ 0\right\}$-end-point-generated. $\square$

Observation 25

Let $(r,\rho )\in \mathcal {C}$ and let $F:[0,1]\multimap [0,1]$ be the set-valued function such that its graph equals to $\Gamma _F = L_{r,\rho }^{-1}$. F is then a USC set-valued function and the generalized inverse limit $\mathop {\lim }\limits _ {\circ \hspace{-1.5pt}-\!\!-\!\!-}\{[0,1],F\}_{n=1}^\infty$ is homeomorphic to $M_{r,\rho }$.

We conclude this paper by stating the following open problems.

Problem 26

Let F and G be fans, which are unions of countable families $\mathcal {F}$ and $\mathcal {G}$, respectively, of Cantor fans such that for all $F_1, F_2\in \mathcal {F}$ and $G_1,G_2\in \mathcal {G}$,

$$ F_1\ne F_2 \implies F_1\cap F_2 = \{(0,0,0,\ldots )\}\ and\ G_1\ne G_2 \implies G_1\cap G_2 = \{(0,0,0,\ldots )\}. $$

If F and G are both $\left\{ \frac{1}{n}\ \mid \ n\in \mathbb {N}\right\} \cup \left\{ 0\right\}$-end-point-generated, are then F and G homeomorphic?

Problem 27

Let X be a non-empty closed subset of [0, 1] and let F and G be fans, which are unions of countable families $\mathcal {F}$ and $\mathcal {G}$, respectively, of Cantor fans such that for all $F_1, F_2\in \mathcal {F}$ and $G_1,G_2\in \mathcal {G}$,

$$ F_1\ne F_2 \implies F_1\cap F_2 = \{(0,0,0,\ldots )\}\ and\ G_1\ne G_2 \implies G_1\cap G_2 = \{(0,0,0,\ldots )\}. $$

If F and G are both X-end-point-generated, are then F and G homeomorphic? If not, find all such X for which they are homeomorphic or find a non-trivial subset of such subsets $X\subseteq [0,1]$.

Problem 28

Let X be a non-empty closed subset of [0, 1] and let F, G be fans such that they are X-end-point-generated. Are F and G homeomorphic? If not, find all such X for which they are homeomorphic or find a non-trivial family of such X.

Problem 29

Characterize all non-empty closed subsets X of [0, 1] for which there exists a fan F such that F is X-end-point-generated or find a non-trivial family of such sets X.

Problem 30

Does there exist a fan which is $\left\{ \frac{1}{2}\right\}$-end-point-generated?