On the SQH Method for Solving Differential Nash Games

Abstract

A sequentialquadratic Hamiltonian schemefor solving open-loop differential Nash games is proposed and investigated. This method is formulated in the framework of the Pontryagin maximum principle and represents an efficient and robust extension of the successive approximations strategy for solving optimal control problems. Theoretical results are presented that prove the well-posedness of the proposed scheme, and results of numerical experiments are reported that successfully validate its computational performance.

1 Introduction

The sequential quadratic Hamiltonian (SQH) scheme has been recently proposed in [4,5,6,7] for solving nonsmooth optimal control problems governed by differential models. The SQH scheme belongs to the class of iterative methods known as successive approximations (SA) schemes that are based on the characterisation of optimality in control problems by the Pontryagin maximum principle (PMP); see [2, 27] and [12] for a recent detailed discussion. The initial development of SA schemes was inspired by the work of L. I. Rozonoèr [32], and originally proposed in different variants by H.J. Kelley, R.E. Kopp and H.G. Moyer [19] and by I.A. Krylov and F.L. Chernous’ko [20, 21]; see [11] for an early review.

The working principle of most SA schemes is the point-wise minimisation of the Hamilton-Pontryagin function introduced in the PMP theory. However, in their original formulation, the SA schemes appeared efficient but not robust with respect to the numerical and optimisation parameters. Twenty years later, a great improvement in robustness was achieved by Y. Sakawa and Y. Shindo [33, 34] by introducing a quadratic penalty of the control updates that resulted in an augmented Hamiltonian. In this latter formulation, the need of coupled updates of the state and control variables of the controlled system limited the application of the resulting method to small-size control problems. This limitation was resolved in the SQH approach where a sequential point-wise optimisation of an augmented Hamiltonian function is considered that defines a suitable update step for the control variable while the state function is updated after the completion of this step. Since the SQH iterative procedure has proved efficient and robust in solving (non-smooth) optimal control problems governed by ordinary- and partial-differential models, it is reasonable to investigate whether this procedure can be successfully extended to differential games.

The first component of a differential game is a differential model that governs the state of the considered system and is subject to different mechanisms of action representing the strategies of the players in the game. Furthermore, objective functionals and admissible set of actions are associated to each player, and in the game the purpose of each player is to minimise its own objective subject to the constraints given by the differential model and the admissible sets. Since we consider non-cooperative games, a suitable solution concept is the one proposed by J. F. Nash in [22, 23], where a so-called Nash equilibrium (NE) for static games with complete information is defined, that is, a configuration where no player can benefit from unilaterally changing its own strategy. In this framework, differential Nash games were pioneered by R. P. Isaacs [16]. However, contemporary to Isaacs’ book, there are the works [25, 26] where differential games are discussed in the framework of the maximum principle. Furthermore, in [1, 21], we find early attempts and comments towards the development of a SA scheme for differential games. Unfortunately, less attention was paid to this research direction and the further development of these schemes for differential games was left out.

It is the purpose of this work to contribute to this development by investigating a SQH scheme for solving open-loop non-zero-sum two-player differential Nash games. In particular, we consider linear-quadratic (LQ) Nash games that appear in the field of, e.g., economics and marketing [13, 18], and are very well investigated from the theoretical point of view; see, e.g., [8, 14, 15, 35]. Moreover, since the solution of unconstrained LQ Nash games can be readily obtained by solving coupled Riccati equations [3, 14], they provide a convenient benchmark for our method. However, we also consider extension of LQ Nash games to problems with tracking objectives, box constraints on the players’ actions, and actions’ costs that include L¹ terms.

In the next section, we formulate a class of differential Nash games and their characterisation in the PMP framework. In particular, we notice that the point-wise PMP characterisation of a Nash equilibrium corresponds to the requirement that, at each time instant, the conditions of equilibrium of a finite-dimensional Nash game with two Hamilton-Pontryagin functions must be satisfied. In Section 3, we present our SQH method for solving differential Nash games and discuss its well-posedness. Specifically, we show that the adaptive choice of the weight of a Sakawa-Shindo-type penalisation can be successfully performed in a finite number of steps such that the proposed update criteria based on the Nikaido-Isoda function are satisfied.

Section 4 is devoted to numerical experiments that successfully validate our computational framework. In the first experiment, we consider a differential LQ Nash game and show that the SQH scheme provides a solution that is identical to that obtained by solving an appropriate Riccati system. In the second experiment, the same problem with the addition of the requirement that the players’ actions must belong to given bounded, closed, and convex sets is solved by the SQH scheme. In the third experiment, we extend the setting of the second experiment by adding weighted L¹ costs of the players’ actions and verify that these costs promote sparsity. In the fourth experiment, we consider the case where each player’s functional corresponds to a tracking problem where the players aim at following different paths. Also in this case, constraints on the players’ actions and L¹ costs are considered. We remark that all NE solutions are successfully computed with the same setting of values of the parameters entered in the SQH algorithm, that is, independently of the problem and of the chosen weights in the players’ cost functionals. A section of conclusion completes this work.

2 PMP Characterization of Nash Games

This section is devoted to the formulation of differential Nash games and the characterisation of their NE solution in the PMP framework. We discuss the case of two players, represented by their strategies $\underline {u}_{1}$ and $\underline {u}_{2}$, which can be readily extended to the case of N players, and assume the following dynamics:

$$ \underline{y}^{\prime}(t)=\underline{f} (t, \underline{y}(t), \underline{u}_{1}(t), \underline{u}_{2}(t)), \qquad \underline{y}(0)=\underline{y}_{0} , $$

(1)

where t ∈ [0,T], $\underline {y} (t) \in \mathbb {R}^{n}$, and $\underline {u}_{1} (t) \in \mathbb {R}^{m}$ and $\underline {u}_{2}(t) \in \mathbb {R}^{m}$, m ≤ n. We assume that $\underline {f}$ is such that for any choice of the initial condition $\underline {y}_{0} \in \mathbb {R}^{n}$, and any $\underline {u}_{1}, \underline {u}_{2} \in L^{2} (0,T;\mathbb {R}^{m})$, the Cauchy problem (1) admits a unique solution in the sense of Carathéodory; see, e.g., [3]. Furthermore, we assume that the map $(\underline {u}_{1},\underline {u}_{2}) \mapsto \underline {y}=\underline {y}(\underline {u}_{1},\underline {u}_{2})$, where $\underline {y}(\underline {u}_{1},\underline {u}_{2})$ represents the unique solution to Eq. 1 with fixed initial conditions is continuous in $(\underline {u}_{1},\underline {u}_{2})$.

We refer to $\underline {u}_{1}$ and $\underline {u}_{2}$ as the game strategies of the players P₁ and P₂, respectively. The goal of P₁ is to minimise the following cost (or objective) functional:

$$ J_{1}(\underline{y},\underline{u}_{1},\underline{u}_{2}):= {{\int}_{0}^{T}} \ell_{1} (t,\underline{y}(t),\underline{u}_{1}(t),\underline{u}_{2}(t)) dt + g_{1}(\underline{y}(T)), $$

(2)

whereas P₂ aims at minimising its own objective given by

$$ J_{2}(\underline{y},\underline{u}_{1},\underline{u}_{2}):= {{\int}_{0}^{T}} \ell_{2} (t,\underline{y}(t),\underline{u}_{1}(t),\underline{u}_{2}(t)) dt + g_{2}(\underline{y}(T)) . $$

(3)

We consider the cases of unconstrained and constrained strategies. In the former case, we assume $\underline {u}_{1}, \underline {u}_{2} \in L^{2} (0,T;\mathbb {R}^{m})$, whereas in the latter case we assume that $\underline {u}_{1}$ and $\underline {u}_{2}$ belong, respectively, to the following admissible sets:

$$ U_{ad}^{(i)} = \{ \underline{u} \in L^{2}(0,T;\mathbb{R}^{m}) : \underline{u} (t) \in K_{ad}^{(i)}, t \in [0,T] \}, \quad i=1,2, $$

(4)

where $K_{ad}^{(i)}$ are compact and convex subsets of $\mathbb {R}^{m}$. We denote with $U_{ad} = U_{ad}^{(1)} \times U_{ad}^{(2)}$ and $U = L^{2}(0,T;\mathbb {R}^{m}) \times L^{2}(0,T;\mathbb {R}^{m})$. Notice that we have a uniform bound on $|\underline {y}(\underline {u}_{1},\underline {u}_{2})(t)|$, t ∈ [0,T], that holds for any $\underline {u} \in U_{ad}$; see [9].

By using the map $(\underline {u}_{1},\underline {u}_{2}) \mapsto \underline {y}=\underline {y}(\underline {u}_{1},\underline {u}_{2})$, we can introduce the reduced objectives $\tilde {J}_{1}(\underline {u}_{1},\underline {u}_{2}):=J_{1}(\underline {y}(\underline {u}_{1},\underline {u}_{2}),\underline {u}_{1},\underline {u}_{2})$ and $\tilde {J}_{2}(\underline {u}_{1},\underline {u}_{2}):={J}_{2}(\underline {y}(\underline {u}_{1},\underline {u}_{2}),\underline {u}_{1},\underline {u}_{2})$. In this framework, a Nash equilibrium is defined as follows.

Definition 1

The functions $(\underline {u}_{1}^{*},\underline {u}_{2}^{*}) \in U_{ad}$ are said to form a Nash equilibrium (NE) for the game $(\tilde {J}_{1},\tilde {J}_{2}; U_{ad}^{(1)}, U_{ad}^{(2)})$, if it holds

$$ \begin{array}{@{}rcl@{}} &\tilde{J}_{1}(\underline{u}_{1}^{*}, \underline{u}_{2}^{*}) \leq \tilde{J}_{1}(\underline{u}_{1}, \underline{u}_{2}^{*}) , \qquad \underline{u}_{1} \in U_{ad}^{(1)}, \\ &\tilde{J}_{2}(\underline{u}_{1}^{*}, \underline{u}_{2}^{*}) \leq \tilde{J}_{2}(\underline{u}_{1}^{*}, \underline{u}_{2}) , \qquad \underline{u}_{2} \in U_{ad}^{(2)}. \end{array} $$

(5)

(A similar Nash game is defined replacing U_ad with U.)

We remark that existence of a NE point can be proved subject to appropriate conditions on the structure of the differential game, including the choice of T. For our purpose, we assume existence of a Nash equilibrium $(\underline {u}_{1}^{*},\underline {u}_{2}^{*}) \in U_{ad}$, and refer to [9] for a review and recent results in this field.

We remark that, if $\underline {u}^{*}=(\underline {u}_{1}^{*},\underline {u}_{2}^{*})$ is a NE for the game, then it satisfies the following:

$$ \underline{u}_{1}^{*} = \underset{\underline{u}_{1} \in U_{ad}^{(1)}}{\arg\min} \tilde{J}_{1}(\underline{u}_{1}, \underline{u}_{2}^{*}) , \qquad \underline{u}_{2}^{*} = \underset{\underline{u}_{2} \in U_{ad}^{(2)}}{\arg\min} \tilde{J}_{2}(\underline{u}_{1}^{*}, \underline{u}_{2}) . $$

(6)

This fact implies that the NE point $\underline {u}^{*}=(\underline {u}_{1}^{*},\underline {u}_{2}^{*})$ must fulfil the necessary optimality conditions given by the Pontryagin maximum principle applied to both optimisation problems stated in Eq. 5, alternatively (6).

In order to discuss these conditions, we introduce the following Hamilton-Pontryagin (HP) functions:

$$ \mathcal{H}_{i}(t, \underline{y},\underline{u}_{1},\underline{u}_{2},\underline{p}_{1}, \underline{p}_{2}) =\underline{p}_{i} \cdot \underline{f}(t,\underline{y},\underline{u}_{1},\underline{u}_{2}) - \ell_{i} (t,\underline{y},\underline{u}_{1},\underline{u}_{2}), \qquad i=1,2 . $$

(7)

In terms of these functions, the PMP condition for the NE point $\underline {u}^{*}=(\underline {u}_{1}^{*},\underline {u}_{2}^{*})$ states the existence of multiplier (adjoint) functions $\underline {p}_{1}, \underline {p}_{2} : [0,T] \rightarrow \mathbb {R}^{n}$ such that the following holds:

$$ \begin{array}{ll} \max\limits_{\underline{w}_{1} \in K_{ad}^{(1)} } \mathcal{H}_{1}(t,\underline{y}^{*}(t),\underline{w}_{1},\underline{u}_{2}^{*}(t),\underline{p}_{1}^{*}(t),\underline{p}_{2}^{*}(t)) & =\mathcal{H}_{1}(t, \underline{y}^{*}(t),\underline{u}_{1}^{*}(t),\underline{u}_{2}^{*}(t),\underline{p}_{1}^{*}(t),\underline{p}_{2}^{*}(t)) , \\ \max\limits_{\underline{w}_{2} \in K_{ad}^{(2)} } \mathcal{H}_{2}(t,\underline{y}^{*}(t),\underline{u}_{1}^{*}(t),\underline{w}_{2},\underline{p}_{1}^{*}(t),\underline{p}_{2}^{*}(t)) & =\mathcal{H}_{2}(t, \underline{y}^{*}(t),\underline{u}_{1}^{*}(t),\underline{u}_{2}^{*}(t),\underline{p}_{1}^{*}(t),\underline{p}_{2}^{*}(t)) , \end{array} $$

(8)

for almost all t ∈ [0,T]. Notice that, at each t fixed, the problem (8) corresponds to a finite-dimensional Nash game.

In Eq. 8, we have $\underline {y}^{*}=y(\underline {u}_{1}^{*},\underline {u}_{2}^{*})$, and the adjoint variables $\underline {p}_{1}^{*}, \underline {p}_{2}^{*}$ are the solutions to the following differential problems:

$$ \begin{array}{@{}rcl@{}} -\underline{p}_{i}^{\prime}(t)& =&\left( \partial_{y} \underline{f}(t,\underline{y}(t),\underline{u}_{1}(t),\underline{u}_{2}(t))\right)^{\top} \underline{p}_{i}(t)-\partial_{y} \ell_{i} (t,\underline{y}(t),\underline{u}_{1}(t),\underline{u}_{2}(t)) , \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} \underline{p}_{i}(T) &=& - \partial_{y} g_{i}(\underline{y}(T)), \end{array} $$

(10)

where i = 1,2, $\partial _{y} \phi (\underline {y})$ represents the Jacobian of ϕ with respect to the vector of variables $\underline {y}$, and ⊤ means transpose. Similarly to Eq. 1, one can prove that Eqs. 9 and 10 are uniquely solvable, and the solution can be uniformly bounded independently of $\underline {u} \in U_{ad}$.

We conclude this section introducing the Nikaido-Isoda [24] function $\psi : U_{ad} \times U_{ad} \to \mathbb {R}$, which we use for the realisation of the SQH algorithm. We have

$$ \psi(\underline{u},\underline{v}):= \tilde{J}_{1} (\underline{u}_{1}, \underline{u}_{2}) -\tilde{J}_{1} (\underline{v}_{1}, \underline{u}_{2}) +\tilde{J}_{2} (\underline{u}_{1}, \underline{u}_{2}) -\tilde{J}_{2} (\underline{u}_{1}, \underline{v}_{2}), $$

(11)

where $\underline {u} = (\underline {u}_{1}, \underline {u}_{2}) \in U_{ad}$ and $\underline {v} = (\underline {v}_{1}, \underline {v}_{2}) \in U_{ad}$. At the Nash equilibrium $\underline {u}^{*} = (u_{1}^{*}, u_{2}^{*})$ it holds

$$ \psi(\underline{u}^{*},\underline{v}) \leq 0, $$

(12)

for any $\underline {v} \in U_{ad}$ and $\psi (\underline {u}^{*},\underline {u}^{*})=0$.

3 The SQH Scheme for Solving Nash Games

In the spirit of the SA scheme proposed by Krylov and Chernous’ko [20], a SA methodology for solving our Nash game $(\tilde {J}_{1},\tilde {J}_{2}; U_{ad}^{(1)}, U_{ad}^{(2)})$ consists of an iterative process, starting with an initial guess $({\underline {u}_{1}^{0}}, {\underline {u}_{2}^{0}}) \in U_{ad}$, and followed by the solution of our governing model (1) and of the adjoint problems Eqs. 9 and 10 for i = 1,2. Thereafter, a new approximation to the strategies $\underline {u}_{1}$ and $\underline {u}_{2}$ is obtained by solving, at each t fixed, the Nash game (8) and assigning the values of $(\underline {u}_{1}(t),\underline {u}_{2}(t))$ equal to the solution of this game.

We remark that this update step is well posed if this solution exists for t ∈ [0,T] and the resulting functions $\underline {u}_{1}$ and $\underline {u}_{2}$ are measurable. Clearly, this issue requires identifying classes of problems for which we can guarantee existence and uniqueness (or the possibility of selection) of a NE point. In this respect, a large class can be identified based on the following result given in [8], which is proved by an application of the Kakutani’s fixed-point theorem; see, e.g., [3] for references. We have

Theorem 3.1

Assume the following structure:

$$ \underline{f}(t,\underline{y},\underline{u}_{1},\underline{u}_{2}) = \underline{f}_{0}(t,\underline{y}) + M_{1}(t,\underline{y}) \underline{u}_{1} + M_{2}(t,\underline{y}) \underline{u}_{2} , $$

and

$$ \ell_{i} (t, \underline{y}, \underline{u}_{1}, \underline{u}_{2}) = {\ell_{i}^{0}}(t, \underline{y}) + {\ell_{i}^{1}} (t, \underline{u}_{1}) + {\ell_{i}^{2}} (t, \underline{u}_{2}), \qquad i=1,2 . $$

Furthermore, suppose that $K_{ad}^{(1)}$ and $K_{ad}^{(2)}$ are compact and convex, the function $\underline {f}_{0}$, ${\ell _{i}^{0}}$ and the matrix functions M₁ and M₂ are continuous in t and $\underline {y}$, and the functions $\underline {u}_{1} \rightarrow {\ell _{1}^{1}}(t,\underline {u}_{1})$ and $\underline {u}_{2} \rightarrow {\ell _{2}^{2}} (t,\underline {u}_{2})$ are strictly convex for any choice of t ∈ [0,T] and $\underline {y} \in \mathbb {R}^{n}$.

Then, for any t ∈ [0,T] and any $\underline {y}, \underline {p}_{1}, \underline {p}_{2} \in \mathbb {R}^{n}$, there exists a unique pair $(\tilde {\underline {u}}_{1},\tilde {\underline {u}}_{2}) \in K_{ad}^{(1)} \times K_{ad}^{(2)}$ such that

$$ \begin{array}{@{}rcl@{}} \tilde u_{1} & = \underset{\underline{v} \in K_{ad}^{(1)}}{\arg\max} \big( \underline{p}_{1} \cdot \underline{f}(t,\underline{y},\underline{v},\tilde{\underline{u}}_{2}) - \ell_{1} (t,\underline{y},\underline{v},\tilde{\underline{u}}_{2}) \big) , \\ \tilde u_{2} & = \underset{\underline{w} \in K_{ad}^{(2)}}{\arg\max} \big( \underline{p}_{2} \cdot \underline{f}(t,\underline{y},\tilde{\underline{u}}_{1},\underline{w}) - \ell_{2} (t,\underline{y},\tilde{\underline{u}}_{1},\underline{w}) \big) . \end{array} $$

With the setting of this theorem, the map $(t,\underline {y},\underline {p}_{1},\underline {p}_{2}) \mapsto \left (u_{1}^{*}, u_{2}^{*} \right )$ is continuous [8]. Moreover, based on results given in [30], one can prove that the functions $(\underline {u}_{1}(t), \underline {u}_{2}(t))$ resulting from the SA update, starting from measurable $({\underline {u}_{1}^{0}}(t), {\underline {u}_{2}^{0}}(t))$, are measurable. Therefore, the proposed SA update is well-posed and it can be repeated in order to construct a sequence of functions $\left (({\underline {u}_{1}^{k}} ,{\underline {u}_{2}^{k}}) \right )_{k=0}^{\infty }$.

However, as already pointed out in [20] in the case of optimal control problems, it is difficult to find conditions that guarantee convergence of SA iterations to the solution sought. Furthermore, results of numerical experiments show a lack of robustness of the SA scheme with respect to the choice of the initial guess and of the numerical and optimisation parameters.

For this reason, further research effort was put in the development of the SA strategy, and an advancement was achieved by Sakawa and Shindo considering a quadratic penalty on the Hamiltonian [33, 34]. We remark that these authors related their penalisation strategy to that proposed by B. Järmark in [17], which is similar to the proximal scheme of R. T. Rockafellar discussed in [29].

For our purpose, we follow the same path of [33] and extend it to the case of Nash games as follows. Consider the following augmented HP functions:

$$ \mathcal{K}_{\epsilon}^{(i)}(t,\underline{y},\underline{u}_{1},\underline{u}_{2},\underline{v}_{1},\underline{v}_{2},\underline{p}_{1},\underline{p}_{2}) := \mathcal{H}_{i} (t,\underline{y},\underline{u}_{1},\underline{u}_{2},\underline{p}_{1},\underline{p}_{2}) - \epsilon | \underline{u} - \underline{v}|^{2} , \quad i=1,2, $$

(13)

where, in the iteration process, $\underline {u} = (\underline {u}_{1}, \underline {u}_{2})$ is subject to the update step, and $\underline {v} = (\underline {v}_{1}, \underline {v}_{2})$ corresponds to the previous strategy approximation; |⋅| denotes the Euclidean norm. The parameter 𝜖 > 0 represents the augmentation weight that is chosen adaptively along the iteration as discussed below.

Now, similar to the SA update illustrated above, suppose that the k th function approximation $({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}})$ and the corresponding $\underline {y}^{k}$ and ${\underline {p}_{1}^{k}}, {\underline {p}_{2}^{k}}$ have been computed. For any fixed t ∈ [0,T] and 𝜖 > 0, consider the following finite-dimensional Nash game:

$$ \begin{array}{@{}rcl@{}} \mathcal{K}_{\epsilon}^{(1)} (t,\underline{y}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2} , {\underline{u}_{1}^{k}}, {\underline{u}_{2}^{k}} , {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) & =& \max\limits_{\underline{u}_{1} \in K_{ad}^{(1)} } \mathcal{K}_{\epsilon}^{(1)} (t,\underline{y}^{k}, \underline{u}_{1}, \tilde{\underline{u}}_{2} , {\underline{u}_{1}^{k}}, {\underline{u}_{2}^{k}} , {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) , \\ \mathcal{K}_{\epsilon}^{(2)} (t,\underline{y}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2} ,{\underline{u}_{1}^{k}}, {\underline{u}_{2}^{k}} , {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) & =& \max\limits_{\underline{u}_{2} \in K_{ad}^{(2)} } \mathcal{K}_{\epsilon}^{(2)} (t,\underline{y}^{k},\tilde{\underline{u}}_{1}, \underline{u}_{2} , {\underline{u}_{1}^{k}}, {\underline{u}_{2}^{k}} , {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) , \end{array} $$

(14)

where $\underline {y}^{k}=\underline {y}^{k}(t)$, ${\underline {p}_{1}^{k}}={\underline {p}_{1}^{k}}(t)$, ${\underline {p}_{2}^{k}}={\underline {p}_{2}^{k}}(t)$, and $({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}} )=({\underline {u}_{1}^{k}}(t), {\underline {u}_{2}^{k}}(t) )$.

It is clear that, assuming the structure specified in Theorem 3.1, the Nash game (14) admits a unique NE point, $(\tilde {\underline {u}}_{1}, \tilde {\underline {u}}_{2} ) \in K_{ad}^{(1)} \times K_{ad}^{(2)}$, and the sequence constructed recursively by the procedure:

$$ ({\underline{u}_{1}^{k}}(t), {\underline{u}_{2}^{k}}(t) ) \rightarrow (\underline{u}_{1}^{k+1}(t), \underline{u}_{2}^{k+1}(t) ) = (\tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2} ) $$

is well defined.

Notice that, in this procedure, the solution to Eq. 14 depends on the value of 𝜖. Therefore, the issue arises whether, corresponding to the step k → k + 1, we can choose the value of this parameter such that the strategy function $\underline {u}^{k+1}=(\underline {u}_{1}^{k+1}, \underline {u}_{2}^{k+1} )$ represents an improvement on $\underline {u}^{k}=({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}} )$, in the sense that some convergence criteria towards the solution to our differential Nash problem are fulfilled.

For this purpose, we define a criterion that is based on the Nikaido-Isoda function. We require that

$$ \psi(\underline{u}^{k+1}, \underline{u}^{k}) \le - \xi \| \underline{u}^{k+1} - \underline{u}^{k} \|_{L^{2}(0,T;\mathbb{R}^{m})}^{2} , $$

for some chosen ξ > 0. This is a consistency criterion in the sense that ψ must be non-positive, and if $(\underline {u}^{k+1}, \underline {u}^{k}) \rightarrow (\underline {u}^{*}, \underline {u}^{*})$, then we must have $\lim _{k \to \infty }\psi (\underline {u}^{k+1}, \underline {u}^{k}) =0$. Furthermore, we require that the absolute value $|\psi (\underline {u}^{k+1}, \underline {u}^{k})|$ monotonically decreases in the SQH iteration process.

In our SQH scheme, if the strategy update meets the two requirements above, then the update is taken and the value of 𝜖 is diminished by a factor ζ ∈ (0,1). If not, the update is discarded and the value of 𝜖 is increased by a factor σ > 1, and the procedure is repeated. Below, we show that a value of 𝜖 can be found such that the update is successful and the SQH iteration proceeds until an appropriate stopping criterion is reached.

Our SQH scheme for differential Nash games is implemented as follows:

In the following proposition, we prove that the Steps 1–6 of the SQH scheme are well posed. For the proof, we consider the assumptions of Theorem 3.1 with further simplifying hypothesis, which can be relaxed at the cost of more involved calculations.

Our purpose is to show that it is possible to find an 𝜖 in Algorithm 1 such that $\tilde {\underline {u}}$ generated in Step 2 satisfies the criterion required in Step 5 for a successful update. We have

Proposition 3.2

Let the assumptions of Theorem 3.1 hold, and suppose that $\underline {f}_{0}$, g_i, ℓ_i, i = 1,2 are twice continuous differentiable and strictly convex in $\underline {y}$ and $\underline {u}$ for all t ∈ [0,T]. Moreover, let M₁,M₂ dependent only on t and suppose that $\underline {f}_{0}$, ℓ_i and g_i, i = 1,2, represent quadratic forms in $\underline {u}$ and $\underline {y}$ such that their Hessians are constant.

Let $(\tilde {\underline {y}}, \tilde {\underline {u}}_{1}, \tilde {\underline {u}}_{2})$, $(\underline {y}^{k}, {\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}})$ be generated by Algorithm 1, Steps 2–3, and denote $\delta \underline {u} = \tilde {\underline {u}} - \underline {u}^{k}$. Then, there exists a 𝜃 > 0 independent of 𝜖 such that, for 𝜖 > 0 currently chosen in Step 2, the following inequality holds:

$$ \psi(\tilde{\underline{u}}, \underline{u}^{k}) \leq -(\epsilon -\theta) \| \delta \underline{u}\|_{L^{2}(0,T)}^{2}. $$

(15)

In particular, if 𝜖 > 𝜃 then $\psi (\tilde {\underline {u}}, \underline {u}^{k})\leq 0$.

Proof

Recall the definition of the Nikaido-Isoda function:

$$ \psi(\tilde{\underline{u}},\underline{u}^{k}):= \tilde{J}_{1} (\tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) -\tilde{J}_{1} ({\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) +\tilde{J}_{2} (\tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) -\tilde{J}_{2} (\tilde{\underline{u}}_{1}, {\underline{u}_{2}^{k}}) . $$

We focus on the first two terms involving J₁; however, the same calculation applies to the last two terms with J₂.

Notice that, with our assumptions, the function $\underline {y}(\underline {u}_{1}, \underline {u}_{2})$ results differentiable. Denote $\underline {y}^{k}=\underline {y}({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}})$, $\tilde {\underline {y}}=\underline {y}(\tilde {\underline {u}}_{1}, \tilde {\underline {u}}_{2})$ and $\tilde {\underline {y}}_{1}^{k}=\underline {y}({\underline {u}_{1}^{k}}, \tilde {\underline {u}}_{2})$, ${\underline {p}_{1}^{k}}= \underline {p}_{1}({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}})$, and define $\delta \underline {y}_{1} := \tilde {\underline {y}} - \tilde {\underline {y}}_{1}^{k}$, and $\delta \tilde {\underline {y}}_{1} := \tilde {\underline {y}}_{1}^{k} - \underline {y}^{k}$.

Consider the augmented Hamiltonian $\mathcal {K}_{\epsilon }^{(1)}$ of player P₁. Similar computations can be done with $\mathcal {K}_{\epsilon }^{(2)}$. It holds

$$ \mathcal{K}_{\epsilon}^{(1)}(t,\underline{y}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}},{\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) \geq \mathcal{K}_{\epsilon}^{(1)}(t,\underline{y}^{k},\underline{w}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}},{\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}), $$

(16)

for any $\underline {w} \in K_{ad}^{(1)}$. Hence, choosing $\underline {w}={\underline {u}_{1}^{k}}$, we have

$$ \begin{array}{@{}rcl@{}} \mathcal{K}_{\epsilon}^{(1)}(t,\underline{y}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}},{\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) &\geq& \mathcal{K}_{\epsilon}^{(1)} (t,\underline{y}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}},{\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) \\ &=& \mathcal{H}_{1}(t, \underline{y}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) - \epsilon |\tilde{\underline{u}}_{2} - {\underline{u}_{2}^{k}}|^{2}. \end{array} $$

Now, compute

$$ \begin{array}{@{}rcl@{}} &&J_{1}(\tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) - J_{1}(\tilde{\underline{y}}_{1}^{k},{\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) = \\ &&={{\int}_{0}^{T}} \Big(\ell_{1}(t,\tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2})- \ell_{1}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) \Big) dt + g_{1}(\tilde{\underline{y}}(T)) - g_{1}(\tilde{\underline{y}}_{1}^{k}(T))\\ && + {{\int}_{0}^{T}} \Big({\underline{p}_{1}^{k}} \cdot \underline{f}(t, \tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2})- {\underline{p}_{1}^{k}} \cdot\underline{f}(t, \tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) \Big) dt\\ && + {{\int}_{0}^{T}} \Big({\underline{p}_{1}^{k}} \cdot\underline{f}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2})- {\underline{p}_{1}^{k}} \cdot\underline{f}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) \Big) dt \\ && = {{\int}_{0}^{T}} \Big(- \mathcal{H}_{1}(t, \tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) + {\underline{p}_{1}^{k}} \cdot\underline{f}(t, \tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) \Big) dt \\ && + {{\int}_{0}^{T}} \Big(\mathcal{H}_{1} (t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) - {\underline{p}_{1}^{k}} \cdot\underline{f}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) \Big) dt \\ && +g_{1}(\tilde{\underline{y}}(T)) - g_{1}(\tilde{\underline{y}}_{1}^{k}(T)) . \end{array} $$

Notice that $\tilde {\underline {y}} = \tilde {\underline {y}}_{1}^{k} + \delta \underline {y}_{1}$. By applying the mean value theorem to second order to the maps $\underline {y} \mapsto {\mathscr{H}}_{1}(\cdot ,\underline {y},\cdot ,\cdot ,\cdot , \cdot )$ and $\underline {y} \mapsto \underline {f}(\cdot , \underline {y}, \cdot , \cdot )$, and $\underline {u}_{1} \mapsto \underline {f}(\cdot , \cdot ,\underline {u}_{1}, \cdot )$, we have

$$ \begin{array}{@{}rcl@{}} &\mathcal{H}_{1}(t, \tilde{\underline{y}}_{1}^{k}+\delta \underline{y}_{1}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) = \mathcal{H}_{1}(t, \tilde{\underline{y}}_{1}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}})\\ &+ \left( ({\underline{p}_{1}^{k}})^{\top} \partial_{y} \underline{f}_{0}(t, \tilde{\underline{y}}_{1}^{k})- \partial_{y}{\ell_{1}^{0}}(t, \tilde{\underline{y}}_{1}^{k})\right)\delta \underline{y}_{1} + \frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1}, \end{array} $$

and

$$ \underline{f}(t, \tilde{\underline{y}}_{1}^{k}+ \delta \underline{y}_{1}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) = \underline{f}(t, \tilde{\underline{y}}_{1}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) + \partial_{y} \underline{f}_{0}(t, \tilde{\underline{y}}_{1}^{k}) \delta \underline{y}_{1} + \frac{1}{2}\delta \underline{y}_{1}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta \underline{y}_{1} $$

and

$$ \underline{f}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}} + \delta \underline{u}_{1}, \tilde{\underline{u}}_{2}) = \underline{f}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) + M_{1}(t) \delta \underline{u}_{1} . $$

With these estimates, we continue the calculation above as follows. Notice that we add and subtract the term $\epsilon |\delta \underline {u}|^{2}$.

$$ \begin{array}{@{}rcl@{}} &&J_{1}(\tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) - J_{1}(\tilde{\underline{y}}_{1}^{k},{\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) = \\ && {{\int}_{0}^{T}} \Big(- \mathcal{H}_{1}(t, \tilde{\underline{y}}_{1}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}})+\mathcal{H}_{1} (t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) \\ && + \partial_{y}{\ell_{1}^{0}}(t, \tilde{\underline{y}}_{1}^{k}) \delta \underline{y}_{1} -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} + ({\underline{p}_{1}^{k}})^{\top}M_{1}(t) \delta \underline{u}_{1} + \frac{1}{2} ({\underline{p}_{1}^{k}})^{\top}\delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \underline{f}_{0} \delta \underline{y}_{1} \Big) dt\\ && +g_{1}(\tilde{\underline{y}}(T)) - g_{1}(\tilde{\underline{y}}_{1}^{k}(T)) + \epsilon |\delta \underline{u}|^{2} - \epsilon |\delta \underline{u}|^{2} \\ && = {{\int}_{0}^{T}} \Big(- \mathcal{K}_{\epsilon}^{(1)}(t, \tilde{\underline{y}}_{1}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}},{\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) - \epsilon|\delta \underline{u}|^{2} + \mathcal{H}_{1}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) \\ &&+ \partial_{y}{\ell_{1}^{0}}(t, \tilde{\underline{y}}_{1}^{k}) \delta \underline{y}_{1} -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} + ({\underline{p}_{1}^{k}})^{\top}M_{1}(t) \delta \underline{u}_{1} + \frac{1}{2} ({\underline{p}_{1}^{k}})^{\top}\delta \underline{y}_{1}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta \underline{y}_{1} \Big) dt\\ &&+ \partial_{y} g_{1}(\tilde{\underline{y}}_{1}^{k}(T))\delta\underline{y}_{1}(T)+ \frac{1}{2} \delta \underline{y}_{1}(T)^{\top} \partial^{2}_{yy}g_{1} \delta \underline{y}_{1}(T). \end{array} $$

Now, we consider the following integration by parts

$$ \begin{array}{@{}rcl@{}} &&{{\int}_{0}^{T}} \Big(({\underline{p}_{1}^{k}})^{\top} M_{1}(t) \delta \underline{u}_{1} + \frac{1}{2} ({\underline{p}_{1}^{k}})^{\top}\delta \underline{y}_{1}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta \underline{y}_{1} \Big) dt = \\ &&-\partial_{y}g_{1}(\tilde{\underline{y}}_{1}^{k}(T)) \delta\underline{y}_{1}(T) - {{\int}_{0}^{T}} \left[({\underline{p}_{1}^{k}})^{\prime}+ (\partial_{y}\underline{f}_{0}(t, \tilde{\underline{y}}_{1}^{k}))^{\top}{\underline{p}_{1}^{k}}\right]\delta \underline{y}_{1} dt . \end{array} $$

Using this result in the previous calculation, we have

$$ \begin{array}{@{}rcl@{}} &&{{\int}_{0}^{T}} \Big(- \mathcal{K}_{\epsilon}^{(1)}(t, \tilde{\underline{y}}_{1}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}},{\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) - \epsilon|\delta \underline{u}|^{2} + \mathcal{H}_{1}(t, \tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2},{\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) \\ && -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} \Big) dt + \frac{1}{2} \delta \underline{y}_{1}(T)^{\top} \partial^{2}_{yy}g_{1} \delta \underline{y}_{1}(T) \\ && + {{\int}_{0}^{T}}\left[ - ({\underline{p}_{1}^{k}})^{\prime} -(\partial_{y}\underline{f}_{0}(t, \tilde{\underline{y}}_{1}^{k}))^{\top}{\underline{p}_{1}^{k}}+\partial_{y}{\ell_{1}^{0}}(t, \tilde{\underline{y}}_{1}^{k}) \right] \delta \underline{y}_{1} dt. \end{array} $$

(17)

Applying again the mean value theorem to second order to the maps $\underline {y} \mapsto {\mathscr{H}}_{1}(\cdot ,\underline {y}, \cdot ,\cdot ,\cdot ,\cdot )$ and $\underline {y} \mapsto \mathcal {K}_{\epsilon }^{(1)}(\cdot ,\underline {y}, \cdot ,\cdot ,\cdot ,\cdot , \cdot ,\cdot )$, we get

$$ \begin{array}{@{}rcl@{}} &&\mathcal{H}_{1}(t, \underline{y}^{k}+\delta \tilde{\underline{y}}_{1}, {\underline{u}}_{1}^{k}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) = \mathcal{H}_{1}(t, \underline{y}^{k}, {\underline{u}}_{1}^{k}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}})\\ &&+ \left( {{({\underline{p}_{1}^{k}})^{\top} \partial_{y} \underline{f}_{0}(t, \underline{y}^{k})- \partial_{y}{\ell_{1}^{0}}(t, \underline{y}^{k})}}\right)\delta \tilde{\underline{y}}_{1} + \frac{1}{2} \delta \tilde{\underline{y}}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \tilde{\underline{y}}_{1}, \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} &&\mathcal{K}_{\epsilon}^{(1)}(t, \underline{y}^{k}+\delta \tilde{\underline{y}}_{1},\tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2} , {\underline{u}}_{1}^{k}, {\underline{u}}_{2}^{k}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) = \mathcal{K}_{\epsilon}^{(1)}(t, \underline{y}^{k},\tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2} , {\underline{u}}_{1}^{k}, {\underline{u}}_{2}^{k}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}})\\ &&+ \left( {{({\underline{p}_{1}^{k}})^{\top} \partial_{y} \underline{f}_{0}(t, \underline{y}^{k})- \partial_{y}{\ell_{1}^{0}}(t, \underline{y}^{k})}}\right)\delta \tilde{\underline{y}}_{1} + \frac{1}{2} \delta \tilde{\underline{y}}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \tilde{\underline{y}}_{1}, \end{array} $$

With these results and replacing the expression of $-({\underline {p}_{1}^{k}})^{\prime }$, we continue the calculation as follows:

$$ \begin{array}{@{}rcl@{}} &&J_{1}(\tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) - J_{1}(\tilde{\underline{y}}_{1}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) = \\ && {{\int}_{0}^{T}} \Big(- \mathcal{K}_{\epsilon}^{(1)}(t, \underline{y}^{k}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}, {\underline{u}_{1}^{k}}, {\underline{u}_{2}^{k}}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) + \mathcal{H}_{1}(t, \underline{y}^{k}, {\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}, {\underline{p}_{1}^{k}}, {\underline{p}_{2}^{k}}) - \epsilon |\delta \underline{u}|^{2} \\ && -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} \Big) dt + \frac{1}{2} \delta \underline{y}_{1}(T)^{\top} \partial^{2}_{yy}g_{1} \delta \underline{y}_{1}(T) \\ && + {{\int}_{0}^{T}} \Big(({\underline{p}_{1}^{k}})^{\top} \left[ \partial_{y} \underline{f}_{0}(t, \underline{y}^{k})- \partial_{y} \underline{f}_{0}(t, \tilde{\underline{y}}_{1}^{k})\right] + \partial_{y} {\ell_{1}^{0}}(t, \tilde{\underline{y}}_{1}^{k})- \partial_{y} {\ell_{1}^{0}}(t, \underline{y}^{k})\Big)\delta\underline{y}_{1} dt \\ && \leq {{\int}_{0}^{T}} \Big(-\epsilon |\delta \underline{u}_{1}|^{2} -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} \Big) dt + \frac{1}{2} \delta \underline{y}_{1}(T)^{\top} \partial^{2}_{yy}g_{1} \delta \underline{y}_{1}(T) \\ && + {{\int}_{0}^{T}} \Big(\delta\underline{y}_{1}^{\top} \partial^{2}_{yy}{\ell_{1}^{0}} \delta \tilde{\underline{y}}_{1} - ({\underline{p}_{1}^{k}})^{\top}\delta\underline{y}_{1}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta\tilde{\underline{y}}_{1}\Big) dt, \end{array} $$

(18)

where in the last integral we applied the mean value theorem to the maps $\underline {y} \mapsto \partial _{y}{\ell _{1}^{0}}(\cdot , \underline {y})$ and $\underline {y} \mapsto \partial _{y} \underline {f}_{0}(\cdot , \underline {y})$.

Therefore, we have shown that

$$ \begin{array}{@{}rcl@{}} J_{1}(\tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) - J_{1}(\tilde{\underline{y}}_{1}^{k},{\underline{u}_{1}^{k}}, \tilde{\underline{u}}_{2}) & \leq& {{\int}_{0}^{T}} \Big(-\epsilon |\delta \underline{u}_{1}|^{2} -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} \\ &&+ \delta\underline{y}_{1}^{\top} \partial^{2}_{yy}{\ell_{1}^{0}} \delta \tilde{\underline{y}}_{1} - ({\underline{p}_{1}^{k}})^{\top}\delta\underline{y}_{1}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta\tilde{\underline{y}}_{1} \Big) dt \\ && + \frac{1}{2} \delta \underline{y}_{1}(T)^{\top} \partial^{2}_{yy}g_{1} \delta \underline{y}_{1}(T). \end{array} $$

With a similar computation, we also obtain

$$ \begin{array}{@{}rcl@{}} J_{2}(\tilde{\underline{y}}, \tilde{\underline{u}}_{1}, \tilde{\underline{u}}_{2}) - J_{2}(\tilde{\underline{y}}_{2}^{k}, \tilde{\underline{u}}_{1}, {\underline{u}_{2}^{k}}) & \leq& {{\int}_{0}^{T}} \Big(-\epsilon |\delta \underline{u}_{2}|^{2} -\frac{1}{2} \delta \underline{y}_{2}^{\top}\partial^{2}_{yy} \mathcal{H}_{2} \delta \underline{y}_{2} \\ && + \delta\underline{y}_{2}^{\top} \partial^{2}_{yy}{\ell_{2}^{0}} \delta \tilde{\underline{y}}_{2} - ({\underline{p}_{2}^{k}})^{\top}\delta\underline{y}_{2}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta\tilde{\underline{y}}_{2} \Big) dt \\ && + \frac{1}{2} \delta \underline{y}_{2}(T)^{\top} \partial^{2}_{yy}g_{2} \delta \underline{y}_{2}(T) , \end{array} $$

where $\tilde {\underline {y}}_{2}^{k}=\underline {y}(\tilde {\underline {u}}_{1}, {\underline {u}_{2}^{k}})$, $\delta \underline {y}_{2} := \tilde {\underline {y}} - \tilde {\underline {y}}_{2}^{k}$ and $\delta \tilde {\underline {y}}_{2} := \tilde {\underline {y}}_{2}^{k} - \underline {y}^{k}$. Thus, we arrive at the following inequality:

$$ \begin{array}{@{}rcl@{}} \psi(\tilde{\underline{u}}, \underline{u}^{k}) &\leq& {{\int}_{0}^{T}} \Big(-\epsilon \left[ |\delta \underline{u}_{1}|^{2} + |\delta \underline{u}_{2}|^{2} \right] -\frac{1}{2} \delta \underline{y}_{1}^{\top}\partial^{2}_{yy} \mathcal{H}_{1} \delta \underline{y}_{1} -\frac{1}{2} \delta \underline{y}_{2}^{\top}\partial^{2}_{yy} \mathcal{H}_{2} \delta \underline{y}_{2} \\ & &+ \delta\underline{y}_{1}^{\top} \partial^{2}_{yy}{\ell_{1}^{0}} \delta \tilde{\underline{y}}_{1} - ({\underline{p}_{1}^{k}})^{\top}\delta\underline{y}_{1}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta\tilde{\underline{y}}_{1} + \delta\underline{y}_{2}^{\top} \partial^{2}_{yy}{\ell_{2}^{0}} \delta \tilde{\underline{y}}_{2} - ({\underline{p}_{2}^{k}})^{\top}\delta\underline{y}_{2}^{\top}\partial^{2}_{yy}\underline{f}_{0} \delta\tilde{\underline{y}}_{2} \Big) dt \\ && + \frac{1}{2} \delta \underline{y}_{1}(T)^{\top} \partial^{2}_{yy }g_{1} \delta \underline{y}_{1}(T) + \frac{1}{2} \delta \underline{y}_{2}(T)^{\top} \partial^{2}_{yy}g_{2} \delta \underline{y}_{2}(T) . \end{array} $$

(19)

Next, we notice that the solutions to the state and adjoint problems are uniformly bounded in [0,T] for any choice of $\underline {u} \in U_{ad}$, and the following estimates hold:

$$ | \delta \underline{y}_{1}(t) | \leq \mathcal{C}_{11} \|\delta \underline{u}_{1} \|_{L^{2}(0,T)}, \quad | \delta \underline{y}_{2}(t) | \leq \mathcal{C}_{22} \|\delta \underline{u}_{2} \|_{L^{2}(0,T)}, \qquad t\in (0,T). $$

(20)

Similarly,

$$ | \delta \tilde{\underline{y}}_{1}(t) | \leq \mathcal{C}_{12} \|\delta \underline{u}_{2} \|_{L^{2}(0,T)}, \quad | \delta \tilde{\underline{y}}_{2}(t) | \leq \mathcal{C}_{21} \|\delta \underline{u}_{1} \|_{L^{2}(0,T)}, \qquad t\in (0,T) ; $$

(21)

see [9] for a proof. By using these estimates in Eq. 19, we obtain

$$ \psi(\tilde{\underline{u}}, \underline{u}^{k}) \leq - (\epsilon - \theta) \| \delta \underline{u} \|_{L^{2}(0,T)}^{2} , $$

where 𝜃 depends on the functions computed at the k th iteration but not on 𝜖. Thus, the claim is proved. □

We remark that in Step 2 of the SQH algorithm, the NE solution $\tilde {\underline {u}}$ obtained in Step 2 depends on 𝜖 so that $\| \tilde {\underline {u}} - \underline {u}^{k} \|_{L^{2}(0,T)}^{2}$ decreases as O(1/𝜖²). In order to illustrate this fact, consider the following optimisation problem:

$$ \max f_{\epsilon}(u):=b u - \frac{\nu}{2} u^{2} - \epsilon (u-v)^{2} , $$

where ν,𝜖 > 0. Clearly, the function f_𝜖 is concave and its maximum is attained at $\tilde u=(b + 2 \epsilon v)/(\nu + 2 \epsilon )$. Furthermore, we have

$$ | \tilde u -v | =\frac{|b - \nu v|}{(\nu + 2 \epsilon)} . $$

Now, subject to the assumptions of Proposition 3.2 and using the estimates in its proof, we can state that there exists a constant C > 0 such that

$$ |\psi(\tilde{\underline{u}},\underline{u}^{k}) | \le C \| \tilde{\underline{u}} - \underline{u}^{k} \|_{L^{2}(0,T)}^{2} , $$

where C increases linearly with 𝜖. On the other hand, since the HP functions are concave, we have that $\| \tilde {\underline {u}} - \underline {u}^{k} \|_{L^{2}(0,T)}^{2}$ decreases as O(1/𝜖²). Therefore, given the value Ψ^k in Step 5 of the SQH algorithm, it is always possible to choose 𝜖 sufficiently large such that $|\psi (\tilde {\underline {u}},\underline {u}^{k}) | \le {\Psi }^{k}$.

In Algorithm 1, we have that $\psi (\underline {u}^{k+1}, \underline {u}^{k}) \to 0$ as $k \to \infty$. Thus, since $\psi (\underline {u}^{k+1}, \underline {u}^{k}) \leq - \xi \|\underline {u}^{k+1} - \underline {u}^{k} \|_{L^{2}}^{2}$, it follows that $\lim _{k} \| \underline {u}^{k+1} - \underline {u}^{k} \|_{L^{2}}^{2} = 0$ and hence the convergence criterion in Step 6 can be satisfied.

We remark that, subject to the assumptions of Proposition 3.2, if $({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}})$ generated by Algorithm 1 satisfies the PMP conditions, then Algorithm 1 stops returning $({\underline {u}_{1}^{k}}, {\underline {u}_{2}^{k}})$.

4 Numerical Experiments

In this section, we present results of four numerical experiments to validate the computational performance of the proposed SQH scheme. We remark that in all these experiments the structure of the corresponding problems is such that in Step 2 of the SQH algorithm the update $\tilde {\underline {u}}(t)$ at any fixed t can be determined analytically.

The first experiment exploits the possibility to compute open-loop NE solutions to linear-quadratic Nash games by solving a coupled system of Riccati equations [14]. Thus, we use this solution for comparison to the solution of the same Nash game obtained with the SQH method.

Our linear-quadratic Nash game is formulated as follows:

$$ \underline{y}^{\prime}(t) = A \underline{y}(t) + B_{1} \underline{u}_{1}(t) + B_{2} \underline{u}_{2}(t), \quad \underline{y}(0)=\underline{y}_{0}, $$

(22)

where

$$ A = \begin{pmatrix} 1 &0 \\ 0&2 \end{pmatrix}, \quad B_{1} = \begin{pmatrix} 1 &0 \\ 0&-1 \end{pmatrix}, \quad B_{2}= \begin{pmatrix} 2 & -1 \\ 0&2 \end{pmatrix} , \quad \underline{y}_{0} = \begin{pmatrix} 2 \\1 \end{pmatrix}. $$

Therefore, $\underline {y}(t) \in \mathbb {R}^{2}$ and $\underline {u}_{i}(t) \in \mathbb {R}^{2}$, t ∈ [0,T].

The cost functionals are as follows:

$$ J_{i} (\underline{y},\underline{u}_{1},\underline{u}_{2})= \frac{1}{2} {{\int}_{0}^{T}} \Big(\underline{y}(s)^{\top}L_{i}(s)\underline{y}(s) + \underline{u}_{i}(s)^{\top}N_{i}(s)\underline{u}_{i}(s) \Big) ds + \frac{1}{2} \underline{y}(T)^{\top} D_{i}\underline{y}(T), $$

(23)

i = 1,2, where the matrices L_i(s),D_i,N_i(s) are given by L₁ = α₁I₂,L₂ = α₂I₂, N₁ = ν₁I₂,N₂ = ν₂I₂, and D₁ = γ₁I₂, and D₂ = γ₂I₂, where I₂ is the identity matrix in $\mathbb {R}^{2}$. In the following experiment, we choose α₁ = 1, α₂ = 10, ν₁ = 0.1, ν₂ = 0.1, γ₁ = 0 and γ₂ = 0.

We consider the time interval [0,T], with T = 0.2, subdivided into N = 2000 subintervals and, on this grid, the state and adjoint equations are solved numerically by a midpoint scheme [3].

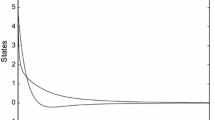
The initial guess $\underline {u}^{0}$ for the SQH iteration are zero functions, and we choose 𝜖 = 10, ζ = 0.95, σ = 1.05, ξ = 10^− 8, Ψ⁰ = 10, and $\mathcal {K}= 10^{-14}$. With this setting, we obtain theNash strategies $(\underline {u}_{1}, \underline {u}_{2})$ depicted in Fig. 1 (left), which are compared with the solution obtained by solving the Riccati system as shown in Fig. 1 (right). We can see that the two sets of solutions overlap.

Fig. 1

Strategies $\underline {u}_{1}$ (left) and $\underline {u}_{2}$ for the LQ Nash game obtained with the SQH scheme (top) and by solving the Riccati system (bottom)

Next, we consider the same setting but require that the players’ strategies are constrained by choosing $K^{(i)}_{ad}= [-2,2] \times [-2,2]$, i = 1,2. With this setting, we obtain the strategies depicted in Fig. 2.

Fig. 2

Strategies $\underline {u}_{1}$ (left) and $\underline {u}_{2}$ for the LQ Nash game with constraints on $\underline {u}$ as obtained by the SQH scheme

In our third experiment, we consider a setting similar to the second experiment but add to the cost functionals a weighted L¹ cost of the strategies. We have (written in a more compact form):

$$ J_{i} (\underline{y},\underline{u}_{1},\underline{u}_{2})= \frac{1}{2} {{\int}_{0}^{T}} \Big(\alpha_{i} | \underline{y}(s)|^{2} + \nu_{i} |\underline{u}_{i}(s)|^{2} + 2\beta_{i} |\underline{u}_{i}(s) | \Big) ds , $$

(24)

where i = 1,2; the terms with D_i, i = 1,2, are omitted. We choose ν₁ = 0.1, ν₂ = 0.01, and β₁ = 0.01, β₂ = 0.1; the other parameters are set as in the first experiment. Furthermore, we require that the players’ strategies are constrained by choosing $K^{(i)}_{ad}= [-10,10] \times [-10,10]$, i = 1,2. The strategies obtained with this setting are depicted in Fig. 3. Notice that the addition of L¹ costs of the players’ actions promotes their sparsity.

Fig. 3

Strategies $\underline {u}_{1}$ (left) and $\underline {u}_{2}$ for the Nash game with L² and L¹ costs and constraints on $\underline {u}$ as obtained by the SQH scheme

In the next experiment, we consider a tracking problem where the cost functionals have the following structure:

$$ \begin{array}{@{}rcl@{}} J_{i} (\underline{y},\underline{u}_{1},\underline{u}_{2}) &=& \frac{1}{2} {{\int}_{0}^{T}} \Big(\alpha_{i} | \underline{y}(s) - \bar{\underline{y}}^{i}(s)|^{2} + \nu_{i} |\underline{u}_{i}(s)|^{2} + 2\beta_{i} |\underline{u}_{i}(s) | \Big) ds \\ &&+ \frac{\gamma_{i}}{2} | \underline{y}(T) - \bar{\underline{y}}^{i}(T)|^{2}, \end{array} $$

(25)

where $\bar {\underline {y}}^{i}$ denotes the trajectory desired by the Player P_i, i = 1,2. Specifically, we take

$$ \bar{\underline{y}}^{1}(t)=\begin{pmatrix} 1 \\ 1 \end{pmatrix} \sin \left( 2 \pi t \right), \qquad \bar{\underline{y}}^{2}(t)=\begin{pmatrix} 1 \\ 1 \end{pmatrix} \cos \left( 2 \pi t \right) . $$

Notice that these trajectories are orthogonal to each other, that is, the two players have very different purposes. For the initial state, we take $\underline {y}_{0}=(1/2,1/2)$.

In this fourth experiment, the values of the game parameters are given by α₁ = 1, α₂ = 10, ν₁ = 10^− 8, ν₂ = 10^− 6, β₁ = 10^− 8, β₂ = 10^− 6, and γ₁ = 1 and γ₂ = 1. Furthermore, we require that the players’ strategies are constrained by choosing $K^{(i)}_{ad}= [-4,4] \times [-4,4]$, i = 1,2. In this experiment, we take T = 1 and N = 10⁴ subdivision of [0,T] for the numerical approximation. The parameters of the SQH scheme remain unchanged. The results of this experiment are depicted in Fig. 4.

Fig. 4

Strategies $\underline {u}_{1}$ (top, left) and $\underline {u}_{2}$ (top, right) for the Nash game with tracking functional as obtained by the SQH scheme. In the middle figures, the values of J₁ and J₂ along the SQH iterations (left) and the evolution of $\underline {y}$ corresponding to $\underline {u}_{1}$ and $\underline {u}_{2}$ (right). In the bottom figures, the values of ψ (left) and of 𝜖 along the SQH iterations

For this concluding experiment, we report that the convergence criterion is achieved after 3593 SQH iterations, whereas the number of successful updates is 1686. Correspondingly, we see that ψ is always negative and its absolute value monotonically decreases, with ψ = − 1.70 × 10^− 10 at convergence. On the other hand, we can see that the value of 𝜖 is changed along the iteration, while the values of the players’ functionals reach the Nash equilibrium. The CPU time for this experiment is 1151.4 s on a laptop computer.

5 Conclusion

A sequential quadratic Hamiltonian (SQH) scheme for solving open-loop differential Nash games was discussed. Theoretical and numerical results were presented that successfully demonstrated the well-posedness and computational performance of the SQH method applied to different Nash games governed by ordinary differential equations.

However, the applicability of the proposed method seems not restricted to these models and appears to be a promising technique for solving infinite-dimensional differential Nash game problems that have been considered recently in different fields of applied mathematics; see, e.g., [10, 28, 31].