Abstract
A confluent and terminating reduction system is introduced for graphs, which preserves the number of their perfect matchings. A union-find algorithm is presented to carry out reduction in almost linear time. The König property is investigated in the context of reduction by introducing the König deficiency of a graph G as the difference between the vertex covering number and the matching number of G. It is shown that the problem of finding the König deficiency of a graph is NP-complete even if we know that the graph reduces to the empty graph. Finally, the König deficiency of graphs G having a vertex v such that \(G-v\) has a unique perfect matching is studied in connection with reduction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a recent paper, Levit and Mandrescu (2016) have given an interesting characterization of graphs having a unique perfect matching and satisfying the König property at the same time. Such graphs are exactly the ones that can be reduced to the empty graph by a simple leaf elimination procedure. The procedure can be implemented in linear time. This result is in line with our conjecture (Bartha and Krész 2010) that the property of having a unique perfect matching is decidable for all graphs in linear time. The König property is, however, too restrictive even for the class of graphs having a unique perfect matching (UPM graphs, for short), which class is already very small to begin with.
In this paper we add a second component, called line reduction, to the leaf elimination procedure. Line reduction, which has been studied by Bartha and Krész (2006, 2009), also preserves the number of perfect matchings and has a linear-time implementation. It is therefore natural to combine leaf elimination with line reduction and see if the resulting reduction can still be implemented in linear time. We give a positive answer to this question in Sect. 4, thus obtaining a larger subclass of UPM graphs that is still decidable in linear time. This class consists of graphs that can be reduced to the empty graph by the help of the combined reduction. Such graphs will be called zero-reducible.
We also investigate the possibility whether, on the analogy of the main result of Levit and Mandrescu (2016), one could come up with a characterization of zero-reducible graphs in terms of the König property. Unfortunately it turns out that such a characterization is not likely to exist. Moreover, in Sect. 5 we prove that the problem of finding the independence number of zero-reducible graphs is still NP-complete. Finally, in Sect. 6 we consider graphs that have a unique near-perfect matching, that is, graphs with a vertex v such that \(G-v\) has a unique perfect matching. We call these graphs almost UPM, and extend the Levit and Mandrescu type characterization of UPM graphs having the König property to almost UPM graphs having the König property.
2 Basic underlying concepts and results
Throughout the paper, we are going to follow the terminology and notation of Lovász and Plummer (1986) concerning elementary concepts in graph theory. Let \(G=(V(G),E(G))\) be an undirected graph. Our concern is with the relationship between the numbers \(\nu (G)\) (the matching number of G), \(\tau (G)\) (the vertex covering number of G), and \(\alpha (G)\) (the independence number of G) in the light of a reduction procedure which has the power to substantially simplify graphs. Two properties of graphs will be of distinguished interest for us. The so called König property (also known as the König–Egervári property), and the property of having a unique perfect matching, abbreviated as the UPM property. By definition, graph G has the König property if \(\nu (G)=\tau (G)\). It is known that \(\nu (G)\le \tau (G)\) for all graphs G. Also, \(\alpha (G)=|V(G)|-\tau (G)\), since the maximum independent sets of G are exactly the complements of the minimum vertex covers. Thus, \(\alpha (G) + \nu (G) \le |V(G)|\) with the two sides being equal iff G has the König property. We introduce the number
as the König deficiency of G.
For any \(v\in V(G)\), \(G-v\) stands for the graph obtained from G by deleting vertex v together with all the edges incident with v. By definition (Gallai 1963), a graph G is factor-critical if \(G-v\) has a perfect matching for each \(v\in V(G)\). A perfect matching of \(G-v\) is then called a near-perfect matching of G. In our discussion we shall use the so called Gallai-Edmonds decomposition (G-E decomposition, for short) of graphs (Edmonds 1965; Gallai 1964; Lovász and Plummer 1986), which splits the set \(V(G)\) into three disjoint subsets D(G), A(G), and C(G) as follows.
D(G): vertices not covered by at least one maximum matching of G;
A(G): vertices in \(V(G){\setminus } D(G)\) adjacent to at least one vertex in D(G);
C(G): vertices in \((V(G){\setminus } A(G)){\setminus } D(G)\).
According to the Gallai-Edmonds Structure Theorem, each connected component of the subgraph of G spanned by D(G) is factor critical, and the subgraph spanned by C(G) has a perfect matching. Moreover, every maximum matching of G composes of:
a perfect matching of C(G),
a near-perfect matching for each component of D(G), and
edges covering all of A(G) together with as many still uncovered vertices in D(G) as possible.
The number of vertices ultimately left uncovered in D(G) is invariant, and is called the (matching-) deficiency of G.
The following two results are quoted from Lovász and Plummer (1986).
Theorem 1
(Lovász and Plummer 1986, Lemma 6.3.6) A graph G has the König property iff, in the G-E decomposition of G, D(G) is an independent set and the subgraph induced by C(G) has the König property.
Notice that D(G) being an independent set is equivalent to the fact that each factor-critical component spanned by D(G) is a single vertex.
Theorem 2
(Lovász and Plummer 1986, Theorem 6.3.7) Let G be a graph having a perfect matching. Then G has the König property iff it does not contain a nice subgraph which is an even subdivision of one of the two graphs in Fig. 1.
Recall that a nice subgraph of G is a subgraph \(G'\) having a perfect matching \(M'\) that can be extended to one of G.
The third result, due to Kotzig (1959), is still the most powerful one in the study of UPM graphs. We quote the result as stated in Lovász and Plummer (1986, Theorem 5.3.10). The result allows UPM graphs to be demolished by successively removing certain cut edges from it. Recall that a cut edgee in G is one the removal of which disconnects the component of G containing e.
Theorem 3
Every UPM graph G contains a matching-positive cut edge, that is, a cut edge belonging to the unique perfect matching of G.
Now we turn to a brief overview of the second fundamental concept used in the paper. An abstract reduction system (Derschowitz and Jouannaud 1990) consists of a set A and a finite number of irreflexive binary relations \(R_1, \ldots , R_n\) over A. It is customary to write \(a\rightarrow _{R_i} b\) for \((a,b)\in R_i\). The reduction is carried out by the relation \(R=\cup _i R_i\) in such a way that a reduces to b if \(a\rightarrow _R^* b\). The relation \(\rightarrow _R ^*\) denotes the reflexive and transitive closure of \(\rightarrow _R\). It is generally not required that \(\rightarrow _R\) be antisymmetric, even though in our case it will be. An element \(a\in A\) is called irreducible or minimal if there exists no \(b\in A\) such that \(a\rightarrow _R b\). (Remember that R is irreflexive.) Let us agree that we simply write \(\rightarrow \) for \(\rightarrow _R\) if R is understood.
Reduction R is confluent (has the Church-Rosser or diamond property) if, for every \(a,b,c\in A\), \(a\rightarrow b\) and \(a\rightarrow c\) imply that \(b\rightarrow ^*d\) and \(c\rightarrow ^* d\) for an appropriate \(d\in A\). Confluence is a vital property with regard to finding irreducible elements in abstract reduction systems. It says that, if \(a\in A\) can be reduced in two different ways: \(a\rightarrow b\) and \(a\rightarrow c\), then b and c can further be reduced (possibly in several steps) to a common element \(d\in A\). A terminating system is one in which there exists no infinite chain \(a_0\rightarrow a_1 \rightarrow \ldots \) of reductions. Notice that termination implies the antisymmetry of \(\rightarrow ^*\). As it is well-known, in a confluent and terminating system every element \(a\in A\) reduces to a unique minimal one \({\hat{a}}\). This minimal element is common to all \(b\in A\) such that \(a \leftrightarrow ^*b\).
3 Reducing graphs
In this section we introduce a confluent and terminating reduction system on graphs, operating with only two component reductions: leaf reduction and line reduction. As mentioned in Sect. 1, both components have been studied earlier separately in Levit and Mandrescu (2016) and Bartha and Krész (2006, 2009), respectively, and it has been observed that they preserve the number of perfect matchings in graphs. Moreover, leaf reduction (elimination) preserves the König deficiency as well.
Definition 1
For graphs G and \(G'\), G is (one-step) leaf-reducible to \(G'\)—notation \(G\rightarrow _\mathbf{f}G'\)—if \(G'\) is obtained from G by deleting a leaf vertex together with the unique vertex adjacent to it.
By the usual terminology, the unique edge \(e=(v,u)\) incident with a leaf v is called pendant. Deleting an edge, together with both of its endpoints, is generally referred to as exploding the edge. Thus, one leaf reduction step amounts to exploding a pendant edge in G. Clearly, leaf reduction by itself is a confluent and terminating reduction system on the set of (isomorphism classes of) graphs. It is also clear that leaf reduction preserves the number of perfect matchings in G, but not necessarily the number of maximum matchings in general. Indeed, every perfect matching of G must cover any leaf with its pendant edge.
From this point on, by a graph we shall mean a multigraph having no loops. Leaf reduction works naturally for multigraphs as well, and the observation in the previous paragraph on the number of perfect matchings remains true.
Recall that a subdividing vertex in \(V(G)\) is one having exactly two neighbors, to which it is connected by a single edge. Let \(c\in V(G)\) be a subdividing vertex in G that is adjacent to the (necessarily distinct) vertices \(f_1\) and \(f_2\). The triple \(r=(f_1,c,f_2)\) is called a redex with centerc and focuses\(f_1\), \(f_2\).
Definition 2
Contracting a redex \(r=(f_1,c,f_2)\) in G (or shrinkingG along r) means deleting the center c and merging the two focuses of r into one vertex, while deleting the (possibly multiple) edge connecting \(f_1\) with \(f_2\). For graphs G and \(G'\), G is (one-step) line-reducible to \(G'\) – notation \(G\rightarrow _\mathbf{l}G'\) – if \(G'\) is obtained from G by contracting one redex.
To be precise, by merging \(f_1\) and \(f_2\) we mean deleting these two vertices from G and replacing them with a new vertex f in \(G'\) such that for every vertex \(v\in V(G)\cap V(G')\), \((f,v)\in E(G')\) iff \((f_1,v)\in E(G)\) or \((f_2,v)\in E(G))\). By this definition, multiplicities of the edges incident with the merged vertices are added up.
Example 1
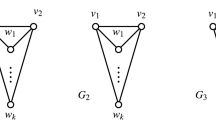
Consider the graph \(G_0\) of Fig. 2 containing four redexes centered at vertices 4, 7, 11, and 14. Contracting the ones at 11 and 14 gives rise to a new redex a in the resulting graph \(G_2\). (In graphs \(G_0\) and \(G_1\) of Fig. 2, small arrows indicate which two vertices are collapsed in one reduction step.) Shrinking \(G_2\) along the redexes at a and 7 yields \(G_3\), showing another new redex b. Finally, shrinking \(G_3\) along the redexes 4 and b results in a single edge, the graph \(r(G_0)\), which is irreducible for \(\rightarrow _\mathbf{l}\).
Line reduction by itself is also confluent and terminating (Bartha and Krész 2006), and it preserves the number of perfect matchings, too.
Theorem 4
The reduction \(\rightarrow =\rightarrow _\mathbf{f}\cup \rightarrow _\mathbf{l}\) is confluent.
Proof
It is sufficient to show that if \(G\rightarrow _\mathbf{f}G_1\) and \(G\rightarrow _\mathbf{l}G_2\), then \(G_1\rightarrow ^*G'\) and \(G_2\rightarrow ^*G'\) for some graph \(G'\). Let \(G\rightarrow _\mathbf{f}G_1\) through a leaf v adjacent to u, and \(G\rightarrow _\mathbf{l}G_2\) via a redex \(r=(f_1,c,f_2)\). The following three cases are possible.
Case A: the vertices \(u,v,c,f_1,f_2\) are pairwise distinct (Fig. 3a). The redex r is then still available in \(G_1\) and the leaf v is present in \(G_2\). The two reductions can be done simultaneously, and for the resulting graph \(G'\), \(G_1\rightarrow _\mathbf{l}G'\) and \(G_2\rightarrow _\mathbf{f}G'\).
Case B: \(c=u\), and consequently \(v=f_1\) or \(v=f_2\) (Fig. 3b). Take \(G'=G_1=G_2\).
Case C: \(u=f_1\) or \(u=f_2\) (Fig. 3c). Let \(G'\) be the graph obtained from G by deleting all of the vertices \(v,u,f_1,c,f_2\). Clearly, \(G_1\rightarrow _\mathbf{f}G'\) and \(G_2\rightarrow _\mathbf{f}G'\).
The proof is now complete. \(\square \)
Since both \(\rightarrow _\mathbf{f}\) and \(\rightarrow _\mathbf{l}\) are terminating, Theorem 4 implies that every graph G can be reduced to a unique minimal graph \({\hat{G}}\) free from leaves and redexes. If G has a perfect matching, then the number of perfect matchings in \({\hat{G}}\) is the same as in G.
Now we investigate the relationship between reduction and the König property.
Proposition 1
For all graphs G and \(G'\), if \(G\rightarrow _\mathbf{f}G'\), then \(k(G)=k(G')\).
Proof
First observe that exploding a pendant edge in G always decrements the size of a maximum matching in the graph. This is a straightforward exercise left to the reader. Now let (v, u) be the edge to be exploded (incident with leaf v), and S be a maximum independent set in G. Assume, without loss of generality, that \(v\in S\). Then \(S-v\) is a maximum independent set for \(G'\). On the other hand, if S is a maximum independent set in \(G'=G-\{u,v\}\), then \(S+v\) is maximum independent in G. Thus, exploding the edge (v, u) will decrement the size of a maximum independent set as well. Since the number of vertices decreases by 2, the number
equals k(G). \(\square \)
Proposition 2
For all graphs G and \(G'\), if \(G\rightarrow _\mathbf{l}G'\), then
Proof
Again, first observe as an easy exercise that the size of a maximum matching is decremented when contracting a redex \(r=(f_1,c,f_2)\) in G. (For, consider the G-E decomposition of G, and discuss the cases \(c\in C(G)\), \(c\in A(G)\) and \(c\in D(G)\).)
As for the maximum number of independent vertices, it may or may not be decremented as a result of contracting r. For example, if G is the redex r itself with \(f_1\) and \(f_2\) not being adjacent, then \(\alpha (G')=\alpha (G)-1\). If, however, \(f_1\) and \(f_2\) are adjacent (i.e., G is a triangle), then \(\alpha (G')=\alpha (G)\). In general, if S is a maximum independent set of G and \(c\in S\), then \(S{\setminus } \{c\}\) is independent in \(G'\). (It may not be maximum, though.) On the other hand, if \(c\not \in S\), then \(f_1\in S\) or \(f_2\in S\). If both \(f_1\) and \(f_2\) are in S, then \(S{\setminus } \{f_1,f_2\}\cup \{f\}\) is independent in \(G'\), where f is the vertex in \(G'\) corresponding to the collapsed pair \(\{f_1,f_2\}\). If only one of \(f_1\) and \(f_2\) is in S (say \(f_1\in S\)), then \(S{\setminus } \{f_1\}\) is independent in \(G'\). Thus, the size of a maximum independent set cannot decrease by more than one as a result of the reduction. Obviously, it cannot increase either, so that
as it was to be proved. \(\square \)
Proposition 2 implies that \(\rightarrow _\mathbf{l}\) preserves the König property, but not the König deficiency in general. Our next theorem is in fact a refinement of Proposition 2. Let \({\bar{H}}\) denote the graph obtained from the graph H in Fig. 1a by deleting the vertices \(v_1\) and \(v_2\). The leaf vertex popping up in \({\bar{H}}\) is then called unsafe. In general, a vertex \(u\in V(G)\) in an arbitrary graph G is unsafe if an instance of \({\bar{H}}\) with possible even subdivisions on its edges can be pasted on G as a subgraph, so that the unsafe vertex of \({\bar{H}}\) coincides with u. If G has a perfect matching, then an unsafe vertex v is nice if the UPM of \({\bar{H}}\) (with its possible subdivisions) can be extended to a perfect matching of G.
Theorem 5
Let \(G\rightarrow _\mathbf{l}G'\) via redex \(r=(f_1,c,f_2)\), and assume that \(G'\) has the König property. Then G does not have the König property iff \((f_1,f_2)\in E(G)\), and, furthermore, for the vertex f in \(G'\) that corresponds to the collapsed pair \(\{f_1,f_2\}\), either \(f\in D(G')\) or \(f\in C(G')\) with f being unsafe and nice.
Proof
Our first observation is that, in order to test the König property for G by Theorems 1 and 2, we do not need to pay attention to the complete graph \(K_4\) appearing as a nice subgraph in C(G), because line reduction preserves the presence of \(K_4\) with even subdivisions. Therefore, by Theorem 2, we can concentrate on the occurrences of the “bad” graph H in Fig. 1a (with even subdivisions) in C(G).
The second key observation is that if \(f_1\) and \(f_2\) are not adjacent in G, then contracting r inside an occurrence of H is essentially equivalent to lifting (not deleting!) two subdividing vertices from an edge in that occurrence. Indeed, since \(f_1\) and \(f_2\) are not adjacent, we can assume without loss of generality that c is one of the subdividing vertices, say on edge e. The subdivision is even, however, therefore there exists another subdividing vertex \(c'\) on e. Again, without loss of generality, we can assume that \(c'\) is adjacent to c, so that contracting r in G will leave the subgraph H intact with two less subdivisions on edge e. Regarding the condition that D(G) be an independent set (i.e., each factor-critical component of the subgraph spanned by D(G) be a single vertex), notice that this condition holds before contracting r iff it holds after contracting it, provided that \(f_1\) and \(f_2\) are not adjacent. (See also the argument under Case a below.) Consequently, the König property could be lost only if \(f_1\) and \(f_2\) are adjacent in G.
Let us assume now that the edge \((f_1,f_2)\) does exist in G. With respect to the G-E decomposition of G and \(G'\), the following three cases are possible.
Case a: \(f\in D(G')\). Clearly, c must then be in \(A(G)\cup D(G)\). The center cannot be in A(G), however, since the surplus of c on D(G) must be positive and the two focusses are in the same connected component of D(G). Therefore the whole redex r is in D(G), implying by Theorem 1 that G does not have the König property.
Case b: \(f\in C(G')\). By Theorem 2, G has the König property iff f is not nicely unsafe in \(G'\).
Case c: \(f\in A(G')\). Again, c cannot be in A(G), because its surplus on D(G) must be positive (and at most one of \(f_1\) and \(f_2\) is in D(G)). Therefore either \(c\in C(G)\) or \(c\in D(G)\), so that the presence of the edge \((f_1,f_2)\) does not make a difference regarding the G-E decomposition of \(G'\). Consequently, G does have the König property.
The proof is now complete. \(\square \)
4 An almost linear-time reduction algorithm
How efficiently can reduction be implemented by an algorithm? This is an important question, since the reduction may substantially decrease the size of the graph, so it could be used as a preamble to some other graph algorithms having a more significant time complexity. Two obvious examples are finding the number of perfect matchings in a graph and deciding if a graph has the König property. The latter example could use Theorem 5 above as a theoretical basis. Other application areas have been mentioned in Bartha and Krész (2009). Line reduction, as described in Bartha and Krész (2009), has been successfully applied in the search of maximum matchings (Korenwein et al. 2018) using parameterized complexity analysis as a theoretical measure, backed up by an experimental study showing a significant speed-up in implementation.
Along this line one may even hope for a polynomial-time algorithm for calculating the König deficiency of graphs that can be reduced to the empty graph. As introduced in Sect. 1, such graphs are called zero-reducible. Indeed, while reversing the steps of the reduction, one might think that a suitable maximum independent set or minimum vertex cover could gradually be built up from scratch for the graph. This appears to be likely, since the class of zero-reducible graphs is just a narrow subclass of the class of UPM graphs, which is already very restricted itself. Disappointingly, however, we are going to show in Section 4 that finding the König deficiency of a zero-reducible graph is an NP-hard problem.
As it is customary in complexity analyses concerning graphs, n and m will stand for the number of vertices and edges in graphs, respectively. If the basis of the reduction is just \(\rightarrow _\mathbf{f}\), then graphs reducible to the empty graph are called zero-leaf-reducible. Leaf reduction by itself can be carried out by a straightforward linear-time (\({\mathcal {O}}(m)\)) algorithm. For a concrete implementation, see Levit and Mandrescu (2016). Thus, zero-leaf-reducibility of graphs is decidable in linear time. Performing line reduction (i.e., obtaining the minimal graph for an input graph G) is a much more complicated issue. A true linear-time algorithm has been worked out for this problem in (Bartha and Krész 2009), building on a single bottom-up pass of a depth-first tree constructed for G. In fact, the algorithm is akin to the so called static tree set union implementation (Gabow and Tarjan 1985) of the well-known union-find problem, where the structure of unions to be performed is known in advance.
Unfortunately, the algorithm in Bartha and Krész (2009) cannot directly be adopted to accommodate leaf reduction. The problem is that, when deleting the vertex adjacent to a leaf, the depth-first tree keeping track of the redex information will fall, and it must be reconstructed. The extra cost incurred is of course intolerable. For this reason, in the present paper we take a completely different approach to implement reduction, even though we firmly believe that the original depth-first algorithm can be fixed somehow to accommodate leaf reduction just by “patching up” the base tree whenever needed. We shall return to this issue shortly.
Our present solution is based on the standard union-find technique by Tarjan (1975) to implement the dynamic union of disjoint sets forming a partition of a given universe set A. For the sake of implementation, A is identified with the set \(\{1,\ldots ,n\}\), and each group S of the current partition is identified by a canonical representant \(i\in S\). Starting from the trivial partition of n groups, one can perform the union of two groups, or find out the (canonical representant of the) group [i] in which a given element i resides. The goal is to keep track of the partitioning information in such a way that the amortized cost of one operation (either union or find) becomes minimal. The concrete description and implementation of different union-find techniques can be found in most undergraduate textbooks on algorithms. The reader is referred e.g. to Sedgewick and Wayne (2011) for a detailed study of this matter.
The fastest way to implement union-find is the so called quick union with path compression method, originally introduced by Tarjan (1975). Groups in the current partition are structured as trees, and the weighted quick-union rule joins the tree of the smaller group to the tree of the larger one as a subtree attached to the root. Path compression means that, whenever a find(i) operation is performed, a pointer is introduced from node i to the root r of the tree that i resides in. Moreover, to speed up subsequent find’s, the pointer to r will be added (and later updated) to each node along the branch from i to r as part of the find(i) operation, which will actually visit these nodes. See Sedgewick and Wayne (2011) for details.
It was shown in Tarjan (1975) that the time required to execute \(m\ge n\) find operations and at most \(n-1\) intermixed unions by this implementation is \({\mathcal {O}}(m\cdot \alpha (m,n))\), where the two-variable function \(\alpha \) (not to be confused with the independence number \(\alpha \)) is related to the functional inverse of the Ackermann function and is very slow growing. The actual definition of \(\alpha \) is complicated (see Tarjan 1975), but the value of \(\alpha (m,n)\) is claimed to remain under 3 for all practical purposes. For this reason, the union-find technique is said to be practically linear-time.
Our idea is to implement the shrinking of a graph G along a redex \(r=(f_1,c,f_2)\) by creating a meta-graph \({\bar{G}}\) having a meta-vertex \(f=\{f_1,f_2\}\), the adjacency list of which is the join of \(f_1\)’s and \(f_2\)’s adjacency lists, excluding the edges between \(f_1\) and \(f_2\). We then proceed iteratively, combining and deleting meta-vertices as the reduction requires. In each step, the meta-vertices of the current meta-graph \({\bar{G}}\) form a partition of V(G), which partition is maintained by union-find. There is one catch, however, which must be avoided. One cannot calculate the exact adjacency list of each newly created meta-vertex, because this would require the full scan of both component adjacency lists to see if there are any edges to be dropped. The cumulative impact of this scan on the overall complexity of the algorithm would of course be fatal. On the other hand, we need to recognize if a meta-vertex becomes a leaf or the center of a redex, that is, its degree becomes 1 or 2. The trick to solve this dilemma is simple. The adjacency lists of the two components of a union will only be joined formally, leaving in the so called “redundant” edges connecting the two focuses, which will be screened out gradually later. We then use a function Check() to perform a smart garbage collection every time a meta-vertex is involved in a reduction step to see if the degree of the meta-vertex has reached 2. The details are as follows.
Algorithm 1. The algorithm maintains a list of meta-leaves Leaves, and a list of meta-redex-centers Redexes. Each vertex on Leaves and Redexes is the canonical representant of the corresponding meta-vertex as a non-empty subset of V(G). As long as either Leaves or Redexes in not empty, the algorithm executes either Step (a) or Step (b), with priority given to Step (a).
Step (a)
- 1.
Take a vertex v from Leaves;
- 2.
For the single vertex u on v’s adjacency list, let \({\bar{u}}=\)find\(\,(u)\), and mark every vertex in \([{\bar{u}}]\) deleted; (Remember that \([{\bar{u}}]\) denotes the group of \({\bar{u}}\).)
- 3.
For every vertex w on \({\bar{u}}\)’s adjacency list do: if w is not marked deleted, then
let \({\bar{w}}=\)find\(\,(w)\);
if \({\bar{w}}\) is on Redexes , then move \({\bar{w}}\) to Leaves ,
else if \({\bar{w}}\) is on Leaves , then remove it from there;
Check\(\,({\bar{w}}\)), and put \({\bar{w}}\) on Leaves or Redexes if Check() returns 1 or 2.
Step (b)
- 1.
Take a vertex c from Redexes;
- 2.
For \(f_1\) and \(f_2\) on c’s adjacency list, let \(\bar{f_1}=\)find\(\,(f_1)\) and \(\bar{f_2}=\)find\(\,(f_2)\);
- 3.
If either \(\bar{f_1}\) or \(\bar{f_2}\) (or both) is on Redexes, then remove it from there; (Note: \(\bar{f_i}\) cannot be on Leaves, because Step (a) has priority over Step (b).)
- 4.
If \(\bar{f_1}=\bar{f_2}\), then c has unnoticeably become ineligible, therefore quit Step (b) without taking any further action;
- 5.
Let \(f=\)union\(\,(\bar{f_1},\bar{f_2})\), and adjust f’s adjacency list by joining \(\bar{f_1}\)’s list to that of \(\bar{f_2}\) or vice versa, depending on the weighted union rule;
- 6.
Mark c deleted; (Note: an ineligible c will not be marked deleted.)
- 7.
Check\(\,(f)\), and put f on Leaves or Redexes if Check() returns 1 or 2.
The description of the function Check() is as follows.
Check(v), vertex v, returns integer;
- 1.
Initialize count:=0;
- 2.
For every vertex u on v’s adjacency list, until count>2 or the list is out, do:
if u is marked deleted or find\((u) =v\), then remove u from the adjacency list of v,
else let count:=count+1;
let u:=next(u) on v’s adjacency list, and repeat 2;
- 3.
If count\(\le 2\), then return count, else return \(-1\).
Analysis of Algorithm 1
Every time it is invoked, the garbage collector method Check() will check if the argument vertex v has become a leaf or redex-center. It does so by identifying some of the redundant edges incident with v. The method scans v’s adjacency list from the beginning and removes every vertex corresponding to a redundant edge until the list is out or more than two non-redundant edges have been found. The number of find operations during the call is therefore at most three greater than the number of redundant edges found. The actual redundancy of an edge will be detected at most once during the algorithm (not from both endpoints, that is), because an edge becomes redundant if one of its endpoints has been deleted or the two endpoints are joined. For this reason, the total number of find operations inside some Check() during the whole algorithm is \(m+3C\), where C is the number of Check() calls.
We claim that \(C\le m\). Indeed, every Check(v) call, either in Step (a) or Step (b), can be associated with the vertex v “losing” one or more degrees, that is, having one or more vertices on v’s adjacency list which has just been deleted. In Step (a3), \({\bar{w}}\) is adjacent to some vertex in \([{\bar{u}}]\) that is being deleted. In Step (b7), f represents the union of \({\bar{f}}_1\) and \({\bar{f}}_2\), each of which is losing a degree by deleting the center c. Consequently, the number of Check() calls cannot exceed m, the number of edges in G. (Mind v’s neighbor that is being deleted, therefore it is losing all of its degrees.)
Other than the find s inside Check(), Step (a) and Step (b) together will perform at most mfind operations in total. Thus, the grand total of find s is at most \(3m+m+m = 5m\), and the total number of union s is at most \(n-1\). Any other cost will clearly remain under the \({\mathcal {O}}(m)\) bound. The overall time complexity of the algorithm is therefore
\(\square \)
Now we return to the question of finding a true linear-time algorithm for reduction. As we have indicated above, the problem is related to the issue of deleting edges from the graph and still being able to maintain a fixed data structure that shows e.g. the cut edges of the graph and/or some other information. This general problem is known in the literature by the name decremental dynamic connectivity. Edges are deleted one-by-one and in the meantime queries are made about the graph being connected or not. It is somewhat more difficult to display the set of cut edges than to show the set of connected components as an answer to a query. Of course, one would hope for an implementation of decremental dynamic connectivity by which the amortized cost of one operation (delete an edge or display the components/cut edges) is constant. Unfortunately, no such implementation exists at present. The best solution for decremental dynamic connectivity uses \({\mathcal {O}}(\log n(\log \log n)^3)\) time (on a pointer machine) for connectivity queries (Thorup 2000) and \({\mathcal {O}}(\log ^4 n)\) time for cut-edge queries (Gabow et al. 2001). Both methods employ search as a fundamental tool.
We believe that an amortized constant-time implementation exists for decremental dynamic connectivity, which solution is structural, rather than search-based. Such a solution would bring the well-known reverse delete minimum spanning tree algorithm in line with Kruskal’s one in the sense that both would require \({\mathcal {O}}(m)\) time only, provided that the set of edges has previously been sorted according to weights. As for now, however, even a \({\mathcal {O}}(\log n)\)-time solution for decremental dynamic connectivity would be a breakthrough result. Other than an efficient implementation for reverse delete, it would also provide an algorithm to decide the UPM property of graphs in \({\mathcal {O}}(m\log n)\) time. Due to Theorem 3, this problem is a special case of decremental dynamic connectivity with cut edge queries, hence the projected \({\mathcal {O}}(m\log n)\) time complexity. Our conjecture is, however, that the UPM decision problem can be tackled by an \({\mathcal {O}}(m)\) algorithm even if general decremental dynamic connectivity fails to be constant-time. The presently fastest algorithm for deciding the UPM property is still the search-based one by Gabow et al. (2001), which uses \({\mathcal {O}}(m\log ^4n)\) time. Needless to say, a structural type constant-time decremental dynamic connectivity implementation would also support a true \({\mathcal {O}}(m)\)-time reduction algorithm to implement our combined leaf-and-line reduction procedure.
5 Computing the König deficiency in zero-reducible graphs
We start out by providing a simple alternative proof of the characterization result obtained by Levit and Mandrescu (2016) on UPM graphs having the König property. In our language, the characterization says that these graphs are exactly the zero-leaf-reducible ones.
Lemma 1
(Levit and Mandrescu 2016, Lemma 4) Every maximum independent set of a non-empty UPM graph G having the König property contains at least one leaf.
Proof
Note that it is implicitly part of the statement that G itself does have a leaf vertex. We prove by induction on the number of vertices in G. If \(|V(G)|=0\), then we have nothing to prove. If G is not empty, then it has a cut edge \(e=(v_1,v_2)\) belonging to its UPM by Theorem 3. We can assume, without loss of generality, that G is connected, so that \(G-\{v_1,v_2\}\) splits up into two uniquely determined disjoint subgraphs \(G_1\) and \(G_2\) the way it is depicted in Fig. 4. In other words, \(G_1+G_2\) is the remainder of G after exploding e. Let S be an arbitrary maximum independent set in G. Then S consists of an independent set \(S_1\) of \(G_1\), an independent set \(S_2\) of \(G_2\), and possibly one of the two vertices \(v_1,v_2\). Since \(k(G)=0\), the König deficiency cannot be positive for \(G_1\) or \(G_2\) either. Indeed, if it was, then the difference between \(\nu \) and \(\alpha \) could not be compensated in G by including only a single extra vertex (namely \(v_1\) or \(v_2\)) in S. Mind that the size of a maximum matching has definitely been incremented by adding the edge e to it. This argument also implies that \(S_1\) and \(S_2\) must be maximum in \(G_1\) and \(G_2\), respectively, and one of \(v_1,v_2\) is in S. Thus, \(G_1\) and \(G_2\) are both UPM graphs having the König property. By the induction hypothesis, both \(S_1\) and \(S_2\) contain at least one leaf (in the respective subgraphs \(G_1\) and \(G_2\), of course). But at least one of these leaves must remain a leaf in G, too, otherwise they would all be adjacent to either \(v_1\) or \(v_2\), meaning that neither \(v_1\) nor \(v_2\) could be in S. The proof is complete. \(\square \)
Corollary 1
(Levit and Mandrescu 2016, Theorem 3) Graph G is zero-leaf-reducible iff it is a UPM graph having the König property.
Proof
We have observed in Proposition 1 that leaf reduction preserves the König deficiency in all graphs. Therefore the corollary follows directly from the implicit statement of Lemma 1 that every non-empty UPM graph having the König property contains at least one leaf vertex. \(\square \)
At this point, even though it is an aside, we take the opportunity to prove a sharper version of Lovász and Plummer (1986, Corollary 5.3.14) on the maximum number of edges in a simple (i.e., no loops or multiple edges) UPM graph.
Theorem 6
If f(n) denotes the maximum number of edges in a simple UPM graph with 2n vertices, then \(f(n)=n^2\). The maximum can only be reached by zero-leaf-reducible graphs.
Proof
As in Lovász and Plummer (1986), we proceed by induction on n. If \(n=0\), then we have nothing to prove. Let G be a UPM graph on 2n vertices (\(n\ge 1\)) having a maximum number of edges. Split G into two disjoint subgraphs \(G_1\) and \(G_2\) along a matching-positive cut edge e as described in the proof of Lemma 1 above. See again Fig. 4. Let \(|V(G_1)|=2n_1\) and \(|V(G_2)|=2n_2\). Then, by definition,
In other words, the maximum value of f is reached by G only if it is reached by both \(G_1\) and \(G_2\), and each vertex in \(G_1\) (\(G_2\)) is adjacent to \(v_1\) (respectively, \(v_2\)). By the induction hypothesis, \(f(n_i)=n_i^2\) (\(i=1,2\)). Observe that the maximum value of the expression \(n_1^2+n_2^2+2(n_1+n_2)+1\) is indeed
which is reached only if either \(n_1=0\) or \(n_2=0\). Thus G, being leaf-reducible to either \(G_1\) or \(G_2\), is zero-leaf-reducible by the induction hypothesis. The proof is complete. \(\square \)
Encouraged by Corollary 1, one would expect a similar characterization of all zero-reducible graphs in terms of a tangible connection between \(\tau \) and \(\nu \). A plausible candidate is articulated in the following conjecture.
Conjecture 1
Let G be a graph having a perfect matching. Then G is zero-reducible iff it can be turned into a UPM graph having the König property by deleting exactly k(G) forbidden edges in an appropriate way.
Recall that a forbidden edge of G is one that is not part of any maximum matching in G. In case of a UPM graph, these are the edges not belonging to the UPM of G.
Example 2
Consider the zero-reducible graph G in Fig. 5a, and observe that \(k(G)=1\). Indeed, \(\nu (G)=5\), but one can only cover 4 matching-positive edges by independent vertices. Yet, it is impossible to delete a single forbidden edge from G to bring k(G) down to 0.
Example 3
Now let G be the graph in Fig. 5b. Clearly, \(\nu (G)=7\) and \(\alpha (G)=4\), so that \(k(G)=3\). By deleting the forbidden edges \(e_i\) (\(i=1,2,3\)), G will have the König property. Yet, one can only reduce G to the multigraph shown in Fig. 5c.
Examples 2 and 3 show that Conjecture 1 fails in both directions. The failure of the conjecture implies that it is not possible to calculate k(G) for a zero-reducible graph G with the following simple greedy algorithm, which appears to be justified by the fact that leaf reduction preserves the König deficiency.
- 1.
Do leaf reduction on G as long as possible; if G is empty, goto step 3.
- 2.
Delete a forbidden edge from G and return to step 1.
- 3.
The number of deleted forbidden edges in step 2 is k(G).
Even if we knew the “appropriate” way to delete edges in step 2, the algorithm would still not work. It gives a wrong answer for G in Example 2, the right one for G in Example 3, but that graph is not zero-reducible.
The irreducibility of the graph G in Fig. 5c raises the following question. Why don’t we disregard the multiplicity of edges during reduction? If we did, our graph in Fig. 5c would be zero-reducible. The reason is to preserve the UPM property during reverse reduction, which could be lost by simply forgetting the multiplicity of edges. (Luckily not in the concrete example graph G, which is UPM to begin with.) Nevertheless, in the end we could still check if the UPM property was lost by de facto reversing the steps of the reduction in practically the same amount of time. This issue is therefore mainly theoretical.
Now we are ready to prove the main result of this section on the intractability of computing k(G) for a zero-reducible graph G.
Theorem 7
Computing k(G) for a zero-reducible graph G is NP-hard, with the corresponding language problem being NP-complete.
Proof
The proof is a reduction from Independent Set. Let G be an arbitrary connected graph. Perform the following transformation steps on G to obtain graph \(G'\).
- 1.
Starting from an arbitrary vertex v as the root, construct a depth-first tree for G.
- 2.
Duplicate every tree edge of G, and drop a subdividing vertex on one of the copies. Furthermore, add a new vertex u to G, together with a “handle” edge \(e=(u,v)\) to the root v.
- 3.
For each newly introduced subdividing vertex w, attach a new triangle to G incident with w. Do the same attachment for the vertex u as well. The resulting graph is \(G'\).
The graph G (left) and the resulting graph \(G'\) (right) of the reduction from Theorem 7
See Fig. 6 for the transformation G–\(> G'\) on a simple example graph G. Dashed lines in the figure identify edges belonging to the depth-first tree. The following three statements should be clear.
- (A):
The graph \(G'\) is zero-reducible, as it is line-reducible to the single edge e.
- (B):
The transformation G–\(> G'\) can be carried out in linear time.
- (C):
\(\alpha (G')=\alpha (G)+ |V(G)|\).
To explain (C), observe that the matching-positive edge of each triangle can be satisfied (i.e., covered) by an independent vertex on either endpoint. Since the total number of triangles is |V(G)| (mind the one incident with u), we have |V(G)| independent vertices in \(G'\) so far. The number of additional independent vertices in \(G'\) is exactly \(\alpha (G)\), since the subdividing vertices are no longer available, and the independent vertices satisfying the triangles cannot be traded in for the sake of collecting more independent vertices in \(G'\) as a whole. See again Fig. 6.
In this way we have found a linear-time (computational) reduction of the general problem of computing \(\alpha (G)\) for an arbitrary (connected) graph G to our problem of computing \(k(G')\) for a zero-reducible graph \(G'\). We have \(\nu (G')=2|V(G)|\) and \(k(G')=\nu (G')-\alpha (G')\), so that
Thus, \(\alpha (G)\) is directly computable from \(k(G')\) once the latter is found. The proof is now complete, knowing that \(\alpha (G)\) is NP-hard to compute. Obviously, the language problem of computing the König deficiency is in NP. \(\square \)
Judging by the simplicity of the above proof, the reader might have the impression that the statement of Theorem 7 is trivial. In order to see how much it is not, consider the following corollary, which would be very difficult to handle in the absence of this theorem.
Corollary 2
Given a graph G and a redex r in G, it is NP-complete to decide if contracting r in G decrements the König deficiency.
Proof
Indeed, by Proposition 2, if \(G\rightarrow _\mathbf{l}G'\) by contracting r, then
Therefore, if e.g. G happens to be line-reducible to a single edge, then its König deficiency can be decremented at most \(|V(G)|/2\) times during reduction. In the light of Theorem 7 this implies immediately that the decision if one reduction step decreases the König deficiency must already be NP-complete. (The problem is obviously in NP.) \(\square \)
6 Characterizing the almost UPM and/or König property
One can find two different definitions in the literature for a graph G to almost have the König property. The obvious one (Levit and Mandrescu 2012) is simply equivalent to the condition \(k(G)=1\). The second definition (Larson and Pepper 2011) postulates that, while G itself does not have the König property, there exists a vertex \(v\in V(G)\) for which \(G-v\) does. It is evident that the classes of graphs satisfying these two definitions are not comparable. Combining the “almost” distinction with the König and/or UPM properties, one obtains the following potential meaningful definitions. For brevity, K will stand for the König property from this point on, just like UPM abbreviates the property of having a unique perfect matching.
Definition 3
An almost K UPM graph is a UPM graph G with \(k(G)=1\).
Definition 4
An almost K and UPM graph is a graph G that is not K or not UPM, but there exists a vertex \(v\in V(G)\) such that \(G-v\) is both K and UPM.
Since the term “almost K and UPM” is rather ambiguous, especially in the context of Definition 3, it needs further clarification. Definition 4 is about a graph G that is definitely not UPM (mind that G and \(G-v\) cannot both be UPM), \(G-v\) is K, while G itself may or may not be K. In other words, G is almost UPM with respect to some \(v\in V(G)\) (i.e., UPM disregarding v) such that \(G-v\) has the König property. To emphasize this meaning, graphs satisfying Definition 4 will rather be referred to as almost K&UPM graphs. Similarly, almost K UPM graphs will be explicitly called (K-1) UPM. In the same vein we define (K-n) UPM graphs as UPM graphs with König deficiency n, and almost (K-n)&UPM graphs as almost UPM graphs G with respect to some vertex \(v\in V(G)\) such that \(G-v\) has König deficiency n. Notice that, e.g. a (K-1) and almost UPM graph can be either almost K&UPM or almost (K-1)&UPM (but not both, of course).
As a further notational convenience, we identify an almost UPM graph as a pointed graph (G, v), indicating the vertex \(v\in V(G)\) for which \(G-v\) is UPM as the designated point in G. The point v will, however, often be omitted from this couple if it is understood or irrelevant. Clearly, the point v in an almost UPM graph G need not be unique, but in general it cannot be arbitrary either.
Our goal is to characterize (K-1) UPM graphs and almost K&UPM graphs in terms of suitable reductions. To understand the connection between these two classes of graphs, let \((G_1,v_1)\) and \((G_2,v_2)\) be two almost UPM graphs with designated points \(v_1\) and \(v_2\), and construct the UPM graph G by taking the disjoint union of \(G_1\) and \(G_2\) and connecting \(v_1\) with \(v_2\) by a (matching-) positive cut edge.
If G is K, then of course both \(G_1-v_1\) and \(G_2-v_2\) must be K and UPM. (Remember the proof of Lemma 1.) Therefore \(G_i\) (\(i=1,2\)) is almost K&UPM. Conversely, if \(G_1-v_1\) and \(G_2-v_2\) are K, then G is either K or K-1, depending on whether one of \(v_1\) or \(v_2\) could be “squeezed in” as a further independent vertex in the union \(S_1\cup S_2\) of appropriate maximum independent sets \(S_i\) of \(G_i\) (\(i=1,2\)).
If G is K-1, then the following cases are possible.
Case A: \(G_1\) (i.e., \((G_1,v_1\))) is K and almost K&UPM, while \(G_2\) is almost (K-1)&UPM.
Case B: both \(G_1\) and \(G_2\) are K-1 and almost K&UPM.
Case C: \(G_1\) is K-1 and almost K&UPM, while \(G_2\) is K-1 and almost (K-1)&UPM.
See Fig. 7 for a graphical summary of these cases. In the figure, circles identify mandatory independent vertices, ones that must be present in every maximum independent set of G. A dashed circle means that the vertex may or may not be mandatory independent in the respective half of the graph, but when it is, it will be lost during the overall count.
An immediate conclusion of the analysis above is that every simple (K-1) UPM graph G has at least one subdividing or leaf vertex. Indeed, by Lemma 1, every K UPM graph, as “one half” \(G_1\) or \(G_2\) of G, has a leaf v, which might turn into a subdividing vertex when connecting it to either \(v_1\) or \(v_2\) according to the decomposition by Fig. 7. By the same token, every almost K&UPM graph, too, has a subdividing or leaf vertex. Along these lines, the characterization of almost K&UPM graphs in terms of reduction is the key to the characterization of (K-1) UPM graphs, which then leads to a linear-time decision algorithm for these graphs. Moving on, we hope to have a similar characterization for (K-2) UPM graphs through a characterization of almost (K-1)&UPM graphs, so we could decide the (K-2) UPM property as well in linear time. Unfortunately one cannot continue this line of reasoning for (K-3) UPM graphs, since these graphs do not necessarily have a subdividing vertex or leaf. See Fig. 8 for the smallest UPM graph with no multiple edges that is free from subdividing vertices and leaves, and verify that \(k(G)=3\), indeed. Nevertheless, a case-by-case analysis according to the decomposition outlined in Fig. 7 can be carried out for all UPM graphs relating to their König deficiency. Such an analysis suggests an inductive method to calculate k(G) for an arbitrary UPM graph G. We know by Theorem 7, however, that this method is not likely to result in an exact polynomial-time algorithm.
In the present study we deal with the characterization of K and almost UPM graphs only, leaving the rest of the work to a forthcoming paper. Clearly, if (G, v) is such a graph, then v must be mandatory independent. Moreover, \(G-v\) is still K. See Fig. 7A, top half.
Lemma 2
Let (G, v) be a pointed graph and \(u\in V(G)\) be a leaf such that \(u\ne v\). If \(G\rightarrow _\mathbf{f}G'\) through eliminating the leaf u, then (G, v) is almost UPM iff \((u,v)\not \in E(G)\) and \((G',v)\) is almost UPM.
Proof
Let \((u,w)\in E(G)\) be the pendant edge to be exploded. Then \(G-v\) is UPM iff \(G-v-u-w\) is UPM, provided that \(v\ne w\). On the other hand, \(v=w\) is impossible if \(G-v\) is UPM. \(\square \)
Corollary 3
If \(G\rightarrow _\mathbf{f}G'\), then G is almost UPM (with respect to some vertex) iff \(G'\) is almost UPM (with respect to a possibly different vertex).
Proof
Let \(G'=G-u-w\) for some leaf vertex u with pendant edge (u, w). First assume that (G, v) is almost UPM. If \(u\ne v\), then \((G',v)\) is almost UPM by Lemma 2. If \(u=v\), then consider the unique positive edge \((w,z)\in E(G)\) and verify that \(G-u-w-z\) is UPM, that is, \((G',z)\) is almost UPM. Conversely, let \((G',z)\) be almost UPM for some vertex z. Then \(z\ne u\) and \(z\ne w\), so that (G, z) is almost UPM again by Lemma 2. \(\square \)
Theorem 8
Graph G is K and almost UPM iff G is leaf-reducible to a single isolated vertex.
Proof
By Proposition 1 and Theorem 3 it is sufficient to prove that every K and almost UPM graph (G, v) different from the single isolated vertex v has a leaf. This is obvious, however, since \(G-v\) is still K, therefore it possesses a leaf vertex in each of its maximum independent sets by Lemma 1. Consequently, not all of \((G-v)\)’s leaves can be blocked by an edge starting from vertex v, which is mandatory independent in G. \(\square \)
Notice that the leaf vertex presented in the above proof is different from v. Therefore we also have a simple reduction algorithm to decide if a pointed graph (G, v) is K and almost UPM (with respect to v, that is). In other words, we have the following corollary.
Corollary 4
Graph (G, v) is K and almost UPM iff it is leaf-reducible to the point v.
Using Theorem 8 and Corollary 4 one can easily decide in linear time if a graph G (pointed graph (G, v)) is K and almost UPM. It is still an interesting open question, however, if one can design a linear-time algorithm to find the set of all points v for which a graph (G, v) is K and almost UPM.
7 Conclusion
Motivated by the characterization (Levit and Mandrescu 2016) of UPM graphs having the König property, we have introduced a confluent and terminating reduction system on graphs, and shown that this reduction can be carried out in practically linear time. As a consequence, zero-reducible graphs, forming a substantial subclass of UPM graphs, are decidable in linear time. We have also given a necessary and sufficient condition for the König property to be preserved in one inverse reduction step. As a negative result, we have proved that the problem of finding the König deficiency of a zero-reducible graph is NP-complete. Finally, we have generalized the Levit and Mandrescu type characterization to almost UPM graphs having the König property.
References
Bartha M, Krész M (2006) Deterministic soliton graphs. Informatica 30:281–288
Bartha M, Krész M (2009) A depth-first algorithm to reduce graphs in linear time. In: Proceedings of the 11th international symposium on symbolic and numeric algorithms for scientific computing, Timisoara, Romania. IEEE Computer Society, pp 273–281
Bartha M, Krész M (2010) Efficient unique perfect matching algorithms. In: Proceedings of the 8th joint conference on mathematics and computer science, Komárno, Slovakia
Dershowitz N, Jouannaud J-P (1990) Rewrite systems. In: van Leeuwen J (ed) Handbook of theoretical computer science, vol B: formal models and semantics. Elsevier, Amsterdam, pp 245–320
Edmonds J (1965) Paths, trees and flowers. Can J Math 17:449–467
Gabow HN, Tarjan RE (1985) A linear-time algorithm for a special case of disjoint set union. J Comput Syst Sci 30:209–221
Gabow HN, Kaplan H, Tarjan RE (2001) Unique maximum matching algorithms. J Algorithms 40:159–183
Gallai T (1963) Neuer Beweis eines Tutte-schen Satzes. Magyar Tud Akad Mat Kutató Int Közl 8:135–139
Gallai T (1964) Maximale Systeme unabhängiger Kanten. Magyar Tud Akad Mat Kutató Int Közl 9:401–413
Korenwein V, Nichterlein A, Niedermeier R, Zschoche P (2018) Data reduction for maximum matching on real-world graphs: theory and experiments. In: Proceedings of the 26th annual European symposium on algorithms (ESA 2018), pp 53:1–53:13
Kotzig A (1959) On the theory of finite graphs with a linear factor II. Mat-Fyz Casopis Slovensk Akad Vied 9:136–159 (in Slovak)
Larson CE, Pepper R (2011) Graphs with equal independence and annihilation numbers. Electron J Comb 18:180
Levit VE, Mandrescu E (2012) Independent sets in almost Konig–Egervary graphs. In: Abstracts of the SIAM conference on discrete mathematics, Halifax, Canada, p 40, abstract MS21
Levit VE, Mandrescu E (2016) Computing unique maximum matchings in ${{\cal{O}}} (m)$ time for König–Egerváry graphs and unicyclic graphs. J Comb Optim 32:267–277
Lovász L, Plummer MD (1986) Matching theory. North Holland, Amsterdam
Sedgewick R, Wayne K (2011) Algorithms. Addison-Wesley, Boston
Tarjan RE (1975) Efficiency of a good but not linear set union algorithm. J Assoc Comput Mach 22:215–225
Thorup M (2000) Near-optimal fully-dynamic graph connectivity. In: Proceedings of the 32nd annual ACM symposium on the theory of computing ACM digital library, pp 343–350
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The second author acknowledges the European Commission for funding the InnoRenew CoE project (Grant Agreement #739574) under the Horizon2020 Widespread-Teaming program and the Republic of Slovenia (Investment funding of the Republic of Slovenia and the European Union of the European regional Development Fund). Miklós Krész is also grateful for the support of the EU-funded Hungarian grant EFOP-3.6.2-16-2017-00015 and the Slovenian ARRS grant J1-9110.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bartha, M., Krész, M. On the König deficiency of zero-reducible graphs. J Comb Optim 39, 273–292 (2020). https://doi.org/10.1007/s10878-019-00466-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-019-00466-2