Solving the maximum vertex weight clique problem via binary quadratic programming

Abstract

In recent years, the general binary quadratic programming (BQP) model has been widely applied to solve a number of combinatorial optimization problems. In this paper, we recast the maximum vertex weight clique problem (MVWCP) into this model which is then solved by a probabilistic tabu search algorithm designed for the BQP. Experimental results on 80 challenging DIMACS-W and 40 BHOSLIB-W benchmark instances demonstrate that this general approach is viable for solving the MVWCP problem.

Appendix

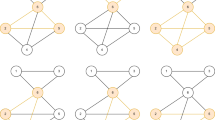
To illustrate the transformation from the MVWCP to the BQP, we consider the following graph (see Fig. 1):

Fig. 1

A graph sample

Its linear formulation according to Eq. (1) is:

$$\begin{aligned} \begin{aligned} Max \ \ f(x)=2x_{1}+3x_{2}+4x_{3}+5x_{4}+2x_{5}+3x_{6} \\ \text {s.t.}\ \ \ \ x_1+x_3 \le 1;\ \ \ \ \ \ \ \ \ \ x_1+x_4 \le 1; \\ x_1+x_6 \le 1;\ \ \ \ \ \ \ \ \ \ x_2+x_4 \le 1;\\ x_2+x_6 \le 1;\ \ \ \ \ \ \ \ \ \ x_3+x_5 \le 1;\\ x_3+x_6 \le 1;\ \ \ \ \ \ \ \ \ \ x_5+x_6 \le 1. \end{aligned} \end{aligned}$$

(6)

Choosing the scalar penalty $P=-15$, we obtain the following BQP model:

$$\begin{aligned} Max\quad f(x)= & {} 2x_{1}+3x_{2}+4x_{3}+5x_{4}+2x_{5}+3x_{6}-30x_{1}x_{3}-30x_{1}x_{4}\nonumber \\&-30x_{1}x_{6}-30x_{2}x_{4}-30x_{2}x_{6}-30x_{3}x_{5}-30x_{3}x_{6}-30x_{5}x_{6} \end{aligned}$$

(7)

which can be re-written as:

$$\begin{aligned} \left( \begin{array}{c} x_1\ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \end{array}\right) \times \left( \begin{array}{cccccc} 2 &{}0 &{}-15 &{}-15 &{}0 &{}-15 \\ 0 &{}3 &{}0 &{}-15 &{}0 &{}-15 \\ -15 &{}0 &{}4 &{}0 &{}-15 &{}-15 \\ -15 &{}-15 &{}0 &{}5 &{}0 &{}0 \\ 0 &{}0 &{}-15 &{}0 &{}2 &{}-15 \\ -15 &{}-15 &{}-15 &{}0 &{}-15&{}3 \\ \end{array}\right) \times \left( \begin{array}{c} x_1 \\ x_2\\ x_3\\ x_4\\ x_5\\ x_6 \\ \end{array}\right) \end{aligned}$$

(8)

Solving this BQP problem yields $x_3=x_4=1$ (all other variables equal zero) and the optimal objective function value is 9.