Abstract
A condensed excited matter called Rydberg Matter (RM) have been studied experimentally for 30 years, but have not sparked widespread attention yet, unlike ordinary Rydberg atoms. RM formed by clusters of Rydberg atoms at a solid surface have a longer lifetime compared to Rydberg atoms, and is liquid-like. This review describes how the RM state is generated, and its potential applications. These include using RM for research into catalysis, space phenomena and sensor applications, or for producing environmentally friendly energy. A background on RM is presented, with its structure and special properties, and the working principle of RM generation. The experimental set-ups, materials, and detectors used are discussed, together with methods to improve the amount of RM produced. The materials used for the catalysts are of special interest, as this should have a large influence on the energy of the RM, and therefore also on the applications. Currently most of the catalysts used are potassium doped iron oxide designed for styrene production, which should give the possibility of improvements. And as there is little knowledge on the exact mechanisms for RM formation, suggestions are given as to where research should start.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The world is still looking for new ways of producing clean energy, as it has been a long time since a truly new method have been developed. The current renewable energy sources are also mostly intermittent, only delivering energy when the conditions are right, so there is a need for green energy that can be turned on when required. For example, the “hydrogen society” has been developing for decades, but there still is not an environmentally friendly way of producing hydrogen that can rival natural gas on price. The usage of hydrogen would also benefit from an improved efficiency, and this is the concern of this review, describing how a condensed excited state of hydrogen atoms can improve efficiency for energy generation and enable multiple other applications. It should be of special interest to anyone researching hydrogen energy production.
Rydberg state is a general term applied to atoms and molecules with a high principal quantum number n, where atoms with n up to 1000 have been detected [1]. This large n gives them their main properties of large sizes, high sensitivity to electric fields, large dipole moments, and very low ionization potentials [2]. These Rydberg atoms can also form a condensed state, called Rydberg Matter (RM). Keeping the characteristic properties of the atoms, while having a longer lifetime and being liquid-like gives some interesting possibilities. These possibilities are getting closer to being realized, and in the coming years RM could have a drastic increase in how well it is known. For example, RM is currently generated using a potassium doped iron oxide catalyst, similar to the ones used for dehydrogenation of ethylbenzene to styrene. So, the research into RM could also give insight as to why alkali metals are such good promoters. And this could be applicable to the iron catalysts used in Fischer–Tropsch and ammonia synthesis also, as Rydberg species have been detected from ammonia catalysts [3,4,5], leading to a very large potential impact on both economy and environment.
The reason for writing this review now is that there are more applications, shown in Fig. 1, being developed that utilize RM, and these applications demand higher quantities of RM than what is needed for research. One of which is the clean energy generated by only using hydrogen as a fuel. Previous reviews on RM have focused on the properties of the clusters that make up RM [6], and on the conditions for forming RM in a gas phase versus on a surface [7]. And a special issue called "Rydberg-Matter and Excited-State Clusters" have also been publish in the field [8]. This review presents what is known, and the information that is needed, about how RM is produced, some of its possible applications, and how close they are to realization.
Theory
Rydberg Background
Rydberg atoms are named after Johannes Rydberg, a Swedish physicist who found the generalized formula relating the spectral lines of an element to each other, which are the specific wavelengths emitted by an element when introduced into a flame. He also realized that the constant used in the formula was universal for all the elements. The constant was named after him, in addition to the atoms in states of high principal quantum number n, Rydberg atoms [9]. Rydberg’s formula can be given as
where En is the energy in eV of the nth level of hydrogen, h is the Planck constant, c is the speed of light in vacuum, and R∞ is the Rydberg constant in wavenumbers. Highly-excited electronic states with an electron (on average) far from the nucleus, can be considered similar to a hydrogen atom, and the formula can be modified to be used on atoms with specifically ordered series of energy levels [1]. These Rydberg atoms have valence electrons with binding energies that decrease with 1/n2, and an orbital radius that increase with n2, leading to exaggerated properties like relatively long lifetime and high sensitivity to electric fields [2]. Due to these properties, the atoms have for example been used in spectroscopy to find the ionization potential of iron period metals [10], and for research on quantum computing [11], photon collisions [12], and sensor applications [1].
In the early 1980′s a theory for the condensation of excited atoms was developed by Manykin et al. [13], and it was predicted to be energetically favored over single excited atoms, with a longer lifetime and delocalized electrons. This was found experimentally around 1990 by Holmlid et al. and named Rydberg Matter (RM), due to the connection to Rydberg atoms [14]. Work has also been done on theoretical estimations of RM using a pseudopotential approach with density functional theory [15]. This was done by modelling the excited atoms as pseudo-atoms in the ground state, and the results compared to experimental data.
The pseudopotential model was further used to describe the thermodynamics and correlation function of the ultracold Rydberg plasma, including the calculations of electron–electron, ion-ion, and electron–ion interaction [16]. The study was done on laser-cooled xenon atoms, where two-photon ionization was used to first excite, and then ionize some of the atoms. The plasma considered is strongly nonideal, where the mean particle potential energy divided by the kinetic energy is significantly larger than unity. The results indicate formation of a short-range order for particles of equal and opposite signs, increasing with nonideality.
Theoretical work has also been done on the kinetic processes in a ultracold nonideal Rydberg plasma, allowing all stages of generation and decay to be traced [17], with further in-depth summary and work on the thermodynamics and kinetic properties [18]. The papers develop a kinetic model to describe the nonideal plasma, and discusses the structural short- and long-range orders, recombination coefficient and the nonideality parameter. The theoretical work was then considered versus experimental results. Simulations also indicate that in the strong nonideality region, the recombination coefficient is several orders of magnitude smaller than in the weakly nonideal region.
Condensed excited state is a broader term than RM, with the condensation of excitons in semiconductors as an example. It was studied with an emphasis on cesium atoms, and the abnormally long recombination time [19]. The lifetime was linked to the large distance in space between initial and final states of valence electrons, and the broad potential barrier that can be formed between them. The mechanisms of decay and their probability was discussed, including intrinsic (radiative and radiationless), and admixture recombination. The latter was exemplified with excited electron capture by an electronegative molecule.
RM is considered as a generalized metallic form with delocalized electrons, forming mostly planar clusters due to the planar shape of the high n atoms. It is metastable in its excited form, having a longer lifetime than other excited states, and the lifetime increases with excitation level. The interionic bond length d, in pm, is determined by the angular momentum l according to
where a0 is the Bohr radius of 52.9 pm. This gives hydrogen RM an interionic bond length of 150 pm in l = 1 [20]. Valence electrons in a circular orbit have the maximum angular momentum, meaning l = n—1 for l > 0. The lowest energy (l value) the valence electrons can have, depends on the inner electrons. For H this is l = 1, while for K this is l = 4, due to the filled shells [21]. The energy of the l values 1–3 are shown in Fig. 2d for hydrogen, compared to two ground state hydrogen atoms. The H–H distance is larger for RM when considering just two atoms, though more than two atoms are usually found with the same distance in a RM cluster, while the H2-H2 distance is greater than 74 pm.

Adapted from Phase transition temperatures of 405–725 K in superfluid ultra-dense hydrogen clusters on metal surfaces, [23], by Leif Holmlid and Bernhard Kotzias, used under CC BY 4.0
a Planar 37 atom cluster. b Octahedral cluster fragment. c Stack of 7-atom planar clusters. d The relationship between energy and interatomic distance for normal H2 and hydrogen RM at energy levels l = 1–3.
The clusters are usually six-fold symmetrical with 7, 19, 37 (Fig. 2a), 61 or 91 atoms, where all the atoms are in the same excitation level. These clusters are proposed to be able to form stacks, with a 7-cluster stack shown in Fig. 2c. The stacks would be easier for smaller clusters to form, due to the larger distance the outer atoms in larger clusters experience, at the same angle of approach [6]. Smaller clusters have also been detected, with 3D shapes like tetragonal, octahedral (Fig. 2b) or icosahedron without the center atom. These form for low l atoms, as for higher l the atom structure is more planar [22]. The large bond distances and the delocalized electrons are suspected to give rise to a large magnetic dipole and an enormous polarizability. RM also has a very narrow range in radio frequency that it can emit and accept radiative energy in, leading it to emitting more energy than receiving until equilibrium is reached. This can be as low as a few degrees Kelvin even when the surroundings are room temperature [6].
The production of RM starts with the thermal emission of ions from a surface and the recombination with a thermal electron. The large size of the Rydberg species gives them long range interactions with the surface, and as they condense to clusters the interaction with the surface decreases, making it easier for the clusters to desorb [24].
Alkali metals are thought to be the easiest to use for making RM, most likely because they have the lowest work function of all the elements, where the work function is the minimum work that must be done to remove an electron from the surface to vacuum at 0 K [25]. It is also unsurprising that an easily ionizable species like RM covering another surface will drastically reduce the work function, useful for example in thermionic energy converters (TICs) [26], which convert thermal to electric energy. Testing was also done on the TIC by Yarygin et al., who observed similarities like the very low work function, and distinctions like the discharge pulse repetition rate [27]. A review on the field is also provided [28], discussing and comparing the TIC efficiency, set-ups and results.
RM can also incorporate impurities into its structure by the way of physisorption or chemisorption [29]. Molecules that are electronegative are shown to exhibit chemisorption, and they will bind valence electrons from the RM, eventually disintegrating the RM cluster at high impurity concentrations. Molecules that have no affinity to electrons are trapped by the van der Waals attraction, which is long range due to the high polarizability of the RM. Here, the chemical identity of RM remains intact, leading to clusters that can accommodate more impurity molecules than there are excited atoms making up the cluster. It is suggested that this can be used to detect the presence of RM, as it leads to a pressure drop, or to maintain high vacuum conditions, removing molecules from the gas phase.
There are also other kinds of Rydberg molecules called heavy Rydberg states and Rydberg clusters. The heavy Rydberg states consist of a positive and a negative ion bound by a Coulomb potential [30]. The same physical laws apply as for the electronic Rydberg states, with the use of mass-scaling, and the large mass leads to easier probing due to slower temporal dynamics. This means that a H+H− system can be described as a hydrogen atom with a H−-ion replacing the electron. These systems could be interesting for storage of quantum information. The replacement of the electron also widens the energy range the heavy Rydberg system can have, compared to the electronic Rydberg states, because of the larger mass [31]. The Rydberg clusters are a pair of oppositely charged atomic clusters with arbitrarily high quantum numbers [32]. The clusters can have a large variety of mass and charge, and a size expected to give in essence classical motion, in addition to being stable compared to Rydberg atoms.
Theory and Working Principle of RM Production
For many chemical reactions, the use of a catalyst can significantly increase the yield and selectivity by creating an alternative pathway for the reaction. For RM, the catalyst works differently. It must be able to remove the condensation energy released, as this energy might remove electrons from the RM and stop the condensation. And it also increases the Rydberg atom density on the surface compared to in the gas phase, increasing the probability that condensation starts [7]. An example of the catalysts currently used for producing RM is shown in Fig. 3a, with a SEM picture of the same kind of catalyst shown in Fig. 3b.
a Photograph of the type of commercial potassium doped iron oxide catalyst that is currently being used for RM production. b SEM picture of the surface of the same commercial catalyst at 15 kV and 3500x. c The reaction steps for forming hydrogen RM on a catalyst surface. (1) The chemisorption of hydrogen gas. (2) Desorption of potassium atoms, ions, and Rydberg atoms. (3) Transfer of energy from potassium to hydrogen atoms. (4) Formation of hydrogen RM
For a catalyst to produce a significant amount of RM, there are several steps that need to be met. First, the atoms and ions desorbing from the heated surface, usually alkali metals, should be Rydberg states, which are then bound close to the surface. At the same time, the catalyst must chemisorb hydrogen gas molecules on the surface. The hydrogen and potassium atoms moving close to the surface can collide and transfer energy from potassium to hydrogen, after which the hydrogen Rydberg atoms can form clusters and RM. A transfer of energy have been proven with collisions between hydrogen Rydberg atoms and deuterium molecules as H* + D2 → HD + D* [33], and a similar transfer should be possible with K* and H. These are the suspected reactions steps, as shown in Fig. 3c, but other mechanisms like potassium Rydberg cluster formation are also possible [20].
When producing RM, a potassium doped iron oxide catalyst is often used. It was developed for industrial production reactions and is studied extensively due to its complexity and usefulness [34,35,36]. For these kinds of catalysts a flux of highly excited potassium Rydberg species have been proven by field ionization method, and this flux corresponded to the catalyst activity [37]. In the sense that the used catalyst had a lower catalytic activity and flux of Rydberg species than the fresh catalyst, even though the total potassium flux was larger for the used catalyst.
The differences from the process of styrene manufacturing are the temperature, pressure and feed gases used. Styrene production uses a temperature of around 850–900 K and 0.1–1.0 bar, with the feed gases being ethylbenzene and steam [34, 38]. This is in contrast to the RM production usually using < 600 K and vacuum conditions, with only hydrogen as the feed gas [39]. In addition, there is some difference between the C-H bonds in ethylbenzene and the bond in H2. This will lead to other demands on the catalyst for RM production than for styrene.
Any catalyst used to produce Rydberg atoms is very dependent on the desorption barrier of the alkali metal, as it controls the desorption flux of atoms, ions and excited states, and what energy the Rydberg atoms will have. There has been much work published on the stabilizers for the potassium iron oxide catalysts and how they affect the desorption barrier [37, 40], and probably much unpublished work also, due to the commercial interest in these catalysts.
The commercial catalyst for styrene production has an active phase that is an equilibrium between KFeO2 and K2Fe22O34, and the effect of doping on the thermal stability of the two phases is large [41]. For the K2Fe22O34 phase, the dopants (Mg, Al, Cr, Mn and Ce) increase the activation barrier for desorption and reduce the flux, while for KFeO2 the same dopants reduce the activation barrier and increase the flux, as seen for the atomic flux in Fig. 4, which shows how large an impact the stabilizers potentially can have for RM production. This is reflected in the change in activation energy of potassium atoms and ions with doping shown in Fig. 5. The effect of Cr3+ substitution for Fe3+ was a stabilization of the potassium in K2Fe22O34, due to blocking of the potassium diffusion pathway in the bulk, that could also be possible with other di- and trivalent ions (Mn2+, Mg2+ and Al3+). The excitation energy for K in the lowest Rydberg-like state (n = 4) has been found to be 3.5 eV, which is close to some of the activation energies for desorption seen in Fig. 5 [20].
Temperature programmed desorption for atomic potassium for a K2Fe22O34 and b KFeO2, undoped and doped with 2% Cr, Mn, Mg, Al, and Ce [41]. Reprinted from Journal of Catalysis, 247, Andrzej Kotorba, Weronika Rożek Irmina Serafin Zbigniew Sojka, Reverse effect of doping on stability of principal components of styrene catalyst- KFeO2 and K2Fe22O34, 238–244, Copyright (2007), with permission from Elsevier
Another catalyst that have been tested was a commercial vanadium oxide catalyst doped with both potassium and cesium, which found the activation barrier for desorption for both elements, while also detecting excited states [42]. Results indicate a slower loss of Cs, even though it was expected otherwise due to the higher vapor pressure of Cs. The barriers found are shown in Fig. 5, where the barrier for Cs is equal to the ionization potential and may indicate that the emission of Cs is as highly excited states with energies close to the ionization limit.
As the addition of alkali metals are so important for several catalytic processes, efforts have been made to discover the mechanism. The effect of the potassium bonding on the surface has been investigated using two phases known to exist on the surface [37]. The activation barrier for desorption is dependent on the strength of the surface bond for the potassium atom. It was found that an ionic bond to the surface, in this case with a desorption barrier for K at 1.76 eV for KAlO2, would not produce any potassium Rydberg atoms. While KFeO2 with a stronger covalent bond of 2.84 eV, would produce Rydberg atoms. This was then correlated to the catalyst activity, which was much higher for KFeO2.
Since the polarizability of Rydberg atoms are so large, increasing rapidly with n due to the dependency on the volume of the electron cloud, the interaction potential between a surface and an atom is also large [44]. This leads to long-range bonding between the Rydberg atoms and the surface that makes long jumps along the surface possible, expected to be up to at least 0.3 mm for a potassium Rydberg state at n = 40. And as might be expected this can give very large diffusion rates.
The large sizes and the closely spaced energy levels of the Rydberg atoms can also enable the formation of complexes from the collision of molecules, which would usually break apart shortly after the collision for ground state atoms [24]. This is due to the short time it takes for the ground state complex to break up, because the excitation energy cannot be removed fast enough. Meaning the lifetime of the ground state complex is shorter than the typical time it takes for IR radiation of the excess energy, stopping a stable complex from forming. For a collision including a Rydberg molecule, some of the excess energy can be transferred to the Rydberg electron, increasing the sticking probability. One example of these collisions is shown in Fig. 6a, where a potassium beam was directed at a surface with desorbing potassium Rydberg clusters, with peaks corresponding to the new cluster mass and direction.
a Potassium beam colliding with, and sticking to Rydberg clusters desorbing at a normal direction from the zirconia surface, leading to peaks corresponding to the new cluster mass and direction [21]. b Variation of excited states with sample voltage at an angle of 16° for the same zirconia surface. a and b reproduced from [24], with the permission of AIP Publishing. c Potassium beam set-up with a heated K metal in a chamber that excites the atoms as they leave, a surface to be studied, and a detector. d Doped catalyst set-up with a heated catalyst that desorbs Rydberg atoms, possible laser for initiating CE, and one or more detectors for TOF
The formation of Rydberg states is a general feature of most non-metals and metal oxides, while the Rydberg states will de-excite rapidly in the vicinity of a metal surface [45]. During the condensation from Rydberg atoms to RM, energy is released, and it needs to be absorbed by the surface for the RM to become stable. Though the surface should not remove electrons from the Rydberg atom, as this will lead to ions that won’t form RM [7].
Another factor that may influence the formation of Rydberg atoms is the distance the thermal electron cloud stretches out from the surface, as this should be comparable to the size of the Rydberg atom. The distance varies for example with Fermi wavelength, being larger for insulators and oxides than metals, while the size of the Rydberg atom is dependent on the principal quantum number n, which can be very large. When the size and distance match, this will enable the atomic and ionic species to cross over to Rydberg species. This was tested with a positive voltage applied to the catalyst, leading to a drastic increase in desorbed Rydberg atoms at 5 V for two different catalysts [24, 43], shown in Fig. 6b for a zirconia surface with an impinging potassium beam. This may also be related to the increased lifetime of Rydberg atoms and molecules with a small electric field found in spectroscopy testing [46, 47].
Experiments have also been conducted to investigate the possibility that excited atoms can condensate in a gas discharge [48]. It was expected from theory that a condensate of excited atoms would give a broadening of the spectral bands, that is shifted to the red side, and this could indicate a condensate. The experiments were done using sodium vapor in an argon buffer gas, with spectral measurements to identify the excited condensate. The buffer gas was there to limit the mean free path of the electrons, so that they would only ionize sodium, and create the highly excited states. A voltage was used to initiate the glow discharge, and the amount of Rydberg atoms was determined by analyzing the light emission of Rydberg series (180–250 nm) with a spectroscope in the range of 180–800 nm. The Rydberg series of sodium was seen with only sodium vapor in the chamber, but when a Na and Ar mixture was used this changed to a red shifted broad emission band, and this was proposed to be from condensed highly excited atoms.
For producing hydrogen RM, another aspect must be considered. The catalyst must also be able to chemisorb the hydrogen gas molecules. More reactive metals bind the atoms stronger to the surface, but this also means it is harder for the atoms to desorb, often leading to a volcano plot for useful catalysts [49]. Though the desorption of the Rydberg hydrogen atoms should be assisted by the formation of clusters, meaning it might be possible to use a more reactive catalyst.
Rydberg Matter Generation and Detection
Materials
The materials used for producing RM have mostly been iron oxide, though several other oxides have also been tested. The different materials and set-ups that have been tested are shown in Table 1. None of these papers have done any comparison as to which material produces the most RM, as they focus on research and properties of RM, and it would be difficult comparing them with the different test set-ups. Ref [42]. gives some insight into the difference of doping with K and Cs in a vanadium oxide catalyst, which could be applicable to other oxides as well, though for commercial catalysts it is also a matter of price.
The difference between the styrene catalysts are usually the promoters and the amount of potassium added. Notable promoters are Cr, Mo, W, Mg, Al, V, Ni and Ce, giving many different variations, but most of them are there for stabilization [50]. The catalysts are usually prepared by wet mixing of Fe2O3 or FeO(OH) with KOH or K2CO3, in addition to the promoters. Extrusions are then calcinated at 400–1000 °C, where BET surface area decreases, and average pore radius increases with increasing temperature.
It is a large variation in the temperature used for producing RM for the different materials, with iron oxide being tested down to room temperature, and it is a general tendency that the doped catalyst set-up uses lower temperatures than the potassium beam. Potassium is also predominant over cesium, probably due to the cost. Most of the tests in the later years have been using iron oxide in the doped catalyst set-up due to the availability and the lower temperatures. And because it gives satisfactory amounts of RM, only a few other materials have been tested.
Using a substrate under the active material has been tested for the potassium beam (PB) set-up. This have not been done with the doped catalyst (DC) set-up, though it could be that layering several materials would improve efficiency, for example with a reservoir of pure K metal like what was used for PB. There are also other non-metallic compounds that could be explored, like organics containing alkali metals.
Set-ups
Two different set-ups have been utilized to produce Rydberg atoms, other than the laser excitation of a gas phase used for spectroscopy. Common for both is the use of a heated surface from where the Rydberg atoms desorb. Some of the materials and set-ups are shown in Table 1.
The potassium beam (PB) set-up is used with a reservoir of potassium metal that is heated so that it will desorb K atoms. The reservoir is placed in a chamber and connected to an emitter. The atoms will then diffuse through a foil, get excited, and desorb as Rydberg atoms, which is directed towards a heated surface at an angle, as seen in Fig. 6c. This can give information on scattering, collision stabilizing and diffusion into the bulk of the surface. One surface that was studied was the potassium doped iron oxide catalyst, using a surface ionization detector [44]. The results gave an indication that the Rydberg species could diffuse over large distances on the catalyst surface, and that they could form clusters.
A heated zirconia layer on top of a nickel foil was used to study collision complex stabilization. Figure 6a was acquired with the surface ionization detector, showing that atoms in the beam stick to the desorbing clusters from the surface instead of breaking them apart [24].
The doped catalyst (DC) set-up differs from the former, in that it does not have a reservoir with a pure K or Cs metal. It consists of a metal oxide catalyst doped with K or Cs, which is then heated to desorb atoms, ions, and Rydberg species. This is shown in Fig. 6d, with two detectors that can be used for time-of-flight (TOF) measurements. In recent years, the catalyst has mostly been a commercial potassium doped iron oxide catalyst for styrene production. This has provided an easy way of producing Rydberg atoms, clusters, and RM for research, with a simple set-up and much lower temperatures needed than for other catalysts.
The RM clusters can for example be fragmented by a Coulomb explosion (CE), initiated with a laser pulse, where the size of the fragments can be determined using neutral TOF to the detector. A CE is caused by the repulsion the ion cores from two bonded atoms experience when the shielding electrons are removed by the laser, while the use of ionic TOF would be problematic since the ion-extracting electric field can interfere with the RM. Using a potassium doped iron oxide catalyst with neutral TOF detection, several new planar cluster sizes were found, including mixed clusters of potassium and hydrogen, for example KH7 and KH11 [20].
Some other materials that have been tested are a vanadium oxide catalyst containing both K and Cs [42], and cryptomelane nanorods, which is potassium doped manganese oxide [43]. For vanadium oxide the atomic and excited state desorption barriers were found for both K and Cs, which indicated a slower loss of cesium, despite what was expected from the vapor pressures. For the cryptomelane nanorods a range of small voltages were applied to the sample, giving a peak in the amount of Rydberg atoms detected. And it was proposed that this peak was caused by matching the energy of the surface electrons and K+ ions.
Detectors
Field ionization is useful for detecting Rydberg species since many of them are easily field ionizable, while not detecting ions and electrons. It consists of an opening for the incoming flux, two electrodes with a hole in each of them and a collector, with a diagram shown in Fig. 7(a) [24]. The first electrode is kept at a high positive voltage, to repel ions and trap electrons. The second electrode is kept at a high negative voltage, almost as high as the positive, which gives an electric field tailored to ionize Rydberg atoms but nothing else. The ions are then accelerated by the positive electrode towards the collector. A given field strength FT, in V/cm, will ionize Rydberg atoms with an effective principal quantum number n given by [3]
a Field ionization detector with an opening for the flux, positive and negative electrodes with holes for the Rydberg atoms, and a collector for the ions. b Dynode-scintillator-photomultiplier with opening for the flux, a catcher foil for neutral particles, negative dynode, scintillator, and PMT. c TOF spectra with hydrogen clusters at energy l = 3, cluster sizes 2–61, and a flight distance of 92.5 mm, allowing the calculation of the kinetic energy and the interatomic distances. Reproduced from Reference [52] with permission from the PCCP Owner Societies. d TOF spectra from potassium clusters at energy l = 4, cluster sizes 2–19 and flight distance of 90 or 92 mm. Reprinted by permission from Springer Nature Customer Service Centre GmbH: Springer, Journal of Cluster Science, [20] Common Forms of Alkali Metals—New Rydberg Matter Clusters of Potassium and Hydrogen, Leif Holmlid, Copyright (2010). Both spectra were acquired with a dynode-scintillator-photomultiplier as the detector
Surface ionization can detect neutral particles in the excited or ground states. It consists of a heated ribbon, for example Re, held at a high positive voltage, and a collector [24]. The particles hit the ribbon, get ionized, and then accelerated to the collector. Ions can also be detected by being redirected by the electric field, without hitting the ribbon.
An ion collector is part of both the field and surface ionization detectors but can also be used by itself to detect ions directly. It consists of a plate that gives out an electric current when ions strike it, which can be measured by a digital electrometer [24].
The dynode-scintillator-photomultiplier combination is often used as detectors for the TOF measurements and is shown in Fig. 7b. It can be used with a dynode to detect field ionizable (Rydberg) species, or without to detect ionizing particles [53, 54]. If used without the dynode, the flux would be directed straight at the scintillator. Incoming Rydberg ions get redirected by the electric field, while the atoms hit the catcher foil and get ionized. The ions are attracted by the negative dynode, impacting on it, producing electrons. These excite the scintillator, which then emit light when it relaxes. The photomultiplier tube (PMT) converts the light to electrons and amplify the signal for easier detection with multiple stages of dynodes. The signal can then be measured, for example on an oscilloscope. And depending on which particles are to be detected, the right scintillator material needs to be chosen.
Time-of-flight (TOF) measurement is a method used in conjunction with other detectors. It is used together with a Coulomb explosion (CE), which is set off by a laser pulse removing some of the bonding electrons from the ion cores in the RM [6]. This forces the ions apart, ejecting the ion or cluster fragment and giving them an energy depending on the internuclear distance and the fragment mass. TOF measures the time from one particle hits the first detector to another particle hits the second detector some distance away, or from the laser enters the vacuum chamber to a particle hits the detector. This time can then be used to calculate the internuclear distance and how energetic the particles are using Coulomb’s law as
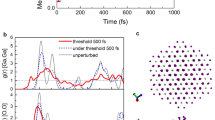
where d is the internuclear distance, ε0 is the vacuum permittivity, e is the unit charge, and Ekin is the sum of the kinetic energy for the particles. Normally, a light particle will break away from a cluster, and therefore acquire most of the kinetic energy. An example of a TOF spectra for hydrogen RM is shown in Fig. 7c, at energy level l = 3 with cluster sizes from 2 to 61, and a flight distance of 92.5 mm [52]. The TOF spectra shown in Fig. 7d is from potassium clusters, giving a larger TOF due to the larger mass. It shows potassium at its lowest energy l = 4, with cluster sizes from 2 to 19, and a flight distance of 90 or 92 mm [20]. And even the largest hydrogen clusters observed (91 atoms) would not give long enough TOF to overlap with potassium. Equations (2) and (4) was derived from this data, relating the kinetic energy to the interatomic distances and the excitation level. This was achieved using a high sample count, together with the integer number of atoms that can make up a cluster fragment, and theoretical calculations.
Several indirect methods of detecting RM have also been proposed, including spectral measurements, second harmonic generation, and detection of inhomogeneity from the speckle structure of transmitted light [48]. Spectral measurements use that when excited atoms or molecules form stable complexes, it broadens the spectral band and shifts it towards the red side. The expectation is that RM will show the same behavior with the Rydberg series. It was predicted that the second harmonic could be generated in RM due to its high polarizability, for example by using a 1064 nm laser and searching for 532 nm radiation. For the speckle structure, an ordered structure produced in a disordered plasma may show up as optical inhomogeneities. This can occur when the inhomogeneities have sizes comparable to or larger than the incident wavelength. Another suggested possibility for the preparation, study and detection of ultra-cold plasma and RM is to use a magneto-optical trap [55]. The experimental set-up included a Zeeman slower, and lasers to cool, excite and probe the atoms. Testing was done on 7Li atoms, and the results gave an estimate of the temperature and density of cold atoms and excited atoms in the trap.
Applications
Catalytic Improvements
Rydberg atoms can have a distinct effect on the catalytic performance, which does not depend on the flux of ground state atoms and ions. The proposed model for how the Rydberg atoms would improve the catalytic performance explains part of why the alkali metals are so efficient promoters for heterogeneous catalysis [56]. It is achieved by having a reactant molecule R react with an excited state of an alkali atom A* on the surface, before reacting further to produce the products. The increased reaction rate come from the large size and reactivity of the Rydberg atom, increasing the sticking probability of the molecule R, and acting as an easily reactive intermediate. This is enabled by the diffusion of alkali metals through the bulk, replacing the lost alkali from the surface. Ions are emitted from the bulk, and acquire electrons on the path to the surface, forming Rydberg atoms in non-equilibrium concentrations.
The reaction H* + D2 → HD + D* involving highly excited Rydberg atoms has been shown to be very similar to the corresponding ionic reaction H+ + D2 → HD + D+. This suggests that the reaction is dominated by the ion–molecule interaction, while the Rydberg electron has little impact [33]. This is attributed to the large distance the electron is from the ion, compared with the range of interactions in the collision. It was tested using crossed molecular beams, where HI molecules were photodissociated, directing the H atoms towards the D2 beam, shown in Fig. 8a. In the interaction volume, the H atoms were excited by two tuned laser beams and collided with the D2 molecules. Using field ionization, the D* Rydberg atoms were detected. In addition to the information this gives about Rydberg atoms and collisions, it can be used to study ionic reactions in a neutral environment, without the adverse effects of ion beam experiments. The similarities and differences were further studied using TOF and field ionization in a microchannel plate detector [57].
a Experimental set-up for testing hydrogen Rydberg atoms with deuterium molecules, with a photolysis laser for dissociating HI, two probe lasers for exciting H atoms, and detectors. Reproduced from Ref [33]. with permission from the PCCP Owner Societies. b Mechanism for converting CO2 to CO over potassium compounds. c Selectivity and conversion for a mixed potassium and iron oxide catalyst. Selectivity from the bottom: CO (yellow), methane (grey), C2-C10 paraffins (red), C2-C10 olefins (blue), and aromatics (green). d Selectivity of C2-C10 olefins and CO2 conversion at 350 °C as a function of time on stream. b, c and d reproduced with permission from Ref. [58]. Copyright 2019, Wiley–VCH (Color figure online)
There are also doubly excited Rydberg atoms with large excitation energies, which could provide the energy necessary to drive any chemical reaction, and are the result of energy pooling in the RM clusters [52]. This pooling can happen during a laser pulse, where a potassium Rydberg atom and excited ion collide, transferring energy to the most excited of them and forming a field ionizable highly excited K*+ ion. The K*+ ion can then be field ionized and detected as a K2+ ion, proving the presence of doubly excited Rydberg atoms with excitation energy over 30 eV, as the electric field was not large enough to ionize a K atom to K2+. The Rydberg species was proposed to increase the catalytic reactivity by contributing energy for the reaction. This process would in theory be most useful for reactions with high activation barriers, like CO2 reforming to useful fuels.
Research in this area have been done using potassium doped iron oxide catalysts, but the presence of RM was not checked for. The reactions are the endothermic reverse water gas shift (RWGS), CO2 + H2 ↔ CO + H2O, and the exothermic Fisher-Tropsch synthesis (FTS), CO + 2H2 → -CH2- + H2O. The conversion of CO2 to valuable chemicals have been shown by several catalysts containing iron oxide and potassium. One was made by mixing Fe2O3 with KO2, and letting it react with CO2 and H2O from the air [58]. The RWGS reaction is enabled by very high K loading, converting the CO2 to CO via potassium bicarbonate/formate as shown in Fig. 8b. The optimal temperature of 350 °C, gives a CO2 conversion of 44.2%, total olefin (C2-C10) selectivity of 62.6%, CH4 selectivity of 13.3%, and CO selectivity of 12.7%, as shown in Fig. 8c. The selectivity and conversion at 350 °C over time is shown in Fig. 8d. Another catalyst was made using impregnation of Fe, Cr and K onto a Nb2O5 support [59]. It was compared to the same catalyst supported on traditional SiO2, being more active and selective to light olefins than the SiO2.
Producing Heat
It would also be possible to use the cluster fragments and charged particles from the CE to produce electricity and heat directly. The heat can for example be generated by a piece of metal thick enough to stop the high energy particles from the CE, while methods to extract more of the energy as electricity are being researched. A test with a set-up similar to the doped catalyst was performed, to see if break-even would be possible to achieve [60]. It used a potassium doped iron oxide catalyst, deuterium gas, and a pulsed laser, but modified to make the energy measurements more accurate. The D2 gas pressure was < 1.0 mbar, the laser was used at 1064 nm instead of a normally lower wavelength to maintain a more constant energy calibration and give less reflection. It used pulses of 5 ns at 10 Hz, giving a nominal laser pulse energy of 0.4 J. And the majority of the tests were done without heating of the catalyst or the feed gas. For accumulating the heat, a 2 cm thick Cu cylinder was used to capture most of the particles, and its temperature measured. Compensations were made for particles that escaped from the small openings in the cylinder, and the heat loss to the D2 gas.
The total heating for a test of 10 min was 2.7 W, resulting in a temperature increase of 1 °C for the 3.2 kg Cu cylinder, while the temperature of the outer reactor wall increased by about 1/5 of this. This is compared to the maximum of 1.2 W that would result from burning the D2 gas with oxygen. Some of the particles were too high energy to be captured by the cylinder, indicating that the efficiency could have been better. The reported results were a gain of 1.5 for the unheated catalyst and 2.0 for the heated, but with a higher suggested gain under optimal conditions.
Understanding Space Physics
RM can also contribute to the understanding of some of the phenomena in space, as it can explain parts of these. This can for example be the diffuse interstellar bands (DIBs), where RM transitions can be assigned to the majority of them [61]. These bands are due to absorptions in the interstellar medium, and 260 of the over 300 are proposed to come from doubly and singly excited atoms, with their frequencies predicted using RM. Absorption in doubly excited states, mostly He, account for 70% of the total DIBs intensity, while the remaining 30% is caused by singly excited He atoms.
Signs of RM can also be found on the surface and in the coma of comets, and examples are made with comets Borelly and Hale-Bopp [62]. RM theory could explain the infrared emission from the coma, line absorption in the emission from the nucleus, and polarization of scattered light from the coma. It is also suggested that smaller weak dipole molecules could be incorporated into the RM, rendering them undetectable with IR or radio observations. These might be released at higher temperatures or stronger solar winds, making them appear to be formed far from the nucleus.
In the alkali atmospheres of the Moon and Mercury, RM can explain several of the problems facing researchers [63]. This could be the assumption that the atmosphere is collision free because of the low density, when the large size of Rydberg atoms and RM could make this possible, and why the alkali atom density depends directly on the sunlight. It would also make the atmosphere more stable with heavier and slower clusters than what is possible with only atoms. And RM clusters can explain the high conductance of the atmosphere that is needed to support the estimated currents around Mercury.
In the sun, RM is proposed to be responsible for the corona temperature and the fast and slow solar winds [64]. The solar winds come from CE in the photosphere for fast, and in the corona for the slow. This gives enough energy to the protons for them to escape the gravity of the sun, while also producing enough energy to explain the high corona temperature.
RM can better explain the unidentified infrared (UIR) emission bands, while reducing the complexity of the current model [65]. These bands are in the 3.3–17 μm wavelengths, with comparable intensities in different surroundings, suggesting a common origin. Currently, the bands are explained by carbonaceous materials, like polycyclic aromatic hydrocarbons. But it might not be enough carbon in space to form enough of them, unlike RM which can form from more abundant elements. The intensities of the bands are also higher than expected coming from stable molecules, and signatures from their precursors would also have been expected to be found, both of which would be explained by RM.
In addition, RM has also been suggested as a part of the dark matter in space [66]. It has several properties that makes it a good candidate, such as a very weak interaction with light, partly stemming from not having any vibrational transitions in the IR range, that makes it appear dark. The large size would fill much space, and it can explain the UIR bands that are observed from all parts of the universe.
Discussion and Outlook
There are many questions about how RM is produced that need to be answered for a more efficient production for the new applications, as the research up until now have focused more on the properties of the RM instead of how it is made. The influence of the desorption barrier and possible differences between different materials with the same desorption barrier on the amount of RM formed should be among the first to be investigated. It is possible that when the desorption barrier is increased, the fraction of Rydberg atoms will increase, but that the total amount of Rydberg atoms will decrease due to the lower total flux. And this will also need to be considered versus alkali depletion for the actual catalyst.
It would furthermore be useful to know if the chemisorption, production of potassium or hydrogen Rydberg atoms, or cluster formation is the rate limiting reaction. Obviously, the elemental composition should also be explored, as there have been very few materials tested, and even though iron oxide is currently the most used, it does not mean it necessarily is the best. Though, iron oxide is a good place to start testing, with how the amount of potassium and the different promoters affect the quantity of RM formed. For iron oxide there is also the question of the phases used for producing the catalysts, and if a magnetic field would have an impact similar to the voltage applied to the cryptomelane and the zirconia. The difference between a bulk and surface layer catalyst should also be investigated, as support material interactions could give even more possibilities to tailor the properties.
The physics of the transition to Rydberg atoms just outside the surface will also need to be understood to optimize the amount of RM produced. Both the cryptomelane nanorods and the zirconia had a large increase in Rydberg atoms desorbed around 5 V, and it should be investigated if this is material specific or not. The question is if this voltage increases the total amount of RM produced, instead of just detected, or if the RM produced decreases because the Rydberg atoms desorbs from the clusters. As can be seen, the knowledge about the specifics of how RM is formed needs to be increased, and any knowledge gained should be able to improve the process.
One application that is possible to realize is the heat generator, as it should be easy to scale up and implement. It has achieved break-even energy wise with suboptimal conditions, but also need to show it can break-even economically. And if a good way to convert some of the charged or high energy particles to electricity was found, it would improve the usefulness considerably, though this might be challenging.
It should also be possible to use RM for sensor applications, like what is done with Rydberg atoms. Rydberg atoms have for example been used for sensing radio frequency (RF) electric fields [67], that have increased the sensitivity limit. They have also been used to measure the phase of an RF field by down-converting it to kHz frequency [68]. It is also suggested that these atoms could be used to detect individual electrons from minute electric field variations, from a distance of 100 μm and resolved in space with a few μm resolution [69]. Research where RM is used as a sensor have not been found, but should be considered for future research, as for example, the longer lifetime could prove useful. Testing have also been done utilizing RM formed from K and N2 Rydberg states as an active medium for a tunable IR laser [70, 71]. It would have low complexity, and would not need expensive cooling, as the catalysts emitting the RM just require heating. The disadvantage is the limited time before the catalysts needs to be replaced.
One drawback is that currently hydrogen is mostly made from natural gas, with a method that is not environmentally friendly. But hopefully new RM applications will incentivize more research into new ways of producing hydrogen, or improve some of the number of possibilities already being worked on [72]. Though the amount of hydrogen needed to produce RM is small.
It should be noted that most of the experimental work on RM have until recently been done by one group in Sweden, but there are currently groups in Norway and Iceland working in the area. This is obviously not optimal, and hopefully more research groups will start experimenting with this material, as more angles of approach are needed.
Conclusion
This review has given an insight into the production of Rydberg Matter and possible applications. Knowledge on how RM is formed have accumulated over the years, but there is still much work that needs to be done to develop a full theory, as the experimental side seems to be further ahead than the theoretical. The development and validation of new detector technologies could also help in this, as there are few options available at the moment. Though, there is currently an easy way to produce RM, with little equipment needed, which should make it possible for more researchers to do testing on RM. And as there has been so little work done with trying to optimize the catalyst, the possibility of improvement should be considerable. More research on the properties, and optimization of the production of RM could lead to applications within sensor technology, optics, particle accelerators, catalyst development and energy production.
References
N. Sibalic and C. S. Adams, in Rydberg Physics (IOP Publishing, 2018).
T. F. Gallagher, Rydberg Atoms (Cambridge University Press, Cambridge, 1994).
K. Engvall, A. Kotarba, and L. Holmlid (1994). Catal. Lett. 26, 101.
A. Kotarba, K. Engvall, J. B. C. Pettersson, M. Svanberg, and L. Holmlid (1995). Surf. Sci. 342, 327.
K. Engvall, L. Holmlid, A. Kotarba, J. B. C. Pettersson, P. G. Menon, and P. Skaugset (1996). Appl. Catal. Gen. 134, 239.
L. Holmlid (2012). J. Clust. Sci. 23, 5.
L. Holmlid (2002). J. Phys. Condens. Matter 14, 13469.
B. K. Teo (2012). J. Clust. Sci. 23, 1.
I. Martinson and L. J. Curtis (2005) Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 235: 17
R. H. Page and C. S. Gudeman (2008). J. Opt. Soc. Am. B 7, 1761.
M. Saffman (2016). J. Phys. B At. Mol. Opt. Phys. 49, 202001.
J. D. Thompson, T. L. Nicholson, Q. Y. Liang, S. H. Cantu, A. V. Venkatramani, S. Choi, I. A. Fedorov, D. Viscor, T. Pohl, M. D. Lukin, and V. Vuletia (2017). Nature 542, 206.
E. A. Manykin, M. I. Ozhovan, and P. P. Poluektov (1983). J. Exp. Theor. Phys. 57, 256.
C. Åman, J. B. C. Pettersson, and L. Holmlid (1990). Chem. Phys. 147, 189.
E. A. Manykin, M. I. Ojovan, and P. P. Poluektov, in Photon Echo and Coherent Spectroscopy 2005, Vol. 6181 (International Society for Optics and Photonics, 2006), p. 618105.
V. S. Filinov, E. A. Manykin, B. B. Zelener, and B. V. Zelener (2004). Laser Phys. 14, 186.
B. B. Zelener, B. V. Zelener, and E. A. Manykin (2004). J. Exp. Theor. Phys. 99, 1173.
E. A. Manykin, B. B. Zelener, and B. V. Zelener (2010). JETP Lett. 92, 630.
E. A. Manykin, M. I. Ojovan, and P. P. Poluektov (2000). Chem. Phys. Rep. 18, 1353.
L. Holmlid (2010). J. Clust. Sci. 21, 637.
L. Holmlid (2019). Phys. Scr. 3, 1.
L. Holmlid (2008). Surf. Sci. 602, 3381.
L. Holmlid and B. Kotzias (2016). AIP Adv. 6, 045111.
J. Wang, K. Engvall, and L. Holmlid (1999). J. Chem. Phys. 110, 1212.
N. D. Lang and W. Kohn (1971). Phys. Rev. B 3, 1215.
R. Svensson and L. Holmlid (1992). Surf. Sci. 269–270, 695.
V. I. Yarygin, V. N. Sidel’nikov, I. I. Kasikov, V. S. Mironov, and S. M. Tulin (2003) J. Exp. Theor. Phys. Lett. 77: 280.
V. I. Yarygin (2012). J. Clust. Sci. 23, 77.
M. I. Ojovan (2012). J. Clust. Sci. 23, 35.
E. Reinhold and W. Ubachs (2005). Mol. Phys. 103, 1329.
A. Kirrander, J. Chem. Phys. 133, (2010).
O. Knospe and R. Schmidt (1996). Z. Phys. -At. Mol. Clust. 37, 85.
E. Wrede, L. Schnieder, K. Seekamp-Schnieder, B. Niederjohann, and K. H. Welge (2005). Phys. Chem. Chem. Phys. 7, 1577.
Y. Sekine, R. Watanabe, M. Matsukata, and E. Kikuchi (2008). Catal. Lett. 125, 215.
G. Ketteler, W. Ranke, and R. Schlögl (2002). J. Catal. 212, 104.
A. Kotarba, I. Kruk, and Z. Sojka (2004). J. Catal. 221, 650.
A. Kotarba, A. Barański, and S. Hodorowicz (2000). Catal. Lett. 67, 129.
Z. Li and B. H. Shanks (2011). Appl. Catal. Gen. 405, 101.
L. Holmlid (2011). Int. J. Mass Spectrom. 300, 50.
I. Serafin, A. Kotarba, M. Grzywa, Z. Sojka, H. Bińczycka, and P. Kuśtrowski (2006). J. Catal. 239, 137.
A. Kotarba, W. Rozek, I. Serafin, and Z. Sojka (2007). J. Catal. 247, 238.
K. Engvall, L. Holmlid, H. Prinz, and H. Hofmann (1991). Catal. Lett. 11, 41.
P. Stelmachowski, Z. Sojka, P. Indyka, P. Legutko, L. Holmlid, T. Jakubek, and A. Kotarba (2015). Phys. Chem. Chem. Phys. 17, 26289.
C. Åman and L. Holmlid (1992). Appl. Surf. Sci. 62, 201.
M. B. Andersson, J. X. Wang, and L. Holmlid (1996). J. Chem. Soc. - Faraday Trans. 92, 4581.
A. Held, L. Y. Baranov, H. L. Selzle, and E. W. Schlag (1998). Chem. Phys. Lett. 291, 318.
L. Y. Baranov, A. Held, H. L. Selzle, and E. W. Schlag (1998). Chem. Phys. Lett. 291, 311.
E. A. Manykin, V. B. Oshurko, and A. N. Fedorov (2011). Tech. Phys. 56, 322.
T. Bligaard and J. K. Nørskov, in Chemical Bonding at Surfaces and Interfaces, 1st ed. (Elsevier, 2008), pp. 255–321.
J. S. Beck and W. O. Haag, in Handbook of Heterogeneous Catalysis, Vols. 5–5 (Wiley-VCH Verlag GmbH, Weinheim, Germany, 1997), pp. 2151–2158.
L. Holmlid (2009). Chem. Phys. 358, 61.
A. Kotarba and L. Holmlid (2009). Phys. Chem. Chem. Phys. 11, 4351.
F. Olofson and L. Holmlid, Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 278, 34 (2012).
L. Holmlid (1998). J. Phys. Chem. A 102, 10636.
B. B. Zelener, S. A. Saakyan, V. A. Sautenkov, A. M. Akulshin, E. A. Manykin, B. V. Zelener, and V. E. Fortov, Coherent Phenom. 2, (2014).
J. B. C. Pettersson, L. Holmlid, and K. Möller (1989). Appl. Surf. Sci. 40, 151.
M. Y. Hayes and R. T. Skodje, J. Chem. Phys. 126, (2007).
A. Ramirez, S. Ould-Chikh, L. Gevers, A. D. Chowdhury, E. Abou-Hamad, A. Aguilar-Tapia, J. L. Hazemann, N. Wehbe, A. J. Al Abdulghani, S. M. Kozlov, L. Cavallo, and J. Gascon, (2019) ChemCatChem 11, 2879.
I. A. da Silva and C. J. A. Mota, Front. Energy Res. 7, (2019).
L. Holmlid (2015). AIP Adv. 5, 087129.
L. Holmlid (2011). Astrophys. Space Sci. 336, 391.
L. Holmlid (2006). Icarus 180, 555.
L. Holmlid (2006). Planet. Space Sci. 54, 101.
L. Holmlid (2017). J. Geophys. Res. Space Phys. 122, 7956.
L. Holmlid (2000). Astron. Astrophys. 358, 276.
S. Badiei and L. Holmlid (2002). Mon. Not. R. Astron. Soc. 333, 360.
S. Kumar, H. Fan, H. Kübler, J. Sheng, and J. P. Shaffer, Sci. Rep. 7, (2017).
M. T. Simons, A. H. Haddab, J. A. Gordon, and C. L. Holloway, Appl. Phys. Lett. 114, (2019).
A. Facon, E. K. Dietsche, D. Grosso, S. Haroche, J. M. Raimond, M. Brune, and S. Gleyzes (2016). Nature 535, 262.
S. Badiei and L. Holmlid (2003). Chem. Phys. Lett. 376, 812.
S. Badiei and L. Holmlid (2005). Appl. Phys. B Lasers Opt. 81, 549.
J. D. Holladay, J. Hu, D. L. King, and Y. Wang (2009). Catal. Today 139, 244.
Funding
Open access funding provided by University Of South-Eastern Norway. This work was supported by the industrial PhD program of Norwegian Research Council (Project Number 297271) and the Norwegian Micro- and Nano-Fabrication Facility (NorFab, Project Number 245963/F50).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The PhD of THA is partially founded by Norrønt AS, and DHZG and SZG are employed by Norrønt AS, which is a company researching RM.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aasen, T.H., Zeiner-Gundersen, D.H., Zeiner-Gundersen, S. et al. A Condensed Excited (Rydberg) Matter: Perspective and Applications. J Clust Sci 33, 839–852 (2022). https://doi.org/10.1007/s10876-021-02031-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10876-021-02031-6