Introduction

In the past 20 years, small metal clusters have been used to model the adsorption of different molecules with the purpose to obtain a good description of the activity of many metal catalysts. Due to the small particles size of a well dispersed catalysts, most or almost all of its atom are surface atoms, so they exhibit structural and reaction properties different from those of the bulk, they are appropriate to surface reactions as the most process in catalysis are. Many previous researches showed that the catalytic properties of clusters are structure dependent, leading to different adsorption energies and sites for different structures of clusters [1–6]. Hydrogen is employed in many modern technologies [7–21], so surface reactions of hydrogen molecules in transition metals have been carried out over the adsorption and desorption of hydrogen and deuterium molecules on well-defined single crystal metals. Axel Pramann et al. [22] studied hydrogen chemisorption rates and electronic structures of small Nb n Al− clusters by photoelectron spectroscopic method. Poulain et al. [23] studied the C2v and C3v reaction of H2 with a Pt4 cluster. Hege Strmsnes et al. [24] studied the chemisorption of molecular hydrogen on a seven atom gold cluster using explicitly correlated wave functions. On the other hand, an area that has attracted recent attention is the effect of chemisorption on the magnetic properties of clusters. For example, Whetten et al. [25] studied the reactivity of Fe n clusters toward H2 and D2, and found the Fermi energy and the band filling could be modulated by adding hydrogen suggests that one could expect interesting effects on magnetic properties. Indeed, Knickelbein et al. [26] recently investigated the effect of hydrogen on the magnetic moment of Fe n clusters in molecular beam experiments and found intriguing results. Knickelbein et al. generated Fe n clusters containing 10–25 atoms in molecular beams and the clusters were saturated with hydrogen. The hydrogenated clusters were subsequently passed through the Stern Gerlach gradient fields. They found that unlike the case of larger nanoparticles and thin films where the hydrogen adsorption quenches the magnetic moment [27], the magnetic moments of the saturated hydrogenated clusters containing 12–25 atoms were higher than those of the free clusters.

Ruthenium is the main element used for hydrogenation and dehydrogenation catalytic reactions. Liu et al. [28] studied adsorption characteristics of atomic nitrogen on ruthenium surfaces, they found that atomic nitrogen always preferably occupies the high coordination sites on Ru surfaces. Carmelo Crisafulli et al. [29] have studied Ni-Ru bimetallic catalysts for the CO2 reforming of methane. Romain Berthoud et al. [30] have studied hydrogen and oxygen adsorption stoichiometries on silica supported ruthenium nanoparticles. Zheng et al. [31] have investigated NH3 decomposition kinetics on supported Ru clusters. Tu et al. [32] have studied the interaction of oxygen with ruthenium clusters by density functional study. Suss-Fink et al. [33] investigated the cluster dication [H6Ru4(C6H6)4]2+ using the a low-temperature 1H-NMR and density functional theory (DFT) calculations, and found the cluster dication [H6Ru4(C6H6)4]2+(1) tends to loose molecular hydrogen to form the cluster dication [H4Ru4(C6H6)4]2+(2). The equilibrium between 1 and 2 can be used for catalytic hydrogenation reactions. Adams et al. investigated the Activation of hydrogen by mixed transitional metal cluster complex [34–37]. Poteau et al. [38] studied spectroscopic and thermodynamic properties of surfacic hydrides on Ru (0001) model surface: the influence of the coordination modes and the coverage by density functional theory and this study partially opens the route to DFT studies of multistep hydrogenation reactions at the surface of ruthenium nanoparticles monitored by spectroscopic techniques. Torsten Gutmann et al. [39] studied hydrido-ruthenium cluster complexes as models for reactive surface hydrogen species of ruthenium nanoparticles by solid-state 2H NMR and quantum chemical calculations and found that the 2H nuclear quadrupolar interaction is a sensitive tool for distinguishing the binding state of the deuterons to the transition metal.

To our knowledge, the study on the adsorption properties of small molecule on ruthenium clusters is still lacking either experimentally or theoretically so far. It would be interesting to know the adsorption ability of ruthenium clusters to small molecules such as the H2 molecule. More precisely, where are the optimal adsorption sites of ruthenium clusters to H2 molecule? Moreover, how does the adsorption of H2 molecule affect the magnetism of the clusters? To answer these questions, we have performed density functional theory (DFT) computations to explore the adsorption behavior of H2 molecule on Ru n clusters. The purposes of this paper include the following: (a) Locate the optimal adsorption sites and (b) analyze the size-dependent structural, electronic, and magnetic properties of the Ru n H2 complexes, and compare with the bare ruthenium clusters.

Computational Methods

Full geometry optimizations were performed using the spin-polarized density functional theory (DFT) implemented in a DMOL package [40]. In the electronic structure calculations, all electron treatment and double numerical basis including d-polarization function (DNP) [40] were chosen. The exchange–correlation interaction was treated within the generalized gradient approximation (GGA) using PBE functional. Self-consistent field calculations were done with a convergence criterion of 10−5 Hartree on the total energy. The density mixing criterion for charge and spin were 0.2 and 0.5, respectively. The Direct Inversion in an Iterative Subspace (DIIS) approach was used to speed up SCF convergence. A 0.001 Hartree of smearing was applied to the orbital occupation. In the geometry optimization, the converged thresholds were set to 0.004 Hartree/Å for the forces, 0.005Å for the displacement and 10−5 Hartree for the energy change. Harmonic vibrational frequencies were calculated for the promising stationary points from a direct structural optimization; if an imaginary vibrational mode was found, a relaxation along coordinates of imaginary vibrational mode was carried out until the true local minimum was actually obtained. Therefore, all isomers for each cluster are guaranteed as the local minima. The on-site charges and magnetic moment were evaluated via Mulliken population analysis [41].

To test the accuracy of the theoretical method, we have calculated the dimers for Ru2 and H2 by using different functionals. For Ru2, the bond length r = 2.26 Å, ω = 364.46 cm−1; the calculated results using PBE functional are in agreement with the previous theory values obtained by all-electron calculation (r = 2.41Å, ω = 380 cm−1) [42] and experimental value by Resonance Raman matrix isolation studies of mass-selected (347.1(9) cm−1) [43]. For H2, the bond length r = 0.748Å, binding energy E b  = 4.665 eV, ω = 4410.896 cm−1. The calculated results using PBE functional are in good agreement with experiment values (r = 0.741Å, E b  = 4.519 eV ω = 4401.21 cm−1) [44]. It indicates that the employed PBE scheme is reliable for the dimer Ru2 and H2. Consequently, the PBE functional are reliable and accurate enough to be applied to describe the properties of the Ru n H2 in this paper.

Results and Discussions

Equilibrium Structures

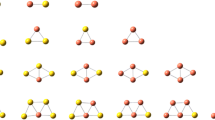
The low-lying isomers of Ru n H2 complexes and their naked counterparts Ru n are displayed in Figs. 1 and 2. The structure and the bond length of the lowest energy structures for Ru n and Ru n H2 are given in Table 1. Here we only present the longest and the shortest interatomic distances between two Ru atoms, two H atoms and Ru–H in Ru n H2 and in the corresponding bare Ru n . The geometries of Ru n H2 and Ru n clusters with considered spin configuration are performed by DFT. The lowest energy geometry of Ru2 is a linear structure. For Ru3, the result is different from those of empirical methods by Tu et al. [45] who have all concluded that the structure of Ru3 is an equilateral triangle. The lowest energy structure we obtained is a triangle (C s ) whose binding energy is 0.819 eV lower than that of equilateral structure. The lowest energy geometry of Ru4 is a quadrangle structure with D4h symmetry. The distorted tetrahedron is 0.348 eV higher than that of the lowest energy geometry. For Ru5, the lowest energy structure is a square pyramid. The trigonal bi-pyramid is an isomer with 0.853 eV higher than the square pyramid. A trigonal prism is the lowest energy structure of Ru6 cluster. The square bipyramid is 0.358 eV higher than that of trigonal prism. The lowest energy structure of Ru7 is a twin square pyramid. The trigonal prism structure face capped a Ru atom is a matastable isomer, it’s energy is 0.0269 eV higher than that of the twin square pyramid. A square prism is the lowest energy structure of Ru8 cluster. Most of lowest energy structures we obtained are similar to the result obtained by Tu et al. [45].

Fig. 1
figure 1

Ground state and some matastable geometries of Ru n clusters. ΔE(eV) is the excess energy of an isomer as compared to the energy of the most stable one. The multiplicity is given in parentheses

Full size image
Fig. 2
figure 2figure 2

Ground state and some matastable geometries of Ru n H2 clusters. The dark circles are the Ru atoms while the white circles are the H atoms. ΔE(eV) is the excess energy of an isomer as compared to the energy of the most stable one. The multiplicity is given in parentheses. The symmetry groups of Ru n H2 clusters are C1 except that of the most stable Ru n H2(n = 1, 4) (Cs, C2v )

Full size image
Table 1 The longest (Max_R Ru–Ru, Max_R Ru–H) and the shortest (Min_R Ru–Ru, Min_R Ru–H) bond lengths(Å) and H–H bond length(Å)(R H–H) of the lowest energy structures of Ru n clusters and Ru n H2 complexes
Full size table

For RuH2, the ground state corresponds to a H–H distance of 2.428Å. The H molecular is therefore activated. For Ru2, the additional hydrogen molecular occupies the on-top site. The Ru–Ru bond length (RRu–Ru) is 2.322Å, 4.31% greater than that in the bare Ru2 dimer. The two Ru–H bond lengths are 1.573 and 1.574Å, respectively. Two Ru–Ru–H angles are both around 90 degree. The H–H bond length (RH–H) is 2.173Å, again indicates that the H2 is activated compared with free H2 molecular.

For n > 2, three different adsorption patterns are found for the Ru n H2 complexes: one H is absorbed on the Ru top site, and another H is absorbed on the bridge site which H atom sits over the Ru–Ru bond for n = 3, 5, 6, 8; bridge site adsorption for n = 4; hollow site and top site adsorption for n = 7. The longest RRu–Ru bond lengths range from 2.493 to 2.598 Å and the shortest from 2.326 to 2.399 Å, the longest RRu–H bond lengths vary from 1.743 to 1.849 Å and the shortest from 1.154 to 1.722 Å, and the bond lengths of H–H are in the range of 2.320 to 3.419 Å, which indicates the H2 is activated.

For Ru2H2, the ground state is quintet state with H–H bond length of 2.173 Å. When one H atom is drawn to one Ru atom and the other H atom to the other Ru atom, the optimized structure (Fig. 2b) is 0.18 eV higher than the ground state. In this structure, both of Ru–Ru–H angles are about 90°.

The most stable structure of Ru3H2 is a triplet state with C1 symmetry. The structure with a H is absorbed on the different top site is metastable isomer, its energy is 0.0861 eV higher than that of the lowest energy structure. In case of Ru4H2, the first and the second H are both absorbed on the adjacent bridge sites. In the lowest energy structure with a triplet state, the H–H distance is 2.530 Å, and the H2 is also activated. The structure with two H atoms absorbed on the top site on the lowest energy structure of Ru4 is metastable isomer, its energy is 0.126 eV higher than that of the lowest energy structure. For Ru5H2, a square pyramid-based structure in a singlet state is most stable, followed by a singlet, triplet and triplet state with 0.293, 0.416 and 0.457 eV higher in energy, respectively.

In the case of Ru6H2, the most stable structure is a trigonal prism-based structure in a triplet state, followed by a singlet with 0.0218 eV higher in energy than the most stable structure. The structure with two H atoms absorbed on the bridge site on the trigonal prism is metastable isomer, the energy is 0.0368 eV higher than that of the lowest energy structure. For Ru7H2, the most stable structure is a singly capped trigonal prism-based structure in a quintuple state, formed by a hollow site adsorption in which one H atom sits above the plane of three Ru atoms and another H atom locates on the Ru atom top. The secondary low-lying isomer of Ru7H2 is a singly capped square bi-pyramid-based structure, which actually corresponds to the third low-lying isomer of pure Ru7 isomer. Other isomers are also presented in Fig. 2. The lowest energy structure of Ru8H2 is square prism-based structure in a quintet state, the single state is 0.0772 eV higher in energy.

According to above analysis, it is shown that the lowest energy structure of Ru n H2 can be obtained by adsorbing H2 in the lowest energy and some meta-table isomers of Ru n clusters. It is interesting to notice that in all cases, the absorbed species does not lead to a rearrangement of the basic cluster, but the hydrogen atom adsorbs to the edge of a Ru–Ru bond with the bond lengthening. The longest and the shortest RRu–Ru (increase with the cluster size overall) as well as RRu–H vary in small ranges overall. In the Ru n H2, H–H bond length is about 2.173–3.419 Å. The values are larger than the bond length of optimized H2 (0.748 Å), which indicates the hydrogen molecular is activated.

Relatives Stability and Electronic Properties

It is known that the relative stability of the different sized cluster can be predicted by calculating the averaged binding energy. The averaged binding energy can be defined as the following formula:

$$ E_b\left[ {{\text{Ru}}_{n}{\text{H}}_{ 2} } \right] = (- E[{\text{Ru}}_{n}{\text{H}}_{ 2} ] + nE\left[ {\text{Ru}} \right] + 2E\left[ {\text{H}} \right] ) / (n + 2 ) $$
(1)
$$ E_b\left[ {{\text{Ru}}_{n}} \right] = (- E[{\text{Ru}}_{n}] + nE\left[ {\text{Ru}} \right] ) /n $$
(2)

where E T (Ru n H2), E T (Ru),E T (H) and E T (Ru n ) represent the total energies of the Ru n H2, Ru, H, Ru n clusters, respectively. The calculated results on the averaged energies for Ru n H2 and Ru n clusters are plotted in Fig. 3. When H2 is adsorbed on the Ru n clusters, the average binding energy is larger than that of Ru n clusters for n = 2–3, the average binding energy is smaller than that of Ru n clusters with cluster size increasing. For n = 2–3, the H atom mainly act with Ru atom. The calculated binding energy (3.577 eV) of Ru–H are larger than that of Ru–Ru (3.19 eV), which indicates the interaction between Ru and H is larger than that of Ru–Ru. So the averaged energy for Ru n H2 clusters is larger than that of Ru n . When n > 3, the H atoms are mainly bond Ru n by the weak interaction, which causes the averaged binding energies of Ru n H2 are smaller than that of Ru n clusters.

Fig. 3
figure 3

Binding energy versus cluster size for Ru n H2 and Ru n clusters

Full size image

The relative stabilities of these clusters can be better understood by calculating the incremental formation energies, i.e., the second order difference of cluster energies, we defined the Δ2 E(n) as the following formula:

$$ \Updelta_{2} E = E(n - 1) + E(n + 1) - 2E(n) $$
(3)

where E T (n) is the total energy of clusters. The second order difference of cluster energies for Ru n H2 and Ru n clusters are all presented in Fig. 4. According to Fig. 4, for Ru n clusters, the peak values appear at n = 3, 5, it shows apparently that the maximum magic number of the relative stability is n = 3, 5 among investigated Ru n clusters. For Ru n H2, particularly high peaks for are found at n = 5, reflecting that the Ru5H2 cluster is more stable than its neighboring clusters. The same magic number 5 indicates the effect of H molecular to the bonding natures of Ru n clusters is small for n > 3, which is consistent with the result of the averaged energy.

Fig. 4
figure 4

Second finite difference of the total energies for Ru n H2 and Ru n clusters

Full size image

To measure the strength of the interaction of H with each of the clusters, we calculated the binding energy of H to each cluster according to:

$$ E(H) = E({\text{Ru}}_{n} {\text{H}}_{ 2} ) - E({\text{Ru}}_{n} ) - 2E({\text{H}}) $$
(4)

The calculated binding energies of H to cluster corresponding to the most energetically favorable chemisorption site are show in Fig. 5, which has a strong dependence on the clusters and increase until n = 2, and then decrease to the lowest value of 5.847 eV at n = 3. The bind energies of H to Ru n cluster then increase in general as the size of the clusters increase, attaining the local maxima for n = 2, 4 and 7. The larger binding energies of H to Ru n cluster (n = 2, 3) indicate the stronger inaction of Ru–H, which is consistent with the result of the averaged energy. The values for bind energies of H to Ru n cluster are 5.847–7.024 eV, and these is larger than that of Ru n cluster(1.597–4.295 eV), which also shows the interaction of Ru–H is larger than that of Ru–Ru.

Fig. 5
figure 5

The binding energies of H to Ru n clusters

Full size image

The electronic properties of clusters are discussed by examining the energy gap between the HOMO and LUMO. The HOMO-LUMO gaps for Ru n H2 and Ru n clusters of the most stable structure are shown in Fig. 6. As can be seen from Fig. 6, when H2 is absorbed on the Ru n clusters, the gaps are usually smaller than those of Ru n cluster, which indicates that the adsorption of the H atoms improves the chemical activity of the host clusters in most cases. However, the exceptional case is n = 2 in which the values of the gap for Ru2 are much larger than those of the Ru2H2 cluster. Interestingly, the energy gap of Ru8H2 is close to that of Ru8, which shows that the adsorption has little effect on the chemical activity with n = 8. Consequently, the Ru n H2 clusters exhibit remarkable difference in terms of the variation of the energy gap as the H atoms are adsorbed onto the Ru n clusters.

Fig. 6
figure 6

The HOMO-LUMO Gaps for Ru n H2 and Ru n clusters

Full size image

In light of the particular phenomenon mentioned above, it is necessary to further study the reason about the changing trend of the gap. Meanwhile, the energy level of the molecular orbital for Ru2 (Ru2H2), Ru5(Ru5H2), which is displayed in Fig. 7, were investigated to further illustrate the electronic property. The obvious characteristic of the molecular orbital for Ru2 is the appearance of the degeneracy of the energy level in the vicinity of the HOMO–LUMO. With the H atoms being adsorbed onto the Ru2 cluster, the degenerate energy level is completely disappeared. Moreover, compared with Ru2, the energy level of the LUMO for Ru2H2 is elevated strongly (about 0.938 eV). In case of Ru5, there is also degenerate orbital in the vicinity of HOMO–LUMO. However, the HOMO and LUMO for Ru5H2 both consist of two degenerate orbitals, respectively. When H atoms are adsorbed onto the Ru5 cluster, the LUMO of Ru5H2 is also reduced (about 0.669 eV) in comparison to Ru5. Apparently, the similar behavior of the reduction of the LUMO for n = 3, 4, 6, 7, results in the decrease of their energy gap.

Fig. 7
figure 7

One electron energy levels in the vicinity of the HOMO and LUMO of the Ru2H2, Ru2, Ru5H2, Ru5 (The dotted lines represent the LUMO levels, and the solid lines represent HOMO levels)

Full size image

In Fig. 8, we give the adsorption energy for Ru n H2 complex. The absorbed energy can be defined as the following formula:

$$ E_{\text{adv}} = E_{{{\text{H}}_{ 2} }} + E_{\text{cluster}} { - }E_{{{\text{cluster}} + {\text{H}}_{ 2} }} $$
(5)
Fig. 8
figure 8

The absorbed energy (Adv) for Ru n H2

Full size image

It is well-known that the chemisorption energies can be used to quantitatively describe the reactivity of H2 on the Ru n clusters. The calculated chemisorption energies corresponding to the most energetically favorable chemisorption site are show in Fig. 8, which has a strong dependence on the clusters and increase until n = 2, and then decrease to the lowest value of 1.182 eV at n = 3. The chemisorption energy then increase in general as the size of the clusters increase, attaining the local maxima for n = 2, 4 and 7. The present results show the Ru3 cluster is of high inertness with respect to the H2 chemisorption, while Ru2, Ru4, and Ru7 clusters are of high activity with respect to the H2 chemisorption. Note that Dhilip Kumar et al. [46] also calculated that the H2 chemisorption energy was found to be the lowest for the stable Ti7 cluster but highest for the most stable cluster Ti13. Experimental measurements indicate that when Ti13 cluster is added as a catalyst to increase the reaction rate of hydrogenation and de hydrogenation processes in alanates [47]. Whether the Ru2 is added as a catalyst to increase the reaction rate of hydrogenation and de hydrogenation processes is to be studied further theoretically and experimentally.

The charge transfer from the Ru n cluster to H2 molecule is an essential factor to determine the H2 adsorption behavior on Ru n clusters. Here we give the charge populations from natural population analysis on H atoms (In Fig. 9). According to the NPA charge population, electron transfer will occur from H atoms to Ru n clusters. The electron transferred number between H atoms and Ru n clusters is about 0.0475–0.158e, this means the interaction between H atoms and Ru n clusters is small. When n = 2, 7, the charges from H atoms to Ru n clusters are more, which is consist with the large absorbed energy in these clusters. For Ru6H2, the charges from H atoms to Ru n clusters are smallest among Ru n H2 complex, this indicates the adsorption has little effect on Ru6, which is the reason that the energy gap of Ru6H2 is close to that of Ru6.

Fig. 9
figure 9

The averaged charge on the H atoms for Ru n H2

Full size image

Magnetic Properties

Figure 10 gives the spin magnetic moment of pure and hydrogenated clusters. For Ru3, the H atoms decrease the spin magnetic moment. For Ru2, Ru4 and Ru7, the H atoms increase the spin magnetic moment. In case of Ru n (n = 5, 6, 8), the H atoms have little impact on the spin magnetic moment. In a previous paper, Fournier et al. have proposed H2 affect on spin magnetic moment of transitional metal clusters can be understood within a simple model [48, 49]. The change in moment is related to the location of the lowest unoccupied orbital of the preceding cluster. The H atom can be considered as a proton and an electron. The additional electron goes to the spin state with lowest LUMO while the proton is screened by the d-states of the neighboring Ru sites. This however, is not the only consideration. If the LUMO of the preceding cluster belongs to the minority manifold (spin down) and the LUMO of majority (spin up) is only slightly higher, the additional electron may still go to majority manifold since the exchange coupling could lead to a rearrangement of the manifolds. To put it simply, it is the difference, δE, between the LUMO of the majority and the minority spin manifolds that controls the change in moment. When this quantity is positive, one expects the moment to increase. On the other hand, when this quantity is highly negative, an addition of H would lead to a decrease in the magnetic moment. To show this correlation, we list in Table 2, the HOMO and LUMO of all the clusters. Note that when δE is less than 0 eV, the spin magnetic moment does decrease upon addition of H2. When δE is close to or more than 0 eV, the spin magnetic moment increases or varies little upon addition of H2.

Fig. 10
figure 10

The total magnetic moment for Ru n H2 and Ru n clusters

Full size image
Table 2 The HOMO and LUMO levels (hartrees) of the majority and minority spin states and δE (eV) in Ru n and Ru n H2 clusters
Full size table

According to above analysis, it again identify the difference between the LUMO of the majority and the minority spin manifolds that controls the change in magnetic moment, the change rule in magnetic moment is different when H2 is adsorbed on different transitional metal clusters. The model may be predict the change in magnetic moment when small molecular is adsorbed on the transitional metal clusters.

Conclusions

We have presented a systematic study on the interaction of the hydrogen atoms with the small Ru n clusters in the size range of two to eight Ru atoms. The lowest energy structures of Ru n H2 clusters can be obtained by substituting H2 in the lowest energy and some meta-stable isomers of Ru n clusters. For n > 2, three different adsorption patterns are found for the Ru n H2 complexes: One H atom binds to the Ru top site, and another H binds to the bridge site for n = 3, 5, 6, 8; bridge site adsorption for n = 4; hollow site and top site adsorption for n = 7. The adsorption energies display oscillation and reach the peak at n = 2, 4, 7, implying their high chemical reactivity. The small electron transferred number between H atoms and Ru n clusters indicates the interaction between H atoms and Ru n clusters is small. It is interesting to note that in all cases, the absorbed species does not lead to a rearrangement of the basic cluster. When H2 is absorbed on the Ru n clusters, the chemical activity of corresponding clusters is dramatically increased. The present studies show that the H absorption can lead to an oscillatory behavior of the magnetic moments. This behavior is rooted in the electronic structure of the preceding cluster and the changes in the magnetic moment are indicative of the relative ordering of the majority and minority LUMO’s. The second order difference indicates 5 is magic number in Ru n H2 and Ru n clusters.