1 Introduction

The Japan Sea is a semi-enclosed marginal sea in the northwestern Pacific Ocean. It is connected to the surrounding seas mainly through three straits: the Tsushima Strait, Tsugaru Strait, and Soya Strait (Fig. 1a). Inflow from the East China Sea and Pacific Ocean occurs from the southwest through the Tsushima Strait and is called the Tsushima Warm Current. Outflows to the Pacific and Okhotsk Sea occur northeast through the Tsugaru and Soya Straits and are called the Tsugaru and Soya Warm Currents, respectively. This oceanic circulation system, designated as the Japan Sea Throughflow (Kida et al. 2016), bifurcates into two branches within the Japan Sea: the coastal and offshore branches (Kawabe 1982a; Yabe et al. 2021). The coastal branch flows along the northern coast of Japan, while the offshore branch flows along the eastern coast of the Korean peninsula as a western boundary current and becomes a zonal jet at 38°N (Ito et al. 2014). The zonal jet is associated with a strong sea surface temperature (SST) front known as the Japan Sea subpolar front (Park et al. 2004, 2007; Ohishi et al. 2019), which exhibits strong air–sea interaction (Zhao et al. 2017). The warm water carried into the Japan Sea by the Tsushima Warm Current occupies the area to the south of this front, and cold water formed within the Japan Sea occupies the area to the north. The Japan Sea Throughflow plays a crucial role in setting up the annual climatological SST field by importing warm water from the south while local monsoonal winds cool the interior (Hirose et al. 1996). This heat-exchange system causes the SST gradient to become more meridional than zonal.

Fig. 1
figure 1

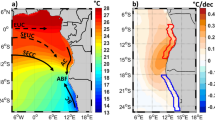
a Annual SST climatology with geographic names and (b) SST trends in the Japan Sea estimated using Optimum Interpolation Sea Surface Temperature annual mean data from the Advanced Very High Resolution Radiometer for 1993–2019 (Banzon et al. 2016). c The same as (b) but the regional zonal band structures are boxed. Blue and red boxes show the areas exhibiting weak and strong SST trends, respectively. The black dashed lines in (a) and (c) indicate the typical path of the Japan Sea Throughflow

Full size image

Studies on temporal variability in SST within the Japan Sea have progressed as the number of direct measurements has increased. Using measurements taken at coastal observatories, Watanabe et al. (1986) examined the interannual variability of SST. Using lag correlations, they found that variability originates from the SST of the East China Sea and is transported into the Japan Sea by the Tsushima Current. Isoda (1994) extended the observation area into the interior along 134°E and found that the decadal variation in SST is correlated with that of Tsushima Warm Current transport. Using gridded temperature data based on the World Ocean Database and complex empirical orthogonal function analysis, Minobe et al. (2004) found that atmospheric variability is responsible for the interannual (less than 7 years) and decadal variability of the SST in the interior of the Japan Sea. More recently, satellite measurements have become the primary means of investigating the spatial variability in SST created by eddies and shifts in the locations of fronts (Park et al. 2004, 2007).

With satellite-measured SST data accumulated for nearly 40 years, long-term trends can now be estimated around the world, and their strength and spatial distribution have gained strong interest in recent years. The northwest Pacific Ocean is described as a hotspot of SST warming (Wu et al. 2020) and exhibits decadal variability in terms of the ocean heat content (Taguchi et al. 2017). Among the seas surrounding Japan, the Japan Sea shows the most significant magnitude of warming (JMA 2020). Lee and Park (2019) examined temporal and spatial differences in the SST trend and found that the intensity of the trend has weakened over the recent 20 years (2000–2020) compared to the previous 20 years (1980–2000). Changes in the Arctic Oscillation index appear to be responsible for this change, in accordance with the findings of Minobe et al. (2004) on decadal variability. In terms of spatial differences within the Japan Sea, Lee and Park (2019) identified a meridionally alternating zonal band structure; there are areas of weak trends around 36°N near the Tsushima Strait and 40°N along the zonal jet, with areas of strong trends along 38°N and 42°N (Fig. 1bc). This alternating band structure reflects the SST trend that occurs during winter. The magnitude of the SST trend within the spatial patterns changes when the analysis periods differ (see Figs. 6 and 7 of Lee and Park 2019). However, the zonal band structure is robust: a weak SST trend forms along the Japanese coast and at 40°N, and a strong one is apparent in the interior.

While the intensity of the spatially averaged trend and characteristics of the spatial distribution of SST trends have been assessed (JMA 2020; Lee and Park 2019), the mechanism behind the formation of the zonal band structure remains unknown. Whether the Japan Sea Throughflow plays a role remains an open question. If it increases SST within the Japan Sea by importing warmer water, the spatial pattern of a zonal band structure will likely form along its path. This structure would be a strong warming trend near the Tsushima Strait, where the throughflow enters the sea, and a warming trend along the zonal jet at 40°N. However, this is the opposite of what is observed; a weak SST trend is apparent near the Tsushima Strait (Fig. 1b). If the throughflow imports water cooler than the interior of the sea, a spatial pattern similar to the observations would be established.

The zonal band structure may further reflect the difference in residence time of surface water within the Japan Sea. A water parcel along the path of the throughflow is advected from the Tsushima Strait to the Tsugaru and Soya Straits, while a water parcel elsewhere will remain within the sea. Thus, the impact of the heating that a water parcel experiences within the Japan Sea is smaller along the throughflow paths, and rendering the SST trend weaker along the path of the throughflow than elsewhere. Kodama et al. (2016) examined the residence times of particles entering the Tsushima Strait; residence times limited the accumulation of nitrate from atmospheric deposits over the Japan Sea (see Fig. 5. of Kodama et al. 2016).

Observations show that atmospheric temperature has been warming in recent years around Japan (Kuroda et al. 2020; Kawase et al. 2023), which can warm the SST. This study uses an idealized model to examine whether the combination of such atmospheric heating and the Japan Sea Throughflow can cause alternating band structures to form within the Sea. We use an idealized model with a flat rectangular coastline to identify the basic process and then employ a realistic bathymetry model to examine the impact of variation in bathymetry. Descriptions of the model setup are provided in Sect. 2. Sections 3 and 4 contain the results of the idealized and realistic bathymetry models, respectively. Differences in residence time created by the throughflow are discussed using a particle tracking model in Sect. 4. Section 5 presents our conclusions and provides future research directions.

2 Methods

2.1 Idealized flat rectangular coastline experiments

An idealized numerical model with a flat rectangular coastline is used to investigate the basic mechanism behind the formation of zonal band structures in the SST trend. The KINACO model (Matsumura and Hasumi 2008) is used as the ocean model with a hydrostatic approximation setting. To create a slowly evolving SST warming trend, we first spin up the model with a steady forcing to reach a steady state (spin-up stage). Then we run two experiments with different surface heat flux (\(Q\)). One with a constant surface heat flux (\(Q=\overline{Q }\)) and the other with an additional surface heat flux anomaly (\({Q= \overline{Q }+ Q}{\prime})\) to emulate the effect of atmospheric temperature warming. The differences between the experiments are examined to elucidate the mechanism underlying the SST trend.

2.1.1 Model setup

The model domain is 1200 km in both the meridional and zonal directions, with a semi-enclosed sea that is 1000 m deep, which represents the Japan Sea (Fig. 2a). Two shallow straits are present at the southwest corner and middle of the eastern boundary, and both are 100 m deep. These straits represent the Tsushima and Tsugaru Straits. Flow through the Soya Strait is neglected for the sake of simplicity. A coastal shelf region exists along the southern and eastern coastlines that connect the two straits, with a slope of 0.001. The maximum depth at the shelf break is 100 m, and the minimum depth is 20 m. The continental slope creates the topographic parameter β, which is important for establishing the coastal branch (Kawabe 1982b; Yoon 1982). The horizontal resolution is 10 km. The vertical resolution varies with depth: 20 m in the upper 200 m, 40 m from 200 to 600 m, and 80 m from 600 m to the bottom.

Fig. 2
figure 2

a The geometry of the idealized model. The black dashed lines indicate the isobaths of the shallow shelf along the southern and eastern coastlines. b Vertical cross section of the initial temperature field at x = 200 km. c Zonal profile of the surface wind stress in the meridional direction. d The temperature field used to restore the SST in SPINUP. e Time series of the basin-averaged SSTs. Black, blue, and red lines indicate the result of the SPINUP, FIXED, and WARM experiments, respectively

Full size image

Constant horizontal viscosity AH and diffusivity KH of 100 m2 s−1 are used with a free-slip lateral boundary condition. The generic length-scale scheme (Umlauf and Burchard 2003) is used to estimate the vertical viscosity AV and diffusivity KV, and a quadratic form with a coefficient of Cd = 0.055 is used for bottom drag.

The initial temperature field resembles the annual climatology estimated using 2005–2017 data from World Ocean Atlas (WOA) 2018 (Locarnini et al. 2019). An SST front is located in the mid-basin (y = 600 km) region to represent the subpolar front (Fig. 2b), and the depth of the thermocline is 200 m to the south of the front and 100 m on the northern side. Salinity is 35 psu and is uniform; therefore, density changes occur only due to changes in temperature.

Inflow occurs from the southwestern strait, and outflow occurs from the eastern strait, with a constant volume transport of 2.2 Sv. This is similar to the magnitude of the Tsushima Current in winter (Takikawa et al. 2004; Fukudome et al. 2010). The temperature of the inflow is set to the initial temperature profile prescribed at the southern boundary. Thus, even if the ocean interior warms, the heat transport of this inflow will remain constant over time. The temperature of the outflow is determined based on the temperature simulated at the eastern boundary, which changes over time.

Zonal wind stress is applied at the sea surface that varies meridionally and is strongest at mid-basin (y = 600 km) (Fig. 2c):

$${\tau }_{x}\left(y\right)=0.025{\text{cos}}\left(\frac{600-y}{600}\pi \right)+0.025$$
(1)

where y is in kilometers. This wind stress remains constant and creates a double gyre circulation within the model domain, which is a major component of the circulation system within the Japan Sea (Yoon et al. 2005; Kim et al. 2020). The maximum wind stress of 0.05 N m−2 is based on the annual mean wind estimate in the J-OFURO3 dataset (Tomita et al. 2019).

The model SST is restored to an idealized meridional profile (Fig. 2d) that resembles the monthly climatology of March near the surface based on 1981–2010 data from WOA 2018 (Locarnini et al. 2019); these simulate the winter SST state. March is used to simulate the winter SST state because it is the coldest month. We restore the model SST rather than employ a prescribed surface heat flux to prevent long-term drift in the SST during spin-up stage. The restoration timescale is 30 days. Wind stress does not affect the surface temperature.

The model temperature of the upper layer reaches a steady state in about 20 years and then is integrated for an additional 7 years (Fig. 2e). We refer to this experiment as SPINUP hereafter.

2.1.2 Warming SST experiment

To examine the mechanism of the warming SST trend, we employ two experiments as mentioned earlier. The first experiment forces the model using a constant surface heat flux (\(\overline{Q }<0\)) based on the average of the last 7 years of SPINUP. A positive sign is used for downward heat flux. We refer to this experiment as the FIXED experiment hereafter. The experiment aims to create an SST field with no long-term trend. Except for the surface heat flux, all other settings are the same as SPINUP. The final day of the 20th year of SPINUP is used as the initial condition and the experiment is integrated for 20 years.

The second experiment applies an anomalous surface heat flux (\(Q{\prime}\)) of 5 W m−2 to FIXED to force a warming trend in SST of about 0.21 °C decade−1, which approximates the observations. This anomalous surface heat flux is temporally and spatially constant and serves to reduce the cooling effect of the surface heat flux used in the FIXED experiment. Note that the total surface heat flux still works to cool the SST (\(\overline{Q }+{Q}{\prime}<0\)). The temperature of the inflow at the southwestern strait does not change. Thus, no anomalous heat input is provided through the straits. We refer to this second experiment as WARM. This experiment thus creates a gradual warming SST field on top of the SST field simulated in FIXED (Fig. 2e); the difference between WARM and FIXED can be used to analyze the SST trend.

2.2 Realistic coastline experiments

To examine the impact of the bathymetry of the Japan Sea, we conduct experiments using ETOPO bathymetry data (Amante and Eakins 2009) (Fig. 3a). Previous studies have suggested that the flow field is affected by bottom topography features such as the Yamato Rise (Hogan and Hurlburt 2000). We conduct three experiments using a realistic bathymetric setting to simulate the SST warming trend. The three experiments are identical to the SPINUP, FIXED, and WARM experiments except for the bathymetry, coastlines, and a center of wind stress located at y = 670 km. We refer to these experiments as R-SPINUP, R-FIXED, and R-WARM, respectively.

Fig. 3
figure 3

a The model geometry used for the realistic coastline experiments. b The locations of particles released in P-TSUSHIMA (the red box) and (c) in P-AIR. Note that particles are shown every 40 km

Full size image

2.3 Heat budget analysis

We analyze the heat balance equation to examine the mechanism behind spatial differences in the SST trend:

$$\frac{\partial T}{\partial t}=-{\nabla }_{H}\cdot \left(\overrightarrow{{u}_{H}}T\right)-\frac{\partial }{\partial z}\left(wT\right)+{K}_{H}{\nabla }_{H}^{2}T+{K}_{V}\frac{{\partial }^{2}T}{\partial {z}^{2}}$$
(2)

On the left side is the tendency term. The right side includes the horizontal heat transport convergence term, vertical heat transport convergence term, horizontal diffusion term, and vertical diffusion term. Equation 2 is integrated vertically across the upper layer:

$$\frac{\partial {T}_{m}}{\partial t}={\left\{-{\nabla }_{H}\cdot \left(\overrightarrow{{u}_{H}}T\right)\right\}}_{m}+\frac{1}{H}\left(wT\right){\left.\right|}_{z=-H}+{\left\{{K}_{H}{\nabla }_{H}^{2}T\right\}}_{m}+\left\{-\frac{{K}_{V}}{H}\frac{\partial T}{\partial z}{\left.\right|}_{z=-H}\right\}+\frac{Q}{{\rho }_{0}{C}_{p}H}$$
(3)

where \({\rho }_{0}\) is the seawater density, \({C}_{p}\) is the specific heat at constant pressure, \(Q\) is the surface heat flux, and H is the depth of the upper layer set to 200 m. If the bathymetry is shallower, then the bottom depth is used. Variables in 200 m represent vertical averages. Tm is the vertically averaged temperature, which will be hereafter termed the SST:

$${T}_{m}= \frac{1}{H}{\int }_{-H}^{0}T dz.$$

Then, we partition each term of Eq. 3 (A) into steady (\(\overline{A }\)) and trend (\({A}{\prime}\)) components:

$$A = \bar{A} + A^{\prime }$$

where \(\overline{A }\) represents FIXED and \({A}{\prime}\) is the difference between WARM and FIXED. The time-mean heat balance equation for FIXED is:

$$0 = \overline {\left\{ { - \nabla _{H} \cdot \left( {\overrightarrow {{u_{H} }} T} \right)} \right\}}_{m} + \overline{{\left\{ {\frac{1}{H}\left( {wT} \right)\left. {} \right|_{{z = - H}} } \right\}}} + \overline{{\left\{ {K_{H} \nabla ^{2} T} \right\}_{m} }} + \overline {\left\{ { - \frac{{K_{V} }}{H}\frac{{\partial T}}{{\partial z}}\left. {} \right|_{{z = - H}} } \right\}} + \frac{{\bar{Q}}}{{\rho _{0} C_{p} H}}$$
(4)

The terms in Eq. 4 from the left represent time means of horizontal and vertical heat transport convergence, horizontal and vertical diffusion, and surface heat flux. The SST trend equation for WARM is:

$$\frac{{\partial T_{m} \prime }}{{\partial t}} = \left\{ { - \nabla _{H} \cdot \left( {\overrightarrow {{u_{H} }} T} \right)} \right\}^{\prime } _{m} + \left\{ {\frac{1}{H}\left( {wT} \right)\left. {} \right|_{{z = - H}} } \right\}^{\prime } + \left\{ {K_{H} \nabla _{H}^{2} T} \right\}^{\prime } _{m} + \left\{ { - \frac{{K_{V} }}{H}\frac{{\partial T}}{{\partial z}}\left. {} \right|_{{z = - H}} } \right\}^{\prime } + \frac{{Q^{\prime } }}{{\rho _{0} C_{p} H}}$$
(5)

The terms in Eq. 5 from the left represents the SST trend (ST), anomalous horizontal heat transport convergence (HH), anomalous vertical heat transport convergence (VH), anomalous horizontal diffusion (HDIF), anomalous vertical diffusion (VDIF) and anomalous surface heat flux (SH). Equation 5 is used to explore the process responsible for the SST trend by examining the spatial averages of each term in the four regions in WARM and R-WARM: coastal branch, offshore branch, southern interior, and northern gyre. The area covered by each region depends on the flow field, and therefore the regions are described separately for each experiment.

2.4 Residence time

Two particle tracking experiments are pursued using R-WARM to examine the residence time of water parcels within the Japan Sea. The first experiment examines the residence time of water parcels that enter from Tsushima Strait at the southwest corner (Fig. 3b), which we refer to as P-TSUSHIMA. The second experiment examines the residence time of water parcels within the Japan Sea affected by surface heat flux (Fig. 3c), which we refer to as P-AIR. Particles accumulate age as long as the particle remains within the model domain, and we use this age to estimate the residence time of water parcels. The detailed methods used to estimate the residence time in each experiment are described below. Particles remain at the same depth and move only in the horizontal direction driven by flow and random walk to represent diffusion. Particles are released at depths of 50 m and 90 m to incorporate the difference in flow with depth.

(a) P-TSUSHIMA

At the beginning of each year, 3000 particles are released into Tsushima Strait; we use data commencing in year 20. The time between when a parcel enters and exits the sea is estimated to be about 120–150 days given the distance of 1200–1500 km and a flow speed of 0.1 m s−1. Thus, the estimated residence time of particles along the path of the throughflow is expected to be less than 1 year, and we take the 20-year average of the distribution of particles at the end of each year. Then, we perform exponential fitting to estimate the decay time scale of particles that entered from the Tsushima Strait along the path of the throughflow. We refer to the fitting result as the residence time of Tsushima Strait water parcels.

(b) P-AIR

Particles are released every 10 km and in each layer, with 8848 and 8587 particles released at depths of 50 m and 90 m, respectively, at the beginning of each year, commencing in year 20. We expect that some particles would remain within the sea much longer than that along the throughflow. We, thus, calculate the 10-year average residence times at the end of each year commencing at year 30. Only particles released within 10 years are considered. We derive the spatial means of particle numbers every 100 km2, this yields the interior residence times at a spatial resolution of 10 km.

3 Idealized flat rectangular coastline experiments

3.1 Mean field

FIXED shows the SST and flow field model in a quasi-steady state (Fig. 4a). The time-averaged field of SST is warm in the southern half of the model domain, particularly near the southwestern strait, where warm water enters. A cold SST region forms in the northern half of the domain. The meridional vertical cross section shows a thick warm layer forming in the south with a strong temperature gradient at mid-basin, around y = 600 km (Fig. 4b). The surface flow field shows inflow from the southwestern strait that bifurcates into a coastal branch and an offshore branch. These two paths comprise the Tsushima Warm Current. The coastal branch flows along the southern and eastern coastlines and then reaches the eastern strait. The offshore branch first flows north as a western boundary and then detaches to become a zonal jet at the latitude of the eastern strait, forming an SST front. The presence of a wind-driven gyre is observed as a cyclonic gyre established in the northern half of the domain with a southward western boundary current, and warm water is advected cyclonically.

Fig. 4
figure 4

Time means of (a) SST and flow field and, (b) the vertical temperature cross section at x = 600 km yielded by FIXED experimental data from years 20–40. The terms in the time-mean heat budget equation of Eq. 4 for FIXED: c The sum of the time-mean horizontal and vertical heat transport convergence terms, d the sum of the time-mean horizontal and vertical diffusion terms, and (e) the time-mean surface heat flux term

Full size image

The time-mean heat balance (Eq. 4) shows that inflow from the southwestern strait bifurcates and introduces heat along the southern and western boundaries (Fig. 4c). The role of diffusion is confined to narrow areas with strong SST gradients, such as the shelf break and the western boundary (Fig. 4d). Surface heat flux cools the SST (Fig. 4e) and is the primary term balancing heat transport convergence.

3.2 SST trend

WARM shows a SST trend of about 0.19 °C decade−1 as a basin average and successfully simulates a meridionally alternating zonal band structure analogous to the observed pattern (Fig. 5a). Here, we will focus on four regions: coastal branch, offshore branch, southern interior, and northern gyre, which are of equal size, with a zonal length of 250 km (from x = 600 to 850 km) and a meridional length of 50 km. The coastal branch is defined as the area in which the depth is shallower than 100 m. The basic heat balance does not qualitatively change as long as areas with abrupt depth changes are excluded.

Fig. 5
figure 5

The terms in the SST trend equation of Eq. 5 for WARM: a ST, b HH, c VH, d HDIF, e VDIF, and f SH. Black contours represent the boundaries of the regions used to obtain areal averages and black arrows shows the names of each region

Full size image

The weakest SST trend is found in the coastal branch. The trend gradually becomes moderate toward the eastern strait, possibly reflecting heat accumulation driven by anomalous surface heat flux. A weak SST trend is also found along the offshore branch. A region of moderate SST warming is found in the southern interior with a magnitude of 0.1–0.2 °C decade−1. The warming signal is also robust toward the east. This SST trend pattern differs from observations, in which a stronger trend is found in the west. The difference may be due to strong fluctuations near the separation point of the western boundary, where it becomes a zonal jet. We discuss this possibility in Sect. 4. A strong warming trend is found in the northern gyre with a magnitude 0.3 °C decade−1. In this region, throughflow is absent and the flow is primarily driven by the wind-stress curl.

3.3 Heat budget of the SST trend

To identify the process responsible for controlling the SST trend in WARM, we will examine the terms of the SST trend equation (Eq. 5). Since the focus of this subsection is on SST trends rather than the mean state, the terms of Eq. 5 will be discussed without using the term “anomalous” hereafter.

For a first approximation, all four regions (coastal branch, offshore branch, southern interior, and northern gyre) show that the warming trend is created primarily by a balance of horizontal heat transport convergence and surface heat flux (Fig. 6a–d). The role of horizontal and vertical diffusion is small. Note that the horizontal and vertical heat transport convergence terms show strong fluctuations near the horizontal boundaries and at the edge of the slope (Fig. 5cd). In these areas, the temporal variability of flow is strong.

Fig. 6
figure 6

Spatial averages of ST, HH, VH, HDIF, VDIF, and SH in Eq. 5 for WARM for the (a) coastal branch, b offshore branch, c southern interior and d northern gyre. RES is the residual. The red bars indicate warming and the blue bars indicate cooling

Full size image

Within the coastal branch, the heat balance is mostly between horizontal heat transport convergence and surface heat flux (Fig. 6a). The magnitude of vertical heat transport convergence and horizontal and vertical diffusions are small. The balance suggests that advection of relatively cold water from the southwestern strait weakens the warming forced by surface heat flux. The magnitude of the surface heat flux is large in this region compared to other areas because the thickness of the water column is limited to 100 m or less due to the slope.

A similar role of horizontal heat transport convergence is found within the offshore branch (Fig. 6b). Surface heat flux is offset by cooling due to horizontal heat transport convergence. The vertical heat transport convergence is also negative, suggesting downwelling of warmer upper-layer water, but its magnitude is much lower than described above. Note that, the sign of vertical heat transport convergence in Eq. 5 depends on the sign of the vertical velocity because it is in heat transport form. The impact of horizontal diffusion becomes positive because the warmer SST trends in the south interior and northern gyre diffuse heat into the offshore branch. The impact of vertical diffusion also becomes positive, suggesting weakening vertical diffusion. The positive impacts of horizontal and vertical diffusion contribute to the stronger increase in SST trends in this area compared to the coastal branch.

Within the southern interior, the reduction in horizontal heat transport convergence creates a stronger warming trend than the coastal and offshore regions (Fig. 6c). The horizontal heat transport convergence maintains a negative value, but its magnitude is greatly reduced. This is consistent with the low flow speed observed in the region. The horizontal diffusion term shows a negative value that is comparable to the impact of the horizontal heat transport convergence and is negative due to horizontal diffusion into surrounding areas with weak SST trends. Vertical heat transport convergence and vertical diffusion show results similar to the offshore branch.

The horizontal heat transport convergence within the northern gyre is lower than those of coastal and offshore branches (Fig. 6d), suggesting that the role played by horizontal flow in the gyre is less significant than in other regions. However, the term is larger than that for the southern interior, possibly because of the stronger flow within the gyre. As vertical heat transport convergence is positive and the horizontal diffusion weakens, the SST trend becomes stronger in the northern gyre than the southern interior. A positive vertical heat transport convergence term reflects upwelling of warmer upper-layer water attributable to Ekman upwelling forced in the northern half of the domain by the wind. The vertical diffusion term remains positive but is slightly smaller than that for the southern interior region.

Heat budget analysis suggests that the primary driver of the establishment of the zonal band structure in the SST warming trend is the changing role of horizontal heat transport convergence. Surface heat flux generally increases SST uniformly across the model domain, while vertical heat transport convergence and diffusion terms are incapable of creating a zonal structure. Flows along the coastal and offshore branches tend to be zonally oriented, and thus explain the difference in horizontal heat transport between the southern interior and the northern gyre.

3.4 Sensitivity to the trend in flow field

The trend in the flow field of WARM may also affect the SST. The strongest signals are found near the separation point of the western boundary current. A weakening of the eastward zonal jet is found, surrounded by eddy-like features (Fig. S1a). These features may affect the SST trend around the jet (Fig. 6a), but their impact appears moderate since most flow changes develop along the SST trend contours. The trend magnitude is less than 0.01 m s−1 decade−1, thus one order of magnitude smaller than that of the mean current.

While the idealized flat rectangular coastline experiment demonstrates the importance of the flow field to the spatial distribution of the SST trend, differences from the observations remain (Fig. 1b), such as a strong SST trend in the southern interior region associated with patches of maxima, which has a trend of strengthening toward the west. We examine the role of realistic coastline and bathymetry settings in Sect. 4.

4 Realistic coastline experiments

4.1 Mean field

R-FIXED shows a mean SST field similar to FIXED, including a warm SST region near the Tsushima Strait (Fig. 7a); the mean flow field exhibits the typical Japan Sea Throughflow pattern. The inflow bifurcating into coastal and offshore branches, with the coastal branch becoming diffused north of the Noto Peninsula, where the shelf along the northern coast of Japan is discontinuous. The offshore branch flows zonally along the SST front and is more stable than in the FIXED experiment. A separation point of western boundary current appears around y = 670 km corresponding to a position of the idealized wind-stress curl zero. An anticyclonic recirculation gyre lies southeast of this separation point. The separation point is northward compared to observations, thus shows overshooting, and we will discuss the impact of this feature on the SST trend in the next section. In the region north of the offshore branch, the flow field is weak.

Fig. 7
figure 7

a Long-term means of SST and the flow field of R-FIXED for years 20–40. b SST warming trend for R-WARM for years 20–40. Black contours indicate the regions used to analyze heat budget: the coastal branch, southern interior, offshore branch, and northern gyre

Full size image

4.2 SST trends

R-WARM simulates a meridionally alternating zonal band structure (Fig. 7b) analogous to the observed pattern (Fig. 1b) and WARM (Fig. 5a). Weak SST trends are found around the Tsushima Strait (y = 200 km) and zonal jet (y = 600 km) while regions of strong SST trends are found in the south (y = 400 km) and north (y = 800 km) of zonal jet. For R-WARM, we will define the coastal branch as the area with a shallow depth of 200 m where the magnitude of the SST trend is less than 0.1 °C decade−1 (Fig. 7b). The offshore branch and southern interior are defined as the areas wherein the magnitudes of the SST trend are below and above 0.1 °C decade−1, respectively. The northern gyre is defined as the various areas north of the zonal jet for which the magnitude of the SST trend is above 0.1 °C decade−1. Regions with depths shallower than 200 m are excluded; we focus on processes in areas away from the slope.

The main difference between R-WARM and WARM in the southern interior is the strong SST trend (greater than 0.25 °C decade−1) in the region east of the Noto Peninsula, where the flow becomes discontinuous along Japanese coast. The SST trend in the southern interior also strengthens toward the west since the separation point is much stable for R-WARM than WARM. We suspect that this difference is due to the formation of a stable recirculation gyre. We generally find that areas with mean currents faster than 0.04 m s–1 area associated with weak SST trends.

4.3 Heat budget of the SST trend

For heat budget analysis, we examine the term of the SST trend equation (Eq. 5). The focus of this subsection is on the trend. Therefore, the terms of Eq. 5 will be discussed here without using the term “anomalous”, similar to subsection 3.3.

In the coastal branch, cooling by the horizontal heat transport convergence balances warming by surface heat flux (Fig. 8a). The diffusion terms are small. It suggests that the advection of water with a lower SST trend than that of the interior is essential to the establishment of the region with the weak SST trend apparent near the Tsushima Strait.

Fig. 8
figure 8

Spatial averages of ST, HH, VH, HDIF, VDIF, and SH in Eq. 5 for R-WARM for the (a) coastal branch, b offshore branch, c southern interior, and d northern gyre region. RES is the residual. The red bars indicate warming, and the blue bars indicate cooling

Full size image

The offshore branch shows a balance between horizontal heat transport convergence and surface heat flux (Fig. 8b). In this case, the effect of horizontal heat transport convergence overwhelms the surface warming by surface heat flux and results in a lower SST trend. The vertical heat transport convergence term is positive, which may be because the offshore branch now includes areas of Ekman upwelling.

In the southern interior, the horizontal and vertical heat transport convergence terms are larger than in the offshore branch (Fig. 8c). This is attributable to strong current fluctuations found near the northern coast of Japan. The sum of the horizontal and vertical heat transport convergences is –1.66 °C decade−1, suggesting that the two terms compensate for each other; this value is smaller than the coastal (–4.11 °C decade−1) or offshore (–1.96 °C decade−1) branches, implying weaker impact of the overall flow field in the southern interior. The difference in the sum of horizontal and vertical heat transport convergences from the offshore branch to the southern interior is approximately 0.3 °C decade−1 and is the primary term responsible for the strengthening of the SST trend from the offshore branch, at –0.04 °C decade−1, to the southern interior, at 0.19 °C decade−1.

In the northern gyre, the horizontal and vertical heat transport convergences and the surface heat flux terms are dominant (Fig. 8d). The horizontal and vertical diffusion terms are small. As is the case for heat budget of the southern interior, the sum of the horizontal and vertical heat transport convergences is -1.26 °C decade−1, thus smaller than the sums for the coastal or offshore branches.

Heat budget analysis suggests that the coastal and offshore branches are strongly influenced by horizontal heat transport convergence, preventing SST warming, similar to WARM. For both the southern interior and northern gyre, significant compensation between horizontal and vertical heat transport convergences is apparent, which results in a weaker impact of the flow field, in turn associated with a stronger SST trend than in other regions.

4.4 Sensitivity to the trend in flow field and wind stress

The trend in the flow field of R-WARM may also affect the SST. We find largest changes occurring near the separation point of the western boundary current (Fig. S1b). Eastward flow increases north of the separation point, implying a northward shift in the position of the zonal jet. This northward shift may partly explain the enhanced SST trend found to the north of the zonal jet. A reduced zonal jet flow speed is also apparent in the eastern half of the Japan Sea. However, their impact appears moderate since most flow changes develop along the SST trend contours.

To examine the sensitivity of the model results on the location of the separation point, the axis of the zero wind-stress curl is moved south (y = 400 km). The separation point moves south, and the overshoot of the western boundary current is much reduced compared to R-WARM and closer to observations (Fig. S2). The recirculation gyre forms southeast of the separation point with a stronger SST trend than the surroundings, which is qualitatively similar to R-WARM but much weaker. The development of the strong warming patch north of the Korean peninsula around 38°N, as observed (Fig. 1a), could be influenced by factors such as the detaching mechanism near the separation point of the wind system. In this study, our focus is on the formation of the zonal band structure of the SST trend, which appears to be robust.

4.5 Residence time

Heat budget analysis was used to examine the SST trend from an Eulerian perspective. We now estimate residence times to examine the trend from a Lagrangian perspective.

4.5.1 Residence time of water masses in the coastal and offshore branches

Particles released from the Tsushima Strait bifurcate and travel along the coasts of Japan and Korea, but eventually merge and exit through the Tsugaru Strait within 1 year (Fig. 9). Particles traveling along the coast of Japan reach the Noto Peninsula in about 130 days and take another 120 days to reach the Tsugaru Strait. Some particles leave the coast and travel westward along with eddies that may reflect planetary baroclinic Rossby waves; these particles eventually join the western boundary current (within 100 days). Particles traveling along the coast of Korea reach the offshore branch region in about 70 days and then travel eastward along the meandering jet to reach the Tsugaru Strait in about 110 days. Some particles disperse and enter the southern interior or the northern gyre.

Fig. 9
figure 9

Snapshots of particles released on day 0 at a depth of 50 m near the Tsushima Strait at a 30, b 70, c 130, and d 180 days. The particles are shown as white dots; annual climatological SSTs as shades of color; and the flow fields as vectors. Time series showing the number of particles at depth of (e) 50 m and (f) 90 m in the coastal and offshore branches (blue and orange dots, respectively). The red solid line is the best-fit exponential curve

Full size image

The time series of particle numbers within the coastal branch indicates residence times of 14 days at 50 m and 13 days at 90 m depth. Little difference in residence time with depth is found. This timescale suggests that the advection of cooler water from the strait directly affects the weak SST trend of the coastal branch.

The time series of particle numbers within the offshore branch demonstrates longer residence times than the coastal branch of 137 days at 50 m and 141 days at 90 m depth. This arises because the particles covers a much longer distance and take some time to reach the offshore branch; we thus estimate the residence time after particle numbers are maximal, therefore about 150 days after the particles are released in the Tsushima Strait. The residence times of 137 and 141 days, which are shorter than a year, align well with the magnitude of the weak SST trend expected in areas where the accumulation of heat is weak.

4.5.2 Residence times of water masses in the southern interior and northern gyre

The particles of P-AIR show the spatial variability of residence times across the entire model domain (Fig. 10a). About 55% of all particles remain in the model domain, while the remainder exit the Tsugaru Strait. Long residence times are found in the recirculation gyre near the western boundary as well as areas west and northeast of the Noto Peninsula and northern gyre; these areas have much longer residence times than the coastal and offshore branches (Fig. 10a). The spatially averaged regional residence times are 0.08 years (29 days) in the coastal branch, 0.72 years (259 days) in the offshore branch, and 1.32 years in the southern interior. This regional pattern of residence time agrees with the pattern of SST trend simulated in the model (Fig. 7b), with strong SST trends in the southern interior, where the residence time is longer than a year. The residence time found in P-AIR is consistent with the results of P-TSUSHIMA; the residence time along the coastal and offshore branches is less than 1 year.

Fig. 10
figure 10

Residence times of particles simulated by P-AIR based on the spatial averages (100 km2) after particle release at (a) depths of 50 m and 90 m, (b) only 50 m, and (c) only 90 m. d Particle age distribution in the southern interior region. The vertical axis shows the sums of areas by the residence times. Blue and orange bars: residence times at 50 and 90 m, respectively

Full size image

Spatially averaged residence time is generally longer at the depth of 90 m than 50 m (Fig. 10b, c). For the coastal branch, the average residence time is 18 days at 50 m and 36 days at 90 m, while for the offshore branch, it is 115 days at 50 m and 407 days at 90 m. This delay is reasonable, as the flow speed is slower at greater depth. Interestingly, in the southern interior region, the residence time is 468 days for 50 m and 486 days for 90 m, which are nearly equal. Particles placed at 50 m generally escape the region but eddies cause some particles to remain. As a result, the age distribution shows a gradual trend of exponential decay as age increases (Fig. 10d). Particles placed at 90 m recirculate and reenter the region after about 1 year. This recirculation causes a peak in the number of particles at about 1 year and rapid decay after about 2.5 years. In terms of spatial variability, eddies near the surface explain the increase in residence time toward the west; particles at the depth become more diffused and thus uniformly distributed. The model results suggest that eddy activity near the surface is important for determining the maximum SST change in the southern interior zonal band, which strengthens toward the west (Fig. 10b).

Comparisons of the residence times and the heat transport convergence terms of Eq. 5 reveal stronger impact of the Japan Sea Throughflow where short residence times are found (Fig. 11). The time sequences of particles' position in the P-AIR show that particles disperse as time passes where the heat transport convergence term is strongly negative, corresponding to where short residence time is found (Fig. 10). These areas are where weak SST trends are found. In contrast, many particles converge in the southern interior and northern gyre, where negative impact of heat transport convergence are weaker, showing positive values in some places. Those areas are where long residence time is found and where strong SST trends are also found.

Fig. 11
figure 11

The numbers of P-AIR particles at a depth of 50m at a 30, b 130, c 230, d 330 days. White dots: Particles. The background color shows the sums of the horizontal and vertical heat transport convergence terms

Full size image

5 Conclusion and future directions

Satellite observations show a trend of SST warming with a meridionally alternating zonal band structure. This study examines the mechanism underlying this observed spatial pattern, and we hypothesize that this structure reflects a difference in residence time within the Japan Sea created by the Japan Sea Throughflow. The accumulation of heat is limited along the path of the throughflow, resulting in weaker SST warming compared to the interior regions.

Using an idealized flat rectangular coastline model with an inflow strait located in the southwest corner and an outflow strait located in the middle of the eastern boundary, we obtain meridional alternating zonal band structures even when spatially uniform atmospheric forcing warms the surface. This pattern arises because the throughflow bifurcates, with one branch flowing along the southern and eastern coastline and another branch that flows along the western boundary and then becomes a zonal jet flowing offshore. As the throughflow exhibits a weaker SST trend than that of the interior, zonal bands of weak SST warming form along the two bifurcating flows while strong SST warming occurs in the area between the flows, thereby establishing a meridionally alternating zonal band structure.

Model experiments with realistic coastline and bathymetry settings suggest that a region with a patch of strong warming forms in the southern interior region due to the presence of a stable recirculation gyre; this area of warming shows a trend of strengthening toward the west. A zonal band with a strong SST trend also originates from the east of Noto Peninsula, where the flow becomes diffused due to the steep shelf. This pattern is also apparent in the observations. Heat budget analysis indicates that the weak SST trends along the coastal and offshore branches are due to cooling induced by horizontal heat transport convergence that balances the surface heat flux, demonstrating the importance of the Japan Sea Throughflow in weakening the SST increase.

Particle release experiments confirm that a difference in residence time underlies the pattern of SST warming trends. Short residence times of about 15–150 days are found along the path of the Japan Sea Throughflow, which limit the impact of surface heat flux while they are much longer in the southern interior region, around 1–3 years. The longest residence times are found within eddies, which create a patch of strong warming near the western boundary of the study domain.

Our model experiments exclude various processes for the sake of simplicity and to focus on the role of the throughflow in driving the spatial variability of the SST warming trend. In reality, both variability in external forcing factors and internal variability exist. Here, we discuss how such variability may affect our results and the direction of future research.

5.1 Variability in external forcing

We focused on a scenario in which the surface heat flux anomaly was constant and served to warm the SST. However, the strength of such an anomaly can change over time. Wang et al. (2022) reported an increase in the net surface heat flux released to the atmosphere over the Japan Sea, which matches with the decline in the SST warming trend (Lee and Park 2019). This situation corresponds to a reduction in the magnitude of the surface heat flux anomaly of our model, which we have kept constant, and thereby weaken the warming trend and may even lead to SST cooling if \(Q{\prime}\) becomes negative. Note that \(\overline{Q }\) in our model represents the surface heat flux required to maintain a steady SST in the Japan Sea and differs from the long-term average of the observed surface heat flux. Hirose et al. (1996) suggest that a surface heat flux of about – 53 \(W \, {m}^{-2}\) is necessary to balance that of the Japan Sea Throughflow. This value is stronger than recent observed values and explains the recent SST warming trend. However, determining exact \(\overline{Q }\) from observations alone is challenging as it is influenced by various factors, such as the strength of the Japan Sea Throughflow. A realistic reanalysis product is necessary to evaluate the role of each process in more detail.

Seasonal variation in atmospheric forcing may increase the role of advection in the interior region. Kim et al. (2020) showed that seasonal varying heat flux leads to the formation of meridional SST gradient structures across a wide area of the Japan Sea that are associated with zonal flow. Increased advection in the interior of the sea may act to reduce the strength of the SST trend and, thus, weaken the contrast between zonal band structures.

Volume transport also change over time and may affect the SST trend. Seasonal variation in the transport of the Japan Sea Throughflow, may increase eddy formation in the southern interior region (Kawabe 1982a; Ito et al. 2014; Yabe et al. 2021). The formation of such eddies may increase residence time, as demonstrated by the particles that become trapped in eddies in P-AIR (Fig. 10b). This process may lead to the formation of the three maxima of SST observed in the southern half of the Japan Sea.

Volume transport monitoring has indicated a slightly increasing trend (to 0.11 Sv decade−1) of the Tsushima Warm Current. Our hypothesis is based on observations that SST warming is weaker in the Tsushima Strait than in the Japan Sea (JMA 2020) and that the volume transport of the Tsushima Warm Current is constant. Although this increasing trend is one order of magnitude lower than the mean volume transport (Kida et al. 2020), the increase may nonetheless be responsible for enhancing the warming trend along the eastern coast of Korea via an increase in meridional heat transport, as the SST gradient runs perpendicular to the direction of flow. Zonal heat transport may remain constant because the zonal SST gradient is small along the coast of Japan and may be partly responsible for creating the observed warming patch near the eastern coast of Korea.

5.2 Internal variability

Changes in internal variability may impact the spatial pattern of the SST trend. Meridional shifts in the subpolar front, which corresponds to the offshore branch in our experiments, are likely to cause changes in SST with a monopole distribution. Specifically, a northward shift of the subpolar front will create a warming trend along the front, while a southward shift will create a cooling trend. Choi et al. (2009) and Park et al. (2007) showed that the interannual shift of this front is 2–3°. However, Chen et al. (2022) found that the decadal meridional shift of the front is characterized by a southward shift of 0.11° decade–1 between 130°E and 135°E and a northward shift of 0.08° decade–1 between 135°E and 138°E. These meridional shifts over decadal time scales appear to be insufficient to explain SST trends at the spatial scale of the Japan Sea. Nonetheless, the observed southward shift between 130°E and 135°E may diminish the SST trend on the western side of the offshore branch, while the northward shift at 135°E–138°E may partly explain the maxima of SST warming found in the observation.

Changes in SST and its spatial distribution over the Japan Sea can lead to changes in atmospheric events, particularly winter snowfall in Japan (Yamamoto and Hirose 2008; Takahashi et al. 2013). The development of the Japan Sea polar air mass convergence zone (JPCZ) causes heavy snow on the Japanese side (Tachibana et al. 2022), and it has been observed that spatial patterns in the SST trend coincide with areas where the JPCZ often develops. While our focus is on the long-term trend from 1993 to 2019, how these long-term changes in SST trends affect atmospheric events, such as snowfall, is a topic for future study.