Dependence of drag coefficient on the spectral width of ocean waves

Abstract

The sea-surface roughness or drag coefficient is ascribed to the effect of various components of ocean waves. Many studies have been focused on the investigation of the dependence of drag coefficient on sea states that are usually denoted by wave age. However, no universally accepted relationship has been obtained up to now and the results are significantly scattered or even contradicted. We reviewed the parameterizations of sea-surface roughness as a function of wave age, and found that the phase speed at spectral peak c_p is an important parameter to characterize the drag coefficient. For the same wave age, drag coefficient increases with increasing c_p. Contrary to the traditional concept, the older waves with greater c_p possesses higher sea-surface roughness for the same wind speed because more wave components participate the air–sea interaction and intensify the wind stress. With the buoy meansurements and the theory of equilibrium range of wind waves, we estimated fricition velocity and proposed that the frequency bandwidth and spectral width of the wave spectrum are more suitable parameters than the traditional wind speed and wave age to be used to parameterize drag coefficient. This study provides a new way to estimate wind stress through the reliable spectra of ocean waves.

1 Introduction

Wind stress or momentum flux through the sea surface is a driving force for ocean waves and ocean circulation. Accurate representation of this stress is important in modeling and forecasting both atmospheric and oceanic dynamics, such as wind wave growth, storm surges, and atmospheric circulation, as well as in interpreting the remotely sensed radar and microwave signatures of the sea surface (Donelan et al. 1993). It depends on the aerodynamic sea-surface roughness, which is, therefore, one of the most important quantities for the description of the physical processes on both sides of the air–sea interface.

The wind stress τ is usually calculated by the bulk formula expressed with the neutral 10-m wind speed U₁₀ and drag coefficient C_D,

$$\tau = \rho_{a} C_{D} U_{10}^{2} ,$$

(1)

where ρ_a is the density of air. The atmospheric boundary layer inside the constant stress layer under neutral conditions is generally assumed to have a logarithmic wind profile, which can be expressed as

$$U(z) = \frac{{u_{*} }}{\kappa }\ln \left( {\frac{z}{{z_{0} }}} \right),$$

(2)

where U(z) is the wind speed at the height of z above sea surface, u_⁎ is the friction velocity of air, κ = 0.4 is the von Kármán constant, and z₀ is the sea-surface roughness length. From Eqs. (1) and (2), C_D can be written as

$$C_{D} = \frac{{u_{*}^{2} }}{{U_{10}^{2} }} = \left[ {\frac{\kappa }{{\ln (10/z_{0} )}}} \right]^{2} ,$$

(3)

where z₀ is in the unit of meter. Therefore, there is a unique relationship between z₀ and the neutral drag coefficient C_D, specifying that the surface roughness specifies the drag coefficient and vice versa.

Accurate evaluation of C_D has been proven to be a major challenge since it requires precise field measurements of fine turbulent fluctuations in the atmospheric boundary layer close to the wavy surface. Considerable research effort has been directed toward obtaining accurate expressions for C_D in terms of wind speed and sea state parameters. Basically, two approaches have evolved, namely, direct parameterization of C_D and indirect parameterization of C_D through a sea-surface roughness z₀ parameterization.

Since the implementation of direct eddy correlation method has led to reliable values of wind stress at moderate wind speeds, the available field data has resulted in a number of quite different parameterizations. It is usually parameterized C_D as a function of mean wind speed U₁₀, but the scatter of experimental data around such parametric dependences is very significant and has not improved noticeably since 1970s (Babanin and Makin 2008; Lin and Sheng 2020; Smith and Banke 1975).

As summarized recently by Zhou et al. (2022), in low to moderate wind speeds (U₁₀ < 20 m/s), previous studies show that C_D increases approximately linearly with wind speed (Anderson 1993; Donelan et al. 2004; Edson et al. 2013; Guan and Xie 2004; Large and Pond 1981; Yelland and Taylor 1996; Smith 1980; Smith and Banke 1975; Wu 1980; Zou et al. 2017). In high winds (U₁₀ > 25 m/s), C_D levels off or decreases with the increasing of wind speed (Bryant and Akbar 2016; Donelan et al. 2004; Hsu et al. 2019; Jarosz et al. 2007; Powell et al. 2003; Sanford et al. 2011; Takagaki et al. 2012; Zhou et al. 2022; Zou et al. 2018). The mechanism of the reduction of C_D has not been clarified (Zhao and Li 2019). In addition, it has often been noted that the act of relating the dimensionless drag coefficient to the dimensional wind speed leads to the inconsistent dimension (Donelan et al. 1990; Johnson and Vested 1992; Zhao and Li 2019).

On the other hand, Charnock (1955) argued on dimensional grounds that the sea-surface roughness should be proportional to the wind stress, and regarded the normalized sea-surface roughness as a constant,

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = \alpha_{C} ,$$

(4)

where g is the gravitational acceleration and α_C is the Charnock coefficient, which was assumed initially to be constant. As shown in Table 1, various values for the Charnock coefficient were determined experimentally over the oceans and laboratories (Edson et al. 2013; Garratt 1977; Geernaert et al. 1986; Kraus and Businger 1994; Liu et al. 2021; Smith 1980; 1988; Wu 1980; Zhao and Li 2019). It should be noted that a constant Charnock coefficient corresponds to a linear dependence of drag coefficient on wind speed (Guan and Xie 2004; Liu et al. 2021; Wu 1980). However, it has long been recognized that a constant α_C does not adequately describe many datasets.

Table 1 Values for Charnock constant from different researchers

Therefore, in addition to wind speed, it is expected that the drag coefficient depends on sea states such as wave age or wave steepness. A more physically sound parameterization is to directly relate the surface drag to the surface roughness elements induced by ocean waves. However, there has been a long on-going debate on how the sea states affecting drag coefficient or sea-surface roughness. The results are significantly different not only quantitatively but also qualitatively.

In this study, we will review the dependence of Charnock coefficient on wave age in Sect. 2. The influence of the phase speed at spectral peak will be discussed in Sect. 3. In Sect. 4, the relation between drag coefficient and the parameters of frequency bandwidth and spectral width will be illustrated, and conclusion will be presented in Sect. 5.

2 Dependence on wave age

It is evident that parameterizing C_D in terms of mean wind speed U₁₀ bears fundamental deficiencies because the mean wind speed U₁₀ does not define the wave properties, like mean or dominant wave height and length, even for ideal wave development situations. It is well-known that the sea-surface roughness is due mainly to surface waves, but it has been difficult to relate the sea-surface roughness to wave parameters in a quantitative way (Donelan et al. 1993). A number of studies suggested that there is a certain relationship between the Charnock coefficients and the sea state represented by the wave age c_p/u_* or c_p/U₁₀ where c_p is the phase speed of waves at the spectral peak.

In fact, researchers commonly attribute some of the scatter in drag coefficient versus wind speed to processes that cannot be represented by the wind speed alone such as the duration of a wind event, the fetch over which the wind is blowing, the depth of the water, etc.—all of which affect the wave age. It is usually regarded that young waves are on average much steeper compared to the old ones (Babanin and Makin 2008; Donelan et al. 1993).

Many authors have tried to improve the description of the sea-surface roughness by parameterizing the Charnock coefficient with wave age. However, there are still lively debates in the research community over this relationship. The common approach to modeling the drag coefficient is to parameterize the normalized sea-surface roughness as a function of wave age using either c_p/u_* or c_p/U₁₀. Stewart (1974) proposed that the Charnock coefficient can be expressed as a function of wave age, which can be conveniently represented as

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = f\left( {{{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} }}} \right. \kern-0pt} {u_{*} }}} \right).$$

(5)

The right side of Eq. (5) can be further expressed as an exponential relationship between the Charnock coefficient and the wave age (Masuda and Kusaba 1987),

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = m\left( {\frac{{c_{p} }}{{u_{*} }}} \right)^{n} ,$$

(6)

where m and n are the coefficients determined based on the field and laboratory observations. When n = 0 and m = α_C, Eq. (6) leads to the classical Charnock relation Eq. (4).

As shown in Table 2 and Fig. 1, in addition to the quantitative difference, these results have given the contradict dependence of Charnock coefficient on wave age. With the positive values of n, it means that the sea-surface roughness increases with increasing wave age and indicates the rougher surface for older waves. With the negative values of n, it represents that the sea-surface roughness decreases with increasing wave age, which indicates the rougher surface for younger waves. Clearly, most investigators have documented greater sea-surface roughness over young and developing wave fields compared to older wave fields.

Table 2 Coefficients m and n in formula of gz₀/u_⁎² = m (c_p/u_⁎)ⁿ proposed by various authors

Fig. 1

Charnock coefficient as a monotonic function of wave age c_p/u_*

Toba et al. (1990) assembled a dataset with a wide range of wave ages by combining open ocean, lake and laboratory data, and led to a conclusion that sea-surface roughness increases with increasing wave age. Donelan et al. (1993) insisted that the laboratory data cannot be lumped together with the field data since the wind-flume waves of a given wave age are smoother than their open-sea equivalents. They argued that the wavenumber density of the laboratory waves is larger than ocean waves, and at high wavenumbers, where flow separation would be a major contributor to wave growth and hence to wind stress, the separation bubbles may merge and create a surface, which acts smoother than one with lower wavenumber densities; that is, closely spaced laboratory waves may shelter each other and leads to smaller sea-surface roughness. Therefore, the two types of waves cannot be used together to determine a single relation between the sea-surface roughness and the wave age. On the other hand, Donelan et al. (1993) insisted that young ocean waves are rougher than old waves in the open ocean. Clearly, it is hard to explain why the young laboratory waves are the smoothest (see the formula derived from laboratory data by Masuda and Kusaba (1987) illustrated in Fig. 1) while the young ocean waves are roughest. These two types of waves should not have essential different characteristics except for the different water depth and fetch. We also note that two mechanisms suggested by Vickers and Mahrt (1997) to explain the negative correlation of sea-surface roughness on wave age: (1) younger waves travel with slower phase speed relative to the wind and thus provide greater bulk shear between the interface and atmospheric surface layer, and (2) younger waves are steeper, which can lead to enhanced flow separation from individual wave crests and stronger pressure drag. Again, if these arguments are also applied to the laboratory waves, it will lead to the conclusion that sea-surface roughness of laboratory waves is greater than that of ocean waves. This inference is contradicted with the observations shown in Table 2 and Fig. 1.

Although most of the authors support that the sea-surface roughness decreases with increasing wave age, their results are significantly different from each other, in which n varies from − 0.008 to − 2.93 (Table 2). No universally accepted form of the scaling has appeared, and it often seems that there are as many wave-age relations as there are datasets with a wave-age dependence (Drennan et al. 2005). As a result, although wave-age formulas were introduced almost 50 years ago, their usefulness has been questioned by many authors. It is obvious that it is difficult to determine the best parameterization in terms of wave age in the calculation of wind stress.

On the other hand, Kitaigorodskii and Volkov (1965) proposed that the sea-surface roughness is related to the function of exp (− κc/u_⁎), where c is the phase speed of waves (Johnson and Vested 1992). For a continuous wave spectrum, Kitaigorodskii (1970) found (Johnson and Vested 1992)

$$z_{0}^{2} = \alpha_{*}^{2} \int_{0}^{\infty } {S\left( k \right)\exp \left[ {{{ - 2\kappa c\left( k \right)} \mathord{\left/ {\vphantom {{ - 2\kappa c\left( k \right)} {u_{*} }}} \right. \kern-0pt} {u_{*} }}} \right]} \, dk,$$

(7)

where α_⁎ is a constant of proportionality, S(k) is the spectral energy density in the wavenumber space, and k is the wavenumber. Equation (7) shows that the smaller the phase speed, the greater the weighted value for sea-surface roughness. In other words, the wave components with high frequencies contribute more to sea-surface roughness than those with low frequencies in the case of the same spectral energy density. It is also clear that the sea-surface roughness increases with the frequency bandwidth of the wave spectrum S(k). For application, Kitaigorodskii (1970) further simplified sea-surface roughness as a function of wave height and wave age

$$z_{0} = 0.075H_{s} \exp \left( { - \kappa \frac{{c_{p} }}{{u_{*} }}} \right),$$

(8)

where H_s is the significant wave height. It is well-known that wave height increases with increasing wave age; thus, this equation implies that, under the restrictions of other factors (e.g., wave height), the sea-surface roughness does not necessarily decrease with increasing wave age.

Following the idea of Kitaigorodskii and Volkov (1965) and the observational data, Johnson and Vested (1992) proposed a similar formula

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = \left\{ \begin{gathered} 0.018\left( {\frac{{c_{p} }}{{u_{*} }}} \right)\exp \left( { - 0.2\frac{{c_{p} }}{{u_{*} }}} \right){,}\quad {{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} < 10}}} \right. \kern-0pt} {u_{*} < 10}} \hfill \\ 0.0808\left( {\frac{{c_{p} }}{{u_{*} }}} \right)^{ - 0.52} {,}\quad {{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} \ge 10}}} \right. \kern-0pt} {u_{*} \ge 10}} \hfill \\ \end{gathered} \right..$$

(9)

To reconcile the contradicted results about the dependence of the sea-surface roughness on wave age, Volkov et al. (2001) proposed the Charnock coefficient as a function of wave age

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = \left\{ \begin{gathered} 0.03\left( {\frac{{c_{p} }}{{u_{*} }}} \right)\exp \left( { - 0.14\frac{{c_{p} }}{{u_{*} }}} \right),\quad {{0.35 < c_{p} } \mathord{\left/ {\vphantom {{0.35 < c_{p} } {u_{*} < 35}}} \right. \kern-0pt} {u_{*} < 35}} \hfill \\ 0.008\left( {\frac{{c_{p} }}{{u_{*} }}} \right)^{ - 0.52} ,\quad {{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} \ge 35}}} \right. \kern-0pt} {u_{*} \ge 35}} \hfill \\ \end{gathered} \right..$$

(10)

Hwang (2005) also pointed out that the dependence of the Charnock coefficient on wave age is non-monotonic when the dataset covers a wide range of wave age by including laboratory and field data. Hwang (2005) proposed

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = 3.14\left( {\frac{{c_{p} }}{{u_{*} }}} \right)^{2} \exp \left[ { - 3.62\left( {\frac{{c_{p} }}{{u_{*} }}} \right)^{0.352} } \right].$$

(11)

As shown in Fig. 2, it is evident the three formulas mentioned above share the common idea that the sea-surface roughness increases with increasing wave age for young waves, and then decreases with increasing wave age for old waves although the mechanism is not clarified. These formulas are consistent with each other qualitatively, but significantly different in quantity.

Fig. 2

The Charnock coefficient as a non-monotonic function of wave age c_p/u_*

However, this reconciled viewpoint was challenged by the recent work of Lin and Sheng (2020) who assembled eight datasets for expanding the range of wave age. Lin and Sheng (2020) suggested that the best fit formula of their datasets can be expressed as

$$\frac{{gz_{0} }}{{u_{*}^{2} }} = \left\{ \begin{gathered} 1.63\left( {{{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} }}} \right. \kern-0pt} {u_{*} }}} \right)^{ - 1.98} ,\quad {{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} < 12}}} \right. \kern-0pt} {u_{*} < 12}} \hfill \\ 1.43 \times 10^{ - 2} \left( {{{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} }}} \right. \kern-0pt} {u_{*} }}} \right)^{ - 0.008} ,\quad 12 \le {{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} < 30}}} \right. \kern-0pt} {u_{*} < 30}} \hfill \\ 4.03 \times 10^{ - 5} \left( {{{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} }}} \right. \kern-0pt} {u_{*} }}} \right)^{1.59} ,\quad {{c_{p} } \mathord{\left/ {\vphantom {{c_{p} } {u_{*} \ge 30}}} \right. \kern-0pt} {u_{*} \ge 30}} \hfill \\ \end{gathered} \right..$$

(12)

On the contrary, Eq. (12) indicates that the sea-surface roughness decreases with increasing wave age for very young waves, and then it is almost independent of wave age. For well-developed waves or swells, the sea-surface roughness begins to increase quickly with wave age. In other words, the youngest and oldest waves are rougher than the moderate waves.

More recently, Zhou et al. (2022) investigated drag coefficient under tropical cyclones and its dependence on sea states by combining upper-ocean current observations and a coupled ocean-wave model. They found that C_D and sea-surface roughness increase with increasing wave age c_p/U₁₀ when the seas are younger (c_p/U₁₀ < 0.6). This result is again contradicted with that of Lin and Sheng (2020). In fact, Zhou et al. (2022) found that the sea-surface roughness decreases with increasing wave age c_p/U₁₀ in the wind range of 25–30 m/s, and increase with increasing wave age c_p/U₁₀ in higher winds. In the different wind ranges, the dependence of sea-surface roughness on wave shows very different behaviors.

It is clear that the dependence of the sea-surface roughness on wave age cannot be clarified by simply expanding the datasets for the wide range of wave age. Some new mechanisms about the dependence of sea-surface roughness on sea state must be revealed before the convincing wave-age-dependent formula can be obtained. This highlights the need to understand more completely the basic physics of the air–sea momentum exchange to get the reliable parameterization of the drag coefficient.

3 Influence of c _p on drag coefficient

As discussed above, influence of the sea state on the drag has proved elusive. Although many wave-age-dependent formulas for the sea-surface roughness or drag coefficient have been proposed, none of them are convincing enough to be applied in the calculation of wind stress. In reality, the wind-speed-dependent formulas usually perform better than those wave-age-dependent formulas. For example, Edson et al. (2013) found that formula for COARE 3.5 with wind-speed-dependent Charnock coefficient matches better than that with wave-age-dependent Charnock coefficient. They suggested the reason is that the inverse wave age u_⁎/c_p varies nearly linearly with wind speed in long-fetch conditions for wind speeds up to 25 m/s. In the other words, the variation of wave age in many datasets is usually due to the change of u_⁎, not c_p, in which the latter varies in a very narrow range for a single dataset, and is the essential parameter denoting the development degree of ocean waves. The decreasing of sea-surface roughness with increasing of wave age suggested by many studies only reflects the varying of wind speed, not c_p. This problem was also noted by Smith et al. (1992) in HEXOS dataset, in which the variation of c_p/u_⁎ is due more to u_* than to c_p.

It reminds us about the ambiguity of the wave age concept for the air–sea interaction applications. Representing the waves by wave age c_p/u_⁎ or c_p/U₁₀ implies “spectral similarity,” that is, that the wave spectrum has a consistent shape for a given wave age. It is supposed that the wave age would be a single most important parameter which defines all the others. However, the wave age is only the ratio of velocities between the dominant wave and wind, the same wave age may correspond to very different values of c_p. The wave age only represents the phase speed of dominant wave relative to wind speed, and cannot reflect the whole wave components from high to low frequencies.

Table 3 summarizes the varying ranges of wind speed U₁₀ and c_p for some observational datasets. For comparison, the corresponding water depths and the maximum values of C_D are also added in Table 3. It can be seen that the U₁₀ ranges are significantly overlapped with each other, but the c_p ranges are significantly different, in which the c_p values roughly increase from shallow to deep waters. It is easy to explain this phenomenon that the longer waves could not exist in shallow water due to the limitation of water depth-induced wave breaking. In deep water, both short and long waves could be found, which are determined by the magnitudes of wind speed and fetch.

Table 3 The variations of wind speed U₁₀ and phase speed at the spectral peak c_p for some observational datasets

From Table 3, it seems to have a trend that C_D increases with increasing c_p. Since the wave spectral peak shifts from high to low frequency with the development of wave field, the greater c_p indicates that more wave components contribute to the sea-surface roughness and intensify the air–sea exchange as suggested by Eq. (7). It can be inferred that the sea-surface roughness would be greater for greater c_p, which is not directly related to wind speed and strongly constrained by fetch and water depth due to wave breaking.

Figure 3 shows the drag coefficient as a function of wave age with various fixed values of c_p according to COARE 3.5 algorithm of Edson et al. (2013). For a fixed c_p, C_D decreases with increasing wave age, which is ascribed to the decreasing of wind speed. For a given wave age, C_D increases with increasing c_p, which is consistent with our inference above. It is suggested that C_D is a multivalued function of wave age, and cannot be regulated by a simple parameterization proposed by some investigators such as Geernaert et al. (1987) and Babanin and Makin (2008).

Fig. 3

Drag coefficient versus wave age for various fixed c_p based on COARE 3.5

Figure 4 is similar to Fig. 3, but Fig. 4 shows drag coefficient versus wind speed with various fixed c_p values while wave age c_p/u_⁎ is limited in the range from 1 to 35, which corresponds to the situation of wind waves. It can be seen that C_D increases with increasing wind speed for a fixed c_p. However, it shows that the smaller the value of c_p, the greater the value of C_D, which means that the laboratory waves would be rougher than ocean wave for the same wind speed. This is contradicted with the current observations because it is evident that laboratory waves of a given age are smoother than their open-sea equivalents (Donelan et al. 1993). Therefore, the COARE 3.5 algorithm is still not appropriate to describe the dependence of sea-surface roughness on sea states.

Fig. 4

Drag coefficient versus wave speed for various fixed c_p based on COARE 3.5

Based on the above analysis, we suppose that c_p is a more important parameter than wave age and wind speed for the parameterization of drag coefficient. The higher the c_p value, the more wave components would contribute to sea-surface roughness, which leads to a greater C_D. Zhou et al. (2022) found that C_D is almost independent of wind speed for wind speeds of 25−55 m/s. In this situation, it is believed that c_p approaches its saturated value due to wave breaking, which leads to the stability of drag coefficient although the wind speed varies a lot.

As mentioned above, the magnitude of c_p is a measure of how many wave components contribute to the sea-surface roughness. Based on the RASEX observations, Vickers and Mahrt (1997) pointed out that with large frequency bandwidth B_w, the wind stress is large for a given wave age and wind speed due to enhanced drag from multiple wave modes. The frequency bandwidth parameter B_w accounts for the breadth of wave spectra due to multiple wave modes. They found an excellent fit to the RASEX data that can be expressed as

$$C_{D} = - 0.5 + (c_{p} /u_{*} )^{ - 2/3} + 0.9B_{w} \lambda_{p} /U_{10} ,$$

(13)

where λ_p is the wave length of the dominant wave that is included on dimensional grounds, the frequency bandwidth B_w has the unit of s⁻¹. Vickers and Mahrt (1997) indicated that the bandwidth parameter may describe the enhancement of the drag coefficient due to swell in the open-ocean case, and may explain the larger drag coefficients in the open-ocean compared to on-shore case in RASEX for a given wave age. In other words, the smaller drag coefficients in shallow water than in deep water are ascribed to the narrower frequency bandwidth in shallow water.

4 Spectral width and drag coefficient

As discussed above, c_p is an important parameter to describe the development of wind waves. The wave field with greater c_p means more wave components involved air–sea interaction, and intensifies the sea-surface roughness. To confirm this inference, we selected the spectra of wind waves measured by the buoys from the National data Buoy Center (NDBC), and estimated the friction velocities based on the concept of equilibrium ranges proposed by Toba (1973) and Phillips (1985).

4.1 Data processing

To clarify this mechanism, a large amount of wave spectra measured by buoys from the National Data Buoy Center (NDBC) are averaged in ensemble for the same c_p of wind waves. In this way, we could obtain various spectra of wind waves denoted by different c_p values in a wide range.

We have chosen the observational data from 102 NDBC buoys in deep water from January 2011 to December 2020. The locations of these NDBC buoys are shown in Fig. 5. The measured spectra of wind waves are selected through the following four criteria:

• 1. The frequency spectrum S(f) has only one significant peak, where f is the wave frequency.

• 2. The angle between the wind and the wave is less than 45°,

• 3. It satisfies with the wave age c_p/U₅ = gT_p/(2πU₅) < 1.27, where T_p is the period at spectral peak and U₅ is the wind speed at 5 m above the sea surface measured by NDBC buoys.

• 4. The significant wave height H_s < 0.03U₅², which is approximately equivalent to the well-developed wind waves.

Fig. 5

Locations of NDBC buoys in the dataset

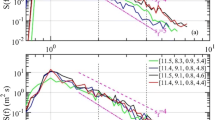
With these criteria, we finally obtained 202, 764 spectra for wind waves. To get the robust wave spectra, we averaged the wave spectra in ensemble for the same T_P and certain range of wind speed within ± 1 m/s. Some ensemble averaged spectra are shown in Fig. 6 in which the spectra multiplied by f⁴ to confirm the equilibrium range of wind waves.

Fig. 6

Examples of ensemble averaged spectra S(f) multiplied by f⁴ with the same T_p in each panel with various wind speeds indicated in the right side. The solid lines with circles are colored by mean values in the U₅ wind speed bins. The vertical dashed line shows the corresponding T_p. The bold solid line indicates the location of the equilibrium range

According to the famous equilibrium range theory by Phillips (1985) and Toba (1973), the frequency spectrum S(f) of wind waves in equilibrium range can be expressed as

$$S\left( f \right) = \left( {2\pi } \right)^{ - 3} \alpha_{T} gu_{*} f^{ - 4} ,$$

(14)

where α_T is Toba constant. The equilibrium range of wind waves is clearly confirmed as shown in Fig. 6. Following the method of Thomson et al. (2013) and Hanson and Phillips (1999), Toba constant can be determined from the directional distribution of wind waves. The values of Toba constant of the ensemble averaged spectra are shown in Fig. 7. It can be seen that α_T is roughly independent of wind speed, and increases slightly with c_p. Therefore, the friction velocity u_⁎ could be obtained in the equilibrium range of wind waves, then U₁₀ can be calculated through Eq. (2), and drag coefficient can be calculated by C_D = u_⁎²/U₁₀² (Juszko et al. 1995). This method has been widely applied to estimate wind stress (Lenain and Melville 2017; Voermans et al. 2020).

Fig. 7

Toba constant of ensemble averaged spectra

To validate u_⁎ from the equilibrium range of wind waves, we compared with the friction velocities calculated by four models. The first model is presented by Voermans et al. (2020) using the wind input source function proposed by Donelan et al. (2005), based on the definition of wind stress in the wave boundary layer (Chalikov and Rainchik 2011; Tsagareli et al. 2010). The second one is given by Takagaki et al. (2012) with the best fit of laboratory and field data for the wind speeds up to 68 m/s. The third and fourth models are from COARE 3.5 with the Charnock coefficient as a function of wave age and wind speed, respectively (Edson et al. 2013). It is noted that the COARE 3.5 algorithm was derived from several datasets through eddy covariance method, which is regarded as the direct measurements of wind stress.

Figure 8 shows the comparisons of the friction velocity u_⁎ from equilibrium range against u_⁎T, u_⁎V, u_⁎CE, and u_⁎Ed derived from the methods of Takagaki et al. (2012), Voermans et al. (2020), COARE 3.5 algorithm (Edson et al. 2013) with the Charnock coefficient as a function of wind speed and wave age, respectively. It is shown that the correlation coefficients are up to r = 0.96, with a little small r = 0.95 in the case of wave-age-dependent COARE 3.5. The smallest root mean square error (RMSE = 0.072 m/s) and bias (= − 0.002 m/s) occur in the case of Voermams et al. (2020). On the contrary, the greatest values of RMSE and bias are obtained in the case of wave-age-dependent COARE 3.5. As a whole, u_* estimated from equilibrium range of wind waves is consistent well with that from the other methods including the eddy covariance method. In the following, we will try to parameterize the drag coefficient with new parameters.

Fig. 8

Comparisons of the friction velocity u_⁎ from equilibrium range with u_⁎T from Takagaki et al. (2012), u_⁎V from Voermans et al. (2020), u_⁎CE and u_⁎Ed from the COARE 3.5 algorithm (Edson et al. 2013) in terms of Charnock coefficient as a function of wind speed and wave age, respectively. The phase speeds at the spectral peak are also shown in the figure

4.2 Parameterization with new parameters

Figure 9 shows C_D versus wind speed with various c_p values. As a function of wind speed, it is surprising that values of C_D are very scattered although C_D still roughly increases with wind speed as a whole. It can be seen that C_D generally increases with increasing c_p, which is consistent with our foregoing inference. Since our results were derived from more complicated wave systems that include various wind speeds and c_p values, C_D does not monotonously increase with increasing wind speed. Instead, for a fixed c_p, it is found that C_D gets saturated at its critical wind speed, and then levels off or decreases with continuously increasing wind speed. The smaller c_p corresponds to the smaller critical wind speed, which means the critical wind speeds in shallow water are smaller than those in deep water. This is consistent with the observations in recent years. In deep water, it is stressed that the critical wind speed depends on the c_p value of wave field concerned. It may be the reason why the critical wind speeds found in deep water are so different by various investigators. For example, Sanford et al. (2011), Black et al. (2007), Bell et al. (2012), Richter et al. (2016), and Holthuijsen et al. (2012) suggested the critical wind speeds are 20, 23, 30, 35, and 40 m/s, respectively, although all the observations were made in open oceans. Here we suppose the main reason is the different c_p ranges involved in different investigations.

Fig. 9

Relationship between C_D and U₁₀ with different values of c_p

As mentioned above, c_p is a kind of measure about how many wave components participate in the air–sea interaction. By taking the frequency bandwidth B_w into account, Vickers and Mahrt (1997) showed that the parameterization of C_D can be improved. In reality, however, we must find a practical way to estimate the frequency bandwidth. Here we define an inverse frequency bandwidth by T_p − T_m, where T_p is the wave period at the spectral peak, and T_m is a mean wave period that is defined as

$$T_{m} = \left( {{{m_{0} } \mathord{\left/ {\vphantom {{m_{0} } {m_{2} }}} \right. \kern-0pt} {m_{2} }}} \right)^{1/2} ,$$

(15)

where m₀ and m₂ are the zeroth and second-order moments of the wave spectrum, respectively. The n-th order moment of the spectrum is defined as

$$m_{n} = \int_{0}^{\infty } {f^{n} S\left( f \right)df} ,\quad n = 0,1,2,3,4, \ldots .$$

(16)

Figure demonstrates the relationship between C_D and the inverse frequency bandwidth T_p − T_m with the values of c_p illustrated for comparison. It is surprising that C_D is well consistent with T_p − T_m, and their relationship can be empirically expressed as

$$C_{D} = \left\{ { - 1.14\left( {T_{p} - T_{m} } \right)^{2} + 8.53\left( {T_{p} - T_{m} } \right) + 11.53} \right\} \times 10^{ - 4}$$

(17)

with the correlation coefficient of 0.94. It also shows that T_p − T_m increases with increasing c_p, in which the drawback of this relationship is the inconsistent dimension of the two sides (Fig. 10). We further use the non-dimensional bandwidth scaled by T_p to parameterize C_D, which is shown in Fig. 11, and this relationship can be expressed as a linear function of non-dimensional bandwidth (T_p − T_m)/T_p

$$C_{D} = \left\{ {65.76{{\left( {T_{p} - T_{m} } \right)} \mathord{\left/ {\vphantom {{\left( {T_{p} - T_{m} } \right)} {T_{p} + 8.28}}} \right. \kern-0pt} {T_{p} + 8.28}}} \right\} \times 10^{ - 4}$$

(18)

with the correlation coefficient of 0.89. It is indicated that C_D increases with the non-dimensional bandwidth linearly with the correlation coefficient as high as 0.89. Compared with wind speed, the non-dimensional bandwidth is more suitable to parameterize C_D.

Fig. 10

Relationship between C_D and the inverse frequency bandwidth T_p − T_m with different values of c_p

Fig. 11

Relationship between C_D and the non-dimensional bandwidth (T_p − T_m)/T_p

Furthermore, we calculate the spectral width of wave spectrum ε, a dimensionless parameter that was defined by Cartwright and Longuet-Higgins (1956),

$$\varepsilon = \left( {1 - {{m_{2}^{2} } \mathord{\left/ {\vphantom {{m_{2}^{2} } {m_{0} m_{4} }}} \right. \kern-0pt} {m_{0} m_{4} }}} \right)^{1/2} .$$

(19)

The spectral width parameter ε is a dimensionless coefficient ranging from 0 to 1.0 (Prasada Rao 1988). The greater ε corresponds to the broader spectral width, in which wave energies are distributed among wider frequency range of ocean waves.

Figure 12 shows that drag coefficient C_D is well consistent with the spectral width parameter ε, and this relationship can be written as

$$C_{D} = \left( {4.85\varepsilon^{2} - 1.20\varepsilon + 0.935} \right) \times 10^{ - 3}$$

(20)

with the correlation coefficient of 0.96. Since the maximum value of ε = 1, Eq. (20) indicates that the maximum of C_D is 4.59 × 10⁻³, which seems to be a reasonable value by observations. It means that the saturated value of C_D is determined by the spectral width, not the wind speed.

Fig. 12

Drag coefficient C_D versus the spectral width parameter ε. The solid line is the best fit of the data

In addition, another spectral width ν defined by Longuet-Higgins (1975) is also tested to parameterized C_D. The definition of ν is

$$\nu = \left( {{{m_{0} m_{2} } \mathord{\left/ {\vphantom {{m_{0} m_{2} } {m_{1}^{2} - 1}}} \right. \kern-0pt} {m_{1}^{2} - 1}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} .$$

(21)

In fact, the spectral width ν can be written as

$$\nu = \left( {\frac{{T_{01}^{2} }}{{T_{m}^{2} }} - 1} \right)^{1/2}$$

(22)

where T₀₁ = m₀/m₁ is the first-order period. It is clear that ν is similar to the non-dimensional bandwidth. The advantage of the spectral width ν is only involved in the second order of moments of wave spectra compared with ε, which has to calculate the fourth order of moments of wave spectra. Figure 13 shows the linear relationship between C_D and ν

$$C_{D} = \left( {9.00\nu - 0.91} \right) \times 10^{ - 3}$$

(23)

with the correlation coefficient of 0.93.

Fig. 13

Drag coefficient C_D versus the spectral width parameter ν. The solid line is the best fit of the data

The advantage of parameterization of drag coefficient in terms of non-dimensional bandwidth and spectral widths through Eq. (18), Eq. (20), and Eq. (23) is that C_D increases with these parameters monotonously. The saturated value of C_D is determined by the maximum value of the spectral width ε and ν for the investigated wave systems. The non-dimensional bandwidth (T_p − T_m)/T_p and spectral width of ε and ν are more suitable to characterize the sea-surface roughness than wind speed and wave age. Based on the parameterizations using these three parameters, the drag coefficient and sea-surface roughness monotonically increase and do not have multiple values. The estimation of wind stress is ascribed to the accurate measurements of spectra of ocean waves, which is more convenient compared to the measurements of turbulent fluxes in the air side, especially at high wind speeds.

In addition, the new version of WAVEWATCH III with the source-sink terms ST6 could robustly capture the high-order moments of wave spectra, and thus the spectral widths. With the results of WAVEWATCH III, Liu et al. (2021) calculated the second-, third-, and fourth-order moments, and compared with buoy measurements in their Fig. 14. Liu et al. (2021) found that the model results of the mean square slope calculated by the fourth moment m₄ are consistent with the buoy observations with correlation coefficient 0.94. Therefore, the wave mode could capture the spectral width robustly and can be used to estimate wind stress through our new parameterizations.

Fig. 14

The spectral width ε versus wave age calculated from 3 NDBC buoys. The black and red solid dots denote the situations of angles between wind and wave directions greater and less than 45°, respectively

The intensity of air–sea momentum flux is determined by how many wave components effectively participate in the air–sea interaction, and it can be denoted by frequency bandwidth and spectral width. In other words, the spectrum of wind waves is directly related to the air–sea interaction. Therefore, we provide a new mechanism for the air–sea interaction and a new method to estimate the wind stress from the wave spectra of ocean waves.

Although the parameterizations with the spectral widths are derived in the case of wind waves, they are expected to be applied in the swell conditions because the spectral width is a robust parameter. Figure 14 shows the spectral width ε versus wave age c_p/U₅ from the measurements of NDBC buoys. To distinguish the situations of different directions between winds and waves, the angles between them greater and less than 45° are denoted by black and red solid dots, respectively. Except for the cases of very small wave ages, the spectral width ε is almost independent of wave age. In the swell conditions (with greater wave ages), ε varies significantly, which is believed to be determined by detailed components of the wave system. Compared with red dots and black dots, it seems that the former varies significantly, and the latter reflects the influence of the misalignment between wind and waves, which keeps ε in a smaller range. Some measurements show that the wind stress is much smaller under strong swell wave conditions because of the swell-induced upward momentum flux. In this situation with low wind speeds and long swells, it is expected that ε is very small due to the absence of high-frequency waves. In this way, our parameterization can capture this behavior to some extent. Obviously, it needs further study to confirm its applicability in swell conditions.

4.3 Validation with the measurements of wind stress by eddy covariance method

The coincident wind and wave observational data were obtained at a fixed platform located in the northern South China Sea (21° 26.5′ N, 111° 23.5′ E), approximately 6.5 km southeast off the coast, where the water depth around the platform is about 16 m. The measurement was conducted from 4 January 2021 to 8 April 2021. Wind and wind stress were measured by an eddy covariance system mounted at a height of 5.5 m above the sea surface, operating at a sampling frequency of 10 Hz. Nortek acoustic wave and current profiler deployed on the sea-bed near the platform by which measured the surface elevation and velocity at 1-h intervals with a sampling frequency of 4 Hz and a duration of 2048 s, from which the directional wave spectra could be derived using the SUV method.

We selected the wind observational data with the wind directions from 55° to 235° in clockwise from the north. Thus, the wind roughly came from the southeast, and the deflection angles between the wind and waves were less than 50°. We further chose the wave data with the wave age less than 3.0, and the significant wave heights smaller than 0.03 U₁₀², which corresponds to the wave height of fully developed wind waves. By these criterions mentioned above, the wave data dominated by wind waves were used to analyze in this study.

Figures 15 and 16 show the variations of drag coefficient with wind speed U₁₀ and the spectral width parameter ε, respectively. Equation (20) is also illustrated in Fig. 16 for comparison. It can be seen that our parameterization of Eq. (20) is roughly consistent with the observational data. It is emphasized that, due to the limited in situ measurements, we could not find enough data in the condition of pure wind waves since the natural seas are usually mixed with wind waves and swells, especially in the shallow water. Therefore, our parameterization should be further validated with more extensive observational data under the wind–sea-dominated conditions in the future.

Fig. 15

Drag coefficient versus wind speed, which were derived from the observational data of wind stress measured at a platform in the South China Sea

Fig. 16

Drag coefficient versus the spectral width parameter ε, which were derived from the coincident observational data of wind stress and wave spectra measured at a platform in the South China Sea. Equation (20) is plotted in the figure (solid line) for comparison

5 Conclusion

It is well-known that ocean waves play an important role on the air–sea momentum flux; the wind stress is directly related to the sea-surface roughness induced by ocean waves. However, the dependence of sea-surface roughness or drag coefficient on wave age is so complicated that none convincing parameterization has been widely accepted until now.

We have reviewed the dependence of sea-surface roughness or drag coefficient on wave age c_p/u_*. It is found that most of the datasets previously used correspond to a narrow range of c_p; thus, the changing of wave age is mainly ascribed to the variation of wind speed. Instead, sea-surface roughness is constrained by c_p as a whole; the higher c_p corresponds to greater sea-surface roughness at the same wind speed. In this situation, more wave components would contribute to the formation of sea-surface roughness and intensify the air–sea interaction.

The traditional concept that younger waves have greater sea-surface roughness than older waves is only valid for the same c_p, in which the wave age varies with the changing of wind speed. For the same wind speed, the sea-surface roughness increases with increasing c_p. In this situation, the drag coefficient is a multivalued function of wave age. For the same c_p, drag coefficient increases with wind speed, and levels off at a critical wind speed, and the critical wind speed increases with increasing c_p. In the open ocean, various critical wind speeds have been observed because of wide range of c_p value. The younger waves with smaller c_p will have smaller sea-surface roughness for the same wind speed. Due to wave breaking and water depth limitation, c_p will reach its saturation and the drag coefficient levels off at the critical wind speed. In the shallow water, however, only the smaller critical wind speeds could be found since the c_p values are significantly suppressed by water depth due to wave breaking and bottom friction.

We suggest that the non-dimensional bandwidth and the spectral widths have more advantages to parameterization of drag coefficient compared with the traditional wind speed and wave age. These parameters are a kind of measure that how many wave components could contribute to the sea-surface roughness. In this situation, drag coefficient is a monotonic increasing function of bandwidth or spectral widths. When the spectral width reaches its maximum, drag coefficient is saturated, which means all available wave components participate in the air–sea interaction. Different wave systems have different maximum values of spectral width, thus correspond to various critical wind speeds as observed by many studies. It is also expected that the parameterizations with spectral width could apply to the situation of swell fields although it remains to be further confirmed.

This study proposed a new way to estimate drag coefficient through the spectral width obtained from wave spectra. It is more convenient compared to the traditional methods of direct eddy correlation and wind profile in the air side and indirect current profile in the water side.