1 Introduction

The East Sakhalin Current (ESC) is located off the western coast of the Sea of Okhotsk, the southernmost marginal sea with sea ice production in the Northern Hemisphere. This current collects riverine discharges from the far-eastern Eurasian Continent, including the Amur River, which is the tenth largest river in the world. This river contains abundant nutrients such as iron, which is an essential micronutrient for phytoplankton growth in the subarctic North Pacific (Nishioka et al. 2014). Although the riverine iron is primarily deposited and sedimented on the ESC upstream shelf, the deposited iron is likely to be resuspended by strong wintertime mixing and therefore mingle with the surrounding water as well as become frozen into the sea ice (Ito et al. 2017) and then transported to the south. The transported mixed water and ice, which contain considerable iron (Kanna et al. 2014, 2018), facilitate the next spring blooms not only in the southern Sea of Okhotsk (Mustapha and Saitoh 2008) but also in the Oyashio and western North Pacific Ocean (Kuroda et al. 2019).

The ESC has two cores (Ohshima et al. 2002) (see also the arrows in Fig. 1a). The coastal core is a wind stress driven current characterized by the arrested topographic waves (ATWs); the ATWs accompanies the coastal current are constrained to the nearshore (Csanady 1978), which extend to Hokkaido Island (Ohshima et al. 2002; Nakanowatari and Ohshima 2014). The other core on the slope is considered the western boundary current (WBC) of the central cyclonic gyre (Ohshima et al. 2002, 2004, 2005). Although the along-shore dynamics of this current have been studied intensively, little information related to the relatively small cross-isobath component of the ESC and its coupled vertical circulation and mixing is available. The ageostrophic cross-isobath current is subtle compared to the along-isobath current, but it is substantial for water mass exchange and for modulating the biogeochemical budgets (Brink 2016) in coastal areas (Federiuk and Allen 1995; Pickart 2000).

Fig. 1
figure 1

Outline of the model setting and an unprocessed model output. a Schematic diagram of the research domain—the Sea of Okhotsk. The black arrows indicate the two ESC cores. The Amur River mouth, which is marked by a petal-like sign, belongs to the river with the largest discharge in the research domain. The area inside the black frame represents the ESC upstream, and we present the horizontal information for this area in the subsequent analysis. The shading and orange contours denote the topography. The blue arrows denote the climatological January-mean wind stress. b The January mean sea ice concentration for the CTRL case. The coloured shading and white contour denote the sea ice concentration. The coloured contour is the isobath with a depth of 500 m. c Model domain northern than 10 °S. The shading denotes the topography. The orange contour is the 500-m isobath. The light grey contours represent COCO’s Mercator grid at every 50 and 30 grid intervals in approximately the N–S and W–E directions, respectively, which is the same as in a

Full size image

It is particularly difficult to observe the temperature and salinity as well as the nutrients in the ESC upstream during the winter because of the presence of sea ice (Mamontova 2021; see also Fig. 1b for the model simulation’s January mean sea ice concentration). Nevertheless, profiling float measurements detected mixed layer formation off the east coast of Sakhalin, which is as deep as 140 m along the shelf break in early winter (Ohshima et al. 2005). This mixed layer is significantly deep, as the mixed layer depth (MLD) in the Sea of Okhotsk is typically suppressed to less than 100 m (Uehara et al. 2012) because of the substantial freshwater input from the rivers around the Sea of Okhotsk, including the Amur River. Further, Ito et al. (2017) observed the resuspension of sediments via high-resolution backscatter measurements using an acoustic Doppler current profiler and found that vertical mixing occurs throughout the water column (> 100 m) near the shelf break in the ESC upstream. They conjectured that the resuspended materials, which contain iron, are entrained to the surface, frozen into the sea ice, and finally transported southward by the ESC.

Considering the difficulty of wintertime hydrographic observations off the Sakhalin, observations of the ESC by an ice breaker off Hokkaido in the south of the Sea of Okhotsk were suggestive, and similar well-mixed water masses were observed at the shelf break (Ohshima et al. 2005, 2001; Mizuta et al. 2004). The mixed water mass has a thickness larger than 200 m and contains sea-ice melting water as well as riverine discharge water from the far-eastern Eurasian Continent (Kanna et al. 2018), while the water over the shallower shelf was stratified. This deep mixed water is characterized by high nutrient and iron concentrations, and it flows out from the Sea of Okhotsk as the Coastal Oyashio and fertilizes the western North Pacific (Kuroda et al. 2019). To obtain a better understanding of these structures, which are adjacent to the shelf break along the ESC, further study of the vertical circulation and mixed-layer formation is required.

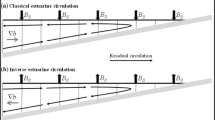
The primary dynamical constituents characterizing the cross-shelf flow of the ESC in winter are a downwelling-favourable northwesterly wind from Siberia, the buoyancy flux from riverine discharge, and bottom friction. The air–sea heat exchange is insulated because sea ice covers the entire ESC coastal region (Fig. 1b). Idealized simulations indicate that when a downwelling-favourable wind drives an along-shelf current that is initially stratified, a well-mixed and relatively stagnant layer is formed inshore adjacent to the downwelling front (Allen and Newberger 1996; Austin and Lentz 2002). Additionally, the surface Ekman transport from the open ocean is blocked because of the coupling between the surface- and the bottom-boundary layers of the nearshore region (Mitchum and Allan 1986). However, once inshore stratification is derived from the riverine freshwater plumes, the cross-shelf overturning structure can be significantly modified via the internal water stress due to a thermal wind shear—the ‘geostrophic stress’. In particular, when the geostrophic stress is higher than the wind stress, the Ekman overturning (EOT) adjacent to the coast is likely to be reversed. Previous coastal studies performed a reversed EOT with idealized simulations, and the geostrophic stress is noticeable inside riverine plumes that are ~ 15 m in depth (Chen and Chen 2017; Moffat and Lentz 2012; Lv et al. 2020), which is where the surface and bottom stresses are balanced. In this study, we focus on the shelf break fronts in the ESC that have deeper structures with a depth of ~ 100 m. Although a few studies have investigated the cross-shelf overturning in a density front of this depth scale (e.g., Shcherbina and Glen 2008), since the surface and bottom boundary layers are typically decoupled, its dynamics have not been effectively explored.

The effects of geostrophic stress on the surface mixed layer across a front were discussed separately in terms of the open ocean, including those associated with the tropical cold tongue as well as the Kuroshio Extension (Cronin and Kessler 2009; Cronin and Tomoki 2016). It was pointed out that the geostrophic stress significantly modifies the Ekman transport and results in upwelling and downwelling structures across the front. This dynamic consequently deepens the MLD on the downwelling side, which suggests that the upwelling/downwelling associated with the cross-shelf overturning impacts the deep mixed layer formation over the shelf break. Note that in the case of the ESC, the surface heat fluxes are insulated by sea ice (Fig. 1b), so the turbulent kinetic energy comes solely from the work of sea ice stress on the sea surface. Further, we disregard the residual overturning due to baroclinic instability (e.g., Spall and Leif 2016) because baroclinic eddies were not observed in the ESC shelf break front in the simulation.

In this paper, we elucidated that a reverse EOT dominates the cross-shelf transport in the ESC upstream by using an ocean general circulation model developed by the Atmosphere and Ocean Research Institute at the University of Tokyo (CCSR Ocean Component Model; hereafter referred to as COCO) (Hasumi 2000). The EOT deepens the mixed layer off the shelf break by blocking the onshore surface Ekman transport under the downwelling-favourable wind that occurs during winter. The reverse EOT, in addition to the accompanied upwelling and downwelling, occurs in the shelf break density front created by the riverine discharges from the far-eastern Eurasian Continent. This shelf break EOT has a depth scale of 100 m. A scaling consideration implies the applicability of this EOT mechanism to various shelf break fronts of an O(100) m depth scale and suggests that the EOT and geostrophic stress significantly impact the water mass formation and material transport between the continental shelves and the open ocean.

2 Methods

2.1 Modelling configuration

The COCO model uses the hydrostatic and Boussinesq approximations, incorporates curvilinear horizontal coordinates (referred to as COCO’s Mercator grids) and couples the sea ice model for diverse applications (Hasumi 2000; Matsuda et al. 2015; Shu et al. 2021). The brine rejection process is included in the sea ice module. In the model settings, sea ice contains 5 psu salinity, and during sea ice formation, the remainder of the salt is released to the ocean. In Matsuda et al.’s (2015) application, the dense shelf water along the middle layer of the west coast of the Sea of Okhotsk was simulated successfully with the COCO model.

In this study, we used COCO V3.4, which adopts the turbulence closure scheme (Noh and Jin 1999) to simulate the evolution of the oceanic surface and bottom boundary layers; however, the COCO model includes a slight modification of the turbulent Prandtl number, following the formulation by Kondo et al. (1978), As for the horizontal viscosity and diffusivity, COCO adopts a biharmonic version of the Smagorinsky viscosity (Smagorinsky 1963) and diffusivity following the formulation by Griffies and Hallberg (2000), which are expressed as follows:

$${B}_{\mathrm{H}}=\frac{1}{8}{\left(\frac{C{\Delta }^{2}}{\pi }\right)}^{2}D,$$

where \({B}_{\mathrm{H}}\) denotes the biharmonic viscosity coefficient as well as the coefficient for the horizontal biharmonic diffusion. \(C\) is a nondimensional parameter, and the value we used in our simulation was 2.5. \(\Delta\) is the spatial variable, and the chosen value is the smaller of \(\Delta x\) and \(\Delta y\). \(D\) has a dimension of \(1/\mathrm{s}\) and denotes the deformation rate or strain (Griffies and Hallberg 2000, for a specific form of \(D\)).

The simulated area encompasses the entire North Pacific Ocean (Fig. 1c) and extends to a southern boundary of \(30^\circ \mathrm{S}\), which was modelled as an open boundary with a sponge layer. Since the open boundary is a considerable distance from our study area, its impact is negligible. For the solid boundaries, we used the non-slip boundary condition without normal flow.

In our simulation, we used the same grid setting as that of Matsuda et al. (2015). The horizontal resolution was finer than 3 km when modelling the Sea of Okhotsk’s north-western continental shelf (Fig. 1a). Since the horizontal scale of the frontal eddies is O(10 km) (e.g., Spall and Leif 2016), the 3-km resolution is considered eddy-permitting. In the vertical direction, 7 surface \(\sigma\) layers were arranged at depths of less than 34 m to represent the surface elevations due to surface gravity waves, whereas 77 levels deeper than 34 m were assigned with z coordinates. The \(\sigma\) coordinate transformation is as follows:

$${z}_{\mathrm{s}}={\sigma }_{\mathrm{s}}\times \left(\eta -{z}_{\mathrm{B}}\right)+{z}_{\mathrm{B}},$$

where \({z}_{\mathrm{B}}\) is the prescribed fixed depth. In this study, it was set as the depth of the seventh layer, which was 34 m. That is, the bottom was considered flat where the bathymetry was shallower than \({z}_{\mathrm{B}}\), i.e., the minimum depth was \({z}_{\mathrm{B}} =\) 34 m. \(\eta\) is the surface water level, and \({\sigma }_{\mathrm{s}}\in [\mathrm{0,1}]\) from the seventh layer to the surface.

We used the six-hourly mean, ERA-Interim from the European Centre for Medium-Range Weather Forecasts, to represent the meteorological force, and the period was June 1980–June 2018 (Dee et al. 2011). We processed the data to a climatological monthly mean. The wind stress \({\overrightarrow{\tau }}_{\mathrm{s}}\) was calculated as folows:

$${\overrightarrow{\tau }}_{\mathrm{s}}={\rho }_{\mathrm{a}}{C}_{\mathrm{D}}\sqrt{({u}_{10}^{2}+{v}_{10}^{2})}{\overrightarrow{u}}_{10},$$

where \({u}_{10}\) and \({v}_{10}\) denote the zonal and meridional winds at a height of 10 m, respectively, and \({\rho }_{\mathrm{a}}\) denotes the air density. \({C}_{\mathrm{D}}\) is the air-ice, or air-water, drag coefficient, which has a value of \(1.3\times {10}^{-3}\) (i.e., the above stress definition with \({C}_{\mathrm{D}}=1.3\times {10}^{-3}\) is used for either case in which the sea surface is covered by ice or not). The above wind stress formula does not consider the impact of the sea surface current and ice velocity, as the 10 m wind of the winter monsoon is O(10 m/s), which is much larger than the surface current speed, which is \(\le\) 0.3 m/s. The air-ice stress drives the sea ice motion by balancing it with the ice-ocean stress, which in turn drives the ocean current. The definition of the ice-ocean stress \({\overrightarrow{\tau }}_{\mathrm{IO}}\) in COCO is as follows:

$${\tau }_{\mathrm{IO}x}={\rho }_{0}{C}_{\mathrm{W}}\sqrt{{({u}_{\mathrm{I}}-{u}_{\mathrm{O}})}^{2}+{({v}_{\mathrm{I}}-{v}_{\mathrm{O}})}^{2}}[\left({u}_{\mathrm{I}}-{u}_{\mathrm{O}}\right)\mathrm{cos}\theta -({v}_{\mathrm{I}}-{v}_{\mathrm{O}})\mathrm{sin}\theta ]$$
$${\tau }_{\mathrm{IO}y}={\rho }_{0}{C}_{\mathrm{W}}\sqrt{{({u}_{\mathrm{I}}-{u}_{O})}^{2}+{({v}_{\mathrm{I}}-{v}_{\mathrm{O}})}^{2}}\left[\left({v}_{\mathrm{I}}-{v}_{\mathrm{O}}\right)\mathrm{cos}\theta -\left({u}_{\mathrm{I}}-{u}_{\mathrm{O}}\right)\mathrm{sin}\theta \right],$$

where \({\rho }_{0}\) is a reference density, and \({C}_{\mathrm{W}}\) is a nondimensional water drag coefficient.\({u}_{\mathrm{I}}\) and \({v}_{\mathrm{I}}\) are the \({x}_{\mathrm{c}}\) and \({y}_{\mathrm{c}}\) components of the ice horizontal velocity, and \({u}_{\mathrm{O}}\) and \({v}_{\mathrm{O}}\) are the \({x}_{\mathrm{c}}\) and \({y}_{\mathrm{c}}\) components of the ocean horizontal velocity. \({(x}_{\mathrm{c}},{y}_{\mathrm{c}})\) denotes the Cartesian coordinate system. \(\theta\) is the rotation angle of the effective ocean flow direction when interacting with sea ice. In terms of the bottom stress, the model adopts a quadratic bottom drag parameterization (Hasumi 2000), and the bottom drag coefficient was set as \(1.3\times {10}^{-3}\). We included the monthly mean freshwater flux, which included the precipitation minus the evaporation and riverine runoff data (Fig. 8a) reported by Dai and Trenberth (2002). The 2-m air temperature, 10-m wind stress, specific humidity, and long-wave and short-wave radiation provide the sea surface boundary conditions to calculate the heat flux, and these data are sourced from the ERA-Interim. Note that we did not restore the sea surface temperature and sea surface salinity to the observed values; without restoration, COCO simulated these values reasonably (e.g., Matsuda et al. 2015). The bathymetry model was obtained from the Japan Oceanographic Data Centre and included a modification reported by Ono et al. (2006).

The simulation included all the external forces as a control case (CTRL case), and additional experiments were conducted to delineate the role of the riverine discharges as follows: the simulation excluding all the riverine discharges is referred to as the ‘no-River’ case; the simulation including only the Amur River discharge is referred to as the ‘Amur-only’ case; and the simulation excluding only the Amur River discharge is referred to as the ‘no-Amur’ case. We executed the model for a 10-year period using data with a CTRL case configuration. Then, we adopted the tenth-year results as the initial conditions in each case for the simulation of another 10-year period to retain the same initial conditions and duration. The averaged January mean for the last 5 years was analysed, and the results were interpolated to the standard grids at a resolution of \(1/30^\circ \times 1/30^\circ\).

2.2 Isobath coordinate

According to the approximately homogeneous w and surface divergence in the along-isobath direction, we calculated the average along the isobath to obtain a representative vertical structure of the ESC, following the definition by Stewart et al. (2019) as follows:

$${\left[\cdot \right]}_{h}={\iint }_{{h}_{1}<h<{h}_{2}}\bullet \mathrm{d}A,\mathrm{ and}$$
$${\overline{\bullet }}_{A}=\frac{{\left[\bullet \right]}_{h}}{A}.$$

Here, A is an area where the grids have a similar depth \(h\). In this study, the depth \(h\) was selected in the COCO model from between the two closest vertical levels \(\left[{h}_{1,} {h}_{2}\right]\). Thus, \({\overline{\bullet } }_{A}\) is an area averaged value inside area A between the two levels \(\left[{h}_{1,} {h}_{2}\right]\). The flat shelf, which is shallower than 34 m, was considered a single isobath. The along-isobath averaged offshore distance \({\overline{x} }_{A}\) was calculated by averaging the offshore distance of each point that belongs to the same isobath within area \(A\). We used the Haversine formula to calculate the distances between the two grids. Note that throughout the paper, we use \((x,y,z)\) to denote the isobath coordinate.

2.3 Data for estimating the geostrophic stress in various coastal areas

The geostrophic stress was globally estimated as summarized in Sect. 3.6 (see Eq. (9)). The data set, which has the CMEMS (the Copernicus Marine Environment Monitoring Service) product identifier GLOBAL_MULTIYEAR_PHY_001_030, was used to estimate the global surface geostrophic current \({\overrightarrow{u}}_{\mathrm{g},\mathrm{s}}\). The sea surface height (SSH) is obtained from a CMEMS global reanalysis product assimilating the satellite altimetry measurements. This product is defined on a regular horizontal grid with the resolution \(1/12^\circ \times 1/12^\circ\), and there are 50 standard levels in the vertical direction. As a reanalysed dataset, the NEMO (Nucleus for European Modeling of the Ocean) platform drives the model component assimilating the sea ice concentration from CERSAT (the Satellite Data Processing and Distribution Center of Ifremer, the French Research Institute for Exploitation of the Sea.). About the runoff, it includes the climatological runoff reported by Dai et al (2009) plus the freshwater fluxes from icebergs for Greenland and Antarctica. The surface mass budget among the evaporation, precipitation and runoff is considered. One of data sets of the product named cmems_mod_glo_phy_my_0.083-climatology_P1M-m, a climatological monthly mean data within the period Jan. 1993–Dec. 2016, was used in this study. The climatological January-mean SSH above the geoid was used to obtain the surface geostrophic current for the Northern Hemisphere, whereas the August-mean SSH above the geoid was used to obtain the surface geostrophic current for the Southern Hemisphere as follows:

$$\overrightarrow{f}\times {\overrightarrow{u}}_{\mathrm{g},\mathrm{s}}=-g\nabla \eta .$$

The SSH above the geoid was also used to define the unit direction vector for the global geostrophic stress estimation.

The ERA-Interim was used to calculate the monthly mean wind stress \(\langle {\tau }_{\mathrm{s}}^{y}\rangle\) and frictional velocity \({u}_{*}=\sqrt{\langle |\overrightarrow{{\tau }_{\mathrm{s}}}|\rangle /{\rho }_{0}}\), where \(\langle \bullet \rangle\) denotes the monthly mean of the six-hourly data.

The General Bathymetric Chart of the Oceans (GEBCO) _2021 grid, i.e., GEBCO’s current bathymetric data set, was used to estimate the depth h of the coastal fronts in the regions chosen for the geostrophic stress estimation. The most recently released data set was gridded on a 15 arc-s interval grid, and furthermore, the under-ice bathymetry value obtained in Greenland was also used.

3 Results and discussion

3.1 Overview of the modelled ESC

In the winter in the Sea of Okhotsk, the northwesterly wind caused by the East Asian Monsoon (dark blue arrows in Fig. 1a) is primarily responsible for driving the ocean circulation, including the boundary currents and the ESC (Ohshima et al. 2002; Mizuta et al. 2003; Nakanowatari and Ohshima 2014). Governed by a climatological January-mean wind velocity, the COCO model reproduced the two ESC cores (Fig. 2a); the coastal branch’s depth is shallower than 50 m, whereas the WBC branch has a depth of approximately 200–500 m. The WBC branch has a density of approximately \(1026 \text{kg/}{\text{m}}^{3}\), and the coastal branch entrains the Amur River discharge with a density of approximately 1021 \(\mathrm{kg}/{\mathrm{m}}^{3}\), covering the northern tip of the Sakhalin (Fig. 2a).

Fig. 2
figure 2

Overview of the upstream ESC. a The light-blue arrows denote the climatological January-mean depth-averaged velocity (as the barotropic current). The black contours denote the climatological January-mean surface density, and the orange contours denote the topography. The yellow-green dotted box indicates the area for which the along-isobath average was processed (see Sect. 2.2; along-isobath averaged: as \({\overline{\bullet } }_{A}\)). b The shading and black contours denote the along-isobath currents. The negative values indicate the southward currents, which are directed towards the reader. The solid and dashed magenta contours denote densities; the former has values from 1023.2 to 1026.2 \(\mathrm{kg}/{\mathrm{m}}^{3}\) at 0.2 \(\mathrm{kg}/{\mathrm{m}}^{3}\) intervals without labels except for the contour at 1026.0 kg/m3. The x-axis represents the offshore distance (see Sect. 2.2). c The shading and solid contours denote the MLD, and the dotted orange contours denote the topography. The orange and red dots denote offshore distances of approximately 20 and 40 km, respectively, along the \(53^\circ\,\mathrm{ N}\) and \(53.5^\circ \, \mathrm{ N}\) latitudes

Full size image

3.1.1 Two ESC cores

The near-shore core of the ESC is interpreted to be arrested trapped waves (ATWs) (Csanady 1978; Simizu and Ohshima 2002; Nakanowatari and Ohshima 2014), which mingles with a density current via the coastal river discharge. Its transport is calculated via the Ekman transport as follows:

$${V}_{\mathrm{ATW}}={\int }_{{l}_{1}}^{{l}_{2}}\frac{\overrightarrow{\tau }}{\rho f}\bullet \mathrm{d}\overrightarrow{l},$$

where \(\mathrm{d}\overrightarrow{l}\) is an integrated path, \({l}_{1}\) and \({l}_{2}\) are the start and end points of an integral path, \(\overrightarrow{\tau }\) is the wind stress over the integral path, \(\rho \sim 1025 \mathrm{kg}/{\mathrm{m}}^{3}\) is the water density, and \(f\sim 1.12\times {10}^{-4} \mathrm{rad}/\mathrm{s}\) is the Coriolis parameter at \(50^\circ \mathrm{N}\).

We calculated \({V}_{\mathrm{ATW}}\) via integration of the Ekman transport \(\frac{\overrightarrow{\tau }}{\rho f}\) along the integral path denoted by the dash-dotted green line in Fig. 3a (cf. Nakanowatari and Ohshima 2014). \({V}_{\mathrm{ATW}}\) was then compared with the model’s simulated transport streamfunction \({\phi }_{1}\) (as the coastal streamfunction was set to zero) as follows:

Fig. 3
figure 3

Two cores of the ESC. a The shading and the black contour denote the streamfunction \({\phi }_{1}\), which was calculated via meridional velocity integration. The red contour denotes the isobath at 200 and 500 m. The dash-dotted green line is the integral path used to calculate the transport according to arrested topographic waves. The purple/red dot is the start/end of the integrated point. b Transport comparison between \({V}_{ATW}\) and \({\phi }_{1}\) at the latitudes 48 °N, 50 °N, 52 °N and 54 °N. For \({\phi }_{1}\), we chose the points with depths of 255, 228, 212, and 197 m for each latitude

Full size image
$${\phi }_{1}={\int }_{E}^{{x}_{\mathrm{c}}^{^{\prime}}}{\int }_{z=0}^{z=H}v\mathrm{d}z\mathrm{d}{x}_{\mathrm{c}},$$

where \(v\) is the meridional velocity of COCO’s output, \(E\) is the eastern boundary of the model domain, \({x}_{\mathrm{c}}^{^{\prime}}\) is any zonal position, and \(H\) is the water depth. We recall that the \(({x}_{\mathrm{c}},{y}_{\mathrm{c}})\) denotes the Cartesian coordinate, and this notation is used throughout the paper. The streamfunction \({\phi }_{1}\) is denoted by the shading and the black contour in Fig. 3a.

Figure 3b presents a comparison between \({V}_{\mathrm{ATW}}\) and \({\phi }_{1}\) at the grid points closest to the 200-m bathymetry along the Sakhalin coast. Since \({V}_{\mathrm{ATW}}\) and \({\phi }_{1}\) match well along the East Sakhalin (Fig. 3b), the near-shore transport simulated by COCO can be explained as the integral of the Ekman flux along the northern and western coasts of the Sea of Okhotsk. It corresponds well with previous studies, e.g., Simizu and Ohshima (2002, Fig. 10). An observed transport at the shallow shelf along Sakhalin Island, shallower than 200 m of depth, was estimated to be 0.8–1.4 Sv by drifter measurements (Ohshima et al. 2002). \({V}_{\mathrm{ATW}}\) estimated by wind and the transport \({\phi }_{1}\) simulated as in Fig. 3b are smaller than the estimation by the drifters. We note, however, that the surface current speed (~ 0.3 m/s) is similar between the simulation and the drifter measurement, and hence, the larger transport estimation by the drifters could be derived from its assumption that the velocity is uniform vertically.

The streamfunction \({\phi }_{1}\) also depicts the offshore core of the ESC over the slope as the WBC of the cyclonic gyre in the central basin (Fig. 3a). For comparison, we calculated streamfunction \({\phi }_{2}\) based on the Sverdrup relation (Ohshima et al. 2004) with the data used by COCO as follows:

$${\phi }_{2}=-\frac{1}{\beta \rho }{\int }_{{x}_{\mathrm{e}}}^{{x}_{\mathrm{c}}^{^{\prime}}}\nabla \times \overrightarrow{\tau }\mathrm{d}{x}_{\mathrm{c}},$$

where \(\beta \sim {1.47\times 10}^{-11}\) is the \({y}_{\mathrm{c}}\) derivative of the Coriolis parameter \(f\), \({x}_{\mathrm{e}}\to {x}_{\mathrm{c}}^{^{\prime}}\) is the zonal integral path from the eastern boundary (deeper than 500 m) to position \({x}_{\mathrm{c}}^{^{\prime}}\), and \(\overrightarrow{\tau }\) is the January-mean wind stress of the ERA-interim (see subsect. 2.1 for details regarding the data).

The Sverdrup transport \({\phi }_{2}\) depicts the cyclonic gyre accompanying the WBC (the figure is not shown). The transport of WBC by \({\phi }_{2}\) is estimated to be ~ 5 Sv. The value is similar to that calculated by Ohshima et al. (2004) and is comparable with the maximum transport value by \({\phi }_{1}\) calculated from COCO’s output (Fig. 3a), which implies that the WBC core of the ESC in the model is consistent with the linear Sverdrup relation. A mooring observation over the slope in the ESC upstream (Mizuta et al. 2003) evaluated the transport to be ~ 10 Sv in January, which is larger than the transport of WBC by \({\phi }_{2}\). The difference could be related to the WBC’s nonlinearity or the interannual variations discussed in Ohshima et al. (2004).

These results imply that the along-shore dynamics of the ESC in COCO’s simulation are consistent with the dynamics in previous studies, and the model results are valuable for the further study of the cross-shelf dynamics.

3.1.2 Along-isobath averaged section of the ESC

To obtain insights into the vertical structure of the upstream ESC, we averaged the variables along the isobaths (range: 34–314 m) from 53.0 to 53.5 °N inside the area marked with yellow–green dots in Fig. 2a. Hereafter, ‘along-isobath averaged’ variable is represented as the notation:

$${\overline{\bullet } }_{A}.$$

as defined in Sect. 2.2 (ref. Stewart et al. 2019); for example, a profile of the ‘along-isobath averaged’ density is denoted by \({\overline{\rho }}_{\mathrm{A}}\).

The variables \({\overline{\rho }}_{\mathrm{A}}\) and \({\overline{v} }_{\mathrm{A}}\) are described in Fig. 2b, where \(v\) is the along-isobath current. The cross- and along-isobath components (\(u,v\)) of the velocity vector \(\overrightarrow{u}\) are denoted by

$$u=\overrightarrow{u}\cdot \widehat{x}, v=\overrightarrow{u}\cdot \widehat{y}$$

and

$$\widehat{y}=\widehat{z}\times \widehat{x},$$

where \(\widehat{x}\), \(\widehat{y}\) and \(\widehat{z}\) are the normal (positive in the offshore direction), tangential and vertical unit vectors of the isobath coordinate \((x,y,z)\), obeying the right-hand rule. The southward along-isobath current \(v\) (direction: toward the reader, Fig. 2b), which is predominantly geostrophic, indicates two cores of the ESC, which is similar to the real system. These cores are separated by a front with a horizontal density gradient, and the frontal isopycnal range is from 1025.2 \(\mathrm{kg}/{\mathrm{m}}^{3}\) at \({\overline{x} }_{\mathrm{A}}= 20\) km to 1025.9 kg/m3 at \({\overline{x} }_{\mathrm{A}}=40\) km, where \({\overline{x} }_{\mathrm{A}}\) denotes the along-isobath averaged offshore distance.

The front originates from the northern shelf of the Sea of Okhotsk and separates the coast into three portions, i.e., a flat shelf (\({\overline{x} }_{\mathrm{A}}\le 20\) km), a gently sloping shelf (20 km \(\le {\overline{x} }_{\mathrm{A}}\le\) 40 km) and the open ocean (\({\overline{x} }_{\mathrm{A}}\ge 40\) km). The shelf break located at \({\overline{x} }_{\mathrm{A}}\sim 40\) km is our focus in the subsequent analysis. Inside the front between the two ESC cores (\(20 \mathrm{km}\le {\overline{x} }_{\mathrm{A}}\le 40 \mathrm{km}\)), we observed a slow \({\overline{v} }_{\mathrm{A}}\) with a minimum current at the bottom (\({\overline{x} }_{\mathrm{A}}\sim 30 {\text{km}}\)). Although this frontal current is slow, the current has a surface intensified structure and exhibits baroclinicity with a typical value of \(\partial v/\partial z\sim -1.0\times {10}^{-3} {\mathrm{s}}^{-1}\). Note that the flat shelf topography (\({\overline{x} }_{\mathrm{A}}\le 20\) km) was constructed according to the requirement dictated by COCO’s settings. Therefore, in the subsequent analysis and discussion, we primarily focus on the formation of overturning over the gently sloping shelf and the deep mixed layer at the shelf break.

On the front’s offshore boundary, there is a region with an MLD > 120 m between the isobaths at 100 and 200 m (Fig. 2c); the MLD is obtained from the water depth where the density increases by 0.125 kg/\({\text{m}}^{3}\) (Kanna et al. 2018; Suga et al. 2004; Levitus 1982) compared to that of the surface density. The MLD value at the shelf break (\({\overline{x} }_{\mathrm{A}}\)~ 40 km) is larger than that in the open ocean by approximately 50 m; in the open ocean, the mixed-layer base is characterized by an isopycnal surface of 1026.0 \(\text{kg/}{\text{m}}^{3}\). The horizontal stratification of the mixed-layer base in the open ocean is broken at the shelf break, where a deep mixed layer is formed, and the isopycnal surface tilts to the bottom. On the inshore boundary of the gently sloping shelf at \({\overline{x} }_{\mathrm{A}}\)~ 20 km, the stratified water is dominant again due to the Amur River discharge.

3.2 Vertical overturning from the flow field in the upstream ESC

To study cross-shelf overturning over the gently sloping shelf, we first examined the divergence in the surface current field at a depth of 7 m in the upstream ESC (Fig. 4a). Despite an almost uniform wind stress (Fig. 1a), we identified a surface region of divergence over the gently sloping shelf in an isobath range of approximately 50–100 m as well as a convergence region located farther offshore in an isobath range of approximately 100–200 m. The divergence coincides with an upwelling, whereas the convergence indicates a downwelling (Fig. 4b, simulated vertical velocity at the depth of 18 m). The surface divergence/convergence and mid-depth vertical motions are nearly homogeneous in the along-isobath direction. Overall, these patterns produce a vertical overturning that entirely occupies the gently sloping shelf on the northern coast of the East Sakhalin. We also noted that there is narrow downwelling adjacent to the coast, which is shown in Fig. 4b and associated with the downwelling-favourable wind.

Fig. 4
figure 4

Surface divergence/convergence field and vertical motion in the upstream ESC. a The shading denotes the climatological January-mean horizontal velocity divergence at a depth of 7 m. The positive values with red shading represent the horizontal velocity divergence, and the negative values with green shading represent the horizontal velocity convergence. The vectors denote the horizontal velocity at the same depth, and the dark green contours denote the topography. b The shading denotes the vertical velocity at a depth of 18 m, where the positive values represent the upward vertical velocity using the reddish-brown shading. The dark green contours denote the topography

Full size image

The vertical overturning over the gently sloping shelf can also be delineated using a combination of the cross-isobath current, \({\overline{u} }_{\mathrm{A}}\), and vertical velocity, \({\overline{w} }_{\mathrm{A}}\) (Fig. 5a). The upward \({\overline{w} }_{\mathrm{A}}\) at \({\overline{x} }_{\mathrm{A}}\)~25 km and downward \({\overline{w} }_{\mathrm{A}}\) at \({\overline{x} }_{\mathrm{A}}\)~40 km correspond to the inshore and offshore boundaries of the front over the gently sloping shelf, respectively. The inshore upward \({\overline{w} }_{\mathrm{A}}\) at \({\overline{x} }_{\mathrm{A}}\)~25 km is unexpected since in the classical EOT, downwelling is generally generated under a downwelling-favourable wind condition, indicating that a reverse EOT is occurring over the gently sloping shelf. Note that the overturning over the flat shelf is not described by the analysis of the along-isobath average because one single value is obtained for each variable, e.g., \({\overline{w} }_{\mathrm{A}}\), over the flat shelf.

Fig. 5
figure 5

Coherence of the vertical overturning and mixed layer deepening. a The shading and black contours denote the vertical velocity. The arrows are the combination of the cross-isobath current and vertical velocity, and the circles denote the start point of each arrow. b The shading denotes the January-mean Richardson Number, \(Ri=\frac{{N}^{2}}{{\left(\frac{\partial u}{\partial z}\right)}^{2}+{\left(\frac{\partial v}{\partial z}\right)}^{2}}\), where \(N\) is the Brunt–Vaisala frequency. The black contours denote the vertical diffusivity Kv, and the dotted line denotes Kv = 0.0001 \({\text{m}}^{2}\text{/s}\), which is close to the background vertical diffusivity. The dashed line denotes Kv = 0.0005 \({\text{m}}^{2}\text{/s}\), which is dominant on the flat shelf. The dodger blue line denotes the MLD

Full size image

The \({\overline{u} }_{\mathrm{A}}\) pattern is consistent with the divergence information provided in Fig. 4a. The surface onshore flow at the flat shelf is approximately \(-0.07\text{ m/s}\), which corresponds to a wind-induced onshore Ekman flow; in this case, as the wind stress and MLD are ~\(0.05 \text{N/}{\text{m}}^{2}\) and ~ 10 m, respectively, we evaluated an onshore Ekman velocity of ~\(-\) 0.05 m/s over the flat shelf. Conversely, the surface cross-shelf flow is weak over the gently sloping shelf, which has a velocity of ~\(-\) 0.01 m/s, causing surface divergence and corresponding upwelling at \({\overline{x} }_{\mathrm{A}}\sim 25\) km between the isobaths of 50 and 100 m. The inshore shallow mixed layer is produced by this upwelling. In contrast, the downwelling occurs farther offshore (\({\overline{x} }_{\mathrm{A}}\gtrsim 40\) km), corresponding to the surface convergence (Fig. 5a). The deep mixed layer forms at a depth of 140 m, corresponding with the downwelling at the shelf break at \({\overline{x} }_{\mathrm{A}}\sim 42\) km (Fig. 5b). Figure 5b also shows that a small Richardson number (\({R}_{i}\)) and a large vertical diffusivity coefficient \({(K}_{\mathrm{v}}\)) are obtained over the gently sloping shelf between the inshore upwelling and offshore downwelling. The mixed layer boundary enveloped Kv is larger than the background diffusivity (= \({10}^{-4} {\text{m}}^{2}\text{/s}\)). These characteristics over the gently sloping shelf are in contrast to the horizontally stratified layer over the flat shelf and open ocean.

3.3 Vertical overturning based on stress distribution in the upstream ESC

To provide a dynamical understanding of the vertical overturning, we analysed the stress since it is a dynamical source of the ageostrophic current. The velocity can be calculated separately by

$$\overrightarrow{u}={\overrightarrow{u}}_{\mathrm{g}}+{\overrightarrow{u}}_{\mathrm{a}},$$

where \({\overrightarrow{u}}_{\mathrm{g}}\) and \({\overrightarrow{u}}_{\mathrm{a}}\) denote the geostrophic and ageostrophic currents, respectively. According to the momentum equation, the ageostrophic current is described by (Chen and Chen 2017; Cronin and Kessler 2009; Cronin and Tomoki 2016) the following:

$$f\widehat{z}\times {\overrightarrow{u}}_{\mathrm{a}}= \frac{1}{{\rho }_{0}}\frac{\partial \overrightarrow{\tau }}{\partial z},$$
(1)

where \(\overrightarrow{\tau }\) denotes the internal stress in the sea water, and \(f\) and \({\rho }_{0}\) denote the Coriolis parameter and a reference density, respectively. The boundary conditions are as follows:

$$\overrightarrow{\tau }={\overrightarrow{\tau }}_{s},\, \mathrm{at}\, z=0,$$
(2a)

and

$$\overrightarrow{\tau }={\overrightarrow{\tau }}_{b},\, \mathrm{at}\, z=-h,$$
(2b)

where \(z=0\) and z =\(-h\) represent the sea surface and bottom, respectively, and \({\overrightarrow{\tau }}_{\mathrm{s}}\) and \({\overrightarrow{\tau }}_{\mathrm{b}}\) denote the wind stress and bottom stress, respectively. The internal water stress \(\overrightarrow{\tau }\) is estimated as follows:

$$\overrightarrow{\tau }={\rho }_{0}{A}_{\mathrm{v}}\frac{\partial \overrightarrow{u}}{\partial z},$$
(3a)

where \({A}_{\mathrm{v}}\) is the vertical viscosity, which is a parameter that was first introduced by Boussinesq as a turbulence measurement parameter in the momentum equation. The along-isobath component of \(\overrightarrow{\tau }\) is denoted by the following:

$${\tau }^{y}\left(x,y,z\right)={\rho }_{0}{A}_{\mathrm{v}}\frac{\partial v}{\partial z}.$$
(3b)

The internal water stress \({\overline{{\tau }^{y}(x,z)}}_{\mathrm{A}}\), derived from Eq. (3b), is depicted in Fig. 6a. The parameter \({A}_{\mathrm{v}}\) is essential for evaluating the frictional force that represents the impact of turbulence, and it has a magnitude of \(0.04\) \({\text{m}}^{2}\text{/s}\) at the middle of the gently sloping shelf (Fig. 6b).

Fig. 6
figure 6

Ageostrophic vertical overturning derived from the stress distribution. a The shading and black contours denote the along-isobath internal water stress. The negative values indicate the southward internal water stress and are directed toward the reader. b The shading and black contours denote the vertical turbulent viscosity Av. The dodger blue line denotes the MLD, and the dotted line represents Av = 0.0001 \({\text{m}}^{2}\text{/s}\). c The shading and black contours denote the cross-isobath Ekman transport \({M}_{e}^{x}\), which is derived from the stress distribution. d The shading and black contours denote the derived vertical velocity. The arrows represent the information of the coupled vertical velocity and the ageostrophic cross-isobath current, both of which are retrieved from the cross-shelf Ekman transport \({M}_{e}^{x}\). The dodger blue line denotes the MLD, and d is a theoretical analogue to Fig. 5a

Full size image

The distribution of \({\tau }^{y}\left(x,y,z\right)\) leads to an ageostrophic cross-shelf transport, as evidenced by Eqs. (1) and (2a), such that

$${M}_{e}^{x}\left(x,y,z\right)={\int }_{z}^{0}\frac{1}{f{\rho }_{0}}\frac{\partial {\tau }^{y}}{\partial {z}^{^{\prime}}}\mathrm{d}{z}^{^{\prime}}=\frac{1}{f{\rho }_{0}}\left[{\tau }_{s}^{y}\left(x,y\right)-{\tau }^{y}\left(x,y,z\right)\right].$$
(4)

Therefore, the cross-shelf ageostrophic velocity \({u}_{\mathrm{a}}\) can be rewritten as follows:

$${u}_{\mathrm{a}}=\frac{\partial }{\partial z}\frac{{\tau }^{y}}{f{\rho }_{0}}=-\frac{\partial {M}_{e}^{x}}{\partial z}.$$
(5a)

Furthermore, due to the near homogeneity of the surface divergence in the along-isobath direction (Fig. 4a), we may presume that the Ekman transport is independent of \(y\). This assumption implies that \({M}_{e}^{x}\) can be viewed as a streamfunction by considering \(\frac{\partial {u}_{\mathrm{a}}}{\partial x}+\frac{\partial {w}_{\mathrm{a}}}{\partial z}=\) 0 because of continuity; here, \({w}_{\mathrm{a}}\) is the vertical velocity derived from the ageostrophic flow. These considerations yield

$${w}_{\mathrm{a}}=\frac{\partial }{\partial x}\frac{{\tau }^{y}\left(z\right)}{f{\rho }_{0}}=\frac{\partial {M}_{e}^{x}}{\partial x}.$$
(5b)

The ageostrophic transport \({M}_{e}^{x}\), which is represented by Eq. (4) and derived from the surface wind stress \({\overline{{\tau }_{s}^{y}(x)}}_{A}\) as well as the model’s generated internal water stress \({\overline{{\tau }^{y}(x,z)}}_{A}\), is depicted in Fig. 6c. The ageostrophic velocity fields \({u}_{\mathrm{a}}\) and \({w}_{\mathrm{a}}\), which are derived from \({M}_{e}^{x}\) using Eqs. (5a) and (5b), represent a clockwise overturning structure centred at \({\overline{x} }_{\mathrm{A}}\sim 30\) km (Fig. 6d), with an upwelling nearshore side and a downwelling offshore side. This \({w}_{\mathrm{a}}\) (Fig. 6d) corresponds well with the \({\overline{w} }_{\mathrm{A}}\) obtained from the COCO-modelled flow field (Fig. 5a). A reverse EOT is thus represented by \({M}_{e}^{x}\) in the ESC upstream, because in a classical EOT a downwelling should be expected to occur on the nearshore side of the shelf. The maximum of \(\left|{\overline{{\tau }^{y}(x,z)}}_{A}\right|\) is approximately \(0.06 \text{N/}{\text{m}}^{2}\) at the middle layer of the gently sloping shelf (Fig. 6a), which is larger than \({\overline{{\tau }_{s}^{y}(x)}}_{A}\sim 0.05 \text{N/}{\text{m}}^{2}\). According to the aforementioned theoretical understanding, we can conclude that this maximum internal water stress, which is higher than the wind stress, primarily produces a reverse overturning (compared to the classical EOT).

Due to this clockwise (reverse) EOT, the surface flow converges at the shelf break at \({\overline{x} }_{\mathrm{A}}\sim 40\) km since there is a usual onshore Ekman transport in the open ocean under the downwelling-favourable wind (Fig. 6c); consequently, a downwelling occurs at \({\overline{x} }_{\mathrm{A}}\sim 40 {\text{km}}\) (Fig. 6d). The deepest mixed layer is produced on the right-hand side of the strong downwelling (see Fig. 6c, an MLD with a dodger line). The divergence/convergence field in COCO’s simulation, which is depicted in Fig. 4a, corresponds well with this EOT’s surface flow, which is represented by \({M}_{e}^{x}\).

In the modelled \({\overline{u} }_{\mathrm{A}}\) (Fig. 5a), the surface flow tends to be directed onshore over the gently sloping shelf, although its divergence and convergence structures are robustly represented (Fig. 4a). This observation suggests that three-dimensional effects such as the pressure gradient could play a significant role in the simulated onshore flow. We attempted to retrieve the cross-shelf flow associated with the along-isobath pressure gradient that results in an onshore geostrophic flow, including the effects due to sea ice (see Appendix 1). However, it is known that cross-shelf geostrophic flow is one of the most difficult variables to retrieve from modelled flow fields (Stewart et al. 2019), and thus, further careful examinations are necessary. As a result, we focused on the divergent and convergent ageostrophic cross-shelf overturning retrieved from the stress distribution as well as on the vertical motion, which corresponds well with the COCO-modelled overturning.

3.4 Effect of geostrophic stress on the stress distribution

The cross-isobath transport from the surface to the bottom at a well-mixed layer, which is represented by \({M}_{e}^{x}\), can be divided into two parts, i.e., the surface transport and bottom transport, such that

$${M}_{e}^{x}= {M}_{e,s}^{x}+{M}_{e,b}^{x},$$

where

$${M}_{e,s}^{x}=\frac{1}{f{\rho }_{0}}\left[{\tau }_{s}^{y}-{\tau }^{y}\left(z\right)\right]\,{ \mathrm{and}\, M}_{e,b}^{x}=\frac{1}{f{\rho }_{0}}\left[{\tau }^{y}\left(z\right)-{\tau }_{b}^{y}\right].$$

Here, the independent variables \(x\) and \(y\) are omitted for neatness. The expression above indicates that the maximum internal water stress, \(\mathrm{max}({\tau }^{y}\left(z\right))\), determines the sign of \({M}_{e,s}^{x}\) and \({M}_{e,b}^{x}\). The \(\mathrm{max}({\tau }^{y}\left(z\right))\) is depicted in Fig. 7a (orange line) in addition to \({\tau }_{s}^{y}\) and \({\tau }_{b}^{y}\) (the solid purple and dotted purple lines, respectively).

Fig. 7
figure 7

Role of geostrophic stress on the vertical overturning. a Various along-isobath stresses are depicted. The surface wind stress is marked by the solid purple line, and the bottom stress is depicted by the dashed purple line. The orange line denotes the maximum internal water stress below a depth of 14 m, while the green line denotes the maximum geostrophic stress. The grey line denotes zero stress. The negative sign denotes the southward direction, and the x-axis denotes the offshore distance. b The shading and red contours denote the geostrophic stress. The dotted yellow line indicates the depths of the maximum internal water stress in terms of distance, and the dotted green line indicates the depths of the maximum geostrophic stress. c The schematic patterns represent the relativity among the surface, bottom, and internal water stresses in the Ekman transport. The role of geostrophic stress in modifying the internal water stress is discussed in the text. The reference coordinate system is shown in the right-bottom corner

Full size image

Defining

$$\delta \tau =\left|\mathrm{max}\left({\tau }^{y}\left(z\right)\right)\right|-\left|{\tau }_{s}^{y}\right|,$$

we can see that \(\delta \tau\) separates the coast into three portions. For \(\delta \tau <0,\) a classical Ekman frictional region is obtained in which the onshore transport occurs under the downwelling-favourable wind; this situation is similar to that on the flat shelf and in the open ocean (comparison between Figs. 6c and 7a). The surface wind stress \({\tau }_{s}^{y}\) is dominant over \({\tau }^{y}\left(z\right)\) because of the large \(Ri\) and small \({A}_{\mathrm{v}}\) over the flat shelf or because \({A}_{\mathrm{v}}\) approaches a background value of \(1.0 \times {10}^{-4}{ \, {\text{m}}}^{2}/\mathrm{s}\) in the open ocean as the depth increases. In contrast, for \(\delta \tau >0\), \(\left|\mathrm{max}({\tau }^{y}\left(z\right))\right|\) \(\mathrm{exceeds} \left|{\tau }_{s}^{y}\right|\sim 0.05 \text{N/}{\text{m}}^{2}\) across the entire layer and produces a surface offshore Ekman transport; specifically, a reverse EOT is produced over the gently sloping shelf between the offshore distances of approximately \(25\)km and \(35 {\text{km}}\) (Fig. 6a, c). Figure 7a indicates that the locations where \(\delta \tau\) changes its sign are close to the inshore and offshore boundaries of the reverse EOT. Furthermore, the bottom onshore flow over the gently sloping shelf (Fig. 6c, d) is considered a bottom Ekman transport because the bottom stress is much smaller than the internal water stress \({\tau }^{y}\left(z\right)\).

To understand the max \((\left|{\tau }^{y}\left(z\right)\right|)\) in the middle layer of the gently sloping shelf, which decides the location of the reverse EOT, we separate the along-isobath stress \({\tau }^{y}\left(z\right)\) into two parts as follows:

$${\tau }^{y}\left(z\right)={\tau }_{\mathrm{p}}^{y}+{\tau }_{\mathrm{a}}^{y},$$
(6)

where \({\tau }_{\mathrm{p}}^{y}\) and \({\tau }_{\mathrm{a}}^{y}\) denote the geostrophic and ageostrophic stresses, respectively. The former, as implied by its name, derives from the vertical shear of the geostrophic current, which is ignored in a classical Ekman solution. Cronin and Tomoki (2016) argued that the stress \(\overrightarrow{\tau }\left(z\right)\) in the frontal region in a mixed layer, such as those in the Kuroshio Extension, is significantly influenced by the geostrophic stress \({\overrightarrow{\tau }}_{\mathrm{p}}\) because of the large horizontal density gradient there.

The geostrophic stress can be evaluated using the thermal wind relation such that

$${\tau }_{\mathrm{p}}^{y}=-{A}_{\mathrm{v}}\frac{g}{f}\frac{\partial \rho }{\partial x},$$
(7)

where \(g\) is the acceleration due to gravity, and \({\tau }_{\mathrm{p}}^{y}\) is depicted in Fig. 7b. COCO’s simulation of the upstream ESC shows the importance of the geostrophic stress over the gently sloping shelf, since it is responsible for the formation of the density fronts caused by the riverine discharges around the Sea of Okhotsk. By substituting Eq. (6) into Eq. (1) and presuming a vertically independent \({\tau }_{\mathrm{p}}^{y}\) and \({A}_{\mathrm{v}}\), we obtained an analytical solution for the ageostrophic current that produces the Ekman transports under the influence of \({\tau }_{\mathrm{p}}^{y}\) (Appendix 2). This derivation indicates that a max (\({\tau }^{y}\left(z\right)\)) may arise when \({\tau }_{\mathrm{p}}^{y}\) exceeds \({\tau }_{\mathrm{s}}^{y}\) as schematically shown in Fig. 7c (right panel). In this case, the surface stress is dragged by the internal geostrophic current, resulting in the surface Ekman transport \({M}_{e,s}^{x}\) in the offshore direction.

The locations of \(\left|{\mathrm{max}(\tau }_{\mathrm{p}}^{y})\right|\) and \(\left|\mathrm{max}({\tau }^{y}\left(z\right))\right|\) are indicated in Fig. 7b by the dashed green and orange lines, respectively. The maximum geostrophic stress, \({\mathrm{max}(\tau }_{\mathrm{p}}^{y})\), is represented by a green line in Fig. 7a. We find that the distribution of \({\tau }_{\mathrm{p}}^{y}\) is similar to that of \({\tau }^{y}\left(z\right)\), and the same is true of the relationship between \({\mathrm{max}(\tau }_{\mathrm{p}}^{y})\) and \(\mathrm{max}({\tau }^{y}\left(z\right))\). A \(\left|{\mathrm{max}(\tau }_{\mathrm{p}}^{y})\right|\) occurs at the middle layer of the gently sloping shelf because of the large \({A}_{\mathrm{v}} (\ge 0.04 {\text{m}}^{2}/{\text{s}})\), which is caused by strong mixing (see Fig. 5b) in conjunction with the vertical thermal wind shear \(\partial v/\partial z\sim {\text{O}}\left({-10}^{-3}\right){\text{s}}^{-1}\) shown in Fig. 2b over the gently sloping shelf. The results shown in Fig. 7a, c imply that \(\left|{\mathrm{max}(\tau }_{\mathrm{p}}^{y}) \right|>\left|{\tau }_{\mathrm{s}}^{y}\right|\) is a necessary condition for \(\delta \tau >0\), which causes a reverse EOT.

3.5 Response of internal water stress and vertical overturning to the riverine discharge

Thermal-wind shear due to baroclinicity is conducive to the production of a substantial geostrophic stress, which results in an internal water stress that is higher than the wind stress. Additionally, the riverine freshwater flux causes the formation of a coastal front in the upstream ESC (Fig. 2a). Since the internal water stress plays a decisive role in the formation of the EOT structure, we performed experiments to test the sensitivity of the internal water stress and the EOT to the riverine freshwater flux.

The rivers included in COCO’s simulation are marked in Fig. 8a. We highlighted the Amur River with a purple dot since it causes a large flux compared to other rivers. However, its wintertime flux is small. The sensitivity experiments are also listed in Fig. 8a. We conducted numerical experiments using the ‘no-River’, ‘Amur-only’ and ‘no-Amur’ cases to contrast with the ‘CTRL’ case.

Fig. 8
figure 8

Sensitivity tests: Impact of the freshwater discharge from the Eurasian Continents on the vertical overturning. a The purple and yellowish dots on the map denote the river’s distribution as defined in the COCO simulation. The purple and yellowish dots in the panel in the right-bottom corner denote the seasonal Amur river and the other river discharges, respectively. b–d Vertical overturning from the modelled flow field. Each column from left to right represents the results for the no-River case, Amur-only case, and no-Amur case. The shading and black contours denote the vertical velocity, and the arrows denote the combination of the vertical and ageostrophic velocity. The bold dodger line represents the MLD. e–g The same as b–d but for the vertical overturning retrieved from the stress distribution. h–j The shading and contour denote the internal water stress of each sensitivity test. The internal water stress values of [0, −0.03, −0.06] are labelled. k–m The density sections (the shading and purple contours) and along-isobath currents (the solid black contours) of the sensitivity tests. Negative along-isobath current values denote southward toward the reader. The purple contours represent isopycnals at the intervals of \(0.2\) and \(0.1 \text{kg}/{\text{m}}^{2}\) for the solid and dashed lines, respectively

Full size image

The vertical overturning based on the flow fields of these three sensitivity experiments (Fig. 8b–d) are well matched to the EOT represented by \({M}_{e}^{x}\) (Fig. 8e–g), which was retrieved from the stress (Fig. 8h–j). The density structures and along-isobath currents are depicted in Fig. 8k–m. Interestingly, only the ‘no-Amur’ case could represent the deep mixed layer of ~ 150 m (Fig. 8m), which is located the farthest offshore among these three cases. This MLD and its location are similar to those in the CTRL case, indicating that the riverine discharge that originates from the eastern coast of the Sea of Okhotsk facilitates the formation of the salinity front over the gently sloping shelf as well as the deep MLD at the shelf break.

On the other hand, the Amur River discharge is not capable of featuring the deep MLD, because the Amur River discharge only contributes to an inshore front (Fig. 8l), which causes a considerable internal water stress adjacent to the flat shelf (Fig. 8i). As a result, the reverse EOT in this case is produced in a shallower layer (Fig. 8c, f).

The ‘no-River’ case exhibits a dissimilar pattern in its density structure, since no coastal front is formed (Fig. 8k); instead, a well-mixed layer is formed over the flat shelf. Therefore, in contrast to the other two sensitivity tests as well as the CTRL case, neither an internal water stress higher than the surface wind stress (Fig. 8h) nor a reverse EOT (Fig. 8b, e) can occur in this case. The inshore upwelling almost disappears because of the absence of the surface divergence. The downwelling found at \({\overline{x} }_{\mathrm{A}}\sim 32\) km is induced by blocking of the onshore Ekman transport due to the well-mixed coastal water mass over the flat shelf. The well-mixed layer and the resulting surface and bottom stress compensation (Mitchum and Allan 1986) concur with an intense \({A}_{\mathrm{v}}\) (a figure depicting this scenario is not included in the paper). These structures are comparable to a simulated structure in the idealized model reported by Allen and Newberger (1996).

In conclusion, the reverse EOT in the CTRL case is driven by the geostrophic stress associated with the density front caused by the freshwater discharge from the far-eastern Eurasian Continent. The Amur River discharge alone cannot produce a density frontal structure that can induce a reverse EOT over the gently sloping shelf or a deep mixed layer at the shelf break in the ESC upstream, but the other riverine discharges support this process.

3.6 Scaling analysis of the geostrophic stress and its applicability to various frontal coastal regions

Thus far, we have demonstrated the importance of geostrophic stress in the cross-shelf flow structure in the ESC upstream. The geostrophic stress has been overlooked in the dynamics of shelf break fronts, which have a depth of O(100 m) or deeper. In related research, Moffat and Lentz (2012) discussed a similar but shallower overturning adjacent to the coast with a depth of approximately 15 m. In their estimation, \({\tau }_{\mathrm{p}}\) is scaled roughly by \({\tau }_{\mathrm{p}}={\rho }_{0}{C}_{\mathrm{b}}{{v}_{\mathrm{g}}}^{2}\), where \({v}_{\mathrm{g}}\) is the geostrophic velocity, and \({C}_{\mathrm{b}}\) is a drag coefficient with a value of \(1.3\times {10}^{-3}\). Applying the same scaling to the well-mixed ESC layer, where \({v}_{\mathrm{g}}\) is approximately equal to 0.1 m/s (Fig. 2a), we obtained \({\tau }_{\mathrm{p}}\sim 0.013 \text{N/}{\text{m}}^{2}\), which is much smaller than \({\tau }_{\mathrm{s}}^{y}\sim 0.05 \text{N/}{\text{m}}^{2}\). In other words, a reverse EOT is not expected in the ESC upstream by this estimation.

Here, we adopted a cubic profile for the vertical viscosity \({A}_{\mathrm{v}}\) (Lentz 1995; Signell et al. 1990; see Appendix 3) while scaling \({\tau }_{\mathrm{p}}\), where \({\tau }_{\mathrm{p}}={\rho }_{0}{A}_{\mathrm{v}}\frac{\partial {v}_{\mathrm{g}}}{\partial z}\). Chen and Chen (2017) considered this profile and characterised \({A}_{\mathrm{v}}\) by its vertical average, although in their case, \({A}_{\mathrm{v}}\) exhibited a parabolic shape for a shallow shelf, where the surface frictional velocity was the same as the bottom frictional velocity. However, for a shelf break such as that in the upstream ESC, the bottom stress is negligible compared to the surface wind stress, because the bottom current is retarded via the thermal–wind relation. Thus, \({A}_{\mathrm{v}}\) exhibits a cubic profile and is characterised by its vertically averaged value as follows:

$${{A}_{\mathrm{v}}}^{\#}=\frac{\kappa {u}_{*}{h}_{\mathrm{mix}}}{12},$$
(8)

where \(\kappa \approx 0.4\) is the von Kármán constant, \({h}_{\mathrm{mix}}\) is the thickness of the vertical well-mixed water, and \({u}_{*}=\sqrt{\langle |\overrightarrow{{\tau }_{\mathrm{s}}}|\rangle /{\rho }_{0}}\) is the frictional velocity. \(\langle \bullet \rangle\) denotes the monthly mean of the hourly data. The superscript # denotes scaled variables and parameters.

We applied this estimation of \({A}_{\mathrm{v}}\) to scale \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) such that

$${{\tau }_{\mathrm{p}}^{y}}^{\#}\sim {\rho }_{0}\frac{\kappa {u}_{*}{h}_{\mathrm{mix}}}{12}\frac{\langle {v}_{\mathrm{g},\mathrm{s}}^{y}\rangle }{h},$$
(9)

where h is the local whole-layer depth, and \({v}_{\mathrm{g},\mathrm{s}}^{y}\) denotes the surface along-isobath geostrophic velocity. A reverse overturning may occur when

$$\left|{{\tau }_{\mathrm{p}}^{y}}^{\#}\right|\ge \left|\langle {\tau }_{\mathrm{s}}^{y}\rangle \right|.$$

Notably, we used \({{u}_{*}}^{2}=\langle \left|\overrightarrow{{\tau }_{\mathrm{s}}}\right|\rangle /{\rho }_{0}\) \(\ge \left|\langle {\tau }_{\mathrm{s}}^{y}\rangle \right|/{\rho }_{0}\) when estimating \({{\tau }_{\mathrm{p}}^{y}}^{\#}\), since \(\langle \left|\overrightarrow{{\tau }_{\mathrm{s}}}\right|\rangle\) is based on the monthly mean absolute wind stress \(\left|\overrightarrow{{\tau }_{\mathrm{s}}}\right|\) (\(\left|\langle {\tau }_{\mathrm{s}}^{y}\rangle \right|\) is the absolute value of the monthly mean of \({\tau }_{\mathrm{s}}^{y}\) that includes both positive and negative values). If we rewrite \(\langle \left|\overrightarrow{{\tau }_{\mathrm{s}}}\right|\rangle /{\rho }_{0}= \alpha \left|\langle {\tau }_{\mathrm{s}}^{y}\rangle \right|/{\rho }_{0}\), then the factor \(\alpha\) represents the stability of the wind direction; this factor becomes \(\alpha \sim 1\) when the wind blows stably in the along-isobath direction as it does in the ESC upstream, where the northwesterly wind along the coast blows most of the time during the winter. In contrast, if the wind has a large variability but a small monthly mean, it corresponds to a large \(\alpha\); the Gulf of Alaska is one example of this case.

Considering the well-mixed ESC layer, where \(\langle {\tau }_{\mathrm{s}}^{y}\rangle \sim -0.05 \text{N/}{\text{m}}^{2}\), \(\alpha \sim 1.484\), and using \({u}_{*}\sim 0.0085 \text{m/s}\), we obtain

$${{A}_{v}}^{\#}=\frac{\kappa {u}_{*}{h}_{\mathrm{mix}}}{12}\sim 0.028{\text{m}}^{2}\text{/s}$$

if the mixed layer depth \({h}_{\mathrm{mix}}\) is scaled to 100 m. The magnitude of the estimated \({{A}_{\mathrm{v}}}^{\#}\) is consistent with the simulated \({A}_{\mathrm{v}}\) after performing a vertical average, which means that \({v}_{\mathrm{g},\mathrm{s}}^{y}\sim 0.18 \text{m/s}\) is a typical velocity in conditions under which \({\tau }_{\mathrm{p}}^{y}\) is significant compared to the surface wind stress. Since the surface geostrophic current \({v}_{\mathrm{g},\mathrm{s}}^{y}\) in COCO’s simulation is approximately \(0.19 \text{m/s}\) (Fig. 2b), the estimation obtained using Eq. (9) implies that the reverse EOT may occur over the ESC shelf break, where \(h\sim 100 {\text{m}}\). This estimation is consistent with that obtained by COCO’s simulation.

A buoyancy-driven geostrophic flow with a vertical shear of \({\text{O}}\left({-10}^{-3}\right) {\mathrm{s}}^{-1}\) in addition to a downwelling-favourable wind is not peculiar to the ESC; it is common to the various shelf break fronts such as those in the Gulf of Alaska (Stabeno et al. 2004). The estimation of \({\tau }_{p}^{y}\) obtained using Eq. (9) is further considered so that it may be applied to various coastal frontal regions under controlled downwelling-favourable wind and a strong coastal current.

The COCO-simulated geostrophic stress \({\tau }_{\mathrm{p}}^{y}\) in areas A3, A4 and A5 as shown in Fig. 9a is compared with the estimated \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) (Fig. 9b). To estimate \({{\tau }_{\mathrm{p}}^{y}}^{\#}\), we used data from the CMEMS to evaluate the geostrophic surface current from the SSH above the geoid (see Sect. 2.3). Here, the along-isobath direction is determined by the SSH instead of the isobaths, since in a coastal region with a complex terrain and multiple extremes, the along-isobath unit vectors exhibit a complicated and unstable direction. The MLD is scaled by \({h}_{\mathrm{mix}}=\) 100 m, because the shelf break fronts were considered at depths of \(\sim 100 {\text{m}}\). The positions for the scaling estimation, which we chose randomly along the front, are represented as numbered dots in Fig. 9a. In Fig. 9b, we observe that the coloured dots are gathered around the line \({\tau }_{\mathrm{p}}^{y}={{\tau }_{\mathrm{p}}^{y}}^{\#}\), indicating that \({\tau }_{\mathrm{p}}^{y}\) scales well with \({{\tau }_{\mathrm{p}}^{y}}^{\#},\) with their root mean square difference being 0.0\(226 \mathrm{N}/{\mathrm{m}}^{2}\).

Fig. 9
figure 9

Scaling analysis: Implications of the significance of geostrophic stress in various frontal coastal regions. a The shading denotes the climatological wintertime mean (the January mean in the Northern Hemisphere and the August mean in the Southern Hemisphere) estimated geostrophic stress along the SSH direction in each region. The vectors are the geostrophic current calculated via the sea surface height above the geoid (see Sect. 2.3). The numbered dots are the selected points located around the coastal front in each region. We chose six representative coastal regions where downwelling favourable winds are dominant. The contours denote the isobaths at 100 and 1000 m. b Geostrophic stress comparison. The x-axis denotes the geostrophic stress value estimated by Eq. (9), and the y-axis denotes the value modelled by the COCO simulation. The numbered dots correspond to those at the positions in a. The COCO simulation includes areas A3–A5. c The y-axis denotes the estimated geostrophic stress in the selected six areas, and the x-axis denotes the surface along-SSH wind stress accordingly. The error bar denotes the root mean square difference between the estimated and modelled geostrophic stresses (= 0.03 \(\mathrm{N}/{\mathrm{m}}^{2}\)) in b

Full size image

We used the SSH of the CMEMS reanalysis to estimate \({v}_{\mathrm{g},\mathrm{s}}^{y}\) because there are almost no observations available in high-latitude coastal regions in winter. We should note that there are some potential defects included in the SSH. The first is the sea ice coverage near the ESC in winter, which makes SSH measurement by satellite impossible. Therefore, the estimated SSH by the CMEMS reanalysis product may also include errors for the area near the ESC in January because of the absence of satellite SSH data. However, the results are still considered as a reasonable estimation in the reanalysis because it includes appropriate physical processes such as riverine discharge and sea ice (see subsect. 2.3), and has an enough resolution (\(1/12^\circ \times 1/12^\circ\)) for the generation of the ATWs (e.g., Simizu and Ohshima 2002). The second potential defect is that the input satellite SSH data from the coastal areas might be contaminated by the land. The first factor may explain why the estimated \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) does not correspond well to the simulated values in the A3 area around the ESC. On the other hand, \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) is close to the simulated values \({\tau }_{\mathrm{p}}^{y}\) in the A4 (East Kamchatka) and A5 (Gulf of Alaska) areas, as there is no sea ice coverage.

This analysis motivated us to evaluate the geostrophic stress in other coastal regions, since it may elucidate the potential dynamical importance of the geostrophic stress. We selected six representative coastal regions (A1–A6 in Fig. 9a). Figure 9a depicts \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) and implies that the geostrophic stress has significant values in various coastal regions. Figure 9c compares \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) in terms of the surface wind stress \(\langle {\tau }_{\mathrm{s}}^{y}\rangle\) to all of the selected coastal positions. In Fig. 9c, the coloured dots tend to concentrate in the shaded quadrants, implying that \({{\tau }_{\mathrm{p}}^{y}}^{\#}\) and \(\langle {\tau }_{\mathrm{s}}^{y}\rangle\) have the same direction. In the yellow-shaded region, where \(\left|{{\tau }_{\mathrm{p}}^{y}}^{\#}\right|>\left|\langle {\tau }_{\mathrm{s}}^{y}\rangle \right|\), the EOT may be reversed by a higher internal water stress. In the pink-shaded region, where \(\left|{{\tau }_{\mathrm{p}}^{y}}^{\#}\right|\le \left|\langle {\tau }_{\mathrm{s}}^{y}\rangle \right|\), a usual EOT is generated while also being retarded by the internal water stress.

This scaling implies that the geostrophic stress may be significant for various coastal areas, although detailed studies should be conducted in each region due to the errors that may have influenced the observed SSH values. Areas such as the upstream ESC, East Kamchatka Current, Labrador Current, Gulf of Alaska and Falkland Current are candidate areas where the reverse EOT could be generated (Fig. 9c). For areas with sea ice coverage that are not as dense as the coast of ESC (e.g., the Labrador Current), the air–sea heat flux cannot be neglected when discussing the mixed layer’s formation. For the area around the East Greenland Current, a very deep frontal structure at the shelf break exists, and as a result, the ratio between the MLD and the whole layer depth largely reduces the estimated geostrophic stress. The estimation represented by Eq. (9) suggests that the geostrophic stress should not be overlooked when evaluating the EOT structures in coastal fronts with depth scales of O(100)m, where cross-shelf overturning is responsible for nutrient entrainment and water exchange between the open ocean and the coastal region.

4 Summary

In this study, we used an Ocean General Circulation Model, IcedCOCO, to establish a realistic regional simulation to determine the formation of the winter deep mixed layer around the shelf break in the Sea of Okhotsk. During the winter, sea ice makes observation difficult. The model results, which simulated the two cores of the East Sakhalin Current and the density fronts over the gently sloping shelf, are instructive in terms of understanding the cross-shelf overturning circulation over the Sakhalin shelf. The density fronts are produced by riverine discharges around the Sea of Okhotsk. The vertical shear due to the thermal wind in the fronts, combined with a significantly large vertical viscosity, generates a large stress in the water column; this stress is known as “geostrophic stress”. A reverse overturning is induced by the larger geostrophic stress than the surface stress, with respect to the classical Ekman overturning, and the reverse overturning incorporates a nearshore upwelling and an offshore downwelling. A deep mixed layer forms with a depth of ~ 120 m in the downwelling region, where a reverse Ekman transport converges with an onshore Ekman transport from the open ocean; this mixed layer is deeper than the open ocean mixed layer, which has a depth of ~ 50 m. Scaling analyses indicate that this mechanism might be applicable to various other shelf break fronts in the world’s oceans.

The overturning over the gently sloping shelf, which we examined in this study, is located between a shallow area, where the water straightforwardly responds to the applied stress with a comparable surface and bottom stress, and a deep area where the depth of the surface boundary layer is far smaller than the whole layer’s depth. Lentz (1995) defined such a coastal transition region as the inner shelf. He examined the inner-shelf circulation in a homogeneous ocean and found that the overturning on the inner shelf is sensitive to vertical viscosity forms. In this paper, we found that stratification further modifies cross-shelf overturning via the geostrophic stress, which directly depends on the vertical viscosity. Although a study by Lentz (1995) provided us with insight into how barotropic water responds to various vertical viscosity profiles in the inner shelf, the effects in conjunction with stratification are still an open question. Spall and Leif (2016) studied restratification/destratification processes in the presence of baroclinic instability from the perspective of potential vorticity and buoyancy budgets with balances among wind stress, geostrophic stress and vertical mixing. They primarily examined cases with strong wind and strong stratification in which baroclinic eddies are dominant. However, density fronts over inner shelf regions are often much weaker, including those in the ESC, where the baroclinic instability may not be dominant or is at most comparable to the effects of geostrophic stress.

Some interesting research targets remain. One target involves the coastal Ekman layer responses to high-frequency variations caused by short-term strong wind events or tidal forcing; in this research, we primarily studied a coastal Ekman layer in a steady state. These effects are likely to cause larger geostrophic stress as well as larger surface and bottom stresses by generating viscosities larger than those of the monthly mean forcing. For example, diurnal tides are strong in the ESC region (e.g., Ohshima et al. 2002; Mizuta et al. 2003), and they likely cause intensive bottom currents and increase the bottom stress and vertical viscosity in the bottom boundary layer. These events may significantly influence the cross-shelf overturning and transport. Another related issue involves determining why a large viscosity occurs at the inner shelf; the answer to this question is important in terms of generating large geostrophic stresses. Furthermore, comparing the simulated cross-shelf and vertical velocity with the observations would be insightful, although obtaining the related data from observations is difficult considering that these variables only have small values. In the case of the East Sakhalin, it is even harder to obtain data during the winter because of the sea ice coverage. Additionally, the effects of sea ice on cross-shelf overturning have not been well examined either.