Abstract
This study examined characteristics of near-inertial internal waves (NIWs) associated with the background mesoscale field near the Tsushima Warm Current. Observational stations off Sado Island were visited recurrently to assess spatiotemporal changes of fine-scale and microscale properties of seawater. Also, NIWs were inspected in terms of relative vorticity and total strain in surface geostrophic motion. During summer expeditions in 2019, current and hydrographic surveys at the rim of an anticyclonic eddy provided clear evidence of downward-travelling NIWs, which were most amplified near the depth of lower pycnocline. The amplification of NIW coincided with elevation in the dissipation rates of turbulent kinetic energy (TKE) and microscale variation of temperature. The fall 2019 expedition found details of wave and turbulence properties associated with the mesoscale structure of paired vortices, where a cyclone and anticyclone were, respectively, adjacent to the east and west. Amplified signals of NIW-related vertical shear and TKE dissipation were found at isopycnals between the dipole cores. From the theoretical perspective of internal wave, the baroclinic term attributable to vertical shear of geostrophic current was interpreted as inducing downward travel of NIW through the lower pycnoclines between the dipole cores. It is also noted that cyclones, passing through the central part of Sea of Japan, can deliver kinetic energy into 10-km scale internal waves as a consequence of interaction between easterly wind and mountainous topography in the Honshu Island.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Tsushima Warm Current (TWC) flowing in the Sea of Japan is known to generate profoundly distorted meanders (e.g., Kawabe 1982a, b; Lee and Niiler 2010; Morimoto and Yanagi 2001; Morimoto et al. 2000; Naganuma 1985). Because of TWC meandering, numerous coherent structures identified by relative vorticity anomaly (RVA) are generated across the sea, particularly along the shelf slope near the Japanese archipelago (e.g., Morimoto et al. 2000; Watanabe et al. 2009). The cross-sea RVA distribution is affected strongly by seasonal changes in the TWC magnitude and the intensity of baroclinic instability (Morimoto and Yanagi 2001; Naganuma et al. 1985). The TWC volume transport is highly dependent on the amount of inflow through the Tsushima Strait, which seasonally builds up typically during summer–fall (Fukudome et al. 2010; Yabe et al. 2020).
Research outcomes in the southeastern part of the Sea of Japan can be an ideal model for studies related to oceanic responses to air disturbances. In fact, storm-driven internal waves have been elucidated clearly in past surveys examining the Sea of Japan (e.g., Byun et al. 2010; Igeta et al. 2009; Jeon et al. 2019; Kawaguchi et al. 2020; Mori et al. 2005; Park and Watts 2005; Noh and Nam 2020; Watanabe and Hibiya 2018). In late summer, atmospheric disturbances associated with tropical and bomb cyclones increase the number dramatically. Most such disturbances originate from southern areas of the North Pacific. As the influences of those cyclones propagate over the sea, they directly stir up near-surface waters and deep waters through internal wave action.
Oceanic motions in the southeastern part of the Sea of Japan are regarded as less contaminated by tidal effects of any kind (Igeta et al. 2009; Kawaguchi et al. 2020; Mori et al. 2005). Short-term oscillations in the northwestern Sea of Japan, proximate to the Korean Peninsula, are regularly influenced by the internal tides (Jeon et al. 2014; Nam and Park 2008; Park and Watts 2006). There, tidal forcing can be crucially important for the local mixing of seawater, e.g., through wave–wave interaction together with wind-generated internal waves (e.g., Noh and Nam 2020).
Mesoscale eddies and internal waves near TWC jets have been investigated recently by the authors in the framework of a research program: the FRA-AORI TWC Observatory (FATO) (e.g., Kawaguchi et al. 2020; Wagawa et al. 2020; Yabe et al. 2020). Key points of the latest findings and remaining questions from the FATO project can be reviewed briefly here. Year-round horizontal current data from an instrument moored off Sado Island (Fig. 1) were analyzed by Kawaguchi et al. (2020). Following a bomb cyclone, they found extraordinary amplification of near-inertial internal waves (NIWs) inside a warm-core eddy. There, the amplified waves occurred near the mid-depth stratification maximum identical to the critical level for NIWs (Kunze 1985; Kunze et al. 1995). They demonstrated that a certain part of the kinetic energy, contained by the primary inertial f, was transferred to smaller scale oceanic motions with multiple-inertial (MI) oscillations (c.f. Mori et al. 2005; Noh and Nam 2020).
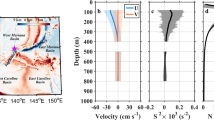
Geographical locations of shipboard and mooring surveys. During three cruises, stationary experiments of turbulence were conducted at the station of FATO, where a year-round mooring was deployed. Over transects of SI and E lines, turbulence, current, and hydrographic surveys were performed. The text presents additional details
As a part of the FATO missions in 2019, the team recurrently visited the mooring site off Sado Island and its nearby areas to conduct stationary and cross-TWC shipboard observations. In the series of surveys, various oceanographic measurements of phenomena such as hydrography, currents, and microstructure, were undertaken near the mooring station, and along and across the TWC axis. The present study specifically assesses temporal and spatial changes of signals from fine-scale internal waves and turbulent-scale mixing associated with mesoscale disturbances.
This report comprises the following sections. Section 2 presents a description of the methodology and observation programs for analyses. In Sect. 3, the dominant frequency of propagating internal waves is inferred from spectral analysis of the moored velocity. Section 4 presents the spatial extent of wave-related turbulent dissipation across the TWC mesoscales. In Sect. 5, details of stationary observations are explained along with their results. In Sect. 6, the atmospheric storm events, potential sources of ocean turbulence, are discussed using a diagnostic mixed-layer slab model. In Sect. 7, discussions of wave propagation through the observed mesoscales are presented in addition to the salient conclusions obtained from this study.
2 Observational programs and data treatment
A suite of physical oceanographic observations was conducted during three periods of scientific cruises in 2019, with research/training vessels: (1) T/S Tenyo-maru of Japan Fisheries and Education Agency during June 21–28; (2) T/S Oshoro-maru of Hokkaido University during July 15–28; and (3) R/V Shinsei-maru of the Japan Agency for Marin–Earth Science and Technology (JAMSTEC) during October 25–31 (Kawaguchi 2019). For convenience, those ship-based expeditions are abbreviated, respectively, herein as (1) TY-06, (2) OS-07, and (3) KS-10. All of the ships traversed the SI line, named after Sado Island, which is nearly perpendicular to the TWC front and which is home to FATO station. On the line, microstructure and hydrographic observations were conducted using a profiler (VMP-250; Rockland Science, Inc.) at horizontal spacings of 10–15 km. The FATO site is located at 137.75° E, 38.75° N, nearly 70 km offshore to the north of Sado Island (yellow circle in Fig. 1). It is at 1780 m water depth.
The quasi-free-falling tethered profiler (VMP-250) was used to obtain underwater microstructure data normally up to 400 m depth. During every expedition, hourly VMP operations were conducted right on the hour for nearly 20 h at FATO station. The instrument collected high-resolution vertical profiles of current shear and temperature gradient at a temporal frequency of 512 Hz as it descended at an approximate speed of 0.5 m s−1. The dissipation rates of turbulent kinetic energy (TKE) and the variance of temperature, expressed, respectively, as ε and χ, were evaluated by integrating the spectral power along a vertical wavenumber coordinate. For ε, the integration limits are kmin = 1 cycles per meter (CPM) for the lower bound and the Kolmogorov wavenumber, expressed as \({k}_{\text{K}}={\left({\nu }^{3}/\varepsilon \right)}^{-1/4}\), for the upper bound, where kK is found using the iteration method (Kawaguchi et al. 2014, 2016), and where \(\nu\) represents the molecular kinematic viscosity. For the χ estimate, the lower bound is chosen ad hoc as kmin = 1 CPM, similarly to ε, whereas the upper bound of wavenumber is the Batchelor wavenumber kB, which is expressed as a function of ε: \({k}_{\text{B}}={\left({\kappa }^{2}\nu /\varepsilon \right)}^{-1/4}\), where \(\kappa\) represents the molecular thermal diffusivity. The electronic noise levels are estimated approximately as the magnitudes of O(10–10) W kg−1 for ε and O(10–11) K2 s−1 for χ.
Slow-response CTD sensors equipped on the VMP-250 acquired the local temperature, salinity, and pressure of seawater at the sampling frequency of 64 Hz during descent, yielding approximately 8 mm vertical resolution if falling at 0.5 m s−1. Raw data from VMP-based CTD observations were compiled to produce 1 m averages of vertical profiles after relevant post-screening procedures (Kawaguchi 2019).
During the TY-06 and KS-10 expeditions, recording of horizontal ocean currents was implemented using a shipboard acoustic Doppler current profiler (SADCP or shipboard ADCP, RDI 38 kHz; Ocean Observer). The 5-min averaged horizontal current was used for analyses later in the study, with manual data screenings based on the echo intensity and percent-good rates. Regarding potential errors in current velocity because of the transducer alignment, the correction proposed by Joyce (1989) was applied to the original SADCP record. The vertical resolutions of the SADCP current were 16 m and 24 m, respectively, for TY-06 and KS-10. For the OS-07 survey, no horizontal velocity was obtained because of technical failures during the SADCP operation.
For the detection of fine-scale wave signals, the SADCP horizontal current and its vertical shear undergo correction of backward rotation for the phase shift because of progressive waves (Shcherbina et al. 2003) as \(u^{\prime } + iv^{\prime } = \left( {u + iv} \right){\text{exp}}\left( { - i\omega \left[ {t - t_{0} } \right]} \right)\), where u and v, respectively, represent the zonal and meridional components in the original coordinate, whereas u’ and v’ are those backward-rotated. Here, t and t0, respectively, denote an arbitrary and an initial time. In the analysis, prominent oscillatory motions are associated with near-inertial internal waves, so that an ad hoc frequency of local inertial (\(\omega \approx f\)) is assumed.
Moreover, a part of year-round mooring velocity (75 kHz Workhorse Long Ranger; Teledyne RD Instruments Inc.) recorded at the FATO site is used for comparison with the shipboard survey results. Particularly, oscillation frequencies in the observed motion are examined in this study. A full description of the mooring system and the data treatment are presented in a separate report (Kawaguchi et al., 2020).
3 Specification of dominant frequency from long-term mooring
Before in-depth analyses of ship-based studies, knowledge about the oscillation frequencies derived from the moored ADCP observation must be explained (Figs. 2, 3).
Time-series of a surface wind stress, b flux of inertial kinetic energy, c predicted inertial motion in SML, d moored raw currents, and e near-inertial bandpass current magnitude (0.8–1.2f) at depth of 138 m, at FATO. Hatched regions show the expedition periods. In a, the inverted triangle denotes an event of passing cyclone, emphasized in Fig. 12
a Frequency spectrum for horizontal current vector from FATO mooring during June 15–October 31, 2019 located at depth of 138 m. Horizontal kinetic energy for CW, CCW, and its total are shown, respectively, by blue, red, and black curves. b Ratio of horizontal kinetic energy between CW and CCW rotation. The reference level of \(\frac{{E}_{\mathrm{CW}}}{{E}_{\mathrm{CCW}}}=\frac{{(\omega +f)}^{2}}{{(\omega -f)}^{2}}\), based on the linear wave theory, is shown as a bold, grey curve. Key oscillation frequencies (f, f + M2, 2f, f + M4, etc.) are shown by vertical dashed lines (see annotations at top of panel). In a, spectral calculation is processed with 30-day Hanning windows, with 18 degrees of freedom. The 90% confidence interval is shown as a vertical bar. The reference level for internal gravity wave (GM), in terms of frequency, is shown as a bold, grey curve. DT and SDT, respectively, represent diurnal and semi-diurnal tides
During the periods of ship-based observation, the horizontal velocity at the depth of upper water is variable along with short-term fluctuations, reflecting some inertial (Fig. 2d). The near-inertial band-passing demonstrates the greatest energetic event during TY06 of the three cruises, attaining nearly 20 cm s−1 velocity magnitude (Fig. 2e). In fact, the frequency spectrum shows that a dominant peak exists for neighboring frequencies of local f: 0.053 CPH (Fig. 3a). In the continuum frequencies, typically between 0.1 CPH and 0.5 CPH, the curve of variance decreases approximately following the slope represented by the canonical curve of Garrett and Munk (1975; GM), shown as grey in Fig. 3a. At the continuum range, the root-mean-square velocity is approximately 0.4 cm s−1, which is slightly smaller than that for GM being 0.7 cm s−1. The CW rotational tendency with time dominates the counterpart of CCW (i.e. ECW/ECCW > > 1) as solely determining the total strength of horizontal kinetic energy (Fig. 3b). The peaks of the rotary energy ratio, ECW/ECCW, generally follow the curve of single-plane wave solution (Gill 1982; Polzin 2008):
According to the yearlong FATO mooring, neither current rotation provides any marked contribution from primary diurnal (DT) or semi-diurnal tidal (SDT) constituents (Fig. 3a). One can readily infer that wave–wave interactions between NIW and any kind of tidal constituent are not really important in the study domain, i.e., the Japanese side of the Sea of Japan (Noh and Nam 2020; Park and Watts 2006). The MI frequencies (i.e., 2f, 3f, 4f, and 5f) present nontrivial peaks of velocity variance, as anticipated. The MI feature has been commonly observed in the southern Sea of Japan (Kawaguchi et al. 2020; Mori et al. 2005). It is also believed that the abundant mesoscale features in the region (Morimoto et al. 2000) can act as an amplifier of MI oscillations through nonlinear resonance occurring between NIWs (Danioux et al. 2008).
4 Evidence of mesoscale eddies, internal waves, and turbulence
4.1 Mesoscale features
The vertical component of mesoscale RVA, defined as \(\zeta_{{\text{g}}} = \frac{{\partial v_{{\text{g}}} }}{\partial x} - \frac{{\partial u_{{\text{g}}} }}{\partial y}\) (where \(u_{{\text{g}}}\) and \(v_{{\text{g}}}\), respectively, denote the zonal and meridional components of geostrophically balanced horizontal velocity), can strongly affect the propagation characteristics of NIWs by modulating the wave frequency (e.g., Kunze 1985; Kunze et al. 1995; Park and Watts 2006). By the linear theory, the internal waves are able to propagate as constrained by the following range of the oscillation frequency:
The upper bound of intrinsic frequency is limited by the local buoyancy frequency, defined as \(N = \sqrt { - \frac{g}{\rho }\frac{{{\text{d}}\rho }}{{{\text{d}}z}}}\), whereas the lower bound is defined as \(\omega_{{{\text{min}}}}\). Here, the vertical axis z points upward, g is the gravitational acceleration, and ρ is the seawater density. The full expression of \(\omega_{{{\text{min}}}}\) is given elsewhere in the literature as (Joyce et al. 2013; Thomas 2017; Whitt and Thomas 2013):
where \({\text{Ri}}_{{\text{g}}} = \frac{{N^{2} }}{{\left( {\partial u_{{\text{g}}} /\partial z} \right)^{2} + \left( {\partial v_{{\text{g}}} /\partial z} \right)^{2} }}\) is the Richardson number of geostrophic flow and \({\text{Ro}}_{{\text{g}}} = \zeta_{{\text{g}}} /f\) is the gradient Rossby number. In Eq. (3), the term of relative strength between the vertical shear of geostrophic current and the density stratification Rig modulates the minimum frequency determined by the effective Coriolis frequency:
\(F = \omega_{{{\text{min}}}}^{{{\text{BT}}}} = \sqrt {f\left( {f + \zeta_{{\text{g}}} } \right)} = f\sqrt {1 + {\text{Ro}}_{{\text{g}}} } .\) (4)
Actually, Eq. (4) is equivalent to an equation from classical wave theory (e.g., Kunze 1985). Comparison of Eqs. (3) and (4) reveals that the baroclinic term Rig serves to revise the estimate of \(\omega_{{{\text{min}}}}\) downward.
We strove to ascertain the horizontal distribution of RVA and baroclinicity for some mesoscale systems along the passage of ship-based observations, i.e., June, July, and October in 2019. In Fig. 4, the near-surface RVA derived from the sea surface height (SSH) is displayed (Yabe et al. 2020), where the near-surface current is assumed to be balanced geostrophically. According to satellite-based images, the southeastern part of the Sea of Japan is apparently filled entirely with numerous coherent eddies and meanders (Morimoto et al. 2000).
Temporal averages of a–c relative vorticity anomaly RVA, d–f Okubo-Weiss parameter OW, g–i total strain TS, for periods of (left) TY-06, (middle) OS-07, and (right) KS-10. Values of RVA and TS are normalized by f, whereas OW is by f2. Eddy structures are identified as \(\mathrm{OW}/{f}^{2} < -2.5 \times {10}^{-4}\) (marked in its color bar). Yellow circles denote the FATO station. In a, c, green arrows indicate a 50-m depth horizontal current from SADCP. In each panel, satellite-based SSH contours, with an interval of 0.02 m, are superimposed. In a–c, SSH-based geostrophic currents are indicated by black arrows. In c, f, i, anticyclonic and cyclonic eddies are designated, respectively, as ACE10 and CE10
The near-surface features of mesoscale eddies, as suggested by RVA, are also confirmed by negative values of the Okubo–Weiss parameter (Okubo 1970), expressed as:
where \(S_{{\text{n}}} = \frac{{\partial u_{{\text{g}}} }}{\partial x} - \frac{{\partial v_{{\text{g}}} }}{\partial y}\) represents the normal strain and \(S_{{\text{s}}} = \frac{{\partial v_{{\text{g}}} }}{\partial x} + \frac{{\partial u_{{\text{g}}} }}{\partial y}\) stands for the shear strain (Fig. 4d–f). In regions of \({\text{OW}} < - 2 \times 10^{ - 12}\) s−2, where the variance of rotation is greater than the sum of those in strain field, the near-surface water is thought to go around the closed contour of SSH without divergence or convergence. Results of earlier studies (e.g., Jing et al. 2017; Noh and Nam 2020; Polzin 2008) suggest that the total strain, defined as \(\sqrt {\left( {S_{{\text{n}}}^{2} + S_{{\text{s}}}^{2} } \right)}\), was able to facilitate the efficient transfer of kinetic energy in mesoscale features to the fine-scale internal waves, and eventually to the microscale turbulence (Fig. 4g–i). Near the FATO station, especially in the region extending southwestward, the anomalous level of total strain is identifiable during KS-10 (Fig. 4i). Linkages between NIWs and surface strain will be addressed in later sections.
During the TY-06 and the OS-07 campaigns, an anticyclonic eddy characterized by negative RVA, being roughly − 0.1f, was identified near FATO station (yellow dots in Fig. 4a, b). The anticyclone remained there for two successive cruises. During TY-06, the FATO station was positioned at a western rim relative to the anticyclone center, but it was even closer to the center of the same eddy during OS-07. Clockwise rotation because of the anticyclone was confirmed from shipboard ADCP observations made during TY-06 (green arrows in Fig. 4a).
In contrast to earlier expeditions, the KS-10 campaign was implemented under the influence of positive RVA circumstances (Fig. 4c). It was approximately when a cyclonic vortex developed quickly and became more coherent. Then, the FATO station was located right on the center of oceanic cyclone. Indeed, the shipboard ADCP along the SI line depicts the near-surface ocean circulation, which rotates counterclockwise (green arrows in Fig. 4c).
In addition, the ship made a zonal transection along the E line (Fig. 1), which crossed the paired vortices consisting of a cyclone at the west and an anticyclone at the east, respectively, designated as CE10 and ACE10. The anticyclone is closely adjacent to the neighboring cyclone, which was on the SI line.
The on-site hydrographic properties are revealed as ships traversing meridionally across the SI line, encompassing the FATO station, for every cruise (Fig. 5). Regarding early summer cases in June and July, the 25.0–27.0 σθ isolines are shown as notably swollen to the shape of a convex lens, which dynamically drives a clockwise rotation (anticyclonic) for current circulation under the geostrophic balance (Fig. 5a, b).
On the SI section, the eddy’s core is present in a region between Sado Island and offshore at approximately 39.25° N latitude (Fig. 4a, b). Therefore, the FATO station is regarded as inside the negative RVA core (Fig. 5a, b). During these expeditions, density stratification (N) shows a shell-like structure, where stubborn (strongly stratified) layers with N = 5–7 cycles per hour (CPH) exist at the top and bottom, respectively, corresponding to isopycnals of approx. 25.0 σθ and 26.5–27.0 σθ (Fig. 5a, b). It is weakly stratified as N < 2 CPH, inside the core, which corresponds to 26.0–26.5 σθ.
During the fall expedition, a concave type of lens structure is found for density stratification (Fig. 5c). The isolines of 24.0–27.0 σθ clearly form an arching curvature towards the surface. The stratification is particularly intense where the isopycnals dome upward, i.e., at around 50 m depth. These isopycnals are regarded as driving a counterclockwise (cyclonic) rotation under the quasi-geostrophic dynamics (Gill 1982). Moreover, the underwater properties of isopycnals are fairly consistent with deductions from the satellite-based RVA distributions (Figs. 4, 5).
The SADCP observation well resolves the mesoscale structure of RVA as it crosses the paired vortex system along the E line (Fig. 6a). For this, the RVA values are estimated as the spatial gradient of SADCP horizontal velocity perpendicular to the line of interest (Fig. 6). In the environment of ACE10, the negative region in RVA is coincident with the downward-arching isopycnals, being 26.5–27.0 σθ, particularly in the upper 200–250 m depth. By contrast, CE10 produces an opposite-signed RVA, i.e., positive, at 150 m or shallower depth (Fig. 6b). The western part of ACE10 is another spot for RVA being positive, apparently as a result of the spatial change in the azimuthal velocity because of the anticyclone (Fig. 6c).
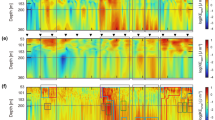
Vertical sections along E line (left) and SI line (right): a, b f-normalized RVA; c, d horizontal normal velocity, where northward and northwestward give, respectively, positive values; e, f squared vertical shear of horizontal velocity, represented by logarithmic scale; g, h vertical shear of back-rotated zonal velocity. Contour lines denote σθ, with intervals of 0.25 and 0.50 kg m−3, respectively, for a–d and e–h. In e–h, vertical profiles of log10 ε from turbulence observations are overlain (see horizontal bars for a reference scale)
4.2 Evidence of internal waves and turbulence
During KS-10, the ship moved across the paired vortices on the E line and SI line (Fig. 1). During the survey, physical properties of fine-scale NIWs and microscale disturbance were investigated closely. The E-line transection took roughly 1.5 days, whereas the SI line was nearly finished in 1 day. Consequently, it can be assumed that during each transect, any oceanic feature larger than mesoscale remained more or less unchanged.
Close inspection of small-scale features along the E line revealed the spatial coincidence of energetic patches between vertical shear of wave-related current and the TKE dissipation rate (Fig. 6e). The amplified NIWs appear at latitudes between 136.0° E and 137.5° E, where wave arrays at some parts are aligned in parallel with isopycnals of 26.5–27.0 σθ. According to the E-line transect, the wave-like structures are distinctly apparent, with characteristic lengths of 10–20 km horizontally and 50–150 m vertically (Fig. 6e, g). The amplified waves can be seen at the depth of lower pycnocline for ACE10 (Fig. 6e). With respect to the spatial distribution of the TKE dissipation, as assessed by ε, it is magnified at the lower pycnocline of ACE10, corresponding to the internal wave features.
Across the CE10 inner core, only the attenuated signature of perturbations is apparent because of fine-scale NIW structure and microscale turbulence (Fig. 6f, h), compared to those for the western half of the E line survey. The most energetic waves are packed at shallow depths within 150 m (Fig. 6f), which are spatially coincident with shoaled isopycnals for the cyclone. At those depths, the ε peaks are found only in a sporadic manner, with magnitudes typically less than O (10–8 W kg−1) (Fig. 6h).
The central part of CE10 and its adjacent areas were characterized by intense total strain (Fig. 4i). There, profound features of internal wave signal are anticipated (Polzin 2008). Indeed, the section of the oceanic cyclone exhibited NIW-related features that are well defined (Fig. 6) irrespective of the fact that the cyclone is seemingly unfavorable for NIW trapping (Kunze 1985). It might also represent the effects of the intense shearing in near-surface geostrophic motions, as described above.
Assuming a dispersion relation for the internal waves, the scale of the horizontal wavelength can be inferred as \({k}_{\mathrm{z}}^{2}=\frac{{N}_{0}^{2}-{\omega }^{2}}{{\omega }^{2}-{f}_{\text{eff}}^{2}}{k}_{\mathrm{H}}^{2}\) (Gill 1982; Massel 2015), where kz and kH, respectively, represent the vertical and horizontal wavenumbers, N0 = 5 CPH denotes the representative buoyancy frequency inside the anticyclone, and wave frequency \(\omega\) is assumed to be in a sub-inertial frequency range of 0.95–0.99f (Jeon et al. 2019; Kawaguchi et al. 2020). One can obtain roughly 20–30 km for the horizontal wavelength if the vertical wavelength is estimated as 100 m, for instance, as shown in Fig. 6g. The linear dispersion theory of internal gravity waves might account for the complex spatial structure in the horizontal current observed during the E line survey.
5 Time evolving features of NIWs and turbulence at FATO
5.1 Hydrography and microstructure
Details of hydrography and microstructures from every stationary observation at FATO station are presented in Fig. 7. During the TY-06 campaign, hydrographic properties were characterized by the existence of warm and saline waters in the upper part of the water column (Fig. 7a). Salinity reaches the distinct maximum of 34.5 at around 30–40 m depth. It then decreases slowly with increasing depth to 34.2 at around 200 m depth, while the temperature is warm exclusively at the top 50 m being warmer than 16 °C. It decreases gradually to 12 °C at 200 m. Density stratification shows the two distinct maxima at 30 m and 200 m depth, representing the anticyclone characteristics (Fig. 5a). Hourly VMP measurements, which were taken for 20 h, revealed intricate patterns characterized by short-term changes in N(z) (Fig. 7a).
During the July expedition, the hydrographic environment is similar to that in the June expedition, except for slightly strengthened near-surface stratification in July (Fig. 7b). The similarity in hydrographic properties found during the two expeditions is readily apparent from the θ–S diagram (Fig. 8).
Some difference is apparent between the turbulent variables examined during the couple of early summer expeditions (Figs. 7, 9). First, during TY-06, ε shows a remarkable peak at intermediate depths of 200–230 m, where the magnitude exceeds ε = O (10–8 W kg−1). Elevation is also found in the temperature gradient variance χ (Fig. 7a) at a slightly wider depth range of 200–250 m, with maximum attained at χ = O(10–6 K2 s−1). During OS-07, microscale variables of both kinds became even less energetic, whereas remnants of turbulent patches exist at similar depths (Fig. 7b).
Vertical profiles of a N, b ε, c χ, and d total shear squared \({u}_{z}^{2}+{v}_{z}^{2}\) for periods of TY-06 (blue), OS-07 (green), and KS-10 (red), where ε and χ are shown on a logarithmic scale. In b–d, the averages are drawn as bold curves, whereas the standard deviations are shown as dotted curves. Hatched regions denote an inferred depth range of critical level
During OS-10, the observed microstructure properties were rather different from those found in earlier expeditions undertaken in early summer (Fig. 7c). Development of surface mixed layer (SML) deepening was readily apparent during the fall expedition. The SML deepens to nearly 40 m, where the temperature is uniformly 18 °C and the salinity is nearly 33.8. Another notable feature that is different from earlier episodes is the strengthening of density stratification around the SML bottom, approx. 40 m, leading to N > 20 CPH. The vertical profile of N consists of the sole peak centered at the SML base (Fig. 9a).
In KS-10, the upper part of water column equivalent to isopycnals of < 25.5 σθ is evidently less saline and colder than those from the other two expeditions (Figs. 7c, 8) by 0.5 in S and by 1.0 °C in θ at an isopycnal of 24.0 σθ. This difference can be inferred as the seasonal variation at the FATO location (Wagawa et al. 2020).
Related to the single peak of stratifications for the fall expedition, the high value of ε is confined mostly within the SML, which is exposed directly to the air (Figs. 7c, 9b). Variation of the temperature gradient more broadly shows the scattering distribution of turbulent-scale energy patches, with confinement along thin isopycnal layers. For both turbulent variables, no apparent peak associated with any amplified current shear can be spotted at remote depths underneath the SML.
The steady-state TKE equation is expressed by the balance among the following terms: (1) production by mean flow shear, designated by P; (2) dissipation attributable to molecular viscosity, D; and (3) buoyancy flux caused by convection, W (Thorpe 2005) as:
One can then introduce the flux Richardson number \({\text{Rf}}\), which is defined as the ratio of the energy removal by buoyancy forces to the production by the shear: \({\text{Rf}} = W/P\). The quantity of \({\text{Rf}}\) can be related to the efficiency factor of:
The efficiency factor is expressed by the following equation (Oakey 1982):
In the specific case of the stationary experiment at TY-06, where ε = 0.5–1.0 × 10–9 W kg−1, χ = 1.0 × 10–6 K2 s−1, N = 3 CPH, and \(\overline{T}_{{\text{z}}}\) = 0.05 °C m−1 (Fig. 7), a back-of-the-envelope calculation yields values of \({\Gamma }\) = 0.14–0.27 and \({\text{Rf}}\) = 0.16–0.38. These estimates are largely consistent with the conventional value of \({\Gamma }\) = 0.2 (Thorpe 2005). Therefore, one can obtain the approximate relation of \({\text{Rf}} = \frac{W}{P} \ll 1\), resulting in \(P \approx D\) from Eq. (6). It is therefore concluded that the shear-produced TKE is consumed proportionally by molecular dissipation, rather than by the work of buoyancy forces.
5.2 Signals of amplified internal waves
Profound wave signals at the middle depth, which occurred during TY-06, can be examined closely though comparison with additional materials.
Vertical shear of horizontal current clearly manifests wave propagation in the vertical sense (Fig. 10a). Current shear images exhibit a couple of crests and troughs of internal waves encountered over a timeframe of approximately 20 h. Considering that the local inertial period is 19.22 h, the oscillatory signals in vertical shear can be attributed to near-inertial internal waves (Igeta et al. 2009; Kawaguchi et al. 2020). Apparently, the iso-phase lines for the wave fluctuation climb upward with time, at a rate of roughly 10 m h−1.
Temporal evolution of wave-related variables at FATO during a TY06 and b KS10: vertical strain, inverted gradient Richardson number Ri−1, zonal and meridional vertical shear, respectively, uz and vz. It is noteworthy that Ri−1 is shown on a logarithmic scale, where the criterion for instability, i.e., Ri−1 = 4, is enclosed by blue contours. In computation of vertical shear, horizontal velocity is smoothed in advance with a 1-h spline filter
Divergence and convergence of motion resulting from the fine-scale internal waves reflects temporal and spatial variation in the vertical density gradient (Thorpe 2005). A convenient measure is the vertical strain expressed as (Alford and Gregg 2001):
where \(\langle {N}^{2}\rangle\) denotes the temporal average of squared N over the stationary observation (Fig. 9a). For the TY-06 (Fig. 10a), one can find a coherent structure in \(\gamma\), characterized by a 20–30 m vertical scale. Irrespective of the indistinct appearance, it allows identification of some coherent signatures propagating; it mostly appears to go upward at a speed of approx. 5 m/h (Fig. 10a). A causal relation linking variations between vertical strain and horizontal current is suspected, but it cannot be readily proved.
An important question remains unresolved: Can the NIW shear explain the observed maximum of dissipation rates? Computing the ratio between the stratification versus vertical shear of horizontal current, i.e., the gradient Richardson number as \(\mathrm{Ri} = {N}^{2}/{\left(\mathrm{d}U/\mathrm{d}z\right)}^{2}\), one can answer this question (Fig. 10a). The inverse function Ri−1 is shown to represent large values conveniently as potentially unstable fluids. For Ri−1 calculation, the SADCP horizontal velocity is spline-filtered to cut off sub-hourly fluctuations. According to the time-vertical section for N (Fig. 7a), the peak exists at depths of 170–200 m, where it is located initially at about 200 m. It then shoals upward by approximately 20 m in several hours. The amplitudes of current shear are recognizably strong at depths of 140–250 m (Figs. 9d, 10a). According to the Ri−1 display, it is more likely to be statically unstable at depths below 200 m, where a highly amplified NIW packet cannot overlap with highly stratified water, which corresponds to the bottom of the mesoscale anticyclone (Fig. 10a).
For discussion of wave packet migration, one can conveniently adopt the rotary spectrum method for the vertical profiles of horizontal velocity vector and its vertical shear, the so-called ‘dropped spectrum’, based on the Fast Fourier Transformation algorithm (Gonella 1972). From that application, one can infer the presence of wave kinetic energy and can distinguish components of downward and upward propagation associated with the near-inertial waves, especially as a function of vertical wavenumbers (Fig. 11) (Pinkel 1984, 2008). For this calculation, the Wentzel–Kramers–Brillouin (WKB) scaling procedure is applied to the vertical coordinate based on the local stratification (Leaman and Sanfornd 1972). The WKB scaling is expected to minimize stretching effects because of local stratification that modulates the internal wave properties, especially in terms of wavelength and wave amplitude. The WKB scaling approximates the situation in which wave-related perturbations are even smaller on the vertical scale than those from the background variation.
Dropped spectra of a horizontal velocity and b its vertical shear during stationary observations of TY-06 and KS-10. Blue and red curves, respectively, show clockwise and counterclockwise rotations with depth, whereas black shows their sum. Dashed curves represent the canonical GM spectrum. For each curve, every 10-min averages of spectra are combined. Blue vertical bars represent 95% confidence intervals with 40 degrees of freedom. For better representation, spectral curves for KS-10 are lowered by 2 decades
Coordinate z* from the WKB approximation is derived as \(\mathrm{d}{z}^{*}=\stackrel{-}{N}(z)/{N}_{0}\mathrm{d}z\), where N0 = 3 CPH and where \(\stackrel{-}{N}(z)\) represents an average profile of N(z) from overall CTD profiles acquired during TY-06 and KS-10 under hourly VMP observations at FATO station (Fig. 11a). In addition, each component of horizontal velocity is scaled using a normalized profile of N. Therefore, it can be assumed to remove the bias in wave amplitude because of the variable stratification (Leaman and Sanfornd 1972). Regarding the zonal component, for example, it is re-coordinated as \({u}^{*}(z)=u(z)/\sqrt{\stackrel{-}{N}(z)/{N}_{0}}\).
In Fig. 11, the spectral density of the horizontal current and its vertical shear are displayed. The CW and CCW components are, respectively, indicative of downward and upward wave energy propagation (Leaman and Sanfornd 1972). The spectral curve for the total horizontal velocity varies along with the semi-empirical spectrum, as proposed originally by Garrett and Munk (1975). The variation implies that the waves distribute their kinetic energy to multi-scale disturbances in an orthodox manner. Particularly, the CW and CCW spectral curves present a notable mutual discrepancy at the wavenumber band between 7 × 10–3 CPM and 1 × 10–2 CPM, which is equivalent to 100–140 m in actual length. In other words, a packet of NIW with 100–140 m vertical wavelength tends to migrate downward rather than upward. Downward propagation of wave kinetic energy, as suggested by upward phase propagation, is fairly common for eddy-trapped NIWs (e.g., Cuypers et al. 2012; Jeon et al. 2019; Joyce et al. 2013; Kawaguchi et al. 2016, 2020).
By contrast, the October survey documented another characteristic of internal waves under the cyclonic eddy. In Fig. 10b, wave-like patterns are apparent at depths of the top 250 m. It is noteworthy that the amplitude of vertical shear is much weaker, being O(10–3 s−2), than that for the anticyclone. According to the figure showing Ri−1, the internal waves were insufficiently powerful to generate an adequate amount of turbulent mixing against local stratification (Fig. 10b). In fact, the strain field shows no marked features corresponding to wave propagation in the density field (Fig. 10b).
According to the dropped spectral analyses (Fig. 11), from the cyclonic eddy observation in KS-10, no significant difference was found between the CW and CCW components. Consequently, the signals of internal waves found in the cyclone are not believed to propagate in either vertical direction. In addition, the total spectral curves of velocity and shear underlie the canonical GM spectra at broad wavenumbers smaller than 2 × 10–2 CPM (50 m or greater actual length). In conclusion, the cyclone-trapped waves are neither very energetic nor radiative.
The NIWs trapped by cyclonic vortices have been reported only rarely in earlier reports of the literature. The diagnostic wave-ray tracing studies based on the WKB wave theory suggest that the incident NIWs into mesoscale features, with positive RVA, might be reflected backward or diffracted to go around (Kawaguchi et al. 2020; Kunze 1985). We presume that the trapped kinetic energy associated with NIWs was unlikely to be delivered from any outer region of the oceanic cyclone. That energy was generated locally from some violent surface wind forcing that took place during tropical cyclones which struck in earlier months (Fig. 2a). This issue is addressed in the following section.
6 Atmospheric forcing: storm events in 2019
The kinetic energy sources for downward-travelling NIWs are most likely to be atmospheric disturbances (Kawaguchi et al. 2016, 2020; Mori et al. 2005). A time-series of surface stress for the FATO site is presented in Fig. 2a, as evaluated from a 10-m wind of the Grid Point Value (GPV) reanalysis calculation. In the model, the surface winds are gridded in 1/16 for longitude and 1/20 degrees for latitude.
The kinetic energy flux for SML and the predicted inertial velocity are presented by the diagnostic calculation of a mixed-layer slab model (D’Asaro 1985; Pollard and Mallard 1970). Rapidly changing wind stress can favorably affect the intense oscillatory current in SML because of the resonance between the surface current and wind. For computation, the SML thickness is assumed to be constant throughout the months of May–October as 30 m. The decaying timescale for the inertial oscillation is set as 3.5 days. A report by Kawaguchi et al. (2020) presents additional details of the computational schemes.
According to the GPV reanalysis output, no noteworthy wind event occurred during TY-06, i.e., between June 21 and 28, irrespective of the profound signals of NIWs (Fig. 2c, d). An intense cyclonic disturbance, with surface stress magnitude of |τ|= 0.2 N m−2 or greater (triangle in Fig. 2a), preceded the observation by a week (Fig. 12a). The cyclone was initially at the Pacific side of Honshu Island. It subsequently entered the Sea of Japan by crossing the same island through its middle. Thereafter, it moved northeastward along the coast in the sea.
As the cyclone moved from west to east in the coastal side of the Sea of Japan, easterly winds blew from land to the sea. In the mid-June low-pressure system, the easterly seaward wind created narrow streak structures in its vertical rotational field, which alternates its sign with certain distance along the coastline (Fig. 12b). The streaky wind shear has an approximate horizontal scale of 10–20 km. The fluctuating features of surface winds might reflect the effects of complex terrain in the Ou mountain range, which extends through the middle of northern Honshu. The wind shear might therefore accompany a vertical current in the water as a result of Ekman pumping, as reported by Gill (1982), defined as:
One can infer that the disturbance attributable to the Ekman pumping ultimately triggered NIWs that distinctly matched the horizontal scale of 10–20 km as large as the mountainous terrain.
During the stationary campaign for the OS-07 expedition, the turbulent variables indicated only attenuated signals of local mixing compared to those for TY-06. With regard to the mid-depth peak, the ε and χ values declined, respectively, to roughly 20% and 5% of the values of the earlier month (Fig. 9b, c). According to the slab model calculation, the on-site surface wind stress added only a modest level of kinetic energy around the inertial frequency (Fig. 2c). Therefore, it can be inferred that the signals of microscale turbulence in the upper part of water column were a remnant of the preceding mixing event, related to the amplified NIWs, as observed in June (Fig. 9b, c).
Regarding the October event, a handful of windstorm events occurred during August–October, caused by violent tropical cyclones that entered and passed over the central Sea of Japan (Fig. 12a). Any of those tropical cyclones might make a potential input of kinetic energy to the internal waves trapped by the oceanic eddies (Fig. 10a). This study examined no details of wave trapping or propagating characteristics for the cyclonic structure.
7 Discussion and conclusions
This study investigated fine-scale internal waves and microstructures of seawater from the viewpoint of their interaction with mesoscale features, emerging around TWC, in the Sea of Japan (Figs. 1, 4). Long-term mooring observations at FATO station, off Sado Island, revealed the predominance of CW horizontal motions oscillating at near-inertial frequency (Figs. 2, 3). The recurrent ship-based surveys revealed the spatial distribution of TKE dissipation because of NIWs along the vertical section of mesoscale systems (Figs. 4, 5, 6).
During the early summer expedition conducted in June, the daylong microstructure campaign at FATO showed that the NIW oscillation and microscale mixing were co-located near the lower pycnocline, corresponding to the critical level, of the anticyclone (Figs. 7, 8, 9, 10). During the time, the SADCP observation exhibited that the trapped NIW propagates upward, which transports the wave kinetic energy in the opposite direction, i.e., downward (Fig. 11). It is noteworthy that the NIW’s vertical propagation was also suggested by the vertical strain inferred from buoyancy (Fig. 10a).
During the KS-10 fall expedition, the dipole paired vortices were surveyed closely with special emphasis on the properties of NIW and its interaction with the background mesoscale system (Fig. 6). Near the dipole system, especially closer to the cyclonic eddy, the satellite-based geostrophic motions indicated distinct horizontal shearing as total strain (Fig. 4). Evidence of the wave-related fine-scale and turbulence kinetic energy was apparently intensified near lower pycnoclines between the cores of cyclone and anticyclone (Fig. 6a).
According to the theoretical solution by Eq. (3), we expect considerable modification in \({\omega }_{\text{min}}\) in the neighborhood of the observed mesoscale field on the E line (Fig. 13a). Values of Rig build up rapidly near inflection points along the isopycnal curves, where they are centered around 136.0°, 136.7°, and 137.8° E (Fig. 13b) (c.f. Joyce et al. 2013; Whitt and Thomas 2013). Near the Rig peaks, the estimate of \({\omega }_{\text{min}}\) is less modulated by the term of baroclinicity. However, some parts located between the isopycnal inflections are rather modulated, so that \({\omega }_{\text{min}}\) becomes significantly lowered. For example, the sub-inertial waves at intrinsic frequency of 0.95f can be guided by the vertical column, propagating from the surface through the water column down to depth of 250 m (constrained by the reach of ADCP beams). For solution of the barotropic limit, i.e., \({\omega }_{\text{min}}^{\text{BT}}=F\), it can propagate within narrower regions determined solely by the signature of negative RVA (Fig. 13b). According to SADCP observations, the amplified NIW feature is identifiable at the low Rig region as coinciding with the lower pycnocline of the dipole vortices (Fig. 13c). The feature then leads us to interpret that the sub-inertial NIWs were guided by a water column in the mesoscale structure, so that it eventually arrived at the intermediate depth.
Vertical section along E line: a f-normalized minimum frequency for propagating internal waves: \(\omega_{{{\text{min}}}}^{{{\text{BT}}}} = f\sqrt {1 + {\text{Ro}}_{{\text{g}}} }\) (color shade) and \(\omega_{{{\text{min}}}}^{{{\text{BC}}}} = f\sqrt {1 + {\text{Ro}}_{{\text{g}}} - {\text{Ri}}_{{\text{g}}}^{ - 1} }\) (blue curve), respectively, representing results with and without the baroclinic component, Rig; b geostrophic Rossby number, Rog; and c geostrophic Richardson number, Rig. Every plot has buoyancy b contoured at a 0.005 m s−2 interval by black solid lines. In a, the region where \(\omega_{{{\text{min}}}}^{{{\text{BC}}}} < 0.95f\) is hatched
Regarding the energy source of downward-propagating NIWs, some cases of synoptic disturbances in the atmosphere were analyzed closely. They travel mostly eastward in the Sea of Japan. Results suggest that the developed air cyclone favorably generates a 10–20 km horizontal shear in the surface Reynolds stress near the northern Honshu Island coastline (Fig. 12a). This stress causes vertical motions of similar scale because of the Ekman pumping in near-surface water. Those motions propagate into the deep water as NIWs (Fig. 12b).
References
Alford MH, Gregg MC (2001) Near-inertial mixing: modulation of shear, strain and microstructure at low latitude. J Geophys Res 106:16947–16968
Byun SS, Park JJ, Chang KI, Schmitt RW (2010) Observation of near-inertial wave reflections within the thermostad layer of an anticyclonic mesoscale eddy. Geophys Res Lett 37:1–6
Cuypers Y, Bouruet-Aubertot P, Marc C, Fuda J-L (2012) Characterization of turbulence from a fine-scale parameterization and microstructure measurements in the Mediterranean Sea during the BOUM experiment. Biogeosciences 9:3131–3139
Danioux E, Klein P, Riviére P (2008) Propagation of wind energy into the deep ocean through a fully turbulent mesoscale eddy field. J Phys Oceanogr 38:2224–22281
D’Asaro EA (1985) The energy flux from the wind to near-inertial motions in the surface mixed layer. J Phys Oceanogr 15:1043–1059
Fukudome K, Yoon J, Ostrovskii A, Takikawa T, Han I (2010) Seasonal volume transport variation in the Tsushima Warm Current through the Tsushima Straits from 10 years of ADCP observations. J Oceanogr 66(4):539–551
Garrett C, Munk W (1975) Space-time scales of internal waves: a progress report. J Geophys Res 80:291–297
Gill AE (1982) Atmosphere ocean dynamics. Academic Press, New York, p 662
Gonella J (1972) A rotary-component method for analyzing meteorological and oceanographic vector time series. Deep Sea Res 19:833–846
Igeta Y, Kumaki Y, Kitade Y, Senju T, Yamada H, Watanabe T, Katoh O, Matsuyama M (2009) Scattering of near-inertial internal waves along the Japanese coast of the Japan Sea. J Geophys Res 114:C10002
Jeon C, Park JH, Park YG (2019) Temporal and spatial variability of near-inertial waves in the East/Japan Sea from a high-resolution wind-forced ocean model. J Geophys Res Oceans 124:6015–6029
Jeon C, Park JH, Varlamov SM, Yoon JH, Kim YH, Sea S, Park YG, Min HS, Lee JH, Kim CH (2014) Seasonal variation of semidiurnal internal tides in the East/Japan Sea. J Geophys Res Oceans 119:2843–2859
Jing Z, Wu L, Ma X (2017) Energy exchange between the mesoscale oceanic eddies and wind-forced near-inertial oscillations. J Phys Oceanogr 45:181–208
Joyce TM (1989) On in situ ‘calibration’ of shipboard ADCPs. J Atmos Oceanic Technol 6:169–172
Joyce TM, Toole JM, Klein KP, Thomas LN (2013) A near-inertial mode observed within a Gulf Stream warm-core ring. J Geophys Res Oceans 118:1797–1806
Kawabe M (1982a) Branching of the Tsushima Current in the Japan Sea. Part I, data analysis. J Oceanogr Soc Jpn 38(2):95–102
Kawabe M (1982b) Branching of the Tsushima Current in the Japan Sea. Part II, numerical experiment. J Oceanogr Soc Jpn 38(4):183–192
Kawaguchi Y (2019) KS-19-22 cruise report, JAMSTEC. http://www.godac.jamstec.go.jp/catalog/doc_catalog/metadataDisp/KS-19-22_all?lang=en. Accessed 1 Dec 2019
Kawaguchi Y, Inoue J, Nishino S, Takeda H, Maeno K, Oshima K (2016) Enhanced diapycnal mixing due to near-inertial internal waves propagating through an anticyclonic eddy in the ice-free Chukchi Plateau. J Phys Oceanogr 46:2457–2481
Kawaguchi Y, Kikuchi T, Inoue R (2014) Vertical heat transfer based on microstructure measurements in ice-free Pacific-side Arctic Ocean: the impact of the Pacific water intrusion. J Oceanogr 70:343–353
Kawaguchi Y, Wagawa T, Igeta Y (2020) Near-inertial internal waves and multiple-internal oscillations trapped by negative vorticity anomaly in the central Sea of Japan. Prog Oceanogr 181:102240
Kunze E (1985) Near-inertial wave propagation in geostrophic shear. J Phys Oceanogr 15:544–565
Kunze E, Schmitt R, Toole JM (1995) The energy balance in a warm-core ring’s near inertial critical layer. J Phys Oceanogr 25:942–957
Leaman KD, Sanford TB (1975) Vertical energy propagation of inertial waves: a vector spectral analysis of velocity profiles. J Geophys Res 80(15):1975–1978
Lee D-K, Niiler P (2010) Eddies in the southwestern East/Japan Sea. Deep Sea Res Part I Oceanograph Res Papers 57(10):1233–1242
Massel SR (2015) Internal gravity waves in the shallow seas. Springer, Berlin, p 163
Mori K, Matsuno T, Senjyu T (2005) Seasonal/spatial variations of the near-inertial oscillations in the deep water of the Japan Sea. J Oceanogr 61:761–773
Morimoto A, Yanagi T (2001) Variability of sea surface circulation in the Japan Sea. J Oceanogr 57:1–13
Morimoto A, Yanagi T, Kaneko A (2000) Eddy field in the Japan Sea derived from satellite altimetric data. J Oceanogr 56:449–462
Naganuma K (1985) Fishing and oceanographic conditions in the Japan Sea (in Japanese, with English Abstract). Umi Sora 67:217–230
Nam S, Park JH (2008) Semidiurnal internal tides off the east coast of Korea inferred from synthetic aperture radar images. Geophys Res Lett 35:1–6
Noh S, Nam S (2020) Observations of enhanced internal waves in an area of strong mesoscale variability in the southwestern East Sea (Japan Sea). Sci Rep 10:9068
Oakey NS (1982) Determination of rate of dissipation of turbulent energy from simultaneous temperature and velocity shear microstructure measurements. J Phys Oceanogr 12:256–271
Okubo A (1970) Horizontal distribution of floatable particles in the vicinity of velocity singularities such as convergence. Deep Sea Res 17:445–454.
Park J-H, Watts DR (2005) Near-inertial oscillations interacting with mesoscale circulation in the southern Japan/East Sea. Geophys Res Lett 32:L10611
Park J-H, Watts DR (2006) Internal tides in the southwestern Japan/East Sea. J Phys Oceanogr 36:22–34
Pinkel R (1984) Doppler sonar observations of internal waves: the wavenumber frequency spectrum. J Phys Oceanogr 14:1249–1270
Pinkel R (2008) Advection, phase distortion, and the frequency spectrum of fine-scale fields in the sea. J Phys Oceanogr 38:291–313
Pollard RD, Mallard RC (1970) Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Res 17:813–821
Polzin KL (2008) Mesoscale eddy-internal wave coupling. Part I: symmetry, wave capture, and results from the mid-ocean dynamics experiment. J Phys Oceanogr 38:2556–2574
Shcherbina A, Talley LD, Firing E (2003) Near-surface frontal zone trapping and deep upward propagation of internal wave energy in the Japan/East Sea. J Phys Oceanogr 33:900–912
Thomas LN (2017) On the modifications of near-inertial waves at fronts: implications for energy transfer across scales. Ocean Dyn 67:1335–1350
Thorpe SA (2005) The turbulent ocean. Cambridge University Press, Cambridge
Wagawa T, Kawaguchi Y, Igeta Y, Honda N, Okunishi T, Yabe I (2020) Detailed water properties of baroclinic jets and mesoscale eddies in the Sea of Japan from a glider. J Mar Syst 201:103242. https://doi.org/10.1016/j.jmarsys.2019.103242
Watanabe M, Hibiya T (2018) A near-inertial current event in the homogeneous deep layer of the northern Sea of Japan during winter. J Oceanogr 74:209–218
Watanabe T, Simizu D, Nishiuchi K, Hasegawa T, Katoh O (2009) Surface current structure of the Tsushima Warm current region in the Sea of Japan derived by satellite-tracked surface drifters. J Oceanogr 65(6):791
Whitt DB, Thomas LN (2013) Near-inertial waves in strongly baroclinic currents. J Phys Oceanogr 43:706–725
Yabe I, Kawaguchi Y, Wagawa T, Fujio S (2020) Anatomical study of Tsushima Warm Current System: principal pathways and its variation. Prog Oceanogr (revised)
Acknowledgements
This study was supported by the Interdisciplinary Research Program of the Atmosphere and Ocean Research Institute of The University of Tokyo. It was also funded by the JSPS KAKENHI Grant Numbers 16H01596 for Y. Kawaguchi and JP18H03741 for T. Senju. The authors thank all members of T/S Tenyo-maru, T/S Oshoro-maru, and R/V Shinsei-maru, who dedicated their best efforts to our data sampling. Data from the science cruises are available via the JAMSTEC data archive system, DARWIN, below: http://www.godac.jamstec.go.jp/darwin/cruise/shinsei_maru/ks-19-22/e. Output data of the GPV reanalysis model developed by the Japan Meteorological Association can be downloaded from the website below: http://database.rish.kyoto-u.ac.jp/arch/jmadata/data/gpv/original. The revised manuscript has been greatly improved by insightful comments from two anonymous reviewers.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kawaguchi, Y., Wagawa, T., Yabe, I. et al. Mesoscale-dependent near-inertial internal waves and microscale turbulence in the Tsushima Warm Current. J Oceanogr 77, 155–171 (2021). https://doi.org/10.1007/s10872-020-00583-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10872-020-00583-1