Abstract
The correlation between transport via the Bering Strait throughflow (BTF) and sea surface salinity (SSS) in the Bering Sea has been examined mainly using an atmosphere–ocean–ice coupled climate model that has an eddy-permitting ocean component. The SSS anomaly in the northwestern Bering Sea is high from winter to spring when the BTF transport anomaly is large in the cold season. Similar features can be seen in an observation dataset and two kinds of ocean data assimilation product. BTF transport is strongly correlated with sea surface height (SSH) in the northeastern Bering Sea, the southwestern Chukchi Sea and the East Siberian Sea. The SSH along the Russian coast in the Arctic Ocean is uncorrelated with the SSH in the Bering Sea, the meaning being that the Arctic SSH affects the BTF and the SSS independently of the SSH in the Bering Sea. The low SSH along the Siberian coast is correlated with easterly wind anomalies over the Laptev Sea and north of the New Siberian Islands. The relationship between the low Siberian-coast SSH and the high SSS in the Bering Sea, however, is not confirmed in 10 years of satellite-derived SSH. Mixed-layer salt budget analysis has revealed that the high SSS anomalies are mainly caused by the increases of horizontal advective salt convergence north of 62.5°N, and by the decreases of sea-ice melting south of 62.5°N, through the strengthening of the near-surface northeastward currents. In the warm season, these two factors fade and the salinization disappears.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Arctic sea ice during summer and autumn has been decreasing, and temperatures have been increasing faster over the Arctic than the global average (e.g., Serreze and Barry 2011; Vaughan et al. 2013). Processes in the Arctic do not only affect the Arctic climate, but their effects also extend to the climate in lower latitudes. Previous studies have indicated that changes in cyclone routes due to the decrease of sea ice in the Barents Sea cause cold winters in Eurasia and East Asia (Inoue et al. 2012; Sato et al. 2014). Is there also a remote effect from the Arctic Ocean to the Bering Sea and the Pacific Ocean?
The Arctic Ocean is connected with the Pacific Ocean by only the Bering Strait, which is approximately 85 km in width and 50 m in depth. The Bering Strait throughflow (BTF) is basically northward (Woodgate et al. 2005, 2012). It is well known that water from the Pacific Ocean that flows though the Bering Strait affects the properties of water in the Arctic Ocean (e.g., Itoh et al. 2012). The current at the Bering Strait sometimes becomes southward in winter (e.g., Woodgate et al. 2015) and sea ice can be transported from the Arctic Ocean to the Bering Sea (e.g., Babb et al. 2013). However, the impacts of changes in the Arctic Ocean on the Bering Sea transmitted through the BTF are not well understood yet. About two-thirds of the change in BTF transport is controlled by the Pacific-Arctic pressure-head (Woodgate et al. 2012). Aagaard et al. (2006) indicated that interannual changes in steric forcing over the Bering Strait were controlled by warm inflow into the Arctic Ocean from the North Atlantic, freshwater accumulation in the southwest Canada Basin, and temperature and salinity changes in the upper Bering Sea. Changes in sea surface height (SSH) in the Arctic Ocean are likely to lead to some changes in the Bering Sea. Danielson et al. (2014) indicated that easterly winds over the western Chukchi Sea (CS) and the East Siberian Sea (ESS) increased the Pacific-Arctic pressure-head through coastal divergence and shelf waves, the implication being that winds over the Arctic Ocean can change the BTF.
There are limited observations in the Arctic Ocean and the Bering Sea, especially in the cold season, and it is still hard to examine oceanographic variations using in situ data only. The present study analyzes the output of an atmosphere–ocean–ice coupled climate model to investigate variations in the Bering Sea that originated in the Bering Strait and the Arctic Ocean; we find interannual variations of sea surface salinity (SSS) and surface currents in the northwestern Bering Sea that are linked with those of BTF transport and Arctic SSH. The continental shelf from the northern Bering Sea to the Chukchi Sea is known as one of the highest biological production regions (e.g., Springer and McRoy 1993), and interannual changes of circulations and water properties in this region are important for biogeochemical research.
In this paper, we show the relationships between the SSS in the Bering Sea, the BTF and the SSH, and discuss the processes of the SSS changes. Section 2 explains datasets and a budget analysis method used in this study. The correlations between the SSS in the Bering Sea and the BTF or the Arctic SSH are shown in Sect. 3. We discuss the salt budget in the northwestern Bering Sea in Sects. 4, and 5 provides the conclusions.
2 Data and method
2.1 Data
2.1.1 Observation products
Objectively analyzed salinity anomaly fields have been produced and released by the Ocean Climate Laboratory Team within the National Centers for Environmental Information. In this study, we utilized the yearly and 3-monthly salinity anomalies from climatologies on one-degree grids from 2005 to 2015 (https://www.nodc.noaa.gov/OC5/3M_HEAT_CONTENT/s_anomaly_data.html). They were computed by objective analysis of all quality-controlled historical salinity data in the World Ocean Database 2013 (WOD13). The objective analysis scheme used for this product was not optimum interpolation but a convergent weighted-averaging scheme (Zweng et al. 2013). The objectively analyzed climatology dataset, World Ocean Atlas 2013 (WOA13) version 2, was also used to evaluate model data (“Appendix”).
We utilized monthly fields of satellite-derived Arctic dynamic ocean topography between 60°N and 81.5°N produced by Armitage et al. (2016). SSH in both the ice-covered and ice-free ocean measured by Envisat and CryoSat-2 were combined to produce this dataset for the period 2003–2014. The data have a horizontal resolution of 2° (longitude) × 0.5° (latitude). Dynamic ocean topography is defined as SSH relative to the geoid, and simply referred to as “SSH” hereafter. In this study, we removed the annual cycle by subtracting each month’s climatology at each grid before analyses.
2.1.2 Data assimilation products
Data assimilation is the process to incorporate observations into the state of a numerical model, and an effective method to estimate a realistic state of the oceans or atmosphere from limited observations and a model simulation. In addition to 9 years of the observation product based on only WOD13 (Sect. 2.1.1), two kinds of ocean data assimilation product were also checked to compare with a climate model: Simple Ocean Data Assimilation (SODA) version 2.2.4 (Giese and Ray 2011) and the Estimated STate of the global Ocean for Climate research (ESTOC) (Osafune et al. 2015). For the SODA reanalyses, the ocean model component used the Parallel Ocean Program (POP) model version 2.0.1 with a horizontal resolution of on average 0.4° × 0.25° and 40 layers in vertical. After the assimilation by a sequential optimum interpolation, output variables were mapped onto a uniform 0.5° × 0.5° grid. On the other hand, the ESTOC used a 4-dimentional variational (4D-VAR) adjoint method to generate a dynamically-self consistent state estimation. The ESTOC was based on version 3 of the Geophysical Fluid Dynamics Laboratory Modular Ocean Model (MOM3) which had a horizontal resolution of 1° in both longitude and latitude, and the number of vertical levels, including the bottom boundary layer, was 46. Sea ice was explicitly dealt with in neither the SODA nor the ESTOC, although surface heat flux was modified when the surface temperature reached the freezing point of seawater in the SODA. The ESTOC included a newly estimated heat and fresh-water surface fluxes through 4D-VAR data synthesis, which was consistent with ocean observations (temperature and salinity) even in sea-ice regions. One should note that these two kinds of ocean reanalysis may not be necessarily reliable enough at high latitudes. Our purpose of using them was to briefly check the consistency among the different products qualitatively. For both the products, we analyzed the data only from 1979, when satellite data became more available.
2.1.3 Model
Even the above data assimilation products are not wholly satisfactory for the investigation of the salinity in the Bering Sea since sea ice was not explicitly dealt with. In this study, we mainly analyzed historical experimental data produced by simulations of the period 1950–2005 using a high-resolution setup of the Model for Interdisciplinary Research on Climate version 4h (MIROC4h) (Komuro et al. 2012; Sakamoto et al. 2012). This historical simulation produced three ensemble members. The three members differ only by their initial conditions. The simulation data of the Coupled Model Intercomparison Project Phase 5 (CMIP5) pre-industrial control experiment on 1st January in the 91st year, 71st year, and 111st year were given for Member 1, 2, and 3 of the historical experiment, respectively, as the initial values on 1st January 1950. Hence, the difference between the members was due to internal variations produced by the model.
The MIROC4h consisted of five model components: atmosphere, land surface, rivers, ocean, and sea ice. The ocean component was the COCO version 3.4 (Hasumi 2000), an eddy-permitting model with a horizontal resolution of 0.28125° zonally and 0.1875° meridionally, and the number of vertical levels, including the bottom boundary layer, was 48. The thickness was 2.50 m for the uppermost layer, and gradually increased to 200 m at the 27th layer (1348-m depth). The first 10 levels were in the upper 60 m. See Sakamoto et al. (2012) for the details. The vertical resolution of the MIROC4h was comparable to or better than other models used for Arctic research (e.g., Clement et al. 2005; Zhang et al. 2010), and fine enough to simulate the mixed layer. In the coordinate system of the MIROC4h, the North Pole and the South Pole were shifted to 77°N, 40°W in Greenland and 77°S, 140°E, respectively. Since the horizontal spacing was not fine enough to resolve mesoscale eddies at high latitudes, harmonic horizontal diffusion of the isopycnal layer thickness was applied for representing eddy-induced transport of tracers. River runoff calculated in the river component was given to uppermost grids facing the mouths of rivers as fresh water flux. The sea ice component was configured with a two-category thickness representation, zero-layer thermodynamics and elastic-viscous-plastic rheology. The horizontal resolution of the sea-ice component was the same as that of the ocean component. On the other hand, the horizontal resolution of the atmospheric components was 0.5625° (T213).
The MIROC4h was developed with the aim of conducting near-term climate prediction experiments in order to contribute to the CMIP5. One of the advantages of the MIROC4h is its top-class horizontal resolution among the CMIP5 models, which is important for simulations around narrow straits. And, since restoring of SSS was not done and no artificial salt flux at the sea surface was yielded, the MIROC4h is suitable for analyses of SSS. The Arctic climate and a realistic sea-ice cover were reproduced reasonably well by the MIROC4h, especially compared with the simulation of its predecessor, the MIROC version 3h (Komuro et al. 2012; Sakamoto et al. 2012). In this study, monthly anomalies, which are differences from monthly climatologies during the 56-year period, are analyzed. Climatologies of BTF transport, SSS, SST, sea-ice concentration (SIC), and SSH in the MIROC4h are compared with observations in “Appendix”. The MIROC4h and the assimilation products simulated the seasonal cycle of BTF transport, although the MIROC4h overestimated BTF transport compared with mooring-based estimates. The climatological mean of the transport through Anadyr Strait in the MIROC4h was 0.5 Sv (1 Sv = 106 m3 s−1) for all three members, which is consistent with the model result of Clement et al. (2005). The transport through Shpanberg Strait was, however, overestimated in the MIROC4h, 0.7 Sv with little seasonal cycle. The Alaskan Coastal Current (ACC) was exaggerated throughout the year due to larger SSH gradient along the Alaskan coast (see Fig. 20b), resulting in the overestimation of BTF transport. However, the monthly mean transports were highly correlated with Anadyr and Bering Straits [correlation coefficient (r) was 0.84–0.88]. On the other hand, the ACC flowed northward in the eastern region, and the monthly mean transports were uncorrelated with Anadyr and Shpanberg Straits (r = − 0.08 – 0.03). These are consistent with the indication of Danielson et al. (2014). The overestimation of the ACC in the basic state will not seriously affect the correlation between BTF transport and SSS in the northwestern part. For the bottom-layer salinity at Bering Strait, while the salinity in January was close to the observation, the model did not well simulate the following quick rise and drop. The salinity at this point might be sensitive to the reproducibility of sea ice or the ACC. The seasonal cycle of the model SSS in the northwestern area, however, approximately agreed with the WOA climatology.
2.2 Salt budget analysis
For each water column integrated from the sea surface to the depth of the mixed layer base D, the rate of change of mixed-layer salt content must be balanced with advection and diffusion of salt, and salt inflow from the surface and from beneath. The advection–diffusion equation of salt for each water column is
S, η, u, v, and w are salinity, SSH, zonal, meridional, and vertical current speed, respectively. P, E, and M are precipitation, evaporation, and surface water flux due to sea ice melting or freezing. K = (K x , K y , K z ) is a vector that consists of horizontal and vertical eddy diffusion coefficients. S i is salinity in sea ice, and was set to 5.0 in the MIROC4h. S m and u m are the average salinity and velocity within the mixed layer. Using the continuity equation, the mixed layer salinity budget can be expressed as:
where W e is the entrainment velocity. S′ m and u′ m are the deviations of salinity and velocity from the averages within the mixed layer. S -D is the salinity just below the base of the mixed layer, and the value 20 m below the base was used in this budget analysis (e.g., Ren and Riser 2009). The left-hand side of Eq. (2) is the rate of change of salinity (salinity tendency). The first and second terms on the right-hand side are the convergences of salt by horizontal advection and the entrainment, respectively. The third and fourth terms describe the effect of E–P and sea-ice freezing minus melting. The diffusion term cannot be calculated from the model output, and is expressed by the residual. In this study, D was determined as the depth at which the potential density or temperature difference from a near-surface value at 10 m depth exceeded +0.03 kg m−3 or ± 0.2 °C (de Boyer Montégut et al. 2004). The salt budget analysis is discussed in Sect. 4.
3 Relationships between SSS, BTF and SSH
3.1 Correlation of SSS with BTF transport
Using the time series of the yearly BTF transport calculated from the A3 mooring shown by Woodgate et al. (2015) (blue line in their Fig. 9a), we selected 2007, 2010, 2011, and 2013 as strong BTF years, and 2005, 2006, 2008, and 2012 as weak BTF years, respectively, to make composites of the WOD13-based SSS anomaly fields, which are available from 2005. Figure 1a shows differences of the composite SSSs between the strong and weak BTF years. Statistical significance of the difference between the two population means was tested using Student’s t test with a 90% confidence level on the assumption that each yearly or 3-monthly value was independent. In the northwestern Bering Sea and south off the root of the Alaska Peninsula, the yearly SSS in the strong BTF case was higher than that in the weak BTF case by more than 0.1 practical salinity unit (psu) and the difference between them was statistically significant. Seasonality can be seen in the SSS differences: the difference was obvious from autumn to spring (Table 1). On the other hand, SSS tended to be lower in the strong BTF case in the southeastern and southwestern parts of the Bering Sea. Figure 1a suggests that the SSS in the northern Bering Sea is correlated with BTF transport. However, since the number of available years is very limited and the confidence level is set to a low value in this case, it is difficult to conclude that there is a relationship between SSS and BTF only from this evidence. Therefore, we further examined the correlation using model and assimilation data.
Difference of a the WOD13-based SSS (psu) and b satellite-derived SSH anomaly means (cm) between the strong BTF years and weak BTF years. Black line is a contour of ± 0.0. Grids where the differences are statistically significant at the 90% confidence level are dotted. The area surrounded with a gray box in a is analyzed in Table 1
Figure 2 shows r between annual mean BTF transport and annual mean SSS—salinity just under sea ice if the sea surface was covered with ice—in the MIROC4h, ESTOC and SODA. In the significance test of r, the effective sample number N e was estimated after taking into consideration serial correlation (Metz 1991):
where N is the number of samples (years in this study), T e is the effective decorrelation time, and r xk (r yk ) is the autocorrelation function of variable x (y) at a lag of k years. Linear trends of x and y were removed when N e and r were calculated. Two of the three members of the MIROC4h and the two assimilation products show significant r in the northwestern Bering Sea in common, which is consistent with Fig. 1a, except for Member 2 of the MIROC4h. However, significant correlation was not seen around the Alaska Peninsula in any datasets. For the MIROC4h, r of Member 1 was the largest, and that of Member 2 was the smallest, although the spatial patterns of r were basically similar to each other. In this paper, the analyses of Member 3, for which the strength of the correlation was intermediate among the three members, are presented in the main text, and the other members, the SODA and ESTOC are shown in the supporting material.
There was obvious seasonality in the relationship between BTF transport and SSS (Fig. 3). In the northwestern Bering Sea, the SSS anomaly associated with the BTF transport anomaly became evident from winter to early summer, and SSS lagged behind the BTF by a few months. We tested averaging windows shorter than 6 months, and no significant correlation was seen if the period of average was 3 months or less (not shown). Some changes in the currents that persist only for a few months will not be enough to change the upper-layer salinity. The SSS averaged over 60.5–64.5°N, 170°E–174°W (gray box in Fig. 3b) regressed by BTF transport was 0.12 psu for Member 1 and 0.09 psu for Members 2 and 3; that is, the area-averaged SSS anomaly rose by approximately 0.1 psu with an increase of the BTF transport anomaly by + 1.0σ. We examined the relationship between BTF transport and SSS in the two different ocean reanalyses. Both the SODA and the ESTOC showed similar spatial patterns of the correlation to Fig. 3b: SSS in the northwestern Bering Sea was high when the BTF was strong. r between BTF transport and the SSS averaged over 60.5–64.5°N, 170°E–174°W is listed in Table 2. The high correlation area in the SODA, however, did not extend to the west of Cape Navarin. While the relationship in the SODA had seasonality similar to Fig. 3a, the season when r became large was different from that in the MIROC4h by a few months, and the seasonal dependence of the correlation was weak in the ESTOC. Although there were some differences from the MIROC4h, the northwestern SSS in the ocean data assimilation products also tended to vary in association with the BTF.
a Lag r between BTF transport and the SSS averaged over 60.5–64.5°N, 170°E–174°W (gray box in b) in Member 3 of the MIROC4h. Both are semiannual means. Pluses indicate that r values are statistically significant at the 95% confidence level. b As in Fig. 2, but for between BTF transport averaged during October–March and SSS averaged during January–June
Sea surface temperature (SST) tended to be high over the Bering Sea when the BTF transport anomaly was large in the cold season (Fig. 4a), and the high SST was related with anomalous southeasterly winds in the northern Bering Sea (Fig. 5). This is consistent with previous studies indicating that anomalous southeasterlies or southerlies associated with the westward shift of the Aleutian Low contributed to the increase of BTF transport (Danielson et al. 2014) and the decrease of sea ice in the Bering Sea (Rodionov et al. 2007; Zhang et al. 2010; Li et al. 2014). The sea surface density in the northwestern Bering Sea was correlated with BTF transport (Fig. 4b), and the correlation was smaller than that of SSS since the effect of positive SSS anomaly on density was offset by that of positive SST anomaly. Figure 4b, however, shows that the density anomalies associated with the BTF changes were dominated by SSS rather than SST.
As in Fig. 3b, but for a SST and b sea surface density in Member 3
As in Fig. 3b, but for between BTF transport and southeasterly wind stress averaged during October–March in Member 3. No time lag between BTF transport and the wind stress
3.2 Correlation of SSH with BTF transport and SSS
Difference of the satellite-derived SSH between the strong and weak BTF years is shown in Fig. 1b. A contrast of high SSH in the Beaufort Sea and low SSH along the Siberian coast can be clearly seen, but the difference was not significantly large around the CS and the Bering Strait on a yearly mean basis. SSH in the strong BTF years tended to be slightly high in the southwestern Bering Sea. This is consistent with Danielson et al. (2014) (their Fig. 14e), who indicated the relationship between the zonal shift of the Aleutian Low and BTF transport in the 2000s. Similar spatial pattern can be seen in 3-monthly means too (not shown).
The increase of BTF transport was strongly correlated with high SSH in the eastern Bering Sea and low SSH in the southwestern CS and the ESS (Fig. 6a). This pattern clearly reflects the across-strait SSH gradient that strengthens the BTF. And, the SSH gradient along the Bering Strait also enhanced to lead to larger BTF transport. There was no time lag between BTF transport and SSH along the coast of eastern Siberia on a monthly basis. The correlation between BTF transport and SSH in the southwestern CS and the eastern ESS was statistically significant throughout the year, and it was larger in summer and relatively small in winter (not shown). There was no correlation between BTF transport and SSH in the Aleutian Basin, which is inconsistent with Danielson et al. (2014) and our Fig. 2. Danielson et al. (2014) focused on a phenomenon that occurred in a specific 12-year period. The long-term correlation analysis used in our study is not suitable to detect a change within a decade.
a r and b r p between BTF transport and the SSH averaged during October–March in Member 3. c r p between the SSS averaged over 60.5–64.5°N, 170°E–174°W (gray box in Fig. 3b) during January–June and the SSH averaged during October–March. These r p’s were calculated by removing the effect of the SSH averaged over 60–65°N, 160–168°W (gray box in a). The area surrounded with a gray box in c is analyzed in Figs. 8, 9, 10, 11, 12, 13. Contours and color are the same as in Fig. 2. Note that the color scale in b is different from those in a and c
The high SSH in the eastern Bering Sea was uncorrelated with the low SSH in the Arctic Ocean. We calculated the partial correlation coefficient (r p) between the Arctic SSH and BTF transport by removing the effect of the SSH in the region 60–65°N, 160–168°W (Fig. 6b). The partial correlation was more than 0.7 along the Siberian coast from the northwestern Bering Sea to the ESS, and more than 0.6 even in the eastern Laptev Sea. This means that the SSH in the southwestern CS and the ESS affects BTF transport independently of the SSH in the Bering Sea. Danielson et al. (2014) also indicated that the SSH anomalies in the western CS and the ESS did not co-vary with those in the eastern Bering Sea using satellite data (their Fig. 11).
The spatial patterns of r (not shown) and r p (Fig. 6c) between SSH and the SSS in the northwestern Bering Sea were similar to those between SSH and BTF transport. The weaker correlation between SSH and SSS is reasonable, because factors other than the Arctic SSH, such as inflow from the Gulf of Alaska and the Aleutian basin, surface freshwater flux, and river runoff, also affect the salinity in the Bering Sea (Aagaard et al. 2006). The correlations between SSH and BTF transport or between SSH and SSS in Member 1 and 2 were similar to the analogous correlations in Member 3. The correlation between the SSS or surface density and the SSH averaged over 66°–72°N, 165E°–170°W was also statistically significant in the northwestern Bering Sea (not shown). On the other hand, SST in the Bering Sea was uncorrelated with the Arctic SSH, except for a small area along the coast south of Cape Navarin. Unlike salinity, temperature is insensitive to the SSH changes in the Arctic Ocean. The same tendencies can be seen in Member 1 and 2.
We checked the relationship between SSH and SSS in the observation datasets. Based on Fig. 7a that shows the WOD13-based salinity anomaly averaged over the northwestern Bering Sea (60.5–64.5°N, 170°E–174°W) during January–June, high SSS years were defined as 2005, 2009–2011, and 2013, and low SSS years as 2006-2008, 2012, and 2014, respectively, to make composites of the satellite-derived SSH in October–March. The difference of the composite SSH between the high and low SSS years shows that SSH was high in the northern Bering Sea and low north of the New Siberian Islands in the high SSS years (Fig. 7b). The difference along the Siberian coast was not significantly large and slightly positive when the SSS anomaly was high, which is contradictory to the model results (Fig. 6). However, the correlation in a 10-year window between the Siberian-coast SSH and the SSS in the northwestern Bering Sea can be nearly zero or positive even for the MIROC4h (Fig. 8). More than 20 years of data may be necessary to confirm this relationship.
a WOD13-based SSS anomaly averaged over 60.5–64.5°N, 170°E–174°W during January–June. b Difference of the satellite-derived SSH anomaly means between the high SSS years and low SSS years (cm). The mean period of the SSH anomaly is October–May. Black line is a contour of ± 0.0 cm. Grids where the differences are statistically significant at the 90% confidence level are dotted
a r in a 10-year window between the Siberian-coast SSH (66–72°N, 165°E–170°W, gray box in Fig. 6c) and the SSS in the northwestern Bering Sea (60.5–64.5°N, 170°E–174°W, gray box in Fig. 3b). The horizontal axis represents the first year of the 10-year window. Horizontal dashed line denotes the correlation throughout the whole period. b As in a, but for 20-year window
The low SSH anomalies along the Siberian coast appear to originate in the Laptev Sea and around the New Siberian Islands (Fig. 6b). The correlation between the SSH averaged over 66–72°N, 165°E–170°W and zonal wind stress (Fig. 9a) indicates that the low SSH anomalies were linked with the easterly wind anomalies over the ESS and the Laptev Sea, and were uncorrelated with the Aleutian Low. These anomalous easterlies caused offshore Ekman transport and the decrease of SSH in the coastal region. The anomalous southeasterlies shown in Fig. 5 also contributed to the SSH drop in the CS. The enhanced Pacific-Arctic pressure-head resulted in the current anomalies from the Bering Sea to the ESS. Figure 9b shows the regression map of the surface current velocity onto the Siberian-coast SSH. The westward current anomalies extended from the southern CS to the ESS and the Laptev Sea. The current anomalies were small and not significant just near the Siberian coast, which might be due to the effect of the Siberian Coastal Current that contains energetic eddies and squirts (Weingartner et al. 1999).
a r between the SSH averaged over 66–72°N, 165°E–170°W (gray box) and zonal wind stress during October–March in Member 3. Contours and color are the same as in Fig. 2. b Regression of surface current velocity onto the SSH averaged over 66–72°N, 165°E–170°W during October–March (color, cm s−1). Black arrows show directions of regressed current velocity. White areas means that neither of the zonal and meridional components are statistically significant at the 95% confidence level. c As in a but for SLP
The spatial distribution of the SSH variation concentrated in the southern CS, the ESS and the Laptev Sea shown in Fig. 6 is similar to the second nonseasonal empirical orthogonal function (EOF) mode of Arctic SSH found by Armitage et al. (2016), the second mode EOF of GRACE data found by Peralta-Ferriz et al. (2014), and the first coupled EOF of ocean mass and zonal wind stress found by Volkov and Landerer (2013). These previous studies indicated that zonal wind anomalies along the Siberian coast, which was related with the Arctic Oscillation, caused onshore/offshore Ekman transport and the rise/drop of SSH in the coastal region. The correlation between the SSH averaged over 66–72°N, 165°E–170°W and sea level pressure (SLP) in the MIROC4h (Fig. 9c) shows a spatial pattern with high SLP around the North Pole and low SLP over Siberia in the case of low Siberian-coast SSH. This is consistent with Peralta-Ferriz et al. (2014) (their Fig. 12), although the correlation is relatively small in the MIROC4h. The high correlation of SSH distributed widely along the Siberian coast shown in Fig. 6 is probably a result of a coincident synoptic-scale response to the zonal wind anomalies, rather than shelf waves propagating from a remote area. In any case, the SSH variations in the southwestern CS and the ESS caused by the zonal wind anomalies are expected to affect the currents in the northern Bering Sea and BTF transport through changes in the Pacific-Arctic pressure-head.
4 Salt budget
The salt budget was evaluated for the northwestern Bering Sea, where the correlation between BTF transport and SSS was high, using the MIROC4h data. The distribution of the maximum mixed layer depth in winter is shown in Fig. 10a. On the shelf the mixed layer reached the bottom in winter. The mixed layer depth reached the maximum in March or April in the southern Bering Sea and around the Bering Strait (Fig. 10b). In some areas, the mixed layer depth peaked in December or January and became shallower after that. This relatively early shallowing was due to the effect of meltwater. The climatological mean of the mixed-layer salinity in the region 60.5–64.5°N, 170°E–174°W (gray box in Fig. 10a) increased from July to November, as a result of the salt convergence due to the horizontal advection and the entrainment (Fig. 10c). From January to June, when salinity decreased, the effects of sea-ice melting and horizontal advection were dominant. The salinity tendency was positive north of 62.5°N in winter mainly due to sea-ice production (not shown). The residual term suggests that much saline water was transported due to eddy diffusion, and that transport reduced the magnitude of the decrease of salinity. Precipitation reduced the salinity in summer, but the contribution of E–P to the salinity change in this area was relatively small. These features were common in all three of the ensemble members. The MIROC4h tended to underestimate sea-ice concentration in the Bering Sea as shown in “Appendix”, and the contribution of sea-ice melting might be greater than in the real world and affect the mixed layer shallowing.
Climatological means of a the maximum mixed-layer depth in winter (m), b the month of the maximum mixed-layer depth just before shallowing (cyan: December, blue: January, green: February, red: March, magenta: April), and c the mixed-layer salinity tendency and its components averaged over the area 60.5–64.5°N, 170°E–174°W (gray box in a) in Member 3. Black, green, blue, cyan, red, and magenta lines in c denote the salinity tendency, horizontal advective convergence, sea-ice melting/freezing, E–P, entrainment, and residual term, respectively
Because the January–June SSS was mainly focused in Sect. 3, we examined the sum of temporal increment of salinity from 3 months before the SSS average period to the end of the period (October–May). Figure 11 shows the regression of each component in Eq. (2) integrated from October to May onto BTF transport in October–March. The spatial pattern of the regressed salinity tendency (Fig. 11a) corresponded to that of r between SSS and BTF transport in Fig. 3b. The contribution of the horizontal advection term to the salinity tendency was dominant north of 62.5°N (Fig. 11b), that is, the salt convergence due to the horizontal advection increased the mixed-layer salinity when the BTF during October–March was strong. On the other hand, south of 62.5°N, the salinity change related with BTF transport was mainly controlled by sea-ice melting (Fig. 11c). The anomalous southerlies, which reinforced the BTF (Fig. 5), also decreased sea ice in the area south of 62.5°N, and led to less dilution and higher SSS. The residual term basically had an opposite effect to the horizontal advection and sea-ice terms, but contributed to the salinity tendency in the vicinity of the coasts (Fig. 11f). The contributions of the entrainment and E–P to the salinity change were small (Fig. 11d, e). River runoff was not considered in Eq. (2). We calculated the correlation between BTF transport averaged during October–March and the river runoff averaged during October–May. The river runoff from the northwestern coast (170°E–173°W) had a statistically significant correlation with BTF transport for Member 1 (r = 0.45) and Member 3 (r = 0.62), but insignificant for Member 2 (r = 0.21). The freshwater from rivers in Russia may have an impact to decrease the SSS. On the other hand, the river runoff from the eastern coast (58–65°N) had no significant correlation with BTF transport for the three members (r = −0.09–0.13).
a Salinity tendency, b horizontal advective convergence, c sea-ice melting/freezing, d entrainment, e E–P, and f residual term regressed by BTF transport averaged during October–March in Member 3 (psu per month). The salinity tendency and its components were averaged during October–May. Grids where values are statistically significant at the 95% confidence level are colored. Note that the color scales in a and e are different from the others
BTF transport is determined by the SSHs in the northeastern Bering Sea and the Arctic Ocean, and local winds over the strait. The spatial distributions of the salinity tendency and its components regressed by the SSH averaged over 66°–72°N, 165E°–170°W in October–March are similar to Fig. 11, although the values are generally smaller than those regressed by BTF transport (not shown). This means that even if only the Arctic SSH changes, the horizontal advection and sea-ice melting vary and affect the mixed-layer salinity. Member 1 and 2 show the same features, except that the salinity tendency regressed by the SSH in Member 2 was not statistically significant at the 95% confidence level in most of the region.
The horizontal convergence of salt changes if the current becomes strong across the contours of salinity. The climatological means of the mixed-layer current simulated by the MIROC4h (Figs. 12a and 13a) were in qualitatively agreement with previous studies. The westward currents in the Gulf of Anadyr in winter were also shown in Danielson et al. (2014) (their Fig. 7c) and Zhang et al. (2010) (their Fig. 6a). The flow toward the Bering Strait was reinforced in the northwestern Bering Sea when the BTF during October–March was strong (Fig. 12b). The near-surface current anomalies traversed the salinity contours east of Cape Navarin, which led to the increase of the horizontal salt convergence. The sea-ice retreat was also assisted by these anomalous currents. The same feature can be seen in the currents regressed by the SSH (Fig. 12c). On the other hand, the current anomalies in the northwestern part were weaker in the warm season (Fig. 13b, c) than in the cold season. The horizontal salt convergence, therefore, did not occur following the anomalous BTF, unlike the cold season. Naturally, the effect of sea ice melting became small after April, and the other terms were small in the warm season as well as the cold season. As a result, the salinity tendency was uncorrelated with the BTF and the seasonality of the correlation shown in Fig. 3a arose.
Mixed-layer current velocity averaged during October–March (color, cm s−1). Arrows show current direction. a Climatological mean, b regression onto BTF transport averaged during October–March, c regression onto the SSH averaged over 66–72°N, 165°E–170°W (gray box in Fig. 6c) during October–March. Black (gray) arrows in b and c denote that both (either) of the zonal and meridional components are statistically significant at the 95% confidence level. Thin contours denote climatological mean SSS with an interval of 0.1 psu. Thick contours show 31, 32, and 33 psu
As in Fig. 12, but for averaged during April–September. b, c show the regressions onto BTF transport and the SSH averaged during April-September, respectively
The northeastward current anomalies in the northwestern Bering Sea were produced in the cold season due to both the strengthened Pacific-Arctic pressure-head caused by the SSH drop along the Siberian coast (Fig. 6) and the Ekman transport induced by the anomalous southeasterly wind (Fig. 5). Danielson et al. (2012) indicated that the southeasterly winds induced greater on-shelf transport along the shelfbreak except within 200 km of Cape Navarin in October–April than the northwesterly winds, and the difference in the transport between the southeasterly and northwesterly winds in May–September are smaller than in October–April. Our results are qualitatively similar to the indications by Danielson et al. (2012). The northeastward (on-shore) current anomalies on the western Bering Shelf traverse the contours of salinity, inevitably resulting in the salinity convergence. Similarly, the convergence of nutrients is easily expected to occur on the western Bering Shelf if the current anomalies cross nutrients contours. Some factors in the Arctic Ocean that change the wintertime Pacific-Arctic pressure-head may affect biological activity in the northwestern Bering Sea in the following spring through the aforementioned processes.
5 Summary
The relationship between BTF transport SSS in the Bering Sea, and SSH in the Arctic Ocean was investigated mainly using an atmosphere–ocean–ice coupled model, MIROC4h, which includes an eddy-permitting ocean model. The MIROC4h simulated the seasonal cycle of BTF transport, although it overestimated the transport compared with previous studies. The interannual variations of SSS in the Bering Sea were correlated with those of BTF transport: SSS in the northwestern Bering Sea was high when BTF transport was large. And there was seasonality in the relationship between SSS and the BTF. The SSS anomaly associated with the BTF anomaly became evident from winter to spring, and SSS lagged behind the BTF by a few months. Similar relationship between the BTF and SSS can be seen in the observation dataset and the two kinds of ocean data assimilation product, although there were some differences from the MIROC4h in the spatial distribution and the timing of large r. SST also became higher with the larger BTF transport anomaly in the cold season, however, the surface density were affected by the SSS anomalies more than the SST.
BTF transport was strongly correlated with SSH in the eastern Bering Sea, the southwestern CS, and the ESS; there was no time lag between the BTF and SSH. The SSH along the Siberian coast was uncorrelated with the SSH in the Bering Sea. The SSH variations in the southwestern CS and the ESS are expected to affect the currents in the northern Bering Sea and BTF transport through changes in the Pacific-Arctic pressure-head, independently of the SSH in the Bering Sea, and resulting in changes in SSS. The spatial distribution of the SSH variation along the Siberian coast was probably a result of a coincident synoptic-scale response to the zonal wind anomalies. The anomalous easterlies in the ESS and the Laptev Sea caused offshore Ekman transport and the decrease of SSH. The anomalous southeasterlies shown in Fig. 5 also reduced SSH in the CS. The low SSH along the Siberian coast associated with the high SSS in the northwestern Bering Sea, however, cannot be confirmed in 10 years of satellite-derived SSH data. More than 20 years of data may be necessary to confirm this relationship, and this still needs to be further investigated.
We evaluated the salt budget in the northwestern Bering Sea. When BTF transport in October–March was large, the horizontal salt advection increased and meltwater decreased; both changes contributed to the mixed-layer salinization, but the horizontal advection term dominated north of 62.5°N, and the sea-ice melting term did south of 62.5°N. The residual term, which mainly represented eddy diffusion, had a role to suppress the magnitude of the salinity tendency. The same features can be seen when the SSH in the southwestern CS and the ESS was low in the cold season. In these cases, the near-surface current across the contours of salinity were reinforced, and the horizontal salt convergence increased in the northwestern part of the Bering Sea. Furthermore, the anomalous southerlies and currents contributed to the sea-ice retreat. The SSH anomalies in the Arctic Ocean affected the currents in Bering Strait and the northwestern Bering Sea, resulting in the salinization. The current anomalies in the northwestern part associated with the BTF or SSH anomalies became weaker in the warm season, which produced the seasonality of the correlation shown in Fig. 3a. Similarly, nutrients in the northwestern Bering Sea, for example, may vary with the Arctic Ocean in winter to lead to affect the biological production in the following spring.
Every numerical model, including the MIROC4h, is imperfect and has their shortcomings. While our analyses of the model have provided new aspects in the Bering Sea, the CS and ESS, the simulation of the MIROC4h are still incomplete for sea-ice concentration in the Bering Sea, salinity in the Arctic Ocean and in the bottom layer at Bering Strait, for example (“Appendix”). Simulated river runoff will have large uncertainty in any model. Furthermore, the effect of steric height is not considered in model simulations. One will need to carefully consider the realistic limits of the numerical models. Further reduction of these uncertainty and incompleteness is necessary to advance Arctic research.
References
Aagaard K, Weingartner T, Danielson SL, Woodgate RA, Johnson GC, Whitledge TE (2006) Some controls on flow and salinity in Bering Strait. Geophys Res Lett 33:L19602. https://doi.org/10.1029/2006GL026612
Armitage TWK, Bacon S, Ridout AL, Thomas SF, Aksenov Y, Wingham DJ (2016) Arctic sea surface height variability and change from satellite radar altimetry and GRACE, 2003–2014. J Geophys Res Oceans 121:4303–4322. https://doi.org/10.1002/2015JC011579
Babb DG, Galley RJ, Asplin MG, Lukovich JV, Barber DG (2013) Multiyear sea ice export through the Bering Strait during winter 2011–2012. J Geophys Res Oceans 118:5489–5503. https://doi.org/10.1002/jgrc.20383
Clement JL, Maslowski W, Cooper LW, Grebmeier JM, Walczowski W (2005) Ocean circulation and exchanges through the northern Bering Sea—1979–2001 model results. Deep-Sea Res II 52:3509–3540. https://doi.org/10.1016/j.dsr2.2005.09.010
Danielson S, Hedstrom K, Aagaard K, Weingartner T, Curchitser E (2012) Wind-induced reorganization of the Bering shelf circulation. Geophys Res Lett 39:L08601. https://doi.org/10.1029/2012GL051231
Danielson SL, Weingartner TJ, Hedstorm KS, Aagaard K, Woodgate R, Curchitser E, Stabeno PJ (2014) Coupled wind-forced controls of the Bering-Chukchi shelf circulation and the Bering Strait throughflow: Ekman transport, continental shelf waves, and variations of the Pacific-Arctic sea surface height gradient. Prog Oceanogr 125:40–61. https://doi.org/10.1016/j.pocean.2014.04,006
de Boyer Montégut C, Madec G, Fischer AS, Lazar A, Iudicone D (2004) Mixed layer depth over the global ocean: an examination of profile data and a profile-based climatology. J Geophys Res 109:C12003. https://doi.org/10.1029/2004JC002378
Giese BS, Ray S (2011) El Niño variability in simple ocean data assimilation (SODA), 1871–2008. J Geophys Res 116:C02024. https://doi.org/10.1029/2010JC006695
Hasumi H (2000) CCSR Ocean Component Model (COCO) Version 2.1, CCSR Report, 13, 68 pp
Inoue J, Hori ME, Takaya K (2012) The role of Barents sea ice in the wintertime cyclone track and emergence of a warm-Arctic cold-Siberian anomaly. J Clim 25:2561–2568. https://doi.org/10.1175/JCLI-D-00449.1
Itoh M, Shimada K, Kamoshida T, McLaughlin F, Carmack E, Nishino S (2012) Interannual variability of Pacific Winter Water inflow through Barrow Canyon from 2000 to 2006. J Oceanogr 68:575–592. https://doi.org/10.1007/s10872-012-0120-1
Komuro Y, Suzuki T, Sakamoto T, Hasumi H, Ishii M, Watanabe M, Nozawa T, Yokohata T, Nishimura T, Oguchi K, Emori S, Kimoto M (2012) Sea-ice in twentieth-century simulations by new MIROC coupled models: a comparison between models with high resolution and with ice thickness distribution. J Meteor Soc Jpn 90A:213–232. https://doi.org/10.2151/jmsj.2012-A11
Li L, Miller AJ, McClean JL, Eisenman I, Hendershott MC (2014) Processes driving sea ice variability in the Bering Sea in an eddying ocean/sea ice model: anomalies from the mean seasonal cycle. Ocean Dyn 64:1693–1717. https://doi.org/10.1007/s10236-014-0769-7
Metz W (1991) Optimal relationship of large-scale flow patterns and the barotropic feedback due to high-frequency eddies. J Atmos Sci 48:1141–1159
Osafune S, Masuda S, Sugiura N, Doi T (2015) Evaluation of the applicability of the Estimated State of the Global Ocean for Climate Research (ESTOC) data set. Geophys Res Lett 42:4903–4911. https://doi.org/10.1002/2015GL064538
Peralta-Ferriz C, Wallace JM, Bonin JA, Zhang J (2014) Arctic ocean circulation patterns revealed by GRACE. J Clim 27:1445–1468. https://doi.org/10.1175/JCLI-D-13-00013.1
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and nighttime marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407. https://doi.org/10.1029/2002JD002670
Ren L, Riser SC (2009) Seasonal salt budget in the northeast Pacific Ocean. J Geophys Res 114:C12004. https://doi.org/10.1029/2009JC005307
Rodionov SN, Bond NA, Overland JE (2007) The Aleutian Low, storm tracks, and winter climate variability in the Bering Sea. Deep-Sea Res II 54:2560–2577. https://doi.org/10.1016/j.dsr2.2007.08.002
Sakamoto TT, Komuro Y, Nishimura T, Ishii M, Tatebe H, Shiogama H, Hasegawa A, Toyoda T, Mori M, Suzuki T, Imada Y, Nozawa T, Takata K, Mochizuki T, Oguchi K, Emori S, Hasumi H, Kimoto M (2012) MIROC4h–A new high-resolution atmosphere-ocean coupled general circulation model. J Meteor Soc Jpn 90:325–359. https://doi.org/10.2151/jmsj.2012-301
Sato K, Inoue J, Watanabe M (2014) Influence of the Gulf Stream on the Barents sea ice retreat and Eurasian coldness during early winter. Environ Res Lett 9:084009. https://doi.org/10.1088/1748-9326/9/8/084009
Serreze MC, Barry RG (2011) Processes and impacts of Arctic amplification: a research synthesis. Glob Planet Change 77:85–96. https://doi.org/10.1016/j.gloplacha.2011.03.004
Springer AM, McRoy CP (1993) The paradox of pelagic food webs in the northern Bering Sea—III. Patterns of primary production. Cont Shelf Res 13:575–599. https://doi.org/10.1016/0278-4343(93)90095-F
Vaughan DG et al (2013) Observations: cryosphere. In: Stocker TF et al (eds) Climate change 2013: the physics science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
Volkov DL, Landerer FW (2013) Nonseasonal fluctuations of the Arctic Ocean mass observed by the GRACE satellites. J Geophys Res 118:6451–6460. https://doi.org/10.1002/2013JC009341
Weingartner TJ, Danielson S, Sasaki Y, Pavlov V, Kulakov M (1999) The Siberian Coastal Current: a wind- and buoyancy-forced Arctic coastal current. J Geophys Res 114:29697–29713
Woodgate RA, Aagaard K, Weingartner TJ (2005) Monthly temperature, salinity, and transport variability of the Bering Strait through flow. Geophys Res Lett 32:L04601. https://doi.org/10.1029/2004GL021880
Woodgate RA, Weingartner TJ, Lindsay R (2012) Observed increases in Bering Strait oceanic fluxes from the Pacific to the Arctic from 2001 to 2011 and their impacts on the Arctic Ocean water column. Geophys Res Lett 39:L24603. https://doi.org/10.1029/2012GL054092
Woodgate RA, Stafford KM, Prahl FG (2015) A synthesis of year-round interdisciplinary mooring measurements in the Bering Strait (1990–2014) and the RUSALCA years (2004-2011). Oceanography 28:46–67. https://doi.org/10.5670/oceanog.2015.57
Zhang J, Woodgate R, Moritz R (2010) Sea ice response to atmospheric and oceanic forcing in the Bering Sea. J Phys Oceanogr 40:1729–1747. https://doi.org/10.1175/2010JPO4323.1
Zweng MM, Reagan JR, Antonov JI, Locarnini RA, Mishonov AV, Boyer TP, Garcia HE, Baranova OK, Johnson DR, Seidov D, Biddle MM (2013) World Ocean Atlas 2013, Volume 2: Salinity. In: Levitus S (ed) A. Mishonov Technical Ed.; NOAA Atlas NESDIS 74. NOAA, Silver Spring, MD, 39 pp
Acknowledgements
This work was supported by the Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (C) (KAKENHI) Grant Number 16K05563. The MIROC4 h and SODA version 2.2.4 data were downloaded from https://esgf-node.llnl.gov/projects/esgf-llnl/, and http://dsrs.atmos.umd.edu/DATA/soda_2.2.4, respectively. (The data of river runoff into the seas are not released to the public for the MIROC4 h.) The ESTOC data are released from http://www.godac.jamstec.go.jp/estoc/e. The WOD13 and HadISST1 data were downloaded from https://www.nodc.noaa.gov/OC5/woa13, and http://www.metoffice.gov.uk/hadobs/hadisst/data/download.html, respectively. The satellite-derived SSH data were supplied by the Centre for Polar Observation and Modelling (http://www.cpom.ucl.ac.uk/dynamic_topography). The authors would like to sincerely thank the editor and anonymous reviewers for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix: comparisons of climatologies between the model and observations
Appendix: comparisons of climatologies between the model and observations
1.1 Climatological seasonal cycle at the A3 mooring site
In this section, seasonal cycles of the model and assimilation products are compared with those observed with a mooring at the A3 site (66°19.6′N, 168°57.5′W) near the Bering Strait. The mean BTF volumetric transport simulated by the MIROC4h during the period 1950–2005 was 1.2 Sv with a maximum of 1.7–1.8 Sv in May or June and a minimum of 0.5–0.6 Sv in January or February for all three members (Fig. 14a). Whereas the MIROC4h tended to overestimate BTF transport compared with mooring-based estimates (Woodgate et al. 2005, 2012), it simulated the BTF seasonal cycle. The BTF volumetric transport in the SODA and ESTOC agreed well with the observations (Fig. 14b–c). The standard deviations of these BTF transports were larger in winter than in summer in all three models.
Climatological means of the BTF volumetric transport. a MIROC4h, b SODA, and c ESTOC. Dashed, chain, and solid lines in a denote Members 1, 2, and 3, respectively. Circles and thin solid line denote the mooring-based estimates reported by Woodgate et al. (2005). Error bars show 95% confidence intervals of the monthly means. For the MIROC4h, only the error bars of Member 3 are shown
The climatological mean of bottom-layer salinity at the A3 site reached a minimum of 32.2–32.3 in January and increased after that; unlike the indication by Woodgate et al. (2005), it did not decrease in the spring and reached a maximum in July of 33.2 (Fig. 15a). In this model, the increase of salinity due to freezing after January was too slow at the strait, and the decrease due to melting was not clearly seen at the Bering Strait. For the SODA and ESTOC, the annual mean and amplitude of salinity were smaller than the observation and the MIROC4h (Fig. 15b–c). Although the salinity in December was close to the observation, the following variation was scarcely reproduced in these products. This is probably due to the lack of sea-ice freezing/melting processes in the assimilation models. The temperatures at the A3 site in the three models was higher than the observations in summer and autumn (Fig. 16). The higher temperature in early winter might have delayed sea-ice formation in the MIRIOC4h (see Fig. 19).
As in Figure 14, but for bottom-layer salinity at the A3 site
As in Figure 14, but for bottom-layer temperature at the A3 site
1.2 Climatological mean fields
Figure 17a–c shows spatial distribution of annual mean SSS and its difference between Member 3 of the MIROC4h and WOA13. The difference was relatively small in the North Pacific and the Bering Sea, but exceeded + 1.0 in the northern part of the Bering Sea. In the Arctic Ocean, the SSS of the MIROC4h was much higher than that of WOA13, especially around the New Siberian Islands and in the Beaufort Sea. The river discharges to the Arctic Ocean simulated in the model might have been insufficient to dilute seawater. In the northwestern Bering Sea, although the seasonal cycle was basically reproduced in the model, the model SSS varied little from late autumn to early spring compared with the WOA SSS (Fig. 17d). For SST, the difference was larger in the Bering Sea, especially in the southeastern part, and relatively small in the Arctic Ocean (Fig. 18a–c). The seasonal cycle of SST in the northwestern Bering Sea was well simulated, and the model SST tended to higher in summer than the WOA SST (Fig. 18d).
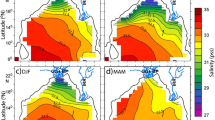
Annual mean of climatological SSS (psu). a WOA13, b MIROC4h (Member 3), and c difference between them (MIROC4h minus WOA13). d Seasonal cycle of the climatological SSS averaged over 60.5–64.5°N, 170°E–174°W (gray box in c). Thin solid line and thick dashed line denote WOA13 and MIROC4h, respectively. In a, b bold and thin contours show SSSs every 5 from 15 to 30, and every 0.5 from 30, respectively. Contour interval is 0.5 and bold contour denotes zero in c
As in Fig. 14, but for SST (°C). In a, b bold and thin contours show SSTs every 5 °C from 0 °C to 15 °C, and every 1 °C from − 1 °C, respectively. Contour interval is 0.5 °C and bold contour denotes zero in c
Climatological means of SIC in the MIROC4h were compared with those of the Hadley Centre’s sea ice and SST dataset, HadISST1 (Rayner et al. 2003). The climatological means of HadISST1 were calculated from the data during 1979–2013. The MIROC4h tended to underestimate SIC, especially in the northeastern Bering Sea, during December–May (Fig. 19). The reason for the less SSS variability in the cold season (Fig. 17d) would be partly that the effect of sea-ice freezing/melting on salinity in the MIROC4h was smaller than the reality.
Climatological SIC during December–May (%). a HadISST1, b MIROC4h, and c difference between them (MIROC4h minus HadISST1). d Seasonal cycle of the climatological SIC averaged over 60.5–64.5°N, 170°E–174°W (gray box in c). Thin solid line and thick dashed line denote HadISST1 and MIROC4h, respectively. Contour interval is 20% in a, b, and 10% in c
Climatological SSH was higher in the Bering Sea and Beaufort Sea, and lower around the Siberian coast both in the satellite-derived data and the MIROC4 h. The high SSH in the Beaufort Sea simulated in the MIROC4h was located farther north off the coast compared with the satellite SSH. The MIROC4h SSH tended to have a negative bias along the Russian coast and the Alaskan coast, and a positive bias around 80°N (Fig. 20a–c). The seasonal cycle of the SSH averaged over 66–72°N, 165°E–170°W was well reproduced in the MIROC4 h, although the amplitude of the model SSH was slightly larger (Fig. 20d).
Annual mean of climatological SSH (cm). a Satellite-derived, b MIROC4h, and c difference between them (MIROC4h minus Satellite). d Seasonal cycle of the climatological SSS averaged over 66–72°N, 165°E–170°W (gray box in c). Thin solid line and thick dashed line denote satellite-derived and MIROC4h, respectively. For each SSH, a domain average over 60–81.5°N, 100°E–130°W was subtracted. Contour interval is 10 cm, and bold contour denotes zero
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kawai, Y., Osafune, S., Masuda, S. et al. Relations between salinity in the northwestern Bering Sea, the Bering Strait throughflow and sea surface height in the Arctic Ocean. J Oceanogr 74, 239–261 (2018). https://doi.org/10.1007/s10872-017-0453-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10872-017-0453-x