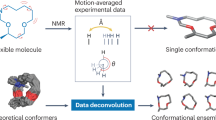
Abstract
Nuclear magnetic resonance (NMR) has the unique advantage of elucidating the structure and dynamics of biomolecules in solution at physiological temperatures, where they are in constant movement on timescales from picoseconds to milliseconds. Such motions have been shown to be critical for enzyme catalysis, allosteric regulation, and molecular recognition. With NMR being particularly sensitive to these timescales, detailed information about the kinetics can be acquired. However, nearly all methods of NMR-based biomolecular structure determination neglect kinetics, which introduces a large approximation to the underlying physics, limiting both structural resolution and the ability to accurately determine molecular flexibility. Here we present the Kinetic Ensemble approach that uses a hierarchy of interconversion rates between a set of ensemble members to rigorously calculate Nuclear Overhauser Effect (NOE) intensities. It can be used to simultaneously refine both temporal and structural coordinates. By generalizing ideas from the extended model free approach, the method can analyze the amplitudes and kinetics of motions anywhere along the backbone or side chains. Furthermore, analysis of a large set of crystal structures suggests that NOE data contains a surprising amount of high-resolution information that is better modeled using our approach. The Kinetic Ensemble approach provides the means to unify numerous types of experiments under a single quantitative framework and more fully characterize and exploit kinetically distinct protein states. While we apply the approach here to the protein ubiquitin and cross validate it with previously derived datasets, the approach can be applied to any protein for which NOE data is available.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The development of methods for determining the structure and dynamics of proteins has been instrumental in elucidating mechanisms behind many important functions, including ligand binding, enzyme-catalysis, allosteric regulation, and folding. Through the use of several nuclear magnetic resonance (NMR) effects, including scalar couplings, longitudinal/transverse relaxation (T1/T2), the heteronuclear nuclear Overhauser effect (NOE), residual dipolar couplings, cross-correlated relaxation, and relaxation dispersion, an extraordinary amount of atomic resolution information can be extracted about the local structure and dynamics of proteins. However, to build a more complete picture of the thermodynamically accessible states of a protein, the determination of an ensemble of atomic resolution structures is often essential. In that regard, homonuclear NOEs, which give information about through space interactions between protons, are of critical importance and have been used in nearly all high-resolution structures determined by NMR.
Most NMR structures are solved using distance-based methods typically considered to be semiquantitative (Borgias and James 1988; LeMaster et al. 1988), in which NOE cross peaks are analyzed with the isolated spin pair approximation (ISPA) that assumes any transfer of magnetization between protons happens solely through space and does not involve the network of neighboring protons. Cross-peaks are often categorized as strong, medium, and weak, then used to derive approximate upper bound distance restraints from which individual structures are solved through computational refinement. Most NMR ensembles deposited in the Protein Data Bank (PDB) consist of about 20 of the best individually determined structures. Although the heterogeneity in these ensembles may reflect true protein flexibility, it often results from the uncertainty due to lack of sufficient restraints or limitations of the modeling procedures.
Several techniques have been employed to enable the determination of more accurate structures and ensembles from NMR data. In the decade around which the first NMR structure was published (Williamson et al. 1985), there was much interest in applying techniques that did not employ the ISPA, but instead treated the full matrix of possible magnetization transfer pathways through neighboring protons (Borgias and James 1988; Keepers and James 1984; Boelens et al. 1988; Yip and Case 1989; Post et al. 1990; Bonvin et al. 1991; Bonvin et al. 1993). However, in most of these approaches, a single conformation was assumed to be a faithful representative of the structural ensemble of the protein. More recently, relaxation matrix calculations were used to reweight an ensemble of conformations using maximum entropy methods (Vasile 2019). Furthermore, other efforts have been made to incorporate additional experimental information into the determination of NMR ensembles, either using RDC (Cornilescu et al. 1998; Lange et al. 2008; Frank et al. 2009; Fenwick et al. 2011; Montalvao et al. 2012; Maltsev et al. 2014) or fast timescale order parameter (S2) (Lindorff-Larsen et al. 2005; Richter et al. 2007; Chen et al. 2007) data. These efforts incorporated one or more of the following features which were probably important to their success: addition of experimental data that directly captures protein dynamics, fitting experimental data to multiple structures simultaneously, and the use of explicit solvent molecular dynamics (MD) refinement with high quality force fields. More recently, the exact NOE (eNOE) approach (Vögeli et al. 2009; Vögeli et al. 2010) has used diagonal peaks, buildup curves, and perdeuteration or relaxation matrix analysis to more accurately determine NOE rates. This has allowed much more precise interatomic distances to be inferred and enabled the determination of multi-state protein ensembles (Vögeli et al. 2012; Chi et al. 2015; Vögeli et al. 2016). However, a notable drawback of nearly all NOE structure determination efforts to date, including the eNOE approach, is that a distinction of time scales for NOE averaging was not attempted and that angular motion is neglected during refinement and at best can only be derived in a post hoc manner using an independently determined reference structure (Vögeli et al. 2009).
This omission is notable because it has been shown that determination of effective internuclear distances requires taking into account fluctuations in the internuclear orientation, and that this can be affected by anisotropic internal motions typical in proteins (LeMaster et al. 1988). One means of incorporating both radial and angular internal dynamics is to explicitly calculate internuclear correlation functions and the resulting NOE rates from molecular dynamics trajectories (Bonvin et al. 1993; Brueschweiler et al. 1992; Peter et al. 2001; Chalmers et al. 2016). While this approach can be used for simulating NMR data and validating MD simulations, it has limited applications in ensemble determination. One notable hybrid approach involved using internuclear order parameters estimated from MD simulations to scale NOE rates calculated from an ensemble of structures (Bonvin et al. 1993). However, this method depends on having an accurate MD simulation and assumes distances average as r−6. Furthermore, it does not guarantee that the resulting ensemble will have accurate angular dynamics, or even the same angular dynamics as the initial MD simulation.
The importance of angular dynamics in proteins has long been appreciated. Through the use of model free (Lipari and Szabo 1982) and extended model free approaches (Clore et al. 1990), along with associated experimental advances (Kay et al. 1989), the determination of Lipari-Szabo order parameters (S2) has become the most widely applied method for elucidating protein dynamics. These values give the amplitude of angular fluctuations of bond vectors within the protein. The strong dependence of the heteronuclear NOE between atoms (e.g. the backbone amide nitrogen/hydrogen) on the amplitude of their relative angular motion, together with T1/T2 measurements, is critical for determining order parameters. The larger the amplitude, or the shorter the timescale of that motion, the more the transfer of magnetization via the NOE is attenuated. This same phenomenon is at work in homonuclear NOE experiments used to determine interatomic distances.
The approach described here, which we call Kinetic Ensemble (KE), explicitly models both the amplitudes and timescales of angular motion involved in homonuclear NOEs. It involves describing atomic motions using a lattice defined by the structural ensemble. Previous studies have used the lattice approach to model toy systems with specialized or approximate spectral density functions (Keepers and James 1984; Brueschweiler et al. 1992; Koning et al. 1990; Liu et al. 1992), making notable contributions to the understanding of methyl rotation and aromatic ring flips (Koning et al. 1990; Liu et al. 1992). The theory described here is a generalization of both the lattice and model free approaches that can handle complex combinations of angular and radial motions in a rigorous manner. The importance of hierarchical protein dynamics has been previously noted (Henzler-Wildman et al. 2007; Smith et al. 2015; Lewandowski et al. 2015), and several techniques have been recently developed to reweight multi-timescale models built from extensive molecular dynamics simulations (Salvi et al. 2016; Wan et al. 2016; Capelli et al. 2018). By contrast, our approach is better suited for modeling such temporally resolved dynamics with an ensemble representation typically used to represent NMR structures, as demonstrated on a protein system using up to five different timescales of molecular motion. We show that the timescale of distance fluctuations has a large impact on how those distances are averaged over a much broader range of timescales than previously appreciated. This is shown to be critical for interpreting NOE data in the context of several state-of-the-art protein ensembles. Despite this, our approach is general and can be applied to ensembles derived solely from NOEs acquired at a single mixing time and does not explicitly require other NMR data.
Results
Kinetic ensemble (KE) approach can be simplified to extended model free formalism
To validate the Kinetic Ensemble approach using a multi-timescale scheme, we used a two-atom, fixed bond length system with two slowly interconverting macrostates, each consisting of two quickly interconverting microstates (Fig. 1). If constructed correctly, this system should recapitulate extended model free formalism (see “Methods”) (Clore et al. 1990). The conformations of the four states were constructed by rotating the two-atom system within a plane. For each macrostate, the angle (θf) between the two microstates was set such that the fast timescale order parameter (S2f) was 0.6. The angle (θs) between the average orientations of the macrostates was set such that the overall order parameter of the system (S2) was 0.57, giving a slow timescale order parameter (S2s = S2/S2f) of 0.95. A transition rate matrix (Q) was constructed to recapitulate fast and slow timescales of motion (τf and τs, respectively, Fig. 1b). The diagonal elements were set to the negative sum of the other elements in the corresponding row (not shown). An eigendecomposition of the resulting matrix yields three unique eigenvalues (0, degenerate − τ−1f, and − τ−1s), indicating two distinct timescales of motion. Upon application of the Kinetic Ensemble approach, the resulting internal correlation functions and spectral densities exactly match those of extended model free theory (Clore et al. 1990), with \(\tau_{c} = 5 \times 10^{ - 9} {\text{s}},\;\tau_{f}^{\prime } = \tau_{f} \tau_{c} /\left( {\tau_{f} + \tau_{c} } \right)\;{\text{and}}\;\tau_{s}^{\prime } = \tau_{s} \tau_{c} /\left( {\tau_{s} + \tau_{c} } \right):\)
As this analysis shows, the Kinetic Ensemble approach simplifies to extended model free when the rate matrix has only three distinct eigenvalues and bond lengths are kept fixed. However, it also handles arbitrarily complex kinetic schemes and bond length variability, as discussed below.
Kinetic Ensemble method can recapitulate Extended Model Free approach a A fixed-distance double atom system showing motion on two timescales with different magnitudes of motion (fast: S2f, slow: S2s) can be represented by four microstates with an angle (θf) between the two pairs of quickly interconverting microstates and another angle (θs) between the average orientations of the two slowly exchanging macrostates. Overall molecular tumbling is ignored here. b In such a system, the slow timescale (τs) can be represented with inter-macrostate rates equal to τ−1s/4. The fast timescale (τf) is captured by an intra-macrostate rate of (τ−1f−1/2τ−1s)/2. c When the internal correlation function for this Kinetic Ensemble is calculated, it is identical to Extended Model Free. d The same is true for the resulting spectral density function, from which NOE rates are determined
Dependence of distance averaging on exchange timescale
As is clear from extended model free theory, the particular timescales at which molecules undergo angular reorientation has a large influence on the spectral densities and resulting experimental observables. The same is true for the timescales at which distances change. For motions occurring much faster than molecular tumbling, the NOE rate is known to be dependent on the r−3 average of interatomic distances (r), while motions occurring much slower show r−6 distance averaging. Mathematically, that can be expressed \(J\left( 0 \right) \propto \left\langle {r^{ - 3} } \right\rangle^{2}\) for fast motion and \(J\left( 0 \right) \propto r^{ - 6}\) for slow motion, assuming the NOE rate is dominated by the \(J\left( 0 \right)\) term, which is true for both the auto (ρ) and cross (σ) relaxation rates of macromolecules. The Kinetic Ensemble approach should implicitly capture this dependence. To test this, we constructed a model system having two states with the same orientation but different distances: one (rA) fixed at 1 Å and the other (rB) varied 1.1–10 Å. While τc was kept fixed, the exchange timescale (τex) was varied around τc plus or minus three orders of magnitude. For each value of τex, the Kinetic Ensemble approach was used to calculate the spectral density function with the population of the first state (pA) set to 0, 0.2, 0.4, 0.6, 0.8, and 1.0. At each τex value, we used the equation \(J\left( 0 \right) = 2\tau_{c} \left( {p_{\text{A}} r_{\text{A}}^{ - n} + \left( {1 - p_{A} } \right)r_{\text{B}}^{ - n} } \right)^{6/n}\) to fit the effective averaging power (n). The resulting values of n are shown in Fig. 2a. When τex is at least two orders of magnitude away from τc, the usual assumptions of distancing averaging are valid. However, at intermediate timescales the averaging power smoothly transitions from three to six. The surprisingly shallow slope of this function at τc indicates that this distance dependence could be used to extract information about dynamics at least an order of magnitude slower than molecular tumbling. This finding agrees with previous work indicating NOE sensitivity to dynamics plus or minus an order of magnitude around τc (Brueschweiler et al. 1992). We found that the averaging powers could be empirically fit with a hyperbolic function similar to that used for bimolecular binding, with the midpoint τ1/2:
Interatomic distance averaging transitions smoothly from a power of three to six a In a double-atom system with states at two distinct distances (r1 and r2), the Kinetic Ensemble approach can be used to understand the dependence of the spectral density function, J(0), on how the averaging of interatomic distances (r) is influenced by the relative timescales of exchange (τex) and overall tumbling (τc). The black points were determined by fitting the black equation to simulations with different populations of the two states. Simulations with τex ≪ τc give the expected ⟨r−3⟩2 dependence and τex ≫ τc give the expected ⟨r−6⟩ dependence. Between those two limits, there is a smooth transition that empirically follows a hyperbolic equation (red). Depending on the ratio of the two distances (rB/rA), the hyperbolic function shifts right or left between the two extremes shown, with τ1/2 being the timescale with an averaging power of 4.5. b As the distance ratio increases, τ1/2 goes from 1.00τc to a plateau value of 1.36τc
The previous two examples illustrate a clear timescale dependence for dipole–dipole interactions between nuclei undergoing either angular reorientation or changes in distance. In a macromolecule, both types of motion are prevalent and convoluted together, precluding the use of simple analytical models (Fig. S4). Whereas most macromolecular modelling efforts neglect one or both types of motion, assume that they are separable, or make implicit assumptions about the timescale, the Kinetic Ensemble approach models the effects of motion in a rigorous manner subject to the structural ensemble and transition rate matrix.
Much internal protein motion occurs at a timescale similar to overall tumbling
To apply the Kinetic Ensemble approach to a more complex biomolecular system, we used the protein ubiquitin. Using high-resolution 2D NOESY experiments, we acquired a set of buildup curves with 34 equally spaced mixing times from 5 to 500 ms at a temperature of 308 K. The signal to noise of this dataset was excellent and showed a high degree of reproducibility in duplicate experiments. To ensure that we had a good basis set of physically realistic ubiquitin structures, we initially analyzed the EROS3 ensemble (Lange et al. 2008), which was generated by refining randomly selected 8 member subsets of 46 crystal structures against NOE and RDC data using explicitly solvated molecular dynamics simulations, with the best 22 subsets selected to produce 176 total ensemble members.
For modeling ubiquitin, we started using a transition rate matrix with the fewest parameters possible, assuming a single timescale of motion with a uniform transition rate between all ensemble members (i.e. an N-site jump model). This poses the least risk for overfitting, while giving the flexibility for the model to explore averaging regimes between r−3 and r−6, and varying amounts of NOE attenuation due to angular dynamics. Given an overall exchange timescale, τensemble, the individual transition rate, k, can be calculated k = τ−1ensemble/N, with number of ensemble members, N = 176. It is trivial to verify the overall exchange timescale, as the eigenvalues of the transition rate matrix contain a single value of 0 and 175 degenerate values equal to − τ−1ensemble. In addition to interconversion between ensemble members, methyl and aromatic group rotations were accounted for as independent exchange processes (see “Methods”).
To determine the timescales that best fit the experimental data, we sampled τc and τensemble on a grid and computed the uncentered correlation with experimental NOE data at each point (Fig. 3). The uncentered correlation is very similar to the Pearson correlation but penalizes data with a non-zero y-intercept (see “Methods”). The agreement with experimental data was much more sensitive to τc, with large decreases in correlation visible with a less than twofold deviation in τc from the optimal value. While τensemble showed comparatively less sensitivity over a much larger range (± 3 orders of magnitude), a distinct peak was seen at around 2.0 ns. After sampling on the grid, the timescales from the best fitting point were numerically optimized to give the best fitting τc value of 4.3 ns. Previous measurements of ubiquitin at 308 K have given very similar tumbling times of 4.0 ns (Sabo et al. 2012), suggesting the protocol can accurately determine kinetics from NOE data. Similarly, an overall ensemble timescale of 2.0 ns is supported by a comparison of backbone amide Lipari-Szabo order parameters and RDC-based order parameters. Previous studies (Lange et al. 2008; Lakomek et al. 2008) have shown that the majority of angular fluctuations throughout ubiquitin are captured by Lipari-Szabo order parameters (\(S_{LS}^{2}\)), which report on motions close to or faster than τc, but some residues show a substantial amount of additional motion (\(S_{rdc}^{2}\)/\(S_{LS}^{2}\)) in RDC-based order parameters (\(S_{rdc}^{2}\)), which report on dynamics up to the millisecond timescale. 2.0 ns would therefore be a reasonable compromise fit of a single exchange timescale to both the sub and supra-τc motions. Motions with timescales much slower than τc affect the NOE by upweighting the contributions of short contacts (through r−6 averaging) without having additional angular attenuation beyond that occurring at fast timescales.
Optimization of time coordinates gives similar tumbling and exchange timescales. Kinetic Ensemble Refinement optimizes the timescale of molecular tumbling (τc) and one or more exchange timescales (in this case just τensemble). When the two are simultaneously optimized for the EROS3 ensemble (purple point), the τc is 4.3 ns, close to previously published tumbling times for ubiquitin. The best τensemble is 2.0 ns, which is within 2.2 times faster than τc (indicated as a dashed line on the τensemble axis). According to Fig. 2, having τensemble within 2.2-fold of τc makes the effective averaging of distances a power of 3.8–4.9, contrary to usual approximations of NOE data that assume powers of either three or six
Modeling an extended hierarchy of timescales
After already modelling a single ensemble timescale, we sought to test whether separating out another, slower ensemble motion would further improve the model. Much of the supra-τc motion in ubiquitin has been attributed to the pincer mode (Lange et al. 2008), which involves opening and closing around the β1–β2 loop and the end of the alpha helix. Extensive relaxation dispersion data strongly suggests that this motion is faster than 3.4 µs (Massi et al. 2005; Smith et al. 2016), giving a range of approximately three orders of magnitude for the kinetics of this motion. Furthermore, even if that level of characterization had not been done, the pincer mode is the largest amplitude motion observed in unbiased MD simulations (Peters and de Groot 2012), suggesting questions about its timescale. This provides a good test case to determine whether NOE data can be better modeled using multiple timescales of internal motions. To compose such a hierarchy as illustrated in Fig. 4a, the overall transition rate matrix was constructed with inter-group rates set to τ−1pincer/N, with N being the total number of structures. The intra-group rates were set to (τ−1 ensemble− (1−Ni/N)τ−1pincer)/Ni, with Ni being the number of structures in the given group (in this case 139 open and 37 closed).
Hierarchical kinetics improve fit to NOE data. a In the hierarchical scheme, different transition rates are used between and within groups of ensemble members (here pincer open and closed). b Starting from a single timescale (orange) slowing down the ubiquitin pincer mode (τpincer) improves correlation with NOE data (green). Subsequent optimization of the ensemble timescale (τensemble) further improves the correlation (purple). c Applying the same optimization protocol to 20,000 sets of randomized groups shows that the enhancement from grouping by pincer state is very significant. d Experimental NOE intensities and theoretical NOE buildups fit to a single timescale. Nearly all NOEs highly overestimated by the model come from those between protons separated by 2–5 bonds (bond separations ≥ 6 are black). Buildups illustrated in e and f are drawn with orange lines. Calculated NOEs show the summed fractional magnetization transfer and observed are arbitrary units, with the limits of the graph set to three times the root mean square (RMS) value. e The I13 QG2-HB buildup showed the greatest improvement after optimization of only τpincer (green), compared with the RMS-normalized experiment (black). It slightly worsens after optimization of τensemble (purple). f The K11 QD-QE buildup showed the greatest improvement after τensemble optimization. g The I13 shows more restricted sampling of chi angles when just open or closed conformations are considered. H) This is mirrored when looking at the I13 structures or CB-CG2 order parameters (S2). The side chains have their CA atoms aligned and the CB-CG2 bond shown with a stick representation. When τpincer is much greater than τc, the population weighted mean order parameter dominates in determining the NOE rate, which results in a net increase in NOE intensities after both timescales are optimized. The overall and mean values compare well to previously determined RDC (Fares et al. 2009) and Lipari-Szabo (Lee et al. 1999) order parameters. i The K11 CD-CE bond vector is more dynamic and shows a much smaller increase in mean order parameter, resulting in a net decrease in calculated NOE intensities
Eigendecompositon of this rate matrix yields exactly three distinct eigenvalues, 0, − τ−1pincer, and − τ−1ensemble. The rate matrix in Fig. S2a was constructed in the same manner. Keeping τensemble fixed at 2 ns, the optimal correlation was found by sampling τpincer on an interval from 2 ns to 1 µs. (Fig. 4b) The correlation improved as the timescale slowed, plateauing at about 100 ns and reaching a maximum at the limit of 1 µs. While a 1 µs pincer motion might be partially visible in relaxation dispersion curves having 3.4 µs resolution, this was not observed experimentally. Nevertheless, because NOE rates are largely insensitive to timescale differences in the regime 25–250 times slower than overall tumbling (i.e. 100 ns–1 µs here), there is little practical effect in using a τpincer somewhat slower than experimentally justified. Using a τpincer of 1 µs, τensemble was then numerically reoptimized from 2 ns to 1.4 ns. This decrease in timescale was likely enabled by reducing the amount of slow timescale “compromise” required. To determine whether the overall increase in uncentered correlation was statistically significant, we repeated that same optimization procedure 20,000 times using randomly grouped sets of 139 and 37 structures. (Fig. 4c) None of these random sets showed improvements greater than the pincer grouping, suggesting a p ≪ 5 × 10−5.
Most previous efforts to model homonuclear NOE data have focused solely on the distance dependence, and therefore typically do not address NOEs between atoms with relatively short covalent bond separations. For these atom pairs, the NOE will be primarily modulated by dynamics in the orientation of the internuclear vector, as it is for backbone amide heteronuclear NOEs. Because the KE approach can rigorously account for both aspects, we have included these low bond separation NOEs in our analysis. As shown in Fig. 4d, which compares experimental intensities to those calculated using a single 2 ns timescale, nearly all atom pairs where the NOE intensity is highly overestimated by the model are separated by 2–5 bonds. This suggests that the orientational motion of the atom pairs is too low and/or the timescale is too slow, both of which result in reduced attenuation of the dipolar interactions. Conversely, the majority of atom pairs having highly underestimated NOE intensities come from those separated by six or more bonds. However, there are a few examples of atoms pairs separated by 2–5 bonds that are predicted to be lower in intensity than actually observed.
One of these, the I13 QG2-HB NOE, is highlighted with an orange line on the right side of Fig. 4d. Upon changing τpincer from 2 ns to 1 µs, this NOE is most responsible for the better correlation coefficient. This NOE shows a relatively large increase in intensity (orange to green in Fig. 4e) because of differences between the overall motion of the I13 side chain and the motion when open or closed. While the chi 1 angle of I13 shows a relatively equal distribution of the 60° and 300° rotamers, the open or closed conformations are more skewed towards one rotamer or the other. (Fig. 4g)
This population shuffling (Smith et al. 2015) of rotamer conformations makes the CB-CG2 order parameters for both the open and closed conformations higher than the overall order parameter (Fig. 4h). In the EROS3 ensemble, the motion of the I13 side chain is thus distinctly hierarchical, showing differences in both average structure and dynamics depending on whether it is open or closed. The CB-CG2 heavy atom order parameter is likely a good proxy for the order parameter between the beta hydrogen and the dynamically averaged position of the gamma 2 methyl group hydrogens. When τpincer ≫ τc, the order parameter that determines the NOE rate is the population weighted mean order parameter of the open and closed states, which is much higher than overall order parameter. This helps explain why increasing τpincer almost three orders of magnitude results in a greater increase in NOE intensity for this pair than others (e.g. Fig. 4f). The difference in fast timescale mean order parameters (determining the NOE rate) and overall order parameters is largely in agreement with previously determined Lipari-Szabo (Lee et al. 1999) and RDC (Fares et al. 2009) order parameters, with the underlying RDC data being used in refinement of the EROS3 ensemble. Though the RDC order parameter is consistent with the ensemble, the experimentally determined Lipari-Szabo parameter is greater than the mean order parameter derived from the EROS3 ensemble. This discrepancy is mirrored in the NOE data, with the experimental buildup curve still exceeding the calculated one. The most straightforward ways to improve the match between the EROS3 ensemble and both datasets would be to either increase the population of the closed conformation or decrease the population of the 60° rotamer in the open conformation.
While increasing τpincer and decreasing τensemble led to a net increase in the NOE intensities for I13 QG2-HB NOE, a net decrease in NOE intensities was also observed for many other pairs. The pair that caused the greatest improvement in correlation after reoptimization of τensemble was K11 QD-QE. This pair was already highly dynamic, with the heavy atom CD-CE order parameter being 0.13. Because the mean open/closed order parameter was not much higher (0.15), increasing τpincer only produced a very small increase in observed NOE intensity. Reoptimization of τensemble from 2.0 to 1.4 ns caused a sizable reduction in NOE intensity below the original prediction. However, there is still a substantial overestimation of the NOE rate for not only K11 QD-QE, but also several other NOEs in the lysine side chain including QD-HG2 and QE-HG2. To improve the model, the kinetics for the side chain could be made much faster. Alternatively, the side chain order parameters could be decreased by increasing the overall mobility or again increasing the population of the closed state. Because the pincer mode was the largest amplitude motion and therefore the most likely to have a detectable kinetic dependence, we did not explore adding additional timescales for lower amplitude motions such as the ubiquitin peptide flip (Smith et al. 2016), but instead turned to changing the composition of the ensemble itself.
Ensemble subselection produces better fits to NOE data
In addition to demonstrating that adding another timescale improved agreement with the NOE data, we also tested how much selecting a refined subset of ensemble members would improve goodness of fit. To do so, we ran a subselection optimization algorithm 100 times starting from different random subsets of the EROS3 ensemble (see “Methods”). The algorithm produced 13–18 member subensembles and consistently improved correlation with the NOE data over the full ensemble (Fig. 5a). By contrast, if random subensembles having same size distribution were generated, the correlations tended to be worse than the full ensemble. This decrease for the random subensembles may stem from the way the EROS3 ensemble was produced, in which 8-member ensembles were collectively fit to NOE/RDC data, each therefore containing a distribution of states that together matched the data. By construction, the full 176-member ensemble would also show a similar overall distribution. However, the generation of small random subsets could very likely miss important states, resulting in lower correlations.
NOE selected subensembles outperform random subensembles. a 100 NOE selected subensembles (blue) produce better uncentered correlations (Ru) than the full ensemble (black), while randomly selected subensembles (red) fit less well than the full ensemble. An Ru cutoff of 0.935 (gray line) was used to pick the top 31 scoring ensembles shown in subsequent panels. b NOE data for the best selected subensemble. The best scoring subensemble shows slightly less overall magnetization transfer. The blue (NOE selected) and black (full ensemble, Fig. 4d) lines have slope RMScalc/RMSobs. c Cross-validation with RDC data (lower Q-factors are better) shows that the random subensembles match the data less well than the full ensemble. However, ensembles selected by NOEs have better backbone N–H (dashed) and N–C′ (solid) RDC Q-factors than the random subensembles, while the side chain data (dotted) is worse. d Part of the decreased side chain performance likely comes from significant changes to overall side chain order parameters, with notable rigidification in a number of residues. Error bars indicate standard deviations. e Those side chains are likely rigidified to counteract an almost tenfold decrease in the ensemble timescale
The best scoring subensemble (Ru = 0.935) was found two out of 100 times by the algorithm and showed slightly lower fractional magnetization transfer than the full ensemble (Fig. 5c). To determine whether the NOE optimized subensembles were truly better than random subensembles of the same size, we cross-validated with the same RDC dataset that was used to produce the EROS3 ensemble (Fig. 5c). Similar to what was observed for the NOEs (Fig. 5a), the random subensembles showed consistently worse reproduction of the RDCs than the full ensemble. However, the NOE selected subensembles showed better Q-factors for backbone RDCs than the random subensembles, indicating that application of the Kinetic Ensemble approach better preserved the orientation/dynamics of backbone bond vectors. Interestingly, the side chain RDCs showed the opposite trend, with the NOE-selected subensembles being worse than those that were randomly selected.
To determine why that might be the case, we examined how use of the NOE data influenced the ensemble side chain order parameters. We found that the 34 side chain methyls for which RDC data was available showed a number of large deviations from the full ensemble order parameters, particularly towards rigidification (Fig. 5e). Notably, the overall order parameter for I13 CB-CG2 increased from 0.25 (consistent with the RDC S2, Fig. 4h) to 0.69 (slightly above the Lipari-Szabo S2). While that improves agreement with the NOE data, it worsens RDC reproduction for this methyl. By contrast, in the τensemble/τpincer model described above, where differing flexibility at two timescales was allowed, it was possible to fit both RDC and Lipari-Szabo/NOE data simultaneously.
Given the difference between models with hierarchical and non-hierarchical kinetics, we also examined the τensemble values derived from the different subensembles (Fig. 5f). While the random subensembles showed a broad distribution of timescales roughly centered on the full ensemble, the NOE selected subensembles had a much narrower distribution almost an order of magnitude faster. We previously hypothesized (Fig. 4h, i) that such faster kinetics and/or reduction in S2 would improve the fits to the NOE data for K11 QD-QE as well as many of the other NOEs coming from short bond separations. The NOE selected S2 for K11 QD-QE was also lower than the full ensemble (also shown in Fig. 5e), supporting the idea that changes in both τensemble and S2 could play a role. However, because dynamics of the entire structure are forced to be on the same timescale, other parts are rigidified (like I13), possibly making the ensemble less representative of the overall flexibility in those regions. This highlights not only the exquisite sensitivity of NOEs to both protein flexibility and kinetics, which hasn’t been possible to analyze with previous theoretical approaches, but also the need to make further refinements to the kinetic schemes employed here to better interpret existing NOE datasets.
Goodness of fit to NOE data is highly correlated with crystal structure resolution
Ubiquitin has been extensively studied by both X-ray crystallography and NMR. To test the ability for the Kinetic Ensemble method to discern structural quality, we used it to compute buildup curves for 176 distinct full-length ubiquitin domain structures, including 115 X-ray crystal, 57 solution NMR, 2 solid-state NMR, and 2 cryo-EM structures (from 64, 47, 2, and 1 PDB entries, respectively). Where multiple alternate conformations existed in the PDB, they were treated as different ensemble members. For NMR structures, all ensemble members were included in the calculations. For this analysis we used crystal/cryo-EM structure resolution as a proxy for quality. In that regard, the goodness of fit to the NOE data showed a surprisingly high correlation with structural quality (Fig. 6).
NOE data agreement is highly correlated with crystal structure resolution. 117 ubiquitin domains from 65 different crystal/cryo-EM structures were used to determine their agreement with the NOE buildup data. Across the full range of resolutions (1.15–4.54 Å), the Pearson correlation coefficient between the resolution and agreement with NOE data is − 0.68. Several structures show unexpectedly high correlations (likely because of molecular replacement into a low-resolution map), or low correlation (because of unusual ubiquitin conformations or poor refinement). When the gray points are removed, the Pearson correlation improves to − 0.87. Both Pearson correlation coefficients are statistically significant (p < 10−16). The Pearson correlation continues to be statistically significant for structures less than 2 Å (p = 0.01, blue) or 1.85 Å (p = 0.05, red), suggesting that NOE data contains higher resolution data than previously thought. When the crystal structures are combined to create a more dynamic ensemble, starting with those at the best resolution, the agreement increases (green line) and reaches a maximum (green point) when all structures 1.74 Å and better are included. This crystal ensemble approaches the best published NMR ensembles to-date in fitting to the NOE data
Several PDB entries showed much better agreement with the NOE data relative to their resolution [5EDV (Lechtenberg et al. 2016) and 4ZUX (Morgan et al. 2016)]. The ubiquitin domains in these macromolecular complexes were solved via molecular replacement using crystal structures of ubiquitin with higher resolution, likely producing better coordinates than would otherwise have been possible. Similarly, several structures showing lower agreement with the NOE data also had more than half of their PDB quality metrics lower than the median values for other structures of similar resolution. When these structures are excluded the correlation coefficient improves to − 0.87.
While discrimination of structural quality over resolutions ranging 1.15–4.5 Å using NOE data could be anticipated, it was much more unexpected to find that significant correlations extended down to resolutions ranging 1.15–1.85 Å (p = 0.05) or 1.15–1.98 Å (p = 0.01). This indicates that NOEs likely have higher resolving capability than was previously appreciated. This high correlation was found despite all the potential confounding factors such as contacts within the crystal lattice, the presence of binding partners, covalent linkages, and differences between the cryogenic temperatures where most of the crystal structures were solved and 308 K where the NOEs were determined. A similar analysis with RDC data yields lower correlations, both quantitatively and visually (Fig. S5). This suggests that NOE data is capable of not only ensemble determination, but also distinguishing high-quality average ground-state structures from those with slightly less quality, which is useful in high-resolution structural refinement.
Despite the clear correlation between NOE data and crystal structure resolution, NMR ensembles still fit the NOE data better than the crystal structures. The top scoring NMR models included single structures optimized against NOEs, RDCs, and J-couplings (1D3Z (Cornilescu et al. 1998), and 2MJB (Maltsev et al. 2014)) as well as ensembles fit against multiple types of NMR data including NOEs (Cornilescu et al. 1998; Lange et al. 2008; Fenwick et al. 2011; Maltsev et al. 2014; Lindorff-Larsen et al. 2005; Richter et al. 2007), RDCs (Cornilescu et al. 1998; Lange et al. 2008; Fenwick et al. 2011; Montalvao et al. 2012; Maltsev et al. 2014), Lipari-Szabo order parameters (Lindorff-Larsen et al. 2005; Richter et al. 2007), and scalar couplings (Cornilescu et al. 1998; Maltsev et al. 2014). (Table 1) Those ensembles included ERNST (Fenwick et al. 2011) (2KOX), MUMO (Richter et al. 2007) (2NR2), DER (Lindorff-Larsen et al. 2005) (1XQQ), EROS (Lange et al. 2008) (2K39), and 2LJ5 (Montalvao et al. 2012). However, combining the 22 ubiquitin domains coming from crystal structures with resolutions 1.15-1.74 Å (Table S1) produces an ensemble whose correlation (Ru = 0.915) exceeds all but four of the NMR ensembles (EROS3, ERNST, MUMO, and DER).
Discussion
Here we have demonstrated a new approach for modeling NOE data which overcomes several shortcomings in the way previous methods have handled protein motion. First, the Kinetic Ensemble approach directly captures the effect that angular motion has on attenuating NOE rates. For protons separated by 2–4 bonds whose interatomic distances are restricted by covalent geometry, this serves as a sensitive probe of angular dynamics, either in the backbone (i.e. between amide and alpha hydrogens), or along side chains. Second, we have shown that the usual assumptions of distance averaging as a power of three or six are only fully valid for motions occurring at least two orders of magnitude slower or faster than the overall tumbling time. In all models we used to fit the experimental data, at least one of the overall exchange timescales was within two orders of magnitude of the tumbling time, indicating that this assumption should be revisited.
As stated above, this study particularly highlights the sensitivity of NOE data to the timescales of angular and through-space motion. The NOE buildup data, when interpreted in the context of a reasonably accurate structural model, is capable of recovering the overall tumbling time with a high degree of accuracy. Furthermore, NOE data can be used to validate hypotheses about the timescales of particular motions, revealing kinetics up to and potentially more than an order of magnitude slower than molecular tumbling.
In the context of structure determination, the quantitative approach used here to directly calculate spectral intensities shows a surprisingly high correspondence between fit to the NOE data and crystal structure resolution. This relationship holds up despite the substantial number of potential confounding factors that make crystal structures deviate from the solution state of a molecule. This suggests that NOE data may contain considerably more information than previously appreciated about the high-precision structural details typically found in the best resolution crystal structures. The Kinetic Ensemble approach could thus be used to help resolve outstanding questions about the similarity between dynamics in solution and other states like a crystal lattice.
When the ubiquitin ensemble was either split into a kinetic hierarchy or trimmed down to a subset of the full ensemble, sizable changes to flexibility and kinetics were observed after Kinetic Ensemble optimization. This practical result is in agreement with what the theory suggests, namely that NOE data is very sensitive to both motional amplitudes and kinetics. This then implies that when interpreting NOE datasets, it is important to correctly model structure, motion, and kinetics. An inaccuracy in any of those three properties will necessarily have an adverse effect on the other two. A NOE-based structural refinement method that ignores any of those properties is making implicit assumptions which could have a sizable impact on the properties it does consider.
One of the most immediately useful applications of the Kinetic Ensemble approach is to augment existing NMR ensemble calculation methods to build more quantitative models of protein structure and motion. Unlike the eNOE approach, only a single mixing time is required, making it applicable to all standard NOE datasets. Starting with a large pool of candidate structures generated using traditional and/or MD-based refinement methods, the Kinetic Ensemble approach can be used to determine optimal subsets (Rangan et al. 2018; Bottaro and Lindorff-Larsen 2018) that collectively reflect not only the structure, but also the dynamics inherent in the NOE data. This approach can also be used to evaluate hypotheses about the relative rates of motions suggested by molecular dynamics simulations.
Furthermore, it is becoming increasingly common to determine structures with a combination of NOE and RDC data. These methods report on motion at different timescales and this study highlights the potential for them to conflict with one another if there is a substantial amount of motion slower than molecular tumbling. If there is sufficient RDC data to extract dynamical order parameters, incorporation of multiple exchange rates provides a means to reconcile the data from these two experiments.
For the quantification of protein dynamics, this approach would be particularly helpful for loop regions, where adjacent protons along the backbone or side chain could be used to directly probe loop flexibility. This would help discern between true dynamics and model uncertainty due to the lower number of medium- and long-range restraints often found in these regions. Furthermore, this could be used to quantify the motion of sidechains that don’t have a methyl group, such polar and charged amino acids critical for catalysis.
Work is currently underway to extend the Kinetic Ensemble approach to allow gradient-based optimization of atomic coordinates in molecular dynamics simulations. Beyond NOE data, the approach could be used to directly model not only the heteronuclear T1/T2 times used in fitting Lipari-Szabo order parameters, but also 1H T1/T2 times, which are typically more difficult to interpret because they depend so much on the large network of proton dipole–dipole interactions. We recently applied the Kinetic Ensemble approach to structurally interpret solid-state proton relaxation-dispersion data (Rovó et al. 2019), which is also sensitive to the proton interaction network. Furthermore, it could be used to better model other kinetically sensitive phenomena, like cross-correlated relaxation (CCR), or incorporate less timescale dependent data like residual dipolar couplings.
Methods
Ubiquitin sample preparation
The cDNA encoding Ubiquitin was expressed in Escherichia coli and the purification protocols were adopted as described earlier (Lazar et al. 1997). Isotopically-labeled (15N, or 15N/13C) and unlabeled Ubiquitin were produced following the same protocol. 15NH4Cl and [13C]-glucose (Cambridge Isotope Laboratories) were used as the sole sources of nitrogen and carbon, respectively.
NMR spectroscopy
The purified ubiquitin samples (15N, 15N/13C, or unlabeled) were used at a concentration of ~ 3 mM in 50 mM sodium phosphate (pH 6.5) containing 100 mM NaCl and 0.05% (w/v) sodium azide. All NMR experiments were carried out at 308 K on a Bruker Avance 900 MHz spectrometer with cryogenic probe. The experiments used for complete resonance assignment were as follows: 3D HNCACB, 3D HCCH-TOCSY, 3D 15N-edited NOESY-HSQC, and 3D 13C-edited NOESY-HSQC (Bax and Grzesiek 1993). A series of 2D [1H-1H]-NOESY experiments with mixing times varying from 5 to 500 ms (equally spaced intervals of 15 ms) were recoded with 300 and 1024 complex points along t1 and t2 dimensions, respectively. The same experiments with NOE mixing times of 80 ms, 155 ms, 215 ms, 305 ms, 410 ms and 500 ms were repeated for error calculation. All NMR data were processed using NMRPipe and analyzed with nmrDraw (Delaglio et al. 1995) and CARA (Keller 2004). CYANA (Güntert and Buchner 2015) was used for stereospecific assignment of 3D NOESY cross peaks. 3D NOE assignments were manually transferred to the 2D experiments and corresponding intensities were determined as a function of NOE mixing time to generate the NOE buildup curves.
Calculation of correlation functions and spectral densities with kinetic ensemble approach
The Kinetic Ensemble method starts with a matrix of transition rates between structures within an ensemble to directly determine correlation functions and spectral densities, from which NMR observables are calculated. An overview of the slower numerical method and a faster analytical solution is shown in Fig. S1. In a transition rate matrix, Q, the rate of a transition from state i to state j is represented by element qij, with i being the row index and j being the column index. The diagonal elements, qii, are defined \({{q}_{ii}}=-\underset{j\ne i}{\mathop \sum}\,{{q}_{ij}}\). The probabilities, pij(τ), of transitioning from state i to state j after a given lag time, τ, can be calculated using the matrix equation, \(P\left(\tau \right)={{e}^{\tau Q}}\). If a system is at a given state (si) at time t, and state (sj) at time t + τ, then one can define a correlation function \(C\left(\tau \right)=\underset{i,j}{\mathop \sum}\,{{\pi}_{i}}{{p}_{ij}}\left(\tau \right){{c}_{ij}}\), where πi is the equilibrium population of a state and cij represents the value of a function, c(si,sj), that gives the strength of the correlation between two different states. NMR observables can then be quantified by evaluating c(si,sj) as shown below.
In the case of NOE calculations, si is defined by the vector \(\overrightarrow {{r_{i} }}\), connecting two nuclei in state i. Given scalar xi, yi, and zi components of that vector and the internuclear distance ri, the cartesian dipole interaction tensor, Di, is defined:
The strength of the correlation for two states (dipole–dipole interaction) can then be calculated as follows:
To aid in computational efficiency, the Di tensor can be recast as a vector:
Such that the normalized trace of the matrix product is equal to the dot product of the vectors:
For the present work, an important property of both the matrix and vector representations of the interaction tensor is that the average value of \(\frac{1}{6}{\text{tr}}\left( {D_{i} D_{j} } \right)\) or \(\overrightarrow {{d_{i} }} \cdot \overrightarrow {{d_{j} }}\). enumerated over two sets of states is equal to applying the same operation once to the average tensor for each set:
This property, which is a straightforward extension of distributivity, enables much more rapid calculation of the correlation function exponential prefactors. It also makes gradient-based optimization computationally feasible, where the goodness of fit of a whole ensemble to NOE buildup data is differentiated with respect to kinetic or structural parameters.
The transition probability matrix, \(P\left( \tau \right) = e^{\tau Q}\), can be calculated by diagonalization of the matrix, \(Q = V \, \varLambda \, V^{ - 1}\), where V is a column matrix of the eigenvectors and Λ is a diagonal matrix with the corresponding eigenvalues. The exponential can then be evaluated \(P\left( \tau \right) = Ve^{\tau \varLambda } V^{ - 1}\). When incorporated into the internal correlation function, \(C_{\text{I}} \left( \tau \right) = \mathop \sum \limits_{i,j} {\mkern 1mu} \pi_{i} p_{ij} \left( \tau \right)c_{ij}\), this produces a multi-exponential decay, \(C_{\text{I}} \left( \tau \right) = \mathop \sum \limits_{i} {\mkern 1mu} a_{i} e^{{\lambda_{i} \tau }}\), with decay rates, −λi, coming from the indidual eigenvalues. The exponential prefactors, ai, associated with each rate can be calculated \(a_{i} = \mathop \sum \limits_{j} {\mkern 1mu} \pi_{j} v_{ji} \mathop \sum \limits_{k} {\mkern 1mu} v_{ik}^{ - 1} c_{jk}\), with \(v_{ji}\) being the element at row j, column i of \(V\). With regularly structured transition rate matrices, as used in this work, the eigenvalues are very often degenerate, and the exponential prefactors can be summed over the eigenvectors associated with a given eigenvalue. If Aλ is the square matrix formed by multiplying the columns of V by the rows of V−1 corresponding to the given eigenvalue, and Π is a diagonal matrix containing the equilibrium state populations, then the exponential prefactor can be calculated via the matrix operation, \(a_{\lambda } = \left( {\varPi A_{\lambda } } \right) \cdot C\). In that formula, standard matrix multiplication is used with Π and Aλ, from which the result is combined with C through the dot product operating over the individual matrix elements.
The rate matrices used in this work produce Aλ matrices with recognizable patterns (Fig. S2c, g). These can be expressed as a linear combination of matrices, Gi. The G matrices are structured such that the rows and columns can be reordered to create a block matrix where all rows and columns contain only a single block with nonzero elements. Even without reordering, this is true for all matrices shown in Fig. S2h except for G3, which requires reordering. The values of the G matrices are set such that all rows sum to 1. Because the group matrices separate states into blocks, it can be shown that \(\left( {\varPi G_{i} } \right) \cdot C = g_{i} = \mathop {\mathop \sum \limits^{{N_{i} }} }\limits_{j = 1} {\mkern 1mu} \frac{{N_{j} }}{N}\left| {\frac{1}{{N_{j} }}\mathop {\mathop \sum \limits^{{N_{j} }} }\limits_{k = 1} {\mkern 1mu} \overrightarrow {{d_{ijk} }} } \right|^{2}\), where N is the number of states, Ni is the number of nonzero blocks in matrix Gi,Nj is the number of states in block j, and \(\overrightarrow {{d_{ijk} }}\) is tensor k of block j of group i. Examples of this equality are shown in Fig. S2d, h. The exponential prefactors can then be rewritten as follows:
where NG is the number of group matrices and kλi is the coefficient associated with a given group matrix (usually a small positive or negative integer). Those coefficients are algorithmically determined from the structure of the rate matrix. While eigendecomposition of the rate matrices and construction of the corresponding Aλ and Gi matrices can be helpful in determining how this calculation should be conducted and validating that it is done correctly, in a production situation this is unnecessary, and the last expression of the above equation can be evaluated directly. This enables a dramatic speedup in the calculations, as eigendecomposition/matrix multiplication has a running time of approximately O(s3) and calculating all cij elements is O(s2), where s is the number of states in the transition rate matrix (i.e. the number of structures in the ensemble). In contrast, this method has a computational complexity of O(sl), where l is the number of unique eigenvalues. This enables the method to scale to very large ensembles. The largest used in this method is 176 members. As discussed below, for methyl–methyl interactions the ensemble is expanded to 1584 members (9 × 176), which would be computationally prohibitive with O(s3) scaling.
Once all aλ coefficients are determined, the spectral density function can be directly evaluated without first determining the correlation function. Taking into account molecular tumbling, assumed to be isotropic, the rotational correlation function is multiplied by the internal correlation function to give the full correlation function \(C\left( \tau \right) = e^{{ - \tau /\tau_{c} }} C_{\text{I}} \left( \tau \right) = e^{{ - \tau /\tau_{c} }} \mathop \sum \limits_{i} {\mkern 1mu} a_{i} e^{{\lambda_{i} \tau }}\). This expression can be simplified using modified eigenvalues, \(\lambda_{i}^{\prime } = \lambda_{i} - 1/\tau_{c}\), making the final correlation function \(C\left( \tau \right) = \mathop \sum \limits_{i} {\mkern 1mu} a_{i} e^{{\lambda_{i}^{\prime } \tau }}\). Fourier transformation of that gives the spectral density function, \(J\left(\omega \right)=-2\underset{i}{\mathop \sum}\,{{a}_{i}}\lambda_{i}^{\prime}/\left(\lambda {{_{i}^{\prime}}^{2}}+{{\omega}^{2}} \right)\). By making the substitution, \(\lambda_{i}^{\prime } = - 1/\tau_{i}^{\prime }\), that expression can be rearranged to \(J\left( \omega \right)=2\underset{i}{\mathop{\sum }}\,{{a}_{i}}\tau_{i}^{\prime }/\left( 1+{{\omega }^{2}}\tau_{i}^{\prime 2} \right)\), which is a generalization of the extended model free spectral density. In the regime where J(0) dominates, \(J\left( 0 \right) = 2\mathop \sum \limits_{i} {\mkern 1mu} a_{i} \tau_{i}^{\prime }\), and the NOE cross relaxation rate is directly proportional to the time constants (\(\tau_{i}^{\prime}\)) associated with molecular motions and the ai coefficients. One of the key advancements made in tinetic Ensemble method is an efficient analytical method to rigorously calculate \(J\left(\omega \right)\) from a temporally partitioned structural ensemble. The magnitude of the coefficients (\({{a}_{i}}\)) are determined by the extent of additional orientational dynamics arising from motions at a given timescale, convoluted with simultaneous changes in internuclear distances.
Methyl and aromatic group rotation
For computational simplicity, many structural modeling programs do not explicitly sample symmetrical hydrogen arrangements on methyl or aromatic groups. However, these structural rearrangements can play a significant role in observed NOE data. These motions can be addressed through either explicit modeling of the rotations or the use of pseudoatoms (Koning et al. 1990; Liu et al. 1992). In this work, we enumerate these rotations by expanding the ensemble to include relabeled methyl and aromatic group atoms and using an expanded transition rate matrix. For a methyl group, the algorithm does the equivalent of tripling the number of ensemble members and then relabeling the methyl atoms such that they hop between three possible conformations. The kinetics of the rotations are modelled using 2 × 2 (aromatic) or 3 × 3 (methyl) transition rate matrices, Qr, in which individual transition rates are set to 1/(2τaromatic) or 1/(3τmethyl), respectively. Because the rotations are treated as being kinetically independent from other protein motions, the overall transition rate matrix, Qo, is calculated using the Kronecker sum of the input and rotation rate matrices, Qo = Q ⊕ Qr. Interactions between atoms on two different rotation groups are handled by additional enumeration. In the present work τaromatic was fixed at 100 µs and τmethyl was fixed at 1 ps. The correlation with NOE data plateaus around those values (Fig. S3), which are also consistent with previously determined timescales of 1 µs–100 ms for aromatic groups (Weininger et al. 2014) and 1–100 ps for methyl groups (Xue et al. 2007).
Calculating spectral intensities
Where necessary, input structures and ensembles were protonated with Reduce (Word et al. 1999). No pseudoatoms were used in the calculations. Spectral densities for all proton dipole–dipole interactions were calculated as described above, including those between equivalent atoms in methyl/aromatic groups. Using those spectral densities, the relaxation matrix, R, was calculated using the well-established Solomon equations (Brüschweiler and Case 1994). Fractional magnetization transfer between protons for a given mixing time, τm, was calculated using the matrix exponential \({{e}^{{{t}_{m}}R}}\). Theoretical NOE intensities between sets of indistinguishable nuclei were determined by summing blocks of the resulting matrix. Where applicable in the Results section, we refer to this summed fractional magnetization transfer using pseudoatom (Q) notation. For crystal structures where there were multiple alternate conformations of atoms available, separate models were created corresponding to each of the alternate conformations, and the structure was scored as an ensemble.
Evaluating goodness of fit
NOE intensities calculated using the Kinetic Ensemble method are typically expressed as fractional magnetization transfer from one nucleus to another. Because the appropriate scaling factor between those values and the experimentally measured NOE intensities is not known a priori, we use an uncentered correlation coefficient, \({{R}_{\text{u}}}\), to determine the goodness of fit. In the uncentered form, the mean values of each set of data are set to zero such that the formula reduces to \({{R}_{\text{u}}}=xy/\sqrt{{{x}^{2}}{{y}^{2}}}\). This has the desired effect of penalizing deviations from a zero y-intercept. However, it is important to note that the uncentered correlation coefficient is higher than the ordinary Pearson correlation coefficient.
Optimization of timescales
Once the correlation function exponential prefactors (\({{a}_{i}}\)) have been calculated for all of the dipole–dipole interactions in a given ensemble, the overall exchange rates (\({{k}_{i}}\)) can be optimized independently of those prefactors. Depending on how a rate matrix is constructed, the eigenvalues (\({{\lambda}_{i}}\)) represent either a single exchange timescale or multiple exchange timescales. For instance, in Fig. S2a, b, the unique eigenvalues each reflect distinct rates, with \(\lambda_{1} = - \;k_{\text{s}}\) and \(\lambda_{2} = \lambda_{3} = - \;k_{\text{f}}\). However, in Fig. S2e, f, one of the unique eigenvalues represents the sum of the exchange rates, with \(\lambda_{3} = - \;(k_{\text{s}} + k_{\text{f}} )\). This happens when the rate matrix is constructed from the Kronecker sum of other rate matrices, as is done for methyl and aromatic group rotation.
Optimization of kinetic coordinates requires determining the gradient of the goodness of fit with respect to the coordinates, \(\partial {{R}_{\text{u}}}/\partial {{\tau}_{i}}\) in the case of the timescales. The most computationally challenging aspect of that calculation is the derivative of \(e^{{\tau_{m} R}}\), where \(\tau_{m}\) is the NOE mixing time and R is the dipole–dipole relaxation matrix (Yip and Case 1989). The computation of this derivative has been previously described (Yip and Case 1989; Jennrich and Bright 1976; Kalbfleisch and Lawless 1985), and involves diagonalization of R and the determination of the derivative of individual elements of R with respect to either the kinetic coordinates. The currently implemented version of the algorithm uses the earlier matrix form of the derivative (Jennrich and Bright 1976; Kalbfleisch and Lawless 1985), which does not take advantage of the sparsity of detectable NOE cross peaks that can significantly reduce the computational cost (Yip and Case 1989). That optimization will be incorporated in future versions of the algorithm. Using \(R_{\text{u}} \left( {\tau_{i} } \right)\) and \(\partial R_{\text{u}} /\partial \tau_{i}\), the timescales are then numerically optimized with the L-BFGS-B algorithm.
Current assumptions
In its current form, the Kinetic Ensemble approach assumes the following have a negligible effect: non-uniform initial magnetization, anisotropic molecular tumbling, dependence of molecular tumbling on internal motions, and solvent hydrogen exchange (e.g. for amide or hydroxyl-protons). The treatment of many of these will be addressed in future work. In that regard, adapting complementary ideas from the eNOE approach to determine initial magnetization would be particularly helpful.
Ensemble subselection
Subensembles were selected from the EROS3 ensemble starting from random ensembles in which each member was either included or excluded with an even probability, resulting in an initial size of approximately 88 members. In successive rounds each of the 176 members had its status as included or excluded swapped one at a time, after which τc and τensemble were optimized using gradient based minimization from their previously optimal values. After evaluating the 176 swaps, the one resulting in the greatest improvement in Ru was accepted. Further rounds of swaps were attempted in the same way until swapping no longer improved the fit to experimental data. To construct the random reference ensembles shown in red on Fig. 5, random subensembles were chosen with the same distribution of sizes as the NOE selected ensembles.
References
Bax A, Grzesiek S (1993) Methodological advances in protein NMR. Acc Chem Res 26:131–138
Boelens R, Koning TMG, Kaptein R (1988) Determination of biomolecular structures from proton-proton NOE’s using a relaxation matrix approach. J Mol Struct 173:299–311
Bonvin AMJJ, Boelens R, Kaptein R (1991) Direct NOE refinement of biomolecular structures using 2D NMR data. J Biomol NMR 1:305–309
Bonvin AM, Rullmann JA, Lamerichs RM, Boelens R, Kaptein R (1993) “Ensemble” iterative relaxation matrix approach: a new NMR refinement protocol applied to the solution structure of crambin. Proteins 15:385–400
Borgias BA, James TL (1988) COMATOSE, a method for constrained refinement of macromolecular structure based on two-dimensional nuclear overhauser effect spectra. J Magn Reson 1969(79):493–512
Bottaro S, Lindorff-Larsen K (2018) Biophysical experiments and biomolecular simulations: a perfect match? Science 361:355–360
Brueschweiler R, Roux B, Blackledge M, Griesinger C, Karplus M, Ernst RR (1992) Influence of rapid intramolecular motion on NMR cross-relaxation rates. A molecular dynamics study of antamanide in solution. J Am Chem Soc 114:2289–2302
Brüschweiler R, Case DA (1994) Characterization of biomolecular structure and dynamics by NMR cross relaxation. Progr Nucl Magn Reson Spectrosc 26:27–58
Capelli R, Tiana G, Camilloni C (2018) An implementation of the maximum-caliber principle by replica-averaged time-resolved restrained simulations. J Chem Phys 148:184114
Chalmers G, Glushka JN, Foley BL, Woods RJ, Prestegard JH (2016) Direct NOE simulation from long MD trajectories. J Magn Reson 265:1–9
Chen Y, Campbell SL, Dokholyan NV (2007) Deciphering protein dynamics from NMR data using explicit structure sampling and selection. Biophys J 93:2300–2306
Chi CN, Vögeli B, Bibow S, Strotz D, Orts J, Güntert P, Riek R (2015) A structural ensemble for the enzyme cyclophilin reveals an orchestrated mode of action at atomic resolution. Angew Chem Int Ed Engl 54:11657–11661
Clore GM, Driscoll PC, Wingfield PT, Gronenborn AM (1990) Analysis of the backbone dynamics of interleukin-1 beta using two-dimensional inverse detected heteronuclear 15 N-1H NMR spectroscopy. Biochemistry 29:7387–7401
Cornilescu G, Marquardt JL, Ottiger M, Bax A (1998) Validation of protein structure from anisotropic carbonyl chemical shifts in a dilute liquid crystalline phase. J Am Chem Soc 120:6836–6837
Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A (1995) NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR 6:277–293
Fares C, Lakomek N-A, Walter KFA, Frank BTC, Meiler J, Becker S, Griesinger C (2009) Accessing ns-mu s side chain dynamics in ubiquitin with methyl RDCs. J Biomol NMR 45:23–44
Fenwick RB, Esteban-Martín S, Richter B, Lee D, Walter KF, Milovanovic D, Becker S, Lakomek NA, Griesinger C, Salvatella X (2011) Weak long-range correlated motions in a surface patch of ubiquitin involved in molecular recognition. J Am Chem Soc 133:10336–10339
Frank AT, Stelzer AC, Al-Hashimi HM, Andricioaei I (2009) Constructing RNA dynamical ensembles by combining MD and motionally decoupled NMR RDCs: new insights into RNA dynamics and adaptive ligand recognition. Nucleic Acids Res 37:3670–3679
Güntert P, Buchner L (2015) Combined automated NOE assignment and structure calculation with CYANA. J Biomol NMR 62:453–471
Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D (2007) A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature 450:913–916
Jennrich RI, Bright PB (1976) Fitting systems of linear differential equations using computer generated exact derivatives. Technometrics 18:385–392
Kalbfleisch JD, Lawless JF (1985) The analysis of panel data under a markov assumption. J Am Stat Assoc 80:863–871
Kay LE, Torchia DA, Bax A (1989) Backbone dynamics of proteins as studied by 15 N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry 28:8972–8979
Keepers JW, James TL (1984) A theoretical study of distance determinations from NMR Two-dimensional nuclear overhauser effect spectra. J Magn Reson 57:404–426
Keller R (2004) The computer aided resonance assignment tutorial. Cantina Verlag, Goldau
Koning TMG, Boelens R, Kaptein R (1990) Calculation of the nuclear overhauser effect and the determination of proton-proton distances in the presence of internal motions. J Magn Reson 1969(90):111–123
Lakomek NA, Walter KF, Farès C, Lange OF, de Groot BL, Grubmüller H, Brüschweiler R, Munk A, Becker S, Meiler J, Griesinger C (2008) Self-consistent residual dipolar coupling based model-free analysis for the robust determination of nanosecond to microsecond protein dynamics. J Biomol NMR 41:139–155
Lange OF, Lakomek NA, Fares C, Schröder GF, Walter KF, Becker S, Meiler J, Grubmüller H, Griesinger C, de Groot BL (2008) Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science 320:1471–1475
Lazar GA, Desjarlais JR, Handel TM (1997) De novo design of the hydrophobic core of ubiquitin. Protein Sci 6:1167–1178
Lechtenberg BC, Rajput A, Sanishvili R, Dobaczewska MK, Ware CF, Mace PD, Riedl SJ (2016) Structure of a HOIP/E2 ~ ubiquitin complex reveals RBR E3 ligase mechanism and regulation. Nature 529:546–550
Lee AL, Flynn PF, Wand AJ (1999) Comparison of 2H and 13C NMR relaxation techniques for the study of protein methyl group dynamics in solution. J Am Chem Soc 121:2891–2902
LeMaster DM, Kay LE, Brünger AT, Prestegard JH (1988) Protein dynamics and distance determination by NOE measurements. FEBS Lett 236:71–76
Lewandowski JR, Halse ME, Blackledge M, Emsley L (2015) Protein dynamics. Direct observation of hierarchical protein dynamics. Science 348:578–581
Lindorff-Larsen K, Best RB, Depristo MA, Dobson CM, Vendruscolo M (2005) Simultaneous determination of protein structure and dynamics. Nature 433:128–132
Lipari G, Szabo A (1982) A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J Am Chem Soc 104:4546–4559
Liu H, Thomas PD, James TL (1992) Averaging of cross-relaxation rates and distances for methyl, methylene, and aromatic ring protons due to motion or overlap. Extraction of accurate distances iteratively via relaxation matrix analysis of 2D NOE spectra. J Magn Reson 1969(98):163–175
Liu S, Chen Y, Li J, Huang T, Tarasov S, King A, Weissman AM, Byrd RA, Das R (2012) Promiscuous interactions of gp78 E3 ligase CUE domain with polyubiquitin chains. Structure 20:2138–2150
Maltsev AS, Grishaev A, Roche J, Zasloff M, Bax A (2014) Improved cross validation of a static ubiquitin structure derived from high precision residual dipolar couplings measured in a drug-based liquid crystalline phase. J Am Chem Soc 136:3752–3755
Massi F, Grey MJ, Palmer AG (2005) Microsecond timescale backbone conformational dynamics in ubiquitin studied with NMR R1rho relaxation experiments. Protein Sci 14:735–742
Montalvao RW, De Simone A, Vendruscolo M (2012) Determination of structural fluctuations of proteins from structure-based calculations of residual dipolar couplings. J Biomol NMR 53:281–292
Morgan MT, Haj-Yahya M, Ringel AE, Bandi P, Brik A, Wolberger C (2016) Structural basis for histone H2B deubiquitination by the SAGA DUB module. Science 351:725–728
Peter C, Daura X, van Gunsteren WF (2001) Calculation of NMR-relaxation parameters for flexible molecules from molecular dynamics simulations. J Biomol NMR 20:297–310
Peters JH, de Groot BL (2012) Ubiquitin dynamics in complexes reveal molecular recognition mechanisms beyond induced fit and conformational selection. PLoS Comput Biol 8:e1002704
Post CB, Meadows RP, Gorenstein DG (1990) On the evaluation of interproton distances for three-dimensional structure determination by NMR using a relaxation rate matrix analysis. J Am Chem Soc 112:6796–6803
Rangan R, Bonomi M, Heller GT, Cesari A, Bussi G, Vendruscolo M (2018) Determination of structural ensembles of proteins: restraining vs reweighting. J Chem Theory Comput 14:6632–6641
Richter B, Gsponer J, Várnai P, Salvatella X, Vendruscolo M (2007) The MUMO (minimal under-restraining minimal over-restraining) method for the determination of native state ensembles of proteins. J Biomol NMR 37:117–135
Rovó P, Smith CA, Gauto D, de Groot BL, Schanda P, Linser R (2019) Mechanistic insights into microsecond time-scale motion of solid proteins using complementary 15 N and 1H relaxation dispersion techniques. J Am Chem Soc 141:858–869
Sabo TM, Bakhtiari D, Walter KF, McFeeters RL, Giller K, Becker S, Griesinger C, Lee D (2012) Thermal coefficients of the methyl groups within ubiquitin. Protein Sci 21:562–570
Salvi N, Abyzov A, Blackledge M (2016) Multi-timescale dynamics in intrinsically disordered proteins from NMR relaxation and molecular simulation. J Phys Chem Lett 7:2483–2489
Schreiner P, Chen X, Husnjak K, Randles L, Zhang N, Elsasser S, Finley D, Dikic I, Walters KJ, Groll M (2008) Ubiquitin docking at the proteasome through a novel pleckstrin-homology domain interaction. Nature 453:548–552
Smith CA, Ban D, Pratihar S, Giller K, Schwiegk C, de Groot BL, Becker S, Griesinger C, Lee D (2015) Population shuffling of protein conformations. Angew Chem Int Ed Engl 54:207–210
Smith CA, Ban D, Pratihar S, Giller K, Paulat M, Becker S, Griesinger C, Lee D, de Groot BL (2016) Allosteric switch regulates protein-protein binding through collective motion. Proc Natl Acad Sci USA 113:3269–3274
van Dijk AD, Fushman D, Bonvin AM (2005) Various strategies of using residual dipolar couplings in NMR-driven protein docking: application to Lys48-linked di-ubiquitin and validation against 15N-relaxation data. Proteins 60:367–381
Vasile F, Tiana G (2019) Determination of structural ensembles of flexible molecules in solution from NMR data undergoing spin diffusion. J Che Infor Model 59(6):2973–2979
Vögeli B, Segawa TF, Leitz D, Sobol A, Choutko A, Trzesniak D, van Gunsteren W, Riek R (2009) Exact distances and internal dynamics of perdeuterated ubiquitin from NOE buildups. J Am Chem Soc 131:17215–17225
Vögeli B, Friedmann M, Leitz D, Sobol A, Riek R (2010) Quantitative determination of NOE rates in perdeuterated and protonated proteins: practical and theoretical aspects. J Magn Reson 204:290–302
Vögeli B, Kazemi S, Güntert P, Riek R (2012) Spatial elucidation of motion in proteins by ensemble-based structure calculation using exact NOEs. Nat Struct Mol Biol 19:1053–1057
Vögeli B, Olsson S, Güntert P, Riek R (2016) The exact noe as an alternative in ensemble structure determination. Biophys J 110:113–126
Wan H, Zhou G, Voelz VA (2016) A maximum-caliber approach to predicting perturbed folding kinetics due to mutations. J Chem Theory Comput 12:5768–5776
Weininger U, Modig K, Akke M (2014) Ring flips revisited: (13)C relaxation dispersion measurements of aromatic side chain dynamics and activation barriers in basic pancreatic trypsin inhibitor. Biochemistry 53:4519–4525
Williamson MP, Havel TF, Wüthrich K (1985) Solution conformation of proteinase inhibitor IIA from bull seminal plasma by 1H nuclear magnetic resonance and distance geometry. J Mol Biol 182:295–315
Word JM, Lovell SC, Richardson JS, Richardson DC (1999) Asparagine and glutamine: using hydrogen atom contacts in the choice of side-chain amide orientation. J Mol Biol 285:1735–1747
Xue Y, Pavlova MS, Ryabov YE, Reif B, Skrynnikov NR (2007) Methyl rotation barriers in proteins from 2H relaxation data Implications for protein structure. J Am Chem Soc 129:6827–6838
Yip P, Case DA (1989) A new method for refinement of macro molecular structures based on nuclear overhauser effect spectra. J Magn Reson 83:643–648
Acknowledgements
Open access funding provided by Max Planck Society. This work was supported by the Max Planck Society, the European Union (European Research Council Grant Agreement 233227 to C.G.), and the Alexander von Humboldt Foundation (C.A.S.).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Smith, C.A., Mazur, A., Rout, A.K. et al. Enhancing NMR derived ensembles with kinetics on multiple timescales. J Biomol NMR 74, 27–43 (2020). https://doi.org/10.1007/s10858-019-00288-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10858-019-00288-8