Fast evaluation of protein dynamics from deficient ¹⁵N relaxation data

Abstract

Simple and convenient method of protein dynamics evaluation from the insufficient experimental ¹⁵N relaxation data is presented basing on the ratios, products, and differences of longitudinal and transverse ¹⁵N relaxation rates obtained at a single magnetic field. Firstly, the proposed approach allows evaluating overall tumbling correlation time (nanosecond time scale). Next, local parameters of the model-free approach characterizing local mobility of backbone amide N–H vectors on two different time scales, S² and R _ex , can be elucidated. The generalized order parameter, S², describes motions on the time scale faster than the overall tumbling correlation time (pico- to nanoseconds), while the chemical exchange term, R _ex , identifies processes slower than the overall tumbling correlation time (micro- to milliseconds). Advantages and disadvantages of different methods of data handling are thoroughly discussed.

Introduction

Analysis of nuclear magnetic relaxation provides insight into the molecular motions of proteins (Palmer 2004; Mayo and Daragan 2005; Ejchart 2007; Charlier et al. 2016; Lisi and Loria 2016). One of the most successful and widely used approaches to the analysis of relaxation data is the model-free approach, MFA (Lipari and Szabo 1982). Two other model-independent descriptions of the internal molecular motions have been developed independently: the two-step model (Halle and Wennerström 1981) and the slowly relaxing local structure model (Tugarinov et al. 2001). In the frame of the MFA, local mobility is described by two parameters, the generalized order parameter, S², which corresponds to the spatial freedom of motion, and the internal correlation time, τ_int, corresponding to the rate of this motion in the pico- to nanosecond time scale, which is smaller than the single correlation time describing an isotropic overall molecular tumbling, τ _R . The additional term, R _ex , accounts for the conformational exchange contribution to R₂ resulting from processes in the micro- to millisecond time scale, often referred to as chemical exchange effects (Stone et al. 1992; Korzhnev et al. 2001).

The most frequently measured protein relaxation parameters are the longitudinal, R₁, and transverse, R₂, relaxation rates of backbone amide ¹⁵N nuclei complemented with ¹⁵N-{¹H} NOEs (Palmer 2004; Reddy and Rainey 2010). Nuclear magnetic relaxation measurements are long lasting, their data reduction is demanding, and interpretation of the results complex (Zhukov and Ejchart 1999; Pawley et al. 2006; Jaremko et al. 2015). Especially NOE measurements are very time consuming owing to their inherently low sensitivity (Fushman 2003) and susceptibility to systematic errors resulting from not fully relaxed spectra and/or saturation transfer due to the exchange with water protons (Ferrage et al. 2008; Gong and Ishima 2007; Grzesiek and Bax 1993; Renner et al. 2002). So it often happens that limited relaxation data (e.g., R₁ and R₂ at a single magnetic field), precluding the determination of all MFA parameters, are solely available. Then, commonly used procedure is to examine the ratio between transverse and longitudinal rates, R₂/R₁, for the estimation of global isotropic correlation time of a protein (Kay et al. 1989). As a prerequisite this procedure requires an efficient rejection from calculation the residues exhibiting skewed R₂/R₁ values owing to intense fast local motions and/or slow conformational exchange. Residues with an NOE (if available) < 0.6 are usually excluded, since in this case the internal motions are likely to skew significantly the R₂/R₁ value. Usually such residues exhibit low experimental R₂/R₁ values. On the other hand, residues undergoing conformational exchange are characterized by high R₂/R₁ values. Routine method of appropriate residue selection can be done by excluding those residues with a R₂/R₁ value outside of ± 1 standard deviation of the mean (Clore et al. 1990).

With the τ _R already estimated, three methods of further analysis of limited relaxation data were independently developed. One of them is based on the observation that one of the MFA parameters, the generalized order parameter, S², can be extracted with a reasonable accuracy from a linear combination of relaxation rates, 2R₂ − R₁ (Habazettl and Wagner 1995). Another method investigates the product of relaxation rates R₁R₂ also giving access to the S² parameter (Kneller et al. 2002). The last method of the S² parameter extraction from R₁ and R₂, measured with the CEST technique to save experimental time and named lean MFA (LMFA), relies on the least squares minimization (Gu et al. 2016). Since all these methods base on the determination of the overall correlation time τ _R from the R₂/R₁ ratio an appropriate data selection seems to be crucial. Therefore, it was proposed to use for this purpose the product of relaxation rates R₁R₂ and claimed that in contrary to the R₂/R₁ ratio, the former allows to distinguish between the effects of motional anisotropy and chemical exchange (Kneller et al. 2002). For convenience, R₂/R₁, 2R₂ − R₁, and R₁R₂ will be further denoted as Q, D, and P, respectively.

This paper describes a comparative analysis of three mentioned above combinations of relaxation rates, which allows to select the optimal method of the MFA parameter elucidation from deficient relaxation data. The utility of this approach is presented by applying it to the relaxation data of four proteins of different size: immunoglobulin-binding domain of streptococcal protein G, GB1 (Idiyatullin et al. 2003), human ubiquitin (Lee and Wand 1999), human S100A1 calcium binding protein in apo state (Nowakowski et al. 2011), and β-lactamase PSE-4 (Morin and Gagné 2009). First limited use of this approach was applied to the ¹⁵N relaxation rates of BacSp222 peptide (Nowakowski et al. 2018).

Method

Equations describing relaxation rates of ¹⁵N nuclei relaxing by dipolar and chemical shift anisotropy mechanisms in terms of spectral density functions are given as (Abragam 1989; Korzhnev et al. 2001):

$${R_1}=\frac{1}{4}{d^2}\left[ {J\left( {{\omega _H} - {\omega _N}} \right)+3J\left( {{\omega _N}} \right)+6J\left( {{\omega _H}+{\omega _N}} \right)} \right]+\frac{1}{3}{c^2}J\left( {{\omega _N}} \right)$$

(1)

$${R_2}=\frac{1}{8}{d^2}\left[ {4J\left( 0 \right)+J\left( {{\omega _H} - {\omega _N}} \right)+3J\left( {{\omega _N}} \right)+6J\left( {{\omega _H}} \right)+6J\left( {{\omega _H}+{\omega _N}} \right)} \right]+\frac{1}{{18}}{c^2}\left[ {4J(0)+3J({\omega _N})} \right]+{R_{ex}}$$

(2)

where $d=\frac{{{\mu _0}}}{{8{\pi ^2}}}\frac{{{\gamma _N}{\gamma _H}h}}{{\left\langle {r_{{NH}}^{3}} \right\rangle }},\quad c={\omega _N}\Delta \sigma$ and other symbols have their usual meaning. It has to be mentioned that in all calculations the vibrationally averaged N–H distance, r_NH = 1.04 Å (Ottiger and Bax 1998) and the chemical shift anisotropy of the ¹⁵N chemical shift tensor Δδ = − 170 ppm (Yao et al. 2010) were used.

The conformational exchange contribution to the transverse relaxation rate, R _ex , is proportional to the square of the ¹⁵N Larmor frequency, ω _N . This term can be written as ${R_{ex}}=\Phi \omega _{N}^{2}$ (Peng and Wagner 1995). The proportionality factor Φ represents the effectiveness of conformational exchange processes and is independent on magnetic field strength facilitating direct comparison of chemical exchange terms determined at different magnetic field strengths for different proteins.

Model-free approach spectral density function takes the form (Lipari and Szabo 1982):

$$J\left( \omega \right)=\frac{2}{5}\left[ {\frac{{{S^2}{\tau _R}}}{{1+{{\left( {\omega {\tau _R}} \right)}^2}}}+\frac{{\left( {1 - {S^2}} \right)\tau }}{{1+{{\left( {\omega \tau } \right)}^2}}}} \right]$$

(3)

where ${\tau ^{ - 1}}=\tau _{R}^{{ - 1}}+\tau _{{\operatorname{int} }}^{{ - 1}}$. Performing the complete MFA analysis of relaxation data for N-residue protein one has to determine 3N local parameters, S², τ_int, and R _ex for each residue. Additionally one global parameter τ _R or six parameters characterizing either isotropic or fully anisotropic overall tumbling, respectively, have to be determined. Extension of the spectral density function for isotropic motion (Eq. 3) to the anisotropic one, based on the formalism developed by Woessner (1962), was implemented to the protein relaxation studies (Tjandra et al. 1995; Baber et al. 2001). Allowing for the positive degree of freedom of a computational task it means that besides R₁, R₂, and ¹⁵N-{¹H} NOE at a single magnetic field, at least one additional set of relaxation parameters has to be measured. It happens, however, that the number of available relaxation data is insufficient, due to sample instability or lack of experimental time and additional data processing has to be applied (Jaremko et al. 2014). Often only R₁ and R₂ relaxation rates at a single magnetic field are at one’s disposal.

A joined analysis of Q = R₂/R₁ and D = 2R₂ − R₁ or P = R₁R₂ values allows obtaining semi-quantitative insight into the protein dynamics owing to the different relations of these quantities to the MFA parameters and, therefore, untangling these parameters from experimental data. The Q parameter is quasi-insensitive to both local MFA parameters, S² and τ_int, in a reasonably broad range of their values (Fig. 1A, B). Therefore, it is well suited for the evaluation of the overall tumbling correlation times of proteins comprising residues with diverse local mobility. On the other hand, the P values are quasi-insensitive to τ_int but decrease considerably with the increased amplitude of local motions, as manifested at smaller values of the S² order parameter (Fig. 1B). The D parameter is even less sensitive to τ_int changes than Q and P, but it displays a modest sensitivity to S² changes. All three quantities, Q, D, and P, are sensitive to the chemical exchange term and increase with the R _ex enlargement (Fig. 1C). Simultaneous effect of S² and τ_int, changes on Q, P and D is shown in Figs. S1–S3 (Supporting Information). One has to be aware of the opposite effects of fast (ps–ns) and slow (µs–ms) motions on the P values. Both these effects can compensate one another leaving the P value unchanged and, thus, hiding chemical exchange effect. The D values are also sensitive to such compensation. They are, however, less sensitive to fast motions and more sensitive to slow ones than P values and, therefore, should retain at least partially the ability of detection of R _ex terms.

Fig. 1

Calculated relationships between normalized Q, D, and P quantities and local parameters of MFA. The presented quantities are normalized in relation to their counterparts in rigid molecules. A Q(τ_int), D(τ_int), and P(τ_int) functions with S² = 0.85 and R _ex  = 0. B Q(S²), D(S²), and P(S²) functions with τ_int = 50 ps and R _ex  = 0. C Q(R _ex ), D(R _ex ), and P(R _ex ) with τ_int = 50 ps and S² = 0.85. Additional input data: τ_R = 5 ns and B₀ = 16.4 T were used in all calculations. Take note that Q and P are superposed in part C

Use of Q, D, and P values in the analysis of a backbone protein dynamics requires several simplifying assumptions bearing a number of consequences. It has been noticed (Peng and Wagner 1992) that the spectral density functions at three highest frequencies J(ω _H  + ω _N ), J(ω _H ), and J(ω _H  − ω _N ) are only a small fraction of two other component J(0) and J(ω _N ) and can be neglected in Eqs. (1) and (2) describing D values (Habazettl and Wagner 1995) or P values (Kneller et al. 2002). As a result following expressions can be written:

$$Q=\frac{2}{3}\frac{{J(0)}}{{J({\omega _N})}}+\frac{1}{2}$$

(4a)

$$D={A_1}J(0)$$

(4b)

$$P={A_2}J(0)J({\omega _N})+{A_3}{[J({\omega _N})]^2}$$

(4c)

$${\text{where }}{A_1}=\left( {{d^2}+\frac{4}{9}{c^2}} \right);{\text{ }}{A_2}=6{\left( {\frac{{{d^2}}}{4}+\frac{{{c^2}}}{9}} \right)^2};{\text{ }}{A_3}=\frac{1}{2}{\left( {\frac{3}{4}{d^2}+\frac{1}{3}{c^2}} \right)^2}$$

In the approach utilizing the Q ratio for the estimation of global correlation time, the assumption τ_int = 0.0 is made resulting in a simplified spectral density function (Kay et al. 1989).

$$J(\omega )=\frac{2}{5}\left[ {\frac{{{S^2}{\tau _R}}}{{1+{{(\omega {\tau _R})}^2}}}} \right]$$

(5)

In order to obtain so estimated global correlation time, τ _R (Q), one has to compute it from Eq. (8) given by Kay et al. (1989). Additionally, neglecting second term in Eq. (4c) and assuming ${({\omega _N}{\tau _R})^2}>>1$ one obtains:

$$Q=\frac{2}{3}{\left( {{\omega _N}{\tau _R}} \right)^2}+\frac{1}{2}$$

(6a)

$$D={A_1}{S^2}{\tau _R}$$

(6b)

$$P={A_2}{\left( {\frac{{{S^2}}}{{{\omega _N}}}} \right)^2}$$

(6c)

Use of the Q values in the evaluation of an overall correlation time results in the τ_R underestimation provided the overall tumbling is isotropic (Korzhnev et al. 1997). Influence of the input τ_R and magnetic field strength values on the value of the apparent τ_R is demonstrated in Fig. 2. In the utmost situations (parts of plots below the dashed line in the Fig. 2 corresponding to intense internal motion: S² = 0.7, τ_int = 100 ps, slow overall tumbling: τ_R = 32 ns and very high magnetic field: 23.5 T) the τ_R evaluation derived from the Q values breaks down; relative errors exceed 25%. Use of Q values retains the sense only if correlation time of internal motion, τ_int, is short and its amplitude small (Fig. S4).

Fig. 2

Normalized values of apparent τ_R evaluated from the Q values, given as a fraction of the synthetic τ_R used in simulations. The τ_R,app/τ_R ratio is shown as a function of B₀ for several τ_R values. Calculations were performed applying sizeable internal motion: S² = 0.7 and τ_int = 100 ps. Performance of the Q-based method is poor for B₀ and τ_R corresponding to plots below the dashed line marking 15% deviation of τ_R,app

In the case of anisotropic tumbling, the determined value of the orientation averaged overall correlation time τ_R = 0.5/(D₁ + D₂ + D₃), can be either larger or smaller than the τ_R value estimated from Q values, depending on the orientation of the N–H vector. Appropriate comparison is presented in Table 1 and Fig. 3.

Table 1 Anisotropic tumbling visibly influences on the Q and D values, while its effect is strongly attenuated regarding P values, with variability ranges 25, 19, and 3%, respectively

Fig. 3

Molecular tumbling is anisotropic (prolate ellipsoid $\left\langle {{\tau _{\text{R}}}} \right\rangle$ = 8 ns, ΔD = 1.5 and η = 0). A sizeable internal motion is assumed: S² = 0.8 and τ_int = 100 ps. The τ_R estimated from the derived Q value can deviate significantly from the expected value of 8 ns marked by a horizontal black line. The deviations depend on the N–H vector orientation relative to the unique axis of diffusion tensor given by an angle α. Deviations depend on the magnetic field strength (red and blue circles). Field dependence nearly disappears for rigid N–H vector (S² = 1.0; red and blue triangles). The tendency of τ _R (α) dependence for oblate ellipsoid ($\left\langle {{\tau _{\text{R}}}} \right\rangle$ = 8 ns, ΔD = 0.67 and η = 0) is opposite in comparison with a prolate ellipsoid (red and blue squares)

Estimation of the average generalized order parameters $S_{{av}}^{2}$ from the experimentally observed P values was proposed by Kneller et al. (2002) using formula:

$$S_{{av}}^{2}=\sqrt {\frac{{\left\langle P \right\rangle }}{{{P_{\hbox{max} }}}}} ,$$

where $\left\langle P \right\rangle$ is experimentally observed 10% trimmed mean value and P_max is determined from the relaxation parameters calculated for a rigid molecule (S² = 1.0, R _ex  = 0.0) which reorients with τ_R(Q). This formula results directly from Eq. (6c). Use of medians is superior to the trimmed mean values since the distributions of Q, D, and P data are most commonly non gaussian (Table S1) and robust statistics has to be used in their description (Maronna et al. 2006). Medians allow not only avoiding influence of outliers but also eliminating residues from the unstructured segments of protein characterized by inherently small Q values and resulting in extremely skewed Q distributions. Robust statistics also facilitates identifying residues undergoing chemical exchange as outliers in Q, D, and P sets. In the following text Q, D, and P medians are solely used and denoted as $\tilde {Q}$, $\tilde {D}$, and $\tilde {P}$. Therefore, the Kneller et al. formula is rewritten as

$$S_{{av}}^{2}=\sqrt {\frac{{\tilde {P}}}{{{P_{\hbox{max} }}}}}$$

(7)

This approach is also extended to the estimation of site specific generalized order parameters, $S_{i}^{2}$ utilizing either D or P values:

$$S_{i}^{2}=\frac{{{D_i}}}{{{D_{\hbox{max} }}}}$$

(8a)

$$S_{i}^{2}=\sqrt {\frac{{{P_i}}}{{{P_{\hbox{max} }}}}}$$

(8b)

One has to be aware of possible systematic deviations of so estimated $S_{i}^{2}$ values. As it was shown earlier, the Q-derived τ_R values are underestimated in isotropically tumbling molecules. Accordingly, the P_max is underestimated as well, resulting in the overestimation of $S_{i}^{2}$ values (Fig. 4). This effect is especially pronounced for slower internal motions (long τ_int) with large amplitudes (small S²) at high magnetic fields. A similar effect was reported for the relaxation data in ATPase α-domain (Gu et al. 2016).

Fig. 4

Normalized values of apparent S² evaluated from D or P values (Eqs. 8a and 8b), given as a fraction of the input S² used in simulations. The $S_{{app}}^{2}/{S^2}$ ratio is shown as a function of the input S² for three B₀ (9.4, 14.1, and 18.8 T) and two τ_int values (10 and 100 ps). Calculations were performed applying overall correlation time τ _R  = 16 ns. Performance of this method becomes poor above the horizontal dashed line representing 10% deviation of the $S_{{app}}^{2}$ values

It is stated that the Q values do not distinguish between the effects of motional anisotropy and chemical exchange (Kneller et al. 2002), while the analysis of P data significantly attenuates the effects of motional anisotropy (c.f. Table 1) permitting rapid identification of residues undergoing chemical exchange, R _ex . It will be shown in the next section, however, that the attenuation of motional anisotropy is not sufficient to identify unequivocally the R _ex influenced residues. The elevated P values not always allow identifying residues affected by chemical exchange. In fact, only simultaneous outlying Q, D, and P values point out unequivocally to the chemical exchange.

Results and discussion

Combined analysis of Q, D, and P values is applied to four proteins for which the large relaxation data sets are available in the literature. Essential information on these proteins is collected in the Table 2.

Table 2 Basic data concerning GB1, ubiquitin, S100A1, and PSE4 proteins

Overall correlation time

The Q, D, and P site specific values for the analyzed proteins at all available magnetic fields are shown in Figs. 5 and S5–S14.The medians of experimentally observed Q = R₁/R₂ values were used for evaluating overall correlation times. Vizualization of this procedure is shown in Figs. S15–S18. Some details are explained in the captions to these figures.

Fig. 5

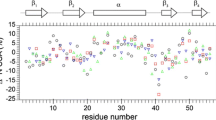
Sequence specific Q, D, and P values calculated from R₁ and R₂ relaxation rates determined for S100A1 protein at 16.4 T. Solid lines represent medians: $\tilde {Q}$ = 10.31, $\tilde {P}$ = 14.68, and $\tilde {D}$ = 23.49. Dashed lines mark the limit of outliers calculated from the formula Q3 + 1.5·IQR, where Q3 is third quartile and IQR is the interquartile range. Residue Glu22 undergoing a chemical exchange is marked with a red circle. Blue circles mark residues with a questionable presence of chemical exchange mechanism

For the proteins analyzed here, the determined τ_R(Q) values are larger than the corresponding values obtained from the MFA analysis as shown in the Fig. 6. Corresponding numerical values are reported in Table S2. The averaged deviations are equal to 18, 5, 2, and 5% for GB1, ubiquitin, S100A1, and PSE4, respectively. The opposite results would be expected from the simulation shown in Fig. 2. However, it is demonstrated in the “Method” section that the anisotropic tumbling can result in the overestimation of τ_R values and one should note that all four proteins reorient anisotropically (Table 3). It is worth noting that the largest discrepancy between Q-based and MFA derived τ_R values appears for GB1 characterized by the strongest tumbling anisotropy. Anisotropic tumbling and, therefore, the possible overestimation of τ_R values can be anticipated from the ratios of principal values of inertia tensor provided the protein structure is available (Mandel et al. 1995).

Fig. 6

Comparison of the overall correlation times τ_R determined by the model-free approach with those obtained from the appropriate $\tilde {Q}$ values. Determination of uncertainties represented by error bars is described in the caption to Table S2

Table 3 Anisotropic tumbling of the analyzed proteins

Anisotropic tumbling as a reason of the divergence between τ_R values obtained from the MFA analysis and Q-based method can be demonstrated analyzing two residues of GB1, Thr17 and Asp40. Their N–H vectors are nearly perpendicular one another. The Q values have been obtained from the R₁ and R₂ relaxation rates and next used in the τ _R (Q) determination. Results are presented in Table 4. The orientation of N–H vectors strongly influences the value of pseudo-isotropic overall correlation time determined using Q value. It has to be pointed out that the median, $\tilde {Q}$, can be skewed due to the non uniform distribution of N–H vector orientations. Regardless of anisotropic tumbling the presented examples of τ_R estimation by means of the Q-based method give suitable results with the average deviation 7% and the largest one 21% for GB1 at 11.7 T as compared with the MFA results.

Table 4 Overall correlation times τ_R determined for GB1 protein from the experimentally derived Q values

Chemical exchange

Residues exhibiting slow conformational mobility in the micro- to millisecond time scale have to be selected and next skipped in the further analysis of fast motions. Elevated Q, P, or D values owing to the chemical exchange mechanism result in non physical values of the generalized order parameter, S² > 1.

None of GB1 residues shows outlying Q, P, or D values being a hallmark of the chemical exchange (c.f. Figs. S5–S7). This observation is consistent with the MFA analysis performed for R₁, R₂, and NOE data at three magnetic fields (Table S3). Both, standard deviations of Φ factors multiplied by an appropriate Student’s t-value and F-test applied to the partial target functions characterizing the fit quality for a given residue with and without assumption of chemical exchange (three or two local parameters) were applied to verify the significance of the MFA-derived Φ factors.

Among the Q, P, and D values calculated for ubiquitin one residue, Asn25, displays the largest values pointing out to the effective chemical exchange mechanism in the relaxation of this residue (c.f. Figs. S8 and S9). This result is consistent with the results of the MFA analysis. Asn25 is the unique residue exhibiting meaningful Φ value (Table S4). Three other residues show large but erratic Q, P, D values. None of them, however, possesses a meaningful Φ value in the MFA analysis.

Glu22 is the unique residue in the S100A1 protein displaying simultaneous large Q, P, and D values, thus clearly exhibiting the chemical exchange mechanism (Figs. 5, S10, and S11). This fact is also consistent with the MFA analysis (Table S5). However, three other residues, Glu3, Gly23 (only at 16.4 T), and Lys25, similarly as Glu22, display distinct P values. So, they can be suspected to undergo a chemical exchange. On the other hand, their Q values and majority of D values are very close to the corresponding medians. Φ factors of Gly23 and Lys25 residues obtained in the MFA analysis reveal the chemical exchange mechanism for these residues but definitely exclude it for Glu3 residue. Summing up, Q values fail to recognize chemical exchange for Gly23 and Lys25 but P values can lead to false recognition of non existing slow motions. D values perform the best at 16.4 T but fail at 9.4 T. None of Q, P, and D parameters is fully immune to the erroneous identification of chemical exchange.

In PSE4 protein (Figs. S12–S14) Q, P, D values for two residues, Thr128 and Ser235, at 11.7 T exceed corresponding outliers’ limits indicating chemical exchange. They also display the largest Φ values in the MFA analysis (Table S6). Nevertheless, not all of Q, P, D values at two higher magnetic fields confirm the efficient chemical exchange. Several other residues show non systematic, outlying Q, P, D values. Three of them, Thr57, Leu221, and Gly236, exhibit meaningful Φ values indicating chemical exchange while for the remaining residues, protruding Q, P, or D values seem to be misleading.

All the above discussed results point out to the possibility of ambiguous or false recognition of chemical exchange involved residues. None of Q, P, and D parameters is fully immune to the erroneous identification of chemical exchange but their values inspected simultaneously usually identify residues influenced by chemical exchange with a high probability.

Generalized order parameters

There are three methods allowing to estimate site specific generalized order parameters S² which describe local fast mobility of a protein backbone. Since such information is important in study of protein function and interactions with other molecules, it is necessary to compare results of these methods. Determination of the isotropic, overall tumbling correlation time, τ _R , from the properly selected Q value makes a starting point of all these methods. Two methods utilizing Eqs. (8a) or (8b) are based on D or P values, respectively. The third method, LMFA, requires fit of back calculated relaxation rates R₁ and R₂ with fixed τ _R (Q) and adjustable S² parameters to the experimental data.

Comparison of the results of these methods with those obtained for the MFA analysis of all available relaxation data as a reference, was performed. Similar conclusions can be reached from the results obtained for each of four investigated proteins. General tendencies can be discussed and presented on the examples of several selected GB1 residues. They are shown in Fig. 7.

Fig. 7

Comparison of S² values and their confidence limits for selected residues of GB1 protein. S² obtained from D values, P values, and LMFA approach are represented by red, green, and blue circles, respectively. The leftmost values are reference MFA derived results. Confidence limits for the MFA and LMFA calculations were obtained as standard deviations from 200 Monte Carlo simulations. Symmetrized confidence limits for S²(D) and S²(P) values were evaluated applying standard method of error propagation

An important conclusion drawn from data shown in Fig. 7 is that confidence ranges of S²(D) are roughly twice larger than corresponding ranges for S²(P) and S²(LMFA). This is a general feature obtained for all residues in all analyzed proteins (total 399 residues). Confidence ranges for S²(P) and S²(LMFA) are comparable, but always larger than those characterizing MFA results for obvious reason of a larger number of data and parameters used in the latter method. Another important factor concerns dispersion of S² values resulting from different methods for the same residue. In the majority of cases S²(D), S²(P), and S²(LMFA) are close each other at a given magnetic field but differ from the S²(MFA) and among the data determined at different magnetic fields (Fig. 7, Thr11 and Glu19). In a number of cases all the data are close each other (Fig. 7, Ala23). Such situation takes place when all individual Q values are close to the corresponding medians $\tilde {Q}$. In the opposite case, when individual Q values differ markedly from medians, all S² values are broadly dispersed (Fig. 7, Asp40).

Whole sets of S² values estimated as the sums of squared differences between S²(MFA) and S²(X) (X = D, P, LMFA) allow to estimate accuracy of each method. Once more P-based and LMFA approaches are comparable and slightly more accurate than the D-based one.

Concluding, P-based and LMFA methods of S² determination perform similarly but the former one is less demanding from the computational standpoint.

Conclusions

The R₁ and R₂ relaxation rates of ¹⁵N nuclei measured at a single magnetic field strength in proteins are not sufficient to perform a formal MFA analysis, but can be utilized for the semi-quantitative evaluation of the overall tumbling correlation time from the median of the set of transverse to longitudinal relaxation rates Q = R₂/R₁. Generalized order parameters S² characterizing amplitude of internal local motions, faster than the overall tumbling, can be site selectively evaluated using either linear combination D = 2R₂ − R₁ or product P = R₂·R₁ or LMFA method. Efficiency of these methods was carefully compared and the P and LMFA methods are comparably accurate while the former is less demanding from the computational standpoint. As the final result one obtains estimation of the overall correlation time, τ_R, and parameters characterizing internal motions, S², on the time scales faster than τ_R. Additionally, residues undergoing conformational motions in the micro- to millisecond time scale can be selected basing on the Q, D, and P outliers.