Introduction

Protein dynamics plays a key role in protein function, including ligand binding, enzyme catalysis, and signal transduction. NMR spectroscopy is a powerful technique for studying such dynamic processes with high resolution across a wide range of time scales, extending from picoseconds to seconds or longer (Palmer 2004; Igumenova et al. 2006). The majority of studies published to date have focused on backbone dynamics through measurement of 15N spin relaxation parameters (Jarymowycz and Stone 2006), but the critical role of side chains in mediating protein function has spawned the development of relaxation methods for methyl groups (Palmer et al. 1993; Muhandiram et al. 1995; Ishima et al. 2001; Millet et al. 2002), methylene groups (Yang et al. 1998), side-chain amides (Boyd 1995), carboxylates/carbonyls (Paquin et al. 2008), secondary amines of arginine and tryptophan (Berglund et al. 1995), and primary amines of lysines (Iwahara et al. 2007).

Aromatic residues occur frequently in the binding interfaces of proteins (Lo Conte et al. 1999). In particular, Tyr and Trp are overrepresented in “hot spots” that contribute a large fraction of the binding free energy (Bogan and Thorn 1998), Tyr is prevalent in antigen-binding sites of antibodies (Lo Conte et al. 1999; Birtalan et al. 2010), and His and Tyr play prominent roles in enzyme catalysis (Bartlett et al. 2002). Thus, it is of great interest to monitor the dynamics of aromatic side chains and changes in this dynamics upon formation of biologically relevant complexes. Furthermore, aromatic residues constitute a significant volume fraction (roughly 25 %) of the protein interior, and therefore represent an attractive complement to methyl-containing residues (which correspond to ca. 50 % of the core) as probes of the dynamics of the hydrophobic core (Wüthrich and Wagner 1975). Previous applications of 13C relaxation have indicated that aromatic side chains show a rich variation in dynamics (Palmer et al. 1993), and theoretical considerations have predicted that 13C relaxation rates should be quite sensitive to the motions of aromatic side chains (Levy and Sheridan 1983).

Relaxation experiments on uniformly 13C-enriched aromatic side chains are seriously hampered by the strong J-coupling between neighboring sites in the aromatic rings. Labeling using 1-13C1- or 2-13C1-glucose solves the problem by creating isolated 13C sites in aromatic side chains, i.e. sites that do not have any 13C–13C one-bond couplings (Teilum et al. 2006; Lundström et al. 2007). Specifically, labeling with 1-13C1-glucose introduces isolated 1H–13C pairs at the Cδ positions of Phe and Tyr, the Cδ1 and Cε3 of Trp, and the Cδ2 and Cε1 of His, while 2-13C1-glucose yields 13C at the Cε positions of Phe and Tyr, and the Cζ3 and Cζ2 of Trp. Thus, the approach results in two complementary labeling patterns of isolated 13C–1H spin pairs suitable for canonical inverse-detected heteronuclear relaxation experiments similar to those developed for 15N spins (Teilum et al. 2006; Boyer and Lee 2008; Sapienza et al. 2011).

However, it is evident that relaxation studies of aromatic 13C spin systems can benefit from further pulse sequence optimization to achieve higher sensitivity. Specifically 13C-labeled protein samples produced using 13C1-glucose are limited in sensitivity by the resulting incorporation level of 50 % (Teilum et al. 2006; Lundström et al. 2007). The inherently fast transverse relaxation of aromatic 13C spins, due in part to their sizeable chemical shift anisotropy (CSA), further reduces the relative sensitivity of these experiments; for example, R 2 is roughly a factor of 4 greater than that of backbone 15N spins. Furthermore, His and Trp residues contain exchangeable protons vicinal to the 1H–13C pairs of interest; chemical exchange of these protons with water might cause differential effects on the intensities of the 1H–13C cross-peaks as a function of the relaxation delay, unless special care is taken to maintain the equilibrium magnetization of water throughout the relaxation period.

Here we present pulse sequences for aromatic 13C relaxation experiments (R 1, R 2 and steady-state {1H}–13C NOE) that include longitudinal-relaxation optimization (Pervushin et al. 2002) and either TROSY (Pervushin et al. 1997, 1998) or PEP-HSQC approaches (Palmer et al. 1991; Kay et al. 1992). As part of these developments, we also demonstrate that neither the two-bond J couplings between 13C spins, nor the dipolar interactions with remote or vicinal protons, adversely affect the relaxation data. The pulse sequences were tested on the carbohydrate binding domain of galectin-3 (Gal3C), which contains all four types of aromatic side chains: Phe, Tyr, Trp, and His. The experiments presented here significantly improve the sensitivity and overall performance compared to ‘standard’ experiments, enabling robust and efficient investigation of aromatic side chain relaxation.

Materials and methods

Expression and purification

The galectin-3 carbohydrate recognition domain (Gal3C; amino acid residues 113–250) was expressed and purified as described previously (Diehl et al. 2009, 2010) using M9 minimal medium containing either 100 % 1-13C1-glucose, or 50 % 1-13C1-glucose + 50 % 12C6-glucose as the sole carbon source. In addition, one partially deuterated sample was produced using M9 minimal medium containing 100 % 1-13C1-glucose in 60 % D2O.

NMR experiments

All NMR spectra were recorded on a Varian DirectDrive 500 MHz spectrometer at 298 K using 0.8 mM Gal3C samples in 5 mM HEPES pH 7.4 and 7 % D2O. Shaped pulses were created using Pbox. Excitation and flip-back 1H EBURP2 pulses (Geen and Freeman 1991) had a bandwidth of 3,300 Hz (6.6 ppm) and offset of −1,400 Hz (−2.8 ppm) from the water resonance. 1H i-SNOB-5 pulses (Kupce et al. 1995) had a bandwidth of 1,350 Hz (2.7 ppm) and offset of 1,250 Hz (2.5 ppm), and 13C REBURP pulses (Geen and Freeman 1991) had a bandwidth of 5,000 Hz (40 ppm). The 1H carrier was set on the water frequency, while the 13C carrier was centered in the aromatic region. For non-L-optimized control experiments the 1H EBURP2 pulses were omitted, the 1H i-SNOB-5 pulses were replaced by rectangular hard pulses, and the water resonance was suppressed using a 3–9–19 WATERGATE sequence (Sklenar et al. 1993).

1H decoupling was applied during the relaxation delays using a series of 1H i-SNOB-5 pulses. In the R 1 experiment, these pulses were spaced 50 ms apart, while in the R 2 experiment they were applied in the center of an 8 ms CPMG block consisting of 8 refocusing pulses that were phase cycled as described previously (Yip and Zuiderweg 2004). Proton saturation in the {1H}–13C NOE experiment was achieved using a train of 180° pulses spaced by 20 ms delays (Ferrage et al. 2008, 2009). Relaxation data were acquired by interleaving relaxation delays and t 1 time points.

Data analysis

Spectra were processed using NMRpipe (Delaglio et al. 1995) and analyzed using NMRview (Johnson and Blevins 1994). Errors in the peak intensitites were estimated from the baseplane noise and duplicate data points. Relaxation data were fittted to mono-exponential decays. Errors in the fitted relaxation rate constants were estimated from the covariance matrix of the Levenberg–Marquardt fitting.

Results and discussion

Pulse sequences

In an effort to optimize the sensitivity of aromatic 13C relaxation experiments, we implemented improved pulse sequences for the measurement of the longitudinal relaxation rate (R 1), the transverse relaxation rate (R 2), and the {1H}–13C NOE, which commonly form the basis for spectral density mapping or model-free analysis of protein dynamics.

The pulse sequences for the R 1, R 2, and {1H}–13C NOE experiments are shown in Fig. 1. Each relaxation experiment was implemented in the framework of either 1H–13C PEP-HSQC or 1H–13C TROSY-HSQC spectra (Fig. 1d–e). The INEPT transfer delays were tuned to a 1H–13C coupling constant of 1 J HC = 155 Hz, which yields near-optimal transfer for most aromatics, except for the Cε1 position of His, which has 1 J HC > 200 Hz.

Fig. 1
figure 1

L-optimized pulse sequences for measuring aromatic 13C relaxation parameters. The pulse sequence of the R 1 relaxation experiment shown in the top panel is divided into two blocks that encode: a polarization transfer from 1H to 13C and the relaxation period; and d the 13C evolution period followed by polarization transfer back to 1H. The R 2 experiment is obtained by replacing block a with block b, and similarly the {1H}–13C NOE experiment is given by block c. The TROSY transfer sequence of block d can be substituted for the PEP-HSQC sequence given in block e. Each of the three relaxation experiments specified by blocks a–c can be combined with either of blocks d or e. Narrow (wide) filled bars represent 90° (180°) rectangular high power pulses. Grey wide bars in block b represent 180° rectangular CPMG pulses attenuated by 6 dB compared to the other hard pulses. Filled bell-shaped bars represent shaped pulses. Narrow bell-shaped bars on 1H represent EBURP2 shapes (bandwidth of 6.6 ppm, shifted 2.8 ppm upfield), while wide bell-shaped bars are i-SNOB-5 pulses (bandwidth of 2.7 ppm, shifted 2.5 ppm downfield). Wide bell-shaped pulses on 13C represent REBURP shapes (bandwidth 40 ppm). Pulsed field gradients (PFG) are indicated as grey open bars. Phases are x unless otherwise indicated. In all sequences τa = 1.5 ms and τb = 1.623 ms. The delay δ varies between blocks: in a, δ = 25 ms; in b, δ = 4 ms; and in c, δ = 10 ms. In all experiments echo/anti-echo selection were made during t1 by reversing ϕ3, GC, and the even-numbered increments of ϕrec. For every second t1 increment ϕ2 and ϕrec were incremented. Durations and strengths of the gradients are G1 = (1 ms, 10 G/cm); G2 = (0.5 ms, 8 G/cm); G3 = (0.5 ms, 12 G/cm); G4 = (0.5 ms, 16 G/cm), G5 = (0.5 ms, 18 G/cm), GC = (1 ms, −50 G/cm), GH = (0.5 ms, 25 G/cm). The phase cycling for the different experiments is: a + d and b + d, ϕ1 = (x, x, x, x, −x, −x, −x, −x), ϕ2 = (y, x, −y, −x), ϕrec = (x, −y, −x, y, −x, y, x, −y); c + d, ϕ2 = (y, x, −y, −x), ϕrec = (x, −y, −x, y); a + e and b + e, ϕ1 = (x, x, −x, −x), ϕ2 = (y, −y), ϕrec = (x, −x, −x, x); c + e, ϕ2 = (y, −y), ϕrec = (x, −x). The phase cycling within the CPMG block is (x, x, y, −y, x, x, −y, y) in b + e, and (y, y, −x, x, y, y, x, −x) in b + d. The phase of the shaped 1H pulse in middle of the CPMG block is x for CPMG block n and −x for n + 1

Full size image

Longitudinal relaxation optimization (L-optimization) involves maintaining the water and aliphatic magnetizations along the +z axis whenever possible (see further below). This was achieved by implementing selective flip-back of the water and aliphatic 1H spins using EBURP2 pulses (Geen and Freeman 1991), as previously applied in the context of the L-GFT-TROSY experiment for aromatic rings (Eletsky et al. 2005). Furthermore, the selective 13C REBURP pulse (Geen and Freeman 1991) in the first INEPT transfer step refocuses only the aromatic carbons to prevent the evolution of 1H–13C couplings of aliphatics in the first INEPT and make possible the re-alignment all aliphatic 1H magnetization back to +z along with the water. The 180° pulses on 1H during the relaxation delays of the R 1 and R 2 experiments and the saturation pulse train of the NOE experiment were implemented as i-SNOB-5 pulses (Kupce et al. 1995) selective for the aromatic region.

In the R 2 experiment (Fig. 1b) an additional gradient (G4) was added before the CPMG block, in order to purge non-refocused magnetization arising as a consequence of the non-uniform 1H–13C coupling constants in aromatic side chains. Off-resonance artefacts of the CPMG refocusing pulses were suppressed by the phase cycle proposed by Yip and Zuiderweg (2004). 1H saturation in the {1H}–13C NOE experiment was achieved using 180° pulses as described (Ferrage et al. 2008, 2009). TROSY selection (Fig. 1d) was implemented in the 13C dimension only (Pervushin et al. 1998), which allows for a simplified TROSY scheme (Eletsky et al. 2005). In the following we describe key aspects of these pulse sequences.

TROSY versus PEP-HSQC detection in specifically 13C-labeled proteins

TROSY detection of aromatic resonances has been shown to be advantageous in experiments developed for uniformly 13C-labeled proteins (Pervushin et al. 1998). Calculations based on the chemical shift tensor of benzene (σ11 = 225 ppm, σ22 = 149 ppm, and σ33 = 15 ppm; Veeman 1984) indicate that the TROSY effect is close to optimal at a static magnetic field strength of 14.1 T, and provides significant sensitivity enhancement at field strengths from 11.7 to 18.8 T (Pervushin et al. 1998). The chemical shift tensors of tryptophan Cδ1 (σ11 = 202, σ22 = 121, and σ33 = 48 ppm; Separovic et al. 1991) and Cε3 (σ11 = 208, σ22 = 137, and σ33 = 15 ppm; Separovic et al. 1999) are comparable to that of benzene, indicating similar TROSY effects for these sites.

Experiments for uniformly 13C-labeled samples include a constant-time evolution period (17.6 ms) to refocus one-bond 13C–13C couplings (Pervushin et al. 1998), which incurs a significant loss in sensitivity. By contrast, in specifically 13C-labeled proteins, the one-bond 13C–13C couplings are eliminated and the evolution period can be kept quite short due to the narrow frequency range of the aromatic region of the 13C spectrum. We tested both TROSY and PEP-HSQC approaches with either constant-time or non-constant time evolution periods on Gal3C at different global correlation times (τ c) by varying the temperature (Supplementary Fig. S1). The non-constant time PEP-HSQC experiment is more sensitive than the TROSY up to a global correlation time of about 13 ns (corresponding to a molecular weight of approximately 16 kDa at 5 °C), but the TROSY version results in narrower linewidths, as expected. We note that the inherent reduction in sensitivity that results from 1- or 2-13C1-glucose labeling (50 % incorporation) is essentially compensated for by the increase in sensitivity that results from the shortened t 1 evolution period of the non-constant time experiment. Thus, aromatic 1H–13C correlation spectra of medium-sized and 13C1-glucose-labeled proteins have comparable sensitivities to those obtained using constant-time TROSY spectroscopy on uniformly 13C-enriched samples (Pervushin et al. 1998), thereby making the former samples very well suited also for other purposes than relaxation studies.

Longitudinal relaxation optimization

In L-optimized spectroscopy (Pervushin et al. 2002), 1H spins not used for polarization transfer and detection are maintained close to equilibrium (i.e. magnetization along +z) throughout the experiment, including the relaxation, t 1 evolution, and acquisition periods. This unperturbed “thermal bath” leads to efficient relaxation of the detected protons, as is well illustrated by comparing the effective relaxation rates in selective versus non-selective inversion recovery experiments (Cavanagh et al. 2007). Thus, L-optimization enables the use of shorter recycle delays and hence improved sensitivity in terms of signal-to-noise (S/N) per unit time. L-optimization is achieved using shaped, frequency-selective pulses to control the aromatic 1H spins separately from the water and aliphatic 1H spins. As described in more detail below, this level of control is critical in any type of quantitative experiment that starts from a non-equilibrium state and involves variable relaxation delays.

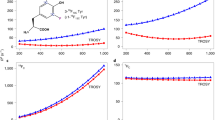
We investigated the benefits of L-optimization by comparing with non-L-optimized pulse sequences. Figure 2a shows the signal-to-noise ratio (S/N) as a function of recovery delay in the R 1 experiment. To find the optimal recovery delay with respect to S/N, we repeated both the L-optimized and non-L-optimized experiments using the same total experimental time for each measured point (Fig. 2b). The optimal recovery time for L-optimized experiments of aromatics was determined to be 0.6 s for Gal3C. The average gain in S/N achieved with L-optimization was 10 % for Phe and Tyr Cδ*, 25 % for His Cδ2 and Cε1, and 35 % for Trp Cδ1. The additional increase in S/N observed for Trp and His is most probably caused by the presence of exchangeable protons vicinal to the 13C sites in question; exchange of these protons for water protons with near-equilibrium magnetization provides an efficient relaxation mechanism for the protons attached to the labeled carbons. The increased S/N is particularly useful in the context of 1-13C1- or 2-13C1-glucose labeling, which restricts the level of 13C incorporation to 50 %, and consequently limits the overall sensitivity of these samples. Phe and Tyr usually have inherently higher sensitivity due to the presence of two chemically identical carbons that contribute to the same peak intensity whenever the two resonances are averaged by rapid ring flips. Thus, L-optimization preferentially augments those side chains (Trp and His) that have the lowest inherent sensitivity, thereby making the signal intensities from the different aromatic sites more uniform on average. This result contrasts with what is observed for 1H–15N correlated experiments, where L-optimization typically leads to a less uniform distribution of signal intensities (Pervushin et al. 2002).

Fig. 2
figure 2

Sensitivity (signal-to-noise ratio, S/N) versus length of the recovery delay for L-optimized (black circles) and non-L-optimized (grey squares) versions of the R 1 pulse sequence. Representative data are shown for different aromatic 13C sites (Trp181 Cδ1, Phe163 Cδ*, Tyr247 Cδ*, and His208 Cε1). a data acquired with a constant number of transients. b data acquired with a constant total experiment time. An optimal recovery time was estimated to 0.6 s for L-optimized and 1.5 s for non-optimized versions (right-hand column). The average gain in S/N for L-optimization is 35 % (Trp Cδ1), 10 % (Phe Cδ*), 10 % (Tyr Cδ*), and 25 % (His Cε1). Similar results are obtained for the R 2 experiment

Full size image

We next verified that the L-optimized pulse sequences yield accurate relaxation rates. Figure 3a–c show a comparison of R 1 decay curves acquired using L-optimized and standard (i.e. non-L-optimized) experiments acquired with a 3.8 s recovery delay to ensure that the aromatic 1H magnetization has relaxed back to equilibrium. The relaxation decays and fitted relaxation rate constants (Fig. 3d) obtained using the L-optimized experiment are identical to those from the standard experiment, provided that 1H decoupling during the relaxation delay is applied as selective pulses on the aromatics. Non-selective 1H 180° pulses (in the context of L-optimization) lead to faster decays and higher apparent 13C R 1 values. This result is a consequence of the intermittent inversion of water and aliphatic 1H magnetization between +z and −z during the relaxation period, which makes the state of the water/aliphatic magnetization at the end of each transient dependent on the length of the relaxation period, which in turn influences the relaxation of aromatic 1H spins, and hence the magnetization available for polarization transfer at the beginning of each ‘scan’. The outcome is that the intensity of the monitored 13C resonances will depend on the length of the relaxation period, thereby affecting the 13C intensity decay curves that define the measured (apparent) relaxation rate constants; similar observations have been reported recently for 15N relaxation experiments (Chen and Tjandra 2011). Therefore, it is critical in L-optimized experiments to maintain the 1H magnetization of water and aliphatics along +z throughout the relaxation delay in order to ensure accurate relaxation measurements.

Fig. 3
figure 3

Dependence of R 1 on the treatment of the 1H magnetization during the variable relaxation delay. a–c Representative relaxation decays (a Phe163 Cδ*; b Phe190 Cδ*; c His208 Cε1) obtained using pulse sequences without (grey squares) or with L-optimization using selective i-SNOB-5 (black circles) or non-selective (open circles) 1H inversion pulses during the relaxation delay. Panel c includes data obtained using rectangular 1H inversion pulses in combination with water flip-back (open triangles). d R 1 rate constants obtained with the different implementations for different types of aromatic side chains, from left to right: His222 Cδ2, Trp181 Cε3, Trp181 Cδ1, Phe198 Cδ*, Phe149 Cδ* + Phe159 Cδ* + Tyr118 Cδ* + Tyr221 Cδ*, Phe163 Cδ*, Phe192 Cδ*, Phe209 Cδ*, His158 Cε1, and His217 Cε1. The non-L-optimized experiment utilized a recycle delay of 3.8 s

Full size image

The results shown in Fig. 3c–d further reveal the extent to which the water and aliphatic magnetizations contribute to the increased relaxation rate of the different aromatic 1H spins achieved with L-optimization. We carried out R 1 experiments in which selective 1H pulses were applied to the water resonance only, thereby restricting the origin of the L-optimization effect to water spin pool. By applying non-selective 1H 180° pulses during the relaxation delay we observe the type of artefacts described in the section above, but only to the extent that the relaxation of the aromatic protons is influenced by the state of the water magnetization. In this experiment, we observe artificially increased R 1 rates for atoms vicinal to sites with exchangeable protons, like Cδ2 and Cε1 in His and Cδ1 in Trp (Fig. 3c–d). By contrast, rates comparable to or slightly higher than those obtained from the standard or L-optimized experiments were observed for other sites, reflecting the signficantly reduced contribution from water in driving the relaxation of these spins. Thus, the water magnetization contributes to L-optimization mainly for 1H spins situated nearby protons that exchange with water, in agreement with the higher intensity gain observed for histidines and tryptophanes (cf. Fig. 2).

L-optimized R2 experiment

The R 2 relaxation experiment can be implemented in a straightforward fashion within the general framework presented above for the R 1 experiment (Fig. 1b). Again, it is advisable that the 1H 180° pulses during the relaxation delay are selective for the aromatics in order to achieve the full benefits of L-optimization. However, the generally shorter relaxation periods needed to sample transverse relaxation decays serve to limit the adverse effects on the 13C relaxation measurements that might arise due to differential recovery of water/aliphatic magnetization as a function of the length of the relaxation period. Indeed, in the present case, L-optimized and non-L-optimized experiments yield identical R 2 rates, within errors (Fig. 4a).

Fig. 4
figure 4

R 2 CPMG in-phase relaxation experiment. a R 2 rate constants for different types of aromatic 13C sites determined using L-optimized (black circles) and non-L-optimized (grey squares) experiments. b Relaxation decays for His 13Cε1 obtained with τb = 1.623 ms (tuned to 1 J HC = 154 Hz) and the purge gradient G4 included (filled circles), or without gradient G4 and τb = 1.623 ms (open triangles) or τb = 1.2 ms (tuned to 1 J HC = 208 Hz, grey triangles)

Full size image

The one-bond 1H–13C coupling constants in aromatic side chains depend on the chemical structure as follows: 1 J HC = 155 Hz for sites in 6-membered rings; 1 J HC = 185 Hz for sites in 5-membered rings with a single directly attached nitrogen, i.e. Cδ2 in His and Cδ1 in Trp; 1 J HC = 205 Hz for sites in 5-membered rings with two directly attached nitrogens, i.e. Cε1 in His. The non-uniform one-bond 1H–13C coupling constants require that non-refocused anti-phase magnetization be purged using a strong gradient pulse (G4 in Fig. 1b). In the absence of the purging gradient and with the refocusing delay optimized for smaller coupling constants (155–185 Hz), the residual anti-phase term gives rise to oscillations in the relaxation decay, as demonstrated for Cε1 in His (Fig 4b). Of course, R 2 rates can alternatively be measured in separate experiments that employ refocusing delays matching the different values of 1 J HC; this approach also serves the purpose to optimize the sensitivity for each class of sites.

While 1-13C1- and 2-13C1-glucose labeling effectively eradicates directly neighboring 13C sites in the aromatic rings, 50 % of the labeled carbons still have another 13C nucleus two bonds away. The two-bond scalar coupling is expected to be small, 2 J CC ≈ 2–7 Hz (Kaski et al. 1996; Witanowski et al. 2007), but is practically impossible to refocus in most cases due to the narrow spectral range covered by the two resonances. We investigated the influence of the 2 J CC coupling on the measured R 2 rates by comparing the results obtained from two different samples labeled using either 100 % 1-13C1-glucose or 50 % 1-13C1-glucose + 50 % 12C6-glucose, resulting in 50 % or 25 %, respectively, of the observed carbons having a two-bond coupling partner (Fig. 5a). The resulting R 2 decays are identical within errors (Fig. 5b), thus verifying that two-bond 13C-13C couplings do not affect 13C R 2 measurements to any appreciable extent.

Fig. 5
figure 5

Influence of two-bond 13C–13C J couplings on measured R 2 relaxation decays. a 13C incorporation pattern in a Phe side chain resulting from labeling with 1-13C1-glucose. Black circles represent 13C-labeled positions while open circles represent 12C. The symbols to the right of the aromatic rings show the net percentages of labeled or unlabeled sites (labeled/unlabeled), and the percentages of 13C sites with or without a two-bond neighbor (labeled–labeled/labeled–unlabeled). Labeling using 100 % 1-13C1-glucose yields 50 % 13C incorporation in the Cδ positions, and 50 % of these 13Cδ have a 13C-labeled two-bond neighbour. Labeling using 50 % 1-13C1-glucose + 50 % 12C6-glucose reduces the relative number of labeled carbons, as well as that of labeled two-bond neighbours, to 25 %. b Representative R 2 relaxation decays for different aromatic side chains in samples labeled using 100 % 1-13C1-glucose (filled circles) or 50 % 1-13C1-glucose + 50 % 12C6-glucose (open circles)

Full size image

{1H}–13C NOE experiment

The {1H}–13C NOE saturation and reference experiments were optimized in a straightforward fashion by finding the shortest possible saturation and recycle periods that still provide full magnetization transfer and recovery. Since the length of the NOE reference experiment is governed by the recovery of the heteronucleus (13C in the present case), L-optimization offers little or no advantage for a medium-sized protein like Gal3C, as shown in Fig. 6. Still, selective 1H pulses for proton saturation are beneficial in order to achieve equal water suppression in both the saturation and reference experiments. For Gal3C, a 1H saturation period of 2 s is sufficient to achieve complete NOE transfer (Fig. 6a). This value is in agreement with the data shown in Fig. 2a, demonstrating that the chosen length of the saturation period is close to 6·T 1 for the aromatic protons. As shown in Fig. 6b, a pre-saturation delay of 1.3 s guarantees full recovery of the 1H magnetization. The recycle delay of the reference experiment is set to 3.3 s (approximately 6·T 1 for aromatic 13C spins), which ensures that the 13C magnetization has relaxed back to equilibrium (Fig. 6c).

Fig. 6
figure 6

Intensity build-up in the aromatic {1H}–13C NOE experiment. a Difference intensity (saturation experiment − reference experiment) of the {1H}–13C NOE experiment shown as a function of 1H saturation time for the pulse sequences that correspond to the L-optimized (black circles) and non-L-optimized (grey squares) versions, using a constant pre-saturation delay of 4 s. b Difference intensity as a function of pre-saturation delays using a 1H saturation time of 2 s. c Intensity originating from 13C excitation (reference experiment) as a function of the recovery delay. Optimal delays are indicated with black arrows: the 1H saturation period is 2 s, and the pre-saturation delay is 1.3 s. The resulting recovery delay of 3.3 s equals approximately 6/R 1, ensuring that the 13C magnetization has completely returned to equilibrium. The data represent the summed intensity of four residues: Phe149 Cδ* + Phe159 Cδ* + Tyr118 Cδ* + Tyr221 Cδ*

Full size image

Vicinal and remote protons do not affect the relaxation of aromatic 13C spins

The interpretation of the 13C relaxation rates in terms of models describing the motion of the aromatic rings is greatly simplified if the relaxation is dominated by the CSA and dipolar interaction with the covalently attached proton (bond length 1.08 Å). We established that there is no detectable influence from 1H spins located near the aromatic 1H–13C moieties of interest. The vicinal protons are expected to be the closest ones, at a distance of 2.14 Å in the case of Phe and Tyr. The dipolar interaction with the vicinal protons is reduced by a factor of approximately (1.08/2.14)6 = 1.7 %, compared to that of the covalently attached proton; consequently, relaxation effects due to vicinal or other neighboring protons are expected to be small. We verified the theroretical prediction by comparing 13C relaxation rates measured on samples that were either fully protonated or partially deuterated to a level of 50–60 % at the vicinal sites (Table S1) and approximately 50 % on average. As shown in Fig. 7, there are no discernable differences in 13C relaxation between these two samples. Thus, we conclude that relaxation measurements on specifically 13C labeled aromatic side chains are unaffected by remote protons.

Fig. 7
figure 7

Comparison of 13C R 1 relaxation in partially deuterated and non-deuterated samples. a–c Representative R 1 relaxation decays measured for two Phe residues (a–b) and one His (c) on a partially deuterated sample (open circles) and non-deuterated sample (black circles). d Fitted R 1 relaxation rate constants for all 13C sites characterized in Gal3C. The deuteration levels at the vicinal sites are estimated to 50–55 % for Phe and Tyr 1Hε, and 60 % for Trp 1Hζ3 (see Table S1)

Full size image

Conclusions

We have shown that L-optimization increases the sensitivity (defined in terms of signal-to-noise per unit time) of 13C relaxation experiments for aromatic side chains by at least 10–35 %. This level of S/N enhancement was attained for a relatively small protein of 16 kDa at a static magnetic field strength of 11.7 T. Significantly higher S/N enhancement are expected for bigger proteins and higher static magnetic field strengths, which both result in slower 1H R 1 relaxation rates and therefore makes L-optimization increasingly advantageous. Proteins larger in size than approximately 25–30 kDa (at 25 °C) benefit further from TROSY-based 13C chemical shift evolution. Furthermore, we demonstrate that the relaxation measurements are not significantly affected by potential complications due to residual two-bond 13C–13C scalar couplings or dipolar interactions with neighboring 1H spins. Precise control of the water and aliphatic 1H magnetizations enables accurate measurements of 13C relaxation rate constants using L-optimized pulse sequences.