Introduction

Exchange experiments involving the transfer of heteronuclear longitudinal magnetization of product operator terms such as I z S z or S z were introduced by Montelione et al. to quantitate transitions between different conformations of biomolecules for which isolated resonances are observed (Montelione and Wagner 1989). These experiments have played an important role in NMR dynamic studies of biological systems ever since, because they provide access to functionally important dynamic processes occurring on time scales ranging from ~0.5 to ~50 s−1. In addition, they offer the possibility to resolve these processes on a per-residue basis and without perturbing the system from thermodynamic equilibrium, a feature that makes NMR spectroscopy an indispensable instrument for the analysis of macromolecular dynamics (Mittermaier and Kay 2009).

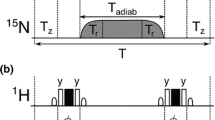
Longitudinal exchange experiments are based on the quantification of magnetization transfer between exchanging conformers during a mixing time. In the standard (frequency-labeled) setup, four peaks are observed for each spin, i.e. two direct correlation (diagonal) peaks and two exchange cross peaks (Fig. 1). In order to measure the interconversion rates between the exchanging conformers, a series of spectra is recorded for a range of mixing times, and the magnitudes of the four peaks are quantified by fitting the appropriate theoretical curves to the experimental data (Fig. 2) (Farrow et al. 1995). Several variants of this setup have been described, including 2D, 3D and pseudo-4D TROSY selected/detected versions (Hwang and Kay 2005; Sahu et al. 2007; Li and Palmer 2009; Sprangers et al. 2005; Nikolaev and Pervushin 2007; Wang et al. 2002) as well as zero-quantum/double quantum coherence versions to resolve chemical shift degeneracy (Robson et al. 2010).

Fig. 1
figure 1

a Scheme of a 2D longitudinal exchange experiment (Montelione and Wagner 1989). After frequency-labeling in an indirect dimension, t 1, magnetization associated with state A (B) (shown in red and black, respectively) either remains A (B) or is converted to B (A) during a variable mixing time (Mix). Subsequent frequency-labeling in the direct dimension (t 2) gives rise to two direct correlation (AA and BB) and two exchange cross peaks (AB, BA), respectively. b If the order of chemical shift evolution (t 1) and mixing times is interchanged, exchange cross peaks are not resolved but remain part of the two direct correlation peaks A and B, which corresponds to the collapse of AA with BA and BB with AB, respectively

Full size image
Fig. 2
figure 2

a Time dependence of normalized direct correlation peaks AA and BB (red and black solid lines, respectively) and exchange cross peaks AB and BA (red and black dashed lines), simulated using (1) and (2). Parameters: k AB = 0.8 s−1, k BA = 1.2 s−1, R A1  = 2.0 s−1, R B1  = 2.0 s−1. b As in a, but without normalization by MAA(0) and MBB(0) (but MAA(0) + MBB(0) set to 1). Exchange cross peaks have equal magnitudes if R A1  = R B1 . c Time dependence of normalized direct correlation peaks A and B [(3), red and black dashed lines], as well as AA and BB [(1), red and black solid lines], using the same parameters as in a. The curves for A and B are identical if R A1  = R B1 . By taking the difference between A and AA (B and BB) curves it is possible to reconstruct the correctly normalized exchange curves AB (BA) shown in a. d As in c but without normalization by MA(0), MAA(0) and MB(0), MBB(0), respectively. Here, the differences between A and AA (B and BB) are equal

Full size image

The apparent simplicity of the analysis of longitudinal exchange experiments is, however, deceiving, as there are several pitfalls that have to be accounted for in order to avoid systematic errors. First, different relaxation properties of the two species result in different transfer efficiencies during INEPT step(s) (Tollinger et al. 2001; Miloushev et al. 2008). Second, and more importantly, the analysis of kinetic properties from this experiment may suffer from substantial systematic errors if the line-widths of the two species are different (Fig. 3). Unless precautions are taken to ensure precise determination of peak volumes, errors due to systematic over- or underestimation of the magnitudes of exchange cross peaks can have a significant impact on the fitting results.

Fig. 3
figure 3

Effect of differential line-broadening in 2D frequency-labeled experiments. a Peaks associated with state A during t 2 detection (AA direct correlation and BA exchange cross peaks) have identical line widths (lw A) in the direct dimension, which can be different from that of BB and AB (lw B). Because quantification of AB (BA) exchange cross peaks requires normalization by AA (BB) direct correlation peaks at zero mixing time, exact peak volumes rather than intensities or partial peak volumes have to be used for analysis of the data. Differences in line-widths during t 1 evolution are irrelevant for the analysis. b Simulation of the effect of approximating peak volumes by intensities for normalized exchange curves, using (2). Parameters: k AB = 1.0 s−1, k BA = 1.0 s−1, R A1  = 2.0 s−1, R B1  =2.0 s−1. Assuming Lorentzian line shapes (where Int = Vol/lw), normalized exchange curves based on intensity measurements are simulated for lw A/lw B = 0.7, 0.8, 0.9, and 1.0. AB and BA exchange curves are shown in red and black, respectively. Only if lw A = lw B, or if exact (direct correlation and exchange cross peak) volumes are used, AB and BA exchange curves are identical, as is expected for k AB = k BA (superimposed red and black dashed lines)

Full size image

Because determining peak volumes by integration requires fitting to a functional form, this is particularly challenging in cases where non-canonical line-shapes (resulting from conformational exchange processes occurring on the ms–μs time scale) are encountered, which are not known a priori. Moreover, it can sometimes be impractical to precisely measure the volumes of small exchange cross peaks with low signal-to-noise ratio, as typically encountered for short mixing times, in particular in the vicinity of strong direct correlation peaks. To circumvent integration, peak volumes are often approximated by partial peak volumes that are obtained by summation of the intensities of data points within a defined interval. Partial peak volumes are, however, dependent on the choice of the summation interval with respect to the line-width (Rischel 1995), thereby complicating the normalization of peaks with different line-widths. To improve the precision in the determination of longitudinal exchange kinetics, a quadratic approximation was proposed for the analysis of the data by employing a composite ratio of exchange and direct correlation peak intensities. This approach does, however, require that equilibrium constants can be determined from other experiments (Miloushev et al. 2008).

Here we present a simple and robust alternative to the standard setup of multidimensional longitudinal exchange experiments for biomolecules. Our approach is based on collecting two complementary data sets, one where exchange cross peaks are resolved, and a second one where they are not. This strategy is reminiscent of (one-dimensional) approaches comparing selective and non-selective inversion recovery measurements, as pioneered by Hoffman and Forsen (1966a, b). Combining the two data sets eliminates systematic errors that can be caused by differential line-broadening and enables reliable quantification of kinetic and relaxation parameters. As an example, we have used this experimental setup to characterize conformational exchange in a selectively 13C labeled sample of a bistable DNA oligomer.

Materials and methods

Sample preparation and conditions

A sample of bistable DNA (TCGTACCGGAAGGTACGAACCTTCCG) (Puffer et al. 2009) was synthesized and purified as described (Kloiber et al. 2011), introducing isolated methyl (13CHD2) labels into thymidines to avoid complications due to cross-correlated relaxation in the methyl group. The NMR sample contained 1.0 mM DNA, 50 mM sodium arsenate buffer, pH6.5, and 100% D2O, All NMR spectra were recorded at 33°C.

NMR measurements

2-Dimensional longitudinal exchange experiments were recorded using pulse sequences that are based on the scheme described by Farrow et al., but employing the exchange of two-spin heteronuclear order, I Z S Z (Farrow et al. 1995). In one experiment 13C frequency labeling preceded the mixing time, while in the second experiment the order of indirect evolution (13C frequency labeling) and mixing times was interchanged. Deuterium decoupling was employed during 13C (t 1) and 1H (t 2) detection. NMR spectra were recorded on a Varian Inova spectrometer operating at a Larmor frequency of 500 MHz. Series of 10 2D spectra (with and without frequency labeling) were collected, with mixing times ranging from 10 to 800 ms. Spectra were recorded as complex data matrices composed of 512 × 38 points, with maximum acquisition times of 127 and 64 ms in the 13C and 1H dimensions, respectively. 32 scans per FID were obtained with a recycle delay of 2 s, resulting in a total experimental time of 18.5 h for each series.

Data analysis

Data were processed and analyzed using NMRPipe and nmrDraw software (Delaglio et al. 1995) and in-house written fitting scripts. The t 1 (t 2) time domain data were apodized using a Gaussian function, linear predicted to 128 data points (t 1), and zero filled to 4,096 × 256 points. Partial peak volumes were obtained by adding the intensities in boxes of 7 × 7, 5 × 5 or 3 × 3 data points centered on the peak maximum. A least-squares fitting procedure was employed to extract k AB, k BA and R A1 , R B1 by fitting the expressions given in (1) and (3) to the measured partial peak volumes, along with MAA(0), MBB(0) and MA(0), MB(0) values, respectively. For comparison, the two direct correlation peaks along with the single resolved exchange cross peak for each spin label were used to extract k AB, k BA and R A1 , R B1 by fitting the appropriate expressions given in (1) and (2) to the measured partial peak volumes (3 × 3 data points). In all cases, experimental uncertainties were estimated via a Monte Carlo approach in which 200 synthetic data sets were generated from the best-fit values of k AB, k BA and R A1 , R B1 by adding random errors based on the signal-to-noise ratio to the best-fit curves. Errors quoted in the paper are the standard deviations in fitted parameters that were obtained in this procedure.

Results and discussion

Our approach relies on recording two separate experiments. The first one is analogous to the two-dimensional experiment described by Montelione et al., where heteronuclear chemical shift evolution precedes the mixing time and four resonances, two direct correlation and two exchange cross peaks, all frequency-labeled in both dimensions, are observed for each spin (Montelione and Wagner 1989). In the second experiment, the order of chemical shift evolution and mixing times is interchanged, so that exchange cross peaks are not resolved but remain part of the corresponding direct correlation peaks (Fig. 1). Analysis of the time dependence of only the direct correlation peaks in the two experiments with and without frequency-labeling eliminates systematic errors that arise from differential line broadening effects, as described below.

In the frequency-labeled experiment, the time dependence of the direct correlation peaks of a two-site exchanging system is given by (Farrow et al. 1995; Palmer et al. 2001)

$$ \begin{aligned} {{{\text{M}}_{\text{BB}} \left( t \right)} \mathord{\left/ {\vphantom {{{\text{M}}_{\text{BB}} \left( t \right)} {{\text{M}}_{\text{BB}} \left( 0 \right)}}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{\text{BB}} \left( 0 \right)}} & = \frac{1}{{\left( {\lambda_{1} - \lambda_{2} } \right)}}\left[ {\left( {a_{11} + \lambda_{1} } \right) \cdot e^{{\lambda_{1} t}} - \left( {a_{11} + \lambda_{2} } \right) \cdot e^{{\lambda_{2} t}} } \right] \\ {{{\text{M}}_{\text{AA}} \left( t \right)} \mathord{\left/ {\vphantom {{{\text{M}}_{\text{AA}} \left( t \right)} {{\text{M}}_{\text{AA}} \left( 0 \right)}}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{\text{AA}} \left( 0 \right)}} & = \frac{1}{{\left( {\lambda_{1} - \lambda_{2} } \right)}}\left[ {\left( {a_{22} + \lambda_{1} } \right) \cdot e^{{\lambda_{1} t}} - \left( {a_{22} + \lambda_{2} } \right) \cdot e^{{\lambda_{2} t}} } \right] \\ \end{aligned} $$
(1)

where MAA and MBB are the magnitudes of the direct correlation peaks corresponding to sites A and B, which are normalized by the amount of magnetization associated with states A and B (the magnitudes of the direct correlation peaks at the start of the mixing period, MAA(0) and MBB(0), respectively). The eigenvalues of the spin density matrix which includes magnetization transfer effects due to chemical exchange, λ 1/2, are given by \( \lambda_{ 1/ 2} = 1/ 2[ - ( {a_{ 1 1} + {\text{a}}_{ 2 2} ) \pm [ ( {a_{ 1 1} - a_{ 2 2} } )^{ 2} + 4a_{ 1 2} a_{ 2 1} ]^{ 1/ 2} }] \), where elements a ij are defined as \( a_{ 1 1} = k_{\text{AB}} + R_{ 1}^{\text{A}} ,a_{ 2 2} = k_{\text{BA}} + R_{ 1}^{\text{B}} ,a_{ 1 2} = - k_{\text{BA}} \) and \( a_{ 2 1} = - k_{\text{AB}} \). Parameters k AB and k BA denote the microscopic kinetic rate constants that describe the interconversion between states A and B, while R A1 and R B1 are the longitudinal relaxation rates of magnetization in sites A and B. Likewise, the normalized magnitudes of the associated exchange cross peaks in the frequency-labeled experiment are given by (Farrow et al. 1995; Palmer et al. 2001)

$$ \begin{aligned} {{{\text{M}}_{\text{AB}} \left( t \right)} \mathord{\left/ {\vphantom {{{\text{M}}_{\text{AB}} \left( t \right)} {{\text{M}}_{\text{AA}} \left( 0 \right)}}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{\text{AA}} \left( 0 \right)}} & = \frac{1}{{\left( {\lambda_{1} - \lambda_{2} } \right)}}\left[ { - a_{21} \cdot e^{{\lambda_{1} t}} + a_{21} \cdot e^{{\lambda_{2} t}} } \right] \\ {{{\text{M}}_{\text{BA}} \left( t \right)} \mathord{\left/ {\vphantom {{{\text{M}}_{\text{BA}} \left( t \right)} {{\text{M}}_{\text{BB}} \left( 0 \right)}}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{\text{BB}} \left( 0 \right)}} & = \frac{1}{{\left( {\lambda_{1} - \lambda_{2} } \right)}}\left[ { - a_{12} \cdot e^{{\lambda_{1} t}} + a_{12} \cdot e^{{\lambda_{2} t}} } \right]. \\ \end{aligned} $$
(2)

In the experiment without frequency labeling only two direct correlation peaks are observed, one of them with a magnitude, MA, that corresponds to the sum of AA and AB, while the magnitude of the second peak, MB, results from BB and AB. The normalized dependencies of MA and MB are then given by

$$ \begin{aligned} {{{\text{M}}_{\text{A}} \left( t \right)} \mathord{\left/ {\vphantom {{{\text{M}}_{\text{A}} \left( t \right)} {{\text{M}}_{\text{A}} \left( 0 \right)}}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{\text{A}} \left( 0 \right)}} & = \frac{1}{{\left( {\lambda_{1} - \lambda_{2} } \right)}}\left[ {\left( {a_{22} - a_{21} + \lambda_{1} } \right) \cdot e^{{\lambda_{1} t}} - \left( {a_{22} - a_{21} + \lambda_{2} } \right) \cdot e^{{\lambda_{2} t}} } \right] \\ {{{\text{M}}_{\text{B}} \left( t \right)} \mathord{\left/ {\vphantom {{{\text{M}}_{\text{B}} \left( t \right)} {{\text{M}}_{\text{B}} \left( 0 \right)}}} \right. \kern-\nulldelimiterspace} {{\text{M}}_{\text{B}} \left( 0 \right)}} & = \frac{1}{{\left( {\lambda_{1} - \lambda_{2} } \right)}}\left[ {\left( {a_{11} - a_{12} + \lambda_{1} } \right) \cdot e^{{\lambda_{1} t}} - \left( {a_{11} - a_{12} + \lambda_{2} } \right) \cdot e^{{\lambda_{2} t}} } \right] \\ \end{aligned} $$
(3)

where MA(0) and MB(0) are the magnitudes of the peaks A and B at zero mixing time.

Using the standard frequency-labeled strategy to extract R A1 , R B1 and k AB, k BA involves simultaneous least-squares fitting of (1) and (2) to exchange cross peaks and direct correlation peaks (Fig. 2). It is obvious from (2), however, that this requires the normalization of the two exchange cross peaks MAB(t), MBA(t) by the direct correlation peaks MAA(0), MBB(0), respectively. Because MAB and MAA (as well as MBA and MBB) have different line widths in the direct (t 2) dimension in most cases (see Fig. 3), special care has to be taken to ensure precise determination of peak volumes in order to avoid errors due to systematic over- or underestimation of exchange cross peak magnitudes, and concomitant over- or underestimation of the corresponding kinetic rate constants.

This complication can be avoided by using the four direct correlation peaks in experiments with and without frequency-labeling, MAA, MBB and MA, MB, respectively, for the analysis of longitudinal exchange. In this case all peaks are normalized by their respective magnitudes at the start of the mixing period, MAA(0), MBB(0) and MA(0), MB(0), with inherently identical line widths. Thus, longitudinal relaxation and kinetic rate constants (R A1 , R B1 and k AB, k BA) can be extracted from the four direct correlation peaks by simultaneous fitting of (1) and (3) to the experimental data, yielding values that are not distorted by differential line-broadening effects. Consequently, the results are independent of the peak integration method, i.e. intensities, partial peak volumes or (exact) peak volumes can be used.

We have applied this simple strategy to a bistable DNA 26-mer that exists in two different conformational (hairpin) sub-states A and B, which interconvert slowly on the NMR chemical shift time scale (Puffer et al. 2009). Both states are populated to a considerable extent at ambient temperature and in aqueous buffer (pH 6.5), and discrete sets of resonances are observed for A and B (Fig. 4). Selective 13C labeling (13CHD2-methyl) in thymidines enables the measurement of longitudinal exchange (2-spin order) between folds A and B in time series of 2-dimensional experiments performed with and without 13C frequency-labeling, respectively. Two thymidines, T4 and T22, were chosen as probes for the interconversion process between the two sub-states because the T22 spin label clearly displays differential line-broadening in folds A and B, consistent with the presence of an A-T/A-T step (A10-T23/A11-T24) in fold B (Lingbeck et al. 1996). Of note, the AB exchange cross peaks of T4 and T22 overlap at 500 MHz and 33°C in the 13CHD2-methyl labeled sample, preventing straightforward analysis of the interconversion process between folds A and B by the standard (frequency-labeled) approach.

Fig. 4
figure 4

Experimental longitudinal exchange data recorded for (T4, T22)-methyl 13C labeled bistable DNA. a Thymidine methyl group region of a 2-dimensional 1H13C correlation spectrum without (top) and with (bottom) frequency-labeling in (t 1) (mixing time 120 ms). Direct correlation peaks of T4 and T22 are labeled. Duplex DNA, which does not participate in the exchange process, is indicated by an asterisk. b Normalized partial peak volumes of A, B, AA and BB direct correlation peaks of spin labels T4 and T22, together with best-fit curves (dashed lines for A, B, solid lines for AA, BB). All four curves ((1) and (3)) were fitted simultaneously to the experimental data for each spin label to yield kinetic rate constants k AB = 0.51 ± 0.08 s−1 (T4), k AB = 0.42 ± 0.07 s−1 (T22), k BA = 0.41 ± 0.07 s−1 (T4), k BA = 0.49 ± 0.06 s−1 (T22), and longitudinal relaxation rate constants R A1  = 1.21 ± 0.04 s−1 (T4), R A1  = 0.67 ± 0.05 s−1 (T22), R B1  = 0.90 ± 0.04 s−1 (T4) and R B1  = 1.59 ± 0.04 s−1 (T22). Uncertainties were derived from a MonteCarlo approach

Full size image

Figure 4 shows the experimental data obtained for the AA, BB, A and B direct correlation peaks in experiments with and without frequency-labeling, together with best-fit curves using (1) and (3). Kinetic rate constants of k AB = 0.51 ± 0.08 s−1 (T4) and k AB = 0.42 ± 0.07 s−1 (T22), as well as k BA = 0.41 ± 0.07 s−1 (T4) and k BA = 0.49 ± 0.06 s−1 (T22) were obtained, with uncertainties derived from a MonteCarlo approach. Despite the considerable difference in line-broadening between folds A and B for T22, the extracted kinetic rates for this spin label are in good agreement with those of T4, which is consistent with a collective two-state conformational transition between the two folds. As expected, the extracted parameters do not depend on the peak integration method: using partial peak volumes by adding the intensities in 7 × 7 grids centered on the peak maximum yields values that are identical (within experimental uncertainties) to the ones obtained using 5 × 5 or 3 × 3 grids, or by using peak intensities.

For comparison, the frequency-labeled data set was used to determine kinetic rate constants by analyzing the single (BA) exchange cross peak that is resolved for each spin label along with its two direct correlation peaks. In this case, only values for one rate constant (k BA) could be determined reliably. Only for the T4 spin label the value of k BA (0.58 ± 0.10 s−1) is in good agreement with the value obtained by analyzing AA, BB, A and B direct correlation peaks, while for T22 the magnitudes of normalized BA exchange cross peaks are overestimated due to considerable line-broadening of fold B, which results in an increase of k BA (1.17 ± 0.21 s−1).

It is evident from (1) and (3) and Fig. 2 that the bi-exponential decays of A and B direct correlation peaks differ from those of the AA and BB direct correlation peaks by an amount that corresponds to the pertinent exchange peak.Footnote 1 Thus, subtraction of normalized AA intensities from A (and BB intensities from B) can, in principle, be employed to formally reconstruct the (correctly!) normalized magnitudes of the corresponding exchange cross peaks AB (BA) that are not affected by differential line-broadening, as they are computed from two peaks with identical line-widths, and irrespective of cross peak overlap. These exchange cross peak intensities can then be analyzed, together with AA and BB direct correlation peaks, as in the conventional frequency-labeled approach using (1) and (2) to obtain longitudinal exchange and kinetic rate constants. We opt not to do so, however, since analysis of the four direct correlation peaks directly is robust and straightforward.

Summary

We have presented an alternative way of analyzing longitudinal exchange in two-state exchanging systems by recording pairs of two- (or more) dimensional spectra with and without frequency-labeling in an indirect dimension. Analysis of the time-dependence of the four (2 + 2) direct correlation peaks that are observed in the two experiments enables reliable and robust quantification of the interconversion rates between the two species, along with their longitudinal relaxation rates. This approach partly resolves the issue of cross peak overlap and eliminates errors caused by differential line-broadening of the two species, thereby expanding the applicability of longitudinal exchange experiments to systems with additional conformational exchange on the ms–μs time scale.

While our approach increases the experimental time by a factor of two, it significantly reduces the number of sources for systematic errors. We recommend to generally use this strategy in cases where (1) resonances show different line broadening, or (2) exchange cross peaks are overlapped or close to intense direct correlation peaks (which may preclude the determination of their exact volumes).